Tilts and shifts in molecular perovskites

Abstract

Molecular perovskites have attracted widespread research attention for their diverse properties. Like inorganic perovskites, these systems are susceptible to displacive phase transitions of rigid octahedra. This study investigates the prevalence of the accessible rigid unit modes—conventional and unconventional tilts and columnar shifts—in the classes of molecular perovskites. Formate-based compounds prefer conventional tilting, as a result of its anti–anti binding mode. Azides, hypophosphites, and dicyanamides show a propensity for unconventional tilts and shifts, which relates to their flexible binding geometries.

---

Recent years have seen a surge of interest in molecular (or hybrid) perovskites.^1–3 These systems exhibit the well-known ABX₃ architecture of perovskite oxides, but the A-site and/or X-site is decorated by a molecular species. As a result, the established chemistry of conventional perovskite oxides is combined with the large number of degrees of freedom associated with molecular frameworks. The different families of molecular perovskites are classified by their X-site anion and include organic halide perovskites,^4,5 Prussian blue analogues (X = cyanide),⁶ formates,^7,8 hypophosphites,⁹ thiocyanates^10,11 azides,^12,13 dicyanamides,^14,15 and dicyanometallates [Fig. 1].^16,17 The currency of these materials stems from their diverse functionality, which holds promise for future applications. By way of example, organic halide perovskites show photovoltaic activity,¹⁸ multiferroic behaviour can occur in formates and azides,^19,20 and barocaloric effects were recently reported in dicyanamides.²¹

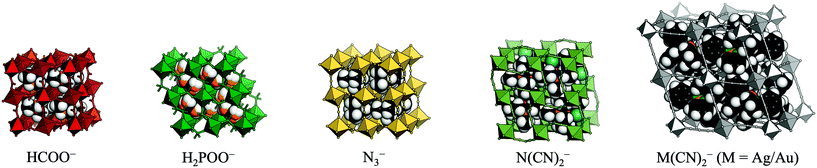Fig. 1 The molecular perovskites under consideration: metal formates, hypophosphites, azides, dicyanamides, and dicyanometallates.

Due to the topological congruence of oxide perovskites and their molecular analogues, many concepts developed for the former can be translated onto the latter. To illustrate, the tolerance factor, originally derived by Goldschmidt,²² has been adapted to account for non-spherical ions and can be used to predict compositional stability windows for a given family.²³ Similarly, the tilting of rigid octahedra—crucial to perovskite physics—can be mapped onto the molecular analogues. The two most prevalent tilting periodicities in perovskite oxides are in-phase tilts, where neighbouring octahedra along the rotation axis rotate in the same direction, and out-of-phase tilts, where the direction of rotation alternates. In Glazer notation, these scenarios are described by “a⁺” and “a⁻”, respectively.²⁴ As the octahedra are corner sharing, adjacent octahedra perpendicular to the rotation axis necessarily tilt in opposite directions. In molecular perovskites, where the octahedra are only corner connected and not corner sharing, this restriction is lifted. Hence, entire layers of octahedra may tilt in a like manner, leading to the concept of “unconventional” tilts.^16,25 Additionally, layers or columns of octahedra can translate collectively, which is referred to as columnar shifts.²⁶ Therefore, the complete set of rigid unit modes (RUMs)—framework distortions where the structural integrity of the octahedra is retained—in molecular perovskites comprise conventional tilting, unconventional tilting and columnar shifts. The latter two are referred to as “unconventional” degrees of freedom, as they have no analogue in conventional oxides, but they contribute to the large structural diversity of molecular perovskites.

Ideal, undistorted perovskites adopt the space group Pm3̄m, but framework distortions reduce this symmetry. The link between symmetry and tilting is well understood in conventional perovskites,^24,27 such that tilt systems can usually be assigned via the space group—if not by inspection. For example, out-of-phase tilting polarised along one axis of the unit cell lowers the symmetry from Pm3̄m to tetragonal I4/mcm symmetry.²⁷ However, clear, unambiguous assignment of tilts and shifts in molecular perovskites can be very challenging, due to the large number of degrees of freedom. Tilts and shifts often coexist, rendering visual assignment difficult, and consequently framework distortions are normally not discussed in detail. Yet an understanding of the active distortion modes is important for the analysis of phase transitions as well as for the ultimate aim of crystal engineering. By way of context, “tilt engineering” in oxide perovskites is an appealing tool for rational materials design.^28,29 The rigid unit modes are often directly implicated in the functionality. For example, the polarity—and potential ferroelectricity—of NH₄Cd(HCOO)₃ arises from the coupling of a tilt and a shift through a hybrid ferroelectric mechanism.^30–32 Moreover, columnar shifts play an active role in the phase transition of [NPr₄]Mn[N(CN)₂]₃ (Pr = propyl, C₃H₇), where a substantial barocaloric effect was found.^21,33

The present study compares the propensity for the rigid unit modes in the various families of molecular perovskites. By using group-theoretical software to analyse a large number of published crystal structures, problems with visual assignment of tilts and shifts are circumvented. The scope is restricted to simple perovskites with polyatomic linker anions: formates, azides, hypophosphites, dicyanamides and dicyanometallates [Fig. 1]. The manuscript first discusses the prevalence of the three types of rigid unit modes in molecular perovskites and proceeds to comparing the structural behaviour of the different families. It will be shown that the preference for certain distortions varies between the different families; e.g. formate perovskites behave largely conventionally, whereas the other systems exhibit varying degrees of unconventional behaviour. The nature of the X-site linker is key in dictating the structural distortions. Lastly, some implications for the development of polar materials are discussed.

As a cautionary note, this study relies on previously published crystal structures and so the results are limited by the accuracy of these crystal structures. A number of factors may impact the accuracy and precision of crystallographic data, including positional disorder, light linker atoms in the vicinity of heavy metals and the collection of low-angle data only. In addition, there may be local deviations from the average structure captured by classical crystallographic techniques.

1 Methods

Each distortion—whether a conventional tilt, unconventional tilt or shift—is associated with a particular propagation vector, k, which is inversely proportional to the periodicity. For example, the out-of-phase conventional tilt has a repeat unit of two octahedra in every direction and hence k = [½, ½, ½]. The distortions can be described by their irreducible representation (irrep) with respect to the (possibly hypothetical) parent structure. In cubic structures, irreps assume the form k_#^±, where k is the Bradley–Cracknell symbol for high-symmetry points in the Brillouin zone.³⁴ To illustrate, the irrep for the out-of-phase tilt is given by R₅⁻. The exact notation of the irrep depends on the setting of the unit cell and here, the A-site is taken as the origin. The software ISODISTORT³⁵ can identify the active irreps in a distorted low-symmetry structure (hettotype) relative to the high-symmetry parent (aristotype). The set of distortions that are sufficient to account for the symmetry of the hettotype are referred to as primary order parameters. Except in simple cases, there is not a unique set of primary order parameters and, here, the set of primary order parameters with the largest amplitudes are chosen. Usually the primary order parameters are accompanied by a set of secondary order parameters, which become symmetry allowed from the primary order parameters. For example, the R₅⁻ distortion leading to I4/mcm symmetry activates the secondary order parameters Γ₁⁺ (symmetric strain) and Γ₃⁺ (tetragonal strain). Further details about group-theoretical analysis of crystal structures can be found in e.g.ref. 27 and 35.

Nine rigid unit modes are accessible to molecular perovskites;³² these are shown along with their irreps in Fig. 2. The two conventional tilt modes (M₂⁺ and R₅⁻) are pictured in red and from each of these, two additional unconventional tilt modes can be generated. As an illustration, allowing neighbouring octahedra in the vertical direction to tilt identically leads to the unconventional tilts transforming as X₅⁻ and M₅⁺. Likewise, if all adjacent octahedra within the plane tilt in the same direction, the Γ₄⁺ and X₁⁻ modes are generated. Hence, there are four unconventional tilt modes in total—two in phase (X₅⁻ and Γ₄⁺) and two out of phase (M₅⁺ and X₁⁻). Finally, there are three distinct periodicities of columnar shifts.³² The first mode corresponds to a shear strain of the lattice and transforms as the irrep Γ₅⁺. The remaining two modes involve alternating displacements of layers or columns of octahedra and correspond to X₅⁻ and M₂⁻, respectively.

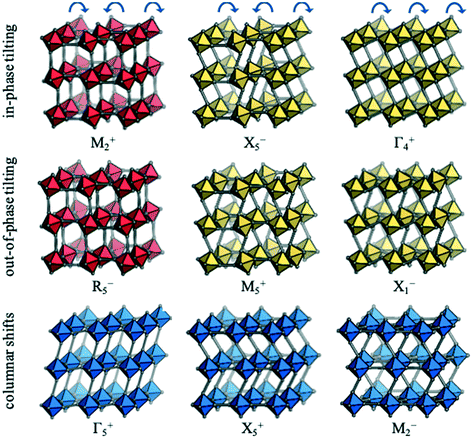Fig. 2 The rigid unit modes accessible to molecular perovskites, along with the corresponding irreps. Conventional tilting is shown in red, unconventional tilting in yellow and columnar shifts in blue. Adapted from ref. 32 under a Creative Commons Attribution 4.0 International License: http://creativecommons.org/licenses/by/4.0/.

The analysis in the present study was performed as follows. Crystal structures of distorted molecular perovskites taken from literature were modified by removing the A-site cation and any pendant hydrogen atoms on the linker molecule. If needed, the structure was converted to the standard setting via the software FINDSYM.³⁶ The resulting structure was decomposed in ISODISTORT³⁵ relative to a hypothetical aristotype structure in space group Pm3̄m with a linear linker. The active irreducible representations corresponding to the shifts and tilts were noted [see ESI†].

2 Results

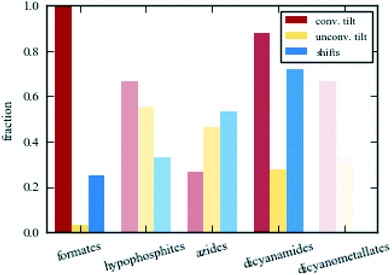
The clearest difference between the various families of molecular perovskites is the varying propensity for conventional tilting. The out-of-phase tilt (R₅⁻) occurs in nearly all formate, hypophosphite, dicyanamide, and dicyanometallate perovskites. It may be polarised along one or more axes with varying relative magnitudes and is frequently very strongly activated. For example, the C2/c phase of [Et₃P(CH₂)₂F]Cd[N(CN)₂]₃ shown in Fig. 1 exhibits a tilt angle of 45° along one axis.³⁷ The in-phase tilt (M₂⁺) is also relatively common in dicyanamides and formates, although not quite as markedly. In contrast, these two modes are scarce in azide perovskites and when present, they are less pronounced relative to the other active distortions. Though not universally present, the out-of-phase tilt is clearly one of the key symmetry-breaking instabilities in the majority of molecular perovskites.

The trends for the unconventional tilts are generally opposite to those for conventional tilts. Azides favour unconventional tilting, which often plays an integral role in their phase transitions. For example, [(CH₃)₂NH₂]Cd(N₃)₃ transitions from R3̄ to P1̄ resulting from a change in the unconventional tilt mode Γ₄⁺ from equal magnitude along the three axes to unequal magnitudes.³⁸ Marked unconventional tilting is rarer in the other families; in particular in the formates. Certain unconventional tilt modes become symmetry allowed from other distortions (e.g. X₅⁻ arises as a secondary order parameter from the common combination of R₅⁻ and M₂⁺ resulting in Pnma symmetry³⁹), yet their magnitudes are insufficient to be observed by inspection. This highlights the need for caution with group-theoretical analysis—the activation of a certain distortion does not imply that it is sufficiently strong to be noticeable. However, an interesting formate system where unconventional tilting does occur is the polar NH₄Cd(HCOO)₃, where X₅⁻ is one of the strongest modes.³⁰ Hypophosphites rarely show the unconventional tilts in Fig. 2, but it will be shown that they can exhibit such tilts with different periodicities. Dicyanamides feature unconventional tilting occasionally, but it is normally less pronounced than the conventional tilts. Thus, unconventional tilting is largely localised to azides and hypophosphites.

Amongst the four periodicities of unconventional tilting, the in-phase tilts (Γ₄⁺ and X₅⁻) dominate. The X₅⁻ distortion is the most frequent and appears in all families where unconventional tilting may occur. The zone-centre tilt, Γ₄⁺, is often present as a secondary order parameter, but only plays an important symmetry-breaking role in some azide perovskites.^38,40 By contrast, the two out-of-phase modes, X₁⁻ and M₅⁺, are scarce. They may be active in systems of such low symmetry that nearly all distortions are symmetry allowed, e.g. [(CH₃)₂NH₂]Mn(H₂POO)₃ (ref. 41) and the triclinic high-pressure phase of [(CH₃)₂NH₂]Fe(HCOO)₃,⁴² yet are normally very weak. As the concept of “rigid units” is less valid in very distorted structures with low symmetry, this approach is perhaps less meaningful for such compounds. However, some important cases of M₅⁺ tilts exist: A-site deficient hypophosphites,⁴³ [PPN]Cd[Ag(CN)₂]₃·3EtOH (PPN = bis(triphenylphosphine)iminium cation) and the low-temperature P2₁ phase of [(CH₃)₂NH₂]Mn(N₃)₃.^13,16 Interestingly, this behaviour is not mirrored by the Cd analogue of the azide system.³⁸ The other out-of-phase unconventional tilt, X₁⁻, occurs in the two low-temperature phases of [(CH₃)₃NH]M(N₃)₃ (M = Mn/Cd)^13,44 but few other cases exist. Consequently, the distribution of the unconventional tilt modes is uneven.

The final set of rigid unit modes are the columnar shifts, where three different periodicities are possible.²⁶ Shifts are relatively common in azides, dicyanamides and hypophosphites and often drive phase transitions.^14,45,46 By way of example, the symmetry lowering from C2/c to P2₁/c in [(CH₃)₃NH]M(N₃)₃ (M = Mn/Cd) or from I4/mcm to P4̄2₁c in [NPr₄]Mn[N(CN)₂]₃ (Pr = propyl, C₃H₇) are both driven by the condensation of a checkerboard shift (M₂⁻).^13,33,44 Shifts may also act as the sole order parameter, as in [N(CH₃)₄]Ca(N₃)₃, where the checkerboard shift polarised along a single axis is sufficient to account for the P4/nmm symmetry.^12,26 Azides are the only family where the shear shift (Γ₅⁺) acts as a primary order parameter. This is particularly obvious in the high-temperature phase of [(CH₃)₃NH]Mn(N₃)₃, where this mode is the only active framework distortion, leading to R3̄m symmetry.¹³ Admittedly, some formates and dicyanometallates exhibit shear shifts, but this is always a result of another, stronger mode—e.g. a conventional tilt.^16,47 In a few cases, formates exhibit layered shifts (X₅⁺) as a primary order parameter, which is often associated with inversion symmetry breaking.³² For example, the condensation of such a shift in [NH₃NH₂]Mn(HCOO)₃ drives a phase transition from Pnna to Pna2₁.⁴⁸ Thus shifts are important for both the structure and properties and feature particularly prominently in azides and dicyanamides.

So far, all the distortions considered have had propagation vectors with components of ½ or 0, i.e. wavelengths of two or infinite number of octahedra. However, other periodicities are also possible, albeit less common. Drawing analogy to the conventional perovskites, certain phases of NaNbO₃ and Ca_0.37Sr_0.63TiO₃ exhibit tilts with k = [½, ½, ¼],^49,50 although most perovskites harbour simple in-phase or out-of-phase tilts. The tilting is considerably more complex in cases where k contains a component of ¼ and the tilt patterns are no longer uniquely described by the propagation vector. In molecular perovskites, these “complex periodicities” are surprisingly common in hypophosphites: four out of the nine hypophosphite perovskites reported to date show such a mode.⁴¹ These distortions typically incorporate both tilt and shift components and always feature some unconventional tilting. A particularly complicated example is the tilt transforming as B₁ (k = [⅙, ½, ⅓]) found in [(CH₃)₂NH₂]Mn(H₂POO)₃ [Fig. 3(a) and (b)].⁴¹ Shifts with k-components of ¼ occur in certain azides and dicyanamides [Fig. 3(c)],^13,51–53 but less frequently than the complex modes in hypophosphites. No such distortions have yet been observed in a formate or dicyanometallate perovskite, although [CH₃NH₃]Co(HCOO)₃ displays an incommensurate phase with modulation wavevector q = 0.1430(2).⁵⁴ Overall, modes with “complex periodicities”—propagation vectors with other values than ½ or 0—appear to be more prevalent in molecular perovskites than in the oxide counterparts.

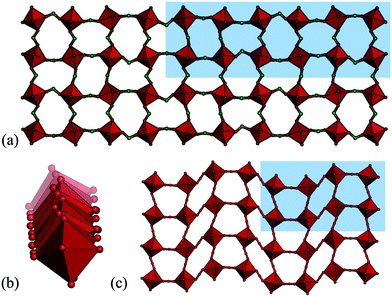Fig. 3 The unusual tilt periodicity (k = [⅙, ½, ⅓]) of [(CH₃)₂NH₂]Mn(H₂POO)₃ shown in (a) two directions and (b) the third direction.⁴¹ (c) The k = [¼, ¼, 0] shift in [cPrNH₃]Mn(N₃)₃ (cPr = cyclopropyl).⁵¹

In addition to enumerating the relative prevalence of the distortion modes, the present analysis facilitates comparisons between the different families of molecular perovskites and the identification of (dis)similar phases. By way of example, the high-temperature Cmce phase of [Et₃P(CH₂)₂F]Cd[N(CN)₂]₃ is isostructural to [(CH₃)₂NH₂]Mn(N₃)₃ at ambient conditions, but distinct from the Cmce phase of [Et₃PPr]Cd[N(CN)₂]₃ (Et = ethyl, Pr = propyl).^13,37,55 Likewise, the Ibam symmetries of [Et₃PPr]Cd[N(CN)₂]₃ and [NPr₄]Fe[N(CN)₂]₃ arise from different distortion modes and these systems are therefore not isostructural.^55,56 However, the Ibam and Cmce phases of [Et₃PPr]Cd[N(CN)₂]₃ presented in ref. 55 were only roughly refined due to suboptimal data quality. The comparison above may be useful for future structural reexamination of these systems. Interestingly, a recurring motif is the conventionally tilted C2/c phase, which occurs in all families of molecular perovskites [Fig. 1].^{7,9,16,37,40,47,57,58} This structure features out-of-phase tilts (R₅⁻) of equal amplitude polarised along two axes of the perovskite unit cell and another out-of-phase tilt of different magnitude along the third direction (a⁻a⁻b⁻ in Glazer notation).²⁴ Yet, the tilt-driven C2/c phase is the only structure appearing in all different families, and such common phases seem to be more of an exception than a rule.

3 Discussion

The above discussion made clear that the structural behaviour varies amongst the families of molecular perovskites. Fig. 4 shows the fraction of distinct phases in each family of molecular perovskites with conventional tilts (red), unconventional tilts (orange) and columnar shifts (blue) as primary order parameters. “Phase” is defined as a unique combination of A, X and space group. Formates are the most conventional family and they always contain a conventional tilt as a primary order parameter. As a result, classical perovskite concepts such as Glazer notation are often invoked.^59–61 Conversely, hypophosphites show considerable unconventional character with numerous columnar shifts and unconventional tilts with “complex” periodicities.⁴¹ Given their deviating distortion preferences, the successful synthesis of mixed X-site formate–hypophosphite molecular perovskites are an interesting achievement.⁶² Such approaches may lead to previously unrealised structural behaviour. The larger molecular perovskites, i.e. azides and dicyanamides, both show a propensity for shifts, but azides generally favour unconventional tilting whereas dicyanamides prefer conventional modes. However, caution should be exerted when attempting to draw quantitative conclusions due to the relatively small set of existing molecular perovskites—compared to the thousands of known oxide perovskites. The colour saturation in Fig. 4 is proportional to the number of structures considered, ranging from ca. 30 formates to 3 dicyanometallates. New molecular perovskites are continuously reported, which will further test the trends identified here. Despite this caveat, it is clear that there is considerable structural diversity in the various classes of molecular perovskites and that general trends can be identified within a given family.

Fig. 4 The percentage of phases in the families of molecular perovskites showing conventional tilts, unconventional tilts and columnar shifts as primary order parameters. “Phase” is defined as a unique combination of A, X and space group. The colour saturation correlates with the number of sampled crystal structures—from ca. 30 for formates to 3 for dicyanometallates.

Having established general trends in the structural behaviour of molecular perovskites, it is tempting to rationalise the observations. Prediction of the precise framework deformation exhibited by a given composition is a tremendous task and requires consideration of the geometry and electronic structure of the linker and the cations. Nevertheless, a few observations regarding the X-site anion can be made. There is no straightforward correlation between unconventional behaviour and the linker length: formate and hypophosphite perovskites are similar in size, yet behave very differently. In addition, two large dicyanometallate perovskites exhibit conventional distortions, similarly to the small formates. Thus, anion length does not appear to be a strong structure-directing factor.

Rather than size, the relative prevalence of the RUMs is related to the preferred binding geometry of the M–X–M moiety. In a simple 2D scenario, conventional tilting requires a cis binding mode of the linker, whereas the two unconventional RUMs give a trans environment [Fig. 5(a)]. Formates serve as a useful illustration, as the metal–formate–metal moiety is close to planar and so the 2D scenario is a good approximation. In its most frequent anti–anti binding mode [Fig. 5(b)], formates bind strictly cis (relative to the O–O vector). This agrees with the predominant distortion modes being conventional tilting. Small shifts sometimes arise due to slight deviations from planarity, yet as a result of the strong tendency for planar binding, these shifts are weak. The only formate perovskite with significant unconventional tilts and shifts features the less common syn–anti binding mode [Fig. 5(c) and (d)].³⁰ As the binding mode is related to the tolerance factor,⁴⁷ this may act as a basis for simple design rules. Azide is the only linear cation considered here and it is agnostic to the binding angle—it can bind in trans and cis and linear geometries.⁶³ Hence both shifts, unconventional tilts and conventional tilts appear in azide perovskites. The paucity of conventional tilts relative to unconventional ones may indicate a preference for trans binding. Hypophosphites and dicyanamides show a broad variety of binding angles and their binding arrangements are not restricted to planar, thus leading to the range of distortions observed.^9,45 It is noteworthy that all the bent linkers appear to favour conventional tilts above unconventional tilts, which again may form the basis of simple design rules. To further explore the binding modes of the anions, and their effect on the resulting structure, theoretical studies would be beneficial.

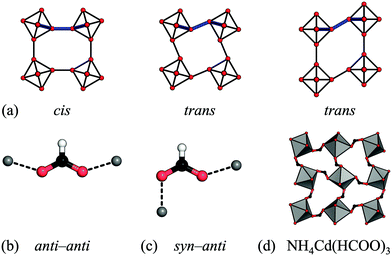Fig. 5 (a) The cis vs. trans binding environments of a linear linker in the presence of conventional tilts, unconventional tilts and columnar shifts. (b) and (c) The binding geometries of the formate anion. (d) The unconventional tilt (X₅⁻) in NH₄Cd(HCOO)₃ is concomitant with syn–anti binding of the formate linker.³⁰

Linker geometry, along with the point symmetry of the A-site cation, also affect the ability to adopt the high-symmetry aristotype Pm3̄m structure. This symmetry requires an undistorted framework and orientationally disordered (or monatomic) A-site cations. A substantial fraction of oxide perovskites exhibit the undistorted parent Pm3̄m symmetry,⁶⁴ yet the sole example of this space group in molecular perovskites are azides with N(CH₃)₄ on the A-site.^13,40 The azide linker can bind linearly between the two metal atoms and the high point symmetry of the tetramethylammonium cation presumably facilitates tumbling. In the systems with bent linkers, disordered tilts—either dynamic or static—are required for high-symmetry phases and can be observed in tetragonal and orthorhombic dicyanamides.⁵⁶ However, the large cations incorporated in the dicyanamide and dicyanometallate frameworks may be too bulky to rotate freely, thus preventing Pm3̄m phases. Both dynamic tilt disorder and A-site tumbling have been separately reported in two different metal formate perovskites,^65,66 suggesting that the aristotype symmetry is in principle attainable.

The nine rigid unit modes accessible to molecular perovskites are unevenly distributed and some modes are considerably more prevalent than others [Fig. 2]. This can be contrasted with oxide perovskites, where the two available distortions are ubiquitous—indeed both appear as primary order parameters in the predominant Pnma phase.⁶⁴ In molecular perovskites, the conventional out-of-phase tilt (R₅⁻) is very common and its integral role is exemplified by the existence of a C2/c phase—driven purely by such tilts—in all families of molecular perovskites. By way of contrast, the unconventional out-of-phase tilts (X₁⁻ and M₅⁺) are rare. One might speculate that perhaps the conventional tilt is sufficiently stable such that most systems with a propensity for out-of-phase tilting will adopt this distortion. Again, computational studies would be a valuable addition to the field.

The rigid unit modes often couple to other distortions, notably the orientational order of the A-site cation. Hence, the deformation of the host framework may sometimes be dictated by the point symmetry of the cation.²⁶ This coupling does not solely arise from templating effects, but the hydrogen-bonding ability can also play a crucial role. To illustrate, imidazolium (C₃H₅N₂⁺) and triazolium (C₂H₄N₃⁺) possess the same five-membered ring structure, but with different hydrogen-bonding capabilities. Thus, they enforce different distortions when encapsulated in hypophosphite perovskites.⁴¹ As a result of the framework–cation coupling, many phase transitions can equally well be considered to arise from A-site cation reorientation and modelled accordingly.^67–69 Of course, phase transitions may also be driven exclusively by cation ordering, e.g. the ferroelectric transition from R3̄c to its non-centrosymmetric subgroup R3c in [MHy]Mn(HCOO)₃ (MHy = methylhydrazinium, CH₃(NH₂)₂⁺) proceeds without noticeable changes to the rigid unit modes.⁶⁰ However, this investigation demonstrate that considerable structural insight can be obtained from consideration of the framework degrees of freedom alone.

Another important distortion mode is the Jahn–Teller effect, which primarily appears in Cu-containing systems.^7,70 A particularly interesting example is [C(NH₂)₃]Cu(HCOO)₃, where the Jahn–Teller distortion drives polar symmetry (Pna2₁) by coupling to other modes.⁷¹ This compound has been predicted to be ferroelectric and B-site substitution leads to the formation of compositional nanoregions reminiscent of relaxor ferroelectrics.^71,72 Analogous structures without a Jahn–Teller distortion adopt the centrosymmetric space group Pnna.⁷⁰ In ref. 32, such systems were labelled “pro-polar”, as the global inversion symmetry can be lifted by introducing a Jahn–Teller distortion. A useful illustration is [TAz]Mn(H₂POO)₃ (TAz = triazolium, C₂H₄N₃⁺) where the coupling of a M₃⁺ Jahn–Teller distortion with the R₅⁻ conventional tilt and X₅⁺ shift will give the polar space group P2₁.³² Similar examples may be identified from the present analysis. By way of example, [FA]Mn(H₂POO)₃, [Ace]Mn(HCOO)₃ and [SPh₃]Mn[N(CN)₂]₃ (FA = formamidinium, (NH₂)CH⁺; Ace = acetamidinium, CH₃C(NH₂)₂⁺; Ph = phenyl, C₆H₅) all contain the correct ingredients to couple to a M₃⁺ Jahn–Teller distortion to break the inversion symmetry.^9,14,73 Thus replacement of Mn²⁺ with Cu²⁺ is likely to give an acentric structure. However, incorporation of Cu in larger molecular perovskites often leads to the preferential adoption of alternative structure types^16,74 and so the realisation of a Cu-containing dicyanamide perovskite may be an experimental challenge.

4 Conclusion

Molecular perovskites represent an intriguing and expanding set of coordination polymers that are attractive from both fundamental and applied perspectives. The present analysis has elucidated the integral role played by the rigid unit modes in the structural behaviour of these systems. Such distortions are ubiquitous in conventional oxide perovskites, yet the presence of polyatomic linkers in molecular perovskites increases the number of accessible modes from two to nine—considering only wavevectors of 0 or ½. These nine modes are not equally prevalent and some of the unconventional tilting modes are particularly scarce. Moreover, the various classes of molecular perovskites show clear differences in their propensities for the various rigid unit modes. Formates, hypophosphites, and dicyanamides generally favour conventional tilts, whereas azide perovskites preferentially adopt structures with unconventional tilting. Columnar shifts are more prominent in the larger molecular perovskites, such as dicyanamides and azides, but also occur to some extent in formates and hypophosphites. The differences relate to the binding geometries of the linkers, where flexible binding modes are conducive to unconventional distortions. It is hoped that this study will ultimately help to understand the structural and functional differences between the different classes of materials and contribute to the development of structure–property relationships in these intriguing coordination polymers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Andrew Goodwin and Chloe Coates (Oxford) are gratefully acknowledged for useful discussions.

References

1. W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099.
2. G. Kieslich and A. L. Goodwin, Mater. Horiz., 2017, 4, 362–366.
3. W.-J. Xu, Z.-Y. Du, W.-X. Zhang and X.-M. Chen, CrystEngComm, 2016, 18, 7915–7928.
4. D. Weber, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1978, 33, 862–865.
5. B. V. Lotsch, Angew. Chem., Int. Ed., 2014, 53, 635–637.
6. A. Ludi, H.-U. Güdel and M. Rüegg, Inorg. Chem., 1970, 9, 2224–2227.
7. E. Sletten and L. H. Jensen, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1752–1756.
8. Z. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 2209–2216.
9. Y. Wu, S. Shaker, F. Brivio, R. Murugavel, P. D. Bristowe and A. K. Cheetham, J. Am. Chem. Soc., 2017, 139, 16999–17002.
10. G. Thiele and D. Messer, Z. Anorg. Allg. Chem., 1980, 464, 255–267.
11. M. J. Cliffe, E. N. Keyzer, M. T. Dunstan, S. Ahmad, M. F. L. De Volder, F. Deschler, A. J. Morris and C. P. Grey, Chem. Sci., 2019, 10, 793–801.
12. F. A. Mautner, H. Krischner and C. Kratky, Monatsh. Chem., 1988, 119, 1245–1249.
13. X.-H. Zhao, X.-C. Huang, S.-L. Zhang, D. Shao, H.-Y. Wei and X.-Y. Wang, J. Am. Chem. Soc., 2013, 135, 16006–16009.
14. J. A. Schlueter, J. L. Manson, K. A. Hyzer and U. Geiser, Inorg. Chem., 2004, 43, 4100–4102.
15. M.-L. Tong, J. Ru, Y.-M. Wu, X.-M. Chen, H.-C. Chang, K. Mochizuki and S. Kitagawa, New J. Chem., 2003, 27, 779–782.
16. J. A. Hill, A. L. Thompson and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 5886–5896.
17. J. Lefebvre, D. Chartrand and D. B. Leznoff, Polyhedron, 2007, 26, 2189–2199.
18. J.-P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Science, 2017, 358, 739–744.
19. K. D. Hughey, A. J. Clune, M. O. Yokosuk, A. al-Wahish, K. R. O'Neal, S. Fan, N. Abhyankar, H. Xiang, Z. Li, J. Singleton, N. S. Dalal and J. L. Musfeldt, Phys. Rev. B, 2017, 96, 180305(R).
20. L. C. Gómez-Aguirre, B. Pato-Doldán, A. Stroppa, L.-M. Yang, T. Frauenheim, J. Mira, S. Yáñez-Vilar, R. Artiaga, S. Castro-García, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, Chem. – Eur. J., 2016, 22, 7863–7870.
21. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga and M. A. Señarís-Rodríguez, Nat. Commun., 2017, 8, 15715.
22. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
23. G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433.
24. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
25. S. G. Duyker, J. A. Hill, C. J. Howard and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 11121–11123.
26. H. L. B. Boström, J. A. Hill and A. L. Goodwin, Phys. Chem. Chem. Phys., 2016, 18, 31881–31894.
27. C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789.
28. F. Li, C. Song, Y. Y. Wang, B. Cui, J. Mao, J. J. Peng, S. N. Li, G. Y. Wang and F. Pan, Sci. Rep., 2015, 5, 16187.
29. M. J. Pitcher, P. Mandal, M. S. Dyer, J. Alaria, P. Borisov, H. Niu, J. B. Claridge and M. J. Rosseinsky, Science, 2015, 347, 420–424.
30. A. S. Antsyshkina, M. A. Porai Koshits, V. N. Ostrikova and G. G. Sadikov, Koord. Khim., 1983, 9, 855–858.
31. N. A. Benedek and C. J. Fennie, Phys. Rev. Lett., 2011, 106, 107204.
32. H. L. B. Boström, M. S. Senn and A. L. Goodwin, Nat. Commun., 2018, 9, 2380.
33. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, Á. Alegría and M. A. Señarís-Rodríguez, Inorg. Chem., 2015, 54, 11680–11687.
34. G. J. Bradley and A. P. Cracknell, The Mathematical Theory of Symmetry in Solids, Clarendon Press, Oxford, 1972.
35. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614.
36. H. T. Stokes and D. M. Hatch, J. Appl. Crystallogr., 2005, 38, 237–238.
37. M.-M. Zhao, L. Zhou, P.-P. Shi, X. Zheng, X.-G. Chen, J.-X. Gao, F.-J. Geng, Q. Ye and D.-W. Fu, Chem. Commun., 2018, 54, 13275–13278.
38. Z.-Y. Du, T.-T. Xu, B. Huang, Y.-J. Su, W. Xue, C.-T. He, W.-X. Zhang and X.-M. Chen, Angew. Chem., Int. Ed., 2015, 54, 914–918.
39. N. A. Benedek and C. J. Fennie, J. Phys. Chem. C, 2013, 117, 13339–13349.
40. Z.-Y. Du, Y.-P. Zhao, W.-X. Zhang, H.-L. Zhou, C.-T. He, W. Xue, B.-Y. Wang and X.-M. Chen, Chem. Commun., 2014, 50, 1989–1991.
41. Y. Wu, T. Binford, J. A. Hill, S. Shaker, J. Wang and A. K. Cheetham, Chem. Commun., 2018, 54, 3751–3754.
42. I. E. Collings, M. Bykov, E. Bykova, M. Hanfland, S. van Smaalen, L. Dubrovinsky and N. Dubrovinskaia, CrystEngComm, 2018, 20, 3512–3521.
43. H. A. Evans, Z. Deng, I. E. Collings, Y. Wu, J. L. Andrews, K. Pilar, J. M. Tuffnell, G. Wu, J. Wang, S. E. Dutton, P. D. Bristowe, R. Seshadri and A. K. Cheetham, Chem. Commun., 2019, 55, 2964–2967.
44. Z.-Y. Du, Y.-S. Sun, S.-L. Chen, B. Huang, Y.-J. Su, T.-T. Xu, W.-X. Zhang and X.-M. Chen, Chem. Commun., 2015, 51, 15641–15644.
45. J. M. Bermúdez-García, S. Yáñez-Vilar, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, J. López-Beceiro, R. Artiaga, M. Dilshad, X. Moya and M. A. Señarís-Rodríguez, J. Mater. Chem. C, 2018, 6, 9867–9874.
46. J. Yang, Y. Huang, T. Fang, K. Qian, W.-B. Chen, X.-F. Yu, Y.-C. Ai, J.-L. Ye and X.-Y. Li, Z. Naturforsch., B: J. Chem. Sci., 2019, 74, 335–339.
47. S. M. Bovill and P. J. Saines, CrystEngComm, 2015, 17, 8319–8326.
48. S. Chen, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem. Front., 2014, 1, 83–98.
49. M. D. Peel, S. P. Thompson, A. Daoud-Aladine, S. E. Ashbrook and P. Lightfoot, Inorg. Chem., 2012, 51, 6876–6889.
50. C. J. Howard, R. L. Withers, K. S. Knight and Z. Zhang, J. Phys.: Condens. Matter, 2008, 20, 135202.
51. K. Qian, Y. Xu, Z. Wang and J. Yang, Z. Naturforsch., B: J. Chem. Sci., 2017, 72, 409–413.
52. J. A. Schlueter, J. L. Manson and U. Geiser, Inorg. Chem., 2005, 44, 3194–3202.
53. M. Mączka, A. Gągor, M. Ptak, D. Stefańska, L. Macalik, A. Pikul and A. Sieradzki, Dalton Trans., 2019, 48, 13006–13016.
54. L. Canadillas-Delgado, L. Mazzuca, O. Fabelo, J. A. Rodriguéz-Velamazán and J. Rodriguez-Carvajal, IUCrJ, 2019, 6, 105–115.
55. L. Zhou, X. Zheng, P.-P. Shi, Z. Zafar, H.-Y. Ye, D.-W. Fu and Q. Ye, Inorg. Chem., 2017, 56, 3238–3244.
56. J. M. Bermúdez-García, M. Sánchez-Andújar, S. Yáñez-Vilar, S. Castro-García, R. Artiaga, J. López-Beceiro, L. Botana, A. Alegría and M. A. Señarís-Rodríguez, J. Mater. Chem. C, 2016, 4, 4889–4898.
57. M. Mączka, A. Ciupa, A. Gągor, A. Sieradzki, A. Pikul, B. Macalik and M. Drozd, Inorg. Chem., 2014, 53, 5260–5268.
58. M.-M. Zhao, L. Zhou, P.-P. Shi, X. Zheng, X.-G. Chen, J.-X. Gao, L. He, Q. Ye, C.-M. Liu and D.-W. Fu, Chem. – Eur. J., 2019, 25, 6447–6454.
59. S. Sobczak, A. Chitnis, M. Andrzejewski, M. Mączka, S. Gohil, N. Garg and A. Katrusiak, CrystEngComm, 2018, 20, 5348–5355.
60. M. Mączka, A. Gągor, M. Ptak, W. Paraguassu, T. Almeida da Silva, A. Sieradzki and A. Pikul, Chem. Mater., 2017, 29, 2264–2275.
61. M. Sánchez-Andújar, L. C. Gómez-Aguirre, B. Pato Doldán, S. Yáñez-Vilar, R. Artiaga, A. L. Llamas-Saiz, R. S. Manna, F. Schnelle, M. Lang, F. Ritter, A. A. Haghighirad and M. A. Señarís-Rodríguez, CrystEngComm, 2014, 16, 3558–3566.
62. Y. Wu, D. M. Halat, F. Wei, T. Binford, I. D. Seymour, M. W. Gaultois, S. Shaker, J. Wang, C. P. Grey and A. K. Cheetham, Chem. – Eur. J., 2018, 24, 11309–11313.
63. X. Liu, F. Li, X. Ma, P. Cen, S. Luo, Q. Shi, S. Ma, Y. Wu, C. Zhang, Z. Xu, W. Song, G. Xie and S. Chen, Dalton Trans., 2017, 46, 1207–1217.
64. M. W. Lufaso and P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 725–738.
65. B.-Q. Wang, H.-B. Yan, Z.-Q. Huang and Z. Zhang, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2013, 69, 616–619.
66. J.-Q. Liu, J. Wu, J. Wang, L. Lu, C. Daiguebonne, G. Calvez, O. Guillou, H. Sakiyama, N. S. Weng and M. Zeller, RSC Adv., 2014, 4, 20605–20611.
67. C. S. Coates, H. J. Gray, J. M. Bulled, H. L. B. Boström, A. Simonov and A. L. Goodwin, Philos. Trans. R. Soc., A, 2019, 377, 20180219.
68. M. Šimėnas, S. Balčiūnas, M. Mączka, J. Banys and E. E. Tornau, Phys. Chem. Chem. Phys., 2016, 18, 18528–18535.
69. M. Šimėnas, A. Ibenskas, A. Stroppa, A. Gągor, M. Mączka, J. Banys and E. E. Tornau, J. Phys. Chem. C, 2019, 123, 19912–19919.
70. K.-L. Hu, M. Kurmoo, Z. Wang and S. Gao, Chem. – Eur. J., 2009, 15, 12050–12064.
71. A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. Cheetham, H. W. Kroto and S. Picozzi, Angew. Chem., Int. Ed., 2011, 50, 5847–5850.
72. E. A. Donlan, H. L. B. Boström, H. S. Geddes, E. M. Reynolds and A. L. Goodwin, Chem. Commun., 2017, 53, 11233–11236.
73. M. Mączka, J. Janczak, M. Trzebiatowska, A. Sieradzki, S. Pawlus and A. Pikul, Dalton Trans., 2017, 46, 8476–8485.
74. F. A. Mautner, S. Hanna, R. Cortés, L. Lezama, M. Gotzone Barandika and T. Rojo, Inorg. Chem., 1999, 38, 4647–4652.

---

Footnote

† Electronic supplementary information (ESI) available: Results from the group-theoretical analysis. See DOI: 10.1039/c9ce01950b

---