The landscape of mechanical properties of molecular crystals†
Abstract
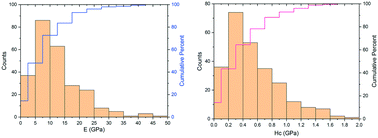
An analysis of compiled literature nanoindentation hardness (Hc) and elastic modulus (E) values of molecular crystals revealed a wide range of mechanical properties (0.001–1.80 GPa for Hc and 0.27–46.8 GPa for E). A global approximately linear relationship between E and Hc is observed and possible reasons for deviation from the line are discussed. A classification scheme for molecular crystals based on E and Hc is proposed. In addition, results suggest that the effectiveness of crystal engineering strategies in modifying both E and Hc follows the order cocrystallization/salt formation > polymorph formation > anisotropy. A clear understanding of the E and Hc landscape lays a foundation for effective optimization of the mechanical properties of molecular crystals through crystal engineering.
- This article is part of the themed collection: Introducing the CrystEngComm Advisory Board and their research


 Please wait while we load your content...
Please wait while we load your content...