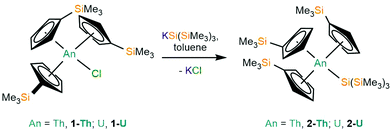Polarised covalent thorium(IV)– and uranium(IV)–silicon bonds

Abstract

We report the synthesis and characterisation of isostructural thorium(IV)– and uranium(IV)–silanide actinide (An) complexes, providing an opportunity to directly compare Th–Si and U–Si chemical bonds. Quantum chemical calculations show significant and surprisingly similar An%:Si%, 7s-, 6d-, and 5f-orbital contributions from both elements in polarised covalent An–Si bonds, and marginally greater covalency in the U–Si vs. Th–Si linkages.

---

The actinides (An) are used for nuclear energy generation, and an improved knowledge of An bonding regimes is important to fully address issues associated with recycling, reprocessing and long-term storage of radioactive An-compounds.¹ An-silicides have been mooted as potential nuclear fuels due to their high An content and greater thermal conductivity than conventional UO₂ fuel rods, and results from fundamental studies of An–Si bonds can potentially be transferable to more applied research for the future adoption of these materials in nuclear fuel cycles.^2–5 Quantification of An chemical bonding can present logistical issues associated with sample transport and local rules at analytical facilities for radioactive samples, but molecular An complexes are ideal model systems for providing these data.^6–8 In comparison to the d-block,⁹ there are relatively few structurally characterised examples of An–metalloid bonds,^10–17 which can be attributed to their polar and kinetically labile bonding regimes resulting from radially contracted An valence orbitals.^1,18

Whilst numerous complexes containing An–C bonds are known for a wide variety of ligand types,^19–23 the molecular chemistry of heavier An–tetrels is in its infancy.^10,14,15 Only one matrix isolation study of An–Si bonding has been reported,²⁴ and molecular examples remain rare;^25,26 the only structurally authenticated polarised covalent U(IV)–Si bond was disclosed in 2001¹⁴ and two silylene complexes exhibiting dative U(III)–Si bonds were reported in early 2020.¹⁵ We envisaged that the hypersilanide ligand, {Si(SiMe₃)₃}⁻, which dominates f-block silanide chemistry^14,27–30 and has notable Zr(IV) and Hf(IV) complexes,^31–33 could be combined with a supporting {An(IV)(Cp′)₃}⁺ (An = Th, U, Cp′ = C₅H₄SiMe₃) framework, providing an opportunity for Th vs. U comparisons. The earliest reports of An(IV)–Si complexes utilised parent Cp (C₅H₅) ancillary ligands,^25,26 thus we reasoned that the increased steric bulk of Cp′ would provide additional kinetic stabilisation of any An–Si linkages.

Salt metathesis reactions of [An(Cp′)₃Cl] (1-An, An = Th, U)³⁴ with one equivalent of KSi(SiMe₃)₃ in toluene, followed by work-up and recrystallisation from pentane, yielded colourless or green plates of [An(Cp′)₃{Si(SiMe₃)₃}] (2-An, An = Th, 74%; U, 64%), respectively (Scheme 1). A U(IV) stannyl complex [U{N(CH₂CH₂NSiⁱPr₃)₃}(SnMe₃)]¹⁹ and a U(IV) silyl complex [U{N(^tBu)(C₆H₃Me₂-3,5)}{Si(SiMe₃)₃}]¹⁶ were both previously prepared by analogous salt metathesis strategies.

Scheme 1 Synthesis of 2-An by the reaction of 1-An with KSi(SiMe₃)₃.

Single crystal XRD data reveals An–Si bond lengths of 3.1191(8) Å (2-Th, Fig. 1) and 3.0688(8) Å (2-U, Fig. S23, ESI†), which are both ca. 0.2 Å longer than the sum of single bond covalent radii reported by Pyykkö of 2.91 Å for Th–Si and 2.86 Å for U–Si.³⁵ Complex 2-Th exhibits the first structurally authenticated example of a Th–Si bond, but we note that the U–Si bond length of 2-U is 0.03 Å shorter than that found for the only previously reported U(IV)–Si bond in [U{N(^tBu)(C₆H₃Me₂-3,5)}₃{Si(SiMe₃)₃}] (3.091(3) Å),¹⁴ likely due to the lower steric demands of Cp′ vs. the amide {N(^tBu)(C₆H₃Me₂-3,5)}⁻. As expected, the U–Si bond length in 2-U is ca. 0.11 Å shorter than those in the U(III)–silylene complexes [U(Cp′)₃{Si(NMe₂)[PhC(N^tBu)₂]}] (3.1637(7) Å) and [U(Cp′)₃{Si[PhC(NⁱPr)₂]₂}] (3.1750(6) Å),¹⁵ which is consistent with the smaller six-coordinate ionic radius of U(IV) (0.89 Å) vs. U(III) (1.025 Å).³⁶ To facilitate the inclusion of a hypersilanide group at the An centres of 2-An the Cp′ ligands rearrange from their orientations in the precursors 1-An³⁴ so that all three Cp′ trimethylsilyl substituents are situated at the opposite side of the molecule to the An–Si bond; a similar arrangement of Cp′ ligands was found for the aforementioned U(III)–silylene complexes.¹⁵ The An⋯Cp_cent distances are statistically indistinguishable between respective 1-An and 2-An pairs, indicating that the ability of the Cp′ ligands to position their trimethylsilyl groups away from the {Si(SiMe₃)₃}⁻ moiety has alleviated the impact on bond distances to the ancillary ligands upon the substitution of chloride with a bulkier ligand. The central Si atoms of the hypersilanide ligands in 2-An deviate significantly from tetrahedral geometries, with mean Si–Si–An bond angles of 116.48(6)° (2-Th) and 116.97(7)° (2-U) indicating significant steric repulsion between the trimethylsilyl substituents; a similar effect was reported for [U{N(^tBu)(C₆H₃Me₂-3,5)}₃{Si(SiMe₃)₃}] (mean Si–Si–An: 115.43(8)°).¹⁴

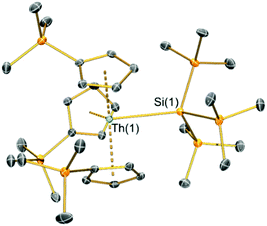Fig. 1 Solid-state molecular structure of 2-Th at 150 K and displacement ellipsoids set at 50% probability; hydrogen atoms and lattice solvent removed for clarity. C, Si and Th atoms are shown as grey, orange, and green respectively. Complex 2-U is essentially isostructural and details of that complex can be found in the ESI† (Fig. S23 and Table S2).

For both 2-Th and 2-U, the ¹H NMR spectra exhibit two Cp′-H resonances for the α- and β-CH positions (2-Th: δ_H = 6.26 ppm, 6.72 ppm; 2-U: δ_H = 0.25 ppm, 0.37 ppm), and two resonances of equal intensity for the two chemically inequivalent trimethylsilyl environments (2-Th: δ_H = 0.34 ppm (Cp–Si(CH₃)₃), 0.66 ppm (Si{Si(CH₃)₃}₃); 2-U: δ_H = −6.67 ppm (Si{Si(CH₃)₃}₃), −5.62 ppm (Cp–Si(CH₃)₃)); as expected these signals are paramagnetically shifted for 5f² U(IV) 2-U. The ²⁹Si{¹H} NMR spectra of 2-An each contain the expected three resonances: for 2-Th a signal at −108.92 ppm is assigned to the Si atom bonded to Th, a shift of 80.64 ppm downfield from KSi(SiMe₃)₃ (δ_Si = −189.56 ppm);³⁷ for 2-U a resonance at −137.09 ppm is attributed to the U-bonded Si atom, a downfield shift of 54.25 ppm from KSi(SiMe₃)₃. To verify the δ_Si assignment of 2-U was not due to the presence of paramagnetically shifted Si(SiMe₃)₄ impurity,³⁰ we added one equivalent of Si(SiMe₃)₄ to a sample of 2-U (Fig. S10 and S11, ESI†) to show that Si(SiMe₃)₄ resonates at different chemical shifts to that of 2-U. Calculated δ_Si chemical shifts (see ESI† for full computational details) for the An-bonded Si atom are −126.3 ppm and −103.9 ppm for 2-Th and 2-U, respectively, and are in good agreement with experiment. These downfield δ_Si shifts from alkali metal precursors are consistent with an increase of metal charge from +1 → +4, resulting in a greater deshielding of electron density on the central Si-atom; the effect is less consistent for 2-U likely owing to the paramagnetic shift and spin orbit coupling effects.^38,39 To the best of our knowledge, these are the first reported chemical shifts of Th–Si and U–Si interactions detected by ²⁹Si{¹H} NMR spectroscopy, precluding literature comparisons. The ²⁹Si NMR data for the Cp′ silicon atoms for 2-An (2-Th: δ_Si = −7.87 ppm; 2-U: δ_Si = −100.89 ppm) and 1-An (1-Th: δ_Si = −8.46 ppm; 1-U: δ_Si = −62.90 ppm) are typical for such complexes, e.g., [Th{C₅H₃(SiMe₃)₂-1,3}₃H] (δ_Si = −8.16 ppm);⁴⁰ [U(Cp′)₄] (δ_Si = −62.80 ppm);³⁴ there is a small change from 1-Th to 2-Th (Δδ_Si = 0.60 ppm downfield) and although there is a 37.70 ppm upfield shift from 1-U to 2-U this is within the upfield limit of reported U(IV) ²⁹Si NMR chemical shifts.⁴¹ The corresponding chemical shift of the U(III) complex, [U(Cp′)₃] (δ_Si = −165.00 ppm),⁴¹ is 64.11 ppm upfield of 2-U, supporting the proposed U(IV) oxidation state of 2-U.

The UV-Vis-NIR spectrum of 2-U (Fig. S17, ESI†) was recorded in toluene (25 mM). A broad charge transfer band spans the ultraviolet and visible regions, tailing off at ∼12 000 cm⁻¹, which is consistent with the dark green colour of 2-U. The NIR region is populated with a series of sharp, weak absorptions (ε = 30–160 M⁻¹ cm⁻¹) of Laporte-forbidden f → f transitions, which are characteristic of intra-configurational transitions of U(IV).⁴²

Powdered samples of 1-U and 2-U were measured by variable-temperature SQUID magnetometry in a magnetic field of 0.5 T. The magnetic moments of 2-U/1-U at 300 K are 2.78/2.93 μ_B and these values tend to zero, decreasing smoothly over the temperature range and reaching 0.77/0.46 μ_B at 2 K (Fig. S18, ESI†). This behaviour is characteristic of a ³H₄ uranium(IV) ion, which is a magnetic triplet at room temperature and a magnetic singlet at low temperature subject to temperature independent paramagnetism.^8,43 A notable feature of these magnetic profiles is the increased low temperature magnetic moment from 1-U to 2-U (0.46 vs. 0.77 μ_B), which we attribute to a ligand field effect.⁴⁴ The addition of ligands to free 5f ions contributes to the loss of the (2J + 1)-fold ground state degeneracy, imparting significant mixing of excited states into the “free ion” ground state. This effect is dictated by the symmetry, orientation, and strength of the ligand field, resulting in variations in the energies between the ground and lowest excited states, impacting on variable temperature magnetic behaviour.⁴⁵ As such, the alteration of the ligand field through the replacement of chloride in 1-U with {Si(SiMe₃)₃}⁻ in 2-U may induce greater mixing of excited multiplets into the ³H₄ ground state term, such that there is an unequal population of excited states between 2-U and 1-U. This stronger ligand field effect of silanide to chloride can be further evidenced by the more pronounced deviation from the theoretical uranium(IV) free-ion χT value at 300 K (1.60 cm³ mol⁻¹ K on the basis of ³H₄ ground state) for 2-Uvs.1-U (0.97 cm³ mol⁻¹ K for 2-Uvs. 1.07 cm³ mol⁻¹ K for 1-U, Fig. S19, ESI†).

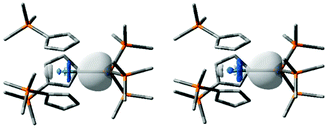
Scalar relativistic, dispersion-corrected, hybrid density functional theory calculations were performed to gain further insight into the nature of the An–Si bonding in 2-An; full details of the methods employed are given in the ESI.† Computed An–Si bond lengths are 3.071 Å and 3.012 Å for 2-Th and 2-U, respectively, in good agreement with those obtained experimentally. Natural localised molecular orbital (NLMO) analysis finds an An–Si σ-bonding orbital in each molecule, mainly localised on the Si atom but with an approximately 30% contribution from the An centre, ca. 5% higher in 2-Uvs.2-Th (Table 1). The metal character is primarily 6d in both cases, with minor but significant 7s and 5f contributions, the latter being ca. 8% higher in 2-Uvs.2-Th. Overall, these data are rather similar, but follow the trend of greater 5f-contribution to the bonding of uranium and greater 6d-contribution to the bonding of thorium. The Si 3s/3p orbital contributions are similar in both cases. Fig. 2 presents images of these polarised σ-bonding NLMOs, and the single An–Si σ-bond description is supported by the Wiberg Bond Indices in Table 1.⁴⁶ Winston et al. previously found that the polarised U–Sn σ-bond in [U{N(CH₂CH₂NSiⁱPr₃)₃}(SnMe₃)] is composed similarly (25 U:75 Sn)¹⁹ to the An-Si bonds in 2-An.

Table 1 NLMO composition of the An–Si bond in 2-An calculated at the DKH2/PBE0/SARC/cc-pVTZ level of theory

Complex	An (%)	Si (%)	An orbital contribution (%)			Si orbital contribution (%)			Wiberg index
			7s	7p	6d	5f	3s	3p
2-Th	28.0	67.0	14.2	0.3	72.0	13.5	36.5	63.3	0.76
2-U	33.1	61.7	12.9	0.1	65.6	21.4	36.8	62.9	0.78

---

Fig. 2 The An–Si bonding NLMOs of 2-Th (−7.408 eV, left) and 2-U (−7.418 eV, right). Hydrogen atoms omitted for clarify. C, Si and An atoms shown as grey, orange, and green, respectively. Isovalue = 0.05 a.u.

Table 2 presents Natural Population and Quantum Chemical Topology (QCT) analysis of 2-An. Both techniques reveal decreased An/Si partial charge separation in 2-U over 2-Th, suggesting increased covalency in the former, supporting the NLMO composition breakdown. Greater An–Si covalency in 2-U is also evidenced by the slightly larger bond critical point (BCP) electron density ρ_BCP and An/Si delocalisation indices DI(An,Si); the BCP energy densities H_BCP are also suggestive of a degree of covalency in both An–Si linkages. These bonding metrics show a higher degree of U–Si covalency in 2-U than the previously reported U(III)–Si model complex [U(Cp′)₃{Si(NCHMes)₂}] (DI(U,Si) = 0.525, ρ_BCP = 0.037, H_BCP = −0.006).⁴⁷ The NPA and QCT spin densities support the U(IV) assignment, and the An–Si BCP ellipticities (Table S3, ESI†) are very close to zero, indicating a spherically symmetric distribution of electron density at the BCP, characteristic of a σ-bond.

Table 2 Partial atomic charges, spin densities and An–Si bonding metrics for 2-An from NPA and QCT analysis at the DKH2/PBE0/SARC/cc-pVTZ level of theory

Complex	NPA			QCT
	q (An)	q (Si)	Spin density (An)	q (An)	q (Si)	An–Si ρBCP	An–Si HBCP	DI (An,Si)	Spin density (An)	V XC (An,Si)
2-Th	1.24	−0.60	—	2.23	−0.13	0.048	−0.013	0.526	—	−0.092
2-U	0.73	−0.51	2.13	2.03	−0.06	0.050	−0.013	0.539	2.08	−0.096

---

Some of us recently reported our first use of the QCT interatomic exchange–correlation energy V_XC as an actinide element covalency metric.⁴⁸ This was found to have excellent agreement with both NBO-based metrics and delocalisation indices. The values for 2-Th and 2-U are given in Table 2. As with all the other data presented, these evidence An–Si covalency that is slightly larger for the U system vs. the Th system.

To conclude, we have reported the synthesis and characterisation of isostructural Th(IV) and U(IV) silanide complexes. Computational analysis of the An–Si bonding in 2-Th and 2-U reveal similar polarised covalent single σ-bonds, though a range of computational metrics consistently show marginally greater covalency in the U–Si bond. The An–Si interactions are kinetically stable in the solid state, and in solution for non-polar solvents. These data confirm a formal +4 oxidation state of 2-U to match analogous Th(IV) 2-Th, and indicate that replacement of a chloride in 1-An with the hypersilanide ligand tends to increase the overall ligand-field splitting; the strong trans-influence of silanide ligands is well-documented in d-block chemistry,⁴⁹ and the strong σ-donor nature of silanides is evidenced here by an increased low temperature magnetic moment of 2-Uvs.1-U.

We thank the University of Manchester for a PhD studentship for B. L. L. R. (Nuclear Endowment), a postdoctoral fellowship to V. E. J. B., and for access to the Computational Shared Facility and associated support services. We also thank the EPSRC (EP/P002560/1, EP/N022122/1, EP/P001386/1, EP/M027015/1) and ERC (CoG612724) for funding. We thank the EPSRC UK National Electron Paramagnetic Resonance Service for access to SQUID magnetometry. We would also like to thank Prof. Christoph Marschner and Dr Johann Hlina for valuable ²⁹Si NMR spectroscopy discussions. Raw research data files supporting this publication are available from Mendeley Data at DOI: http://10.17632/4d9rwvp77h.3.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. L. R. Morss, N. M. Edelstein and J. Fuger, The Chemistry of the Actinide and Transactinide Elements, Springer, Netherlands, Dordrecht, 4th edn, 2010.
2. J. T. White, A. T. Nelson, J. T. Dunwoody, D. D. Byler, D. J. Safarik and K. J. McClellan, J. Nucl. Mater., 2015, 464, 275–280.
3. T. L. Wilson, E. E. Moore, D. Adorno Lopes, V. Kocevski, E. Sooby Wood, J. T. White, A. T. Nelson, J. W. McMurray, S. C. Middleburg, P. Xu and T. M. Besmann, Adv. Appl. Ceram., 2018, 117, S76–S81.
4. U. E. Humphrey and M. U. Khandaker, Renewable Sustainable Energy Rev., 2018, 97, 259–275.
5. S. He and J. Cai, Ann. Nucl. Energy, 2020, 140, 107303.
6. M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406.
7. N. Kaltsoyannis and S. T. Liddle, Chem, 2016, 1, 659–662.
8. S. T. Liddle, Angew. Chem., Int. Ed., 2015, 54, 8604–8641.
9. S. T. Liddle, Molecular metal–metal bonds: compounds, synthesis, properties, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015.
10. M. Porchia, U. Casellato, F. Ossola, G. Rossetto, P. Zanella and R. Graziani, J. Chem. Soc., Chem. Commun., 1986, 1034–1035.
11. M. S. Winston, E. R. Batista, P. Yang, A. M. Tondreau and J. M. Boncella, Inorg. Chem., 2016, 55, 5534–5539.
12. S. G. Minasian, J. L. Krinsky, J. D. Rinehart, R. Copping, T. Tyliszczak, M. Janousch, D. K. Shuh and J. Arnold, J. Am. Chem. Soc., 2009, 131, 13767–13783.
13. S. T. Liddle, J. McMaster, D. P. Mills, A. J. Blake, C. Jones and W. D. Woodul, Angew. Chem., Int. Ed., 2009, 48, 1077–1080.
14. P. L. Diaconescu, A. L. Odom, T. Agapie and C. C. Cummins, Organometallics, 2001, 20, 4993–4995.
15. I. J. Brackbill, I. Douair, D. J. Lussier, M. A. Boreen, L. Maron and J. Arnold, Chem. – Eur. J., 2020, 26, 2360–2364.
16. S. T. Liddle and D. P. Mills, Dalton Trans., 2009, 5992.
17. D. Patel and S. T. Liddle, Rev. Inorg. Chem., 2012, 32, 1–22.
18. The Rare Earth Elements: Fundamentals and Applications, ed. D. A. Atwood, Wiley, Hoboken, 2012.
19. S. A. Johnson and S. C. Bart, Dalton Trans., 2015, 44, 7710–7726.
20. M. Gregson, A. J. Wooles, O. J. Cooper and S. T. Liddle, Comments Inorg. Chem., 2015, 35, 262–294.
21. P. L. Arnold and I. J. Casely, Chem. Rev., 2009, 109, 3599–3611.
22. O. Walter, Chem. – Eur. J., 2019, 25, 2927–2934.
23. S. T. Liddle, Coord. Chem. Rev., 2015, 293–294, 211–227.
24. H. S. Hu, F. Wei, X. Wang, L. Andrews and J. Li, J. Am. Chem. Soc., 2014, 136, 1427–1437.
25. M. Porchia, N. Brianese, U. Casellato, F. Ossola, G. Rossetto, P. Zanella and R. Graziani, J. Chem. Soc., Dalton Trans., 1989, 677–681.
26. W. A. King and T. J. Marks, Inorg. Chim. Acta, 1995, 229, 343–354.
27. M. M. Corradi, A. D. Frankland, P. B. Hitchcock, M. F. Lappert and G. A. Lawless, Chem. Commun., 1996, 2323–2324.
28. M. Niemeyer, Inorg. Chem., 2006, 45, 9085–9095.
29. R. Zitz, J. Hlina, K. Gatterer, C. Marschner, T. Szilvási and J. Baumgartner, Inorg. Chem., 2015, 54, 7065–7072.
30. R. Zitz, J. Hlina, H. Arp, D. Kinschel, C. Marschner and J. Baumgartner, Inorg. Chem., 2019, 58, 7107–7117.
31. B. K. Campion, J. Falk and T. D. Tilley, J. Am. Chem. Soc., 1987, 109, 2049–2056.
32. J. Arnold, H. G. Woo, T. D. Tilley, A. L. Rheingold and S. J. Geib, Organometallics, 1988, 7, 2045–2049.
33. J. Arnold, M. P. Engeler, F. H. Elsner, R. H. Heyn and T. D. Tilley, Organometallics, 1989, 8, 2284–2286.
34. C. J. Windorff, M. R. MacDonald, J. W. Ziller and W. J. Evans, Z. Anorg. Allg. Chem., 2017, 643, 2011–2018.
35. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
36. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
37. C. Marschner, Eur. J. Inorg. Chem., 1998, 221–226.
38. P. Hrobárik, V. Hrobáriková, A. H. Greif and M. Kaupp, Angew. Chem., Int. Ed., 2012, 51, 10884–10888.
39. L. A. Seaman, P. Hrobárik, M. F. Schettini, S. Fortier, M. Kaupp and T. W. Hayton, Angew. Chem., Int. Ed., 2013, 52, 3259–3263.
40. R. R. Langeslay, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2016, 138, 4036–4045.
41. C. J. Windorff and W. J. Evans, Organometallics, 2014, 33, 3786–3791.
42. D. E. Morris, R. E. Da Re, K. C. Jantunen, I. Castro-Rodriguez and J. L. Kiplinger, Organometallics, 2004, 23, 5142–5153.
43. D. R. Kindra and W. J. Evans, Chem. Rev., 2014, 114, 8865–8882.
44. J. A. Seed, H. R. Sharpe, H. J. Futcher, A. J. Wooles and S. T. Liddle, Angew. Chem., Int. Ed., 2020, 59, 15870–15874.
45. J. van Leusen, M. Speldrich and P. Kögerler, Topics in Organometallic Chemistry, Springer, 2019, vol. 64, pp. 391–410.
46. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
47. X. W. Chi, Q. Y. Wu, J. H. Lan, C. Z. Wang, Q. Zhang, Z. F. Chai and W. Q. Shi, Organometallics, 2019, 38, 1963–1972.
48. V. E. J. Berryman, J. J. Shephard, T. Ochiai, A. N. Price, P. L. Arnold, S. J. Parsons and N. Kaltsoyannis, Phys. Chem. Chem. Phys., 2020, 22, 16804–16812.
49. M. Simon and F. Breher, Dalton Trans., 2017, 46, 7976–7997 , and references cited therein.

---

Footnote

† Electronic supplementary information (ESI) available: Full synthetic details, crystallography, NMR, FTIR and electronic spectra, magnetism and DFT calculations. CCDC 2019267–2019269. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cc06044e

---