Visualizing the helical stacking of octahedral metallomesogens with a chiral core†
Go
Watanabe
 *a,
Hideyo
Watanabe
b,
Kota
Suzuki
b,
Hidetaka
Yuge
b,
Shintaro
Yoshida
a,
Takuyoshi
Mandai
a,
Shigetaka
Yoneda
a,
Hisako
Sato
*a,
Hideyo
Watanabe
b,
Kota
Suzuki
b,
Hidetaka
Yuge
b,
Shintaro
Yoshida
a,
Takuyoshi
Mandai
a,
Shigetaka
Yoneda
a,
Hisako
Sato
 c,
Mitsuo
Hara
c,
Mitsuo
Hara
 *d and
Jun
Yoshida
*d and
Jun
Yoshida
 *b
*b
aDepartment of Physics, School of Science, Kitasato University, 1-15-1, Kitasato, Minami-ku, Sagamihara 252-0373, Japan. E-mail: go0325@kitasato-u.ac.jp
bDepartment of Chemistry, School of Science, Kitasato University, 1-15-1, Kitasato, Minami-ku, Sagamihara 252-0373, Japan. E-mail: yoshidaj@kitasato-u.ac.jp
cDepartment of Chemistry, Graduate School of Science and Engineering, Ehime University, 2-5, Bunkyo-cho, Matsuyama 790-8577, Japan
dDepartment of Molecular and Macromolecular Chemistry, Graduate School of Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Japan. E-mail: mhara@chembio.nagoya-u.ac.jp
First published on 16th September 2020
Abstract
A combination of grazing-incidence X-ray diffraction and molecular dynamics simulation studies led to the visualization of the stacking structure of a helical columnar liquid crystal formed by enantiopure octahedral metallomesogens with ΔΛ chirality. The helical structure was elucidated as a hybrid of two major proposed structures.
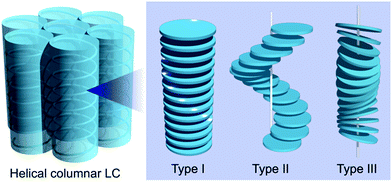
The introduction of chirality to liquid crystals (LCs) often leads to the spontaneous formation of macroscopic chiral structures.1,2 A nematic (N) LC, typically formed by achiral rod-shaped (calamitic) molecules, is well known to show a phase transition to a chiral nematic (N*) LC with a μm-scale helical pitch upon doping with chiral molecules.3,4 The introduction of chirality to columnar (Col) LCs mainly formed by discotic molecules5,6 can also induce macroscopic chiral structures, such as a helical stack of chiral mesogens.7–9 Helical Col LCs have attracted widespread research attention, for example, polar switching/ferroelectric materials, organic semiconductors with densely packed structures, and reaction fields for asymmetric reactions.10,11 In parallel, several stacking structures have been proposed for helical Col LCs; the major proposed structures are shown in Fig. 1 (types I, II, and III).10 Although the rational preparation of each helix type is necessary for the further development of helical Col LCs, it is currently challenging to even determine the helix type.12 Molecular dynamics (MD) simulation based on detailed experimental data has been used as a powerful method to reveal the detailed structure of LCs. In fact, MD simulations for non-helical Col LCs have been actively performed in recent years.13,14 However, the MD simulations with all-atom models have been applied to only helical Col LCs with type I structures, to the best of our knowledge.15–17
A series of octahedral metallomesogens firstly reported by Giroud-Godquin and Rassat18 and later investigated in detail by Swager's group19,20 is unique and unconventional in the sense that they have propeller-shaped chirality at the molecular core (ΔΛ chirality). The effect of ΔΛ chirality on the resulting stacking structures was investigated indirectly; the introduction of enantiopure alkyl chains at the periphery of the octahedral mesogen resulted in the partial intercolumnar separation of the diastereomeric mixture.20
Our research group has investigated chiral octahedral metal complexes, including enantiopure Ru-C8 (Fig. 2a), as dopants for inducing N* phases, focusing on clarifying the relation between the molecular ΔΛ chirality and the resulting helical structures in N* phases.21–24 During the course of this study, we found that enantiopure Ru-C8 aggregates in a nematic liquid crystal medium.25 Here, we report the columnar liquid-crystalline behaviour of enantiopure Ru-C8 itself. Based on the X-ray diffraction (XRD) and molecular dynamics (MD) simulation studies, the helical stacking structure of enantiopure Ru-C8 was elucidated as a hybrid of types II and III. The role of the core ΔΛ chirality in determining the resulting helical structure deduced from the analysis of the simulated structure will be discussed.
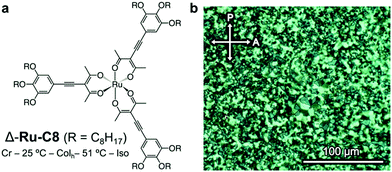 | ||
| Fig. 2 (a) Molecular structure and phase behavior of the Δ isomer of Ru-C8. (b) Polarized optical micrographs of the textures displayed by Δ-Ru-C8 in a Colh phase at 40 °C (after annealing). | ||
The phase behavior of Δ-Ru-C8 was examined via differential scanning calorimetry (DSC, Fig. S4, ESI†), polarized optical microscopy (POM, Fig. 2b), and XRD. The mesophase observed in Δ-Ru-C8 was identified as a hexagonal columnar (Colh) phase. When Δ- or Λ-Ru-C8 was cooled from the isotropic state to room temperature, it showed little indication of crystallization under POM observation. Their slow crystallization was confirmed by the time-course change of POM textures and XRD patterns (Fig. S5 and S6, ESI†). The details of the slow crystallization behavior are described in the ESI.†
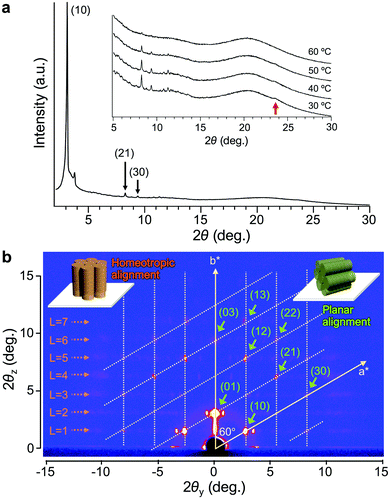
The XRD analysis of Δ-Ru-C8 with a 1D detector reveals several diffraction peaks attributed to a Colh phase with a lattice parameter of a = 3.3 nm (Fig. 3a), in addition to a broad diffraction corresponding to the alkyl halo and a peak at d = 0.38 nm (indicated by a red arrow in Fig. 3a), which is attributed to the repeat distance between adjacent mesogens, such as π–π stacking inside the columns. In contrast, a broad diffraction was observed around 2θ = 3–4°. To confirm the origin of this diffraction and obtain detailed structural information, GI-XRD analysis was conducted for the thin films of Δ- and Λ-Ru-C8, prepared by spin-coating their chloroform solutions on glass plates.
The GI-XRD image of Δ-Ru-C8 taken at 37 °C shows spot-like reflections in the out-of-plane region (Fig. 3b). Since no surface treatment was performed on the glass plate, columns with planar and homeotropic alignments most likely co-existed on the glass plate. Indexing of most spots was possible by considering a reciprocal lattice of the Colh phase with a planar alignment (green columns in the inset of Fig. 3b).26,27 The lattice parameter of the Colh phase was deduced to be a = 3.2 nm, almost identical to that obtained from the 1D XRD analysis. In contrast, several reflections that are not on the grid points of the reciprocal lattice still remain: weak broad reflections highlighted by orange dotted arrows in Fig. 3b. The broad reflections periodically appear along the out-of-plane direction (L = 1, 2, 3… in Fig. 3b). Similar periodic reflections (layer-lines) were observed for helical Col LCs as the first- and higher-order reflections based on the intracolumnar helix.28–31 The GI-XRD measurement of helical columns with a homeotropic alignment affords periodic broad reflections along the out-of-plane direction (orange columns in the inset of Fig. 3b). Based on the layer-lines, a helical pitch (p) was deduced to be 5.2 nm. Given the helical pitch (p = 5.2 nm) and the periodic distance between adjacent mesogens (d = 0.38 nm), a single pitch was deduced to comprise approx. 14 molecules. The simulated diffraction pattern based on these parameters matches fairly well with the experimental reflections (Fig. S7, ESI†). A similar diffraction pattern was also observed for the other enantiomer, Λ-Ru-C8 (Fig. S8, ESI†).
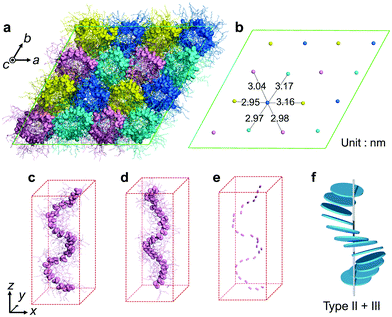
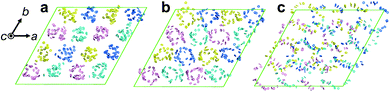
To clarify the helical structure in enantiomeric Ru-C8, we then performed all-atom molecular dynamics (MD) simulations for Δ-Ru-C8 based on the experimentally obtained structural information (approx. 14 molecules form a helical pitch of 5.2 nm) under periodic boundary conditions. As the initial structure, 16 columns with 2-fold helical pitches were positioned in the hexagonal lattice cell with dimensions of 12.95 nm × 12.95 nm × 10.60 nm. All the MD simulations were carried out using the program GROMACS 2016.6. The simulation details are provided in the ESI.† In the initial structure, Δ-Ru-C8 molecules were placed in a type I manner with the neighboring molecules rotated ca. 25° to each other, because the configurations without rotation resulted in an overlap of the ligands and the formation of undesirable void spaces between the columns. When 14 molecules were initially placed without tilting to form an M helical pitch, the calculations either did not reach the equilibrium state or resulted in structures without 2D periodicity. We then examined the initial configurations, in which 14 molecules were placed with the C3 axis of each mesogen tilted approximately 5° from the column axis to form an M helical pitch. After the equilibration run at 310 K for 200 ns, the two-dimensional hexagonal packing of Δ-Ru-C8 molecules was confirmed (Fig. 4a, b and Fig. S9–S14, ESI†). The helical stacking in a single column is shown in Fig. 4c, in which the neighboring atoms of ruthenium (Ru core) and other atoms are represented by spheres and stick models, respectively. The C3 axes of each molecule in a single column are shown in Fig. 4e. The position and direction of each mesogen gradually rotate around the column axis, confirming the presence of a helical structure that is a hybrid of types II and III (Fig. 4f and Fig. S15, ESI†). The average lattice parameter of the hexagonal lattice obtained from the MD simulation was a = 3.04 ± 0.03 nm, consistent with the experimentally obtained value (a = 3.2 nm by GI-XRD). The equilibrium structure with an M helix is hereafter denoted as M-Δ-Ru-C8 (Fig. 4a and Fig. S16a, ESI†).
For comparison, we also examined the initial condition, under which 14 tilted Δ isomers were set to form an opposite P helix. After the equilibrated run at 310 K for 200 ns, deformed P helices were obtained (P-Δ-Ru-C8, Fig. S16b, ESI†). We then examined another initial condition, under which 14 tilted Λ-isomers were set to form a P helix (P-Λ-Ru-C8, Fig. 4d and Fig. S16c, S17, ESI†). The resulting helical structure was almost antipodal to that of M-Δ-Ru-C8, indicating that Δ and Λ isomers favor the formation of M and P helices, respectively.
In M-Δ-Ru-C8, Ru-C8 molecules with roughly Y-shaped molecular structures stack along the column axis, directing one ligand to the inner space of the helix, and spreading the other two ligands to the exterior of the helix. Three phenylene rings in each Δ-Ru-C8 molecule are shown in Fig. 5a–c; they were positioned at the interior of the helix formed by the Ru core, close to the helix framework, and outside the helix. Intermittent π-stacking was observed between the phenylene rings positioned in the interior of the helix (Fig. 5a and Fig. S18a, ESI†), consistent with the XRD study (observation of the peak at d = 0.38 nm). In contrast, no π-stacking was observed between the other two phenylene rings (Fig. 5b and c). Similar stacking behavior is also observed in P-Λ-Ru-C8 (Fig. S19, ESI†). When each Ru-C8 molecule is viewed along the C3 axis (at the center of the Y-shape), the three methyl groups protrude along the C3 axis (Fig. S20a, ESI†), disturbing the efficient packing. To avoid steric repulsion, the Y-shaped molecules need to be slipped and twisted with each other, keeping the π-stacking (Fig. S18b and c, ESI†); the twisting direction (M or P) reflects the chiral structure of each mesogen, as shown in Fig. S16 (ESI†). The hybrid helical structure of types II and III is rational in terms of the π-stacking interaction and steric repulsion between chiral cores.
In addition to the molecular structure, we further consider the effect of dipolar interactions in the helix formation.32,33 The core structure of Ru-C8, [Ru(acacC2Ph)3], was deduced to have a dipole moment of ca. 0.92 Debye along the C2 axis based on the DFT calculation (Fig. S20a, ESI†). Although [Ru(acacC2Ph)3] ideally has D3 symmetry, it is slightly distorted and the paramagnetic spin is distributed to some extent over one of the three ligands.34 Hence, [Ru(acacC2Ph)3] has a dipole moment along the C2 axis. To examine the effect of dipolar interactions in M-Δ-Ru-C8, the dipole moments were then calculated for each Ru-C8 molecule in a single column using the molecular coordinates obtained by MD simulations (Fig. S20b, c and S21, ESI†). The variable magnitudes of dipole moments are attributed to the fluctuation of the terminal alkyl chains. The distribution of dipole moments in a single column viewed along the side and top of the column highlights the balanced distribution of dipole moments in the xz and xy planes (Fig. S20c and S21, ESI†); the dipoles were cancelled within a helical pitch. The analysis of MD simulation results indicates that the interplay of steric repulsion, π–π interaction, and dipolar interaction is a driving force for enantiopure Ru-C8 to form the helical structure.
In this paper, we mainly discussed the intermolecular interactions inside a column, which led to a helical assembly of octahedral metallomesogens; molecules stack with both the molecular position and the C3 axis rotating along the column axis. In contrast, each resulting helical column, a hybrid of types II and III, is not a simple cylinder. Hence, helical columns need to assemble collectively to minimize the total energy of the system. The importance of efficient molecular packing has already been recognized for the cases of so-called star-shaped mesogens with three arms.35–37 Because star-shaped molecules have “free space” between the arms, their assembly structures are stabilized by filling the space with neighboring molecules or guests.38 In our case, neighboring columns have similar helical manners to fill the “free space” (Movie S1, ESI†). The helical structure information appears to be transferred between neighboring columns, leading to the stabilization of the whole helical columnar assemblies as a hexagonal columnar phase.
In conclusion, the helical Col LC system was established using enantiopure octahedral metallomesogens with ΔΛ chirality at the molecular core (Δ- or Λ-Ru-C8). A combination of GI-XRD and MD simulation studies led to the visualization of the helical stacking structure as a hybrid of two major proposed structures, types II and III. Both type II and III structures have been proposed as basic structures for helical Col LCs, whereas the all-atom MD simulation of the hybrid structure is reported for the first time in this article, to the best of our knowledge. We believe that the revealed correlation between the core chiral mesogen and the helical stacking structure will lead to the rational development of helical Col LCs, including the control of stacking type.
We gratefully acknowledge Prof. Takahiro Ichikawa (Tokyo University of Agriculture and Technology) for his assistance in the XRD measurements and helpful discussions on this project. This work was financially supported by JSPS KAKENHI (Grant Numbers JP18K14283, JP19K05508, JP19H02537, JP19H05718, and JP20H05217). J. Y. and H. S. acknowledge the financial support from JST MIRAI (Grant Number JPMJMI18GC). G. W. and J. Y. acknowledge the financial support from Kitasato University Research Grant for Young Researchers. The computations were performed at the Research Center for Computational Science, Okazaki, Japan.
Conflicts of interest
There are no conflicts to declare.Notes and references
- J. W. Goodby, M. A. Waugh, S. M. Stein, E. Chin, R. Pindak and J. S. Patel, J. Am. Chem. Soc., 1989, 111, 8119–8125 Search PubMed.
- Chirality in Liquid Crystals, ed. H.-S. Kitzerow and C. Bahr, Springer-Verlag, New York, 2001 Search PubMed.
- G. Solladié and R. G. Zimmermann, Angew. Chem., Int. Ed. Engl., 1984, 23, 348–362 Search PubMed.
- N. Katsonis, E. Lacaze and A. Ferrarini, J. Mater. Chem., 2012, 22, 7088 Search PubMed.
- Handbook of Liquid Crystals, ed. J. W. Goodby, C. Tschierske, P. Raynes, H. Gleeson, T. Kato and P. J. Collings, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2014 Search PubMed.
- T. Kato, T. Yasuda, Y. Kamikawa and M. Yoshio, Chem. Commun., 2009, 729 Search PubMed.
- J. Malthête, J. Jacques, N. H. Tinh and C. Destrade, Nature, 1982, 298, 46–48 Search PubMed.
- G. Scherowsky and X. H. Chen, J. Mater. Chem., 1995, 5, 417 Search PubMed.
- R. J. Bushby and O. R. Lozman, Curr. Opin. Colloid Interface Sci., 2002, 7, 343–354 Search PubMed.
- F. Vera, J. Luis Serrano and T. Sierra, Chem. Soc. Rev., 2009, 38, 781 Search PubMed.
- T. Wöhrle, I. Wurzbach, J. Kirres, A. Kostidou, N. Kapernaum, J. Litterscheidt, J. C. Haenle, P. Staffeld, A. Baro, F. Giesselmann and S. Laschat, Chem. Rev., 2016, 116, 1139–1241 Search PubMed.
- T. Metzroth, A. Hoffmann, R. Martín-Rapún, M. M. J. Smulders, K. Pieterse, A. R. A. Palmans, J. A. J. M. Vekemans, E. W. Meijer, H. W. Spiess and J. Gauss, Chem. Sci., 2011, 2, 69–76 Search PubMed.
- D. Andrienko, V. Marcon and K. Kremer, J. Chem. Phys., 2006, 125, 124902 Search PubMed.
- M. Yoneya, T. Makabe, A. Miyamoto, Y. Shimizu, Y. Miyake, H. Yoshida, A. Fujii and M. Ozaki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062505 Search PubMed.
- V. Marcon, D. W. Breiby, W. Pisula, J. Dahl, J. Kirkpatrick, S. Patwardhan, F. Grozema and D. Andrienko, J. Am. Chem. Soc., 2009, 131, 11426–11432 Search PubMed.
- D. Chakrabarti and D. J. Wales, Phys. Rev. Lett., 2008, 100, 127801 Search PubMed.
- X. Feng, V. Marcon, W. Pisula, M. R. Hansen, J. Kirkpatrick, F. Grozema, D. Andrienko, K. Kremer and K. Müllen, Nat. Mater., 2009, 8, 421–426 Search PubMed.
- A. M. Giroud-Godquin and A. Rassat, C. R. Seances Acad. Sci., Ser. 2, 1982, 294, 241–243 Search PubMed.
- H. Zheng and T. M. Swager, J. Am. Chem. Soc., 1994, 116, 761–762 Search PubMed.
- S. T. Trzaska, H.-F. Hsu and T. M. Swager, J. Am. Chem. Soc., 1999, 121, 4518–4519 Search PubMed.
- J. Yoshida, H. Sato, A. Yamagishi and N. Hoshino, J. Am. Chem. Soc., 2005, 127, 8453–8456 Search PubMed.
- J. Yoshida, H. Sato, N. Hoshino and A. Yamagishi, J. Phys. Chem. B, 2008, 112, 9677–9683 Search PubMed.
- G. Watanabe and J. Yoshida, J. Phys. Chem. B, 2016, 120, 6858–6864 Search PubMed.
- J. Yoshida, S. Tamura, K. Hoshino, H. Yuge, H. Sato, A. Yamazaki, S. Yoneda and G. Watanabe, J. Phys. Chem. B, 2018, 122, 10615–10626 Search PubMed.
- J. Yoshida, G. Watanabe, K. Kakizawa, Y. Kawabata and H. Yuge, Inorg. Chem., 2013, 52, 11042–11050 Search PubMed.
- J.-G. Ha, J. Song, J.-K. Lee, B.-K. Cho and W.-C. Zin, Chem. Commun., 2012, 48, 3418 Search PubMed.
- M. Hara, T. Orito, S. Nagano and T. Seki, Chem. Commun., 2018, 54, 1457–1460 Search PubMed.
- W. Pisula, Ž. Tomović, C. Simpson, M. Kastler, T. Pakula and K. Müllen, Chem. Mater., 2005, 17, 4296–4303 Search PubMed.
- M. Peterca, M. R. Imam, C.-H. Ahn, V. S. K. Balagurusamy, D. A. Wilson, B. M. Rosen and V. Percec, J. Am. Chem. Soc., 2011, 133, 2311–2328 Search PubMed.
- J. Shu, D. Dudenko, M. Esmaeili, J. H. Park, S. R. Puniredd, J. Y. Chang, D. W. Breiby, W. Pisula and M. R. Hansen, J. Am. Chem. Soc., 2013, 135, 11075–11086 Search PubMed.
- M. L. Nguyen, J. Byun, S. Kim, J. W. Hyun, K. Hur, T. J. Shin and B. Cho, Angew. Chem., Int. Ed., 2019, 58, 2749–2753 Search PubMed.
- N. V. Madhusudana, Mol. Cryst. Liq. Cryst., 2004, 409, 371–387 Search PubMed.
- T. Nozawa, P. Brumby and K. Yasuoka, Int. J. Mol. Sci., 2018, 19, 2715 Search PubMed.
- J. Yoshida, K. Tateyama and H. Yuge, Dalton Trans., 2020, 49, 2102–2111 Search PubMed.
- M. Lehmann and M. Hügel, Angew. Chem., Int. Ed., 2015, 54, 4110–4114 Search PubMed.
- K. Bader, T. Wöhrle, E. Öztürk, A. Baro and S. Laschat, Soft Matter, 2018, 14, 6409–6414 Search PubMed.
- M. Hügel, M. Dechant, N. Scheuring, T. Ghosh and M. Lehmann, Chem. – Eur. J., 2019, 25, 3352–3361 Search PubMed.
- M. Lehmann, M. Dechant, M. Lambov and T. Ghosh, Acc. Chem. Res., 2019, 52, 1653–1664 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc05930g |
| This journal is © The Royal Society of Chemistry 2020 |