Open Access Article
Open Access ArticleRotational dynamics of the imidazolium ion in cyanide-bridged dielectric framework materials†
Anthony E.
Phillips
 *a,
Guanqun
Cai
*a,
Guanqun
Cai
 a and
Franz
Demmel
a and
Franz
Demmel
 b
b
aSchool of Physics and Astronomy, Queen Mary University of London, London E1 4NS, UK. E-mail: a.e.phillips@qmul.ac.uk
bISIS Facility, Rutherford Appleton Laboratory, Didcot, OX11 0QX, UK
First published on 28th August 2020
Abstract
Reorientation of organic cations in the cubic interstices of cyanoelpasolite molecular perovskites results in a variety of structural phase transitions, but far less is known about these cations’ dynamics. We report quasielastic neutron scattering from the materials (C3H5N2)2K[MIII(CN)6], M = Fe,Co, which is directly sensitive to the rotation of the imidazolium ion. The motion is well described by a circular three-site hopping model, with the ion rotating within its plane in the intermediate-temperature phase, but tilting permanently in the high-temperature phase. Thus the two rhombohedral phases, which are crystallographically rather similar, have markedly different dynamics. The activation energy of rotation is about 10 kJ mol−1 and the barrier between orientations is 6 kJ mol−1. Our results explain two anomalous features in these materials’ dielectric constants.
The well-known, deceptively simple cubic framework structure of Prussian blue can adopt a multitude of variations, together comprising the broad family of “Prussian blue analogues” AxM′y[M(CN)6]z·nG. Over the past decade, many new materials have been reported in the specific family AI2BI[MIII(CN)6], where the B cation is an alkali metal while M is a first-row transition metal. These form stoichiometric structures analogous to “ordered perovskite” or elpasolite, with B+ and [M(CN)6]3− cations alternating to form the framework and an A+ cation occupying each cubic interstice (Fig. 1a). Significantly, these interstices are large enough for the A+ cation to be a small organic ion such as imidazolium,1 guanidinium, acetamidinium,2 or (poly)methylammonium.3,4 Unlike monatomic ions, such cations may have intrinsic dipole or higher-order multipole moments, giving rise to both dielectric switching behaviour and complex, unusual forms of crystallographic order.5
Understanding and controlling this behaviour requires detailed investigation not only of the subtle atomic structure but also of the guest ion dynamics. Although dynamic information is routinely inferred from electrical and NMR measurements, few atomistic models of these materials’ dynamics have been reported. An ideal technique for this purpose is incoherent quasielastic neutron scattering (QENS), which is sensitive to both the geometry and timescale of atomic motion. Because of the very high incoherent scattering cross section of the 1H nucleus, the QENS signal is invariably dominated by contributions from hydrogen atoms, making this a useful technique for probing the motion of organic guest ions within framework materials. QENS is especially suitable for the cyanide materials considered here, since the framework is entirely inorganic, so that the signal arises essentially from the guest ions alone. Furthermore, it has the advantage over NMR spectroscopy that it is equally applicable to paramagnetic and diamagnetic metal ions M3+. QENS has recently been used to elucidate the motion of the guest ions in the A = (CH3)nNH4–n+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6,7 and CH3C(NH2)2+
6,7 and CH3C(NH2)2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 members of the cyanoelpasolite family.
8 members of the cyanoelpasolite family.
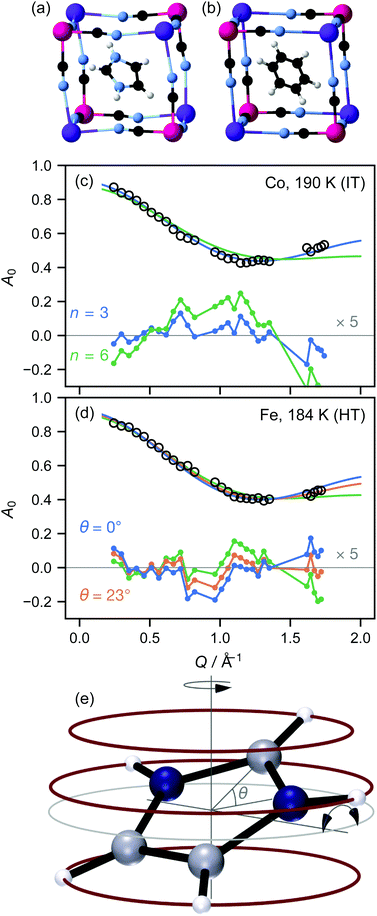
We here report measurements on the imidazolium salts (C3H5N2)2K[MIII(CN)6], M = Fe,Co. We have previously measured the local9 and long-range crystallographic structure10 of these materials, while Zhang and co-workers have reported crystallographic, electrical, and NMR data.1,11 The target materials have three phases: a low-temperature (LT) phase crystallising in space group C2/c, where the imidazolium ions are ordered (Fig. 1(a)); an intermediate-temperature (IT) phase in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ; and a high-temperature phase in R
; and a high-temperature phase in R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The phase transition temperatures are 110 K and 199 K for Co, 157 K and 184 K for Fe: thus the IT phase exists over a somewhat larger temperature range for the Co material. In the IT and HT phases, the imidazolium ion is disordered about the threefold axis; for convenience, the resulting toroid of electron density is typically represented in an atomistic crystal structure as a “benzene ring” (Fig. 1(b)). The crystallographic differences between these phases are extremely subtle: on cooling from the HT to the IT phase, the cyanide ions move slightly away from the lost mirror plane10 and bend somewhat less at the metal ion.9 On the other hand, 2H-NMR shows a distinct shift in the dynamics at the HT–IT transition, which has been attributed to librations of the imidazolium ion out of its plane.
m. The phase transition temperatures are 110 K and 199 K for Co, 157 K and 184 K for Fe: thus the IT phase exists over a somewhat larger temperature range for the Co material. In the IT and HT phases, the imidazolium ion is disordered about the threefold axis; for convenience, the resulting toroid of electron density is typically represented in an atomistic crystal structure as a “benzene ring” (Fig. 1(b)). The crystallographic differences between these phases are extremely subtle: on cooling from the HT to the IT phase, the cyanide ions move slightly away from the lost mirror plane10 and bend somewhat less at the metal ion.9 On the other hand, 2H-NMR shows a distinct shift in the dynamics at the HT–IT transition, which has been attributed to librations of the imidazolium ion out of its plane.
Our measurements were performed on the OSIRIS instrument (ISIS Neutron and Muon Source). Samples were crystallised from aqueous solution by previously reported methods.1 Each sample was ground finely and loaded into an annular aluminium can, then mounted in a CCR. The annular geometry was chosen to minimise multiple scattering. We collected data using the 002 orientation of the pyrolytic graphite analyser, which gives data to Q = 2 Å−1; beyond this point, Bragg diffraction peaks make it difficult to obtain reliable measurements. Data were initially processed in Mantid;12 fitting to non-standard functions was then performed in Python (see ESI†).
The QENS signal gives a direct measurement of the autocorrelation between the positions of each atom at different times. The experimentally measured quantity is the incoherent scattering function S(Q,ω). For the case of rotating molecules, this can be written in terms of scattering vector Q and energy transfer ω as13
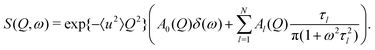 | (1) |
The localised motion causes an elastic contribution represented by the delta function and a sum of quasielastic contributions with Lorentzian line shapes. The structure factors Al(Q) are characteristic of the geometry of motion, while the correlation times τl depend on its timescale and are independent of the momentum transfer Q. The mean-square atomic displacement 〈u2〉 is analogous to the U parameter in crystallography except that it reflects only molecular vibrations and librations, not molecular rotation (which appears elsewhere in the scattering function).
We initially focused our analysis on A0(Q), known as the elastic incoherent structure factor (EISF), because it can be evaluated independently of any prior model, since it is simply the fraction of the total scattering that is elastic. From the crystallographic structure, a natural first model of the H motion is hopping around a circle. Since the imidazolium ion sits on a crystallographic threefold axis, the minimum plausible number of sites for each H atom is three. However, the crystallographic disorder might suggest that atoms hop over shorter distances between six or more sites, up to the limit of continuous rotation. We therefore fitted the data using the standard expressions for three- and six-site rotation; in fact, within the Q range probed here, a six-site model is effectively indistinguishable from continuous rotation (see ESI†). We initially fixed the radius of the circle at the radius of the imidazolium ion taken from the low-temperature crystal structure, r = 2.018 Å.
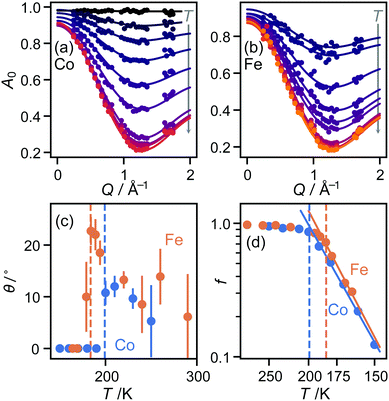
In both the intermediate- and high-temperature phases of both materials, the three-site model fitted the experimental data substantially better than models with six or more sites (Fig. 1(a and b)). Further inspection, however, showed that in the high-temperature phase, there were suspicious correlations between the residuals even of the three-site fit: the experimental data appeared scaled by a small factor in Q, implying that the effective radius r of molecular motion in this phase is less than its theoretical value. Of course, there is no physically plausible means for the imidazolium ion itself to shrink. However, the radius of rotation for any given proton can be less than the molecular radius if the molecule is tilted away from the rotation axis (Fig. 1(c)). Allowing this tilt angle θ to refine gave a substantially improved fit only in the HT phase (Fig. 1(b)).
We therefore adopted a three-site model, giving the expression for the EISF
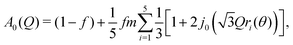 | (2) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) sin(x)/x is the zero-order spherical Bessel function. (If we allow hopping between tilts of ±θ, this expression becomes more complicated but changes numerically very little: see ESI.†) There are three refined parameters: the tilt angle θ, which determines the rotation radii r1,…,r5 of the five protons; the fraction f of ions rotating on the OSIRIS time scale; and a correction m for multiple scattering, which is ideally 1 but will refine to slightly smaller values if multiple scattering is significant.14 This model gave a good fit to our data for both materials at all temperatures (Fig. 2(a and b)). The best-fit tilt angles are shown in Fig. 2(c). In the intermediate phase, the tilt angle refined to zero. (The exception is Fe at 180 K, nominally just below the transition; this may reflect a small error in either the sample temperature or the nominal transition temperature, or be associated with the onset of the phase transition.) In the high-temperature phase, the fitted tilt angle ranges from about 8° to 25°. The tilt angle appears to be maximum immediately above the phase transition, decreasing gradually with temperature in the HT phase.
sin(x)/x is the zero-order spherical Bessel function. (If we allow hopping between tilts of ±θ, this expression becomes more complicated but changes numerically very little: see ESI.†) There are three refined parameters: the tilt angle θ, which determines the rotation radii r1,…,r5 of the five protons; the fraction f of ions rotating on the OSIRIS time scale; and a correction m for multiple scattering, which is ideally 1 but will refine to slightly smaller values if multiple scattering is significant.14 This model gave a good fit to our data for both materials at all temperatures (Fig. 2(a and b)). The best-fit tilt angles are shown in Fig. 2(c). In the intermediate phase, the tilt angle refined to zero. (The exception is Fe at 180 K, nominally just below the transition; this may reflect a small error in either the sample temperature or the nominal transition temperature, or be associated with the onset of the phase transition.) In the high-temperature phase, the fitted tilt angle ranges from about 8° to 25°. The tilt angle appears to be maximum immediately above the phase transition, decreasing gradually with temperature in the HT phase.
To check that this result is consistent with these materials’ known structure, we revisited our published single-crystal diffraction data.10 In both materials, the C⋯C distance across the “benzene ring” indeed decreases at the IT–HT phase transition. Moreover, estimating the tilt angle from this decrease, cosθ = dHT/dIT, gave a value of 9° in each case, in agreement with the QENS result. The tilt angles proposed here cover approximately the same range as previously reported from NMR for the Co material, ranging from 2° at 190 K to 24° at 340 K.11 However, there is some disagreement in the trend proposed through the HT phase. We return to this issue below.
The refined fraction f of imidazolium ions rotating on the timescale of this experiment increased rapidly with temperature from 150 K upwards through the IT phase, then far more gradually from about 90% to 100% in the HT phase. Fitting this fraction to an Arrhenius model (Fig. 2(d)), f = f0exp(−Ea/kT), gave activation energies of 10.9(7) kJ mol−1 (Fe) and 10.1(4) kJ mol−1 (Co), in reasonable agreement with the NMR value of 11.0 kJ mol−1 (Co) over the same region.11 However, the QENS result sheds new light on this result: rather than interpreting it as an increase in the speed of molecular rotation, as proposed from the NMR data, we see instead that it is the fraction of moving molecules that increases. Again, we return below to the question of the speed of molecular rotation itself. The multiple-scattering correction m refined to values between 0.8 and 0.9 for both materials at all temperatures, with no obvious trend in variation with temperature.
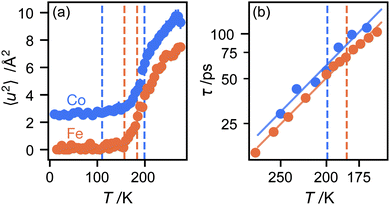
We now consider the mean squared displacement 〈u2〉, which we determined using (1) from an “elastic window scan” of the elastic scattering as a function of temperature (Fig. 3(a)). In both materials the mean squared displacement begins to rise more rapidly at around 160 K. Although this corresponds approximately to the LT–IT transition in the Fe material, the almost identical behaviour of the Co material suggests that this is a coincidence, corresponding to the H atoms’ vibrational motion entering the OSIRIS time window rather than any physical change in their behaviour. Interestingly, in the Co material the IT–HT phase transition corresponds to a distinct decrease in the gradient. This implies that a vibrational or librational mode is stiffening with temperature, rather than softening as one might expect in general. Specifically, it directly contradicts the NMR suggestion that the libration amplitude increases linearly with temperature from the IT–HT transition.11 While there appears to be some sign of similar behaviour in the Fe material, the corresponding phase transition is so close to the observable limit that this is difficult to verify from our data. We can rationalise the apparent stiffening, in combination with the tilt angles refined from the EISF, as follows. In the IT phase, the molecule librates in its plane with increasing amplitude 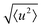 but always about the untilted position. In the HT phase, the molecule becomes permanently tilted, but increasing the libration amplitude further involves a steeper energy curve, so that the gradient of 〈u2〉 with temperature decreases.
but always about the untilted position. In the HT phase, the molecule becomes permanently tilted, but increasing the libration amplitude further involves a steeper energy curve, so that the gradient of 〈u2〉 with temperature decreases.
Finally, we return to the timescale associated with molecular rotation itself. In a three-site model, there is a single inelastic structure factor A1 and corresponding correlation time τ1. The data fit well to this model (see ESI†), given correlation times in the range 20–100 ps over the temperature range studied here, with rotation in the Co material slightly slower than Fe, perhaps because the unit cell volume is slightly smaller. Plotting the correlation times as a function of temperature in an Arrhenius plot (Fig. 3(b)) gives identical values of the energy barrier to rotation, within experimental error: 6.0(5) kJ mol−1 for the Co material and 5.93(13) kJ mol−1 for Fe. There appears to be little difference in these values between the IT and HT phases. These values are plausible for motion that disrupts several van der Waals and hydrogen-bonded interactions between the host framework and guest ions. They are only about half the value of the activation energies to molecular rotation, suggesting that, once molecules shake free of their initial static positions, the energy barrier to continued rotation is smaller.
This model is consistent with published measurements of the dielectric constants.1,11 Indeed, it explains two unusual features that appear not to have been previously discussed. First, the dielectric constant in the imidazolium plane increases with temperature below the IT–HT phase transition, which is extremely rare for orientational dielectrics.15 We attribute this anomalous behaviour to the increase in the fraction of ions that rotate and hence contribute to the dielectric constant. Second, the dielectric constant perpendicular to this plane is slightly larger in the HT than the IT phase. This can be explained by hopping between tilt angles of ±θ, which have opposite perpendicular dipole moments.
In conclusion, we have put forward a model for the geometry and timescale of the motion of the imidazolium ion in our target framework materials, based on incoherent quasielastic neutron scattering data. Our work is in good agreement with previous studies, in particular giving comparable activation energies to those from NMR and supporting the model that the imidazolium ion rotates in its plane in the IT phase but is tilted in the HT phase. However, the unique advantages of this method allow us to elaborate this model in three ways. First, we have demonstrated that the molecular motion is best described by hopping about a threefold rotation axis, the minimum consistent with the crystallographic symmetry. This emphasises that, despite the apparent toroidal symmetry of the crystallographic disorder, the molecular dipoles are not free to rotate continuously but hop between specific low-energy conformations. Modifying the intermolecular interactions can thus tune these dynamics. Second, we suggest that the tilting in the HT phase is not simply libration with an increasing amplitude, but rather reflects a permanent tilt angle. Moreover, this angle does not increase gradually from the IT–HT transition, but rather increases rapidly at the transition and may then subsequently decrease slightly. Third, we have shown that two distinct energy scales are involved: a larger initial barrier to rotation, and a smaller barrier between rotational orientations. We hope that these results will lead to a better understanding of the dielectric behaviour of this family of materials. More generally, our results illustrate the exceptional suitability of QENS for achieving atomistic understanding of dynamics in tuneable dielectric framework materials.
We thank ISIS Neutron and Muon Source for the award of beamtime (RB1620286 and RB1720204). GC thanks the Chinese Scholarships Council for funding.
Conflicts of interest
There are no conflicts of interest to declare.Notes and references
- W. Zhang, Y. Cai, R. Xiong, H. Yoshikawa and K. Awaga, Angew. Chem., Int. Ed., 2010, 49, 6608–6610 CrossRef CAS.
- W.-J. Xu, K.-P. Xie, Z.-F. Xiao, W.-X. Zhang and X.-M. Chen, Cryst. Growth Des., 2016, 16, 7212–7217 CrossRef CAS.
- W. Zhang, H.-Y. Ye, R. Graf, H. W. Spiess, Y.-F. Yao, R.-Q. Zhu and R.-G. Xiong, J. Am. Chem. Soc., 2013, 135, 5230–5233 CrossRef CAS.
- W.-J. Xu, S.-L. Chen, Z.-T. Hu, R.-B. Lin, Y.-J. Su, W.-X. Zhang and X.-M. Chen, Dalton Trans., 2016, 45, 4224–4229 RSC.
- C. S. Coates, H. J. Gray, J. Bulled, H. L. B. Boström, A. Simonov and A. L. Goodwin, Philos. Trans. R. Soc., A, 2019, 377, 20180219 CrossRef CAS.
- M. Rok, G. Bator, W. Medycki, M. Zamponi, S. Balčiūnas, M. Šimėnas and J. Banys, Dalton Trans., 2018, 47, 17329–17341 RSC.
- M. Rok, G. Bator, B. Zarychta, B. Dziuk, J. Repeć, W. Medycki, M. Zamponi, G. Usevičius, M. Šimėnas and J. Banys, Dalton Trans., 2019, 48, 4190–4202 RSC.
- M. Rok, G. Bator, B. Zarychta, B. Dziuk, D. K. Skałecki, W. Medycki and M. Zamponi, Cryst. Growth Des., 2019, 19, 4526–4537 CrossRef CAS.
- H. D. Duncan, E. O. R. Beake, H. Y. Playford, M. T. Dove and A. E. Phillips, CrystEngComm, 2017, 19, 7316–7321 RSC.
- A. E. Phillips and A. D. Fortes, Angew. Chem., Int. Ed., 2017, 56, 15950–15953 CrossRef CAS.
- X. Zhang, X.-D. Shao, S.-C. Li, Y. Cai, Y.-F. Yao, R.-G. Xiong and W. Zhang, Chem. Commun., 2015, 51, 4568–4571 RSC.
- Mantid: A high performance framework for reduction and analysis of neutron scattering data, DOI:10.5286/software/mantid.
- M. Bée, Quasielastic neutron scattering, Adam Hilger, Bristol and Philadelphia, 1988 Search PubMed.
- M. Songvilay, Z. Wang, V. G. Sakai, T. Guidi, M. Bari, Z.-G. Ye, G. Xu, K. L. Brown, P. M. Gehring and C. Stock, Phys. Rev. Mater., 2019, 3, 125406 CrossRef CAS.
- J. Hunger, A. Stoppa, S. Schrödle, G. Hefter and R. Buchner, ChemPhysChem, 2009, 10, 723–733 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc05238h |
| This journal is © The Royal Society of Chemistry 2020 |