A curious case of dynamic disorder in pyrrolidine rings elucidated by NMR crystallography

Abstract

A pharmaceutical exhibits differing dynamics in crystallographically distinct pyrrolidine rings despite being nearly related by symmetry, with one performing ring inversions while the other is constrained to torsional librations. Using ¹³C solid-state magic-angle spinning (MAS) NMR and DFT calculations, we show that this contrast originates from C–H⋯H–C close contacts and less efficient C–H⋯π intermolecular interactions observed in the transition state of the constrained pyrrolidine ring, highlighting the influence of the crystallographic environment on the molecular motion.

---

Pharmaceutical products are most often manufactured in their solid forms, benefiting the patient with a convenient route of administration.¹ During the development stage, solid forms are thoroughly characterized in order to identify potential risks associated with stability, polymorphic conversion,^2,3 and the ability to form hydrates or solvates.⁴ Characterization may include X-ray crystallography and using the derived structural model to assess the risks of making a particular solid form into a medicine. The occurrence of crystallographic disorder arising from mobility (i.e. dynamic structural disorder) or the accessibility of multiple conformations/orientations (i.e. static structural disorder) poses several challenges in the risk assessment, due in part to the uncertainty on the atomic positions.

Solid-state NMR spectroscopy is a powerful tool for investigating crystallographic disorder, with the potential to exploit several pharmaceutically-relevant nuclei (¹H, ¹³C, ¹⁵N) and the ability to probe specific sites in the structure.^5,6 NMR crystallography is capable of distinguishing static from dynamic structural disorder, has been used for investigating dynamics in pharmaceuticals,^7–10 and can be used to improve structural models.^11–17 Conversely, the presence of dynamics may not be immediately apparent from X-ray data, especially for data acquired at low temperatures due to a “freezing” of the motion.

Here, we combine solid-state NMR and DFT calculations in an NMR crystallography approach to investigate a development compound, 1a, which features a curious case of structural disorder. Despite there being two molecules in the asymmetric unit (Z′ = 2) each related by pseudosymmetry, surprisingly only one of the two pyrrolidine groups in the structural model appears to be disordered. The solid-state NMR experiments allow the motion and thermodynamic parameters to be characterized in 1avia¹³C spin–lattice relaxation time measurements, while the computations allow the origins of these contrasting dynamics to be understood.

The compound investigated herein, 1a, consists of the salt (the counterion is referred to as “a”) of a pharmaceutical compound (1) in a 1 : 1 stoichiometric equivalence. The structural model, determined by X-ray crystallography at 150 K, suggests the presence of a pair of 1a related by C₂ pseudosymmetry, with the disorder in one of the pyrrolidine groups of 1 breaking this symmetry. As shown in Fig. 1a, where the red dashed lines represent the rest of the undisclosed structure, a pyrrolidine group appears to be relatively “ordered” (henceforth referred to as C^ord), while the other group appears to be disordered (henceforth referred to as C^dis) over two positions with occupancies of 0.5 each. However, while C^ord appears to be ordered, the situation is ambiguous as its anisotropic displacement ellipsoids have some distortions (see Fig. S3 of the ESI†), suggesting the presence of vibrations. The crystallographic environment surrounding the two pyrrolidine groups differ in that C^dis interacts more closely with the counterion a while C^ord interacts primarily with other molecules of 1. All contacts (within 3 Å) involving the pyrrolidine groups are shown in Fig. S4 of the ESI.† In order to confirm the contrast in the dynamics of the pyrrolidine groups, variable temperature ¹H–¹³C cross polarisation (CP) magic-angle spinning (MAS) solid-state NMR experiments and ¹³C spin–lattice relaxation time measurements, T₁(¹³C), have been performed.

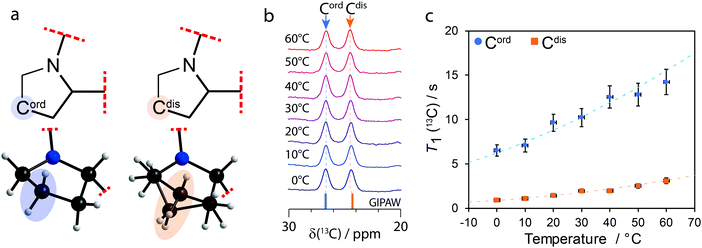Fig. 1 (a) Diagram of the partial molecular structure and depiction of the structural model of 1a showing the ordered (C^ord) and disordered (C^dis) carbon atoms on their respective pyrrolidine groups. (b) Variable temperature ¹H–¹³C CPMAS (ν_L(¹H) = 400 MHz; ν_MAS = 10 kHz) solid-state NMR spectra of 1a showing the 20 to 30 ppm region and (c) T₁(¹³C) of C^ord and C^dis as a function of temperature. The dashed lines in (c) show the fits using eqn (S1)–(S3) of the ESI† and the values from Table 1.

When there are two molecules in the asymmetric unit, a doubling of ¹³C resonances can be observed if the crystallographic environments between otherwise chemically equivalent sites are sufficiently distinct. As shown in Fig. 1b, a ¹³C chemical shift difference of 2.2 ppm is observed between C^ord (δ(¹³C) = 26.7 ppm) and C^dis (δ(¹³C) = 24.5 ppm). The ¹³C signals have been assigned to their sites in the structural model using gauge-including projector augmented-wave (GIPAW)¹⁸ DFT calculations as part of CASTEP.¹⁹ The calculations were performed for both conformations of C^dis, and the average GIPAW calculated δ(¹³C) chemical shifts are 26.7 ppm and 24.3 ppm for C^ord and C^dis, respectively, resulting in a computed difference of 2.4 ppm. These calculated results, shown on Fig. 1b as sticks, are in excellent agreement with the experimental results.

As the pyrrolidine groups consist of saturated heterocycles, they can exhibit dynamics in the form of ring inversions,^20,21 analogous to those observed in cyclohexane.^10,22 In order to investigate the dynamics, ¹H–¹³C solid-state CP MAS NMR and T₁(¹³C) measurements were performed at 10 °C steps between 0 °C and 60 °C. As shown in Fig. 1b, there are no significant changes to the ¹³C chemical shifts of C^ord or C^dis as the temperature is increased, and this is also true for all the other resonances (not shown on the figure). Supported by differential scanning calorimetry (see Fig. S5 of the ESI†), this suggests that no phase changes or major structural changes are occurring between these temperatures.

Fig. 2 Calculated relative energies as a pyrrolidine group achieves a ring inversion performed on models of (a) C^ord and (b) C^dis using: the original structural model of 1a (teal diamonds), 1a maintaining periodicity but with the counterion removed (red squares), and an isolated molecule of 1 (purple circle). A depiction of the models are shown above to provide a frame of reference for the conformations. (c–f) Diagrams showing all atoms within distances shorter than the sum of their van der Waals radius and near hydrogen atoms in either pyrrolidine group of the optimized structural models of 1a when: (c) C^ord is puckered up, (d) C^ord is puckered down, (e) C^dis is puckered up, (f) C^dis is puckered down. The structure in (d) was obtained from DFT optimizations and has not been experimentally observed. The arrows highlight the carbon atoms of interest.

The T₁(¹³C) at 20 °C for C^ord and C^dis were 9.7 s and 1.4 s, respectively, and all T₁(¹³C) values are shown on Fig. 1c and have been tabulated in Table S1 of the ESI.† These short T₁(¹³C) suggest that both C^ord and C^dis are dynamic. To place these values into context, the T₁(¹³C) at 20 °C of the rigid carbons of 1a are >100 s, whereas the T₁(¹³C) of rotating methyl groups on 1a are 11 s and 15 s at 20 °C. The relationship between T₁(¹³C), the correlation times (τ_c), and the activation energy are well known, and have been interpreted using the Bloembergen–Purcell–Pound model.^23–25 Assuming it follows the Arrhenius equation, measuring the T₁(¹³C) relaxation times as a function of temperature allows for the activation energy to be extracted (see eqn (S1)–(S3) of the ESI†).

A plot of T₁(¹³C) as a function of the temperature is shown in Fig. 1c, with the fits using eqn (S1)–(S3) (ESI†) being in excellent agreement with the experimental results (R_c² > 0.96). The extracted activation energies are 11 ± 2 kJ mol⁻¹ for C^ord and 16 ± 3 kJ mol⁻¹ for C^dis, with all parameters being summarized in Table 1. The higher activation energy of C^dis is attributed to dynamics in the form of ring inversions, which is also supported by the X-ray structure. In contrast, having a single favourable conformation, short T₁(¹³C) relaxation times, and anisotropic displacement ellipsoids suggesting the presence of vibrations, we associate the lower experimental activation energy of C^ord to torsional librations rather than ring inversions. The activation energy of C^dis is very similar in value with the calculated energy of 17.2 kJ mol⁻¹ for the pyrrolidine group in proline performing a ring inversion.²⁶

Table 1 Experimental thermodynamic parameters obtained from fitting the T₁(¹³C) in Fig. 1c for 1a using eqn (S1)–(S3) (see the ESI), including the correlation coefficient (R_c²), as compared to the DFT-calculated activation energies performed on complete ring inversions

Group	E a (kJ mol^−1)	τ 0 (s)/× 10^−14	a	R c ^2	Comment
a Calculated using DFT as part of CASTEP (see Fig. 2a and b).
C^ord	11 ± 2	4 ± 3	0.11	0.96	Experimental
	31.7				Calculated
C^dis	16 ± 3	4 ± 2	0.10	0.98	Experimental
	17.8				Calculated

---

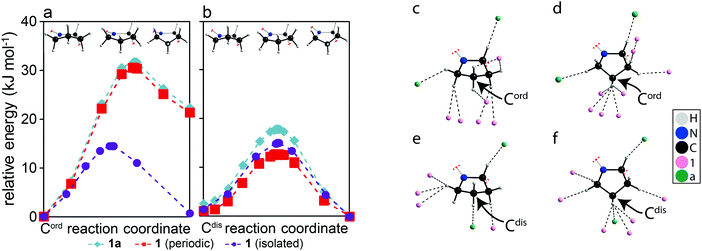
In order to understand why C^dis is capable of exhibiting ring inversions while C^ord is only librating, transition state calculations were performed using CASTEP. The calculations performed on the full structures, shown as teal diamonds in Fig. 2a and b, indicate that the two conformations of the pyrrolidine group, puckered up (left) and down (right), have approximately equal energies for C^dis, whereas a 22.3 kJ mol⁻¹ energy difference is observed for C^ord. These results suggest that both conformations of C^dis are energetically favourable, while only the conformation that was experimentally observed in the structural model for C^ord is favourable. Further, the calculated transition state energy barrier for C^dis relative to the puckered down conformation is 17.8 kJ mol⁻¹, in excellent agreement with the experimentally measured activation energy of 16 ± 3 kJ mol⁻¹. We propose that this energy barrier is low enough to permit the pyrrolidine ring to undergo dynamics in the form of ring inversions, with both conformations of C^dis being accessible. In contrast, the transition state energy of a ring inversion for C^ord is 31.7 kJ mol⁻¹ relative to the starting geometry, which is not in agreement with the experimental NMR results of 11 ± 2 kJ mol⁻¹. The clear discrepancy between the computational and experimental results for C^ord suggests that for this ring, the barrier for a ring inversion is too high, and thus libration is observed experimentally.‡ To understand why C^dis is exhibiting ring inversions while C^ord is only librating, a series of structural models were created. The first set of models consisted of structure 1a but the counterions “a” have been removed while maintaining periodicity (red squares in Fig. 2a and b), and the second set consisted of completely isolating either molecule of 1 in a cell enlarged by 9 Å along the a, b, and c axes of the unit cell (purple circles in Fig. 2a and b). These models allow interactions arising from the crystal packing to be removed selectively.²⁷

As shown in Fig. 2a and b, there is a clear contribution to the transition state energies from crystal packing. The intermolecular interactions involving C^ord and C^dis can be identified based on the molecules involved, either between two molecules of 1 (denoted here as 1⋯1) or between molecules of 1 and a (denoted here as 1⋯a). In the case of C^dis, removing the counterion a has lowered the calculated energy barrier by 5.1 kJ mol⁻¹, whereas a reduction of 2.8 kJ mol⁻¹ was observed upon isolating the molecule 1 that has C^dis. In contrast, isolating the molecule 1 that has C^ord reduced the energy barrier of C^ord by 17.2 kJ mol⁻¹, whereas removing the counterion a merely reduced the barrier by 1.2 kJ mol⁻¹. Notably, in the isolated molecule of 1, the energy of both conformations of C^ord are now nearly the same, and the energy barriers are similar for both C^dis and C^ord due to the removal of the intermolecular interactions. Evidently, the intermolecular interactions involving C^ord and C^dis are distinct, with 1⋯1 interactions playing a larger role in the energy barrier for C^ord and 1⋯a interactions being more important for C^dis.

The interactions in the structural model were analysed in detail and are shown in Fig. 2c–f, illustrating all atoms within distances shorter than the sum of their van der Waals radius and near hydrogen atoms for both conformations (puckered up & down) of both pyrrolidine rings. C^ord exhibits mostly 1⋯1 interactions (Fig. 2c and d), whereas C^dis presents both 1⋯1 and 1⋯a interactions (Fig. 2e and f). In the case of C^dis, there are six and eight atoms within this specified radius of any hydrogen atom in the ring when puckered up and down, respectively, compared to eight and ten atoms for C^ord in the same conformations. The significance of these interactions was further investigated using DFT calculations performed on molecular cluster models (tabulated in Table S2 of the ESI†).²⁸

The energy barrier for the ring inversions of C^dis appears to originate primarily from the weakening of C–H⋯O interactions originating from 1⋯a, with a difference of 7.4 kJ mol⁻¹ between the puckered up conformation and the transition state, thus destabilizing the transition state of C^dis. This further supports the results obtained from the calculations presented in Fig. 2b, where removing the counterion reduced the energy barrier of C^dis. However, the overall calculated energy barrier (17.8 kJ mol⁻¹) is still small enough to allow ring inversions to occur. In terms of C^ord, the destabilizing 1⋯1 interactions originate mainly from a build-up of close contacts between neighbouring pyrrolidine hydrogens (C–H⋯H–C), and in part due to less efficient C–H⋯π interactions in the transition state. Overall, this imposes a much greater energy barrier for a ring inversion to occur (31.7 kJ mol⁻¹), and results in a higher relative energy for the puckered down conformation. This explains why a significant reduction in the energy barrier for C^ord was observed in the isolated molecule (cf.Fig. 2a).

In order to investigate the wider significance of the phenomenon investigated here, we have searched the Cambridge Structural Database (in version 5.41)²⁹ for disordered pyrrolidine rings using the structure on Fig. 1a as the search query. Full details on the analysis can be found in Section 4 of the ESI.† We have identified 179 examples where the pyrrolidine ring exhibits structural disorder, with 20 structures having a Z′ = 2 and a case of contrasting disorder akin to our compound 1a (see Table S3 of the ESI†). Further, pyrrolidine ring inversions are shown to have implications on the structure of proline^26,30,31 and proline-containing peptides.^32,33 Evidently, disorder in pyrrolidine rings is not a rare occurrence, and is likely also in other five-membered rings. Interestingly, while intermolecular interactions have previously been shown to play a role in dynamics,^34–36 their influence has been manifested here as two pseudosymmetric pyrrolidine groups exhibiting distinct dynamics.

In conclusion, the disorder observed in C^dis of compound 1a has been attributed to the occurrence of dynamics in the form of ring inversions with an activation energy of 16 ± 3 kJ mol⁻¹. Despite the pseudosymmetry of the structure (Z′ = 2), ring inversions were only observed for C^dis while C^ord was constrained to torsional librations with an activation energy of 11 ± 2 kJ mol⁻¹. DFT calculations suggest that the constraints on C^ord originate from neighbouring C–H⋯H–C and less effective C–H⋯π intermolecular interactions between 1⋯1 in the transition state and the ring inversion product.

This work was funded by Innovate UK and AstraZeneca (Grant number: KTP11570). We thank Dr G. Whitehead and Dr I. J. Vitorica-Yrezabal at the University of Manchester for X-ray crystallography services, Prof. J. Lewandowski from the University of Warwick for discussions about the NMR relaxation analysis, and Dr R. Storey from AstraZeneca for the DSC results. Data for this study are provided as a supporting data set from WRAP, the Warwick Research Archive Portal at https://wrap.warwick.ac.uk/142932/.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. B. M. Couillaud, P. Espeau, N. Mignet and Y. Corvis, ChemMedChem, 2019, 14, 8–23.
2. R. Censi and P. Di Martino, Molecules, 2015, 20, 18759–18776.
3. S. L. Morissette, S. Soukasene, D. Levinson, M. J. Cima and O. Almarsson, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 2180–2184.
4. E. Pindelska, A. Sokal and W. Kolodziejski, Adv. Drug Delivery Rev., 2017, 117, 111–146.
5. G. A. Monti, A. K. Chattah and Y. G. Linck, Annu. Rep. NMR Spectrosc., 2014, 83, 221–269.
6. P. C. Vioglio, M. R. Chierotti and R. Gobetto, Adv. Drug Delivery Rev., 2017, 117, 86–110.
7. T. Venâncio, L. M. Oliveira, T. Pawlak, J. Ellena, N. Boechat and S. P. Brown, Magn. Reson. Chem., 2019, 57, 200–210.
8. D. C. Apperley, A. F. Markwell, I. Frantsuzov, A. J. Ilott, R. K. Harris and P. Hodgkinson, Phys. Chem. Chem. Phys., 2013, 15, 6422–6430.
9. M. Dračínský and P. Hodgkinson, CrystEngComm, 2013, 15, 8705–8712.
10. G. A. Facey, T. J. Connolly, C. Bensimon and T. Durst, Can. J. Chem., 1996, 74, 1844–1851.
11. R. F. Moran, D. M. Dawson and S. E. Ashbrook, Int. Rev. Phys. Chem., 2017, 36, 39–115.
12. A. S. Tatton, H. Blade, S. P. Brown, P. Hodgkinson, L. P. Hughes, S. O. Nilsson Lill and J. R. Yates, Cryst. Growth Des., 2018, 18, 3339–3351.
13. R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45(suppl 1), S174–S186.
14. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
15. B. Elena, G. Pintacuda, N. Mifsud and L. Emsley, J. Am. Chem. Soc., 2006, 128, 9555–9560.
16. C. M. Widdifield, J. D. Farrell, J. C. Cole, J. A. K. Howard and P. Hodgkinson, Chem. Sci., 2020, 11, 2987–2992.
17. C. M. Widdifield, S. O. Nilsson Lill, A. Broo, M. Lindkvist, A. Pettersen, A. Svensk Ankarberg, P. Aldred, S. Schantz and L. Emsley, Phys. Chem. Chem. Phys., 2017, 19, 16650–16661.
18. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
19. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
20. G. Pfafferott, H. Oberhammer, J. E. Boggs and W. Caminati, J. Am. Chem. Soc., 1985, 107, 2305–2309.
21. K. F. Dziubek and A. Katrusiak, Phys. Chem. Chem. Phys., 2011, 13, 15428–15431.
22. F. A. L. Anet and A. J. R. Bourn, J. Am. Chem. Soc., 1967, 89, 760–768.
23. D. A. Torchia and A. Szabo, J. Magn. Reson., 1982, 49, 107–121.
24. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712.
25. P. A. Beckmann, Phys. Rep., 1988, 171, 85–128.
26. J. Kapitán, V. Baumruk, V. Kopecký Jr, R. Pohl and P. Bour, J. Am. Chem. Soc., 2006, 128, 13451–13462.
27. J. R. Yates, T. N. Pham, C. J. Pickard, F. Mauri, A. M. Amado, A. M. Gil and S. P. Brown, J. Am. Chem. Soc., 2005, 127, 10216–10220.
28. A. Halme, M. J. Quayle, S. O. Nilsson Lill, A. Pettersen, M. Fransson and C. Boissier, Cryst. Growth Des., 2019, 19, 3670–3680.
29. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
30. H. S. Park, B. J. Byun, D. Motooka, K. Kawahara, M. Doi, T. Nakazawa, Y. Kobayashi and Y. K. Kang, Biopolymers, 2012, 97, 629–641.
31. A. Muralidharan, J. R. Schmidt and A. Yethiraj, J. Phys. Chem. B, 2020, 124, 5899–5906.
32. S. K. Sarkar, D. A. Torchia, K. D. Kopple and D. L. VanderHart, J. Am. Chem. Soc., 1984, 106, 3328–3331.
33. M. Sonea, H. Yoshimizub, H. Kurosua and I. Ando, J. Mol. Struct., 1993, 301, 227–230.
34. P. M. J. Szell, S. Zablotny and D. L. Bryce, Nat. Commun., 2019, 10, 916.
35. S. Khazaei and D. Sebastiani, J. Chem. Phys., 2016, 145, 234506.
36. J. Baudry, J. Am. Chem. Soc., 2006, 128, 11088–11093.
37. J. Claudot, W. J. Kim, A. Dixit, H. Kim, T. Gould, D. Rocca and S. Lebègue, J. Chem. Phys., 2018, 148, 064112.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental procedures, equations, and results. See DOI: 10.1039/d0cc05236a

‡ The expected mean absolute error in absolute interaction energies (IE) for PBE-TS calculations is 1.5 kJ mol⁻¹,³⁷ and errors in relative IEs are expected to be even smaller.

---