Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Active learning and neural network potentials accelerate molecular screening of ether-based solvate ionic liquids†
Wujie
Wang
 ,
Tzuhsiung
Yang
,
William H.
Harris
and
Rafael
Gómez-Bombarelli
,
Tzuhsiung
Yang
,
William H.
Harris
and
Rafael
Gómez-Bombarelli
 *
*
Department of Materials Science and Engineering Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02319, USA. E-mail: rafagb@mit.edu
First published on 16th June 2020
Abstract
Solvate ionic liquids (SIL) have promising applications as electrolyte materials. Despite the broad design space of oligoether ligands, most reported SILs are based on simple tri- and tetraglyme. Here, we describe a computational search for complex ethers that can better stabilize SILs. Through active learning, a neural network interatomic potential is trained from density functional theory data. The learned potential fulfills two key requirements: transferability across composition space, and high speed and accuracy to find low-energy ligand-ion poses across configurational space. Candidate ether ligands for Li+, Mg2+ and Na+ SILs with higher binding affinity and electrochemical stability than the reference compounds are identified. Lastly, their properties are related to the geometry of the coordination sphere.
Solvate ionic liquids (SILs) consist of chelated metal cations and small molecular anions. They are synthesized by mixing a salt and a ligand, commonly an oligoether. Prepared in an equimolar ratio, the cation (e.g., Li+, Na+, or Mg2+) and the oligoether form a stable coordination complex where oxygen donors in the ligand coordinate the cation. This results in SILs with better thermal and oxidative stability than the two components alone and high ionic conductivity like a conventional IL. The properties of these SILs can be tuned by adjusting the ligand chemistry.1–4 SILs synthesized with tri- and tetraethylene glycol dimethyl ethers (triglyme (G3) and tetraglyme (G4), respectively) and lithium bis(trifluoromethylsulfonyl)imide (LiTFSI), have been extensively studied in experiments1,3,5,6 and molecular dynamics simulations,7–10 and demonstrate the potential of SILs as a promising alternative to conventional ILs for electrolyte applications. Hence, finding SILs with desired melting temperature, oxidative stability, transport properties and cation-ligand association can advance battery technologies. We screen a combinatorial library of 103 ether molecules seeking to maximize ligand-ion binding energy, the electrochemical stability of the chelate, and the size of the complex. Neural-network-accelerated atomistic simulations allow identifying a number of synthetically accessible ligands with stronger affinities than the baselines and mapping the chemical space of oligoether–ion interactions for SILs (Scheme 1).
An optimal novel SIL ligand would form strongly-coordinated chelates with small hydrodynamic radius and weak ionic interaction to allow high cation transference number, low viscosity, and low melting temperature.2,11 Common salts are typically not dissociative enough to form SILs, which results in the need to use complex and expensive anions such as TFSI.12 New ligands with higher binding affinities than current glymes can enable SILs with less costly – but also less dissociative – anions than TFSI by strongly solubilizing ions. The chemical space of ligands for SILs is vast, even if only ether derivatives are considered, since small variations in alkyl spacers can have large effects on the binding energy. Charting this design space experimentally is slow and costly. Virtual screening allows quantification of the ion-ligand binding energy with accurate ab initio simulations by identifying the ligand-ion pose with the lowest energy and comparing with the energies of free ligand and ion.13
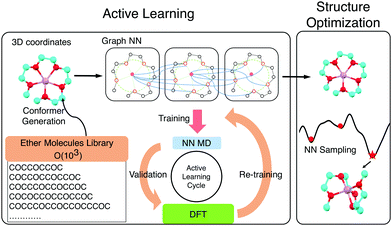
The exhaustive configurational sampling needed to evaluate every ion and ligand pair is computationally demanding, because the ion-ligand potential energy surface (PES) has many local minima. Algorithms such as simulated annealing or seeding gradient-based optimization from different random guesses can perform such global optimization but are typically too costly to be combined with quantum chemical methods. Classical force fields are possible alternatives to the expensive ab initio methods for sampling. However, they describe electrostatic interactions poorly and struggle to capture the interactions between ions and lone pairs. This results in inaccurate structure guesses which, in the best case, require extensive refinement with, and in the worse case, do not correspond with the global minimum of the quantum chemical PES. In order to combine higher accuracy and fast sampling, we trained neural network (NN) interatomic potentials based on graph convolutions (GC)14,15 using density functional theory (DFT) energies and atomic forces for a set of reference chemistries. An active learning (AL) strategy was used to acquire training data efficiently by carrying out DFT only on areas with high model uncertainty.16,17
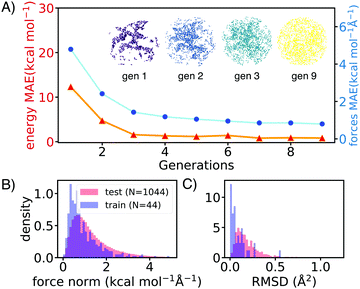
AL augments the data space and automatically improves the model by iteratively acquiring training data and deploying molecular dynamics (MD) simulations with the learned potential. Additional DFT simulations are carried out on points in the trajectory for which the model is uncertain. CGNN models trained with this approach showed high accuracy both in terms of energies and forces at the end of the AL loop, and also in predicting converged ion-binding structures that agree with the DFT refined ones (Fig. 1).
The screened library enumerates over 1000 linear and branched oligoethers with methyl and/or ethyl capping groups, alkyl spacers of length one to five, and up to six ether oxygens. A reference dataset of 44 oligoethers was used for training. Starting geometries were obtained using RDKit,18 followed by DFT optimizations at BP86-D3/def2-SVP level of theory using ORCA,19 and augmented with randomly-generated ion–molecule poses. Normal mode sampling of each DFT-optimized configuration was performed at 500 K to obtain non-equilibrium geometries, upon which energy and gradient calculations were performed. This produced an initial training set of around 5000 geometries. The first generation of GCNN was trained on these energy and gradient values. Constant-energy NN MD runs were then performed for 10–200 ps to explore the configurational space. The predicted energies and forces at a fraction of frames were then validated by DFT calculations and added to the training data for a new model. The procedure was repeated until the accuracy of forces and energies converged. Fig. 1 shows the improvements in force and energy accuracy for all generations of NN models trained on Li–oligoethers chemical space. After several rounds of training, the resulting NN model for Li–ether complexes shows accurate energy (0.83 kcal mol−1) and force predictions (0.50 kcal mol−1 Å−1) on newly-sampled poses from NN MD. At the end of learning cycle the training set was composed of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 763 geometries. To understand how AL helps explore configurational space, we performed t-distributed stochastic neighbor embedding (t-SNE) analysis20 on SOAP fingerprints21 of NN-generated configurations and colored the data by generations (Fig. 1A). The configurations in the 1st generation do not cover enough configurational space and hence showed poor performance when the learned potential is used to run MD (Fig. 1A). As the evolution progresses, the diversity in configurational space was systematically improved in keeping with the validation accuracy of the model.
763 geometries. To understand how AL helps explore configurational space, we performed t-distributed stochastic neighbor embedding (t-SNE) analysis20 on SOAP fingerprints21 of NN-generated configurations and colored the data by generations (Fig. 1A). The configurations in the 1st generation do not cover enough configurational space and hence showed poor performance when the learned potential is used to run MD (Fig. 1A). As the evolution progresses, the diversity in configurational space was systematically improved in keeping with the validation accuracy of the model.
We then applied the trained NN models to sample and optimize the conformations of more than 1000 oligoethers with each of the three cations. The NN-optimized geometries are shown to be close to equilibrium geometries which are obtained with DFT refinements at BP86-D3/def2-SVP level of theory, as shown in small forces and RMSD (Fig. 1B). The low-energy geometries were refined using a long-range-corrected hybrid DFT functional, wB97X-D3/def2-TZVP.21 We first applied our workflow on well-studied crown ether binding with Li+ and Na+. It was found that the calculated binding energies correlate well with experimental data measured in gas-phase and correlate reasonably with solvent data (see Table S2, ESI†). The [Li-18C6]+ crown ether–lithium complexes form SILs2 with [TFSI]−,22 but show varied binding behaviors across solvents.23,24 DFT calculations of the binding energy of [Li-18C6] in organic solvents predict weak binding, despite its known ability to form SILs. Hence, we primarily utilize gas-phase DFT results as a proxy for the binding affinity of oligo–ethers in SILs.
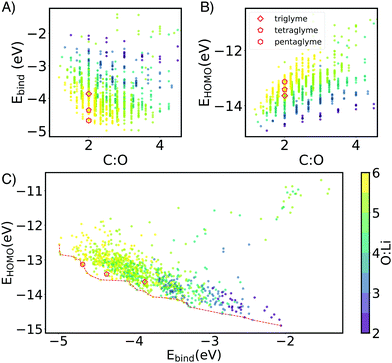
Through this NN-accelerated virtual screening workflow for ion-ligand complexes, we identified synthetic targets that have stronger binding strength than and comparable oxidative stability to the state-of-the-art G3 and G4 ligands. A few selected complexes from our screened molecules, shown in Fig. 2, are predicted to be more stable than Li(G3)+ and Li(G4)+ baseline molecules by 0.2–0.3 eV while maintaining a similar EH level.
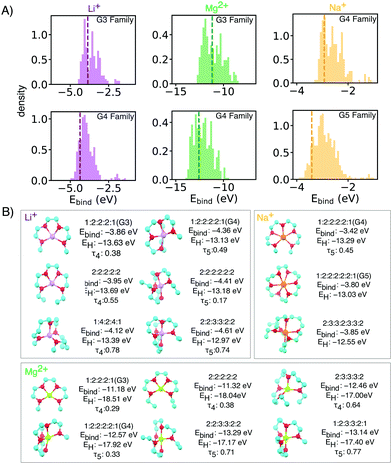 | ||
| Fig. 2 (A) Binding energy distributions and (B) selected symmetrical structures from DFT optimization (w-B97xD3/def2-TZVP) that demonstrate stronger binding energy than baselines for each glyme families of interests with different ion. Some asymmetrical oligoethers may have superior properties, but are likely less synthetically accessible, and thus reported in the ESI.† In the X:X:X:X short notation,: represents the oxygen and X is the number of carbons spacers or caps. Dashed vertical lines mark the energy of baseline glyme molecules (G3, G4 or G5). | ||
Li+ binding can be improved by increasing the number of oxygen atoms and by increasing spacer length (Fig. 3). The longer carbon spacers facilitate the arrangement of oxygen atoms around the ion and therefore to the formation of favorable oxygen coordination structures. In particular, having 3-C spacers is beneficial because it contributes to the formation of a six membered-ring with low strain energy.25 Linear energy decomposition analysis suggests that larger rings contribute more to the binding energy (Fig. S5 in ESI†). This hypothesis is further supported by geometrical analysis using τ, an index ranging from 0 to 1 that captures the deviation from an ideal coordination structure, a value of 1 corresponding to the lowest-energy coordination structure (tetrahedral and bi-pyramidal for 4- and 5-coordinated structures respectively).26 Strongly-binding ethers have high τ4 and τ5. In comparison, the baseline G3 and G4 complexes are closer to square planar (4-coordination) and square pyramidal (5-coordination) geometries, resulting form the constraints imposed by the short spacers.
Because the hydrodynamic radius of SIL complexes is related to their self-diffusion,27 and hence to their conductivity, we have estimated the solvent-excluded volume of the converged ion-ligand complexes using a spherical probe with radius 1.9 A. Fig. S6 in ESI† reports how the larger ethers, which usually have higher affinities, are bulkier and might be more viscous.
The HOMO level of the complex was used as a surrogate for oxidative stability (ESI,† Fig. S7 reports the correlation between ionization potential and HOMO levels). As shown in Fig. 3B and C the predicted stability follows the opposite trend to binding energy: as the length of the spacers increases, HOMO values become less negative (less oxidatively stable). This compensation effect between binding strength and oxidative stability is reflected in Fig. 2C. The Pareto front of HOMO and Ebind traces the line connecting all the optimal points, so that one property cannot be improved without sacrificing the other. Interestingly G3 and G4 form SILs but are not on the Pareto for Li+ which suggests that it is possible to improve over them in both binding and stability. G5 lies on the Pareto front, but is known not form a SIL in experiments.
Batteries based on sodium and magnesium are promising and earth-abundant alternatives for lithium, but they lack effective and stable electrolytes, so a similar analysis was performed for Mg2+ and Na+ complexes. Fig. S4 (ESI†) reports the Ebind and HOMO level for Mg2+ and Na+ complexes. The trends about spacers are similar to Li+, although in the case of Mg2+, the number of ether oxygen atoms is a more dominating factor regardless of spacer. Interestingly, for both Mg2+ and Na+, G3, G4 and G5 lie on the Pareto front of HOMO and Ebind, implying that increased binding would come at cost in stability, and vice versa, for any of the other Pareto-optimal oligoether we have identified.
Mg2+ has a similar ionic radius as Li+ and thus the proposed ligands for Li+ are also good candidates for Mg2+ SILs. Top candidates have more than 1 eV improvement in binding energy over reference glymes. Mg2+ complexes we calculated to have very deep HOMO levels due to the double positive charges (Fig. S5A, ESI†). However, due to stronger electrostatic interactions, [Mg(Glyme)](TFSI) has very high melting points which hinder its use at room temperature.28 Our proposed molecular libraries include side chain modifications and bulkier capping alkyl groups which can be used to tune SIL melting temperature by increasing van der Waals interactions. Such design strategies have proven effective for tuning the melting temperature and viscosity of conventional ionic liquids,29 [Mg(Glyme)](TFSI)228 and [Li(Glyme)](TFSI).11 Selected geometries with side akyl groups for Mg2+ ether complexes which have high binding energies in are reported in the ESI† (Fig. S2).
Experiments show relatively weaker binding in Na[Glyme]+ than the smaller lithium ion. This results in higher presence of uncoordinated glymes which compromise the stability of the electrolytes.30 Our simulations are in keeping, the larger radius of sodium ions results in weaker ion–dipole interactions and lower affinity than Li+ by about 1 eV. We thus focused on potential candidates from the G4 and G5 families (Fig. 2), and observed relatively minor improvement over the baseline.
Design of optimal ligands for a desired ion requires exploring a complex compositional and configurational design space. By combining fast and transferable machine learning with accurate DFT simulations through active learning, over 1000 candidate oligoethers have been evaluated as ligands for Li+, Mg2+ and Na+ SILs. The tradeoff between affinity, electrochemical stability and size have been charted, and candidate ethers with better predicted properties than the baseline compounds have been identified.
The authors thank Bo Qiao for insightful discussions and providing helpful comments. W. W. thanks the Toyota Research Institute, T. Y. thanks Sumitomo Chemical, and W. H. thanks the MIT Energy Initiative for financial support. The computations in this paper were executed at the Massachusetts Green High-Performance Computing Center with support from MIT Research Computing.
Data availability
The training data and optimized geometries are available for download at https://github.com/learningmatter-mit/MLElectrolytes.Conflicts of interest
There are no conflicts to declare.Notes and references
- K. Ueno, K. Yoshida, M. Tsuchiya, N. Tachikawa, K. Dokko and M. Watanabe, J. Phys. Chem. B, 2012, 116, 11323–11331 CrossRef CAS PubMed.
- T. Mandai, K. Yoshida, K. Ueno, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2014, 16, 8761–8772 RSC.
- K. Ueno, R. Tatara, S. Tsuzuki, S. Saito, H. Doi, K. Yoshida, T. Mandai, M. Matsugami, Y. Umebayashi, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2015, 17, 8248–8257 RSC.
- H. M. Kwon, M. L. Thomas, R. Tatara, A. Nakanishi, K. Dokko and M. Watanabe, Chem. Lett., 2017, 46, 573–576 CrossRef CAS.
- K. Yoshida, M. Nakamura, Y. Kazue, N. Tachikawa, S. Tsuzuki, S. Seki, K. Dokko and M. Watanabe, J. Am. Chem. Soc., 2011, 133, 13121–13129 CrossRef CAS PubMed.
- K. Dokko, N. Tachikawa, K. Yamauchi, M. Tsuchiya, A. Yamazaki, E. Takashima, J.-W. Park, K. Ueno, S. Seki, N. Serizawa and M. Watanabe, J. Electrochem. Soc., 2013, 160, A1304–A1310 CrossRef CAS.
- Y. Sun and I. Hamada, J. Phys. Chem. B, 2018, 122, 10014–10022 CrossRef CAS PubMed.
- A. Thum, A. Heuer, K. Shimizu and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2020, 22, 525–535 RSC.
- W. Shinoda, Y. Hatanaka, M. Hirakawa, S. Okazaki, S. Tsuzuki, K. Ueno and M. Watanabe, J. Chem. Phys., 2018, 148, 193809 CrossRef PubMed.
- M. Callsen, K. Sodeyama, Z. Futera, Y. Tateyama and I. Hamada, J. Phys. Chem. B, 2017, 121, 180–188 CrossRef CAS PubMed.
- T. Tamura, K. Yoshida, T. Hachida, M. Tsuchiya, M. Nakamura, Y. Kazue, N. Tachikawa, K. Dokko and M. Watanabe, Chem. Lett., 2010, 39, 753–755 CrossRef CAS.
- M. Huang, S. Feng, W. Zhang, J. Lopez, B. Qiao, R. Tatara, L. Giordano, Y. Shao-Horn and J. A. Johnson, Chem. Mater., 2019, 31, 7558–7564 CrossRef CAS.
- B. Qiao, S. Mohapatra, J. Lopez, G. Leverick, R. Tatara, Y. Shibuya, Y. Jiang, A. France-Lanord, J. C. Grossman, R. Gómez-Bombarelli, J. Johnson and Y. Shao-Horn, ChemRxiv, 2020 DOI:10.26434/CHEMRXIV.12152820.V1.
- D. K. Duvenaud, D. Maclaurin, J. Aguilera-Iparraguirre, R. Gómez-Bombarelli, T. Hirzel, A. Aspuru-Guzik and R. P. Adams, Advances in Neural Information Processing Systems, 2015, pp. 2215–2223 Search PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. J. Kindermans, A. Tkatchenko and K.-R. R. Müller, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- S. J. Ang, W. Wang, D. Schwalbe-Koda, S. Axelrod and R. Gomez-Bombarelli, ChemRxiv, 2020 DOI:10.26434/CHEMRXIV.11910948.V1.
- RDKit: Open-source cheminformatics, http://www.rdkit.org, [Online; accessed 05-June-2020].
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- L. Van Der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- R. E. Dillon and D. F. Shriver, Chem. Mater., 1999, 11, 3296–3301 CrossRef CAS.
- A. R. Fakhari and M. Shamsipur, J. Inclusion Phenom. Mol. Recognit. Chem., 1996, 26, 243–251 CrossRef CAS.
- J. D. Lin and A. I. Popov, J. Am. Chem. Soc., 1981, 103, 3773–3777 CrossRef CAS.
- T. Dudev and C. Lim, J. Am. Chem. Soc., 1998, 120, 4450–4458 CrossRef CAS.
- L. Yang, D. R. Powell and R. P. Houser, J. Chem. Soc., Dalton Trans., 2007, 955–964 RSC.
- J. M. Slattery, C. Daguenet, P. J. Dyson, T. J. Schubert and I. Krossing, Angew. Chem., Int. Ed., 2007, 46, 5384–5388 CrossRef CAS PubMed.
- K. Hashimoto, S. Suzuki, M. L. Thomas, T. Mandai, S. Tsuzuki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2018, 20, 7998–8007 RSC.
- S. Murray, R. O'Brien, K. Mattson, C. Ceccarelli, R. Sykora, K. West and J. Davis, Angew. Chem., Int. Ed., 2010, 49, 2755–2758 CrossRef CAS PubMed.
- P. Geysens, V. S. Rangasamy, S. Thayumanasundaram, K. Robeyns, L. Van Meervelt, J. P. Locquet, J. Fransaer and K. Binnemans, J. Phys. Chem. B, 2018, 122, 275–289 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc03512b |
| This journal is © The Royal Society of Chemistry 2020 |