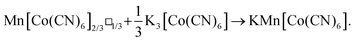Open Access Article
Open Access ArticleFilling vacancies in a Prussian blue analogue using mechanochemical post-synthetic modification†
John
Cattermull
a,
Samuel
Wheeler
b,
Kevin
Hurlbutt
b,
Mauro
Pasta
 b and
Andrew L.
Goodwin
b and
Andrew L.
Goodwin
 *a
*a
aDepartment of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford OX1 3QR, UK. E-mail: andrew.goodwin@chem.ox.ac.uk; Tel: +44 (0)1865 272137
bDepartment of Materials, University of Oxford, Parks Road, Oxford OX1 3PH, UK
First published on 4th June 2020
Abstract
Mechanochemical grinding of polycrystalline powders of the Prussian blue analogue (PBA) Mn[Co(CN)6]2/3□1/3·xH2O and K3Co(CN)6 consumes the latter and chemically modifies the former. A combination of inductively-coupled plasma and X-ray powder diffraction measurements suggests the hexacyanometallate vacancy fraction in this modified PBA is reduced by approximately one third under the specific conditions we explore. We infer the mechanochemically-driven incorporation of [Co(CN)6]3− ions onto the initially-vacant sites, coupled with intercalation of charge-balancing K+ ions within the PBA framework cavities. Our results offer a new methodology for the synthesis of low-vacancy PBAs.
Prussian blue analogues (PBAs) are an important and topical family of battery materials with a number of considerable advantages over longer-established charge storage systems.1–3 On the one hand, they are chemically versatile, inexpensive, and easily made by aqueous precipitation from widely-available precursors. And, on the other hand, PBA electrochemistry is characterised by a combination of high specific capacity for Na+/K+ insertion, rapid charge/discharge rates, and long cycle lives.4
One key limitation of PBA chemistry as battery materials is the remarkably strong tendency for vacancy incorporation within the PBA structure.5,6 Whilst hexacyanometallate vacancies help improve structural stability and increase bulk ionic conductivity, their presence reduces specific capacity.4 Increasing energy density therefore requires synthetic routes that minimise vacancies.7
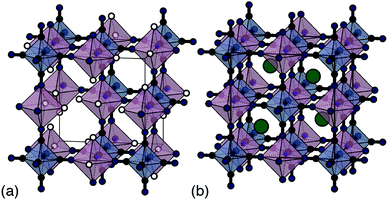
Traditional PBA synthesis routes usually yield samples with nominal compositions M[M′(CN)6]2/3□1/3·xH2O (here M and M′ are di- and trivalent transition-metal cations, respectively, and the symbol □ represents a M′-site vacancy).8 The corresponding structure is based on the simple cubic lattice; M2+ and [M′(CN)6]3− species decorate alternate sites with one third of the hexacyanometallate sites occupied by coordinated and zeolitic water [Fig. 1(a)].5 While vacancies increase ionic conductivity9 and can even help stabilise the structure during electrochemical cycling,10 their presence limits charge capacity. From an electrochemical perspective, the ideal PBA composition is instead the non-defective system AM[M′(CN)6] (A = monovalent alkali metal cation) because there is now scope for two separate one-electron processes—e.g. M(III)[M′(III)(CN)6] ⇌ AM(II)[M′(III)(CN)6] ⇌ A2M(II)[M′(II)(CN)6]—and hence a much improved theoretical charge-storage capacity [Fig. 1(b)].11
The two most widely-employed approaches for reducing vacancy concentrations are to bias crystallisation with large excesses of alkali cation12 and/or to employ chelating agents (e.g. citrate) to slow down precipitation kinetics.13,14 Both types of approach involve considerable precursor waste, which is an important consideration in scale-up. Moreover they have proven to be successful only for the synthesis of PBAs in their fully reduced state.12 Consequently there is strong interest in developing alternative approaches to vacancy reduction in this family.4
Influenced by the use of mechanochemistry to allow post-synthetic metallation of a variety of porous frameworks,15–17 and also its recent application to PBA synthesis,18–20 we sought to establish whether the technique might help reduce the vacancy fraction in PBAs. Our reasoning was that the success of chelation strategies13,14 implies vacancies are largely a kinetic—rather than thermodynamic—phenomenon in PBAs, and so milling may provide an atom-efficient methodology for overcoming the kinetic barrier to ion incorporation. A mechanochemical approach would also offer a scalable21 and green22 alternative for vacancy reduction in PBAs.
We synthesised polycrystalline samples of the canonical PBA Mn[Co(CN)6]2/3·xH2O following the approach of ref. 6 and 23. This particular PBA has the dual advantages of high M-site lability (high-spin d5 configuration of Mn2+)—which we expected to facilitate structural reorganisation in the solid-state—and an inert M′-site configuration (Co3+, low-spin d6) to avoid unwanted side-reactions during milling. By virtue of these choices, this proof-of-concept system is not itself a viable cathode material; nevertheless we anticipate any demonstration of control over vacancy fractions in this canonical material will motivate further studies on electrochemically-active PBAs. Stoichiometric quantities of Mn[Co(CN)6]2/3·xH2O and K3[Co(CN)6] were loaded within a ball-mill, and the mixture milled for up to three hours. The reaction we hoped to effect is given by the (idealised) scheme
Small fractions of the reaction mixture were removed at successive time intervals to allow interrogation of the PBA composition as a function of milling time.
Inductively-coupled plasma (ICP) measurements of these milled samples gave the compositional variation shown in Fig. 2(a), where we plot the Co/Mn ratio ϕ = f(Co)/f(Mn). Note that, in preparing our samples for ICP analysis, we removed any remaining K3[Co(CN)6] through washing, and digested the insoluble PBA in a nitric acid solution. Our focus is on Mn and Co compositions, since ICP analysis of K content is notoriously unreliable.7 We infer K content on the basis of charge-balance. For the as-prepared sample, ϕ = 0.700(17), which suggests the initial composition was K0.10Mn[Co(CN)6]0.70□0.30·xH2O. Milling increases the value of ϕ such that after three hours ϕ = 0.80(3); the PBA composition is now K0.40Mn[Co(CN)6]0.80□0.20·xH2O. The evolution of ϕ with milling time t is well fit by the simple expression
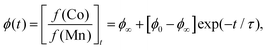 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2).
2).
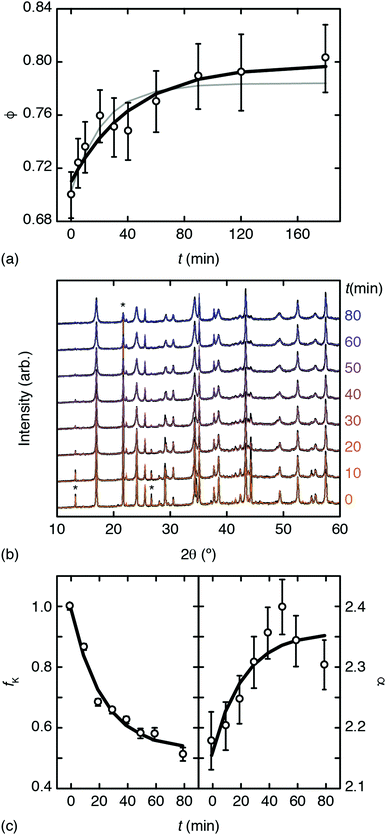 | ||
| Fig. 2 Evidence for mechanochemical vacancy filling in Mn[Co(CN)6]2/3. (a) Variation in Co/Mn ratio with milling time as determined using ICP. The bold line shows the fit to data obtained using eqn (1); the fine grey line is the corresponding fit when all data sets are included. (b) PXRD traces (black lines) and fits (coloured lines) for milled samples; successive curves are shifted vertically by a constant amount. Three reflections associated with K3[Co(CN)6] are marked with an asterisk. (c) Phase fractions and intensity ratios extracted from (b) as discussed in the text. The bold lines show the fit-to-data using eqn (1). | ||
Powder X-ray diffraction (PXRD) measurements also support this interpretation. We carried out a new set of milling experiments under identical conditions but focussing on the initial 80 minutes. Again we extracted small fractions of the reaction mixture throughout milling at intervals of 10 minutes up to one hour, and after 80 minutes. The PXRD patterns collected for these fractions (Cu Kα radiation) evolved smoothly as a function of milling time [Fig. 2(b)]. In particular, we observed a monotonic decrease in the intensities of reflections associated with K3[Co(CN)6]. In order to quantify this point we carried out a combination of Pawley and Rietveld refinements. We used the former to model the PBA component (so as not to presume its composition) and the latter for K3[Co(CN)6] (and an Al2O3 standard); full details are given as ESI,† including discussion of our treatment of preferred orientation effects and of peak broadening. By fixing the relative intensities assigned to the PBA reflections we refined a corresponding phase scale factor fPBA for each data set. The evolution of the relative K3[Co(CN)6] scattering fraction fK is then given by
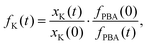 | (2) |
But there is direct evidence too from PXRD reflection intensities of incorporation of K+ and [Co(CN)6]3− within the PBA structure. The ratio
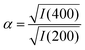 | (3) |
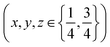 increases the strength of the former type relative to that of the latter. Fixing the PBA scale factors fPBA as above and allowing the reflection intensities to refine, we can determine the experimental variation in α with milling time [right-hand panel of Fig. 2(c)]. While the uncertainty in α is not small, we nonetheless observe the expected trend: namely, that its value increases with milling time, consistent with intercalation of K+. For completeness, we note that we also notice a systematic variation in PBA lattice parameter accompanying intercalation (see ESI† for further discussion).4,24
increases the strength of the former type relative to that of the latter. Fixing the PBA scale factors fPBA as above and allowing the reflection intensities to refine, we can determine the experimental variation in α with milling time [right-hand panel of Fig. 2(c)]. While the uncertainty in α is not small, we nonetheless observe the expected trend: namely, that its value increases with milling time, consistent with intercalation of K+. For completeness, we note that we also notice a systematic variation in PBA lattice parameter accompanying intercalation (see ESI† for further discussion).4,24
Taking together our ICP and PXRD results, we carried out a collective empirical fit of all our data using the functional form of eqn (1) with a common characteristic time-scale τ. These collective fits are shown in Fig. 2(a and c); their consistency implies that the observed trends in chemical composition, phase fractions, and diffraction intensities arise from a single common process. Hence we conclude there is evidence for mechanochemical insertion of K3[Co(CN)6] into this PBA, that involves simultaneous filling of hexacyanocobaltate vacancies and intercalation of K+ cations.
Of course our analysis does not shed light on the mechanism of this filling process. That—under the conditions we study here—the limiting fraction of vacancies is non-zero suggests an inhomogeneous distribution of filled vacancies in the PBA component of our mixture. A reasonable hypothesis is that hexacyanometallate migration in the solid-state is itself facilitated by M′-site vacancies, such that filling inhibits further reaction. In such a scenario, one expects the interior of PBA particles to remain defective as their surfaces react. With this in mind, increasing milling rate may allow a reduction in particle size that in turn translates to higher filling fractions. Our very preliminary measurements have at least found that reducing milling rate does indeed reduce both peak broadening and vacancy filling (see ESI†)—and so this is an obvious avenue for further investigation. Porosity measurements—which are notoriously difficult to interpret for PBAs25,26 as a result of their complex and varied pore networks6,27—may nonetheless provide useful additional insight into vacancy filling. Likewise we cannot yet say definitively whether hexacyanometallate anion incorporation is limited to the M′ site, or whether intercalation on the A-site is also possible, such as has been observed for complex ions in the related thiocyanate PBAs.28
In the context of optimising PBA-based battery materials a number of obvious follow-up experiments must now be carried out. First, it is important to show that vacancy filling in redox-active PBAs is possible (our own preliminary study of Mn[Fe(CN)6]2/3 suggests it may be; see ESI†). Second, the vacancy filling fraction should be maximised by varying milling rate, exploiting ion and liquid assisted grinding approaches,22,29,30 controlling the degree of PBA hydration, and/or pre-milling reagents. And, third, the crucial link to electrochemical performance remains to be made. Other variations on the theme may also be possible, such as milling with varying A3[M(CN)6] salts to generate multivariate PBAs.31,32 Our key result here, of course, has been to demonstrate that post-synthetic control over vacancy fraction is at least possible in PBAs using a mechanochemical approach. The exploitation of mechanochemistry in post-synthetic modification of this type remains somewhat under-explored,33 and a broader implication of our work is that similar control over vacancy fractions in other porous materials (e.g. metal–organic frameworks34,35) may now be possible.
The authors gratefully acknowledge funding from the E. R. C. to A. L. G. (Grant 788144) and the John Fell Oxford University Press Research Fund to M. P.
Conflicts of interest
There are no conflicts to declare.References
- J. Qian, C. Wu, Y. Cao, Z. Ma, Y. Huang, X. Ai and H. Yang, Adv. Energy Mater., 2018, 8, 1702619 CrossRef.
- Y. Xu, S. Zheng, H. Tang, X. Guo, H. Xue and H. Pang, Energy Storage Mater., 2017, 9, 11–30 CrossRef.
- B. Wang, Y. Han, X. Wang, N. Bahlawane, H. Pan, M. Yan and Y. Jiang, iScience, 2018, 3, 110–133 CrossRef CAS PubMed.
- K. Hurlbutt, S. Wheeler, I. Capone and M. Pasta, Joule, 2018, 2, 1950–1960 CrossRef CAS.
- A. Ludi, H.-U. Güdel and M. Ruegg, Inorg. Chem., 1970, 9, 2224–2227 CrossRef CAS.
- A. Simonov, T. De Baerdemaeker, H. L. B. Boström, M. L. Ros Gómez, H. J. Gray, D. Chernyshov, A. Bosak, H.-B. Bürgi and A. L. Goodwin, Nature, 2020, 578, 256–260 CrossRef CAS PubMed.
- S. Wheeler, I. Capone, S. Day, C. Tang and M. Pasta, Chem. Mater., 2019, 31, 2619–2626 CrossRef CAS.
- A. G. Sharpe, The Chemistry of Cyano Complexes of the Transition Metals, Academic Press, London, 1976 Search PubMed.
- Y. Moritomo, K. Igarashi, J. Kim and H. Tanaka, Appl. Phys. Express, 2009, 2, 085001 CrossRef.
- Y. Kurihara, Y. Matsuda and Y. Moriotomo, Jpn. J. Appl. Phys., 2013, 52, 017301 CrossRef.
- X. Wu, C. Wu, C. Wei, L. Hu, J. Qian, Y. Cao, X. Ai, J. Wang and H. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 5393–5399 CrossRef CAS PubMed.
- Y. Moritomo, Y. Kurihara, T. Matsuda and J. Kim, J. Phys. Soc. Jpn., 2011, 80, 8–11 Search PubMed.
- R. Chen, Y. Huang, M. Xie, Z. Wang, Y. Ye, L. Li and F. Wu, ACS Appl. Mater. Interfaces, 2016, 8, 31669–31676 CrossRef CAS PubMed.
- C. Li, R. Zang, P. Li, Z. Man, S. Wang, X. Li, Y. Wu, S. Liu and G. Wang, Chem. – Asian J., 2018, 13, 342–349 CrossRef CAS PubMed.
- Y. Neinska, C. Minchev, R. Dimitrova, N. Micheva, V. Minkov and V. Kanazirev, Stud. Surf. Sci. Catal., 1994, 84, 989–996 CrossRef CAS.
- H. Ali-Moussa, R. N. Amador, F. Martinez, F. Lamaty, M. Carboni and X. Bantreil, Mater. Lett., 2017, 197, 171–174 CrossRef CAS.
- M. D. Marquez-Medina, S. Mhadmhan, A. M. Balu, A. A. Romero and R. Luque, ACS Sustainable Chem. Eng., 2019, 7, 9537–9543 CrossRef CAS.
- Y. Sun, C. Liu, J. Xie, D. Zhuang, W. Zheng and X. Zhao, New J. Chem., 2019, 43, 11618–11625 RSC.
- W. Gong, M. Wan, R. Zeng, Z. Rao, S. Su, L. Xue, W. Zhang and Y. Huang, Energy Technol., 2019, 7, 1900108 CrossRef.
- W. Gong, R. Zeng, S. Su, M. Wan, Z. Rao, L. Xue and W. Zhang, J. Nanopart. Res., 2019, 21, 274 CrossRef CAS.
- D. E. Crawford, C. K. G. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Green Chem., 2017, 19, 1507–1518 RSC.
- S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2012, 41, 413–447 RSC.
- J. Song, L. Wang, Y. Lu, J. Liu, B. Guo, P. Xiao, J.-J. Lee, X.-Q. Yang, G. Henkelman and J. B. Goodenough, J. Am. Chem. Soc., 2015, 137, 2658–2664 CrossRef CAS PubMed.
- C. D. Wessells, R. A. Huggins and Y. Cui, Nat. Commun., 2011, 2, 550 CrossRef PubMed.
- S. S. Kaye and J. R. Long, J. Am. Chem. Soc., 2005, 127, 6506–6507 CrossRef CAS PubMed.
- R. Roque-Malherbe, F. Lugo and R. Polanco, Appl. Surf. Sci., 2016, 385, 360–367 CrossRef CAS.
- S. S. Kaye and J. R. Long, Catal. Today, 2007, 120, 311–316 CrossRef CAS.
- M. J. Cliffe, E. N. Keyzer, A. D. Bond, M. A. Astle and C. P. Grey, Chem. Sci., 2020, 11, 4430–4438 RSC.
- T. Friščić, S. L. Childs, S. A. A. Rizvi and W. Jones, CrystEngComm, 2009, 11, 418–426 RSC.
- T. Friščić, D. G. Reid, I. Halasz, R. S. Stein, R. E. Dinnebier and M. J. Duer, Angew. Chem., Int. Ed., 2010, 49, 712–715 CrossRef PubMed.
- M. Pasta, R. Y. Wang, R. Ruffo, R. Qiao, H.-W. Lee, B. Shyam, M. Guo, Y. Wang, L. A. Wray, W. Yang, M. F. Toney and Y. Cui, J. Mater. Chem. A, 2016, 4, 4211–4223 RSC.
- C. D. Wessells, M. T. McDowell, S. V. Peddada, M. Pasta, R. A. Huggins and Y. Cui, ACS Nano, 2012, 6, 1688–1694 CrossRef CAS PubMed.
- V. Valtchev, G. Majano, S. Mintova and J. Pérez-Ramrez, Chem. Soc. Rev., 2013, 42, 263–290 RSC.
- H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525–10532 CrossRef CAS PubMed.
- M. J. Cliffe, W. Wan, X. Zou, P. A. Chater, A. K. Kleppe, M. G. Tucker, H. Wilhelm, N. P. Funnell, F.-X. Coudert and A. L. Goodwin, Nat. Commun., 2014, 5, 4176 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cc02922j |
| This journal is © The Royal Society of Chemistry 2020 |