Nickel(II)-methyl complexes adopting unusual seesaw geometries†
Ethan A.
Hill‡
,
Norman
Zhao‡
 ,
Alexander S.
Filatov
,
Alexander S.
Filatov
 and
John S.
Anderson
and
John S.
Anderson
 *
*
Department of Chemistry, The University of Chicago, 5735 S. Ellis Ave, Chicago, IL 60637, USA. E-mail: jsanderson@uchicago.edu
First published on 22nd January 2020
Abstract
We report four-coordinate nickel(II)-methyl complexes of tris-carbene borate ligands which adopt rare seesaw geometries. Experimental and computational results suggest the structural distortion from threefold symmetry results from a combination of electronic stabilization of the singlet state, strong field donors, and constrained angles from the chelating ligand.
Nickel-alkyl complexes have been invoked as important intermediates in a host of chemical transformations including the production of acetic acid and cross-coupling reactions.1–6 In all reported examples of crystallographically characterized Ni(II)-methyl complexes, a diamagnetic, square planar geometry is observed and many attempts to synthesize such species in other, four-coordinate geometries have proven unsuccessful frequently leading to reduction or other degradation.7–11 Despite this, catalytically active Ni(II)-alkyl species may likely exhibit or transition through different coordination geometries.12–14 For example, other synthetic Ni(II) complexes can be found in tetrahedral geometries in addition to the more common square planar geometries. While a square planar geometry is favored due to electronic stabilization of the d8 Ni(II) ion, a tetrahedral geometry may be favored with suitably bulky or chelating ligands.15
An alternative geometry for four-coordinate metal centers that has rarely been observed is a seesaw geometry. In fact, only a handful of examples of Ni(II) complexes in this geometry have been reported.13,16–18 In these cases, steric bulk is used to enforce the desired geometry. For example, the first of these reported by Bröring and co-workers utilized a tripyrranato ligand which positions methyl substituents within the square plane, forcing halide ligands above this plane.19–21 Other examples include those by Gossage and Baruah where homoleptic complexes of Ni(II) were synthesized with bulky propan-2-ylidene and oxazoline substituents that prevent planarization of the Ni(II) coordination environment.14,22 Another recent example of a seesaw geometry at a Ni(II) center involves a diisopropylpyrazole-substituted carbazole ligand to enforce steric crowding of the square plane.13 Finally, an example of a ligand-constrained geometry around a Ni(II) center can be seen in a complex bound to a triphosphacyclododecane ligand.23 This ligand binds in a facial manner with strongly donating trialkylphosphines which are proposed to enforce a low-spin state at nickel. Due to the constrained ligand environment, the coordination geometry distorts to accommodate the low-spin state but cannot fully isomerize to a square planar geometry. These examples demonstrate the lengths required to enforce this geometry at a d8 Ni(II) center.
We have been interested in exploring the chemistry of late transition metals supported by chelating and strongly donating tris-N-heterocyclic carbene (NHC) borate scaffolds.24,25 These ligand scaffolds typically enforce a pseudo-tetrahedral geometry, but also favor low-spin states due to the strong donor properties of the carbene ligands. These factors suggest that Ni(II) complexes supported by this ligand would have geometric frustration between an electronically preferred square planar geometry and a chelate-enforced pseudo-tetrahedral geometry. We therefore rationalized that Ni(II) complexes of this ligand with suitably strong ligand fields might display unusual geometries and electronic structures.26–28 Here we report the isolation and characterization of two Ni(II)-methyl complexes supported by a strongly donating tris-carbene borate ligand which display unusual seesaw geometries.
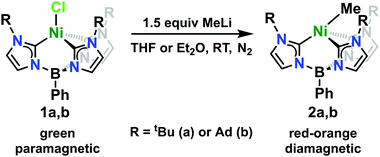
The Ni(II)-chloride complexes were first synthesized by initial deprotonation of the proligand, [PhB(RImH)3][OTf]2 (where R = tBu or Ad), with in situ generated lithium diisopropylamide (LDA) followed by metalation with tetraethylammonium tetrachloronickelate ([Et4N]2[NiCl4]) to yield PhB(tBuIm)3NiCl and PhB(AdIm)3NiCl (1a and 1b) in low but synthetically viable yields (see ESI†). The title complexes, PhB(tBuIm)3NiMe and PhB(AdIm)3NiMe (2a and 2b), were synthesized by treatment of the Ni(II)-chloride complexes 1a and 1b with a solution of methyllithium following a similar reported procedure for related complexes of cobalt (Scheme 1).29 Complexes 2a and 2b can be isolated as red, microcrystalline solids in good yield. These complexes are thermally unstable at room temperature, but pure solids can be stored at −35 °C for weeks to months without noticeable decomposition. Despite their intense, red-orange color in solution, complexes 2a and 2b display no distinct absorption features by UV-vis spectroscopy with only trailing absorbances from the UV region of the spectra into the visible region. Contrary to the parent Ni(II)-chloride complexes 1a and 1b, both complexes 2a and 2b are diamagnetic. However, 1H NMR spectra of both the Cl and Me complexes in C6D6 indicate C3-symmetric geometries in solution at room temperature (see ESI†).
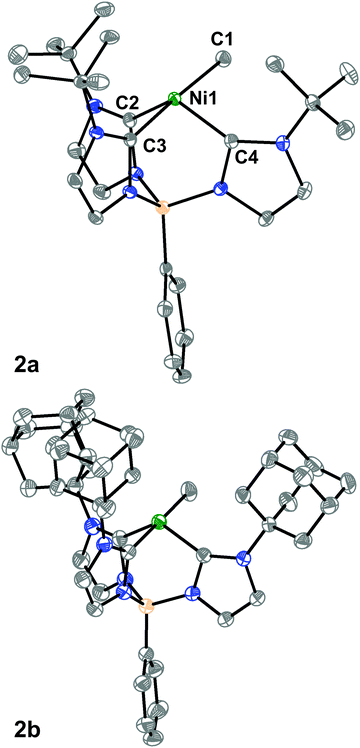
We then turned to single-crystal X-ray diffraction (SXRD) measurements to probe the structures of these Ni complexes in the solid-state. As expected from their threefold symmetric NMR spectra, complexes 1a and 1b are pseudo-tetrahedral in the solid-state and have a C3-axis with a B–Ni–Cl angle of 177.92(6)° and 178.8(2)°, respectively (see ESI†). In contrast, while the room temperature 1H NMR spectra of the methyl complexes 2a and 2b are consistent with a C3-symmetric structure, an unusual seesaw coordination geometry at the Ni(II) centers is observed in their solid-state structures (Fig. 1). The metrical parameters of the Ni centers in complexes 2a and 2b are consistent with a seesaw geometry around the Ni(II) center composed of three carbon donors from the tris-carbene borate ligand and a fourth from the bound methyl group. The Ni-methyl carbon atom distances are nearly identical between the two complexes at 1.965(2) and 1.959(2) Å, respectively. Additionally, there is no evidence of agostic interactions between the Me hydrogen atoms and the Ni(II) center. The two widest C–Ni–C angles which describe the seesaw geometry are 177.19(8)° and 121.49(8)° for 2a and 177.80(7)° and 121.25(7)° for 2b. Using both of these angles, a geometry index parameter τ4 can be calculated to describe the coordination environment of the Ni(II) center between square planar (τ4 = 0) or tetrahedral (τ4 = 1).30,31 For both 2a and 2b, the τ4 parameter is calculated to be 0.43, indicating a nearly perfect mono-vacant, trigonal bipyramidal or seesaw geometry around the Ni(II) center. These are the first such cases to be crystallographically characterized.§
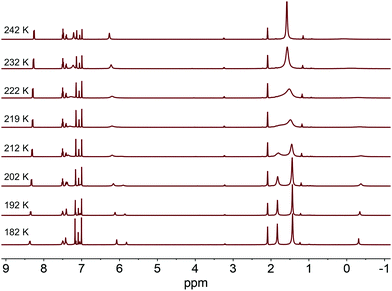
With the disparity between solid-state and solution structural data, we sought to better understand the dynamics of complexes 2a and 2b in solution. Variable temperature 1H NMR experiments were conducted in d8-toluene to determine an isomerization barrier, ΔG‡ (Fig. 2).32,33 In these complexes, the barrier being measured represents the energy to reorient the methyl substituent from between one pair of NHC groups to between a different pair through either an effective lever mechanism or via B–Ni–Me linearization to a C3-symmetric isomer (see below).34 For an NHC resonance of 2a (labeled with an asterisk in Fig. 2), a coalescence temperature of 215 K was determined and from the value of Δν, the peak-to-peak splitting in Hz of the fully resolved asymmetric structure, a barrier to isomerization was calculated to be 10.4 ± 0.5 kcal mol−1. In the case of 2b with the larger adamantyl groups, we anticipated a higher calculated barrier. However, the calculated value for the analogous imidazol-2-ylidene proton resonance is the same within an estimate of the error. From the coalescence temperature of 225 K and the measured Δν values, a barrier of 10.9 ± 0.5 kcal mol−1 was calculated (see ESI†). This suggests that while the adamantyl groups are bulkier, extending further away from the Ni center, this does not appreciably alter the barrier to isomerization in this complex.
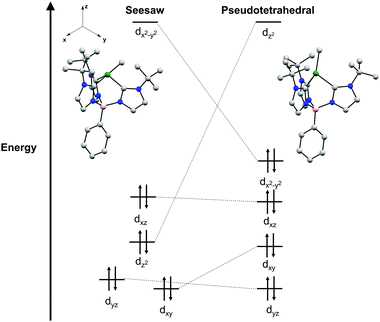
A point of interest upon studying complexes 2a and 2b was to rationalize the observed seesaw structures in the solid-state. A crude examination of the geometries a four-coordinate Ni(II) complex may adopt indicates three possible isomers as discussed above: tetrahedral, square planar, and seesaw. The parent chloride complexes 1a and 1b are characterized as high-spin S = 1 complexes in a pseudo-tetrahedral geometry. Given the additional strong field methyl ligand in complexes 2a and 2b, it is likely that diamagnetic, low-spin Ni(II) species would be most stable.35 While low-spin Ni(II) complexes are typically found in square planar geometries, the chelate ring of the tris(carbene)borate scaffold precludes the complex from distortion to a square planar geometry that would be otherwise electronically favored. Additionally, this stronger ligand field disfavors pseudo-tetrahedral geometries, as this would qualitatively result in occupation of a high energy, antibonding orbital (Fig. 3). As a result, the intermediate seesaw geometry is most stable, distorted away from pseudo-tetrahedral but restricted from planarization.
This qualitative description of the preference for seesaw geometries observed in complexes 2a and 2b is also supported by density functional theory (DFT) calculations. The geometry optimization of 2a in a singlet electronic configuration yields a structure that is in agreement with its solid-state structure. Geometry optimization of 2a in a triplet state shows instead a pseudo-tetrahedral geometry, similar to the geometry seen in 1a and 1b (see ESI†). The DFT calculations predict the S = 0 seesaw geometry to be 31 kcal mol−1 lower in energy than the corresponding S = 0 pseudo-tetrahedral isomer but only 11 kcal mol−1 lower than the S = 1 threefold symmetric species (see ESI†). Qualitative comparison of the frontier molecular orbitals of singlet 2a reveals that deviation from a pseudo-tetrahedral to seesaw geometry stabilizes the dz2 orbital (Fig. 3). This results in a single, high-lying dx2–y2 orbital that remains unoccupied with a clustering of occupied orbitals at overall lower energy than those in the pseudo-tetrahedral geometry. This qualitative orbital depiction for the seesaw geometry is similar to the classical depiction of square planar d-orbital splitting, further suggesting such a geometry would be preferred in this system if not for the chelate ring constraint imposed by the tris-carbene borate ligand.
The DFT calculations above suggest that an isomerization mechanism involving a linear S = 1 transition state is energetically reasonable, but we also wanted to probe the feasibility of a lever type mechanism for this isomerization computationally. In this mechanism the Me group migrates between NHC groups without linearizing to a pseudo-tetrahedral symmetry (see ESI†).34 The CMe–Ni–Ccarbene–Ncarbene dihedral angle was held fixed at 0° and the Ni–Me group allowed to move between a pseudo-tetrahedral orientation and close proximity to the R-group of the NHC in order to find a low energy intermediate which would model the transition state for this isomerization (see ESI†). In doing so, a conformer higher in energy by 20 kcal mol−1 relative to the seesaw geometry was found. This energy is high enough to rule out this pathway as operative given the ∼10 kcal mol−1 energy barrier calculated from the variable temperature 1H NMR experiments. Given the computed relative energies of the S = 0 (+31 kcal mol−1) and S = 1 (+11 kcal mol−1) pseudo-tetrahedral isomers, it is likely that the isomerization proceeds through the S = 1 C3-symmetric isomer. This conclusion is also supported by the relatively broad Ni–CH3 proton resonance at room temperature that shifts with temperature displaying Curie behavior (see ESI†). This effect is likely the result of perturbation from a minor amount of the paramagnetic, pseudo-tetrahedral isomer at room temperature as has been previously observed.36 Interestingly, this observation suggests that paramagnetic Ni-methyl intermediates are accessible at room temperature in the current system, and that similarly high-spin Ni(II)-alkyl complexes may be reasonable intermediates in catalysis.
The Ni(II)-methyl complexes 2a and 2b are the first examples of such species to be found in a seesaw coordination geometry as revealed by their solid-state structures. Variable temperature 1H NMR spectroscopy demonstrates that this distortion also occurs in the solution state and has an electronic origin as opposed to arising from any solid-state crystal packing. Using DFT calculations, the observed structures are rationalized by an overall lowering of filled orbitals by distortion from pseudo-tetrahedral to a seesaw geometry. This geometry is proposed to be favored over square planar geometry due to the chelate constraint of the tris(carbene)borate ligand. This work shows that Ni-alkyl species with chelating ligands can adopt this geometry and draws attention to the potential effects of this distortion and electronic structure on the reactivity of Ni intermediates in catalytic transformations.
This work was supported by an NSF CAREER award to JSA: Grant No. 1654144. NZ is supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1746045. NSF's ChemMatCARS Sector 15 is principally supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant number NSF/CHE-1834750. Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357.
Conflicts of interest
There are no conflicts to declare.Notes and references
- P. A. Lindahl, J. Biol. Inorg. Chem., 2004, 9, 516–524 CrossRef CAS PubMed.
- X. Zhao, H.-Y. Tu, L. Guo, S. Zhu, F.-L. Qing and L. Chu, Nat. Commun., 2018, 9, 3488 CrossRef PubMed.
- L. Guo and M. Rueping, Acc. Chem. Res., 2018, 51, 1185–1195 CrossRef CAS PubMed.
- J. Hu, Y. Zhao, J. Liu, Y. Zhang and Z. Shi, Angew. Chem., Int. Ed., 2016, 55, 8718–8722 CrossRef CAS PubMed.
- D. Nianios, S. Thierbach, L. Steimer, P. Lulchev, D. Klostermeier and S. Fetzner, BMC Biochem., 2015, 16, 10 CrossRef PubMed.
- M. Can, F. A. Armstrong and S. W. Ragsdale, Chem. Rev., 2014, 114, 4149–4174 CrossRef CAS PubMed.
- E. Carmona, F. González, M. L. Poveda, J. L. Atwood and R. D. Rogers, J. Chem. Soc., Dalton Trans., 1980, 2108–2116 RSC.
- P. Stoppioni, P. Dapporto and L. Sacconi, Inorg. Chem., 1978, 17, 718–725 CrossRef CAS.
- C. E. MacBeth, J. C. Thomas, T. A. Betley and J. C. Peters, Inorg. Chem., 2004, 43, 4645–4662 CrossRef CAS PubMed.
- P. J. Schebler, B. S. Mandimutsira, C. G. Riordan, L. M. Liable-Sands, C. D. Incarvito and A. L. Rheingold, J. Am. Chem. Soc., 2001, 123, 331–332 CrossRef CAS PubMed.
- N. Shirasawa, T. T. Nguyet, S. Hikichi, Y. Moro-oka and M. Akita, Organometallics, 2001, 20, 3582–3598 CrossRef CAS.
- S. A. Macgregor, Z. Lu, O. Eisenstein and R. H. Crabtree, Inorg. Chem., 1994, 33, 3616–3618 CrossRef CAS.
- J. Ghannam, T. Al Assil, T. C. Pankratz, R. L. Lord, M. Zeller and W.-T. Lee, Inorg. Chem., 2018, 57, 8307–8316 CrossRef CAS PubMed.
- A. Tarai and J. B. Baruah, Dalton Trans., 2018, 47, 4921–4930 RSC.
- T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2nd edn, 2013 Search PubMed.
- C. A. Grapperhaus, J. A. Bellefeuille, J. H. Reibenspies and M. Y. Darensbourg, Inorg. Chem., 1999, 38, 3698–3703 CrossRef CAS PubMed.
- R. Graziani, M. Vidali, U. Casellato and P. A. Vigato, Transition Met. Chem., 1978, 3, 99–103 CrossRef CAS.
- J. Li, D. Tian, H. Song, C. Wang, X. Zhu, C. Cui and J. P. Cheng, Organometallics, 2008, 27, 1605–1611 CrossRef CAS.
- M. Bröring, S. Prikhodovski and C. D. Brandt, J. Chem. Soc., Dalton Trans., 2002, 4213–4218 RSC.
- M. Bröring, S. Prikhodovski and C. D. Brandt, Inorg. Chim. Acta, 2004, 357, 1733–1738 CrossRef.
- M. Bröring, S. Prikhodovski, C. D. Brandt and E. C. Tejero, Chem. – Eur. J., 2007, 13, 396–406 CrossRef PubMed.
- J. A. Adjei, A. J. Lough and R. A. Gossage, RSC Adv., 2019, 9, 3956–3964 RSC.
- P. G. Edwards, F. Ingold and M. B. Hursthouse, Chem. Commun., 1998, 545–546 RSC.
- M. K. Goetz, E. A. Hill, A. S. Filatov and J. S. Anderson, J. Am. Chem. Soc., 2018, 140, 13176–13180 CrossRef CAS PubMed.
- M. K. Goetz and J. S. Anderson, J. Am. Chem. Soc., 2019, 141, 4051–4062 CrossRef CAS PubMed.
- R. A. Juarez, W.-T. Lee, J. M. Smith and H. Wang, Dalton Trans., 2014, 43, 14689–14695 RSC.
- I. Nieto, R. P. Bontchev and J. M. Smith, Eur. J. Inorg. Chem., 2008, 2476–2480 CrossRef CAS.
- S. B. Muñoz, W. K. Foster, H.-J. Lin, C. G. Margarit, D. A. Dickie and J. M. Smith, Inorg. Chem., 2012, 51, 12660–12668 CrossRef PubMed.
- R. E. Cowley, R. P. Bontchev, E. N. Duesler and J. M. Smith, Inorg. Chem., 2006, 45, 9771–9779 CrossRef CAS PubMed.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC.
- D. Rosiak, A. Okuniewski and J. Chojnacki, Polyhedron, 2018, 146, 35–41 CrossRef CAS.
- H. Shanan-Atidi and K. H. Bar-Eli, J. Phys. Chem., 1970, 74, 961–963 CrossRef CAS.
- J. Sandström, Dynamic NMR Spectroscopy, Academic Press, London, 1982 Search PubMed.
- M. Mauksch and P. v. R. Schleyer, Inorg. Chem., 2001, 40, 1756–1769 CrossRef CAS PubMed.
- J. Cirera, E. Ruiz and S. Alvarez, Inorg. Chem., 2008, 47, 2871–2889 CrossRef CAS.
- B. Le Guennic, T. Floyd, B. R. Galan, J. Autschbach and J. B. Keister, Inorg. Chem., 2009, 48, 5504–5511 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1968521–1968524. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cc09249h |
| ‡ These authors contributed equally. |
| § Determined by searching the Cambridge Crystallographic Database using Conquest by limiting a 4-coordinate Ni center with two pairs of ligand bond angles restricted between 150–180° and 110–130° |
| This journal is © The Royal Society of Chemistry 2020 |