Polar nano-region structure in the oxynitride perovskite LaTiO₂N

Abstract

We investigated the multiscale characters of the crystal structure of the oxynitride perovskite LaTiO₂N. While X-ray diffraction results identified the average structure as being centrosymmetric, we detected a signature of unknown structural deformation. By viewing the local structure, we unveiled the formation of a polar structure at the nanoscale.

---

Oxynitride perovskites with AMX₃ structure (A = alkali earth metal, rare earth; M = Ti, Zr, Nb, Ta, W; X = O, N)^1–7 are emerging materials that hold promise as visible-light responsive photocatalysts^4,8–11 and chromatically tunable non-toxic pigments.¹² The ability to modify their electronic states by replacing oxygen with nitrogen^11,13–16 has attracted attention, in particular for developing lead-free dielectric materials that are stable in air and water. BaTaO₂N exhibits a high dielectric permittivity of ∼5000 without phase transition and with minimal temperature dependence,^4,17 and a ferroelectric behavior has been reported in SrTaO₂N.^18,19 The interplay between structure and high permittivity mechanisms is expected to be revealed.

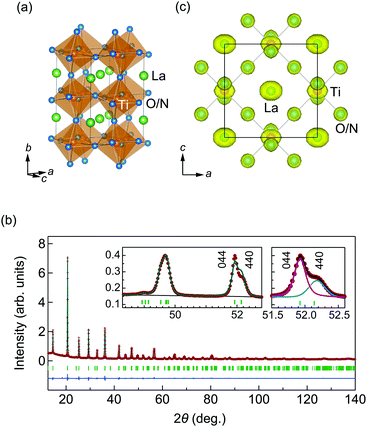
In this study, we focus on the oxynitride LaTiO₂N, which has a band gap of 2.1 eV and permittivity of 750 (bulk) and 1220 (film) without a phase transition.^8,20,21 In electronic state calculations, the epitaxial strain in the thin film gives rise to a spontaneous polarization of 59 μC cm⁻².²² Clarke et al., Logvinovich et al., and Chen et al. have claimed that this compound crystallizes in a triclinic, I1̄ structure with partial O/N trans-order on the TiO₄N₂ octahedron.^2,23,24 In contrast, Yashima et al. have reported crystallization in the orthorhombic Imma space group with O/N site disorder, where O and N atoms occupy random anion sites.¹⁴ The Imma type perovskite can be described by the a⁰b⁻b⁻ Glazer tilt system^25,26 with a √2 × 2 × √2 unit cell (Fig. 1a). The Imma and I1̄ structures are centrosymmetric space groups with the Ti atoms located at the inversion center.²⁷

Fig. 1 (a) The crystal structure of LaTiO₂N. The La, Ti, and O/N atoms are represented by green, orange, and blue balls. (b) The powder XRD pattern of LaTiO₂N with a wavelength of λ = 0.999175 Å at 300 K. The plots correspond to observed (red crosses) and calculated (deep green line) signals, difference profiles (blue line), and positions of Bragg peaks (green tick marks). The left inset shows the enlarged pattern at around 2θ = 50 deg. with 044 and 440 reflections. The right inset shows the profile deconvolution of 044 (magenta line) and 440 (blue line) reflections. (c) The isosurface of MEM electron density at 4 e Å⁻³ for LaTiO₂N.

We present average and local structure analyses of LaTiO₂N through measurements of synchrotron X-ray diffraction (XRD), extended X-ray absorption fine-structure (EXAFS) and atomic pair distribution function (PDF) from neutron total scattering. Our XRD results led us to identify the average structure as orthorhombic Imma, and not triclinic I1̄. Local structure analyses from EXAFS and PDF further revealed polar nano-region (PNR) formation as widely observed in relaxors^28–30 with high permittivity. The PNR in LaTiO₂N probably arises from short-range O/N cis-order instead of chemical disorder in the relaxor. The strong relation between the local structure and the functionality of the material is a characteristic of mixed anion systems,³¹ including oxynitrides.

Details of synthesis, characterization, and structure determinations are provided in the ESI.† The XRD pattern for the LaTiO₂N powder at 300 K can be seen in Fig. 1b. We approached the structural analysis following the Imma structure previously reported in the literature,¹⁴ which resulted in the reasonable weighted-profile R-factor R_wp = 2.6%.³² The site disordered O/N atoms were assigned with the occupancies of occ(O) = 2/3 and occ(N) = 1/3. The refined structural parameters listed in Table S1 (ESI†) agree with the previous results.¹⁴ However, we note inconsistencies between the observed and the calculated intensities, in particular for reflections such as 044, 440, 165, and 561 (Fig. 1b, left inset). Habu et al. also reported similar inconsistencies in neutron diffraction patterns,²¹ and suggested that they could be explained by lowering the symmetry to a triclinic, I1̄ structure. No lattice distortion or violation of the extinction conditions for the Imma structure was detected in our high-resolution XRD and electron diffraction (ESI†), however, motivating further investigation of the inconsistency.

We fit the profiles of the 044 and 440 reflections using pseudo-Voigt functions (Fig. 1b, right inset). The linewidth and intensities were estimated by the quantities H(044)/H(440) = 0.70 and I(044)/I(440) = 1.9, respectively. The difference in linewidth can be accounted for by size-strain broadening in the a-axis direction. The intensities, however, differ significantly from the calculated structure factor based on the Imma model, giving I(044)/I(440) ∼ 0.87. This implies that the Imma model cannot account for the observed intensities. To determine a more favorable structural model, we attempted to refine the candidate structures among non-isomorphic subgroups of Imma (ESI†). None of the trials in the lower symmetry models provided a close fit to the experimental data, however.

We then examined the MEM calculation based on the XRD data,³³ resulting in the electron densities depicted in Fig. 1c. Elongated electron densities were found for many atoms, suggesting anisotropic displacements from the equilibrium position along the a-axis. From the average structure, however, it was not possible to determine whether they were static or dynamic, and we proceeded to analyze the local structure for more insight into the structural character.

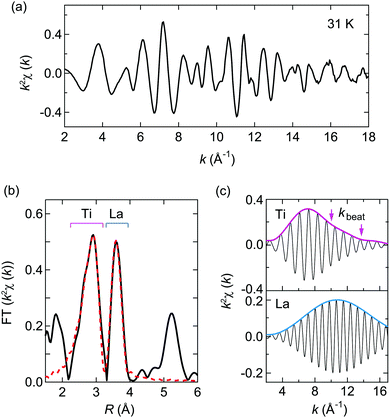
The La K-edge EXAFS measurement of LaTiO₂N was performed at a low-temperature of 31 K in order to suppress the influence of thermal motion. Plots of the k²-weighted EXAFS oscillation k²χ(k) and R-space magnitude of the Fourier transformation (FT) are shown in Fig. 2a and b, respectively.³⁴ In the radial direction without phase-correction, the peak amplitudes ∼2.9 and ∼3.6 Å correspond to the La–Ti (6 + 2 neighboring Ti) and La–La (4 + 2 neighboring La) shells, respectively. Bond distances from the fit result in R_La–Ti = 3.370(6) and 3.402(6) Å, and R_La–La = 3.945(9) and 3.969(9) Å, where the relative distance is the trial parameter based on the Imma structure from the XRD measurement.

Fig. 2 (a) The k²-weighted EXAFS oscillation k²χ(k) of LaTiO₂N at 31 K at the La K-edge. (b) The magnitude of the Fourier transformed spectrum (black line) and the calculated profile (red dashed line). (c) Fourier-filtered EXAFS oscillations and amplitudes transformed in the range of 2.25–3.25 Å for Ti (upper panel) and 3.32–3.99 Å for La (lower panel) in (b). Kinks exist at k_beat = 10.0 and 13.8 Å⁻¹ in the Ti profile, as indicated by the arrows.

To examine the further distortion, we employed a Fourier-filtered back transformation.³⁵ Plots of the Fourier-filtered EXAFS oscillations and amplitudes for La–Ti (2.25–3.25 Å) and La–La (3.32–3.99 Å) shells are shown in Fig. 2c. We found kinks, as indicated by the arrows, at k_beat ∼ 10.0 and 13.8 Å⁻¹ in the La–Ti shell. The kinks stem from the beat from the phase difference of EXAFS oscillations along with different bond distances ΔR in the shell. Based on the relation ΔR = π/(2k_beat), we can estimate the ΔR of the La–Ti bond distances to be ΔR = 0.16 and 0.11 Å. Considering that the La–Ti distances in the average Imma structure are 3.41 and 3.44 Å, the estimated ΔR values signal the presence of unknown distortion. As the beats were absent in the La–La shell, they cannot be attributed to static disorder or dynamical fluctuation in the structure, implying that there were no local modulations longer than 0.1 Å in terms of the La atom positions. We propose therefore that static modulation of the equilibrium positions arose in this compound.

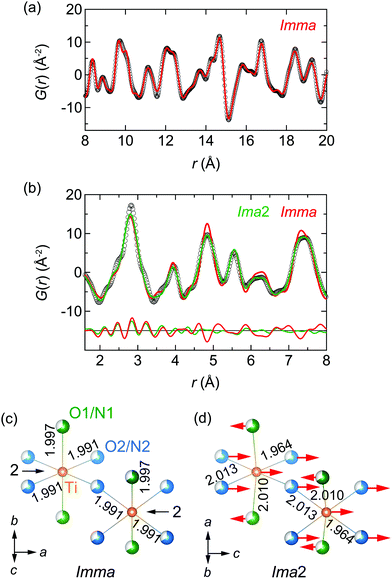
We proceeded to a multiscale data treatment through PDF analysis from neutron total scattering data.³⁶ First, we fitted G(r) in the range 1.6 < r < 20 Å at 300 K based on the Imma structure, shown in Fig. S3 (ESI†). We noted that the refined patterns were not well reproduced at short-range (r < 8 Å). Hence, we separated the fitting area into short (1.6 < r < 8 Å) and medium (8 < r < 20 Å) ranges. The medium-range plot is shown in Fig. 3a. We refined the structural parameters based on the Imma structure, resulting in a pattern agreeing reasonably well with G(r), with a weighted R-factor R_w = 9.4%.³⁷ The parameters are given in Table S1 (ESI†), and coincide closely with those for XRD analyses.

Fig. 3 (a) PDF data (black circles) for LaTiO₂N at 300 K in the range of 8 < r < 20 Å. The red line indicates the centrosymmetric Imma model. (b) PDF data (black circles) in the range of 1.6 < r < 8 Å. The calculated patterns from Imma, and non-centrosymmetric Ima2 models are represented by the red and green lines, respectively. The lower curves are the difference profiles between the experimental data and the calculated patterns. (c and d) Imma and Ima2 structures from PDF analyses. The unit cells of Imma and Ima2 are related by (a, b, c)_Imma = (c, a, b)_Ima2. Ti, O1/N1, and O2/N2 atoms are represented by orange, green, and blue balls, respectively. The O/N disordered state is signified by partially colored balls. The arrows indicate the relative displacements from the Imma average structure. Ti–O/N bond lengths are shown in angstroms. Two-fold rotational axes run through the Ti atoms along the a and c-axes for the Imma and Ima2 structures, respectively.

The short-range plot shown in Fig. 3b still failed to be reproduced well by the Imma model. To assess the structure with a more reasonable model in this range, we considered candidates among non-isomorphic subgroups of Imma. Taking into account the extinction rules used in XRD and electron diffraction measurements, only Ima2, a polar point group²⁷ (see details in the ESI†), remains as a feasible candidate. With our knowledge of the previous EXAFS results, we proceeded assuming that the Ti atom is shifted by ΔR along the polar c-axis of Ima2. Refining all structural parameters according to Ima2 symmetry, a reasonable fit to G(r) resulted with R_w = 11.6%. The structural parameters obtained are given in Table S1 (ESI†).

The results of the PDF analysis show that the crystal structure of LaTiO₂N can be regarded as polar Ima2 at the nanoscale and non-polar Imma in the average structure. Fig. S4 (ESI†) shows the calculated curve for 1.6 < r < 20 Å fixed for the Ima2 structure, resulting in substantial discrepancies with the experimental data. Hinuma et al. have proposed effects originating from dynamical polarization at the picosecond scale,³⁸ however our findings indicate the polar shift to be static.

Fig. 3c and d illustrate the local structure of the Imma (O/N disorder) and Ima2 (disorder) models from the PDF analyses, respectively, where the unit cells are related by (a, b, c)_Imma = (c, a, b)_Ima2.²⁷ The arrows represent the atomic displacements from the Imma average structure. In the Ima2 model, Ti and O2/N2 atoms shift by 0.130(14) and 0.127(8) Å in the +c-axis direction, and the O1/N1 atom shifts by 0.033(12) Å in the −c-axis direction. The La atom was needed in the polar structure to fix the Imma equilibrium position. The bond length of Ti–O1/N1 is modified from 1.997(1) Å in Imma to 2.010(2) Å in Ima2. The bond length of Ti–O2/N2 is modified from 1.9910(1) Å in Imma to 1.964(11) and 2.013(11) Å in Ima2.

Finally, we investigated the O/N order of the anion sites. In LaTiO₂N, O/N disorder^2,14 and partial trans-order^23,24 have been proposed at the long-range scale. In our study, we performed PDF analyses for complete trans-order and cis-order models in a unit cell at short-range, r < 8 Å, as illustrated in Fig. S5a (ESI†). The O/N orders are introduced to the Ima2 disordered structure. The final values of R_wp are described in Fig. S5a (ESI†). While the trans-ordered models led to little refinement, the cis-ordered models delivered improvements, suggesting cis-ordering as a feasible O/N ordered state in the compound. However, one issue reported in the literature is that bulk cis-ordering is associated with an anti-polar state.³⁹ In our study, since the polar region emerges below 8 Å, a size effect may affect polarization in conjunction with cis-ordering. We need further studies on the O/N ordering through the NQR and polarized photoemission spectra, which would enable visualization of the O/N ordering.

The polar structure in the nano-scale observed in this study bears resemblance to PNR formation in the relaxor Pb(Mg_1/3Nb_2/3)O₃ (PMN).^28–30 The dielectric permittivity in the relaxor is maximized with broadened features at low temperature, possibly from phase transitions becoming smeared out due to its heterogeneity. In another example, Withers et al. have proposed that the diffuse intensity in electron diffraction in BaTaO₂N results in a one-dimensional PNR state due to random strain from chemical disorder.⁴⁰ Unlike these cases for a classical PMN relaxor or BaTaO₂N, the PNR in LaTiO₂N can most likely be ascribed in terms of short-range O/N cis-order instead of chemical disorder. Taking into account that ferroelectric materials in general exhibit high permittivity due to their large polarization, the PNR may be closely tied to the high permittivity in LaTiO₂N.

In conclusion, we conducted crystal structure analyses of the oxynitride perovskite LaTiO₂N via a multiprobe study using synchrotron XRD measurements, EXAFS, and neutron PDF analysis. We advocate that the average structure of LaTiO₂N should be regarded as Imma, and not I1̄. We highlight the polar structure observed at the short-range scale of r < 8 Å, which deviated from centrosymmetric at the long-range scale. Our results demonstrate the power of combining multiprobe and multiscale analyses. Further insight into this structure can likely be gained through electronic state calculations incorporating polar shift, O/N order, and size effects. We think that the mechanism of PNR formation will give significant guidelines for designing high permittivity materials in oxynitride and, more commonly, mixed-anion systems.

We thank Y. Kuramoto for fruitful discussions. This work was supported by the MEXT Elements Strategy Initiative to Form Core Research Center (JPMXP0112101001) and JSPS KAKENHI (No. 16K05434). The synchrotron XRD, EXAFS and neutron scattering experiments were performed with the approval of the Photon Factory Program Advisory Committee (No. 2016S2-004 and 2016V002) and the Neutron Science Proposal Review Committee of IMSS, KEK (No. 2014S06), respectively. The crystal structure diagrams were created using the software VESTA.⁴¹

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. E. Günther, R. Hagenmayer and M. Jansen, Z. Anorg. Allg. Chem., 2000, 626, 1519–1525.
2. S. J. Clarke, B. P. Guinot, C. W. Michie, M. J. C. Calmont and M. Rosseinsky, Chem. Mater., 2002, 14, 288–294.
3. S. J. Clarke, K. A. Hardstone, C. W. Michie and M. Rosseinsky, Chem. Mater., 2002, 14, 2664–2669.
4. Y. I. Kim, P. M. Woodward, K. Z. Baba-Kishi and C. W. Tai, Chem. Mater., 2004, 16, 1267–1276.
5. A. Fuertes, J. Mater. Chem., 2012, 22, 3293–3299.
6. S. H. Porter, Z. Huang and P. M. Woodward, Cryst. Growth Des., 2014, 14, 117–125.
7. N. Cordes and W. Schnick, Chem. – Eur. J., 2017, 23, 11410–11415.
8. A. Kasahara, K. Nukumizu, G. Hitoki, T. Takata, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. A, 2002, 106, 6750–6753.
9. A. Kasahara, K. Nukumizu, T. Takata, J. N. Kondo, M. Hara, H. Kobayashi and K. Domen, J. Phys. Chem. B, 2003, 107, 791–797.
10. K. Maeda and K. Domen, J. Phys. Chem. C, 2007, 111, 7851–7861.
11. X. Wang, Z. Li and Z. Zou, Phys. Chem. Chem. Phys., 2015, 17, 19631–19636.
12. M. Jansen and H. P. Letschert, Nature, 2000, 404, 980–982.
13. C. M. Fang, G. A. de Wijs, E. Orhan, G. de With, R. A. de Groot, H. T. Hintzen and R. Marchand, J. Phys. Chem. Solids, 2003, 64, 281–286.
14. M. Yashima, M. Saito, H. Nakano, T. Takata, K. Ogisu and K. Domen, Chem. Commun., 2010, 46, 4704–4706.
15. E. Orisakwe, R. Marchal, B. Fontaine, R. Gautier and J.-F. Halet, J. Ceram. Soc. Jpn., 2016, 124, 1056–1062.
16. A. Kubo, G. Giorgi and K. Yamashita, Chem. Mater., 2017, 29, 539–545.
17. Y.-I. Kim and P. M. Woodward, J. Solid State Chem., 2007, 180, 3224–3233.
18. D. Oka, Y. Hirose, H. Kamisaka, T. Fukumura, K. Sasa, S. Ishii, H. Matsuzaki, Y. Sato, Y. Ikuhara and T. Hasegawa, Sci. Rep., 2014, 4, 4987.
19. S. Kikkawa, S. Sun, Y. Masubuchi, Y. Nagamine and T. Shibahara, Chem. Mater., 2016, 28, 1312–1317.
20. A. Ziani, C. L. Paven-Thivet, L. L. Gendre, D. Fasquelle, J. C. Carru, F. Tessier and J. Pinel, Thin Solid Films, 2008, 517, 544–549.
21. D. Habu, Y. Masubuchi, S. Torii, T. Kamiyama and S. Kikkawa, J. Solid State Chem., 2016, 237, 254–257.
22. N. Vonruti and U. Aschauer, Phys. Rev. Lett., 2018, 120, 046001.
23. D. Logvinovich, L. Bocher, D. Sheptyakov, R. Figi, S. G. Ebbinghaus, R. Aguiar, M. H. Aguirre, A. Reller and A. Weidenkaff, Solid State Sci., 2009, 11, 1513–1519.
24. D. Chen, D. Habu, Y. Masubuchi, S. Torii, T. Kamiyama and S. Kikkawa, Solid State Sci., 2016, 54, 2–6.
25. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
26. H. T. Stokes, E. H. Kisi, D. M. Hatch and C. I. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 934–938.
27. International Tables for Crystallography, ed. T. Hahn, Kluwer Academic, Dordrecht, 4th edn, 2002, vol. A.
28. I.-W. Chen, P. Li and Y. Wang, J. Phys. Chem. Solids, 1996, 57, 1525–1536.
29. A. A. Bokov and Z.-G. Ye, J. Mater. Sci., 2006, 41, 31–52.
30. V. V. Shvartsman and D. C. Lupascu, J. Am. Ceram. Soc., 2012, 95, 1–26.
31. H. Kageyama, K. Hayashi, K. Maeda, J. P. Attfield, Z. Hiroi, J. M. Rondinelli and K. R. Poeppelmeier, Nat. Commun., 2018, 9, 772.
32. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15–20.
33. F. Izumi and R. A. Dilanian, Recent Research Developments in Physics, Transworld Research Network, Trivandrum, 2002, vol. 3, part II, pp. 699–726.
34. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
35. C. J. Zhang and H. Oyanagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 064521.
36. T. Otomo, K. Suzuya, M. Misawa, N. Kaneko, H. Ohshita, T. Fukunaga, K. Itoh, K. Mori, M. Sugiyama, Y. Kameda, T. Yamaguchi, K. Yoshida, Y. Kawakita, K. Maruyama, S. Shamoto, S. Takeda, S. Saitoh, S. Muto, J. Suzuki, I. Ino, H. Shimizu, T. Kamiyama, S. Ikeda, Y. Yasu, K. Nakayoshi, H. Senda, S. Uno and M. Tanaka, MLF Annual Report 2009, J-PARC, 2011, vol. 10-05, pp. 62–63.
37. C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Bozin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
38. Y. Hinuma, H. Moriwake, Y.-R. Zhang, T. Motohashi, S. Kikkawa and I. Tanaka, Chem. Mater., 2012, 24, 4343–4349.
39. J. P. Attfield, Cryst. Growth Des., 2013, 13, 4623–4629.
40. R. L. Withers, Y. Liu, P. Woodward and Y.-I. Kim, Appl. Phys. Lett., 2008, 92, 102907.
41. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available: Synthesis, structure determination, and crystallographic data. See DOI: 10.1039/c9cc07029j

---