What’s novel in the new Eurachem guide on uncertainty from sampling?
Analytical Methods Committee, AMCTB No. 96
First published on 23rd April 2020
Abstract
A second edition of the Eurachem guide, Measurement uncertainty arising from sampling (UfS),1 has recently been published (Fig. 1), in collaboration with CITAC, Eurolab, Nordtest and the Royal Society of Chemistry’s Analytical Methods Committee. This Technical Brief aims to explain how this new second edition differs significantly from the first edition that was published in 2007. The stated objective of this new edition is to incorporate several recent research developments, and to explain how they can be integrated into the estimation of measurement uncertainty in different situations. Both editions are based on the general concept that primary sampling is the first part of the measurement process, and thus usually an important contributor to the uncertainty of any measurement value. The two main approaches to estimating UfS are based upon either empirical methods or numerical modelling. Six worked examples, showing these two approaches, cover a range of application sectors, including food, animal feed, soil and water.
Use of the uncertainty factor
One significant new development is the option of using the Uncertainty Factor as an alternative way to express measurement uncertainty (AMCTB 88).2 The upper and lower confidence limits of a measurement value are expressed by multiplying and dividing the measurement value by the uncertainty factor, rather than by the traditional approach of adding and subtracting the uncertainty. This approach is more accurate when the relative expanded uncertainty value is large, typically over 20%, and also where the frequency distribution of the uncertainty is approximately log–normal rather than normal. These two conditions often apply to measurement uncertainty that arises from the sampling process, particularly when the spatial distribution of the analyte in the test material is substantially heterogeneous. However, these two conditions can also apply to purely analytical sources of uncertainty, such as those described for the measurement of the proportion of genetically modified organisms (GMO) in soya Fig. 2, (AMCTB 18).3 | ||
| Fig. 1 The cover of the Eurachem guide, Measurement uncertainty arising from sampling (used with permission from Eurachem). | ||
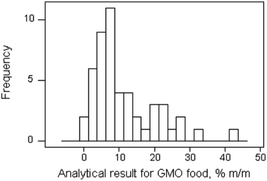 | ||
| Fig. 2 Log–normal frequency distribution of proficiency test measurements of GMO in soya (AMCTB 18),3 that suggests that the uncertainty factor may be the most applicable way to express measurement uncertainty in purely analytical systems, as well as for UfS. | ||
The guide also explains two options for how measurement uncertainty can be calculated by combining the component arising from sampling, expressed as an uncertainty factor, with that arising from chemical analysis, expressed in the traditional way as a relative uncertainty.
Reducing the cost of UfS estimation using an unbalanced design
A second new development in the methods described in the guide is the use of an unbalanced experimental design to reduce the cost of estimating UfS by the duplicate method (AMCTB 64).2 The first edition of the guide described the use of a balanced design for the empirical estimation of the measurement uncertainty as a whole, and its two components in the sampling and analytical steps. This balanced design has analytical duplicates on both of the two sample duplicates. The new edition of the guide stresses the advantage of using an unbalanced design, with an analytical duplicate on only one of the two sample duplicates. This design reduces the extra cost of estimating the uncertainty by 33%. The software RANOVA2 can implement the unbalanced design, and can also express the ANOVA results as both the expanded relative uncertainty and the new uncertainty factor, is freely available from the AMC software webpage (https://www.rsc.org/Membership/Networking/InterestGroups/Analytical/AMC/Software/index.asp).Estimating UfS using sampling proficiency testing data
The third development is a more comprehensive method for the estimation of UfS that uses measurements made in a procedure called Sampling Proficiency Testing (SPT, AMCTB 78).2 In the first edition of the UfS guide this approach was discussed in theory, but the new edition now refers to the first practical example of the use of SPT data for UfS estimation.4 In this approach multiple samplers each apply whatever sampling protocol they consider appropriate to achieve the same stated objective for the same sampling target. Using a balanced design across all of the different samplers, it is then possible to include the ‘between-sampler’ bias in the estimate of UfS, in addition to the components that were previously included. The first practical SPT (concerned the measurement of the moisture content of a 20 ton batch of fresh butter) gave an uncertainty estimate that was a factor of 2.2 larger than that from the duplicate method applied to just a single sampler. The cost of the estimation of UfS with SPT measurements will usually be higher than that incurred using the simpler duplicate method. However, this extra expenditure can be justified when the financial consequences of underestimating the UfS are high, for example when characterising a sampling target of high financial value that may be lost by a consequent misclassification.Application of UfS estimation to new situations
The fourth development covered in the new guide is the increased range of measurement types and situations where UfS estimation has been applied and reported. One such application is for measurements made in situ, where the test material has not been removed from its original location but measured in place. For in situ measurements, the taking of a sample is almost indivisible from the rest of the measurement process. This means that the situation is more complex than for traditional ex situ measurements made in an external laboratory, partially because of the spatial heterogeneity of the analyte concentration in the test material. Even when an in situ measurement probe is placed at the same nominal location on the sampling target, the analyte heterogeneity will thereby increase the measurement uncertainty. This is due to the higher level of UfS that is present in an in situ measurement when compared against an ex situ measurement, where the test material has usually been homogenized during laboratory test-sample preparation.UfS can be estimated for in situ measurements using an empirical approach such as the duplicate method.5 Duplicated positioning of the measurement probe, using the same sampling protocol, can be used to give a ‘sample duplicate’. Similarly, duplicated measurements made without moving the probe can be used to give an ‘analytical duplicate’. The systematic component of the uncertainty cannot be estimated only with measurements on a matrix-matched certified reference material (CRM). This is because a CRM is usually a dried, ground, homogenized and often compacted material that is physically very different from the test material, which may well be moist, not ground, heterogeneous and unconsolidated in the measurement situation. Comparison will also be required, therefore, between the measurements made in situ and those made ex situ, with an independent analytical method for the same measurand, on samples taken from the same sampling target.
‘On site’ measurements, are made when a sample has been taken from its original location, usually prepared and homogenised, and measured close in a field lab to the sample’s original location. This situation is intermediate in complexity between the traditional ex situ measurements, and the in situ measurements just discussed. For an example of the determination of total petrol hydrocarbons (TPH) in stockpiled soil, the ex situ measurement made by the on-site method were compared against those made in a remote laboratory under more controlled conditions. The substantially higher concentration values measured on site may be partially due to loss of volatile analytes between the field and the laboratory, despite precautions being taken to minimize this loss.6
UfS in passive measurements of radioactive decay
Application of UfS estimation to the measurement of 137Cs in soil, by gamma ray spectrometry at a nuclear decommissioning site, has illustrated some interesting new issues.7 The passive nature of sampling for in situ use of γ-ray spectrometry, means that a very large mass of test material (e.g. 200–1000 kg) can form the ‘test portion’ of this analytical method. This contrasts with the very limited mass of test material (e.g. ∼0.5 kg) usually physically extracted for the ex situ measurement, also by γ-ray spectrometry. When the duplicate method was applied, the measurement UfS for the in situ measurements was found to be seven times lower than that for the ex situ measurements. This is undoubtedly due to the much greater mass interrogated by the in situ γ-ray spectrometry, which is therefore much more representative of the sampling target. This effect is slightly offset by the 30% lower analytical component of the uncertainty, due to the longer counting time typically used for ex situ determinations, making the overall expanded measurement uncertainty comparable at around 40%. However, the cost of each in situ measurement is about one tenth of an ex situ measurement, so it is economically justified to take many more in situ than ex situ measurements. Overall, when four times more in situ measurements are made than ex situ measurements, it was found that the standard error on the mean value of 137Cs for the whole site is reduced by a factor of two using the in situ measurement approach, at around half the cost.UfS estimation at the micro-scale
The final area of new application of UfS estimation is to a range of different spatial scales. This is particularly the case for instrumental measurements made using ‘beam sampling’ at scales ranging from the millimetre to the micron scale (AMCTB 84).2 At these smaller scales, analyte heterogeneity becomes increasingly important. The heterogeneity is often the main component of the UfS and hence the dominant source of the measurement uncertainty. Studies using PXRF at the millimetre scale, and SIMS at the micron scale, have used the duplicate method to estimate both the UfS, and the analyte heterogeneity. When the UfS is included in the uncertainty estimate, it is possible to show that these in situ measurements can be fit-for-purpose (FFP, such as the spatial mapping of element concentration), despite having higher uncertainty than is usual for bulk analysis. With an increasing use of in situ measurement devices in many sectors of society, at all spatial scales, reliable methods of estimating the UfS of beam measurement procedures can enable their FFP to be judged.The second edition of the UfS guide reflects the increasing adoption of the general principles described in the first edition, but with improvements to some of the methods of estimating and expressing UfS, and a wider range of applications. There are still many areas of chemical measurement where the importance of UfS has not yet been recognised or quantified, such as the pharmaceutical, clinical and manufacturing sectors. Hopefully this new edition will enable these new application areas to be investigated resulting in improvements in sampling practises.
Michael H. Ramsey
This Technical Brief was prepared for the Analytical Methods Committee with contributions from members of the AMC Sampling Uncertainty Expert Working Group and approved on 21 February 2020.
Further Reading
- Eurachem/EUROLAB/CITAC/Nordtest/AMC Guide: Measurement uncertainty arising from sampling: a guide to methods and approaches, M. H. Ramsey, S. L. R. Ellison and P. Rostron, Eurachem, Second edn, 2019, ISBN (978-0-948926-35-8), available from http://www.eurachem.org Search PubMed.
- RSC Publishing Themed Collection, Analytical Methods Committee Technical Briefs, http://rsc.li/amctb.
- AMC Technical Briefs Webpage, https://www.rsc.org/Membership/Networking/InterestGroups/Analytical/AMC/TechnicalBriefs.asp.
- M. H. Ramsey, B. Geelhoed, A. P. Damant and R. Wood, Improved evaluation of measurement uncertainty from sampling by inclusion of between-sampler bias using sampling proficiency testing, Analyst, 2011, 136(7), 1313–1321, 10.1039/c0an00705f.
- M. H. Ramsey and K. A. Boon, Can in situ geochemical measurements be more fit-for-purpose than those made ex situ?, Appl. Geochem., 2012, 27, 969–976, DOI:10.1016/j.apgeochem.2011.05.022.
- K. A. Boon and M. H. Ramsey, Judging the fitness of on-site measurements by their uncertainty, including the contribution from sampling, Sci. Total Environ., 2012, 419, 196–207, DOI:10.1016/j.scitotenv.2011.12.001.
- P. Rostron, J. A. Heathcote and M. H. Ramsey, Evaluation of uncertainties in in situ and ex situ gamma measurements on land areas with low contamination levels, J. Radiol. Prot., 2015, 35, 391–399, DOI:10.1088/0952-4746/35/2/391.
| This journal is © The Royal Society of Chemistry 2020 |


