An indirect Raman spectroscopy method for the quantitative measurement of respirable crystalline silica collected on filters inside respiratory equipment

Abstract

This article describes the development of an analytical method to measure respirable crystalline silica (RCS) collected on filters by a miniature sampler placed behind respirators worn by workers to evaluate their ‘true’ exposure. Test samples were prepared by aerosolising a calibration powder (Quin B) and by pipetting aliquots from suspensions of bulk material (NIST 1878a and Quin B) onto filters. Samples of aerosolised RCS collected onto polyvinyl chloride PVC filters were ashed and their residue was suspended in isopropanol and filtered into a 10 mm diameter area onto silver filters. Samples were also collected by the Health and Safety Executive's (HSE) miniature sampler from within the facepiece of a respirator on a breathing manikin during a simulated work activity. Results obtained using Raman spectroscopy were compared with X-ray diffraction (XRD) measurements, which was used as a reference method and a linear relationship was obtained. Raman has similar estimates of uncertainty when compared with the XRD methods over the measurement range from 5 to 50 μg and obtained the lowest limit of detection (LOD) of 0.26 μg when compared with XRD and Fourier Transform Infrared FTIR methods. A significant intercept and slope coefficient greatly influenced the higher LOD for indirect XRD method. The level of precision and low LOD for Raman spectroscopy will potentially enable workplace measurements at lower concentrations below the Workplace Exposure Limit (WEL) than are achieved using current analytical instrumentation. Different inward leakage ratio (ILR) measurement approaches were compared using six aerosolised sandstone dust tests. For the three highest inward leakage ratios the Portacount® obtained higher values than the RCS mass or the miniWRAS ratios, the latter of which reporting both particle number and quartz mass concentration. However, these limited ILR data were insufficient to establish statistical correlations between the measurement methods.

---

Introduction

The term respirable refers to a health-related definition for the mass distribution of aerodynamic particle size diameters that are less than 16 μm and with a median aerodynamic diameter of 4 μm with the potential to penetrate to the alveoli of the lung.¹ The inhalation of respirable-sized crystalline silica (RCS) is a potential hazard to the health of thousands of workers in the United Kingdom because of the widespread use of materials containing crystalline silica. It is estimated that a total of 560 000 workers are potentially exposed to RCS in Great Britain (GB).² Crystalline silica is a common naturally occurring mineral and exposure to excessive levels of RCS generated when working on materials containing crystalline silica can cause lung diseases, including silicosis³ and cancer.⁴

There are many processes which can generate RCS, especially those which involve working with powered tools on materials containing crystalline silica, where airborne levels of RCS remain high despite following the principles of good practice given in the Control of Substances Hazardous to Health (COSHH) regulations 2002.⁵ In addition to the use of engineering and organisational controls, Respiratory Protective Equipment (RPE) is often required to manage any residual risk and help ensure worker exposures are below the Workplace Exposure Limit (WEL).

Respirators are classified in terms of their assigned protection factors (APF). For example, in the United Kingdom, a type of RPE known as a Filtering Facepiece 3 (FFP3) respirator is allocated an assigned protection factor (APF) of 20. The value of 20 assumes that the respirator is capable of reducing airborne concentration inside the respirator by at least 1/20^th of the concentration outside. APFs are based on the 5^th percentile of workplace data and are intended to be a reasonable worst-case estimate of protection in the workplace. Some studies indicate that RPE does not always prevent exposures reaching regulatory exposure limits when used in workplace conditions.^6–8

Currently, there isn't a method which measures the personal RCS exposure a worker is subject to in their breathing zone inside a respirator. The exposure of a worker wearing RPE is routinely assessed by measuring the RCS concentration obtained from a sampler placed outside the RPE, but within the breathing zone of the worker.

A miniature respirable sampler was developed by the Health and Safety Executive (HSE) to collect dust after penetrating into a respirator to determine a more reliable measure of RCS exposure in the workplace. The HSE miniature sampler has the potential to provide a hazard specific measure of the worker's ‘true’ exposure^9,10 and provide data for studies to investigate the APF when working with crystalline silica. Estimates indicate that the mass of RCS collected from within the facepiece of the FFP3 type respirator, will be below the limits of detection (LOD) of current X-ray diffraction (XRD) and Fourier-transform infrared (FTIR) analytical methods for RCS measurement, if the tight-fitting FFP3 respirator is performing to its APF specification. Raman spectroscopy was investigated as new approach to measure RCS at lower filter mass loadings levels¹¹ by micro-concentrating an aerosol sample onto a small measurement area (5 mm in diameter). A similar feasibility study using semi-portable Raman equipment was conducted by Zheng et al.¹² and both feasibility studies demonstrate that the Raman technique was more sensitive (reported LODs for RCS when using Raman are from 0.02 to 0.55 μg) than the established XRD and FTIR methods. LODs for RCS analysis when using current XRD and FTIR methods range from about 3 to 10 μg for both instruments^13–15 on deposit areas that can range from 16 mm to about 22 mm in diameter. Wei et al.¹⁶ recently demonstrated a LOD of 0.33 μg for RCS using a cascade IR laser focused on a smaller deposit area (1.7 mm in diameter). An advantage of using Raman spectroscopy is that its measurement response more specifically measures the crystalline silica and is able to distinguish between different polymorphs. FTIR measures the absorption of energy from the vibrational and stretching frequencies of molecular bonds. Similar absorbance is found for amorphous silica, which is considered to have lower toxicity than crystalline silica,¹⁷ other polymorphs of crystalline silica and for some silicate minerals that have similar molecular silicon and oxygen bonds. This article describes the validation of a Raman spectroscopy analysis method for the measurement of aerosols of RCS using a silver filter as the analysis substrate. There are two main analytical approaches used in measurement methods for RCS. The first is known as a direct on-aerosol sampling filter analysis approach where the dust on, for example, a polyvinyl chloride (PVC) filter is analysed without further processing.¹⁵ The second is known as an indirect approach, where the sample dust is recovered from the aerosol sampling filter and deposited onto another filter for analysis by the instrument.^18,19 The method employed for this work is an indirect analysis approach where the dust is recovered from a polyvinylchloride (PVC) filter and deposited onto the silver filter. A silver filter is used routinely by some XRD methods for the measurement of aerosol particulate,¹⁹ therefore little modification of current sampling protocols would be necessary to adopt a Raman analysis approach and the filters can be analysed by both techniques for comparative purposes. The silver filter provides a relatively flat surface when compared with other membrane filters, which is important when using a microscope to focus on the aerosol particulate during Raman analysis. This substrate provides little interference for the most common polymorphs of crystalline silica (quartz and cristobalite) and may have the potential to provide a resonance enhanced Raman response when the particles are in close contact with its surface. XRD is the established technique currently employed for the measurement of RCS. XRD analysis is considered less prone to influence from other mineral interferences and changes in measurement response due to differences in the median particle sizes of the measured dust than FTIR, which is the other most commonly used technique. In this work, XRD is used as the reference method and the performance of Raman and XRD measurements were compared when measuring laboratory prepared test samples and when measuring samples from a simulated work task conducted in a calm air chamber.

Particle number concentration measurements are used to assess the fit of masks and respirators on an individual. However, workplace exposures are measured and assessed against exposure limits in terms of mass concentration and the relationship between the two when measuring workplace aerosols is not known. The APFs used for the classification of RPE for workplace provision is based on limited mass concentration inward leakage data, collected from the workplace supported by expert opinion. APFs provide information about the level of protection a type of RPE is expected to achieve in the workplace when compared with mass based exposure limits. Instruments measuring number concentration have been proposed for workplace studies,^20,21 however, any estimates of APFs from these instruments would need to assume that the number concentration based leakage ratio is equivalent to the mass concentration based leakage ratio. In this article, RCS mass concentration inward leakage ratios (ILRs) were compared with those based on particle number concentration values from the Portacount® and miniWRAS instruments. The Portacount® is an instrument commonly used for fit-testing of tight-fitting negative pressure respirators and determines an inward leakage ratio based on a count of the number of particles outside the respirator to those inside the respirator while a series of fit-testing exercises are undertaken. The miniWRAS measures a wider particle size range and reports particle number concentration and mass if it is assumed the all the particles are spherical and have the same density.

Methods

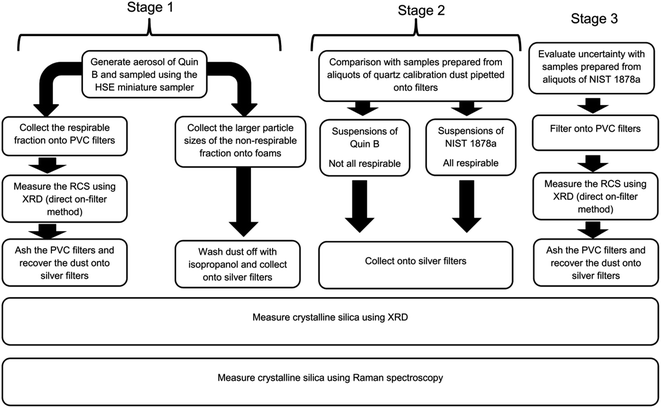
An outline of the structure of the first three stages of this study is provided in Fig. 1. The first stage used the HSE miniature respirable sampler and compared the performance of XRD and Raman when measuring respirable and non-respirable samples of RCS collected from aerosols of calibration dust Quin B. Samples analysed were either deposited directly onto PVC filters or in-directly onto silver filters. The second stage compared the response trend lines of the aerosolised samples collected in the first stage with those of the bulk calibration material (Quin B) and that of a certified reference material of respirable sized quartz NIST 1878a that had been suspended in isopropanol and directly pipetted onto silver filters. For the third stage replicate samples of the certified reference material, NIST 1878a, were also prepared by directly pipetting aliquots from an isopropanol suspension on PVC filters to estimate and compare the uncertainty of the XRD and Raman methods.

Fig. 1 The analytical measurement process.

Stage 1: aerosol preparation of samples using the HSE miniature sampler

Aerosols of respirable quartz (Quin B, Institut National de Recherche et de Sécurité (INRS), France) were generated and sampled onto 13 mm diameter 5 μm pore size polyvinylchloride (PVC) filters (SKC Ltd, Blandford Forum, Dorset, UK) using the HSE miniature sampler.⁹ The procedure to collect these calibration samples is described in HSE's method for the determination of hazardous substances (MDHS) 101 RCS.¹⁵ In brief, the quartz calibration powder of high crystallinity (Quin B) was placed in a glass bowl at the bottom of a bell-type jar and was aerosolised using a short burst of pressurised air. The jar was earthed to reduce agglomeration of particles. The aerosol was sampled using the HSE miniature sampler which was placed at the top of the jar. The HSE miniature sampler uses polyurethane foam (PUF) to first remove the larger sized particles (non-respirable) by filtration from the smaller respirable sized ones, which pass through and are collected on a 13 mm diameter PVC filter. The selection of particles through the foam is dependent on the flow of air. The HSE miniature sampler was calibrated at its specified flow rate for the selection of respirable dust at 0.8 l min⁻¹ using a TSI 4100 flow calibrator (TSI Inc, Shoreview, USA).⁹ The mass of quartz collected on each filter was determined gravimetrically using a balance with a readability of 6 decimal places (Sartorius UK Ltd, Epsom, UK). This was followed by direct on-aerosol filter XRD measurements using standard XRD flat sample holders, modified to include a mask with a 13 mm diameter hole to hold the filters steady at their centre. Each PVC filter was then placed in a glass bottle and ashed using a low temperature plasma asher (Emitech K1050X, Quorum Technologies Ltd, Ashford, UK). The filters were ashed in air at 50% power for 12 h and then in oxygen for 4 h at 95% power. About 5 ml of 99.9% purity isopropanol (Fisher Scientific UK Ltd) was added to the bottle after it was removed from the asher and had cooled. The isopropanol and residue were then sonicated for about five minutes and the suspension was filtered onto 0.45 μm pore size silver filters. The area of the sample deposit was constrained to 78.6 mm² using a bespoke 10 mm diameter filtration funnel. A washer, with a hole of the same diameter as the funnel, was placed under the filter to ensure the uniform spread of sample.

Non respirable dust collected on the PUF particle selectors was also prepared for Raman and XRD analysis. The sample foams were placed into glass bottles, covered with isopropanol and sonicated for 5 minutes. The foams were then washed with more isopropanol, removed from the bottle and the liquor was filtered, (as described above) onto a 10 mm diameter area on fresh silver filters.

Stage 2: comparison with standard materials NIST 1878a and Quin B

The preparation of calibration standards by pipetting aliquots of calibration dust onto a silver analysis filter is common practice in some measurement methods for RCS.^18,19 This approach allows the deposition of a known amount of dust that is traceable to a calibrated metric. It is frequently used because the alternative method to prepare calibration filters, by collecting samples of aerosol onto filters, does not easily permit the preparation of replicate samples; as the aerosol generation cannot be accurately repeated. The bulk quartz power, NIST 1878a (National Institute for Science and Technology, United States) was selected because it is a quartz certified reference material that is completely respirable sized²² and closely represents the particle size of dust collected on the filter after the aerosol is separated into its respective fraction by a respirable sampler.

To test the difference between the response from the aerosol generated samples and a respirable quartz certified reference material, aliquots from a stock suspension of (10 μg ml⁻¹) NIST 1878a in isopropanol were pipetted onto silver filters to provide a trend line of mass and response. The slopes of the trend lines of the bulk materials were compared with the slope of the response from the respirable Quin B collected on the filters from the respirable sampler. A t-test was used to compare the similarity of the slopes of their mass response relationships to confirm that the two dusts were similar after their respective processing with a 95% level of confidence. The null hypothesis is that there is no difference between the slopes, so a probability value of less than 0.05 would indicate that there was a significant difference at the 95% level of confidence. A similar mass response trend line was developed directly from aliquots of the calibration material Quin B, which contains a significant proportion of particles that are not respirable for comparison with trend lines obtained for the quartz dust collected from the foam samples. Each trend line contained samples from two separate suspensions.

Stage 3: uncertainty and repeatability precision

The precision, from the measurement of different replicate samples, was calculated to estimate the uncertainty of the indirect analysis process over the mass loading range between 0.5 to 60 μg. Replicate samples were prepared by filtering aliquots from a suspension of quartz standard reference material (SRM) NIST 1878a in isopropanol (10 μg ml⁻¹) onto PVC filters using the same procedure described above. Five replicate aliquots were filtered at six mass loadings levels, by taking 0.05, 0.1, 0.5, 1, 2 and 5 ml aliquots of stock solution. A 0.45 μm pore size silver filter was placed behind the PVC sample filter to provide support, slow the filtration speed and to check for breakthrough of particles. The PVC filters were measured using XRD, and ashed following the same procedure for the test samples prepared from the respirable Quin B collected on filters. The residues were then transferred to silver filters using the procedure described previously and then quantified using XRD and Raman spectroscopy. The percent relative standard deviations (RSD) for the mean mass value of the Raman measurements were compared with those obtained using XRD measurement of the most sensitive quartz reflection at a 2θ angle of 26.6 degrees made on the same samples. The repeatability precision was calculated from three repeated measurements on a single filter at each mass loading.

Calibration and Raman measurement conditions

Measurement conditions were based on those described in a feasibility study using 5 mm diameter deposit area.¹¹ An In-Via Raman microscope (Renishaw Ltd, Gloucester, UK) with near infrared laser (785 nm) excitation, CCD camera, and a grating with 1200 l mm⁻¹ was used to collect Raman spectra between 314 and 906 cm⁻¹. This range was set to avoid the broad Raman band below 300 cm⁻¹, which was attributed to a trace of silver oxide. Raman spectra were collected from 50 to 90 points along a predetermined line using a ×20 microscope objective with a numerical aperture of 0.4. The minimum area of the focused laser was about 4.5 μm². An automated microscope stage and focus facilitated an operator free data collection process. The automated focus was set to operate for every third field of view position. Spectra were collected at each field of view position using the same laser power and exposure time. Each spectrum was collected by the instrument's laser at 100% power of 500 mW at its source with three accumulations of seven seconds. The integrated areas under the Raman response at 464 cm⁻¹ for quartz was measured by fitting a Gaussian model using the standard algorithms in the manufacturer's WiRE 4 software package for each spectrum collected. The band fitting software in this package was also applied to model and subtract the presence of interference. The mean band area response was calculated for each sample. Spectra that were shown to have saturated the detector were excluded from this calculation. Trends lines were drawn to compare the average area counts and mass. A silicon (Si) wafer was measured before the analysis of a test sample and used as an external standard to compensate for daily fluctuations in laser intensity. The integrated area from the silicon wavenumber shift at 520 cm⁻¹ was measured with a ×50 objective at 10% laser power for 1 s. The average area measurement, calculated for each calibration and test sample, was corrected for fluctuations in laser intensity using the ratio between the area count collected when the silicon was first measured and the average collected on the day of the filter measurement.

X-ray diffraction measurements

The quantity of quartz in test samples was also determined using an X-pert Pro MPD instrument (PANalytical Ltd, Cambridge, UK) with focusing Bragg–Brentano geometry. The instrument used the second set of standard instrumental conditions described in Table A1 of the International Standards Organisation (ISO) standard method ISO 16258-1; 2015.¹⁴ The instrument was fitted with a broad focus copper tube set at 50 kW and 45 mA, automatic scattering and receiving slits set to provide an illumination length of 18 mm and an array detector with the detection area set at 2.12 degrees. The area of the most intense 101 quartz reflection at a 2θ angle of 26.6 degrees was measured for 420 s for each 0.03 degree interval over the range 25.9–27.3 degrees. Tube drift was corrected using the measurement of an aluminium plate as an external standard.

Limit of detection of the Raman measurement

Ten clean PVC filters were prepared for analysis using a plasma asher and the procedure described for the preparation of filter samples from the HSE miniature sampler. The ashed residue of each PVC filter was suspended in isopropanol and then filtered into a 10 mm diameter area onto a 25 mm diameter 0.4 μm pore size silver filter. About 90 spectra were obtained from each filter and the area of any band at the position for the quartz shift close to 464 ± 4 cm⁻¹ in each spectra was quantified using the instruments WIRE™ software. The limit of detection was calculated from the standard deviation of the average Raman area response of the detected quartz shift from ten silver filters. The calculated standard deviation was multiplied by three to estimate the 99% level of confidence.

Limit of detection for XRD analysis

The LOD values for the direct on-aerosol filter XRD measurement of the quartz on 13 mm diameter PVC filters and the indirect XRD measurement approach involving the deposition of the aerosol dust onto a silver filter were measured in two ways. For the direct method ten clean 13 mm diameter PVC filters were first measured by XRD. Subsequently, for the indirect method the same filters were then ashed, their residue suspended in isopropanol, filtered onto a 10 mm diameter area on a silver filter and measured by XRD again. The LOD values for both the direct and indirect measurement approaches were calculated from the average variation of the scatter in the XRD pattern for one degree around the primary quartz reflection at the 2θ angle of 26.6 degrees. The standard deviation of the area measurements of the blank filters was then multiplied by 3. For comparison, the LODs were also calculated following the approach in Stacey²³ to provide an LOD for each measured filter. Stacey²³ showed that direct measurement of the background scatter could provide LOD values that were comparable to the more traditional approach using the measured responses for each sample. A short Matlab script (Mathworks, Cambridge, United Kingdom) was used to fit a line of best fit with a polynomial equation to the scatter around the 2θ angle of 26.6 degrees. The standard deviation of the scatter was multiplied by 1.66 (3/2) to obtain the 99% level of confidence of positive scatter above the line of best fit. The LOD was calculated as a mass by multiplying the standard deviation with the calibration coefficients obtained from the fitted mass response trend lines.

Collection of samples from a simulated work activity

To assess the measurement procedure for inward leakage tests, samples were collected from aerosols generated from a simulated work activity in a calm air chamber. The calm air chamber consisted of three chambers, one on top of the other, with an air flow (about 0.4 m s⁻¹) from the top to the bottom. The work activity involved the power cutting of a sandstone pavement block. Two square chambers, of approximately 1 m³, sit on top of each other separated by an aluminium honeycomb layer (approximately 6 cm deep) to improve laminar flow. A third, pyramid shaped chamber, is sited above the first two and incorporates a deionising fan to allow mixing and reduce charge, as described in previous work.^9,24 In these experiments, a mitre saw with a diamond cutting disc was bolted to a frame in the top pyramid shaped chamber and the deionising fan was situated on top of the honeycomb directly below the simulated work task positioned between the two square boxes. A ‘Sheffield’ manikin head²⁵ was situated in the centre of the bottom chamber and connected to a breathing machine. The breathing machine had a sinusoidal breathing pattern, with tidal volume 1.5 l and rate of 20 breaths per minute (total respiratory minute volume 30 l min⁻¹). This breathing rate and volume were selected to represent a worker conducting sustained hand and arm work over a full shift with breaks.²⁶ The safety in mines personal dust, respirable sampler (SIMPEDS) is frequently used for routine workplace monitoring of respirable dust in the United Kingdom. Three SIMPEDS were positioned equidistant in a line across the chamber in front of the manikin to collect the respirable dust concentration of the chamber. The SIMPEDS were positioned between 10 to 30 cm from the FFP3 respirator placed on the manikin. The inlets for these SIMPEDS samplers were at the level of the mouth on the Sheffield manikin head. PVC filter samples from the SIMPEDS were measured for RCS using XRD and the routine HSE analytical method MDHS 101 (ref. 15) to obtain a measure of the RCS concentration in the chamber. This approach replicates the current standard practice to assess a workers' exposure to aerosols containing RCS, where the sample is collected outside the respirator using the SIMPEDS sampler. The loadings on the filters for the SIMPEDS were much higher than those measured from the HSE miniature sampler within the facepiece of the respirator, therefore the secondary and tertiary quartz XRD reflections at 2θ angles of 20.9 and 50.1 degrees were also quantifiable and measured using the direct on aerosol filter approach specified in MDHS 101. The average of two of the three measured reflections providing the most consistent values for each sample was reported as the mass of RCS from the SIMPEDS sampler. The average RCS value from all three SIMPEDS samplers was used to calculate the concentration of RCS inside the chamber. An FFP3 respirator was positioned over the nose and mouth of the Sheffield head. Two HSE miniature samplers were fixed within the facepiece of the respirator using the same procedure for fixing tubes from particle counting instruments to RPE for face-fit tests.¹⁰ The leakage of crystalline silica into the facepiece was calculated from the ratio of the concentration of RCS from the miniature sampler inside the facepiece, measured using Raman, and the average concentration of RCS on filters from the three SIMPEDS samplers that collected the aerosol concentrations outside the respirator. It has been shown that the performance of the SIMPEDS and HSE miniature sampler to collect respirable aerosol is not significantly different when measuring concentrations of RCS up to 4 mg m⁻³ and with 282 μg as a maximum mass collected on the PVC filter in the miniature sampler. The trend lines diverge from the ideal 1 : 1 relationship at higher mass loadings.⁹

Particle size measurements for the simulated work activity

Two Portacount® (TSI Inc, Shoreview, USA) and two mini Wide Range Aerosol Spectrometer (miniWRAS) aerosol sizing instruments (GRIMM Aerosol Technik Ainring GmbH, Germany) were used in these tests for the comparison of inward leakage values. The Portacount® instrument, which measures the concentration of the number of particles, is commonly employed for inward leakage and face fit testing and has the smallest particle size measurement range. This instrument mostly counts particles from 0.02 μm to a particle diameter of 1 μm. The Portacount® instruments were operated from outside the chamber. One tube from the Portacount® instrument was fixed into the respirator whilst the other was positioned to sample the chamber atmosphere. The miniWRAS instruments were employed as they measure a much wider particle size range. They use two different detectors to cover the particle size range from 0.01 to 32 μm (particle diameter) in 42 sizing channels. This instrument counts the smaller and nano-sized particles (0.010 μm to 0.2 μm) using a unipolar diffusion charger with time multiplexed electrode and Faraday cup electrometer and uses an optical cell for the larger sized particles (0.25 μm to 35 μm). The mass concentration can be estimated if it is assumed that the particles are spheres with the same density. Two miniWRASs were placed inside the bottom of the chamber and operated remotely using wireless technology. The inlet for one miniWRAS was fed into the respirator positioned on the Sheffield manikin head whilst the other miniWRAS was set up to sample the concentration of dust inside the chamber. Potential losses of dust due to electrostatic attraction to the walls of the sampling tubes to the instrument were evaluated and minimised before the experiments. The mass median diameters of the aerosols were calculated by loading the raw data from the miniWRAS into a spreadsheet, converting each particle size bin into a particle volume, multiplying by the number of particles and then the density (2.65 g cm⁻³) to obtain the mass distribution. Tablecurve 2D (version 5.01) software was used to fit a curve to cumulative particle size model and calculate the median mass particle size diameter (MMD). Alarms were set on both the miniWRAS and Portacount® instruments to warn of very high concentrations that could lead to an increased risk of particle counting errors; for example, due to the coincidence of particles within the optical beam at high concentrations. In addition, a deionising fan was used during all experiments to reduce the potential for multiply charged particles and thus reduce counting errors for the electron mobility spectrometer, which is used in the miniWRAS to measure the smaller and nano-sized particles.

Results

Fig. 2 shows the median for the accumulated spectra for a sample of 60 μg, 10 μg and 0.5 μg of NIST 1878a deposited into a 10 mm diameter area onto a 0.45 μm pore size silver filter. Table 1 reports trend line coefficients and coefficients for determination (r²) for the Raman measurements of crystalline silica (quartz) in NIST 1878a and Quin B and aerosolised sub-fractions of Quin B. An intercept is not given when it is not significantly different from zero with a 95% level of confidence.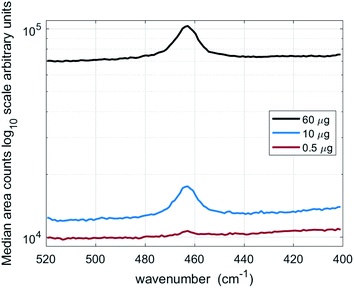

Fig. 2 Median of accumulated spectra from 90 fields of view for filters containing 60 μg, 10 μg and 0.5 μg of respirable quartz (NIST 1878a).

Table 1 Load ranges, trend line equations and coefficients of determination for the Raman spectroscopy calibrations used in this study^a

Quartz dust	Calibration approach	n	Mass range (μg)	Trend line equation	Coefficient of determination
a n denotes the number of samples measured.
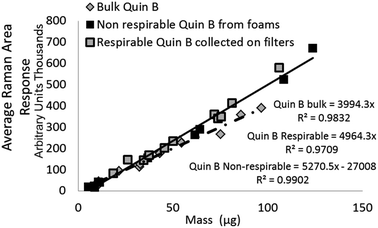
Quin B	Indirect – respirable dust recovered from aerosol sampling filter	11	13 to 106 (gravimetric mass)	Y = 4964x	0.97
	Indirect – non-respirable dust recovered from foam particle selectors	14	5 to 586 (gravimetric mass)	Y = 5411x − 38 099	0.99
	Indirect – non-respirable dust recovered from foam particle selectors (limited mass range)	10	5 to 100 (gravimetric mass)	Y = 4947x	0.98
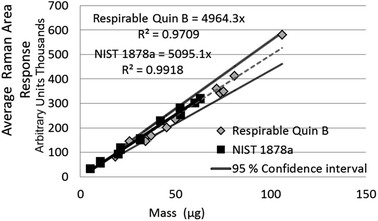
NIST 1878a	Measurement of aliquots from a suspension	14	5 to 60 (theoretical mass)	Y = 5095x	0.99
Quin B	Measurement of aliquots from a suspension	13	10 to 90 (theoretical mass)	Y = 3994x	0.98

---

The difference between the calibration trend line slopes for Raman measurement of NIST 1878a and aerosolised respirable Quin B (Fig. 3) was not significant (p = 0.33). For ease of comparison, the 95% level of confidence is also shown in Fig. 3 for the respirable Quin B results. The other Raman mass response relationships, for the measurement of crystalline silica dust collected by the PUF foam (i.e. with particle sizes larger than respirable) and measurement of the bulk material Quin B (with a large proportion of non-respirable particles), are significantly different at the 95% level of confidence (p < 0.05). However, detector signal saturation occurred at loadings of the non-respirable Quin B above 100 μg when a counting time of seven seconds was applied so counting times were reduced for the highest loaded foam dust calibration samples with non-respirable Quin B to avoid the saturation. The counting time for the highest loaded foam dust calibration sample was 3 seconds for each accumulation. To comply with the calibration measurement conditions we assumed that the difference in response was proportional to the change in measurement time. Each measured band area was multiplied by (7/n), where n is the counting time used to avoid saturation. A linear trend line relationship was observed over the whole mass range with a coefficient of determination of 0.99. When the mass range for the crystalline silica collected in the foams is restricted to samples below 100 μg the slopes of the trend lines for the measurement of respirable Quin B collected on the silver filters and the non-respirable Quin B (Fig. 4) are not significantly different (p = 0.93).

Fig. 3 The difference in average Raman area response at 464 cm⁻¹ between two quartz calibration powders Quin B and NIST 1878a. Quin B was aerosolised and the respirable fraction was collected on PVC filters which were ashed and redeposited onto silver filters. Aliquots of the bulk powder of the certified reference material of respirable quartz (NIST 1878a) were filtered directly onto silver filters.

Fig. 4 The difference in Raman response between the respirable fraction of Quin B collected by the HSE miniature sampler, the non-respirable fraction of the Quin B collected by the foam particle separators and aliquots of the bulk powder Quin B filtered directly onto silver filters.

Table 2 reports the trend line equations and coefficients of determination for the XRD measurements at each stage of the measurement process (Fig. 1) when measuring quartz on the same samples. The trend line slope coefficient when comparing the Raman and XRD measurement values for respirable Quin B was 1.01 with a coefficient of determination of 0.98. The trend line slope coefficients for the mass response relationships of the direct on-aerosol filter XRD measurements of RCS on PVC filters and when collected indirectly onto silver filters, following sampling with the HSE miniature sampler of respirable Quin B are different at the 95%. The slope coefficients for XRD measurements of the bulk certified reference material of respirable quartz (NIST 1878a) pipetted onto silver filters were statistically similar with the respirable Quin B collected with the HSE miniature sampler when the PVC filters were ashed and then recovered onto silver filters (p = 0.35); but not with direct on-aerosol PVC filter measurements for respirable Quin B, the non-respirable Quin B collected on the foams, or the aliquoted bulk Quin B (all p < 0.05). The slope of the trend line obtained from aliquots of bulk Quin B was statistically similar to that of the non-respirable quartz collected on the foams (p = 0.32).

Table 2 Load ranges, trend line equations and coefficients of determination for the X-ray diffraction calibrations used in this study^a

Quartz dust	Calibration approach	n	Mass range (μg)	Trend line equation	Coefficient of determination
a n denotes the number of samples measured.
Quin B	Direct on-aerosol sampling filter (PVC)	17	13 to 106 (gravimetric mass)	Y = 0.441x	0.97
	Indirect – respirable dust recovered from aerosol sampling filter	17	13 to 106 (gravimetric mass)	Y = 0.419x − 1.61	0.99
	Indirect – non-respirable dust recovered from foam particle selectors (limited mass range)	14	5 to 586 (gravimetric mass)	Y = 0.505x	0.99
NIST 1878a	Measurement of aliquots from a liquid suspension	13	5 to 60 (theoretical mass)	Y = 0.390x − 1.26	0.99
Quin B	Measurement of aliquots from a liquid suspension	11	10 to 60 (theoretical mass)	Y = 0.518x	0.98

---

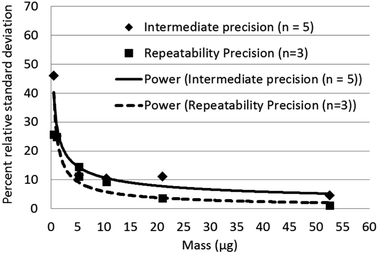
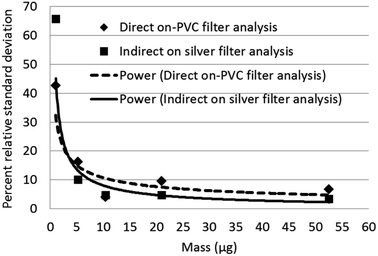
Limits of detection calculated for Raman, and XRD were compared with published values for infrared analysis in Table 3. Raman has the lowest calculated limits of detection for quartz. The intermediate precision for Raman measurement was between 4 to 11 percent relative standard deviation (RSD) (Fig. 5) over the measurement range 6 to 60 μg and increased to 45% at 0.50 μg. The trend line equation for the intermediate precision for the indirect Raman method was y = 29.6x^−0.44. The XRD limits of detection in terms of mass determined using the more traditional approach were 2.3 μg for the direct on-aerosol filter approach and 5.6 μg for the indirect analysis approach. The average standard deviation of the XRD background scatter determined using the Matlab calculation was 0.623 for direct on-aerosol filter measurement and 0.442 for the indirect analysis approach on a silver filter. The precision for XRD measurement (Fig. 6) was from 4 to 16% when measuring with PVC filters for the direct on-aerosol filter approach and decreased to 3 to 10% RSD when measuring the quartz dust recovered on silver filters over the mass range 4 to 47 μg. The % RSD increased to 45 and 66% respectively for the PVC and silver filters with a loading of about 1 μg. The trend line equation for the intermediate precision for the XRD indirect method was y = 46.8x^−0.76. No XRD precision measurements were obtained for mass loadings of quartz below 1 μg because these were not detected.

Table 3 Limits of detection for quartz achieved for each technique and a comparison with values from recently published work. The entries in bold indicate those values that were measured by this work

Technique	Description	Number of measurements	Calculated limit of detection (μg)
a The limit of detection was dependent on the counting time (5 to 30 s) at each field of view. The LODs quoted are for a deposition method. Lower LODs were obtained using a focused collection approach. b A method limit of detection was estimated using Partial Least Squares (PLS) modelling.
X-ray diffraction	Direct on 13 mm diameter PVC aerosol filter	10	1.5 to 3
	Indirect 10 mm diameter area on silver filters	8	5.1 to 6.1
Raman	Indirect 10 mm diameter area on silver filters	10 × 90 spectra	0.26
	Aliquots on 5 mm diameter areas^11	5 × 50 spectra	0.055
	1, 1.5 and 3 mm diameter areas^12	3 × 15 spectra	0.055 to 3^a
Infrared	Direct on 9 mm diameter PVC aerosol filter^36	12	0.5 to 1.5
	Cascade laser focused into 1.7 mm area deposit^16	Not known^b	0.33

---

Fig. 5 Intermediate and repeatability measurement precision for Raman analysis of certified reference material NIST 1878a (respirable quartz) when sample is recovered from the aerosol PVC sampling filter and deposited onto a 10 mm diameter area on a silver filter.

Fig. 6 Intermediate measurement precision of XRD measurement of certified reference material NIST 1878a (respirable quartz) for the principle quartz reflection at a 2θ angle of 26.6 degrees for the direct on-aerosol filter and the indirect measurement approaches.

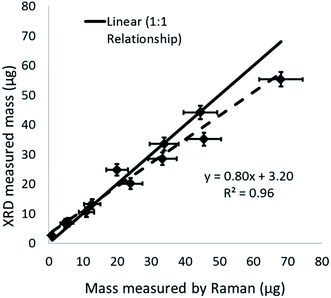
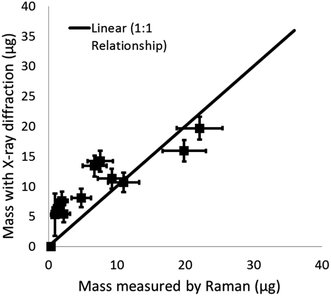
Simulated work activity

The proportion of crystalline silica in the stone was determined using the XRD Rietveld method with nickel oxide as an internal standard. The bulk sandstone used for cutting contained 89% crystalline silica (quartz) with 9% feldspar (microcline), and 2% mica (muscovite 2M1). XRD and Raman results for quartz collected on the PUF particle selector (i.e. non-respirable fraction) inside the HSE miniature sampler during tests in the calm air chamber are compared in Fig. 7. Mass loadings for these foam samples ranged from 0.87 to 63 μg. XRD and Raman measurements collected on the filters (i.e. the respirable fraction) in the miniature sampler inside the respirator are shown in Fig. 8; these, as anticipated, show lower mass loadings. If both the XRD and Raman results are exactly the same they should follow the ideal 1 : 1 relationship. The error bars in Fig. 7 and 8 show the 95% level of confidence for each of pair of measurements which were calculated from the intermediate precision for indirect analytical approach applied for each instrument.

Fig. 7 A comparison of Raman and XRD measurements on the same samples when measuring the fraction of quartz collected from the particle size selective foams in miniature samplers placed inside a face filtering particulate respirator on a breathing manikin.

Fig. 8 A comparison of Raman and XRD measurements on the same samples when measuring the respirable crystalline silica (quartz) emitted from the cutting of a sandstone block and collected on the PVC filters from miniature samplers placed inside a face filtering particulate respirator on a breathing manikin.

On average, 95% of particles (by number) emitted from the cutting process and measured by the miniWRAS were less than 0.68 μm for the outside aerosol and 0.58 μm for the aerosol inside the respirator (Fig. 9). The mass median diameters measured by the miniWRAS of the aerosol outside and inside the respirator were between 4.35 μm to 9.47 μm and 4.29 μm to 5.60 μm, respectively. The mass median diameter (MMD) inside the respirator increased as the outside concentration increased following the equation:

MMD inside the respirator = 0.212 (MMD outside) + 3.54 (1)

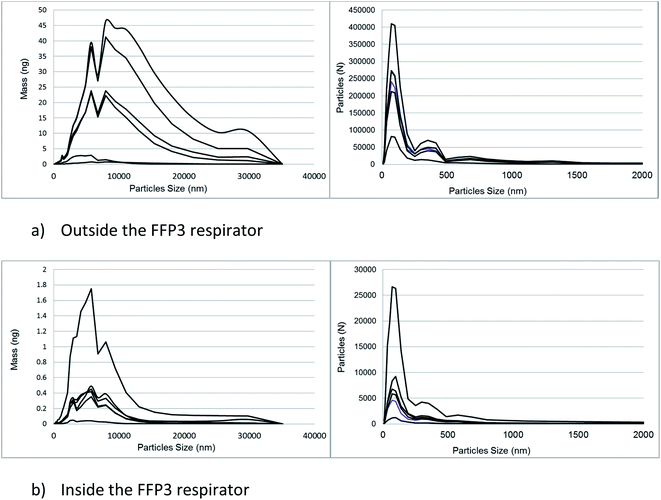Fig. 9 A comparison of the mass and particle number distributions of the emission generated by cutting sandstone using a diamond blade.

The coefficient of determination was 0.89 and the MMD were reported in μm. The filter samples were weighed to determine the mass of respirable dust collected by the respirable samples positioned inside and outside the mask. The proportion of crystalline silica, determined using Raman spectroscopy, in the respirable dust samples collected inside the respirator (median = 34%) decreased with reducing mass and inward leakage ratio and was less than the proportion in the respirable dust samples outside (median = 73%). Fig. 9 shows the number and mass distribution of particle sizes detected by the miniWRAS in the aerosols outside and inside the respirator. Generally, the proportions of particle sizes inside and outside the respirator remained reasonably consistent over the whole particle size range. An example of this effect is provided in Fig. S1 (ESI†). An inward leakage ratio (ILR) is the ratio of the concentration of particles measured inside the respirator divided by the concentration of aerosol outside the respirator. Table 4 compares the percentage ILRs determined from the Raman measured RCS mass concentrations with the particle number concentration ratios measured by the Portacount® instrument and number and mass concentrations measured by the miniWRAS in terms of the percentage leakage into the respirator. The ILR values from the respirable dust measurements are not shown because the values for the in-mask samples are generally close to their limit of quantification; however, the ILR for the highest in-mask respirable dust sample collected from test 6 with a mass loading of 37 μg was 13.4.

Table 4 Inward leakage ratio (ILR) percentages calculated from each metric and instrument used in the calm air chamber experiments when challenged to an aerosol of sandstone dust generated using a power saw

Metric	Concentration of particles (Portacount® ILR) percent (%)	Concentration of particles (miniWRAS ILR) percent (%)	Respirable mass concentration (miniWRAS ILR) percent (%)	Respirable crystalline silica concentration (Raman ILR) percent (%)
Test 1	1.14	0.49	0.36	0.60
Test 2	2.16	1.42	1.18	1.97
Test 3	2.87	11.39	13.40	2.49
Test 4	3.49	2.36	1.79	1.06
Test 5	6.91	2.09	1.72	3.05
Test 6	27.88	13.25	10.71	6.69

---

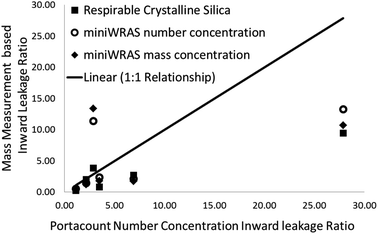
The relationship between the ILRs based on the Raman measured RCS mass concentration and those determined using number concentration from the Portacount® instrument are shown in Fig. 10. Qualitatively, the three highest ILRs from the Portacount®, which are calculated from the ratios of particle number concentrations, were much higher than the miniWRAS, measuring both number and mass concentrations and the respirable crystalline silica concentration ILR values (Fig. 10). The highest particle concentration measured the Portacount® was 17 025 particles per cm³ which is within the upper limit specified by the manufacturer of 2.5 × 10⁵ particles per cm³. However, the miniWRAS obtained particle concentrations that were 2× to about 4× more than the Portacount®. The largest particle concentration measured by the miniWRAS was 50 000 particles per cm³.

Fig. 10 Trend line between the percent inward leakage ratios (ILR) determined by the Portacount® instrument using particle number concentration and those determined measuring the mass of respirable quartz.

Discussion

The advantage of Raman spectroscopy over XRD when measuring low concentrations of RCS collected from inside respirators are demonstrated in this work. The Raman obtains measurements that are comparable with XRD and has similar uncertainty estimates with a much lower LOD.

Raman photon scatter originates from a small fraction of the applied laser photons and the laser energy is potentially sufficient to cause photoluminescence (emission and fluorescence) effects in particles. The fluorescence effects are often much greater than the magnitude of the Raman bands and can swamp the detector; however, no samples in this work were not measurable because of fluorescence. In addition, other particles in close proximity of the analyte of interest may enhance the magnitude of the Raman shift or absorb the Raman photons as they are emitted. The measurement strategy applied in this work helps the Raman system overcome potential issues associated with fluorescence and stray Rayleigh scattering. The choice of laser wavelength to reduce the risk of fluorescence, the averaging of accumulated micrometre area spectra, the spatial separation of particles and the characteristics of a respirable dust sample collected on a filter surface all play their role to reduce the effect of interference.

The accumulation and averaging of multiple micrometre area spectra across the surface of a uniformly distributed sample permits the exclusion of occasional spectra with saturation or too much interference; since the average should be relatively consistent, provided sufficient spectra are collected. Measuring low concentrations also improves the spatial separation of particles and reduces interference effects. For example, a feasibility study¹¹ measuring 20% quartz in a photon absorbing hematite (Fe₂O₃) mineral mixture in deposit areas of 5 mm in diameter showed that quartz was measurable to a specific particle density before absorption reduced the response. XRD measurement has similar issues with absorption in mixtures of hematite²⁷ which is overcome using a standard to correct for the reduced transmittance. The larger 10 mm diameter deposit areas applied in this work enables measurement of higher loadings that are more able to cope with routine sample deposits and the LOD is sufficient to enable an improved measurement despite a loss of sensitivity, due to a reduced particle density per unit mass, when compared with the feasibility study.¹¹ It's possible to exclude the occasional spectra with a high fluorescence and interference and still obtain an accurate result if the density of particles (and therefore the average) is reasonably consistent across the surface of the filter and sufficient spectra from a sample are analysed.

A major technical challenge is to determine, with reasonable accuracy, whether a respirator is performing to the APF it is expected to achieve in the workplace. Sensitive measurements are needed because of the small mass of RCS collected during sampling. Where high exposure to RCS is likely to occur, an FFP3 respirator or another type of respirator with an equivalent or higher APF may be worn during workplace tasks, in addition to other control measures. Therefore, potentially short sampling times and the low WEL for RCS (100 μg m⁻³ as an 8 h time weighted average) highlight the importance of using a technique with a sufficiently low limit of detection. Table 3 shows that the Raman method has the lowest LOD for the measurement of RCS on test filters compared to XRD, FTIR, and cascade IR methods. In this study, the expected mass of RCS collected on a filter from the miniature sampler within the facepiece of tight-fitting respirator is above the Raman method limit of detection when a worker is wearing a respirator for 1 h, the respirator is performing to its APF of 20 and the challenge concentration of RCS outside the respirator matches expected concentration for the workplace exposure limit i.e. 1/8^th of 100 μg m⁻³ (the 8 h WEL). This theoretical calculation indicates that Raman spectroscopy is a technique that can be used to assess the applicability of the APF when sampling for an hour. In practice, the RCS concentrations are likely to be higher than this because respirators are generally worn for work tasks with the potential to produce the highest exposures despite the use of other control measures. Further improvements to the Raman sensitivity and LOD beyond those achieved in this study are also potentially possible by collecting scans from more measurement points, by increasing measurement time in each measurement point¹² or, by further concentrating the sample into a smaller deposit area.¹¹ However, concentrating the sample into a smaller area may also increase the risk of interference, absorption and fluorescence from other particles. Zheng et al.¹² reported a direct proportional relationship between increases in sensitivity of the Raman response with decreasing circular deposit areas with diameters from 3 to 1 mm. A proportional relationship with deposit area is also shown when comparing our current work using 10 mm deposit area with our previous work on 5 mm diameter area (ESI Fig. S2†).¹¹ Therefore, analysts can potentially apply the technique to any deposit area size without further calibration by applying a predictable factor, assuming the particle density does not increase the risk of interfering factors.

An evaluation of this and recent work highlights the importance of the deposit area in determining the sensitivity and LOD for all the analysis techniques involved with the measurement of RCS (Table 3). Generally, the LOD is reduced as the deposit area decreases. Samples are usually collected and measured on 25 or 37 mm diameter filters. Concentrating the sample improves the response for techniques like Raman, which examine a small area in each field of view measured. Concentrating the sample into a 9 or 10 mm diameter area for XRD and IR analysis, also moves the whole sample within the full width of the infrared beam, which is between 7 mm to 9 mm or the area that provides most XRD response, which is about 15 mm in diameter. A deposit area of 10 mm in diameter should also reduce the possibility of obtaining a trend line relationship for XRD or IR with a significant negative intercept; since there is no potential for mass to be outside the analysis area that does not contribute to the measurement response. The change in LOD with measurement area suggests that LODs obtained by industry practitioners could be different from those stated in national or international methods for indirect RCS analysis, if the deposit area is not specified.

Comparison of the quantification of RCS determined by XRD and Raman (Fig. 7 and 8) from the calm air chamber experiments demonstrates that the results reported have a linear relationship. The slight differences between the Raman and XRD values are probably caused by the influence of a negative intercept coefficient, where the intercept was significantly different from zero, for one of the two measurement techniques. For example, Fig. 8 shows XRD measured values have a positive bias towards higher values when comparing XRD and Raman measurements on the same samples at low measurement levels less than 15 μg. Although, the lowest mass for test samples with a measurable XRD response was about 1 μg, the application of the intercept provides a higher estimated LOD of about 5 to 6 μg (Table 3). The observed number (about 1 μg) does not agree with the calculated XRD LOD value of 5 μg to 6 μg; which is similar to the LODs currently reported in analytical methodology.^14,15,19 The LODs for the XRD methods were confirmed using the two different approaches discussed in the methodology section. Further investigation showed that, the variability of the X-ray scatter reflected from the filter and sample holder obtained from measurements on the silver filters (for the indirect analysis approach) was lower than that obtained from measurements on the PVC filters (for the direct on-aerosol filter approach); which has a higher X-ray scatter but lower LOD. This seems to indicate that the over prediction of the LOD for the indirect XRD analysis approach is due to the application of the intercept coefficient for the XRD calibration trend line response and that in this instance a nonlinear trend line relationship might be more suitable to fit loadings close to the intercept. The XRD method adopted by the Occupational Safety and Health Administration (OSHA) in the United States uses a polynomial curve to fit logarithmically transformed data;¹⁸ which assumes the relationship between mass and XRD response is curved. Forcing the XRD results herein through zero produces a trend line Y = 0.393 with a coefficient of determination (r²) of 0.99. The correspondence between the Raman and XRD values now converge around the 1 to 1 line for the ideal relationship (Fig. S3 ESI†).

Fig. 3 demonstrates a close match between the mass response of NIST 1878a and the aerosolised ‘Quin B’ when collected on a filter after the PUF particle selector. This level of significance (p = 0.36) demonstrates the suitability of this NIST 1878a as a standard for the indirect analysis method, where dust is recovered from the aerosol sampling filter and deposited onto another filter for analysis. The comparability of the NIST 1878a powder provides an opportunity for analysts to prepare calibration, replicate and quality control standards from a liquid suspension rather than employ a more elaborate and less repeatable process of collecting a dust sample from a generated aerosol. Moreover, an improved calibration approach is to include laboratory test samples prepared onto the filters used for collection of the aerosol and to develop a trend line with the intercept forced through zero or to model a curve towards zero at low mass loadings.

The samples with non-respirable quartz dust from the foams had the highest loaded masses measured by Raman and were used to assess the upper limits of measurement. A linear Raman measurement response was obtained up to 586 μg with a coefficient of determination of 0.99. Higher loaded masses (greater than 100 μg) were affected by high saturation of the detector and were only measurable by reducing the measurement time during data collection. A significant factor limiting the upper measurement threshold appears to be the saturation of signal at the detector rather than absorption of the Raman response due to the density and depth of the dust sample. A technique to compensate for this is to reduce the counting time during analysis and mathematically correct the measured area counts to comply with the measurement counting conditions for the calibration (Fig. 3). The laser energy could also be reduced; however, it would be more convenient if the detector were able to accommodate the increase in counts from the sample.

The response of many techniques measuring RCS is affected by differences in particle sizes²² however, previous work¹¹ has shown that Raman was not significantly affected when measuring Quin B and NIST 1878a, which have different mass median diameters (3.7 and 7.2 μm, respectively), over a limited mass measurement range with a maximum mass of 12 μg. In this work, the mass responses for the respirable and the non-respirable fractions of Quin B collected by the miniature sampler are also not statistically different (Fig. 4) when the measured range is restricted to those samples less than 100 μg, however, the trend response for the bulk Quin B powder is significantly different. Many of the mass response values for the bulk Quin B coincide with the trend lines for the respirable and non-respirable Quin B collected by the miniature sampler at lower measured masses below 50 μg (Fig. 4). The mass response trend lines also tend to converge as they approach zero. There could be several reasons for this including; firstly, the particle size distribution of the bulk material will not be the same as the aerosolised dust because the heavier particles tend to fall out quicker, and secondly, the particle size distribution is also less diverse for lower mass samples improving the uniformity of the particle size distribution and consistency of measurements. For example, the d₅₀ of the aerosol size distributions was reduced as the aerosol concentration decreased (Fig. 9). The advantage of a multiple point measurement approach (with each point having a small (micro) sampling area) is that it is likely to reduce the particle size dependence of the measurements when mass loadings are low. Each sampling point measured using Raman looks at a very small part of the available sample and the measurement will encounter larger numbers of smaller sized particles at low concentrations than the larger sized particles. The occurrence of larger sized particles in each measured sampling point increases at higher mass loadings, which may change the average sample response for sample masses higher than 50 μg. A multiple point micro measurement approach may also reduce the particle size dependency of the measurement response for other techniques e.g. XRD and FTIR.

This work demonstrates that Raman and XRD have the similar analytical uncertainty over the range from about 5 to 60 μg when measuring test samples (Fig. 5 and 6); however, Raman has a much lower LOD. The lower LOD enables Raman measurements of RCS to potentially meet all the European requirements in EN 482:2012 + A1:2015 (ref. 28) for the performance of occupational hygiene analytical methods when measuring regulatory limit values at mass loadings below those currently possible using traditional XRD and FTIR methods. EN 482:2012 + A1:2015 has three requirements for long term measurements to assess worker exposures against an occupational exposure limit. These are;

• The measurement range of the method must be from 0.1 to 2 times the exposure limit,

• The expanded relative uncertainty of the measurement (including sampling) should be less than or equal to 30% when measuring from 0.5 to 2 times the exposure limit,

• And the expanded relative uncertainty (including sampling) should be less than or equal to 50% when measuring from 0.1 to 0.5 times the exposure limit.

A Raman measurement at 10 μg on low particle density test samples free of interference meets all these requirements. This statement assumes the sampling errors are 11.8% as specified in ISO 24095,²⁹ the sampling and measurement precision are combined as the square root of the sum of squares and the uncertainty is multiplied by a coverage factor of 2. A mass of 10 μg would equate to an air concentration of about 10 μg m⁻³ being sampled for 7 h using a respirable sampler at a typical flow rate of 2.2 l min⁻¹. This theoretical concentration value of 10 μg m⁻³ is 10% of the WEL in GB and 20% of the current regulatory limit for RCS in the United States.³⁰ However, it is not currently known if the Raman approach will have the same level of performance with more complex dust mixtures with a greater particle density, and in samples collected with the types of aerosol samplers and filter diameters that are more commonly employed for work exposure assessments or reassurance testing.

Raman was successfully employed for the measurement of RCS within a facepiece respirator samples using mass measurement instruments.

The placing of an FFP3 respirator on a breathing manikin reduced the number of particles leaking into the masks across all particle sizes when compared with the number of particles in the chamber outside the respirator (Fig. 9). This general reduction in numbers of particles inside the facepiece of the FFP3 respirator compared with outside also resulted in a decrease in the mass median aerodynamic diameter inside the respirator due to a smaller number of larger particles that contributed most to the sample mass. For example, a single 10 μm diameter particle of quartz is about 1000 times heavier than a single particle with a diameter of 1 μm; so, a relatively small number of larger particles of about 10 μm can have a significant impact in terms of mass. Whether a larger diameter particle (e.g. greater than 10 μm in diameter) is present inside an FFP3 respirator might be due to probability and not necessarily as a result of any particular property of the respirator. For example, there is a lower probability of observing larger diameter particles inside a respirator if they are not present in significant numbers in the outside aerosol. The relative consistency of the percentage proportions of particles inside and outside the respirator at each particle size range recorded by the miniWRAS is in contrast with other work,³¹ although charts in Rengasamy and Eimer³² indicate that the relative ILR can be fairly consistent in certain conditions over the nanoparticle size range when investigating leakage with sealed FFP3 respirators. In this study, there was no attempt to deliberately put a hole through the respirator and the most likely leakage route would have been around the nose piece and chin of the respirator through a soft rubber type of seal rather than through the value.

A comparison of particle number concentration measurements using the Portacount® and mass concentration measurements of RCS using Raman spectroscopy is currently not generally applicable to workplace practice. Instruments reporting particle number concentration measurements are specifically used to help assess the fit of worker's RPE and mass based measurements are used to derive APFs to assess protection of RPE from work based tasks were exposures and exposure limits are measured in terms of their mass concentration. The Portacount® obtained higher ratios for the three highest ILRs (Fig. 10) than the RCS mass determined by Raman spectroscopy or the miniWRAS, which reports both number and mass concentrations.

All aerosol measuring instruments have errors associated with both the aerosol sampling and measurement which combine and contribute to the overall uncertainty of the reported concentration value. The uncertainty of an inward leakage ratio value is the addition of the uncertainty of both the two measurements (outside and inside the mask). When a respirator is performing to its APF the leakage will be low and the in-mask measurement will usually make the largest contribution to the overall uncertainty of the ILR. The counting errors made by optical particle number concentration instruments like the Portacount® and the optical detector in the miniWRAS, used for the larger sized particles, are well established.³³ Optical particle sizing instruments are calibrated using uniform spheres with a specific refractive index. The calibration particles' characteristics may differ from the those measured from a workplace aerosol and the instruments often need a calibration that is specific for the expected matrix due to the nature of light scattered by the particles.³⁴ Large counting errors are also attributed to the coincidence of particles at high concentrations, the fluctuation of concentrations of particles in the size range just smaller than the lowest detectable particle size and Rayleigh scatter.³³ The miniWRAS uses an electrical mobility spectrometer to count particles at the lowest sizes, for particle sizes below 1 μm, however, counting errors can also occur from multiply charged particles.³⁵ For this study, particle number concentrations were kept below thresholds specified by the manufacturer that cause an increase in the risk of particle coincidence, and a deionising fan was also included to reduce the potential for agglomeration of multiple charged particles. We discount the possibility that the Portacount® measured lower a concentration of particles outside the respirator due to the coincidence of particles (so increasing the ILR) because the concentrations measured are within the manufacturers' specification and the risk of this event significantly affecting the ratio is low. Differences between instruments are better explained by the different particle size measurement range and metric used by each instrument. For example, although the relative proportions of large and small particles leaking into a respirator in the tests were relatively consistent when using the miniWRAS over the whole particle size range, the increase in absolute number of smaller sized particles (less than 0.5 μm in diameter) is greater than the increase in absolute number of larger diameter particles (Fig. 9) when the particle concentration is higher i.e. for the higher ILR values. Therefore, the Portacount®, measuring the smallest size range in terms of particle number concentration (mostly less than 1 μm) is potentially more sensitive when a leak occurs in these tests than the miniWRAS which measures particle diameters from 0.01 μm to 32 μm.

Recently published work involving the measurement of artificial aerosols of salt (NaCl) has found that the Portacount® obtained ratios that were twice as high as those obtained with a flame photometer, which measures all particle sizes sampled containing NaCl.²¹ It was also confirmed that the particle size distribution inside the mask was similar to that found outside and when measuring particle size diameters below 10 μm.²¹ These findings are similar to the observations in this work, which used more realistic aerosols of mineral dust generated from a simulated work task and the procedures applied in the workplace for the collection of samples to measure the mass concentration of RCS. This article highlights the advantage of using Portacount® instruments for its current employed purpose, which is for face fit testing in ambient environments, because its sensitivity when measuring small particle sizes is high. The main purpose of the RCS specific measurement by Raman spectroscopy is not to assess fit but to determine the actual exposure of workers when wearing respirators. The hazard specific RCS measurement is potentially more accurate for this purpose when compared with a particle counting measurement that has to assume all the particles are RCS and have the same spherical shape and same density to convert a number to a mass concentration value.

However, the limited data from this study is insufficient to determine any true statistical correlation between particle number and mass based measurements, although large differences were observed between the other instruments and high Portacount® particle number ILRs in these tests. Further workplace and laboratory measurements are needed to confirm these data.

Conclusion

Raman spectroscopy is a viable technique for the analysis of RCS from low concentrations of dusts collected after penetrating the facepiece of a tight-fitting FFP3 respirator. This work also indicates the potential of Raman to provide workplace measurements of RCS at lower mass concentrations below the WEL than are currently possible with traditional analysis techniques (XRD and FTIR instruments) as Raman spectroscopy has the lowest reported LOD.

The sample deposit area is a significant factor that affects measurement sensitivity and LOD for all analytical techniques measuring RCS (i.e. XRD, IR and Raman). Smaller sample deposit areas improve measurement sensitivity because the sample either becomes more concentrated or more of the sample is within the analysis area of the instrument.

Results from XRD and Raman are comparable, and it is recommended that a zero intercept is included in the XRD trend line relationship or to model the intercept towards zero for low mass measurements.

Saturation of the detector, when the sample loading is high (about 100 μg), is a significant potential limitation for Raman measurement when measuring densely loaded samples.

An analytical approach based on the measurement of multiple micro-sized points within a sample may reduce the dependence of measurement response on particle size for some techniques.

An FFP3 respirator placed over the mouth of the breathing manikin reduced the particle number and mass concentrations within the respirator compared to outside across all measured particle sizes. A linear relationship was observed between the mass median diameter of the particles within the facepiece of an FFP3 respirator and the mass median diameter of the challenge aerosol outside the respirator.

Instruments reporting particle number concentration measurements are specifically used to help assess the fit of worker's RPE and mass based measurements are used to derive APFs which are used to assess protection of RPE from work based tasks. The limited data from this study suggest that these distinct roles are appropriate for each measurement metric. Further workplace and laboratory measurements are needed to confirm these comparisons of inward leakage data.

Disclaimer

This publication and the work it describes were funded by the Health and Safety Executive (HSE). Its contents, including any opinions and/or conclusions expressed, are those of the authors and do not necessarily reflect HSE policy.

Conflicts of interest

There are no known conflicts of interest.

Acknowledgements

Thanks to Ian Pengelly, Laurie Davies, Margaret Wade and Susan Hambling (Health and Safety Executive) for their technical and editorial reviews. Thanks also to Rhiannon Mogridge (Health and Safety Executive) for her support with the calm air chamber tests, calibrating the breathing manikin and looking after the Portacount® and miniWRAS instruments and to Timothy Yates for his support with developing the Matlab code.

References

1. CEN, EN 481:1993, Workplace atmospheres—Size fraction definitions for measurement of airborne particles, European Committee for Standardisation, Brussels, 1993.
2. T. Brown, J. W. Cherrie, M. Van Tongeren, L. Fortunato, S. Hutchings and L. Rushton, The burden of occupational cancer in Great Britain lung cancer, Health and Safety Executive, Bootle, Liverpool, 2012.
3. HSE, EH75, Respirable Crystalline Silica, Variability in fibrogenic potency and exposure–response relationships for silicosis, Health and Safety Executive, 2003, Report No. ISBN 978 0 7176 2191 0.
4. L. Rushton, S. J. Hutchings, L. Fortunato, C. Young, G. S. Evans and T. Brown, et al., Occupational cancer burden in Great Britain, Br. J. Cancer, 2012, 107(suppl. 1), S3–S7.
5. HSE, The Control of Substances Hazardous to Health Regulations 2002 (as amended), Health and Safety Executive, Crown, Norwich, United Kingdom, 2005.
6. M. Hery, M. Villa, G. Hubert and P. Martin, Assessment of the performance of respirators in the workplace, Ann. Occup. Hyg., 1991, 35(2), 181–187.
7. S. Chazelet, P. Wild, E. Silvente and C. Eypert-Blaison, Workplace Respiratory Protection Factors during Asbestos Removal Operations, Ann. Work Exposures Health, 2018, 62(5), 613–621.
8. S. Steinle, A. Sleeuwenhoek, W. Mueller, C. J. Horwell, A. Apsley and A. Davis, et al., The effectiveness of respiratory protection worn by communities to protect from volcanic ash inhalation; Part II: Total inward leakage tests, Int. J. Hyg. Environ. Health, 2018, 221, 977–984.
9. P. Stacey, A. Thorpe, R. Mogridge, T. Lee and M. Harper, A New Miniature Respirable Sampler for In-mask Sampling: Part 1—Particle Size Selection Performance, Ann. Occup. Hyg., 2016, 60(9), 1072–1083.
10. R. Mogridge, P. Stacey and J. Forder, A New Miniature Respirable Sampler for In-mask Sampling: Part 2—Tests Performed Inside the Mask, Ann. Occup. Hyg., 2016, 60(9), 1084–1091.
11. P. Stacey, K. T. Mader and C. Sammon, Feasibility of the quantification of respirable crystalline silica by mass on aerosol sampling filters using Raman microscopy, J. Raman Spectrosc., 2017, 48(5), 720–725.
12. L. Zheng, P. Kulkarni, M. E. Birch, K. Ashley and S. Wei, Analysis of Crystalline Silica Aerosol Using Portable Raman Spectrometry: Feasibility of Near Real-Time Measurement, Anal. Chem., 2018, 90(10), 6229–6239.
13. ISO, ISO 19087:2018, Workplace air—Analysis of respirable crystalline silica by Fourier-Transform Infrared spectroscopy, International Organisation for Standardisation, Geneva, Switzerland, 2018.
14. ISO B, 16258-1, Workplace Air – Analysis of Respirable Crystalline Silica using X-Ray Diffraction. Part 1. Direct-on-filter Method (ISO), ed. ISO, British Standards Institution, Chiswick, London, 2015.
15. HSE, Methods for the Determination of Hazardous Substances, MDHS 101/2 Crystalline Silica in Respirable Airborne Dust, Direct On-Filter Analyses by Infrared Spectroscopy and X-Ray Diffraction, Health and Safety Executive (HSE), Crown, Norwich, United Kingdom, 2014.
16. S. Wei, P. Kulkarni, K. Ashley and L. Zheng, Measurement of Crystalline Silica Aerosol Using Quantum Cascade Laser-Based Infrared Spectroscopy, Sci. Rep., 2017, 7(1), 13860.
17. J. K. McLaughlin, W. H. Chow and L. S. Levy, Amorphous silica: A review of health effects from inhalation exposure with particular reference to cancer, J. Toxicol. Environ. Health, 1997, 50(6), 553–566.
18. OSHA, Method ID142, Crystalline Silica. Quartz and Cristobalite, in Industrial Hygiene Chemistry Division, ed. OSHA, Salt Lake Technical Center, Sandy, UT 84070-6406, United States, 2015.
19. NIOSH, Silica, Crystalline, by XRD (filter redeposition) Method 7500, ed. K. Ashley, Department of Health and Human Services, National Institute for Occupational Safety and Health, 2003.
20. S.-A. Lee, S. A. Grinshpun, A. Adhikari, W. Li, R. Mckay and A. Maynard, et al., Laboratory and Field Evaluation of a New Personal Sampling System for Assessing the Protection Provided by the N95 Filtering Facepiece Respirators against Particles, Ann. Occup. Hyg., 2005, 49(3), 245–257.
21. C. Sun, C. Thelen, I. Sancho Sanz and A. Wittmann, Evaluation of a New Workplace Protection Factor-Measuring Method for Filtering Facepiece Respirator, Saf. Health Work, 2020, 11(1), 61–70.
22. P. Stacey, E. Kauffer, J.-C. Moulut, C. Dion, M. Beauparlant and P. Fernandez, et al., An International Comparison of the Crystallinity of Calibration Materials for the Analysis of Respirable alpha-Quartz Using X-Ray Diffraction and a Comparison with Results from the Infrared KBr Disc Method, Ann. Occup. Hyg., 2009, 53(6), 639–649.
23. P. Stacey, A study to assess the performance of an “X-ray powder diffraction with Rietveld” approach for measuring the crystalline and amorphous components of inhalable dust collected on aerosol sampling filters, Powder Diffr., 2019, 1–9.
24. P. Stacey, T. Lee, A. Thorpe, P. Roberts, G. Frost and M. Harper, Collection Efficiencies of High Flow Rate Personal Respirable Samplers When Measuring Arizona Road Dust and Analysis of Quartz by X-ray Diffraction, Ann. Occup. Hyg., 2014, 58(4), 512–523.
25. CEN, EN 149:2001 + A1:2009, Respiratory protective devices—Filtering half masks to protect against particles—Requirements, testing, marking, Comité Européen De Normalisation, Brussels, Belgium, 2009.
26. ISO, ISO/TS 16976-1:2015, Respiratory protective devices—Human factors. Part 1: Metabolic rates and respiratory flow rates, International Standards Organisation, Geneva, Switzerland, 2015.
27. M. Mecchia, C. Pretorius, P. Stacey, M. Mattenklott and E. Incocciati, X-Ray Absorption Effect in Aerosol Samples Collected on Filter Media, ed. T. Lee and M. Harper, ASTM International, West Conshohocken, PA, United States of America, 2013.
28. CEN, EN 482:2012 + A1:2015, Workplace exposure. General requirements for the performance of procedures for the measurement of chemical agents, Comité Européen De Normalisation, Brussels, Belgium, 2015.
29. ISO, ISO 24095:2009, Workplace air – Guidance for the measurement of respirable crystalline silica, International Standards Organisation, Geneva, Switzerland, 2009, ISBN 978 0 580 58960 7.
30. Rules and Regulations, Final Rule. Occupational Exposure to Respirable Crystalline Silica, Occupational Safety and Health Administration, 2016.
31. W. C. Hinds and G. Kraske, Performance of Dust Respirators with Facial Seal Leaks: I. Experimental, Am. Ind. Hyg. Assoc. J., 1987, 48(10), 836–841.
32. S. Rengasamy and B. C. Eimer, Total Inward Leakage of Nanoparticles Through Filtering Facepiece Respirators, Ann. Work Exposures Health, 2011, 55(3), 253–263.
33. A. E. Martens, Errors in Measurement and Counting of Particles Using Light Scattering, J. Air Pollut. Control Assoc., 1968, 18(10), 661–663.
34. N. Sang-Nourpour and J. S. Olfert, Calibration of optical particle counters with an aerodynamic aerosol classifier, J. Aerosol Sci., 2019, 138, 105452.
35. N. Takegawa and H. Sakurai, Laboratory Evaluation of a TSI Condensation Particle Counter (Model 3771) Under Airborne Measurement Conditions, Aerosol Sci. Technol., 2011, 45(2), 272–283.
36. T. Lee, L. Lee, E. Cauda, J. Hummer and M. Harper, Respirable Size-Selective Sampler for End-of-Shift Quartz Measurement: Development and Performance, J. Occup. Environ. Hyg., 2017, 14(5), 335–342.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ay00165a

---