Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new class of ratiometric small molecule intracellular pH sensors for Raman microscopy†
Liam T.
Wilson
 a,
William J.
Tipping
a,
William J.
Tipping
 b,
Lauren E.
Jamieson
b,
Lauren E.
Jamieson
 b,
Corinna
Wetherill
b,
Zoë
Henley
c,
Karen
Faulds
b,
Corinna
Wetherill
b,
Zoë
Henley
c,
Karen
Faulds
 *b,
Duncan
Graham
*b,
Duncan
Graham
 *b,
Simon P.
Mackay
*b,
Simon P.
Mackay
 d and
Nicholas C. O.
Tomkinson
d and
Nicholas C. O.
Tomkinson
 *a
*a
aDepartment of Pure and Applied Chemistry, WestCHEM, Thomas Graham Building, University of Strathclyde, 295 Cathedral Street, Glasgow, G1 1XL, UK. E-mail: Nicholas.Tomkinson@strath.ac.uk
bCentre for Molecular Nanometrology, WestCHEM, Department of Pure and Applied Chemistry, Technology and Innovation Centre, University of Strathclyde, 99 George Street, Glasgow, G1 1RD, UK
cGlaxoSmithKline Medicines Research Centre, Gunnels Wood Road, Stevenage, SG1 2NY, UK
dStrathclyde Institute of Pharmacy and Biomedical Science, University of Strathclyde, 161 Cathedral Street, Glasgow, G4 0RE, UK
First published on 2nd July 2020
Abstract
Intracellular pH (pHi) homeostasis is intertwined with a myriad of normal cellular behaviors as well as pathological processes. As such, small molecule probes for the measurement of pHi are invaluable tools for chemical biology, facilitating the study of the role of pH in cellular function and disease. The field of small molecule pHi sensors has traditionally been dominated with probes based on fluorescent scaffolds. In this study, a series of low molecular weight (<260) oligoyne compounds have been developed which exhibit pH sensitive alkyne stretching frequencies (νalkyne) in Raman spectroscopy. The modular design of the compounds enabled tuneability of their pKa(H) through simple structural modification, such that continuous pH sensitivity is achieved over the range 2–10. Alkyne stretching bands reside in the ‘cell-silent’ region of the Raman spectrum (1800–2600 cm−1) and are readily detectable in a cellular environment with subcellular spatial resolution. This enabled the application of a pH sensitive oligoyne compound to the ratiometric sensing of pHi in prostate cancer (PC3) cells in response to drug treatment. We propose that probes based on Alkyne Tag Raman Imaging offer an entirely new platform for the sensing of pHi, complementary to fluorescence microscopy.
Introduction
pH homeostasis is essential for normal physiology. Regulation of both intracellular (pHi) and extracellular (pHe) pH plays a key role in many processes including cell proliferation1 and differentiation,2,3 protein synthesis,4 the acetylation and deacetylation of histones5 and metabolism.6,7 Given the importance of pH in many critical functions it is unsurprising that many diseases are associated with aberrant pH profiles. For example, pHi and pHe dysregulation have been linked to Alzheimer's disease8 and cancer.9,10 The development of methods to determine the role of pH homeostasis in cellular processes and its relationship to disease is therefore of great interest.pHi can be determined using fluorescent probes, the most commonly used being BCECF (2′,7′-bis-(2-carboxyethyl)-5-(and-)-carboxyfluorescein)11 and its derivatives.12 BCECF has been used extensively in mammalian and plant cells12–15 and living tissues,16,17 providing accurate pH measurement and excellent sensitivity at concentrations as low as 0.1 μM.18 However, there are limitations of BCECF and related fluorescent sensors such as photostability, phototoxicity and probe retention.19 These deficiencies limit the use of many probes, particularly in extended real time monitoring of live cells. Whilst efforts have been made to address these problems,12 significant challenges remain. In addition, diffuse absorption and emission spectra hinder the analysis of multiple fluorescent probes simultaneously (multiplexing), since spectral overlap limits the number of resolvable features within the spectra (especially where ratiometric sensors are used).20,21
Intracellular pH sensing has also been achieved by Surface Enhanced Raman Scattering (SERS) using functionalised metal nanoparticles.22–26 These nanoparticles bear a surface coating of organic molecules with pH-dependent Raman spectra, which are detectable inside cells with excellent sensitivity, owing to the SERS effect.27 Nanoparticle sensors, however, can suffer from reproducibility and accuracy issues arising from nanoparticle inhomogeneity,22 and the possible off target effects and toxicity of nanoparticles within cells remain unclear.27 We propose that small-molecule Raman pH sensors have the potential to address these issues.
An emerging technique, which is complementary to fluorescence microscopy, is Alkyne Tag Raman Imaging (ATRI).28,29 Alkynes have key vibrational modes that occur in the ‘cell-silent’ region of the Raman spectrum (1800–2600 cm−1), in which few vibrational modes from endogenous biomolecules exist.29 Alkyne bands can be detected in a cellular environment using spontaneous Raman microscopy or nonlinear variants such as Stimulated Raman Scattering (SRS).30 The first example of ATRI in cells was the use of ethynyldeoxyuridine (EdU, 1, Fig. 1A) which was metabolically incorporated into DNA for its visualization in cells.28 Since then, functionalisation of small biomolecules with alkyne ‘tags’ has enabled visualization of the intracellular distribution of drugs,31 natural products,32,33 sugars34,35 and lipids36–38 using Raman and SRS microscopy. Alkyne-tags have also been metabolically incorporated into macromolecules such as RNA and proteins for single-step imaging by SRS.39
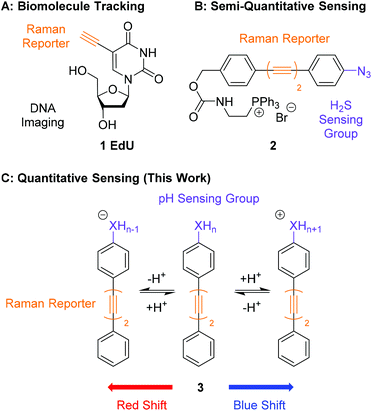 | ||
| Fig. 1 Comparison of the work presented in this manuscript with previous work in ATRI. (A) Structure of EdU, first used to visualise and track intracellular DNA by Raman microscopy.28 (B) Structure of 2, a bisarylbutadiyne sensor of H2S for use in SRS microscopy.20 (C) General structure of a pH sensitive bisarylbutadiyne for quantitative pH sensing (this work). | ||
An application of ATRI that remains unexplored is the development of sensors and probes for the quantification of endogenous biomolecules and ions. A pioneering report by Min and co-workers demonstrated the suitability of chemically reactive oligoyne scaffolds in the development of a ratiometric sensor for H2S (2, Fig. 1B).20 This sensor contained an azide group in conjugation with a bisarylbutadiyne scaffold which was reduced to the corresponding aniline in the presence of H2S. This chemical transformation induced a Raman shift change in the alkyne band, enabling the detection of intracellular H2S by SRS microscopy. Whilst this clearly demonstrates that Raman microscopy can be used to develop intracellular sensors, it relies on an irreversible chemical process rendering the detection semi-quantitative. The development of quantitative probes for use in a cellular environment would require any change in the shift of a Raman band to be bought about through a rapid and reversible chemical transformation, such as protonation/deprotonation. Sodeoka and Fujita reported the simultaneous imaging of the protonated and deprotonated forms of carbonylcyanide p-trifluoromethoxyphenylhydrazone (FCCP) in HeLa cells, using a pH sensitive C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretch, suggesting pH did represent a potential strategy for quantitative sensing.40 Within this work we report bisarylbutadiynes sensitive to environmental pH, and their application to ratiometric pHi determination by Raman microscopy (3, Fig. 1C). These molecules rely on reversible protonation/deprotonation events to induce a Raman shift change, enabling quantitative measurement of pH. These small molecule ratiometric pH sensors that are low molecular weight (MW <260), modular, readily tuneable, and possess good photostability,21 represent a novel platform for pH sensing at the cellular level. Using Raman microscopy as the method for detection provides additional experimental data including a direct measure of distribution for endogenous biomolecules (proteins, lipids and nucleic acids).
N stretch, suggesting pH did represent a potential strategy for quantitative sensing.40 Within this work we report bisarylbutadiynes sensitive to environmental pH, and their application to ratiometric pHi determination by Raman microscopy (3, Fig. 1C). These molecules rely on reversible protonation/deprotonation events to induce a Raman shift change, enabling quantitative measurement of pH. These small molecule ratiometric pH sensors that are low molecular weight (MW <260), modular, readily tuneable, and possess good photostability,21 represent a novel platform for pH sensing at the cellular level. Using Raman microscopy as the method for detection provides additional experimental data including a direct measure of distribution for endogenous biomolecules (proteins, lipids and nucleic acids).
Results and discussion
Electron delocalization influences alkyne stretching frequency
The design of our pH-sensitive probes was based around the fact that 4-ethynylaniline 4 (Fig. 2) has a lone pair of electrons on the aniline nitrogen that is in conjugation with the alkyne. Protonation of the aniline to give 4H+ would result in the nitrogen and the alkyne no longer being conjugated. We reasoned this could manifest itself in a detectable change in the Raman shift observed for the alkyne group. In support of this we performed DFT calculations on 4 and 4H+ which clearly showed that 4 had a significant contribution of the aniline lone pair to the calculated HOMO of the molecule whereas the aniline nitrogen made no contribution to the calculated HOMO of 4H+. Additionally, 4 displayed an unsymmetrical distribution of the HOMO across the alkyne triple bond, while distribution was more symmetrical in 4H+. The calculations suggested that the difference in the Raman stretching frequency of the two species 4 and 4H+ was Δνalkyne = 21 cm−1. We hypothesised that the calculated sensitivity of the Raman spectrum of 4 to protonation could be exploited to develop alkyne-based probes for the determination of environmental pH.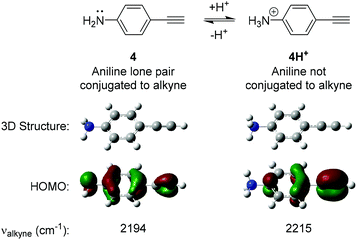 | ||
| Fig. 2 Results of Density Functional Theory (DFT) calculations on 4-ethynylaniline 4 and its protonated analogue 4H+. DFT calculations were carried out using B3LYP/6-311(G)++(d,p). | ||
Development of pH sensitive diynes
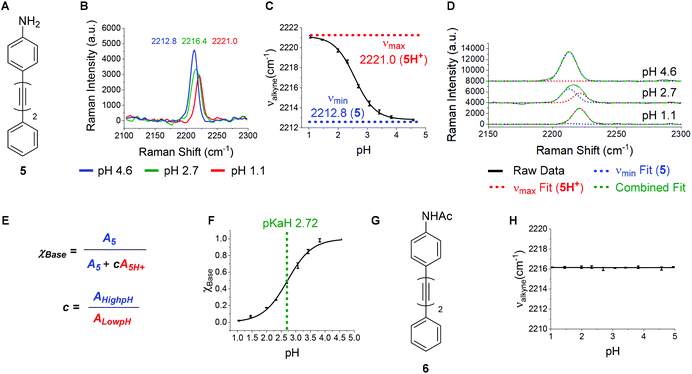
A bisarylbutadiyne scaffold was selected for our compounds, as it has been shown that the increased hyperpolarizability associated with the alkyne stretching vibrations of this functionality results in high Raman-scattering intensity,21,29 giving rise to lowered detection limits in solution. We synthesised aniline 5 (Fig. 3A) and aimed to assess the sensitivity of its Raman spectrum to pH. Due to the experimental complications associated with thermodynamic pKa(H) determination in water for hydrophobic molecules,41 we generated pKa(H) estimates for all compounds prepared in mixtures of 30% w/w EtOH/H2O under conditions of constant ionic strength (I = 0.2) and temperature (20 °C). The buffer solutions used (diyne analysis buffers), and their preparation, are described in the Experimental section. The experimental pKaH derived for 5, and all other compounds, is valid only under the conditions of solvent, ionic strength and temperature studied. Fig. 3B shows overlays of the alkyne region of the Raman spectra of 5 at pH 1.1, 2.7 and 4.6. At pH 4.6, the unprotonated microspecies 5 dominates, and the observed νalkyne is at a minimum (2212.8 cm−1) due to π-electron donation from the aniline lone pair.Conversely, at pH 1.1, the protonated microspecies 5H+ dominates and the observed νalkyne is near maximum (2221.0 cm−1) due to diminished π-electron donation. At pH 2.7, near the experimental pKa(H), the spectrum observed is a combination of contributions from both microspecies, and the apparent νalkyne is intermediate in value (2216.4 cm−1). Fig. 3C shows a plot of the apparent νalkyne of compound 5 across a range of indicated pH values. Asymptotes of the sigmoidal curve provided the maximum and minimum alkyne stretching frequency values (νmax = 2221.0 and νmin = 2212.8 cm−1) corresponding to the peak centres of the protonated 5H+ and parent microspecies 5, respectively. The difference between these two values is designated Δνalkyne (8.2 cm−1). In order to determine pKaH we assumed the observed alkyne peak at any given pH value was a linear additive combination of the peaks arising from 5 and 5H+. As shown in Fig. 3D, the combined fits effectively described the observed peaks at different pH values. The peak areas of 5 (A5) and 5H+ (A5H+) were determined, correcting for differing intrinsic peak intensities, allowing the mole fraction of conjugate base (χBase) to be determined as a function of pH (Fig. 5E).
Fitting the data to a Boltzmann function enabled the estimation of pKaH from the inflection point of the sigmoid (Fig. 3F), giving a value of 2.72 ± 0.02. This pKaH measurement of 5 was validated using UV-Visible spectroscopy under the same conditions of ionic strength and temperature (Fig. S3†), which indicated a pKaH of 2.66, consistent within 0.06 units of the value obtained by Raman, providing strong confidence in the methods used.
To test the hypothesis that the pH sensitivity of νalkyne exhibited by 5 could be attributed to aniline protonation, we synthesised the corresponding acetamide 6 (Fig. 3G). Pleasingly, 6 showed no change of the νalkyne over the pH range 1.1–5.0 (Fig. 3H). In line with our hypothesis we attribute this to the absence of a basic nitrogen lone pair.
Encouraged by the positive results obtained with aniline 5, we synthesised a series of diyne compounds 7–18 which exhibited pH sensitivity in different ranges (Fig. 4). Compounds were designed to incorporate aromatic substituents in conjugation with the diyne moiety which could be expected to influence π-electron density within the molecule. In addition, substituents were selected which had an expected pKa(H) 2–10, with the rationale that protonation/deprotonation events in solution would influence π-electron density in the alkyne chain, and in turn the observed νalkyne. Plots of νalkyne variance as a function of pH were constructed for compounds 7–18 (Fig. S4†). As predicted, compounds 5 and 7–18 showed sigmoidal relationships between νalkyne and environmental pH, and pKa(H) values could be determined using the multiple curve fitting method discussed previously. Plots of χBase as a function of pH can be found in Fig. S5.†Fig. 4 details the apparent pKa(H), νmax, νmin and Δνalkyne values for compounds 5 and 7–18. As discussed above, aniline 5 showed a pKaH of 2.7 and a decrease in νalkyne with increasing pH, consistent with an increasing proportion of the microspecies 5 (decreasing 5H+). Aniline 7 showed a similar trend. Notably, 7 exhibited an increased pKaH (3.2) and diminished Δνalkyne (4.6, compared to 8.2 for 5), likely arising from reduced conjugation due to the meta-substitution pattern.
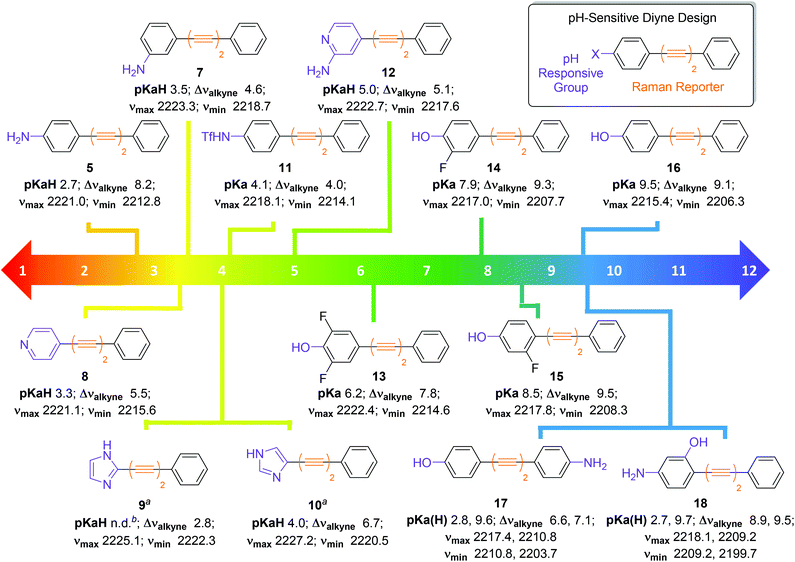 | ||
| Fig. 4 Design and structures of diyne compounds 5 and 7–18 showing experimental pKa(H), νmax, νmin and Δνalkyne values. Data were derived from plotting mean νalkyne values (n = 3, ±standard deviation) of 5 and 7–18 (100 μM in diyne analysis buffers) as a function of pH. Curves were fitted to Boltzmann functions in OriginPro 2018 and asymptotes afforded νmax, νmin and Δνalkyne values. Multiple peak fitting in OriginPro2018 at fixed peak centres derived from νmax and νmin enabled determination of ABase and AAcid as a function of pH, and values of AHighpH and ALowpH were derived from spectra at extreme pH values. Plots of χBase as a function of pH were constructed according to eqn (1), and data were fitted to Boltzmann functions. pKa(H) values were derived from the inflection points of these curves. Notes: aExperiments carried out at a compound concentration of 200 μM; bpKaH could not be determined. | ||
Unlike most compounds studied, pyridine derivative 8 (pKaH = 3.3) showed an increase of νalkyne with increasing pH. We reason that, given the π-deficient electron withdrawing nature of the pyridine ring, protonation of the nitrogen atom induced increased conjugation with the alkynes, which resulted in a decreased stretching frequency for the microspecies 8H+. Imidazoles 9 and 10 showed the opposite trend to the pyridine species 8, as the protonated microspecies 9H+ and 10H+ exhibited increased νalkyne upon protonation. We reason that, as imidazoles are π-excessive and electron donating, protonation induced decreased conjugation with the alkyne. We were unable to accurately determine a pKaH value for imidazole 9 as multiple curve fitting reported inconsistent values for ABase and AAcid, likely due to the small Δνalkyne of 2.8.
Triflamide 11 (pKa = 4.1) displayed a decrease in νalkyne on increasing pH, as the deprotonated analogue of 11 is expected to have increased conjugation with the alkyne chain. Aminopyridine 12 exhibited a pH dependence in line with that of pyridine 8, displaying a predictably higher pKaH (5.0). Phenols 13–16 exhibited a decrease in νalkyne upon increasing pH consistent with an increased π-electron delocalization upon deprotonation to the phenolate. It is noteworthy that the observed pKa values of these compounds were readily tuneable by incorporation of inductively withdrawing fluorine atoms in proximity to the phenolic oxygen allowing variance in the observed pKa of >3 pH units (cf. compounds 13 and 16).
It also proved possible to include two pH sensitive groups within the molecule providing two pKa(H) values for a single compound. For example, the bifunctional molecule 17, which contains an aniline and a phenol group on different aromatic rings displayed two discrete inflection points, the first at the pKaH of the aniline (2.8) and the second at the pKa of the phenol (9.6). The related compound 18, where the two functional groups are on the same aromatic ring, also showed inflection points for the aniline (pKaH = 2.7) and the phenol (pKa = 9.7). With the ability to finely tune pKa(H) values by the introduction of either electron donating or electron withdrawing groups on the aromatic ring(s), bespoke pH probes can be designed to provide sensitivity over multiple pH ranges.
The modular design of compounds 5 and 7–18 enabled rational tuning of their pKa(H) by substitution of the pH responsive group. Between the 14 diyne compounds prepared, there are compounds capable of pH-sensitivity for any pH value between 2–10 and this work provides the foundation for the design of oligoyne pH sensors for Raman microscopy across the physiological pH range. We have shown that detectable changes in νalkyne (3–18 cm−1) can be induced by protonation/deprotonation events. Other researchers have shown22,24,37 that larger changes in the base νalkyne values of oligoynes can be engineered by isotopic labelling of alkynes (>20 cm−1), and increasing the number of alkyne groups present in the molecule (>40 cm−1). It stands to reason, therefore, that the use of pH sensitive oligoynes with different alkyne chain lengths could enable visualization of multiple species simultaneously, with complete resolution, to enable multiplexing of multiple pH sensors, designed to report on discrete microenvironments.
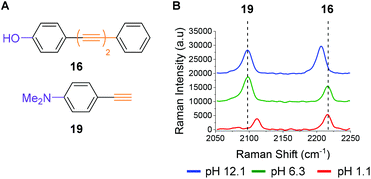
To illustrate the potential for multiplexing, we captured spectra of phenol 16 and commercially available dimethylaniline derivative 19 (Fig. 5A) in a single solution at different pH values (Fig. 5B). The Raman peaks corresponding to the alkyne group(s) of both compounds are clearly resolved at pH 12.1 (blue line), pH 6.3 (green line) and pH 1.1 (red line), enabling visualization of pH sensitivity for both compounds. The spectra indicate that at high pH (12.1) a different microspecies of compound 16 is present in solution when compared to the spectra obtained at lower pH (6.3 and 1.1). They also indicate that at low pH (1.1) dimethylaniline derivative 19 is present as a different microspecies to the spectra recorded at higher pH (6.3 and 12.1). These experiments show that through judicious design multiplexing of pH sensitive Raman probes should be possible.
Intracellular pH sensing
For the purposes of developing an intracellular pH sensor, compounds with pKa(H) values close to physiological pH ranges were desirable.6 The apparent pKa(H) values reported in Fig. 4 served as a guide for assessing suitability of the diyne compounds for intracellular pH sensing. Based on the data accrued, phenol 13 appeared to be a promising candidate for use as a cytosolic pH sensor due to its apparent pKa of 6.2 (Fig. 6A). Prior to investigation within a cellular environment, the photostability of 13 in solution was established by acquiring 120 consecutive spectra (acquisition time = 0.5 s) followed by integration of the alkyne peak using OriginPro 2018 (Fig. S6†). In addition, 13 was evaluated for any potential cellular toxic effect. Exposure of PC3 cells to 25 μm 13 for 6 h showed no change in cell count when compared to a DMSO control (Fig. S7†).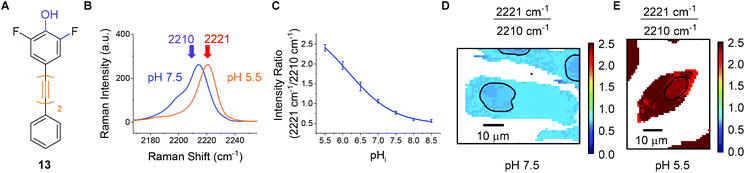 | ||
| Fig. 6 Raman imaging of PC3 cells treated with phenol 13 (25 μM, 30 min) fixed to discrete pHi values using the method of Thomas.42 (A) Structure of phenol 13. (B) Overlaid sample spectra from PC3 cells fixed to pHi 7.5 (blue) and 5.5 (orange). Spectra are presented within the range 2170–2260 cm−1 and normalised to the maximum intensity within that range. (C) Calibration curve for 13 in PC3 cells. Average 2221/2210 cm−1 intensity ratios from PC3 cells (n = 5, ±standard deviation, 532 nm, 0.5 s, 5 μm step size in x and y) were plotted at the indicated pHi values. Data were fitted to a Boltzmann function in OriginPro 2018. (D) and (E) False colour images representing the 2221/2210 cm−1 signal intensity ratios (532 nm, 0.5 s, 1 μm step size in x and y), in PC3 cells, fixed to pHi 7.5 and 5.5 respectively. The nuclear regions are highlighted by black bands. | ||
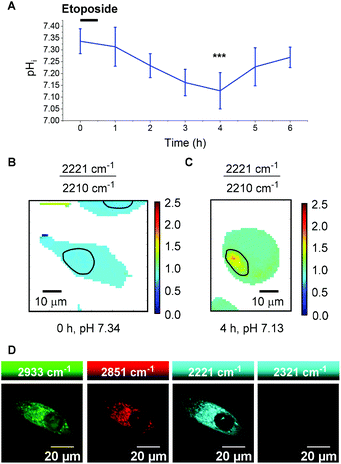
To quantitatively determine pH, 13 required calibration within the environment of interest. For the purposes of cellular pH sensing, the method of Thomas42 was used to calibrate our selected compound. Nigericin is an H+/K+ ion transporter which is commonly used to calibrate fluorescent pH probes.18,43,44 Cells were treated with 13 (25 μM, 30 min), and nigericin (25 μM) was used to equilibrate pHi with pHe in high K+ buffer solutions at pH values of 5.5, 6.0, 6.5, 7.0, 7.5, 8.0 and 8.5. The cells were then imaged using a Raman microscope. Under these conditions νmax and νmin were determined to be 2221 cm−1 and 2210 cm−1 respectively. Fig. 6B shows sample spectra from PC3 cells treated with 13 (25 μM, 30 min) and fixed to the pHi values of 5.5 (orange) and 7.5 (blue), illustrating the change in spectroscopic properties of 13 in response to pHi. Fig. 6C shows a plot of average 2221/2210 cm−1 signal intensity ratios derived from Raman maps of PC3 cells across the pHi range measured (n = 5 cells per condition, 5 μm step size in x and y, ±standard deviation). The data were fitted to a Boltzmann function to generate a calibration curve, enabling us to relate the 2221/2210 cm−1 ratio of 13 to pHi. Fig. 6D and E show false colour images of the 2221/2210 cm−1 ratio in PC3 cells fixed to pH 7.5 and 5.5 respectively. The Raman maps from which these derive were acquired at a resolution of 1 μm in x and y. These false colour images, and all others reported in this manuscript and ESI† were generated using a custom MATLAB® script reported in previous publications.38,45 As with fluorescent sensors, a minimum intensity cut-off should be established prior to ratiometric analysis, because ratios vary significantly as signal intensity decreases toward the threshold of detection.19 We established that the signal intensity of 13 was lowest within cell nuclei (Fig. S9†), due to minimal nuclear penetration of the probe compounds. This distribution pattern is consistent with analogous oligoyne molecules.21,29,32,33 As such, although the 2221/2210 cm−1 ratio appears to be consistent throughout the cells in Fig. 6D and E, we chose to exclude nuclear regions from interpretation and these are highlighted by black bands.
It is clear, however, from Fig. 6D and E that the 2221/2210 cm−1 ratio is consistent throughout the cytoplasm of the PC3 cells and varies as a function of pHi. Having calibrated 13 within a cellular environment, we aimed to determine whether this probe could be used to monitor and quantify changes in pHi in response to drug treatment. It has been reported that apoptosis is accompanied by a decrease in pHi.46 Treatment of 6 plates of PC3 cells with etoposide (80 μg mL−1, 30 min) induced apoptosis.47 Following incubation periods of 0.5, 1.5, 2.5, 3.5, 4.5 or 5.5 h, 13 (25 μM) was added and the cells were imaged after a further 30 minutes (n = 6 cells per time point, 532 nm, 0.5 s, 5 μm step size in x and y). From these data the 2221/2210 cm−1 ratio was extracted from average spectra at each time point and related to pHi using the calibration curve shown in Fig. 6C. Fig. 7A shows a plot of pHi over time. The average 2221/2210 cm−1 ratio at 0 h (no etoposide treatment) of 0.843 ± 0.027, corresponds to a pHi of 7.34 ± 0.05. The pHi steadily decreased over time, reaching a minimum at 4 h of 7.13 ± 0.08 (***p < 0.01), before showing signs of recovery. The change in pH and cellular recovery is consistent with observations with HL-60 cells.47,48 This experiment was repeated, with consistent results (Fig. S10†). For visual clarification, high resolution maps (1 μm step size in x and y) were acquired at the 0 and 4 h time points. Fig. 7B and C show false colour representations of the 2221/2210 cm−1 ratio in PC3 cells at 0 h and 4 h respectively. As before (cf.Fig. 6), low alkyne signal was observed in the nuclear regions of these cells (Fig. S11†), and so pHi data in these regions (highlighted by black bands) was excluded from interpretation. It is clear that the cell at 4 h post etoposide treatment (Fig. 7C) has a higher 2221/2210 cm−1 ratio and thus lower pHi than the cell at 0 h (Fig. 7B), in agreement with the data in Fig. 7A, showing that 13 can be used to effectively monitor and quantify changes in pHi of live cells in response to drug treatment.
A distinct advantage of Raman spectroscopy over other cellular imaging techniques is the rich information provided on compartmentalisation, the location of organelles and the distribution of endogenous biomolecules such as lipids and proteins. This is determined in a label free manner, therefore, each piece of experimental data gathered within this investigation provides considerable further knowledge, as demonstrated by identification of nuclear regions through lipid to protein ratio analysis (Fig. S9 and S11†) This data could not be obtained using spontaneous Raman microscopy in conjunction with a fluorescent probe, due to photobleaching, and the obscuring of Raman data by the fluorescence response.
To demonstrate the compatibility of 13 with advanced Raman imaging techniques, live PC3 cells were treated with 13 (25 μM, 30 min) and imaged by SRS microscopy for improved spatial resolution. Fig. 7D shows false colour images of 2933 cm−1 (CH3, protein), 2951 cm−1 (CH2, lipid), 2221 cm−1 (alkyne, 13) and 2321 cm−1 (off-resonance) channels in a single PC3 cell. The 2221 cm−1 channel confirms the extranuclear, cytoplasmic distribution of 13 with subcellular resolution, demonstrating the compatibility of this probe of this probe for intracellular pH sensing. We aim to extend the current capability of this probe by performing ratiometric SRS imaging for high-resolution pH sensing.
Experimental
DFT calculations
DFT calculations were performed using the Gaussian09 suite of programs.49 Structures were optimised and then characterised using frequency calculations at the B3LYP/6-311(G)++(d,p) level of theory.Buffer preparation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of 0.2 M HCl and 0.2 M KCl in 30 wt%. EtOH, to give corrected51 pH values of 1.05 and 1.45 respectively.
1 mixtures of 0.2 M HCl and 0.2 M KCl in 30 wt%. EtOH, to give corrected51 pH values of 1.05 and 1.45 respectively.
For etoposide treatment experiments, cells in 6 separate dishes were treated with 80 μg mL−1 etoposide from a 16 mg mL−1 stock solution in DMSO for and incubated for 30 min at 37 °C and 5% CO2. Dishes were aspirated and washed twice with PBS and refilled with DMEM. Each dish was incubated for a further time of 0.5, 1.5, 2.5, 3.5, 4.5 or 5.5 h at 37 °C and 5% CO2. Incubation periods were interrupted 30 min prior to their end point and cells were treated with 25 μM 13, then returned to the incubator for 30 min. Then they were then aspirated and washed twice with PBS, before refilling with PBS prior to imaging.
Raman spectroscopy
All Raman spectra were acquired on a Renishaw inVia Raman microscope equipped with a 532 nm Nd:YAG laser giving a maximum power of 500 mW, 1800 lines per mm grating. Prior to spectral acquisitions, the instrument was calibrated using the internal silicon standard at 520 cm−1.Stimulated Raman scattering microscopy
An integrated laser system (picoEMERALD™ S, Applied Physics & Electronics, Inc.) was used to produce two synchronised laser beams at 80 MHz repetition rate. A fundamental Stokes beam (1031.4 nm, 2 ps pulse width) was intensity modulated by an electro-optic-modulator with >90% modulation depth, and a tunable pump beam (700–960 nm, 2 ps pulse width, <1 nm (10 cm−1) spectral bandwidth) was produced by a built-in optical parametric oscillator. The pump and Stokes beams were spatially and temporally overlapped using two dichroic mirrors and a delay stage inside the laser system and coupled into an inverted laser-scanning microscope (Leica TCS SP8, Leica Microsystems) with optimised near-IR throughput. SRS images were acquired using 40× objective (HC PL IRAPO 40×, N.A. 1.10 water immersion lens) with a 10 μs pixel dwell time over a 512 × 512 frame. The Stokes beam was modulated with a 20 MHz EoM (Zurich Instruments). Forward scattered light was collected by a S1 N.A. 1.4 condenser lens (Leica Microsystems). Images were acquired at 8-bit image depth. The laser powers measured after the objective lens were in the range 10–30 mW for the pump beam only, 10–50 mW for the Stokes beam only and 20–70 mW (pump and Stokes beams).UV-Visible spectroscopy
Solutions of 5 and 11 were prepared using by diluting an aliquot from a stock solution (2 μL, 12.5 mM, EtOH) to a volume of 1 mL using diyne analysis buffer at the desired pH. The resulting final concentration of 5 or 11 was 25 μM. Samples were equilibrated to a room temperature of 20 °C prior to spectral acquisition. Spectra were recorded using an Agilent Cary 60 UV-Visible spectrometer between 250 and 800 nm at a resolution of 0.5 nm.Data processing
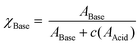 | (1) |
These data were fitted to Boltzmann functions in OriginPro 2018, and pKa(H) values were derived from inflection points.
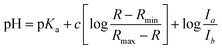 | (2) |
R is the ratio of emission intensity at two wavelengths. Rmax and Rmin are maximum and minimum limiting values of R (determined from the asymptotes of plots of R vs. pH), and c is the slope. Ia/Ib is the ratio of the absorption intensity in acid to the absorption intensity in base at the wavelength chosen for the denominator of R.52 pKa(H) was determined from the y intercept minus log(Ia/Ib).
Conclusions
In summary, we have reported the development of a bespoke suite of low molecular weight diyne compounds which exhibit pH sensitive Raman spectra. Using a modular design strategy, the pKa(H) values of the series were tuned to achieve sensitivity across a physiologically-relevant pH range (2–10) in order to detect and monitor changes in pH. Following calibration, we demonstrated that compound 13 could be used to ratiometrically determine pHi in PC3 cells and, significantly, to monitor change in pHi in response to a homeostatic disruptor, in this case exemplified by administration of the chemotherapeutic agent etoposide. The probe molecule 13 proved to be photostable, non-toxic and cell penetrant, providing the first example of an environmentally sensitive small molecule to enable accurate pH determination by Raman microscopy. Central to the success of these quantitative probes was the use of a rapid and reversible chemical equilibrium to influence the Raman spectrum of the bioorthogonal alkyne. The ability to use Raman microscopy for quantitative sensing using ratiometric probes represents an exciting new application of ATRI which could be used to detect other important ions and biomolecules of relevance to disease. We believe that the work presented here represents an entirely novel platform for pH sensing in a cellular environment which will find broad applicability in the chemical and life sciences.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the University of Strathclyde, the EPSRC and GlaxoSmithKline for financial support. We are extremely grateful to Dr Alison Nordon for her insight and advice in curve fitting analysis to determine experimental pKa(H) values.Notes and references
- M. Flinck, S. H. Kramer and S. F. Pedersen, Acta Physiol., 2018, 223, e13068 CrossRef CAS PubMed.
- J. D. Gross, J. Bradbury, R. R. Kay and M. J. Peacey, Nature, 1983, 303, 244–245 CrossRef CAS PubMed.
- B. Ulmschneider, B. K. Grillo-Hill, M. Benitez, D. R. Azimova, D. L. Barber and T. G. Nystul, J. Cell Biol., 2016, 215, 345–355 CrossRef CAS PubMed.
- S. J. Fuller, C. J. Gaitanaki and P. H. Sugden, Biochem. J., 1989, 259, 173–179 CrossRef CAS PubMed.
- M. A. McBrian, I. S. Behbahan, R. Ferrari, T. Su, T.-W. Huang, K. Li, C. S. Hong, H. R. Christofk, M. Vogelauer, D. B. Seligson and S. K. Kurdistani, Mol. Cell, 2013, 49, 310–321 CrossRef CAS PubMed.
- J. R. Casey, S. Grinstein and J. Orlowski, Nat. Rev. Mol. Cell Biol., 2010, 11, 50–61 CrossRef CAS PubMed.
- W. B. Busa and R. Nuccitelli, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 1984, 246, R409–R438 CrossRef CAS.
- T. A. Davies, R. E. Fine, R. J. Johnson, C. A. Levesque, W. H. Rathbun, K. F. Seetoo, S. J. Smith, G. Strohmeier, L. Volicer, L. Delva and E. R. Simons, Biochem. Biophys. Res. Commun., 1993, 194, 537–543 CrossRef CAS PubMed.
- M. Schindler, S. Grabski, E. Hoff and S. M. Simon, Biochemistry, 1996, 35, 2811–2817 CAS.
- H. Izumi, T. Torigoe, H. Ishiguchi, H. Uramoto, Y. Yoshida, M. Tanabe, T. Ise, T. Murakami, T. Yoshida, M. Nomoto and K. Kohno, Cancer Treat. Rev., 2003, 29, 541–549 CrossRef CAS PubMed.
- T. J. Rink, J. Cell Biol., 1982, 95, 189–196 CAS.
- J. Han and K. Burgess, Chem. Rev., 2010, 110, 2709–2728 CrossRef CAS PubMed.
- T. Speake and A. C. Elliott, J. Physiol., 1998, 506, 415–430 CrossRef CAS PubMed.
- A. Varadi and G. A. Rutter, Endocrinology, 2004, 145, 4540–4549 CrossRef CAS PubMed.
- D. Pérez-Sala, D. Collado-Escobar and F. Mollinedo, J. Biol. Chem., 1995, 270, 6235–6242 CrossRef PubMed.
- I. D. Weiner and L. L. Hamm, Am. J. Physiol.: Renal, Fluid Electrolyte Physiol., 1989, 256, F957–F964 CAS.
- C. Hille, M. Berg, L. Bressel, D. Munzke, P. Primus, H.-G. Löhmannsröben and C. Dosche, Anal. Bioanal. Chem., 2008, 391, 1871–1879 CAS.
- P. A. Valant and D. H. Haynes, J. Fluoresc., 1992, 2, 191–206 CrossRef CAS PubMed.
- B. K. Grillo-Hill, B. A. Webb and D. L. Barber, in Methods in Cell Biology, Elsevier, 2014, vol. 123, pp. 429–448 Search PubMed.
- C. Zeng, F. Hu, R. Long and W. Min, Analyst, 2018, 143, 4844–4848 RSC.
- F. Hu, C. Zeng, R. Long, Y. Miao, L. Wei, Q. Xu and W. Min, Nat. Methods, 2018, 15, 194–200 CrossRef CAS PubMed.
- C. E. Talley, L. Jusinski, C. W. Hollars, S. M. Lane and T. Huser, Anal. Chem., 2004, 76, 7064–7068 CrossRef CAS PubMed.
- J. Kneipp, H. Kneipp, B. Wittig and K. Kneipp, J. Phys. Chem. C, 2010, 114, 7421–7426 CrossRef CAS.
- J. Kneipp, H. Kneipp, B. Wittig and K. Kneipp, Nano Lett., 2007, 7, 2819–2823 CAS.
- A. Pallaoro, G. B. Braun, N. O. Reich and M. Moskovits, Small, 2010, 6, 618–622 CrossRef CAS PubMed.
- L. E. Jamieson, A. Jaworska, J. Jiang, M. Baranska, D. J. Harrison and C. J. Campbell, Analyst, 2015, 140, 2330–2335 RSC.
- C. Zong, M. Xu, L.-J. Xu, T. Wei, X. Ma, X.-S. Zheng, R. Hu and B. Ren, Chem. Rev., 2018, 118, 4946–4980 CrossRef CAS PubMed.
- H. Yamakoshi, K. Dodo, M. Okada, J. Ando, A. Palonpon, K. Fujita, S. Kawata and M. Sodeoka, J. Am. Chem. Soc., 2011, 133, 6102–6105 CrossRef CAS PubMed.
- H. Yamakoshi, K. Dodo, A. Palonpon, J. Ando, K. Fujita, S. Kawata and M. Sodeoka, J. Am. Chem. Soc., 2012, 134, 20681–20689 CrossRef CAS PubMed.
- F. Hu, L. Shi and W. Min, Nat. Methods, 2019, 16, 830–842 CAS.
- S. F. El-Mashtoly, D. Petersen, H. K. Yosef, A. Mosig, A. Reinacher-Schick, C. Kötting and K. Gerwert, Analyst, 2014, 139, 1155 RSC.
- W. J. Tipping, M. Lee, A. Serrels, V. G. Brunton and A. N. Hulme, Chem. Sci., 2017, 8, 5606–5615 RSC.
- J. Seidel, Y. Miao, W. Porterfield, W. Cai, X. Zhu, S.-J. Kim, F. Hu, S. Bhattarai-Kline, W. Min and W. Zhang, Chem. Commun., 2019, 55, 9379–9382 RSC.
- F. Hu, Z. Chen, L. Zhang, Y. Shen, L. Wei and W. Min, Angew. Chem., Int. Ed., 2015, 54, 9821–9825 CrossRef CAS PubMed.
- R. Long, L. Zhang, L. Shi, Y. Shen, F. Hu, C. Zeng and W. Min, Chem. Commun., 2018, 54, 152–155 RSC.
- H. J. Lee, W. Zhang, D. Zhang, Y. Yang, B. Liu, E. L. Barker, K. K. Buhman, L. V. Slipchenko, M. Dai and J.-X. Cheng, Sci. Rep., 2015, 5, 7930 CrossRef CAS PubMed.
- F. Hu, L. Wei, C. Zheng, Y. Shen and W. Min, Analyst, 2014, 139, 2312–2317 RSC.
- L. E. Jamieson, J. Greaves, J. A. McLellan, K. R. Munro, N. C. O. Tomkinson, L. H. Chamberlain, K. Faulds and D. Graham, Spectrochim. Acta, Part A, 2018, 197, 30–36 CrossRef CAS PubMed.
- L. Wei, F. Hu, Y. Shen, Z. Chen, Y. Yu, C.-C. Lin, M. C. Wang and W. Min, Nat. Methods, 2014, 11, 410–412 CrossRef CAS PubMed.
- H. Yamakoshi, A. F. Palonpon, K. Dodo, J. Ando, S. Kawata, K. Fujita and M. Sodeoka, Chem. Commun., 2014, 50, 1341–1343 RSC.
- J. Reijenga, A. van Hoof, A. van Loon and B. Teunissen, Anal. Chem. Insights, 2013, 8, ACI.S12304 CrossRef PubMed.
- J. A. Thomas, R. N. Buchsbaum, A. Zimniak and E. Racker, Biochemistry, 1979, 18, 2210–2218 CAS.
- D. G. Nicholls and S. J. Ferguson, in Bioenergetics, Elsevier, 2013, pp. 13–25 Search PubMed.
- M. R. James-Kracke, J. Cell. Physiol., 1992, 151, 596–603 CrossRef CAS PubMed.
- L. E. Jamieson, C. Wetherill, K. Faulds and D. Graham, Chem. Sci., 2018, 9, 6935–6943 RSC.
- D. Lagadic-Gossmann, L. Huc and V. Lecureur, Cell Death Differ., 2004, 11, 953–961 CAS.
- M. A. Barry, J. E. Reynolds and A. Eastman, Cancer Res., 1993, 53, 2349–2357 CAS.
- The choice of PC3 cells was based on previous experience using this cell line. See ref. 45.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Available: https://gaussian.com/g09citation.
- C. Mongay and V. Cedra, Ann. Chim., 1974, 64, 409–412 CAS.
- W. J. Gelsema, C. L. de Ligny, A. G. Remijnse and H. A. Blijleven, Recl. Trav. Chim. Pays-Bas, 2010, 85, 647–660 CrossRef.
- T. Myochin, K. Kiyose, K. Hanaoka, H. Kojima, T. Terai and T. Nagano, J. Am. Chem. Soc., 2011, 133, 3401–3409 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Analytical data, experimental procedures and 1H, 19F and 13C NMR spectra for all compounds reported. Raman spectra of all compounds reported, pKa(H) determination plots, and additional Raman data pertaining to pH measurement in PC3 cells. See DOI: 10.1039/d0an00865f |
| This journal is © The Royal Society of Chemistry 2020 |