Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mathematical chromatography deciphers the molecular fingerprints of dissolved organic matter†
Urban J.
Wünsch‡
 *a and
Jeffrey A.
Hawkes
*a and
Jeffrey A.
Hawkes
 b
b
aChalmers University of Technology, Architecture and Civil Engineering, Water Environment Technology, Sven Hultins Gata 6, 41296 Gothenburg, Sweden. E-mail: wuensch@chalmers.se
bAnalytical Chemistry, Department of Chemistry – BMC, Uppsala University, Uppsala, Sweden
First published on 9th January 2020
Abstract
High-resolution mass spectrometry (HRMS) elucidates the molecular composition of dissolved organic matter (DOM) through the unequivocal assignment of molecular formulas. When HRMS is used as a detector coupled to high performance liquid chromatography (HPLC), the molecular fingerprints of DOM are further augmented. However, the identification of eluting compounds remains impossible when DOM chromatograms consist of unresolved humps. Here, we utilized the concept of mathematical chromatography to achieve information reduction and feature extraction. Parallel Factor Analysis (PARAFAC) was applied to a dataset describing the reverse-phase separation of DOM in headwater streams located in southeast Sweden. A dataset consisting of 1355 molecular formulas and 7178 mass spectra was reduced to five components that described 96.89% of the data. Each component summarized the distinct chromatographic elution of molecular formulas with different polarity. Component scores represented the abundance of the identified HPLC features in each sample. Using this chemometric approach allowed the identification of common patterns in HPLC–HRMS datasets by reducing thousands of mass spectra to only a few statistical components. Unlike in principal component analysis (PCA), components closely followed the analytical principles of HPLC–HRMS and therefore represented more realistic pools of DOM. This approach provides a wealth of new opportunities for unravelling the composition of complex mixtures in natural and engineered systems.
Introduction
Dissolved Organic Matter (DOM) is a ubiquitous, reactive pool of organic compounds that ultimately originates from terrestrial or aquatic plant matter.1,2 Prior to its remineralization, DOM is subjected to continuous reactions over timescales of days to millennia.3 This reaction cascade creates an extremely diverse mixture of dilute compounds. Determining the composition of DOM at any given time presents a significant challenge.4,5 Among the array of analytical techniques used to fingerprint DOM, high-resolution mass spectrometry (HRMS) is generally considered to be the most advanced with regard to specificity and molecular insight.6,7In direct infusion mode, hundreds of mass spectral transients are collected and averaged, routinely generating more than 106 data points consisting of 103 to 104 molecular formulas. Since each molecular formula represents an unknown number of structural isomers, the true complexity far exceeds the observed size of the dataset.8,9 This complexity presents a significant barrier in the interpretation of molecular formula fingerprints, as it is unclear to what extent a formula represents a single compound or different isomers. High performance liquid chromatography (HPLC) fractionation offers a promising alternative to direct infusion HRMS since it physically separates DOM prior to detection. After fractionation, the complexity of each obtained mass spectrum decreases and the interpretation may be simplified, although the smearing of isomeric mixtures throughout the elution demonstrates that the mass spectral peaks are not isomerically pure.10–13 While manual fraction collection is labour-intensive, the online coupling of HPLC and HRMS fully automates the measurement procedures.14,15
Compared to direct infusion HRMS, the formulaic complexity of HPLC–HRMS datasets increases by orders of magnitude. For each environmental sample, hundreds of different mass spectra are collected, increasing the total number of assigned formulas.14,16,17 This additional information aids the characterization of DOM, but simultaneously complicates the extraction of meaningful information. HPLC–HRMS peaks have lower signal-to-noise ratios than the traditional direct infusion method as limited signal averaging occurs. Since chromatograms of DOM represent unresolved humps, the abundance of single analytes cannot easily be deduced.13,18 Instead, complex mass spectra in broadly eluting fractions must be analysed. However, the visual analysis of raw data is overburdened by the large number of spectra, and statistical analyses capable of extracting information from direct infusion datasets (such as principal component analysis) require unfolding of the multidimensional data. These analyses are typically conducted in statistical programming environments such as R or MATLAB using built-in functions and user-built scripts. As of the publication of this article, community-driven software only covers molecular formula assignment and basic exploration of variance for direct-infusion data.19,20 To fully exploit the potential of HPLC–HRMS, such tools could be expanded upon to include data analysis routines that isolate systematic variation from HPLC–HRMS datasets.
Contrary to direct infusion, HPLC–HRMS analyses generate three-dimensional datasets that can benefit from tensor rank decompositions through models such as parallel factor analysis (PARAFAC).21,22 These models decompose the raw data into a set of terms that, when multiplied together and summed up, describe the systematic variability in the dataset. PARAFAC has been widely applied in DOM research to distinguish between different fluorescence spectra by fitting a set of excitation and emission spectra to fluorescence landscapes. In fluorescence applications, PARAFAC is often able to account for more than 99% of the raw data and is thus able to reduce hundreds of fluorescence matrices to typically less than six components.23 Besides information on fluorescence spectra, the component abundances are commonly used to distinguish water masses or elucidate the biogeochemistry of DOM.24,25
The PARAFAC model assumes rigidly aligned data and linear detector responses and is capable of distinguishing between highly similar analyte spectra. PARAFAC thus naturally follows the analytical principles of HPLC–HRMS and can extract chemically meaningful information under ideal conditions. Consequently, Bro et al. (2010) have coined the phrase “mathematical chromatography” for data analysis approaches that isolate analyte information from complex spectra.26 In addition to spectral decomposition, such approaches also allow rigorous testing of data quality. While difficult to notice in raw data, artefacts caused by retention time shifts, or matrix effects in the ion source may be spotted more easily during PARAFAC modelling.27 Despite this, visual analyses of in silico fractions, determination of bulk dissimilarities prior to clustering, and principal component analysis of unfolded datasets are the dominant data reduction strategies to date.14–16,28,29
The aim of our study was to achieve information reduction and feature extraction in HPLC–HRMS by three-way analysis. PARAFAC was applied to a previously published reverse-phase separation dataset describing the DOM composition of headwater streams in southeast Sweden.28 Once the validity of the identified statistical model was confirmed, the goal was to chemically evaluate the isolated features and relate shifts in their abundance to geochemical parameters.
Materials and procedures
Sample collection and preparation
Samples were collected and processed as described previously.28 Briefly, 74 randomly selected forested headwater streams in southeast Sweden were sampled in autumn 2016. All samples were stored unfiltered in the dark at 4 °C for approximately five months after sampling. The long-term storage of samples likely affected the sample composition, removing more labile and chemically reactive compounds and leaving the more stable DOM in solution. On the day of measurements, specific volumes of samples were transferred to 2 mL Eppendorf vials so that 11.25 μg dissolved organic carbon (DOC) was present in each sample vial, while 2 mL of blanks were transferred. The water in samples and blanks was subsequently removed by vacuum evaporation at 45 °C, after which samples were reconstituted in 150 μL 1% (v/v) formic acid to a final concentration of 75 mg L−1 DOC.Reverse-phase liquid chromatography
Reverse-phase chromatography separations were performed on an Agilent 1100 series instrument with an Agilent PLRP-S series column (150 × 1 mm, 3 μm bed size, 100 Å pore size). Solvent A (0.1% formic acid, 0.05% ammonia, and 5% acetonitrile) was pumped at a flow rate of 100 μL min−1 and 80 μL of sample were injected for each sample. The elution of DOM was achieved through a step-wise increase in concentration of solvent B (100% acetonitrile) from zero initially, followed by 20%, and ending in >45% solvent B (Fig. S1†). This step-wise elution leads to three broad humps of elution: poorly retained compounds, compounds eluted with 20% acetonitrile, and compounds eluted with 45% acetonitrile. This strategy increases signal to noise ratio compared with a gradual gradient elution. Note that there is a large time delay between solvent composition change and elution, due to dead volume.Mass spectrometry detection was carried out with an Orbitrap LTQ-Velos-Pro (Thermo Scientific, Germany) with electrospray ionization (ESI, negative mode) as ion source. Transient ions were collected in the range of m/z 150–1000 at an instrumental resolving power set to 105. An external calibration with the manufacturer's calibration mixture was followed by an internal calibration using six ubiquitous ions in the range of m/z 251–493. Further details on the chromatographic method and mass spectrometric detection are given elsewhere.14,28
Data processing
Vendor software was used to produce centroided m/z data for each transient, and transients were filtered for noise after considering peaks with mass defect 0.6–0.8 as noise and removing all peaks with intensity lower than the mean + three standard deviations of these peak intensities. Molecular formulas were assigned within the range C4–40, H4–80, O1–40, N0–1, S0–1 in the mass range m/z 170–700 using the closest formula in the theoretical list for assignment. Additionally, assignments were constricted to O/C 0–1, H/C 0.3–2, a double bond equivalent minus oxygen less than or equal to 10, and a mass defect of −0.1 to 0.3 (decimal after the nominal mass). Formulas detected in process blanks were excluded from further analysis. Formulas were also removed from consideration in samples if the intensity did not exceed the noise + ten standard deviations in at least ten sequential transients at some point in the elution. This molecular formula assignment and data treatment yielded 2052 unique molecular formulas. Several sequential intensities (typically 3–4) were summed to a chromatographic resolution of 0.1 min to favour analyte signals over instrument noise and to reduce computational requirements.To yield a more quantitative dataset in subsequent analyses, the DOC normalization was reversed by accounting for the sample-specific volume that yielded the constant amount of carbon dissolved for chromatographic analysis. For statistical modelling, the retention time window of 5.0–22.9 min was selected, yielding a preliminary dataset size of 74 samples × 2052 molecular formulas × 180 retention times (Fig. 1). All mass spectra were divided by a factor of 4.92 × 107 to avoid machine precision errors during statistical modelling.
The median detection rate for formulas across all samples and retention times was 31.2%. Since excessive missing numbers can obstruct meaningful statistical modelling, formulas that were detected in less than 10% of measurements (including samples and retention times) were excluded from further analysis (N = 661). An additional 36 molecular formulas were removed from the dataset due to noticeably unique chromatograms (Fig. S2†). As can be seen in Fig. S2,† these formulas often constituted genuine analytes with narrow chromatograms. However, as the goal was to analyse the dominating patterns, these unique features were excluded. Overall, outliers accounted for a total of 2.3% of the dataset (between 1.6 and 4% for different samples). Combined with the removal of the 661 scarcely observed formulas, this led to the exclusion of 697 molecular formulas. The remaining 1355 formulas represented 96.4 ± 0.4% of the total signal observed for samples and 95.0 ± 3.1% of the total signal observed at different retention times (Fig. S3†).
Chromatographic sections with missing observations of at least 2 min (20 observations or more) were set to zero while leaving a gap of missing numbers of 0.7 min to each end of the section. This aimed to reduce the amount of missing observations by assuming that non-detects represent the true absence of an ion. Every 2nd retention time (after t = 7 min) was excluded, which reduced the chromatographic resolution to 0.2 min between t = 7.0 and 22.9 min. Since DOM chromatograms are relatively broad, it was assumed that this step would not lead to a systematic loss of information but would only reduce computational expenses. Furthermore, all data above retention times of 22.2 min was excluded since chromatograms often showed high, somewhat random variation. The final modelled dataset size was therefore 74 × 1355 × 97 (samples × formulas × retention times). Fig. S4† visualizes the quantitative impact of each of the data processing steps detailed above.
Chemometric analysis
In traditional chromatography, peaks mostly consist of single analytes and indicate the abundance of a chemical species. In the case of DOM, chromatograms are broad and unresolved since many chemical species with highly similar composition elute simultaneously at any given time. Here, the aim was to isolate groups of molecular formulas with indistinguishable chromatographic elution profiles using PARAFAC. Under these conditions, PARAFAC does not isolate single analyte peaks, but rather isolates groups of analytes and isomers. In the following, we use the term chromatographic feature to mean a non-resolved peak, and reserve the word peak for true analyte peaks (which are rare in DOM) or resolved mass spectrometry peaks, which usually contain information from numerous isomers with the same formula.9,13 The use of the term elution profile or chromatographic feature of components or formulas does not imply single analyte peaks, but always refers to complex mixtures unless specifically stated otherwise.All data processing and modelling was carried out using PLS_Toolbox (v8.61, Eigenvector Research Inc.) in MATLAB (v9.7, MathWorks Inc.). HPLC–HRMS signals were decomposed with the PARAFAC model into a set of trilinear terms and residuals as follows:22
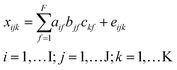 | (1) |
x ijk represents the jth molecular formula in the ith sample at the kth retention time that is described with the proportional abundance a of the fth component (also referred to as “scores”), its formula loadings b and retention time loadings c. The term eijk represents the unexplained residual variability of the ith sample, the jth molecular formula and the kth retention time. PARAFAC models were fit using the alternating least squares (ALS) algorithm starting with random orthogonalized numbers. ALS repeatedly assumes two of the three model parameters (e.g. a and b) as known and estimates the third (e.g. c). In the next iteration, a different parameter is estimated by assuming two other parameters as known. Once the model fit between iterations does not improve beyond a set threshold (here: 10−12), the model is assumed to have converged. PARAFAC models were fit by constraining the terms a, b, and c to nonnegative values. Each model was initialized 50 times with orthogonalized random numbers and only the least squares solution was further inspected. In combination with the small convergence criterion, picking the best out of 50 solutions minimized the likelihood that the identified solution was a local minimum instead of the global solution.
Models with two to nine components were considered; each model's core consistency and percentage of explained variance was used as screening criteria to diagnose the likelihood of overfitting and to assess improvement in model fit with increasing component number.30 Subsequently, the appropriateness of component elution profiles, randomness of model residuals, and split-half validation was used to further evaluate the robustness and validity of potential models:22 A model is considered appropriate if it can be obtained when only part of the dataset is given, its residuals are mostly random, and elution profiles resemble plausible chromatographic features.
As an alternative to PARAFAC, nonnegative matrix factorization (multivariate curve resolution, MCR) models were fit to individual sample chromatograms. MCR decomposes chromatogram x into f components, each with an elution profile c and corresponding mass spectrum s as follows:31
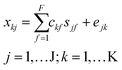 | (2) |
In eqn (2), xkj represents the jth molecular formula at the kth retention time. The part of xkj that the bilinear MCR model does not explain is expressed in the error term ejk. MCR models were fit using the ALS algorithm in PLS_Toolbox with a convergence criterion of 10−6 (as explained above) and using five nonnegative components for all 74 samples. Each model was initialized with the five most dissimilar mass spectra (based on Euclidean distances of normalized spectra) at different retention times.
Results
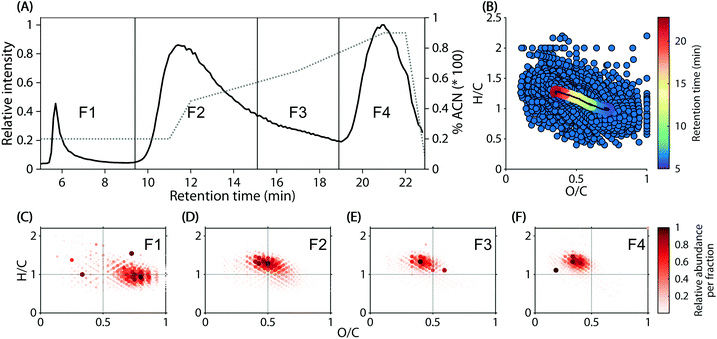
Reverse-phase chromatograms of the 74 headwater stream samples showed three major, unresolved features at approximately 5.5–9 min, 9–19 min, and 19–22.5 min (Fig. 1A), due to the step-wise increase of acetonitrile in the mobile phase. Within the chromatogram, a decrease in polarity (water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) octanol partitioning coefficient) from early to late elution was observed (Fig. 1B). The weighted average molecular composition shifted steadily from O/C 0.70 and H/C 1.00 at 5 min to O/C 0.36 and H/C 1.23 at 22.9 min (Fig. 1B, coloured line). These observations were supported by the formula composition in four arbitrarily defined in silico fractions (Fig. 1C–F).
octanol partitioning coefficient) from early to late elution was observed (Fig. 1B). The weighted average molecular composition shifted steadily from O/C 0.70 and H/C 1.00 at 5 min to O/C 0.36 and H/C 1.23 at 22.9 min (Fig. 1B, coloured line). These observations were supported by the formula composition in four arbitrarily defined in silico fractions (Fig. 1C–F).
Exploratory phase and model validation
The three broad elution humps hinder the distinction of co-eluting chromatographic features by in silico fractionation. Instead, we aimed to isolate features in the HPLC chromatograms using the three-way PARAFAC model. Two to nine PARAFAC components explained 89.4–97.7% of the data and the corresponding models had a steadily decreasing core consistency between 99% (two components) and 3% (nine components, Fig. S5†). All models covered the elution observed in Fig. 1 and always contained components with multiple broad elution features at different retention times. With an increasing number of components, some features separated into different components, while others remained unresolvable (Fig. S6†). Starting at seven components, multiple components with highly correlated retention time loadings were observed. As this indicates overfitting, only up to six components were considered.From a viewpoint of chromatographic separation and functional grouping of molecular formulas, it was unclear which model was appropriate. Split-half validations were carried out with four- to six-component models since these models showed good feature distinction and little evidence of overfitting. The split-half validation was successful for the four- and five-, but not the six-component model (Fig. S7†). This was likely due to the high degree of correlation between some of the features in the six-component model. Ultimately, the five-component model was therefore chosen to approximate the HPLC–HRMS dataset.
The five-component model explained 96.89% of the dataset and had a core consistency of 56.9%. All samples had similar levels of residuals, i.e. no outlier samples could be identified. In general, the linear combination of components reproduced the chromatographic elution profiles and mass spectra well (Fig. 2 depicts some examples). However, residuals increased sharply with decreasing signal strength. This meant that the model could not reproduce less abundant signals as well as the dominant ones (Fig. S8†).
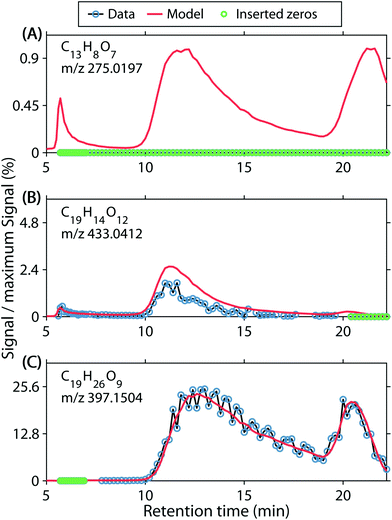
For a dataset with over 9 × 106 elements, a detailed residual analysis is challenging. Initially, data and modelled data were compared for many randomly selected molecular formula chromatograms (Fig. S9† shows some examples). This resulted in the identification of several issues. First, false positive abundances were identified by counting the cases in which PARAFAC estimated a non-zero chromatogram, but the data only contained zeros or missing observations (Fig. 3A). This seemingly false estimation was observed for 7.7% of all formula chromatograms, but only amounted to 0.12% of the data intensity (Table 1). Formulas with this type of modelling error were generally estimated to have a low signal and were found to have properties of typical low-abundance DOM (Fig. S10A and F†).
| Group | % chromatograms | % data | % modelling error |
|---|---|---|---|
| Underestimated | 2.5 | 0.12 | 3.9 |
| Overestimated | 4.8 | 0.10 | 3.2 |
| False positive | 7.7 | 0.12 | 3.9 |
| Random | 23.9 | 0.8 | 25.7 |
| Other/uncategorized | 61.0 | 2.0 | 63.3 |
Secondly, systematic over- and underestimations were observed. We counted overestimations as chromatograms in which more than 80% of residuals were negative (Fig. 3B). We acknowledge that the first error set ‘false positive abundances’ may be a subset of ‘overestimations’, where the signal is below the detection limit. Conversely, underestimations were counted as chromatograms in which more than 80% of residuals were positive. Underestimated chromatograms primarily occurred for formulas with m/z <300 (Fig. S10B and G†), and H/C < 1.4, O/C < 0.7, whereas formulas with narrow features at the edges of the chromatograms were often overestimated. Therefore, overestimations almost exclusively occurred for formulas with H/C 1.3–1.7 and O/C 0.2–0.35, or H/C 0.6–1.2 and O/C 0.7–0.85 (Fig. S10C and H†). Combined, 7.33% of all formula chromatograms were either over- or underestimated and the corresponding residuals accounted for 7.2% of the modelling error (Table 1).
Lastly, we observed random residuals in many cases (Fig. 3C). Residuals were classified as random when they did not fall into any other category, their absolute median was <0.001, and the number of positive and negative residuals each accounted for between 40 and 60% of the raw chromatograms (not counting zeros or missing observations). Since detector noise occurred presumably randomly, PARAFAC modelled smooth chromatograms and the random noise was left unexplained. This type of model residual amounted to 0.8% of the overall data, 25.7% of the modelling error, and was observed in 23.9% of chromatograms (Table 1). Moreover, random residuals were found for formulas across almost the entirety of the covered compositional space (Fig. S10D and I†).
The model error stemming from random noise, false estimations, and over- and underestimations accounted for 1.4% of the data. Together with the 96.9% of data explained by the five-component PARAFAC model, 98% of the data was accounted for. The remaining two percent of unmodelled data likely belonged to one of the categories above but the model residuals could not be easily classified with the selected criteria.
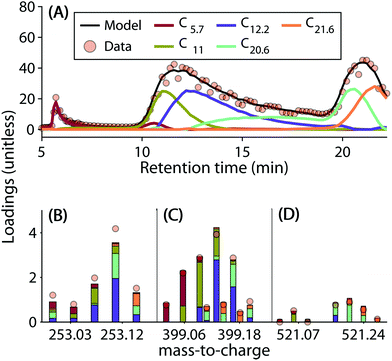
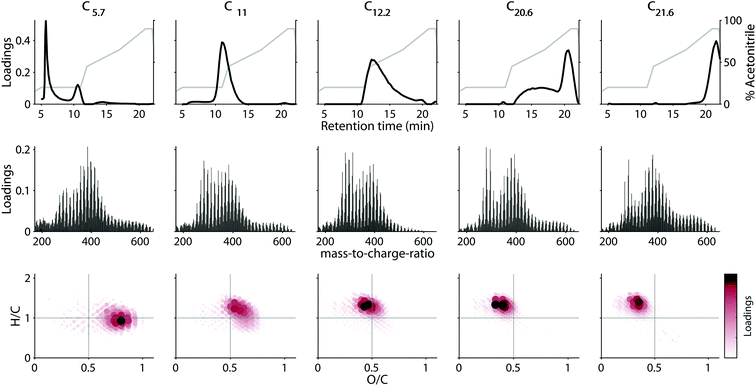
Component properties
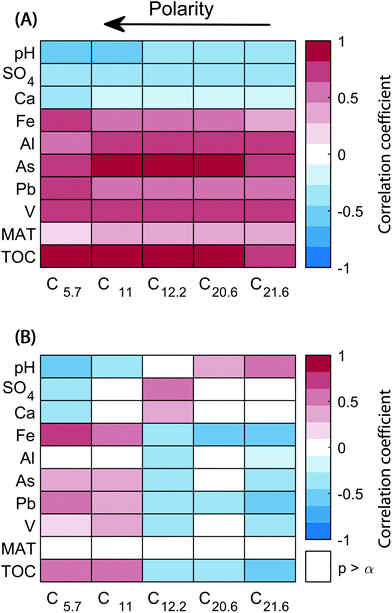
The loadings of the validated five-component model are shown in Fig. 4. Most components had strongly overlapping chromatographic profiles with retention time maxima at 5.7, 11, 12.2, 20.6, and 21.6 minutes. Each component will henceforth be referred to by these maxima (e.g. C5.7). Note that—in contrast to in silico fractionation14,15,28—PARAFAC distinguishes between signals arising from overlapping features and separates their contributions into components. Three of the five components (C11, C12.2 and C21.6) had skewed, but almost unimodal elution profiles, while C5.7, and C20.6 showed multiple chromatographic features (Fig. 4 top row). All five components were broad, and by definition contained a single mass spectrum with varying abundance over the retention. This demonstrates the high isomeric diversity of these natural mixtures, but suggests that different isomers behave similarly across geographical gradients.Each component covered a different compositional space in the van Krevelen diagram (Fig. 4, bottom panel). The weighted-average (wa) polarity decreased with increasing retention time maximum from O/Cwa and H/Cwa 0.72 and 0.97 for C5.7 to 0.34 and 1.30 for C21.6. No direct connection between polarity and mass-to-charge ratio (m/z) or double bond equivalent (DBE) was apparent (Table 2). However, mass spectra of components eluting at similar retention times were generally most similar (Fig. S11†). The chemodiversity (number of molecular formulas with loadings larger than zero) differed only slightly between the five components (Table 2). From the molecular perspective, the dominant molecular formulas were usually present in several components (Fig. S12†), highlighting the isomeric diversity hidden behind each formula,13,32 and revealing for the first time that isomers can be grouped by behaviour across environments.
| Comp. | m/zwa | H/Cwa | O/Cwa | DBEwa | %var. | C i |
|---|---|---|---|---|---|---|
| C5.7 | 373.3 | 1.0 | 0.7 | 9.0 | 3.6 | 789 |
| C11 | 366.5 | 1.1 | 0.6 | 8.4 | 23.4 | 759 |
| C12.2 | 349.5 | 1.2 | 0.5 | 7.6 | 41.1 | 776 |
| C20.6 | 378.0 | 1.3 | 0.4 | 8.1 | 34.2 | 794 |
| C21.6 | 386.4 | 1.3 | 0.3 | 8.2 | 22.4 | 803 |
The scores of components reflect the abundance of the five different chromatographic features per sample. Connections between changes in the abundance of each feature and biogeochemical parameters were explored with a covariance analysis (Fig. 5A). All components correlated positively with total organic carbon and metals such as Pb, As, Al, V, and Fe (except for Fe and C21.6). On the other hand, inverse correlations were observed with pH, SO4, and Ca abundances. A second analysis was carried out with relative component scores (score divided by the sum of scores in a sample), where the score of each component corresponds to its contribution to the overall sample composition (Fig. 5B). The covariance of components C5.7 and C11 with TOC, Pb, As, and Fe remained largely unchanged, but were weaker. In contrast, C14.2, C20.6, and C21.6 showed a tendency to correlate inversely with previously directly correlated variables (and vice versa).
Discussion
The decomposition of multivariate datasets with PARAFAC occurs under the assumption that the analysed dataset is low-rank trilinear.22,33 First, this implies that the HPLC–HRMS data can be described with a reasonable number of components. Additionally, the mass spectrum and chromatogram of an individual analyte should only vary in concentration. In complex mixtures, this requirement expands to groups of environmentally or analytically indistinguishable analytes. Lastly, the total intensity of a signal – except for random detector noise – should equal the sum of all its constituents. The compounds that constitute a molecular formula are expected to ionize with a near constant efficiency, irrespective of the samples they occur in or retention time at which they elute. In the following section, we first evaluate whether these key assumptions were met before further discussing the modelling outcome.Validity of the PARAFAC model
Under ideal conditions, electrospray-ionization HRMS responds linearly to changing analyte concentrations and a chromatographic separation occurs in a reproducible fashion.34 However, during the analysis of complex samples such as those containing DOM, numerous factors can introduce artefacts and prohibit ideal conditions for analysis.35Compared to direct infusion measurements, matrix effects may play a more important role in HPLC–HRMS analyses. As analytes may coelute with interfering species, ionization efficiencies may change over the course of an LC separation. Such matrix effects can introduce non-linearity, increase noise, or lead to the complete loss of an analyte via ionization suppression.36 Because samples were not desalted prior to analysis in our study, complexing metals that retain on the column with DOM (like iron and copper) could also interfere with the ESI spray in a non-consistent manner throughout the chromatogram.37,38 The variation in solvent composition and pH is also likely to affect desolvation and ionisation of carboxylic acids.39–42 Furthermore, large organic polymers (probably derived from lignin) are not detected by ESI-MS, and may further interfere with desolvation or ionisation.29
Chromatographic misalignments can also prevent a systematic description of HPLC–HRMS data with PARAFAC.21 When the same chemical species in two samples elutes at different retention times, a single PARAFAC component cannot account for the abundance of the analyte. Changes in analyte retention may be due to the imperfect replication of the elution program between two injections, changes in the stationary phase properties over multiple injections, or small changes in the temperature conditions. During statistical modelling, misalignments may contribute to the modelling error in mild cases. In more severe cases, the model may describe the misalignments directly by fitting components with highly similar mass spectra and slightly shifted elution profiles. The loadings of the five-component PARAFAC model suggest that the model was not directly impacted by chromatographic misalignments since all components described visibly different elution phenomena. However, some mild cases of misaligned chromatograms may have contributed to the model residuals discussed below.
A relatively large degree of noise in the detection of individual ions suggests that the stability of the ESI was low at times. In the case of abundant ions, PARAFAC was able to distinguish random noise from the systematic underlying variation of analytes (Fig. 3C). In our residual analysis (Fig. 3 and Table 1), purely random residuals accounted for the largest identifiable proportion of unexplained variance, and random modelling error occurred in almost all molecular fractions of DOM. This indicates that random noise is an important source of imprecision in HPLC–HRMS analyses. Linear models such as PARAFAC thus help to isolate the systematic variation in noisy HPLC–HRMS chromatograms.
The estimation of less abundant analytes with PARAFAC was more challenging. In approximately 7.7% of all formula chromatograms, the model estimated the ion in question to be present while not a single detection was recorded (Fig. 3A). These ions may have either been present but not detected by the instrument, or absent and falsely estimated by PARAFAC. These explanations point towards matrix effects in the ion source or modelling with too few components, respectively. At present, it is difficult to assess which of the two explanations accounts for seemingly false-positive PARAFAC estimations.
In this context, it should be noted that formula chromatograms containing zeros do not indicate a true absence of an ion, but only failure of the signal to exceed the signal-to-noise threshold. In agreement with this, the group of formulas that were categorized to be false-positive present often had properties typically observed for low-abundance DOM (e.g. occurrence at the edges of the mass spectrum, Fig. S10A and F†). A lower signal-to-noise cut-off would allow better insight into the less abundant ions but would also significantly increase dataset size and computational expense.43 Here, we opted against adjusting the data processing routine as the issue accounted for a relatively small proportion of the modelling error.
As noted above, interfering species can adversely affect the linear detector-response in HPLC–HRMS. Estimating the impact of non-linearity has been difficult due to the complex nature of DOM mass spectra. In this context, PARAFAC offers a unique opportunity for a more quantitative assessment. Since PARAFAC describes the data with a linear combination of rigid mass spectra and chromatograms, non-linearity cannot be accommodated (Fig. 3B).44 Non-linearity due to matrix effects can be identified as systematic deviations of the data from the established model.
Here, we observed that approximately 2.5% of chromatograms were systematically underestimated while 4.8% were overestimated. However, both types of modelling error only accounted for 0.22% of the data or 7.2% of the modelling error (Table 1). This demonstrates that non-linear signals are in fact encountered in HPLC–HRMS, but only a small proportion of the data seems affected. It was noteworthy that over- and underestimations were compositionally more selective than other types of modelling errors. Overestimated formulas mostly either eluted as a sharp feature at the beginning or end of each run (Fig. S10C†). Difficulty of accounting for the behaviour these relatively narrow and sharp features may in part be due to retention time misalignments (as discussed above).27 In contrast, underestimated formulas had distinctly low m/z values (<300). This suggests that matrix effects leading to underestimations are especially important for ions with low m/z.
While the identification of rare or uniquely behaving formulas was not the primary goal of this study, the detailed analysis of model residuals may in future also be used for the purpose of studying emerging contaminants or metabolomic targets. There is an increasing interest in such compounds that exist as part of DOM.45 Since the relevant molecular formulas are known, our approach could be modified to target specific formulas and isomers. A PARAFAC model would describe their dynamics well if these specific compounds behave like the remainder of DOM. In contrast, a detailed analysis of model residuals may reveal meaningful information if the behaviour of targeted compounds differs significantly from the complex, broadly eluting background.
Overall, the five-component PARAFAC model (Fig. 4) captured the patterns in much of the modelled dataset, (Fig. 2 and S9†) and was found to represent random halves as well as the overall dataset (Fig. S7†). A linear combination of five components explained almost 97% of the data. This represents a significant reduction of complexity, and – since additional features were isolated from a broadly overlapping bulk chromatogram – also a step towards enhanced information-recovery in HPLC–HRMS analysis of complex mixtures.
Alternatives to PARAFAC
In cases where HPLC–HRMS datasets do not follow the assumptions behind the PARAFAC model, alternative approaches to data reduction and feature isolation may be more appropriate. A particularly popular approach is nonnegative matrix factorization (also referred to as multivariate curve resolution, MCR).31 MCR is a bilinear model that can produce results that compare well to PARAFAC solutions.46 Alternative, more constrained approaches, such as principal component analysis (PCA) have been widely applied to mass spectra of DOM to relate changes in DOM composition to environmental processes.28,47–49Here, we observed a good agreement between MCR models describing individual samples and the global PARAFAC model (Fig. S13†). MCR might be particularly valuable when HPLC–HRMS datasets consist of too few samples for conventional PARAFAC. Models can be fit to each individual sample, as MCR does not require three-dimensional data. This allows the identification of elution patters in individual samples (as seen in Fig. S13†).50 Conversely, when its assumptions are upheld, the application of PARAFAC is simpler when three-way data are analysed. Unsurprisingly, three-way PARAFAC is less susceptible to random detector noise than sample-by-sample bilinear MCR (Fig. S13†). For an excellent discussion of sources of model error in MCR and a detailed tutorial review, we refer the reader to Tauler and Maeder (2009) and de Juan et al. (2014).31,51
In cases where neither PARAFAC nor MCR deliver satisfying results, PCA may be an alternative. PCA is a bilinear model and thus requires unfolding of HPLC–HRMS data or sample-by-sample modelling. PCA primarily explores deviation from an average composition, which requires mean-centring and scaling.52 Thus, component loadings differ from the initial raw data, which can be a hurdle when users are more accustomed to typical mass spectra. Moreover, PCA components are orthogonal and may thus have loadings that do not necessarily follow the natural structure of the underlying data.53 Many HRMS studies of DOM have employed some type of data reduction method that involves calculating pairwise sample distances followed by multidimensional scaling into principle coordinates. These methods usually require peak intensities to be scaled to a normalised total value and also force trends into orthogonal components, which may not be realistic in environmental data. In contrast, MCR and PARAFAC can account for the high similarity between measured phenomena, follow the relevant analytical principles, and do not require much pre-processing.22,31
One disadvantage of all above-mentioned approaches is that they focus on describing the chromatographic elution of analytes. In contrast, most applications of HPLC–HRMS intend to relate the composition of complex samples to environmental processes. Such environmental processes may coincide with the modelled polarity, but it is possible that the formulas in an identified polarity fraction (“component”) are controlled by entirely different environmental processes. Thus, relating the sample composition (as identified by PARAFAC) to environmental processes may not lead to satisfying results. Regression methods, such as N-way partial least squares (N-PLS) may help to identify the chemical fractions that are controlled by certain environmental processes.54 PLS-based methods are already common tools in disciplines such as metabolomics,55 but have not been employed in HPLC–HRMS analysis of DOM to our knowledge.
Polarity distribution of DOM across Swedish headwater streams
Each of the five PARAFAC components provided insights on the abundance and chemical complexity of different molecular fractions. In HPLC–HRMS, chromatographic separation is the main source of variation. Therefore, each PARAFAC component groups molecular formulas that co-eluted as a response to the increasing acetonitrile concentration in the mobile phase.A HPLC separation of DOM prior to mass spectrometric analysis has been utilized as a method to decrease isomeric complexity in many studies.10,12,14–16,28,32 As chromatograms routinely consist of broad humps, a separation of DOM into its analytes remains unachieved. In this regard, chemometric approaches such as PARAFAC serve to maximise feature distinction by utilizing the collected spectral information to identify patterns. Despite these improvements, the components in our study did not represent individual compounds but rather groups of compounds with identical chromatographic elution. To further improve the physical separation of DOM compounds, multidimensional chromatography is necessary. Sequential dimensions of chromatography offer superior separation and improve the identification of molecular species.12,17 In cases where single analyte peaks are obtainable, a statistical decomposition would no longer be required since pure analyte spectra are already extracted. However, under the scenario of co-elution in multi-dimensional chromatography, multi-way modelling would still provide an advantageous information-reduction and -extraction strategy.
By comparing the loadings of each of the five PARAFAC components, an estimate of contribution from distinguishable groups of isomers from within the complexity of each molecular formula can be obtained (Fig. 2). The three examples shown in Fig. 2 demonstrate that some molecular formulas were described by one or two components, but others were split more evenly between the majority of the six components. Higher mass formulas tend to be more hydrophobic and were less often detected in the first component (C5.7). The highest abundance ions were more often detected above the noise level and needed more components to be described. For these reasons, there was a slight tendency for higher mass ions to require less components, and higher abundance ions to require more components to be described by the model (Fig. S12†). Even after the application of PARAFAC, isomers were not fully resolved. Each PARAFAC component had relatively broad elution profiles, most likely caused by a range of isomers with highly similar polarity and behaviour.
The composition of DOM across 74 headwater streams in southeast Sweden showed that the five organic matter fractions mainly tracked the abundance of total organic carbon itself, but also many metals (Pb, V, As, Al, and Fe). Conversely, pH and sulphate weakly correlated with decreasing amounts of organic matter. While the strong positive correlation between total organic carbon and all its polarity fractions is expected, the relative contribution of different fractions responded differently. Overall, the weak correlations between relative scores and biogeochemical variables indicated that the composition of DOM did not vary drastically between the 74 streams, as noted previously.28 Only the two most polar fractions tended to show increasing importance with total organic carbon, and inversely correlated with changes in pH, sulphate, and calcium. The strongest relationship of a component's relative score with a measured geochemical parameter was the most acidic and hydrophilic component, C5.7 with iron, which is likely to have a close relationship with carboxylic acid rich DOM in solution.
As noted above, a PARAFAC analysis of HPLC–HRMS data itself does not necessarily identify fractions with common environmental reactivity. The disconnect between HPLC-based polarity fractions and environmental reactivity may explain the weak correlations observed in Fig. 5 (bottom). In its current form HPLC–HRMS is a valuable tool to extract more molecular features from complex samples. To identify which of the (partially) separated isomers are tied to environmental processes, multiway regression models may ultimately be more promising. However, such approaches have not yet been explored for DOM-type HPLC–HRMS datasets. In the present study, the low degree of compositional variation would present a significant challenge to regression models, since many formulas and isomers were correlated in their abundance.
It was previously found in this sample set that there was a relationship between higher molecular mass compounds and mean annual temperature using principle coordinate analysis (PCoA).28 No similar trend was found here using PARAFAC component scores. The underlying assumptions of PARAFAC and PCoA are fundamentally different, making a direct comparison difficult. However, since PARAFAC more closely follows the analytical principles of HPLC–HRMS, trends found between PARAFAC scores and geochemical parameters are likely more robust than those found with PCoA.
During sample preparation, DOC was adjusted with the goal of injecting a constant amount of carbon into the HPLC–HRMS system. This common practice in DOM mass spectrometry aims to fill the detector trap (ion cyclotron resonance or Orbitrap) with a consistent number of ions, typically 106, for consistent mass accuracy and space-charge effects.56–58 Additionally, while the dynamic range of peak intensities within DOM is enormous (spanning several orders of magnitude43,59), the dynamic range of detectors is usually only on the order of thousands. This means that sample concentrations, which spanned an order of magnitude in this sample set, need to be normalised in order to observe a fair representation of ions. Because the scores obtained by PARAFAC are theoretically quantitative, we scaled the results back to environmental levels by multiplying them by the factor used to concentrate the samples.
The resulting relationship between PARAFAC component scores and bulk DOC concentrations was quite well explained by a linear regression (sum of scores vs. DOC: R2 = 0.79, p < 0.001). However, the ratio of sum of scores to DOC decreased with increasing DOC, indicating that an increasing proportion of DOC at high concentrations was not ionisable and thus not contributing to PARAFAC components (Fig. S14†). This corresponds well with recent evidence of a coloured, high molecular weight pool of DOM in terrestrial samples that does not ionise by ESI.29 This pool of ESI-invisible, coloured pool of DOM is gradually removed when DOC decreases across the aquatic environment.60,61 For terrestrial DOM containing coloured, ESI-invisible material, using DOC concentration to ensure equal conditions in the detector trap may result in under-filling of detector cells if automatic gain control is not available. Furthermore, the post hoc correlation of optically active DOM with electrospray ionisable DOM may give misleading results as the various pools do not necessarily overlap.62,63 Recent advances in multivariate data fusion provide the flexible mathematical framework necessary to jointly analyse the composition of DOM with different analytical tools.53 However, further work is required to determine the extent to which DOM samples are ionised by techniques such as ESI, as well as the extent to which DOM absorbs and fluoresces light, in order to properly investigate the overlap and molecular nature of these pools.
Our results indicate that the sum of modelled ions generally followed ionisable DOC concentrations. This was despite the fact that not all assigned ions were modelled and that the true quantity of non-ionisable species was unknown. The good agreement between DOC and PARAFAC scores demonstrates that HPLC–HRMS measurements provide compositional insight that also relates to the abundance of ionisable DOC in general.
Conclusion and future perspectives
A HPLC–HRMS dataset describing the polarity distribution of DOM in 74 headwater streams in southeast Sweden was analysed with a multiway chemometric approach. Despite considerable molecular diversity, only five PARAFAC components described 96.89% of the dataset. The remaining variability was due to a combination of matrix effects and measurement noise. The statistical components isolated almost all ionisable DOM into groups of isomers within molecular formulas that co-eluted due to their highly similar polarity and co-varied across the landscape in predictable patterns. It is quite remarkable that only five components described almost all data. The abundance of all components increased with total organic carbon and decreased with pH. On the other hand, the relative contribution of low oxygen, saturated DOM increased at lower pH and decreased for streams containing higher total organic carbon and iron.Overall, the integration of a chemometric approach greatly simplified the analysis of HPLC–HRMS data. 7178 mass spectra and 1355 formulas were reduced to a linear combination of only five components. Each of these components summarized the information of all three measurement modes (sample, formula, elution). Whereas in silico fractionation integrates coeluting groups of molecular formulas, PARAFAC utilized the spectral information to distinguish between them and identified their contribution regardless of co-elution. Future applications of HPLC–HRMS of complex samples may improve based on PARAFAC decompositions. For example, elution profiles may be optimized based on the elution profiles of statistical components, rather than the more complex raw mass spectra.
While the incorporation of a supervised chemometric model such as PARAFAC introduces an additional data analysis step, it provides superior information recovery and maximises the potential of HPLC–HRMS analyses. Since PARAFAC follows key analytical principles, its components are as interpretable as raw data. The insight provided by the statistical model can be related to the processes affecting DOM by relating component scores to other geochemical and environmental information.
Data availability
All HPLC–HRMS data, geochemical sample parameters, and model scores and loadings are available on Dryad (https://doi.org/10.5061/dryad.nk98sf7pp) as comma-separated files. The Dryad data submission does not include MATLAB scripts, but contains the intermediate data products with which all results can be recreated platform-independently. Please refer to the usage notes of the Dryad data submission for further details.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
U. J. W. acknowledges funding from the Swedish Research Council (FORMAS 2017-00743) and the Åforsk Foundation (grant number 19-499). J. A. H. acknowledges funding from the Swedish Research Council (Vetenskapsrådet 2018-04618).References
- R. Benner, in Biogeochemistry of Marine Dissoved Organic Matter, ed. D. A. Hansell and C. A. Carlson, Academic Press, San Diego, 2002, pp. 59–90 Search PubMed.
- C. A. Carlson and D. A. Hansell, in Biogeochemistry of Marine Dissolved Organic Matter, Elsevier Inc., 2nd edn, 2014, pp. 65–126 Search PubMed.
- D. A. Hansell, Annu. Rev. Mar. Sci., 2011, 5, 120717164858000 Search PubMed.
- N. Hertkorn, C. Ruecker, M. Meringer, R. Gugisch, M. Frommberger, E. M. Perdue, M. Witt and P. Schmitt-Kopplin, Anal. Bioanal. Chem., 2007, 389, 1311–1327 CrossRef CAS PubMed.
- P. Schmitt-Kopplin, D. Hemmler, F. Moritz, R. D. Gougeon, M. Lucio, M. Meringer, C. Müller, M. Harir and N. Hertkorn, Faraday Discuss., 2019, 218, 9–28 RSC.
- S. L. McCallister, N. F. Ishikawa and D. N. Kothawala, Limnol. Oceanogr. Lett., 2018, 3, 444–457 CrossRef.
- M. Derrien, S. R. Brogi and R. Gonçalves-Araujo, Water Res., 2019, 163, 114908 CrossRef CAS PubMed.
- N. Hertkorn, M. Frommberger, M. Witt, B. P. Koch, P. Schmitt-Kopplin and E. M. Perdue, Anal. Chem., 2008, 80, 8908–8919 CrossRef CAS PubMed.
- M. Zark, J. Christoffers and T. Dittmar, Mar. Chem., 2017, 191, 9–15 CrossRef CAS.
- B. P. Koch, K. U. Ludwichowski, G. Kattner, T. Dittmar and M. Witt, Mar. Chem., 2008, 111, 233–241 CrossRef CAS.
- E. N. Capley, J. D. Tipton, A. G. Marshall and A. C. Stenson, Anal. Chem., 2010, 82, 8194–8202 CrossRef CAS PubMed.
- T. A. Brown, B. A. Jackson, B. J. Bythell and A. C. Stenson, J. Chromatogr. A, 2016, 1470, 84–96 CrossRef CAS PubMed.
- J. A. Hawkes, C. Patriarca, P. J. R. Sjöberg, L. J. Tranvik and J. Bergquist, Limnol. Oceanogr. Lett., 2018, 3, 21–30 CrossRef CAS.
- C. Patriarca, J. Bergquist, P. J. R. Sjöberg, L. Tranvik and J. A. Hawkes, Environ. Sci. Technol., 2018, 52, 2091–2099 CrossRef CAS PubMed.
- D. Kim, S. Kim, S. Son, M.-J. Jung and S. Kim, Anal. Chem., 2019, 91, 7690–7697 CrossRef CAS PubMed.
- T. Reemtsma, A. These, A. Springer and M. Linscheid, Water Res., 2008, 42, 63–72 CrossRef CAS PubMed.
- T. Spranger, D. van Pinxteren, T. Reemtsma, O. J. Lechtenfeld and H. Herrmann, Environ. Sci. Technol., 2019, 53, 11353–11363 CrossRef CAS PubMed.
- J. K. Geuer, B. Krock, T. Leefmann and B. P. Koch, Mar. Chem., 2019, 215, 103669 CrossRef CAS.
- T. Leefmann, S. Frickenhaus and B. P. Koch, Rapid Commun. Mass Spectrom., 2018 DOI:10.1002/rcm.8315.
- N. Tolić, Y. Liu, A. Liyu, Y. Shen, M. M. Tfaily, E. B. Kujawinski, K. Longnecker, L. J. Kuo, E. W. Robinson, L. Paša-Tolić and N. J. Hess, Anal. Chem., 2017, 89, 12659–12665 CrossRef PubMed.
- D. Bylund, R. Danielsson, G. Malmquist and K. E. Markides, J. Chromatogr. A, 2002, 961, 237–244 CrossRef CAS PubMed.
- R. Bro, Chemom. Intell. Lab. Syst., 1997, 38, 149–171 CrossRef CAS.
- U. J. Wünsch, R. Bro, C. A. Stedmon, P. Wenig and K. R. Murphy, Anal. Methods, 2019, 11, 888–893 RSC.
- C. A. Stedmon, S. Markager and R. Bro, Mar. Chem., 2003, 82, 239–254 CrossRef CAS.
- K. R. Murphy, C. A. Stedmon, T. D. Waite and G. M. Ruiz, Mar. Chem., 2008, 108, 40–58 CrossRef CAS.
- R. Bro, N. Viereck, M. Toft, H. Toft, P. I. Hansen and S. B. Engelsen, TrAC, Trends Anal. Chem., 2010, 29, 281–284 CrossRef CAS.
- J. M. Amigo, M. J. Popielarz, R. M. Callejón, M. L. Morales, A. M. Troncoso, M. A. Petersen and T. B. Toldam-Andersen, J. Chromatogr. A, 2010, 1217, 4422–4429 CrossRef CAS PubMed.
- J. A. Hawkes, N. Radoman, J. Bergquist, M. B. Wallin, L. J. Tranvik and S. Löfgren, Sci. Rep., 2018, 8, 16060 CrossRef PubMed.
- J. A. Hawkes, P. J. R. Sjöberg, J. Bergquist and L. J. Tranvik, Faraday Discuss., 2019, 218, 52–71 RSC.
- R. Bro and H. A. L. Kiers, J. Chemom., 2003, 17, 274–286 CrossRef CAS.
- A. de Juan, J. Jaumot and R. Tauler, Anal. Methods, 2014, 6, 4964–4976 RSC.
- S. Sandron, N. W. Davies, R. Wilson, A. R. Cardona, P. R. Haddad, P. N. Nesterenko and B. Paull, Chromatographia, 2018, 81, 203–213 CrossRef CAS.
- N. D. Sidiropoulos and R. Bro, in Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 2000, pp. 1–4 Search PubMed.
- W. M. Johnson, M. C. Kido Soule and E. B. Kujawinski, Limnol. Oceanogr.: Methods, 2017, 15, 417–428 CrossRef.
- P. J. Taylor, Clin. Biochem., 2005, 38, 328–334 CrossRef CAS PubMed.
- R. King, R. Bonfiglio, C. Fernandez-Metzler, C. Miller-Stein and T. Olah, J. Am. Soc. Mass Spectrom., 2000, 11, 942–950 CrossRef CAS PubMed.
- R. M. Boiteau, J. N. Fitzsimmons, D. J. Repeta and E. A. Boyle, Anal. Chem., 2013, 85, 4357–4362 CrossRef CAS PubMed.
- G. Becher, G. Oestvold, P. Paus and H. M. Seip, Chemosphere, 1983, 12, 1209–1215 CrossRef CAS.
- K. M. Peru, M. J. Thomas, D. C. Palacio Lozano, D. W. McMartin, J. V. Headley and M. P. Barrow, Chemosphere, 2019, 222, 1017–1024 CrossRef CAS.
- L. Tang and P. Kebarle, Anal. Chem., 1993, 65, 3654–3668 CrossRef CAS.
- T. L. Brown and J. A. Rice, Anal. Chem., 2000, 72, 384–390 CrossRef CAS PubMed.
- M. Oss, A. Kruve, K. Herodes and I. Leito, Anal. Chem., 2010, 82, 2865–2872 CrossRef CAS PubMed.
- D. C. Palacio Lozano, R. Gavard, J. P. Arenas-Diaz, M. J. Thomas, D. D. Stranz, E. Mejía-Ospino, A. Guzman, S. E. F. Spencer, D. Rossell and M. P. Barrow, Chem. Sci., 2019, 10, 6966–6978 RSC.
- R. Bro, C. A. Andersson and H. A. L. Kiers, J. Chemom., 1999, 13, 295–309 CrossRef CAS.
- J. A. Pemberton, C. E. M. Lloyd, C. J. Arthur, P. J. Johnes, M. Dickinson, A. J. Charlton and R. P. Evershed, Rapid Commun. Mass Spectrom., 2019 DOI:10.1002/rcm.8618.
- X. Zhang, R. Marcé, J. Armengol and R. Tauler, Chemosphere, 2014, 111, 120–128 CrossRef CAS PubMed.
- R. L. Sleighter, Z. Liu, J. Xue and P. G. Hatcher, Environ. Sci. Technol., 2010, 44, 7576–7582 CrossRef CAS PubMed.
- O. J. Lechtenfeld, B. P. Koch, B. Gašparović, S. Frka, M. Witt and G. Kattner, Mar. Chem., 2013, 150, 25–38 CrossRef CAS.
- T. Riedel, M. Zark, A. V. Vähätalo, J. Niggemann, R. G. M. Spencer, P. J. Hernes and T. Dittmar, Front. Earth Sci., 2016, 4, 1–16 Search PubMed.
- F. Marini, A. D'Aloise, R. Bucci, F. Buiarelli, A. L. Magrì and A. D. Magrì, Chemom. Intell. Lab. Syst., 2011, 106, 142–149 CrossRef CAS.
- R. Tauler and M. Maeder, in Comprehensive Chemometrics, Elsevier, 2009, pp. 345–363 Search PubMed.
- R. Bro and A. K. Smilde, Anal. Methods, 2014, 6, 2812–2831 RSC.
- U. J. Wünsch, E. Acar, B. P. Koch, K. R. Murphy, P. Schmitt-Kopplin and C. A. Stedmon, Anal. Chem., 2018, 90, 14188–14197 CrossRef PubMed.
- R. Bro, J. Chemom., 1996, 10, 47–61 CrossRef CAS.
- P. S. Gromski, H. Muhamadali, D. I. Ellis, Y. Xu, E. Correa, M. L. Turner and R. Goodacre, Anal. Chim. Acta, 2015, 879, 10–23 CrossRef CAS PubMed.
- A. V. Tolmachev, M. E. Monroe, N. Jaitly, V. A. Petyuk, J. N. Adkins and R. D. Smith, Anal. Chem., 2006, 78, 8374–8385 CrossRef CAS PubMed.
- D. K. Williams and D. C. Muddiman, Anal. Chem., 2007, 79, 5058–5063 CrossRef CAS PubMed.
- D. F. Smith, D. C. Podgorski, R. P. Rodgers, G. T. Blakney and C. L. Hendrickson, Anal. Chem., 2018, 90, 2041–2047 CrossRef CAS PubMed.
- R. P. Rodgers, M. M. Mapolelo, W. K. Robbins, M. L. Chacón-Patiño, J. C. Putman, S. F. Niles, S. M. Rowland and A. G. Marshall, Faraday Discuss., 2019, 218, 29–51 RSC.
- G. A. Weyhenmeyer, M. Fröberg, E. Karltun, M. Khalili, D. Kothawala, J. Temnerud and L. J. Tranvik, Glob. Change Biol., 2012, 18, 349–355 CrossRef.
- S. J. Köhler, D. Kothawala, M. N. Futter, O. Liungman and L. Tranvik, PLoS One, 2013, 8, 1–12 Search PubMed.
- S. Wagner, R. Jaffé, K. Cawley, T. Dittmar and A. Stubbins, Front. Chem., 2015, 3, 1–14 CrossRef PubMed.
- R. H. S. Hutchins, P. Aukes, S. L. Schiff, T. Dittmar, Y. T. Prairie and P. A. del Giorgio, J. Geophys. Res.: Biogeosci., 2017, 122, 2892–2908 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9an02176k |
| ‡ Present address: Sven Hultins Gata 6, 41296 Gothenburg, Sweden. |
| This journal is © The Royal Society of Chemistry 2020 |