Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stochastic electrochemistry at ultralow concentrations: the case for digital sensors
Taghi
Moazzenzade
 ,
Jurriaan
Huskens
,
Jurriaan
Huskens
 and
Serge G.
Lemay
and
Serge G.
Lemay
 *
*
MESA+ Institute for Nanotechnology, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands. E-mail: s.g.lemay@utwente.nl
First published on 29th November 2019
Abstract
There is increasing demand, in particular from the medical field, for assays capable of detecting sub-pM macromolecular concentrations with high specificity. Methods for detecting single bio/macromolecules have already been developed based on a variety of transduction mechanisms, which represents the ultimate limit of mass sensitivity. Due to limitations imposed by mass transport and binding kinetics, however, achieving high concentration sensitivity additionally requires the massive parallelization of these single-molecule methods. This leads to a new sort of ‘digital’ assay based on large numbers of parallel, time-resolved measurements aimed at detecting, identifying and counting discrete macromolecular events instead of reading out an average response. In this Tutorial Review we first discuss the challenges inherent to trace-level detection and the motivations for developing digital assays. We then focus on the potential of recently developed single-entity impact electrochemistry methods for use in digital sensors. These have the inherent advantage of relying on purely electrical signals. They can thus in principle be implemented using integrated circuits to provide the parallelization, readout and analysis capabilities required for digital sensors.
Introduction
Healthcare is developing toward solutions attuned to the needs of patients based on real-time, precise and reliable data.1 Important enablers are sensing devices to monitor, treat and coach patients. Particularly interesting in analyzing the molecular landscape of diseases such as cancer are so-called liquid biopsies, which probe circulating factors in biofluids including cell-free DNA (cfDNA) and RNA (cfRNA), proteins, extracellular vesicles, and circulating tumor cells (CTCs).2 Among these biomarkers, oligonucleotides constitute the most important class for such applications.2,3 To name but two examples, tumor DNA has been found to circulate freely in bodily fluids such as blood and urine,4,5 and it has been proposed that drugs can be targeted against aberrant transcription pathways in cancer patients by monitoring messenger RNA expression levels.6,7 As the natural concentrations of such biomarkers in liquid biopsies can be extremely low (pM or lower), analytical devices with ultrahigh sensitivities are required.Surface-based “solid-phase” biosensors are an important class of analytical methods for biomolecular detection. In a typical surface-based biosensor, the sensing element surface is functionalized with receptors, and specific interaction of the biomarkers with these recognition elements transduce to a measurable signal. The quantity of analyte bound to the surface of the transducer is inferred through a variety of means that includes optical,8 mechanical,9,10 electrochemical,11 and magnetic responses,12 from which the concentration in the original sample can be deduced. Different strategies have been implemented for boosting the sensitivity of surface-based sensors via ameliorating the efficiency of the recognition elements,13 transducers,9 and electronic components of the biosensors. Nevertheless, designing reliable analytical approaches for the detection of analytes at low concentrations within a practical time scale remains demanding.
The affinity and kinetics of a particular biomarker-receptor pair are largely predetermined. However, targeted recognition elements have been engineered for increasing the binding affinity. For instance, substituting DNA with PNA improves the affinity via diminishing the electrostatic repulsion between the target DNA and the probe.13 Similarly, introducing electrostatic interaction in the binding site residues of antibodies via mutagenesis can boost the affinity of antibodies against their antigens.14 However, the mutations can destabilize the engineered antibodies thermodynamically and make them more vulnerable in further sensing procedures such as immobilization.14,15 Besides, engineering the recognition elements for improving the affinity may undermine their selectivity. Hence, improving the performance of the recognition elements of the biosensors represents a major challenge. Boosting the response of the detection element (or, alternatively, suppressing aspecific background signals) is therefore an appealing alternative.
Many electrochemical methods have been developed to monitor the binding of biomolecules to surface-immobilized probes and thus provide specific recognition of targets. A broad array of chemical schemes further exists to assist binding of the target or boost sensitivity, often in combination with a DNA pre-amplification step in the case of nucleic acids.16–21 These platforms require minimum amounts of captured analyte to transduce the event to a measurable signal. As a rule these schemes employ ‘macroscopic’ electrochemical methods even when the readout electrodes are miniaturized, and efforts to downscale electrodes in the hope of higher sensitivity do not automatically translate into higher overall performance.
Here we first discuss the challenges of sensing at low concentrations (pM, fM) via ensemble sensing systems. We summarize the fundamental physical impediments and outline the key parameters in surface-based sensing: mass transport and kinetics. Here we use the detection of short oligonucleotides as a prototypical example application. We argue that there exists an opportunity for new sensor concepts based on massively parallelized single-entity measurements. Early attempts have focused mostly on optical methods.22–24 Purely electrical transducers are however highly desirable since they can be implemented using integrated circuits to provide massive parallelization at low cost. In the second part of the manuscript, we therefore review electrochemical sensory systems with the capability to sense analytes and particles with a digital on/off mode.
The challenges
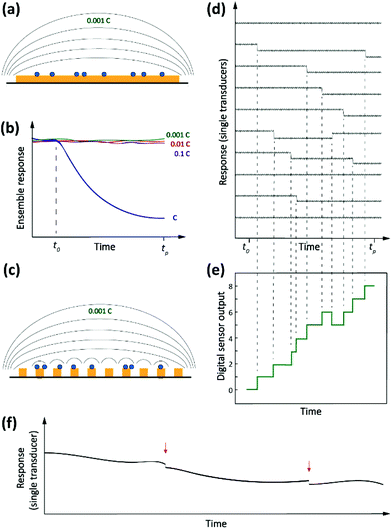
Miniaturization can increase the sensitivity of a sensing element and improve its signal-to-noise ratio.25,26 Moreover, it allows analysis of small-volume samples as encountered in single-cell analysis. However, in a sensor where the rate of analyte transport is limited by diffusion, shrinking the size of transducers decreases the probability of interaction between analytes and sensing elements. Hence, although scaled-down transducers can detect ultra-low amounts of analyte due to their superior electrostatic, photonic, electrochemical or magnetic performance, transport of analyte to the sensing element can quickly become the limiting factor for sensing over a practical time scale. This is illustrated in Fig. 1a, which shows that the expected collision rate between an analyte and a sensor quickly becomes impractical for nanoscale sensors at fM level concentrations.27,28 For example, if we consider that the transducer is sensitive enough to convert the adsorption of one target molecule into a measurable signal, the time scale of sensing for transducers with a size of 1 μm to 10 nm ranges from ∼1 hour to ∼1 day for 1 fM samples. In addition, most sensors are unable to convert a single molecule interaction event and require more analyte molecules for a detectable signal. Hence, the time scale of the sensing becomes impractical and stability of the transducer, bioreceptor, and analytes become an issue.27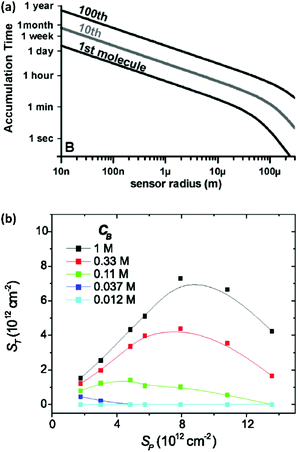 | ||
| Fig. 1 (a) Time required for the diffusive flux of 20 bp DNA molecules with a diffusion coefficient of 150 μm2 s−1 to a hemispherical sensing element for an analyte concentration of 1 fM. Reprinted from ref. 24. (P. E. Sheehan and L. J. Whitman, Nano Lett., 2005, 5, 803–807). (b) Plot of hybridization of target oligonucleotide (ST) as a function of probe density (Sp) and the buffer concentration CB (here defined as moles per litre of phosphate in the pH 7.4 potassium phosphate buffer). Reprinted from ref. 30. (P. Gong and R. Levicky, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5301–5306. Copyright 2008 National Academy of Sciences). | ||
It is possible to decrease the time scale of collision between analytes and a sensing element via imposing fluid flow. This is not as effective as might be assumed, however. At high convective flow rates the collision rate between analyte and a sensor surface scales only as the 1/3 power of the flow velocity (in other words, increasing the pressure by a gigantic factor of 1000 results in a mere 10-fold gain in the collision rate).29 In principle, this problem can be alleviated by implementing simultaneous fluid flow and nanoscale confinement to guide analyte toward the sensing elements.30
Returning to the diffusion-limited regime, the calculation in Fig. 1a was performed with an optimistic assumption of instant and irreversible binding of analyte molecules to the sensing element. In practice, however, analytes do not necessarily adsorb to the sensor as soon as they encounter its surface. Binding and dissociation of biomolecules, for example to a sensor surface, is a dynamic process.31,32 This complicates sensor design because, besides the intrinsic kinetic properties of the recognition elements, their density is also an important factor (especially for highly charged capture probes such as DNA).33,34 Hence, in addition to diffusional mass transport, the recognition event can also become the rate-limiting step.
To appreciate this point more fully, it is interesting to perform some numerical estimates. Consider a simple capture reaction described by Langmuir kinetics. The number of analytes bound to the surface, Nbound, after an incubation time, t, obeys
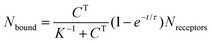 | (1) |
Here Nreceptors is the total number of receptors on the surface, CT is the target concentration in solution, K is the binding constant and τ is the time constant for reaching equilibrium. For illustration purposes, we focus on short oligonucleotides (20 base pairs) under favourable binding conditions (probe density of 5 × 1012 molecules per cm2). For this system, typical values are K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1 ≈ 1 nM and τ ≈ 105 s.35 For a trace target concentration of 1 pM, this means that only about 0.1% of the receptors are occupied at equilibrium (t → ∞). For a measurement time of order 100 s, a desirable value for point-of-care applications, the occupancy Nbound/Nreceptors drops another factor 1000 such that only one receptor in a million is occupied. If one desires a statistically meaningful measurement, it is further necessary to count a significant number of targets. For ca. 10% statistical error, for example, this corresponds to Nbound ≈ 100 and, correspondingly, Nreceptors ≈ 108. Importantly, these receptors occupy a significant surface area of order (100 μm)2 and do not physically fit on a typical miniaturized sensor.35 Increasing the density of probe DNA does not solve this problem since electrostatic repulsion hampers hybridization at high densities, as illustrated in Fig. 1b. On the other hand, lowering the density below 1 × 1012 molecules per cm2 is kinetically favorable and can overcome the electrostatic barrier.33 However, in this regime the number of capture probes per surface area is low (1 molecule/100 nm2), limiting sensitivity.27
−1 ≈ 1 nM and τ ≈ 105 s.35 For a trace target concentration of 1 pM, this means that only about 0.1% of the receptors are occupied at equilibrium (t → ∞). For a measurement time of order 100 s, a desirable value for point-of-care applications, the occupancy Nbound/Nreceptors drops another factor 1000 such that only one receptor in a million is occupied. If one desires a statistically meaningful measurement, it is further necessary to count a significant number of targets. For ca. 10% statistical error, for example, this corresponds to Nbound ≈ 100 and, correspondingly, Nreceptors ≈ 108. Importantly, these receptors occupy a significant surface area of order (100 μm)2 and do not physically fit on a typical miniaturized sensor.35 Increasing the density of probe DNA does not solve this problem since electrostatic repulsion hampers hybridization at high densities, as illustrated in Fig. 1b. On the other hand, lowering the density below 1 × 1012 molecules per cm2 is kinetically favorable and can overcome the electrostatic barrier.33 However, in this regime the number of capture probes per surface area is low (1 molecule/100 nm2), limiting sensitivity.27
The above back-of-the-envelope calculation represents an order-of-magnitude estimate for one specific system but highlights the difficulties inherent in pM-level detection. Measuring the average response of a mm-scale sensor to ca. 100 macromolecules represents a formidable challenge. Even if more favourable conditions are assumed, such as extending the incubation time, one is still left with a situation in which a small integer number of targets must generate a signal large enough to be detected. Achieving the absolute sensitivity to detect such a signal by optical, mechanical or electrical means is not the only challenge, however. The relatively long incubation times also mean that high stability is required to detect the signal against a background that includes slow fluctuations due to temperature stability as well as low-frequency (so-called 1/f) noise in the readout electronics. These sources of drift can easily mask a small signal.
Digital sensors
Driven by the nanotechnology explosion of the last decades, most fields of science have witnessed the development of methods for detecting and studying single entities ranging from artificial (nano)particles and living cells to individual (bio/macro)molecules. The detected signals differ from those commonly encountered in macroscopic measurements in that they are inherently stochastic. Instead of a smooth, average response, one observes sharp spikes, steps or other discrete features that reflect single-entity-scale events such as binding, conformational changes, bond breaking, etc. Detection of single analytes corresponds to the ultimate level of mass sensitivity. However, this does not automatically translate into a high sensitivity in terms of concentration. This is because, in order to achieve this absolute level of mass sensitivity, it is usually necessary for single-entity transducers to have dimensions that are not too much larger than those of the entity being detected. This limits their capabilities for trace-level analysis since, as we argued above, these applications require very large numbers of receptors that in turn require a large detection area. Therefore, in order to adapt single-entity techniques to ultra-low concentration measurements, it becomes necessary to employ large numbers of transducers in parallel. Each individual sensor is capable of detecting discrete microscopic events, but only in the aggregate do they provide the ability to detect ultra-low concentrations. This concept is illustrated schematically in Fig. 2.How would a digital36 sensor work for measuring concentration? Returning to our example of Langmuir kinetics for short DNA oligos, note that at short times (t ≪ τ) eqn (1) simplifies to
| Nbound = NreceptorskonCTt | (2) |
There is an additional subtle advantage to using single-entity transducers. We already mentioned that real-world detection techniques suffer from background drift. If a single-entity signal is measured in real time, however, drift and offsets become much less of an issue. It is much easier to detect sharp, sudden events in the presence of slow drift than it is to detect a small change in response after a long time interval. This is illustrated in Fig. 2f.
We refer to the combination of discrete, time-resolved signals and high degree of parallelization as digital sensors, in analogy to the discrete and parallelized nature of digital integrated circuits.
Electrochemical methods are in principle well-suited to the implementation of digital sensors. This is because parallelization can be achieved relatively straightforwardly and in a cost-effective manner if implemented in the form of integrated circuits. This renders single-entity electrochemical methods an interesting candidate for attempting to build new sensors based on the principle of digital detection.
The Coulter counter, a classic stochastic electrochemical assay
A classic example of a stochastic electrochemical sensing system for single-entity detection and characterization is the resistive pulse sensing (RPS). This system is the advanced exemplar of the classic Coulter counter approach, originally introduced in 1953.37 In Coulter counters, particles passing through a nano/micro pore cause discrete transients in the ionic current flowing through the pore. The sensing system consists of two electrolyte-filled reservoirs separated by an insulating membrane and possessing a single micro-nanoscale pore. The two reservoirs contain electrodes that are used for applying a transmembrane potential difference across the nanopore, such that ions flow through the pore and an ionic current (ic) is established. Particles driven through the pore temporarily block the ionic current by displacing the conductive electrolyte (Fig. 3a). The resulting transient increase in the electrical resistance leads to a detectable step-like decrease in the current-time response. However, the decreased current pulse is ephemeral and the current is restored to its baseline value immediately after the particle has passed entirely through the pore (Fig. 3b). The magnitude, duration and frequency of the current-time resistive pulse provide information about the size, shape, surface charge, and concentration of the particles.38 Initially applied to micron-scale analytes such as cells, this approach developed further following progress in micro- and nanofabrication techniques39,40 and was extended to characterize the size, geometry, surface charge, and mass transport kinetics of nanoscale objects and macromolecules.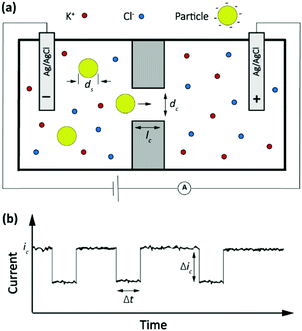 | ||
| Fig. 3 (a) Schematic representation of a resistive pulse sensing system. (b) The current transient properties upon particles passing through the pore. | ||
The amplitude of pulses upon blocking the ionic current, Δic, depends on the geometries of the pore and of the particle as given by the equation
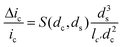 | (3) |
Here ic is the baseline current, ds is the diameter of particle, dc is the pore size, lc′ is the channel length considering the “end effect” (lc′ = lc + 0.8 dc), and S(dc,ds) is a numerical correction factor.39,41,42
The frequency of the pulses is directly proportional to the particle concentration.43 In a channel with well-defined geometric shape and known chemical properties, the pulse duration, Δt, and characteristic signature have been associated with the charge density of nano objects,44 the shape and structure of macromolecules45 and the translocation dynamics of asymmetric nanoparticles.46 For instance, in a biological nanopore (α-hemolysin protein channel) the blockade lifetime is related to the length of translocating polynucleotides.43 In addition, the pulse duration and characteristic signature can provide information about the molecular configuration and folding.45 More recently this approach has been extended to a broad palette of analytes, culminating in the sequencing of nucleic acids.47
Impact stochastic electrochemistry
Another, more recent approach to detect single entities in micro- or nanoscale regions is impact stochastic electrochemistry. This is also an amperometric sensing approach in which the collision of particles with an electrode surface leads to discrete changes in the current-time response. Depending on the electrical or catalytic properties of the colliding particles, different types of signals can be detected in the form of characteristic step- or spike-like transients that appear in the current curve. Different types of information such as size, electroactivity, shape, and surface charge can be extracted from these current transients. While still in its infancy, exploiting these methods for macromolecular detection has been demonstrated in specific cases.36,48–50 Three main classes of approaches based on the impact principle are current blockade, current amplification and capacitive impact, as summarized in Fig. 4.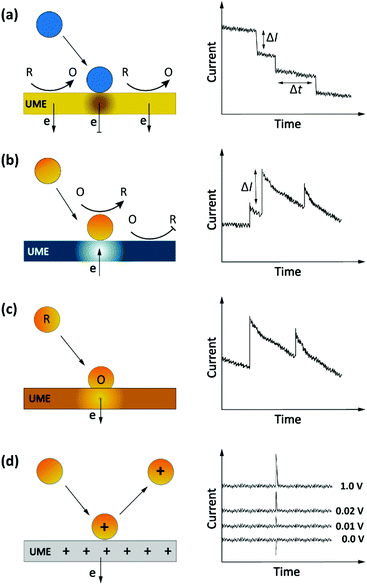 | ||
| Fig. 4 Schematic representation of impact stochastic electrochemical sensors. (a) Current blockade impact:51 step-like decreases in the current–time transients upon collision of the insulator particles. (b) Mediated faradaic impact: staircase-shaped increases in the current–time transient due to a redox reaction catalyzed by the nanoparticles. The catalytic nanoparticles play the role of working electrodes to carry out a heterogenous electron-transfer reaction while the inert electrode works solely to establish electrical contact to the nanoparticles.52 (c) Direct faradaic impact: electron transfer takes place by electro-dissolution of particles reaching the electrode. The measured current change upon the collision is proportional to the number of atoms in the cluster.53 (d) Capacitive impact: current transients upon particle collision result from either charging of the particle or obstruction of the electrical double layer of the electrode. In both cases the polarity of the spikes can invert upon changing the applied potential. | ||
Current blockade impact
In blocking-based measurements, binding of individual non-electroactive particles to the electrode surface hampers the mass transfer of a redox mediator present in the solution. Under potentiostatic control, mass-transport-limited oxidation or reduction of this mediator at the surface of a miniaturized electrode leads to a steady-state current. In an electrolyte solution containing micro/nanoparticles, proximity of the particles to the electrode surface blocks the steady-state mass transport of redox molecules. Hence, stochastic interaction of particles with the electrode surface can be sensed as discrete, step-like decreases in the current-time response (Fig. 4a).51 The average step magnitude, ΔI, is approximately proportional to the projected area of the particle on the electrode, inversely proportional to the diameter of the electrode and proportional to the concentration of the redox mediator.As a complication, due to the nonuniformity in diffusive flux of the redox molecules, particles adsorbing on the edges of the disk electrode block a higher current density and therefore lead to larger step heights.49,51 Furthermore, due to the difference in current density between the edge and center of the disk electrode, the dynamic displacement of adsorbed particles from the center to the edge of the electrode may lead to unwanted steps in the current response that are not representatives of adsorption events.54
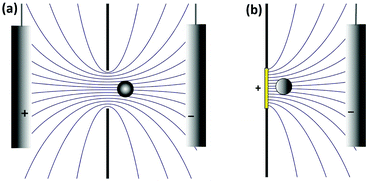
It is interesting to note that the current blockade mechanism is conceptually related to that of the Coulter counter, as sketched in Fig. 5. In the Coulter counter, the migration of ions is obstructed by the analyte particle, whereas it is the diffusion of the redox mediator that is obstructed in current blockade. Because both the electrostatic potential and the mediator concentration profile are governed by the Laplace equation, however, the distortion of the migrational or diffusional fluxes around the particles are very similar in the two cases.
Current amplification impact
The impact detection approach has also been applied to studies of the electrocatalytic activity of metal nanoparticles at the single particle level. Here the sensing mechanism is faradaic reactions involving the (usually conductive) nanoparticles.55 These sensing systems can be separated into two distinct classes: mediated impact and direct impact.53The current step magnitude upon diffusion-controlled electrocatalysis of the redox species on the adsorbed particle on planar electrode can be expressed by the following equation:
ΔI = 4π(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)nFDCr 2)nFDCr | (4) |
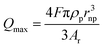 | (5) |
In this equation, Qmax is the maximum transferred charge, ρp is the mass density of the nanoparticle, rnp is the particle radius, and Ar is the relative atomic mass.57 This approach has been extended to sensing of non-metallic nanomaterials and electrochemical size monitoring of organic nanoparticles has been studied.59
Capacitive impact
Particle collisions can have additional consequences beyond faradaic charge transfer and current blockade. Collisions can also remove charge from the electrode surface or disrupt its electrical double layer, a process known as capacitive impact. Both conductive and insulating particles can exhibit this phenomenon in different manners.53 For example, this sensing system has been implemented for characterizing the capacitive properties of graphene nanoplatelets (GNPs). In this approach, the stochastic collision of GNPs with an electrode modify the charge at the electrode–electrolyte interface. Depending on the applied potential, electrons can leave or enter the electrode to compensate this charge redistribution.60 These events can be observed as transients in the current-time response (Fig. 4d). Moreover, the polarity of the spikes will be inverted by using an applied potential that is either higher or lower than the potential of zero charge (PZC) of either the electrode or the particle, as shown in Fig. 4d.61 Determining the PZC of colliding particles can also help to elucidate the nature of the electric double layer of electrodes.60Analyte transport in impact electrochemistry
Before they can be detected by impact electrochemistry, analyte particles must make their way to the surface of the electrode. In general this mass transport includes contributions from diffusion, migration and convection:| J = Jdiff + Jmig + Jconv = −D∇C + μCE + Cv | (6) |
Here J, C, D and μ are the local flux, the concentration, the diffusion coefficient and the electrophoretic mobility of the particles, respectively, E is the electric field and v the electrolyte flow velocity. Impact electrochemistry measurements usually do not involve convection so we take v = 0 and ignore this contribution here.
In a well-designed electrochemical experiment, the electric field is usually negligible through the use of a supporting electrolyte. Migration may however play a larger role in impact experiments. This is because the electrophoretic mobility of colloidal particles is of the same order of magnitude as that of small ions and largely independent of particle size, whereas the diffusion coefficient scales as the inverse of the particle size. Thus, the larger the particle, the more important the electric field becomes. This counterintuitive observation can be used to selectively influence the rate of mass transport, for example in current blockade impact experiments.51
It is thus useful to estimate the conditions under which migration dominates over diffusion. For a hemispherical electrode of radius r0, the electric field has radial symmetry with magnitude
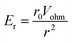 | (7) |
Here r is the radial distance from the center of the electrode and Vohm is the potential difference between the electrode and bulk solution (i.e. the ohmic drop). Assuming that particles that reach the electrode are immobilized or consumed, the corresponding total collision rate from migration, Γmig, is
| Γmig = 2πμC0r0Vohm | (8) |
Here C0 is the bulk particle concentration (this simplification ignores the depletion near the electrode caused by diffusion but this is sufficient to estimate the crossover between diffusion and migration). The corresponding collision rate from diffusion is
| Γdiff = 2πDC0r0 | (9) |
This calculation indicates that Γmig becomes larger than Γdiff when
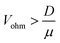 | (10) |
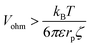 | (11) |
The critical value of Vohm above which migration dominates thus decreases with increasing rp. Numerical substitution indicates that the critical potential is ≈10 μV for a particle with rp = 1 μm and ζ = −27 mV. It is thus possible for migration to be negligible for the transport of a small redox mediator while it dominates the motion of larger particles.
How large is Vohm? This of course depends on the nature of the experiment. We first consider the Coulter counter. Here Vohm originates from the potential applied between the two reservoirs, Vapp. This potential can be divided between the resistance of the pore itself, Rpore, and the resistance of the solution on either side of the pore (the so-called access resistance), Racc. The ohmic drop is then Vohm = VappRacc/(Rpore + 2Racc). For a pore that is much shorter than its diameter, Rpore ≪ Racc and thus Vohm ≈ Vapp/2. It is thus rather straightforward to apply sufficient potential to ensure that transport to the pore is driven by electrophoresis rather than diffusion, as is commonly done in Coulter counters.
We now turn to current blockade electrochemistry. Here an ohmic drop develops because salt ions must move to compensate the charge injected by oxidation or reduction of the redox mediator. The ohmic drop is then RaccI, where I is the faradaic current. The access resistance for a disk electrode is given by Racc = ρ/4r0, where ρ is the resistivity of the electrolyte, while the diffusion-limited mediator current is I = 4nFCmDmr0, where n is the number of electrons transferred, Cm is the mediator concentration and Dm is the mediator diffusion coefficient. This yields
| Vohm = nρFCmDm | (12) |
Interestingly, this result is independent of the electrode radius. For 1 mM ferrocene dimethanol in aqueous 0.3 M KCl solution (n = 1, D ≈ 5 × 10−10 m2 s−1, ρ ≈ 0.2 Ωm) eqn (12) gives Vohm ≈ 10 μV. Comparing this value with eqn (11) indicates that transport of particles with r0 > 1 μm will be dominated by migration under these conditions. Increasing the mediator concentration or decreasing the supporting electrolyte concentration (thus increasing ρ) will cause smaller particles to become controlled by migration. Also note that the direction of the migrational flux depends on the polarity of Vohm. For negatively charged particles (ζ < 0) an oxidation reaction for the mediator attracts the particles toward the electrode while a reduction reaction repels them, preventing access to the electrode at sufficiently high reduction currents.
Other forms of impact electrochemistry besides current blockade do not require a mediator and are thus in principle free of migrational effects. In practice, however, unwanted background reactions take place to some degree, leading to a finite faradaic current. The magnitude of the ohmic drop can again be estimated as Vohm = RaccI = ρI/4r0, where in this case I is the experimentally measured background current.
Summary and outlook
In this Tutorial Review we have discussed some of the main challenges inherent in detecting trace amounts of macromolecular species with high degrees of specificity using electrochemical methods. We have argued that, while recently developed nanoscale assays allow detecting single entities ranging from nanoparticles to bio/macromolecules, these cannot be directly employed for analytical applications at ultra-low concentrations. Doing so will further require massive parallelization in the form of large numbers of individually addressable electrodes and readout systems, thus creating a ‘digital’ assay based on the counting of single discrete events. Electrochemical methods are well suited for this purpose as they can be integrated with microfabricated circuitry to implement this parallelization. We then focused on impact electrochemistry, a set of methods for detecting and characterizing single micro- and nanoscale entities. While this has not yet been achieved experimentally, these methods provide a route for the realization of an electrochemical digital sensor. An important question has not yet been addressed by the impact electrochemistry community, however: how does one best translate a biomolecular recognition event into an impact electrochemistry signal?Conflicts of interest
S. G. L. is co-inventor of an ongoing patent application for a biomedical device based on impact electrochemistry.Acknowledgements
We acknowledge financial support from the TopSector High-Tech Systems & Materials in the TKI project “Early cancer diagnostics”.Notes and references
- C. M. Christensen, J. H. Grossman and J. Hwang, The innovator's prescription: a disruptive solution for health care, McGraw-Hill, New York, 2009 Search PubMed.
- G. Siravegna, S. Marsoni, S. Siena and A. Bardelli, Nat. Rev. Clin. Oncol., 2017, 14, 531–548 CrossRef CAS PubMed.
- A. Sassolas, B. D. Leca-Bouvier and L. J. Blum, Chem. Rev., 2008, 108, 109–139 CrossRef CAS.
- N. Bellassai and G. Spoto, Anal. Bioanal. Chem., 2016, 408, 7255–7264 CrossRef CAS PubMed.
- J. Das, I. Ivanov, L. Montermini, J. Rak, E. H. Sargent and S. O. Kelley, Nat. Chem., 2015, 7, 569–575 CrossRef CAS PubMed.
- W. Verhaegh, H. van Ooijen, M. A. Inda, P. Hatzis, R. Versteeg, M. Smid, J. Martens, J. Foekens, P. van de Wiel and H. Clevers, Cancer Res., 2014, 74, 2936–2945 CrossRef CAS PubMed.
- W. Verhaegh and A. van de Stolpe, Oncotarget, 2014, 5, 5196–5197 CrossRef PubMed.
- B. Liedberg, C. Nylander and I. Lunström, Sens. Actuators, 1983, 4, 299–304 CrossRef CAS.
- J. Fritz, M. Baller, H. Lang, H. Rothuizen, P. Vettiger, E. Meyer, H.-J. Güntherodt, C. Gerber and J. Gimzewski, Science, 2000, 288, 316–318 CrossRef CAS.
- R. Mukhopadhyay, M. Lorentzen, J. Kjems and F. Besenbacher, Langmuir, 2005, 21, 8400–8408 CrossRef CAS PubMed.
- A. Idili, A. Amodio, M. Vidonis, J. Feinberg-Somerson, M. Castronovo and F. Ricci, Anal. Chem., 2014, 86, 9013–9019 CrossRef CAS PubMed.
- L. Hien, L. Quynh, V. Huyen, B. Tu, N. Hien, D. Phuong, P. Nhung, D. Giang and N. Duc, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2016, 7, 045006 Search PubMed.
- C. Briones, E. Mateo-Marti, C. Gomez-Navarro, V. Parro, E. Roman and J. Martin-Gago, Phys. Rev. Lett., 2004, 93, 208103 CrossRef CAS PubMed.
- A. Fukunaga and K. Tsumoto, Protein Eng., Des. Sel., 2013, 26, 773–780 CrossRef CAS PubMed.
- A. Fukunaga, S. Maeta, B. Reema, M. Nakakido and K. Tsumoto, Biochem. Biophys. Rep., 2018, 15, 81–85 Search PubMed.
- J. A. Hansen, R. Mukhopadhyay, J. Ø. Hansen and K. V. Gothelf, J. Am. Chem. Soc., 2006, 128, 3860–3861 CrossRef CAS PubMed.
- P. Miao, Y. Tang and J. Yin, Chem. Commun., 2015, 51, 15629–15632 RSC.
- H. D. Hill and C. A. Mirkin, Nat. Protoc., 2006, 1, 324 CrossRef CAS.
- G. Liu, Y. Wan, V. Gau, J. Zhang, L. Wang, S. Song and C. Fan, J. Am. Chem. Soc., 2008, 130, 6820–6825 CrossRef CAS PubMed.
- J. Zhang, S. Song, L. Zhang, L. Wang, H. Wu, D. Pan and C. Fan, J. Am. Chem. Soc., 2006, 128, 8575–8580 CrossRef CAS PubMed.
- Y. Xiao, A. A. Lubin, B. R. Baker, K. W. Plaxco and A. J. Heeger, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16677–16680 CrossRef CAS PubMed.
- A. Johnson-Buck, X. Su, M. D. Giraldez, M. Zhao, M. Tewari and N. G. Walter, Nat. Biotechnol., 2015, 33, 730 CrossRef CAS PubMed.
- E. W. Visser, J. Yan, L. J. Van IJzendoorn and M. W. Prins, Nat. Commun., 2018, 9, 2541 CrossRef PubMed.
- W. Jing, Y. Wang, Y. Yang, Y. Wang, G. Ma, S. Wang and N. Tao, ACS Nano, 2019, 13, 8609–8617 CrossRef CAS PubMed.
- Y. Zhang, B. Zhang and H. S. White, J. Phys. Chem. B, 2006, 110, 1768–1774 CrossRef CAS PubMed.
- M. B. Viani, T. E. Schäffer, A. Chand, M. Rief, H. E. Gaub and P. K. Hansma, J. Appl. Phys., 1999, 86, 2258–2262 CrossRef CAS.
- P. E. Sheehan and L. J. Whitman, Nano Lett., 2005, 5, 803–807 CrossRef CAS PubMed.
- P. Nair and M. Alam, Appl. Phys. Lett., 2006, 88, 233120 CrossRef.
- T. M. Squires, R. J. Messinger and S. R. Manalis, Nat. Biotechnol., 2008, 26, 417 CrossRef CAS PubMed.
- J. Fritzsche, D. Albinsson, M. Fritzsche, T. J. Antosiewicz, F. Westerlund and C. Langhammer, Nano Lett., 2016, 16, 7857–7864 CrossRef CAS PubMed.
- C.-S. Goh, D. Milburn and M. Gerstein, Curr. Opin. Struct. Biol., 2004, 14, 104–109 CrossRef CAS PubMed.
- T. E. Ouldridge, P. Šulc, F. Romano, J. P. Doye and A. A. Louis, Nucleic Acids Res., 2013, 41, 8886–8895 CrossRef CAS.
- P. Gong and R. Levicky, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5301–5306 CrossRef CAS PubMed.
- L. Simon and R. E. Gyurcsányi, Anal. Chim. Acta, 2019, 1047, 131–138 CrossRef CAS PubMed.
- J. Tymoczko, W. Schuhmann and M. Gebala, ACS Appl. Mater. Interfaces, 2014, 6, 21851–21858 CrossRef CAS PubMed.
- J. E. Dick, A. T. Hilterbrand, L. M. Strawsine, J. W. Upton and A. J. Bard, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 6403–6408 CrossRef CAS PubMed.
- W. H. Coulter, US Pat, 2656508, 1953 Search PubMed.
- M. Don, JALA, 2003, 8, 72–81 Search PubMed.
- R. DeBlois and C. Bean, Rev. Sci. Instrum., 1970, 41, 909–916 CrossRef.
- J. Li, D. Stein, C. McMullan, D. Branton, M. J. Aziz and J. A. Golovchenko, Nature, 2001, 412, 166–169 CrossRef CAS PubMed.
- R. R. Henriquez, T. Ito, L. Sun and R. M. Crooks, Analyst, 2004, 129, 478–482 RSC.
- L. Sun and R. M. Crooks, J. Am. Chem. Soc., 2000, 122, 12340–12345 CrossRef CAS.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770–13773 CrossRef CAS PubMed.
- D. Kozak, W. Anderson, R. Vogel, S. Chen, F. Antaw and M. Trau, ACS Nano, 2012, 6, 6990–6997 CrossRef CAS PubMed.
- C. Plesa, D. Verschueren, S. Pud, J. van der Torre, J. W. Ruitenberg, M. J. Witteveen, M. P. Jonsson, A. Y. Grosberg, Y. Rabin and C. Dekker, Nat. Nanotechnol., 2016, 11, 1093–1097 CrossRef CAS PubMed.
- H. Wu, Y. Chen, Q. Zhou, R. Wang, B. Xia, D. Ma, K. Luo and Q. Liu, Anal. Chem., 2016, 88, 2502–2510 CrossRef CAS PubMed.
- D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. Di Ventra, S. Garaj, A. Hibbs and X. Huang, in Nanoscience and technology: A collection of reviews from Nature Journals, World Scientific, 2010, pp. 261–268 Search PubMed.
- S. J. Kwon and A. J. Bard, J. Am. Chem. Soc., 2012, 134, 10777–10779 CrossRef CAS PubMed.
- J. E. Dick, C. Renault and A. J. Bard, J. Am. Chem. Soc., 2015, 137, 8376–8379 CrossRef CAS PubMed.
- A. D. Castañeda, N. J. Brenes, A. Kondajji and R. M. Crooks, J. Am. Chem. Soc., 2017, 139, 7657–7664 CrossRef PubMed.
- B. M. Quinn, P. G. van't Hof and S. G. Lemay, J. Am. Chem. Soc., 2004, 126, 8360–8361 CrossRef CAS PubMed.
- X. Xiao and A. J. Bard, J. Am. Chem. Soc., 2007, 129, 9610–9612 CrossRef CAS PubMed.
- S. V. Sokolov, S. Eloul, E. Kätelhön, C. Batchelor-McAuley and R. G. Compton, Phys. Chem. Chem. Phys., 2017, 19, 28–43 RSC.
- A. Boika, S. N. Thorgaard and A. J. Bard, J. Phys. Chem. B, 2012, 117, 4371–4380 CrossRef PubMed.
- N. V. Rees, C. E. Banks and R. G. Compton, J. Phys. Chem. B, 2004, 108, 18391–18394 CrossRef CAS.
- X. Xiao, F.-R. F. Fan, J. Zhou and A. J. Bard, J. Am. Chem. Soc., 2008, 130, 16669–16677 CrossRef CAS PubMed.
- Y. G. Zhou, N. V. Rees and R. G. Compton, Angew. Chem., Int. Ed., 2011, 50, 4219–4221 CrossRef CAS PubMed.
- E. J. Stuart, K. Tschulik, C. Batchelor-McAuley and R. G. Compton, ACS Nano, 2014, 8, 7648–7654 CrossRef CAS PubMed.
- W. Cheng, X. F. Zhou and R. G. Compton, Angew. Chem., Int. Ed., 2013, 52, 12980–12982 CrossRef CAS PubMed.
- J. Poon, C. Batchelor-McAuley, K. Tschulik and R. G. Compton, Chem. Sci., 2015, 6, 2869–2876 RSC.
- C. E. Banks, N. V. Rees and R. G. Compton, J. Phys. Chem. B, 2002, 106, 5810–5813 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |