Tap water fingerprinting using a convolutional neural network built from images of the coffee-ring effect

Abstract

A low-cost tap water fingerprinting technique was evaluated using the coffee-ring effect, a phenomenon by which tap water droplets leave distinguishable “fingerprint” residue patterns after water evaporates. Tap waters from communities across southern Michigan dried on aluminum and photographed with a cell phone camera and 30× loupe produced unique and reproducible images. A convolutional neural network (CNN) model was trained using the images from the Michigan tap waters, and despite the small size of the image dataset, the model assigned images into groups with similar water chemistry with 80% accuracy. Synthetic solutions containing only the majority species measured in Detroit, Lansing, and Michigan State University tap waters did not display the same residue patterns as collected waters; thus, the lower concentration species also influence the tap water “fingerprint”. Residue pattern images from salt mixtures with an array of sodium, calcium, magnesium, chloride, bicarbonate, and sulfate concentrations were analyzed by measuring features observed in the photographs as well as using principal component analysis (PCA) on the image files and particles measurements. These analyses together highlighted differences in the residue patterns associated with the water chemistry in the sample. The results of these experiments suggest that the unique and reproducible residue patterns of tap water samples that can be imaged with a cell phone camera and a loupe contain a wealth of information about the overall composition of the tap water, and thus, the phenomenon should be further explored for potential use in low-cost tap water fingerprinting.

---

Introduction

Need for innovation in drinking water monitoring

With tap water crisis events that continue to occur in both developed and developing nations, the desire for low-cost tap water testing that is practical for application by citizens is high. When a teacher, student, household, or community member would like to test their tap water, they are faced with single use paper test strips, probes, standard analytical methods for measuring water quality, or water testing fees for hundreds or even thousands of different water quality parameters. Challenges exist in choosing which water constituents to test and which methods to apply, both of which can be difficult since there is little to no tap water education in typical K-12 and university systems. In this work, experiments were conducted to determine if the coffee-ring effect, precipitation reactions, and convolutional neural networks (CNN) could be harnessed for low-cost “fingerprinting” of tap water samples as a whole, rather than measuring one contaminant at a time.

How does the coffee-ring effect work?

The coffee-ring effect offers low-cost separation of particles in aqueous samples due to the physics of water droplet drying on hydrophobic substrates. This phenomenon occurs when water evaporates evenly from a water droplet surface with a pinned diameter, such that the droplet shrinks in height while the diameter remains constant.^1,2 The shrinking height of the droplet correlates to a decrease in contact angle at the pinned surface through droplet drying, squishing particles into concentric circles by size.¹ The phenomenon was termed nanochromatography after separation resolutions on the order 100 nm were demonstrated for mixtures of fluorescently labeled antibodies, B-lymphoma cells, and E. coli at particle volume fractions on the order of <0.04%.¹ Force balance analysis suggests nanoscale separation is possible for low particle volume fractions due to the difference in the magnitude of adhesion versus surface tension forces for large (1 μm) and small (40 nm) particles at the drop edge, where surface tension forces move particles towards the center of the drop and substrate-particle adhesion forces hold particles in place.¹

Most existing studies on the coffee-ring effect have been conducted on particles or biological molecules, sometimes in buffer solutions or biofluids where particle-like species deposit on the outer edge forming concentric rings of particles separated by size and soluble salts deposit throughout the center of the drop (Fig. 1).^1,3–5 Particles within a drop are known to deposit on the outer edge when the fluid flow that delivers particles to the drop edge is faster than the surface capture effect, the latter which occurs if the concentration of particles at the surface of the droplet is high or if water evaporation is accelerated.⁶ Tap water solutions, however, are composed largely of dissolved ions rather than particles. Within dissolved salt solutions, the majority of the particles observed in the residue patterns must form as water evaporates and increases ion concentrations above solubility limits of their respective salts; however, very little work has been conducted to document the coffee-ring patterns for complex mixtures of salts.⁷ It is expected that in mixed salt solutions both the coffee-ring effect and the fundamental characteristics of the salts that form will control the location, sizes, and shapes of each salt in the resulting residue pattern, with the least soluble salts that form particles quickly separated by size at the drop edge. Thus, features such as the sizes, shapes, colors, quantity, and location of particles within the coffee-ring residue of a water sample are expected to correlate to water chemistry. The coffee-ring effect has previously been partnered with Raman spectroscopy to quantify cyanotoxins in environmental water, signs of ocular damage in human tear fluid, and osteoarthritis determinants in knee fluid; however, the patterns produced due to the coffee-ring effect have not been harnessed without expensive chemical analysis instrumentation to record composition of the deposited residues.

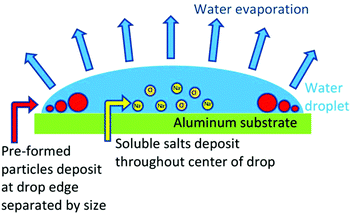Fig. 1 Nanoscale separation of particles within a drying droplet is provided by the phenomenon known as the coffee-ring effect.¹

Image analysis via convolutional neural network (CNN)

Machine learning methods, especially deep learning artificial neural networks (ANNs) are increasing in popularity in research and engineering to solve problems that are challenging to solve with traditional analysis techniques. Convolutional neural networks (CNNs) have been widely tested and successfully used for image analysis, especially in segmentation problems, such as differentiating between an object and the background.^8,9 With the development of more advanced CNN architectures (e.g., CNN models involving more layers, new activation functions, more options for objective functions to calculate error, more sophisticated model structures) and use of graphics processing units with higher computational speeds, CNNs are being developed to analyze a growing variety of data types, including medical images,^10–14 electron microscopy images,¹³ DNA data,^15–17 spectra,^18–20 and chemical structures.^21,22 For example, CNN models have proven the ability to identify brain tumors in magnetic resonance images (MRI) faster and more accurately than the state of the art tools and can identify the pancreas in computerized tomography (CT) images, both of which are challenging analysis problems because of anatomical variability.^10,11 In chemistry, CNN models are being trained using 2D and 3D images of molecular structure for quantitative structure–activity relationship (QSAR) modeling to predict toxicity²³ and to predict therapeutic use classes of drugs.²⁴ CNN models have also been trained to assign surface-enhanced Raman spectroscopy (SERS) spectra to classes of metabolites and to assign bundles of SERS spectra (8 × 8 pixel hyperspectral images) to the concentration of rhodamine 800 dye at femtomolar concentrations for single molecule detection.^18,20 Additional applications include identifying the types and positions of defect structures in silicon doped graphene from unprocessed scanning transmission electron microscopy images,²⁵ predicting chemical reactivity,²² and diagnosing faults in the chemical process industry.²⁶ Limitations of CNNs include the computational cost of model training,^7,16 the sensitivity of classification to unbalanced datasets (unequal numbers of samples in different classes can result in poor model performance),²⁷ and the necessity of experienced users to modify model structure and tune parameters for every individual CNN application. However, the accuracy of classification results observed and the wide variety of cases in which it can be applied ensures use of CNN will continue to grow.

The goal of this research was to determine if the residue patterns of tap water samples imaged with a cell phone camera and loupe were sufficiently reproducible, sensitive, and correlated to water chemistry to be valuable for low-cost analyses. Specific objectives were to create a library of images of residue patterns for real and synthetic tap waters, determine if the residue patterns were reproducible for a given water chemistry, document the response of the fingerprint to changes in composition of majority species (sodium, calcium, magnesium, chloride, bicarbonate, sulfate), and apply machine learning image analysis techniques to differentiate between residue patterns. These objectives were met by photographing residue patterns for a variety of collected tap water solutions and increasingly complex synthetic water solutions with a cell phone camera through a jeweler's loupe, measuring features observed in residue patterns, and correlating residue features to water chemistry, and creating a CNN to classify residue pattern images to groups with similar water chemistry.

Experimental

Water samples

Thirty tap water samples were collected from communities across southern Michigan, utilizing a variety of water treatment systems (Table 1, Table SI-1‡). One liter of each water sample was collected in a hydrochloric acid washed polypropylene bottle from the water supply at a public park, community center, or city building water fountain or restroom tap. Samples were stored at 4 °C until analysis using the coffee-ring effect and standard methods. Samples were not filtered before measurement. Conductivity was measured by a Hach HQ40D portable conductivity meter and intelliCAL™ CDC401 standard conductivity probe, and pH was measured with a Orion Star A211 pH meter and Orion 8135BNUWP Ross Ultra Fast pH probe (Thermo Scientific). Chloride, sulfate, phosphate, fluoride, bromide, and nitrate concentrations were measured by ion chromatography with a Dionex series 2000i/sp instrument. Bicarbonate was measured by titration to pH of 4.5 using standard method 2320.²⁸ Metals were measured by Varian 710-ES Axial ICP-OES and samples were digested by nitric acid using standard method 3030 E. One replicate sample was measured for every ten samples, and values that deviated from expected (from annual municipal water quality reports or previous measurements) were repeated.

Table 1 Measured water quality data for tap water samples collected across Michigan and treatment information from annual municipal water quality reports and system operators. Averages and standard deviations are listed for values conducted in replicate

City	Water treatment	pH	Cond. (μS cm^−1)	Na^+ (mM)	Ca^2+ (mM)	Mg^2+ (mM)	K^+ (mM)	Cl^− (mM)	SO4^2− (mM)	HCO3^− (mM)	PO4^3− (mM)	Cu (mM)	Fe (mM)
MSU - academic hall	Chlorine, fluoride, phosphate, sodium hydroxide	6.96	823	1.08	2.24	1.54	0.041	0.91	0.92	6.94	0.01	6.1 × 10^−3	2.2 × 10^−2
Durand	Iron removal filters, chlorine	6.72	388	0.31	0.16	0.11	0.075	1.10	0.47	4.88	0.02	1.6 × 10^−3	2.4 × 10^−3
Kalamazoo	Chlorine, fluoride, and phosphate	8.52	976	3.17	1.06	1.29	0.060	3.11	0.39	6.23	0.01	1.2 × 10^−3	4.1 × 10^−3
Portland	Chlorine, phosphate	6.94	909	0.76	0.53	2.86	0.109	0.05	0.12	7.51	BD	1.1 × 10^−3	1.1 × 10^−3
Battle Creek site A	Chlorine, fluoride, and phosphate	6.99	672	1.76	1.80	1.04	0.035	1.14	0.51	5.48	0.02	4.0 × 10^−3	7.9 × 10^−4
Battle Creek site B	Chlorine, fluoride, and phosphate	7.22	673	1.60	1.77	1.04	0.035	1.16	0.50	5.47	0.02	8.9 × 10^−3	2.0 × 10^−2
Charlotte	Chlorine, phosphate	7.01 ± 0.29	1215 ± 23	3.79	2.53	3.32	0.252	4.10	0.54	6.89	0.02	3.9 × 10^−4	4.4 × 10^−3
Fowlerville	Chlorine, phosphate	7.14	978	4.63	1.10	0.91	0.158	3.53	0.24	6.07	0.01	7.8 × 10^−4	9.4 × 10^−3
Lansing site A	Lime softening	8.70	609	4.29	0.55	0.56	0.082	2.33	1.34	0.99	0.01	3.1 × 10^−4	2.5 × 10^−3
Lansing site B	Lime softening	7.04	535	3.79	0.63	0.49	0.079	1.91	1.16	0.83	0.01	1.4 × 10^−3	5.9 × 10^−4
East Lansing	Lime, ferric chloride, filtration, chloramine, fluoride, phosphate	6.61	361	1.43	0.58	0.56	0.063	1.10	0.50	1.39	0.01	1.8 × 10^−3	5.3 × 10^−3
Howell	Lime softening	8.15	453	2.76	0.55	0.54	0.092	1.83	0.62	1.29	0.01	6.9 × 10^−4	6.6 × 10^−3
MSU - residence hall	Ion exchange, chlorine, fluoride, phosphate, sodium hydroxide	7.34	880	19.57	0.07	0.04	0.025	1.16	0.84	7.09	0.01	1.3 × 10^−3	2.3 × 10^−2
Williamston	Iron removal, softening, chlorine, phosphate	7.51	710	6.02	0.99	0.53	0.075	0.93	0.43	6.83	0.02	1.0 × 10^−2	6.4 × 10^−4
Genoa Twp Soft	Household water softener, private well	7.04 ± 0.23	1920 ± 30	18.65 ± 0.47	0.20 ± 0.015	0.20 ± 0.035	0.03 ± 0.025	9.7 ± 0.3	0.61	8.55	BD	8.1 × 10^−4	BD
Genoa Twp Untreated	Private well; untreated	7.24	1940	6.69	3.81	1.98	0.120	11.16	0.60	8.26	BD	4.5 × 10^−4	4.7 × 10^−2
Rest stop Okemos	Chlorinated if bacteria found	7.36	516	3.08	1.41	0.46	0.141	0.09	0.15	6.19	BD	3.4 × 10^−4	1.7 × 10^−3
Rest stop Zeeland	Chlorinated if bacteria found	7.05	560	3.35	1.04	0.82	0.085	0.79	0.21	5.38	BD	2.7 × 10^−4	9.3 × 10^−3
Rest stop I96/M66	Chlorinated if bacteria found	7.07	546	1.22	1.76	1.19	0.029	0.05	0.12	6.86	BD	2.5 × 10^−4	4.0 × 10^−2
Rest stop Fenton	Chlorinated if bacteria found	6.96	606	2.71	1.10	1.21	0.090	1.20	0.14	5.64	BD	4.1 × 10^−3	1.3 × 10^−2
Allegan	Reverse osmosis and iron removal filters, phosphate, fluoride, chlorine	6.53	295	1.41	0.73	0.52	0.019	0.63	0.17	2.51	0.02	1.8 × 10^−3	6.0 × 10^−3
Genoa Twp RO	Reverse osmosis of private well after household water softener	6.64	264	3.23	0.08	0.02	0.006	1.27	0.11	1.37	BD	4.8 × 10^−4	4.8 × 10^−4
Detroit	Great Lakes Water Authority (GLWA), Water Works Park plant	6.21	226	0.43	0.59	0.34	0.023	0.51	0.26	1.55	0.02	1.8 × 10^−3	5.4 × 10^−3
Flint	GLWA, Lake Huron plant	6.86	219	0.32	0.07	0.02	0.022	0.52	0.23	1.64	0.04	4.4 × 10^−3	5.6 × 10^−3
Swartz Creek	GLWA, Lake Huron plant	5.87	209	0.41	0.08	0.03	0.024	0.51	0.23	1.61	0.02	6.9 × 10^−4	4.9 × 10^−3
Grand rapids	Lake Michigan Filtration Plant	7.17	304	0.44	0.89	0.26	0.030	0.63	0.33	2.2 ± 0.04	0.02	4.9 × 10^−3	1.9 × 10^−2
Holland	Holland Board of Public Works Water Filtration Plant	6.76	302	0.74	0.85	0.51	0.034	0.60	0.29	2.45	BD	3.7 × 10^−3	5.7 × 10^−3
Wyoming	Donald K. Shrine Water Treatment Plant	7.16 ± 0.03	302 ± 8	1.30 ± 0.005	0.905 ± 0.005	0.5 ± 0.001	0.036 ± 0.002	0.61 ± 0.01	0.34 ± 0	2.17	BD	BD	BD

---

In order to determine the effects of specific ions on residue patterns, synthetic water samples containing various concentrations of the main components in tap water were prepared, including synthetic hard freshwater (192 mg L⁻¹ NaHCO₃, 120 mg L⁻¹ MgSO₄, 120 mg L⁻¹ CaSO₄·2H₂O, and 8 mg L⁻¹ KCl) and mixtures of NaCl, NaHCO₃, CaCl₂, MgCl₂, CaSO₄, MgSO₄, and Na₂SO₄. Salt mixtures were designed to examine ranges that may be observed in real tap waters; thus, the low and high concentrations tested of every salt do not match. Simplified synthetic tap waters were created to mimic concentrations of calcium, magnesium, sodium, chloride, sulfate, and total carbonate species observed in tap water. Complex synthetic tap waters also contained phosphate, nitrate, fluoride, copper, and iron (Table SI-2‡). Natural organic matter was not added because larger organic molecules typically deposit on the outer edge of the drop where the organics can't be identified from images alone.^1,2,29

Collection of coffee-ring residue patterns

Two microliter droplets of each water were gently pipetted onto aluminum substrates (6061 with mirror-like finish, McMaster-Carr 1655T1). Substrates from the manufacturer were used directly after peeling off the plastic film that protects the mirror-like finish. Samples were left uncovered for 20–30 minutes or until dry without being moved, touched, or disturbed from the moment of deposition on the slide (Fig. SI-1‡). Relative humidity in the lab ranged from 47–52% and temperature 23–25 °C over the course of the coffee-ring effect experiments. Samples were imaged with a SamSung S6 cell phone through a Fancii 30× triplet loupe (Amazon.com) with the LED light on (Fig. 2). At least five drops were imaged for each sample, and residues that were not round due to lack of pinning to the surface were repeated. Relative humidity and temperature were recorded for each experiment with a Fisher Scientific Traceable Relative Humidity/Temperature Meter (11-661-13). Reproducibility of water residue patterns was examined by three researchers testing a subset of water samples on several substrates.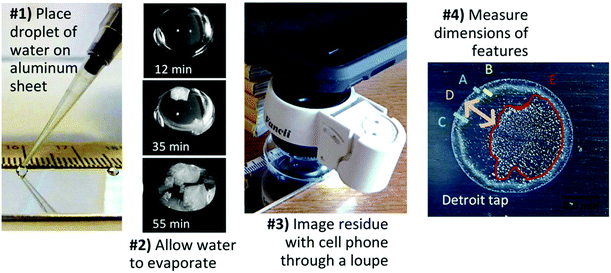

Fig. 2 Tap water fingerprints were captured by drying droplets on aluminum and photographing with a cell phone camera thru a loupe.

Image processing, principal component analysis (PCA), and cluster analysis

Residue pattern photographs were cropped manually with ImageJ to dimensions of 700 by 600 pixels. Scales bars of 0.5 mm were added in ImageJ using ruler tape captured in photographs as a reference, dimensions of features in residues were measured, and processed images were saved in JPEG format. Images were converted to black and white, noise removed, and particles measured in Matlab software version R2017b (im2bw, medfilt2, and regionprops functions). Principal component analysis (PCA) was conducted on both particle measurements and on the image files themselves using Python version 3.6.4 (matplotlib, numpy, and sklearn packages; Fig. SI-2‡). Measured water chemistry for each tap water sample was plotted on a trilinear classification diagram using GW_Chart (Version 1.29.0.0, USGS) with samples sorted according to treatment. The cluster analysis algorithm CLARA was used to group samples into six groups using all thirteen of the measured parameters after normalization by subtracting the mean from the measured value and dividing by its standard deviation.³⁰ The cluster analysis result was visualized in a two dimensional map using the two main components identified by principal component analysis with the R factoextra package.

Convolutional neural network

A convolutional neural network (CNN) model was created to classify images. Ten residue images from each water sample were used for model training and testing, five of which were from fresh samples and five collected after storage at 4 °C. The first three replicates of each water sample for each condition (fresh and stored) were used for training the model (180 images), and the last two replicates were used for testing the model (120 images). Image pre-processing involved resizing each image from 470 by 470 pixels to 300 by 300 pixels and converting from color to gray-scale (Table SI-3‡). The brightness was normalized for each image by dividing the brightness value for each pixel in an RGB channel by the overall sum of the brightness values of all pixels for that RGB channel.

A CNN model was built with two convolutional layers and three fully connected layers in Python (Fig. SI-3‡). In the first layer eight filters were used to extract pattern features, and sixteen filters were used in the second layer to extract deeper pattern features. After the convolutional layers, three fully connected layers were used to fit the data. The fitting method was a stochastic gradient descent (SGD) with probability calculations through the SoftMax function. The batch size was five for each optimization process. Samples were randomly selected by their weights which were set equal at the beginning but updated after each optimization process by their classification result. The learning rate was 10⁻⁴ in the model training process. In each iteration, five samples were randomly selected from 180 training samples by their weights with replacement, and every 36 iterations consisted of one epoch. After each epoch, training accuracy, testing accuracy, training loss, and testing loss were calculated. Two hundred epochs were processed for each model and ten independent models were trained. The test dataset accuracies of the last one hundred epochs and the last epoch model were recorded for analysis.

Results and discussion

Coffee-ring residue patterns for each Michigan tap water are unique

Michigan State University and the surrounding communities frequently rely on groundwater sources with minimal treatment (chlorine and phosphate, sometimes with fluoride) or hardness removal by lime softening or ion exchange. Rural communities also frequently use on point-of-use or point of entry treatment such as home water softeners or reverse osmosis systems. Many communities near Great Lakes coastlines utilize surface water sources and conventional treatment. The Great Lakes Water Authority (GLWA) treats and distributes water to a substantial fraction of Michigan's population in the east from Lake Huron or the Detroit River and many communities in the west utilize Lake Michigan. Tap water collected from the sampled Michigan communities displayed a wide range of chemical compositions (Table 1).

The coffee-ring residue patterns for each type of tap water were unique, and waters with similar chemistry displayed similar residue features (Fig. 3). Reproducibility was evaluated initially by imaging five droplets of each sample on the same slide, and most residue patterns displayed nearly identical features across replicates (Table SI-4‡). Lime softened water showed variability across replicates, with some samples displaying a thin film of particles across the entire drop and others producing a clearing in the center. A subset of samples were analyzed by three analysts with varying levels of experience. Mirrored aluminum 6061 substrates were chosen due to low cost, availability, compatibility with the loupe and cell phone camera for imaging, and ease of use for inexperienced users; substrates were inspected before use for scratches or defects and only smooth areas without blemishes were used for the coffee-ring effect experiments. Nanopure water and synthetic hard freshwater were applied as controls. The substrates contained residue remaining from the manufacturer that was captured in images of nanopure water controls (Table SI-5‡). A trend was not observed between residue patterns for samples and the residue pattern or lack of residue pattern in the nanopore water controls (Table SI-5‡). Tap water samples were tested on multiple substrates to ensure that variation observed in the patterns was not due to the substrate (Tables SI 4–6‡). All analysts produced more consistent data across a single slide than across different slides. Despite variability between substrates, MSU water from academic buildings (hard water) displayed similar patterns on substrates tested across all researchers. Untreated groundwater from the rest stop was characteristically more variable, displaying one of two patterns with a thin film of small particles and either a white ring at the outer edge or a circular segment to one side. Residue patterns for lime softened water from East Lansing were typically consistent across a single slide, but showed two types of patterns with several concentric rings at the drop edge and either a clear center or a thin film of feathery particles across the center surface. Neither the nanopure blank nor synthetic hard freshwater were sufficient to predict which samples would produce thin films of particles for the lime softened water. A similar result was observed for softened Lansing water (Table SI-5‡). Synthetic lime softened water may function as a more sensitive positive control for future experiments. Only analyst 1 observed the residue pattern for Detroit with the center scattering of particles concentrated on one side of the drop; this result was attributed to a lab bench at an angle of approximately 1° (Table SI-5‡). Residue patterns that displayed variability across substrates were still sufficiently unique from samples with different chemistry to identify what type of drinking water treatment was applied. The results of these experiment suggest that a more uniform substrate and level surface may be required to reduce variability for applications beyond identifying the tap water source from a library of residue fingerprints. It is well established that the hydrophobicity of the substrate influences the coffee-ring effect;^7,31–33 thus, the substrate used for training datasets must be consistent with that of unknown samples. Additional variables that must be controlled during coffee-ring effect experiments include temperature,^6,34 humidity,^6,35,36 and the volume of the droplet³⁷ (further evaluation of the durability of the protocol is included in the ESI and Table SI-6‡).

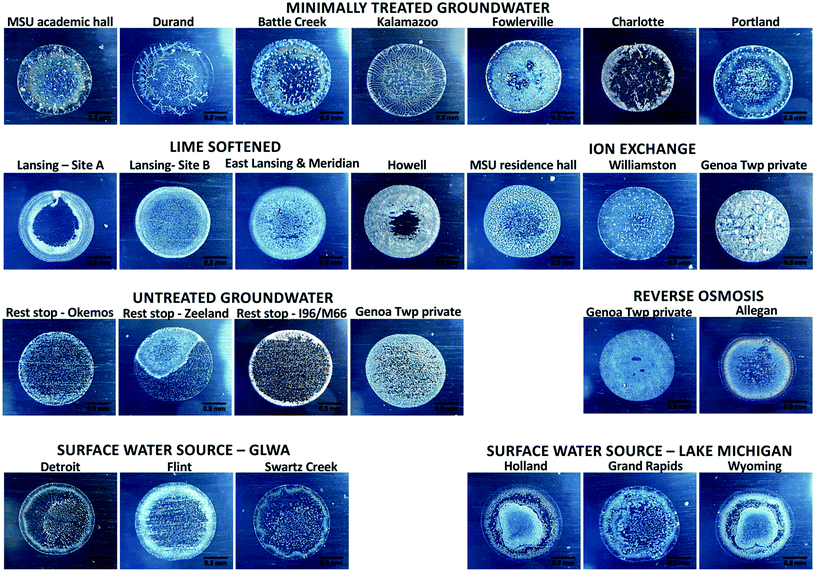Fig. 3 Coffee-ring residue patterns of freshly collected Michigan tap waters. The lab temperature was 24–25 °C and relative humidity 52% for this experiment. Replicates are included in Table SI-4.‡

Synthetic tap water solutions containing six main constituents do not fully explain the environmental samples

Synthetic tap water solutions were created to reflect components measured in Lansing (lime softened groundwater), MSU (minimally treated hard water), and Detroit water (surface water with conventional treatment). A synthetic mixture of simplified Lansing water containing only the six major components (calcium, magnesium, sodium, chloride, sulfate, and total carbonate species) displayed many features observed in Lansing waters on various slides, but the simplified synthetic Detroit and MSU waters were different than the collected tap water samples (Table 2). The simplified synthetic Detroit water had particles deposited at the drop edge like the environmental sample, but the rings, color, and center were different. Adding iron, copper, nitrate, fluoride, and phosphate caused the synthetic residue pattern for Detroit water to become closer to the environmental sample, but still did not capture all the features. Additional studies must be conducted to determine the influence of pH and organic matter on the residue patterns as well. The complex synthetic Detroit water sample captured the yellow and blue coloring observed in the concentric ring at the inner drop edge, possibly due to the presence of phosphate and iron forming insoluble salts. The MSU tap water still did not resemble the collected water after addition of the lower concentration components. This finding provides further evidence that lower concentration species, pH, or particulates likely play a role in defining residue patterns.

Table 2 Simplified synthetic tap water compared residue patterns to real tap water, with measured pH of each solution listed below the image (24 °C, 47% relative humidity). Replicate images are shown in Table SI-8‡

	Collected tap water	Simplified synthetic	Complex synthetic
Lansing
MSU
Detroit

---

Residue patterns document water chemistry

Simple synthetic mixtures demonstrate trends between water chemistry and particle, shape, size, and location of deposition. To confirm that trends in particle shapes and sizes in coffee-ring patterns are influenced by the identities and concentrations of solutes, three salt synthetic mixtures were created of NaCl with CaCl₂ and MgCl₂, NaHCO₃ with CaCl₂ and MgCl₂, Na₂SO₄ with CaSO₄ and MgSO₄, and NaHCO₃ with CaSO₄ and MgSO₄ at concentrations relevant to tap waters. In the presence of calcium and magnesium chloride, NaCl caused large uniform particles to be distributed across the drop, while NaHCO₃ caused smaller and more densely packed flakes and feathering patterns at the higher concentrations (Table 3). These features could be quantified by measuring the average area of particles and the number of particles for each set of images. For example, the average area of particles decreased with decreasing NaCl concentration in the presence of 3.0 mM CaCl₂ and 1.5 mM MgCl₂, and the average number of particles decreased with decreasing NaHCO₃ concentration in the presence of 0.5 mM CaCl₂ and 0.25 mM MgCl₂ (Fig. 4). It was hypothesized that because NaCl and NaHCO₃ are highly soluble, both produced thin films of particles that were likely deposited through surface capture or settling rather than the coffee-ring effect as ions remain dissolved through most of the droplet evaporation process. Crystal formation was sensitive to differences in slides; a similar result was found on additional slides, though the large distinct, uniformly sized NaCl particles did not form at the lower concentrations of calcium and magnesium chloride (Table SI-9‡). Intricate particle shapes were observed for mixtures of sodium bicarbonate with calcium and magnesium chlorides, but the shapes of the particles were not identical across all batches of slides. Additional experiments are required with higher quality substrates to determine how the shape of the bicarbonate particles correlates to the matrix water chemistry and surrounding conditions.

Fig. 4 Particle areas and particle counts for simplified synthetic mixtures of three salts.

Table 3 Simple synthetic mixtures analyzed at 24 °C and 48% relative humidity

	NaCl 10 mM	NaCl 5.0 mM	NaCl 2.5 mM	NaHCO3 10 mM	NaHCO3 5.0 mM	NaHCO3 2.5 mM
							Nanopure
3 mM CaCl2, 1.5 mM MgCl2
1 mM CaCl2, 0.5 mM MgCl2							Synthetic hard water
0.5 mM CaCl2, 0.25 mM MgCl2

---

	Na2SO4 5.0 mM	Na2SO4 2.5 mM	Na2SO4 1.25 mM	NaHCO3 10 mM	NaHCO3 5.0 mM	NaHCO3 2.5 mM
							Nanopure
3 mM CaSO4, 1.5 mM MgSO4
1 mM CaSO4, 0.5 mM MgSO4							Synthetic hard water
0.5 mM CaSO4, 0.25 mM MgSO4

---

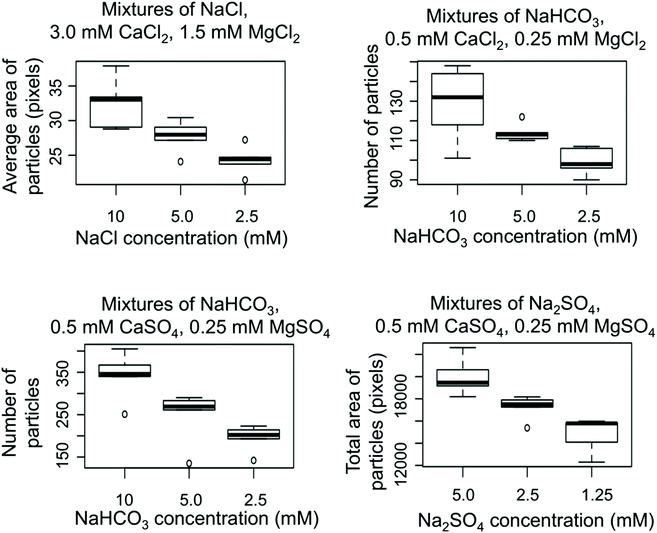
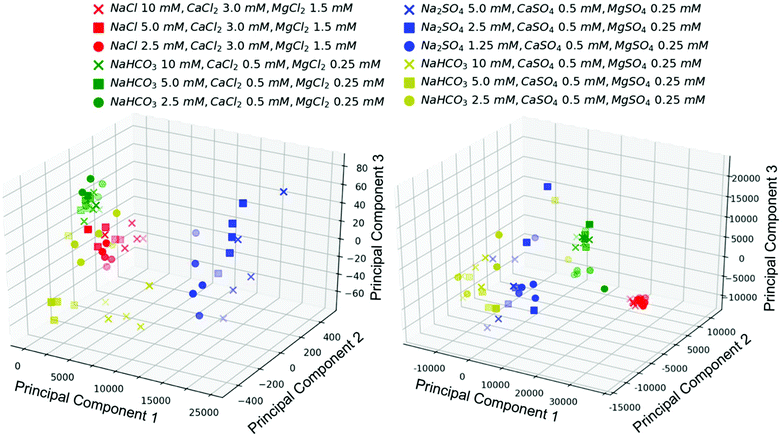
Simple synthetic mixtures containing sulfate salts of sodium, magnesium, and calcium had multiple concentric rings at the drop edge, likely due to differences in solubility between calcium sulfate, magnesium sulfate, and sodium sulfate. Again, the number of particles decreased with decreasing sodium sulfate concentration in the presence of 0.5 mM CaSO₄ and 0.25 mM MgSO₄ (Fig. 4). Adding bicarbonate to the mixture at the same concentration of calcium and magnesium sulfate caused the concentric rings at the drop edge to be eliminated to create a thin film of densely packed very small uniform particles, except for the lowest sulfate and bicarbonate concentrations (Table 3), though the number of particles still decreased with sodium bicarbonate concentration (Fig. 4).

PCA conducted on the image files themselves (five replicates of each image) was compared to PCA on the measurements of particle sizes and numbers within the images. In both cases, three principal components were useful in clustering the images into groups with similar ions, but not sufficient to group samples by concentrations of components (Fig. 5). Three principal components explained around 50% of the variability of the data set for PCA conducted on the image files (Fig. SI-4‡). PCA is valuable for highlighting variability in a dataset, but it does not take into account subimages or subpatterns (such as rings at the drop edge versus the center of the residue pattern);³⁸ thus, it is not surprising that PCA on the image files was not sufficient to differentiate between images with different concentrations of ions despite clear qualitative differences in residue patterns. Specific measurements of features within the images or a convolutional neural network designed from a larger dataset may be more valuable in determining concentrations of species (Fig. 4).

Fig. 5 Principal component analysis (PCA) on particle measurement data (left) and PCA conducted on image files (right).

Similar residue patterns were observed for collected tap water samples with similar water chemistry. Cluster analysis and trilinear classification diagrams were used to group samples with similar water chemistry, with cluster analysis taking all the collected water chemistry data into account and the trilinear diagram only using data for the species with the highest concentrations typical of freshwaters (calcium, magnesium, sodium, potassium, chloride, sulfate, carbonate, and bicarbonate). In general, the cluster analysis and the trilinear diagrams grouped samples with those from the same treatments together (Fig. 6, Fig. SI-5‡). Cluster analysis, however, did not group ion exchange samples together, more effectively separated minimally treated groundwaters, and lumped reverse osmosis samples with surface waters. The trilinear plot showed the ion exchange samples clearly distinct from the rest, plotted the reverse osmosis samples closer to the minimally treated groundwaters, and the lime softened waters separated clearly from the surface waters. These findings highlight that the water chemistry for the ion exchanged samples are related in terms of the higher concentration components, but the overall water chemistry more closely matches samples from other groups.

Fig. 6 Cluster analysis of water chemistry data.

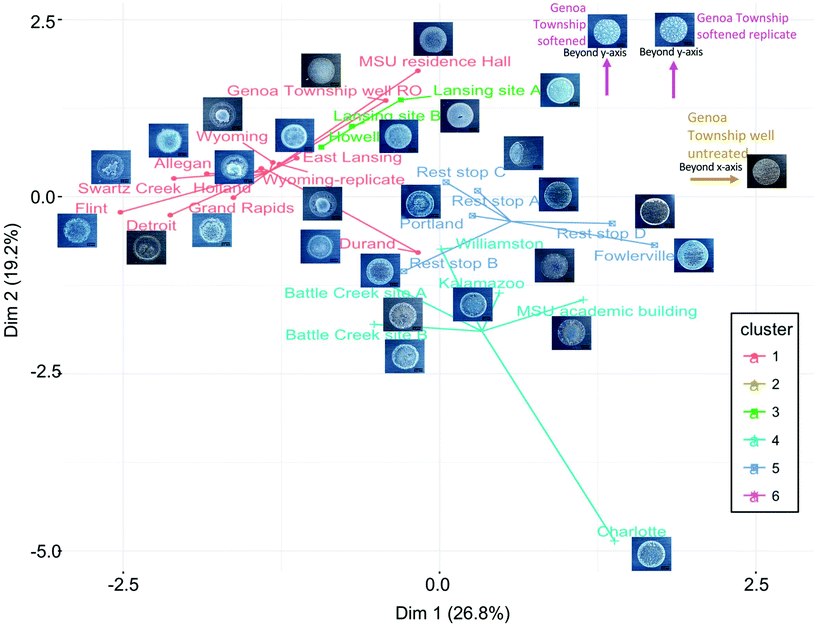
Inspection of the coffee-ring residue photographs according to the groupings visualized by cluster analysis and trilinear diagrams uncovers patterns in the crystals that may associate with a given water chemistry (Fig. 6). For example, each ion exchange sample that clustered together on the trilinear diagram had a thin film of particles with larger crystals scattered across the drop, but each image also displayed attributes of the group assigned through cluster analysis when the lower concentration species were accounted for. Trends in the dataset can also be determined from comparing residue patterns from synthetic mixtures, samples with similar composition of the six main water components, and samples with similar overall water chemistry. The residue patterns for tap waters treated by similar methods displayed characteristic features representative of that treatment, such as several concentric rings with a strong secondary ring near the outer edge for surface water, colorful concentric rings with smaller particles scattered throughout for hard groundwaters with minimal treatment, a thin film of fine particles for reverse osmosis treated groundwater, a strong outer ring of white with small particles densely spread across the drop for untreated groundwater, large crystals scattered across the drop for ion exchange, and a white/gray thin film of small particles or dense concentric rings of small particles with feathering patterns for lime softened water (Fig. 3). Tap water samples contain high concentrations of dissolved ions when droplets are placed on the substrate, so particles form and grow as water evaporates from the drop as observed previously for solutions of NaCl or CaSO₄.⁷ Therefore, particles of the least soluble salts that grow quickly upon their concentrations exceeding solubility limits are expected to form particles early enough during drying to be transported by the coffee-ring effect to the drop edge, unless they grow large enough to settle first. Particles that do not form until the drop is nearly dry are expected to be deposited through the surface capture effect or settling and be found across the center of the drop. Calcium and magnesium carbonates and sulfates are less soluble than sodium and chloride containing salts;^39,40 therefore, it is logical that hard waters would display an outer ring at the drop edge and waters softened by ion exchange (containing more sodium than calcium or magnesium) would display thin films of particles. Additional mixtures must be analyzed to verify the qualitative patterns described here.

Convolutional neural network (CNN) model assigned images to groups with similar water chemistry. CNN models have previously been proven effective in object detection and image classification.^41–43 Herein a CNN model was developed and tested to assign residue images into classes with similar water chemistry data as determined by cluster analysis. Overall, after building the model from a library of similar training images, the CNN model was effective with 80% accuracy in assigning residue images from the test set into groups with similar water chemistry. To achieve higher accuracy, a larger dataset would be needed to train the model.

Specifically, in the CNN model developed here the average and standard deviation of the accuracy for the last 100 epochs for ten independent CNN models was 76.7 ± 3.0% (Fig. 7). Only six of the test images were misclassified in the class one group of images that contained a total of 48 images (largely from surface waters with RO samples and a few others mixed in), but two of the test images were misclassified from class two that contained a total of four images all from the high TDS genoa township untreated well water (Fig. 7). All of the misclassified images from class two were instead placed into class four that contained minimally treated groundwaters and one ion exchanged sample. Two out of twenty-four images from class four and two out of twenty-four images in class five (minimally treated and untreated groundwaters) were misclassified into class one. A few additional images were also misclassified between class four and five; in qualitative comparing residue images, images of class four and class five are more similar than images in other classes, which is logical considering these both classes largely contain minimally treated and untreated groundwaters.

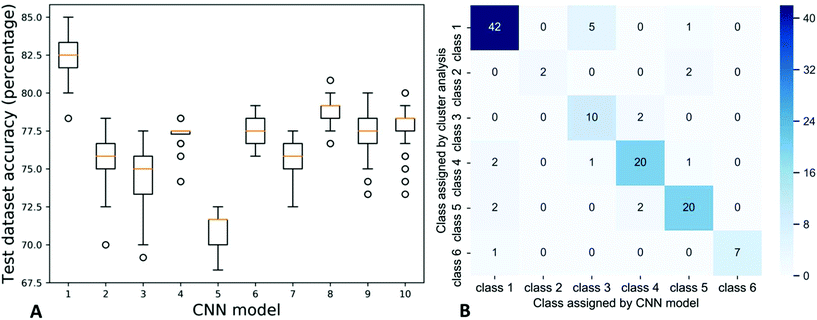Fig. 7 Testing dataset accuracies of ten CNN models (left) and the confusion matrix of the first trained model (right).

There were a few of the test images that were misclassified more often than others (Table SI-10‡). Five of the test images with a misclassification percentage over 70% had a coffee-ring residue pattern that was notably different from replicates of the same sample. For example, two MSU residence hall samples had a clearing in the center of the residue pattern while the rest had a complete thin film across the entire drop; the two samples with clearings were misclassified in over 70% of the models (Tables SI-10 and SI-3‡). Two of the images with a misclassification percentage over 70% were from class two which had the lowest number of replicates. The low number of images causes the model to be less sensitive to this class despite the distinct large crystal pattern.^44,45 Three images were often misclassified without a clear reason (Table SI-10‡).

The percentage of images that were properly classified into class one was much higher than most of the other classes. Class one had the most images, so in the model training process the model is skewed to more accurately predict the class one images.^46,47 Generally with CNN models the accuracy is improved by using a larger dataset of images during model training to allow the model to capture more information and detail.^44,45 Overall, class one, three, four and five had similar accuracy around 80%, but due to the low number of samples the accuracies of classes two and six were around 40–50% (Fig. SI-6‡). About half images in class one had less than 1% mis-classification percentage and most images in class two and six had high mis-classification percentages.

Conclusions and future outlook

Both the coffee-ring effect and convolutional neural networks (CNNs) remain underutilized techniques to be harnessed for tap water analysis. Herein we show proof of concept experiments that document the unique fingerprints provided by the coffee-ring effect for tap water solutions from various cities across Michigan and the reproducibility of the phenomenon, demonstrate that low concentration species as well as major ions influence the residue patterns, provide evidence that the patterns indeed document water chemistry within the sample, and demonstrate the ability of a CNN in assigning images to water chemistry. The low-cost substrate employed in this work caused variability between experiments, especially for batches of substrates purchased at different times; however, the variability was included in the training dataset, so the CNN was still able to classify the images with 80% accuracy. Additional work is required to identify the appropriate substrate that is widely available for a low cost test. Quality control metrics are critical for identifying variation in experiments, and lime softened water was much more sensitive to experimental variation than the hard synthetic water used as a control for this study. Traditional PCA on image files is insufficient for differentiating between images of water samples with different concentrations of components, likely due to lack of consideration of subregions such as the outer coffee ring; however, with a larger dataset a CNN model will be especially valuable for differentiating between water chemistries and assigning unknown images to groups from a library of images. A larger library of residue patterns and a corresponding CNN model must be trained to move this technology from qualitative tap water quality analysis to a quantitative technique and to further identify features of the residue patterns.

Despite the use of a low-cost and variable aluminum slide, using a pipette, $18 jeweler's loupe, and cell phone camera, each type of tap water tested displayed unique characteristics, water samples with similar water chemistry produced residue patterns with similar features, waters from two locations in a city were more similar than samples from different cities, and the CNN model was able to assign samples to groups with similar water chemistry. This evidence suggests that this method should be further considered for low-cost water quality fingerprinting.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Michigan State University, Lyman Briggs College, the College of Engineering, the Department of Civil and Environmental Engineering, and the Honors College for supplying student support for this project, including a Professorial Assistantship to Alyssa Sanderson, Engineering Summer Undergraduate Research Experience (EnSURE) positions for Selett Allen and Alyssa Sanderson, and a Summer Undergraduate Research Academy (SURA) position for Selett Allen with the Michigan Louis Stokes Alliance for Minority Participation (MI-LSAMP).

References

1. T.-S. Wong, T.-H. Chen, X. Shen and C.-M. Ho, Nanochromatography driven by the coffee ring effect, Anal. Chem., 2011, 83, 1871–1873.
2. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Capillary flow as the cause of ring stains from dried liquid drops, Nature, 1997, 389, 827.
3. J. Filik and N. Stone, Drop coating deposition Raman spectroscopy of protein mixtures, Analyst, 2007, 132, 544–550.
4. D. Zhang, M. F. Mrozek, Y. Xie and D. Ben-Amotz, Chemical segregation and reduction of Raman background interference using drop coating deposition, Appl. Spectrosc., 2004, 58, 929–933.
5. K. A. Esmonde-White, S. V. Le Clair, B. J. Roessler and M. D. Morris, Effect of conformation and drop properties on surface-enhanced Raman spectroscopy of dried biopolymer drops, Appl. Spectrosc., 2008, 62, 503–511.
6. Y. Li, Q. Yang, M. Li and Y. Song, Rate-dependent interface capture beyond the coffee-ring effect, Sci. Rep., 2016, 6, 24628.
7. N. Shahidzadeh, M. F. Schut, J. Desarnaud, M. Prat and D. Bonn, Salt stains from evaporating droplets, Sci. Rep., 2015, 5, 10335.
8. E. Shelhamer, J. Long and T. Darrell, Fully Convolutional Networks for Semantic Segmentation, IEEE Trans. Pattern Anal. Mach. Intell., 2017, 39, 640–651.
9. J. M. Alvarez, T. Gevers, Y. LeCun and A. M. Lopez, in Computer Vision – ECCV 2012, ed. A. Fitzgibbon, S. Lazebnik, P. Perona, Y. Sato and C. Schmid, Springer, Berlin, Heidelberg, 2012, pp. 376–389.
10. H. R. Roth, A. Farag, L. Lu, E. B. Turkbey and R. M. Summers, in Medical Imaging 2015: Image Processing, International Society for Optics and Photonics, 2015, vol. 9413, p. 94131G.
11. M. Havaei, A. Davy, D. Warde-Farley, A. Biard, A. Courville, Y. Bengio, C. Pal, P.-M. Jodoin and H. Larochelle, Brain tumor segmentation with Deep Neural Networks, Med. Image Anal., 2017, 35, 18–31.
12. W. Zhang, R. Li, H. Deng, L. Wang, W. Lin, S. Ji and D. Shen, Deep convolutional neural networks for multi-modality isointense infant brain image segmentation, NeuroImage, 2015, 108, 214–224.
13. D. C. Cireşan, A. Giusti, L. M. Gambardella and J. Schmidhuber, in Proceedings of the 25th International Conference on Neural Information Processing Systems, Curran Associates Inc., USA, 2012, vol. 2, pp. 2843–2851.
14. Z. Zhang, L. Chen, Y. Wang, T. Zhang, Y.-C. Chen and E. Yoon, Label-Free Estimation of Therapeutic Efficacy on 3D Cancer Spheres Using Convolutional Neural Network Image Analysis, Anal. Chem., 2019, 91, 14093–14100.
15. M. Wang, C. Tai, E. Weinan and L. Wei, DeFine: deep convolutional neural networks accurately quantify intensities of transcription factor-DNA binding and facilitate evaluation of functional non-coding variants, Nucleic Acids Res., 2018, 46, e69.
16. H. Zeng, M. D. Edwards, G. Liu and D. K. Gifford, Convolutional neural network architectures for predicting DNA–protein binding, Bioinformatics, 2016, 32, i121–i127.
17. N. G. Nguyen, V. A. Tran, D. L. Ngo, D. Phan, F. R. Lumbanraja, M. R. Faisal, B. Abapihi, M. Kubo and K. Satou, DNA Sequence Classification by Convolutional Neural Network, J. Biomed. Sci. Eng., 2016, 09, 280–286.
18. F. Lussier, D. Missirlis, J. P. Spatz and J.-F. Masson, Machine-Learning-Driven Surface-Enhanced Raman Scattering Optophysiology Reveals Multiplexed Metabolite Gradients Near Cells, ACS Nano, 2019, 13, 1403–1411.
19. O. Alharbi, Y. Xu and R. Goodacre, Simultaneous multiplexed quantification of nicotine and its metabolites using surface enhanced Raman scattering, Analyst, 2014, 139, 4820–4827.
20. W. J. Thrift and R. Ragan, Quantification of Analyte Concentration in the Single Molecule Regime Using Convolutional Neural Networks, Anal. Chem., 2019, 91, 13337–13342.
21. M. Hirohara, Y. Saito, Y. Koda, K. Sato and Y. Sakakibara, Convolutional neural network based on SMILES representation of compounds for detecting chemical motif, BMC Bioinf., 2018, 19, 526.
22. C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, A graph-convolutional neural network model for the prediction of chemical reactivity, Chem. Sci., 2019, 10, 370–377.
23. Y. Matsuzaka and Y. Uesawa, Optimization of a Deep-Learning Method Based on the Classification of Images Generated by Parameterized Deep Snap a Novel Molecular-Image-Input Technique for Quantitative Structure–Activity Relationship (QSAR) Analysis, Front. Bioeng. Biotechnol., 2019, 7, 65.
24. J. G. Meyer, S. Liu, I. J. Miller, J. J. Coon and A. Gitter, Learning Drug Functions from Chemical Structures with Convolutional Neural Networks and Random Forests, J. Chem. Inf. Model., 2019, 59, 4438–4449.
25. M. Ziatdinov, O. Dyck, A. Maksov, X. Li, X. Sang, K. Xiao, R. R. Unocic, R. Vasudevan, S. Jesse and S. V. Kalinin, Deep Learning of Atomically Resolved Scanning Transmission Electron Microscopy Images: Chemical Identification and Tracking Local Transformations, ACS Nano, 2017, 11, 12742–12752.
26. H. Wu and J. Zhao, Deep convolutional neural network model based chemical process fault diagnosis, Comput. Chem. Eng., 2018, 115, 185–197.
27. M. Buda, A. Maki and M. A. Mazurowski, A systematic study of the class imbalance problem in convolutional neural networks, Neural Networks, 2018, 106, 249–259.
28. APHA, AWWA and WEF, Standard Methods for the Examination of Water and Wastewater, American Public Health Association, Washington, DC, 21st edn, 2005.
29. H. Y. Erbil, G. McHale and M. I. Newton, Drop Evaporation on Solid Surfaces: Constant Contact Angle Mode, Langmuir, 2002, 18, 2636–2641.
30. Encyclopedia of Database Systems, ed. L. Liu and M. T. Özsu, Springer US, Boston, MA, 2009, pp. 330–330.
31. D. Zhang, Y. Xie, M. F. Mrozek, C. Ortiz, V. J. Davisson and D. Ben-Amotz, Raman Detection of Proteomic Analytes, Anal. Chem., 2003, 75, 5703–5709.
32. C. Ortiz, D. Zhang, Y. Xie, V. J. Davisson and D. Ben-Amotz, Identification of insulin variants using Raman spectroscopy, Anal. Biochem., 2004, 332, 245–252.
33. X. Zhong, J. Ren and F. Duan, Wettability Effect on Evaporation Dynamics and Crystalline Patterns of Sessile Saline Droplets, J. Phys. Chem. B, 2017, 121, 7924–7933.
34. P. Takhistov and H.-C. Chang, Complex Stain Morphologies, Ind. Eng. Chem. Res., 2002, 41, 6256–6269.
35. V. Chhasatia, A. Joshi and Y. Sun, Effect of relative humidity on contact angle and particle deposition morphology of an evaporating colloidal drop, Appl. Phys. Lett., 2011, 97, 231909–231909.
36. D. Kaya, V. A. Belyi and M. Muthukumar, Pattern formation in drying droplets of polyelectrolyte and salt, J. Chem. Phys., 2010, 133, 114905.
37. C. Ortiz, D. Zhang, Y. Xie, A. E. Ribbe and D. Ben-Amotz, Validation of the drop coating deposition Raman method for protein analysis, Anal. Biochem., 2006, 353, 157–166.
38. V. Kadappa and A. Negi, A Theoretical Investigation of Feature Partitioning Principal Component Analysis Methods, Pattern Anal. Appl., 2016, 19, 79–91.
39. M. M. Benjamin, Water Chemistry, Waveland Press, 2nd edn, 2014.
40. D. R. Lide, CRC Handbook of Chemistry and Physics, 85th edn, Taylor & Francis, 2004.
41. A. Krizhevsky, I. Sutskever and G. E. Hinton, in Proceedings of the 25th International Conference on Neural Information Processing Systems, Curran Associates Inc., USA, 2012, vol. 1, pp. 1097–1105.
42. O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh, S. Ma, Z. Huang, A. Karpathy, A. Khosla, M. Bernstein, A. C. Berg and L. Fei-Fei, ImageNet Large Scale Visual Recognition Challenge, Int. J. Comput. Vis., 2015, 115, 211–252.
43. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke and A. Rabinovich, 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, 2015, pp. 1–9.
44. E. Junqué de Fortuny, D. Martens and F. Provost, Predictive Modeling With Big Data: Is Bigger Really Better?, Big Data, 2013, 1, 215–226.
45. D. Martens, F. Provost, J. Clark and E. J. de Fortuny, Mining Massive Fine-grained Behavior Data to Improve Predictive Analytics, MIS Q, 2016, 40, 869–888.
46. N. Japkowicz and S. Stephen, The Class Imbalance Problem: A Systematic Study, Intell. Data Anal., 2002, 6, 429–449.
47. B. Krawczyk, Learning from imbalanced data: open challenges and future directions, Prog. Artif. Intell., 2016, 5, 221–232.

---

Footnotes

† Data and CNN model are available at https://doi.org/10.5281/zenodo.3550247

‡ Electronic supplementary information (ESI) available: Replicate images, synthetic tap water recipes, a trilinear plot for the collected tap waters, and detailed descriptions of residue patterns according to water chemistry. See DOI: 10.1039/c9an01624d

---