Soft-trilinear constraints for improved quantitation in multivariate curve resolution†
Elnaz
Tavakkoli
 ab,
Hamid
Abdollahi
b and
Paul J.
Gemperline
ab,
Hamid
Abdollahi
b and
Paul J.
Gemperline
 *a
*a
aDepartment of Chemistry, East Carolina University, Greenville, North Carolina 27858, USA. E-mail: gemperlinep@ecu.edu
bDepartment of Chemistry, Institute for Advanced Studies in Basic Sciences, P.O. Box 45195-1159, Zanjan, Iran
First published on 11th November 2019
Abstract
Nowadays, hyphenated chemical analysis methods like GC/MS, LC/MS, or HPLC with UV/Vis diode array detection are widely used. These methods produce a data matrix of mixtures measured during the analytical process. When a set of samples is to be analyzed with one data matrix per sample, the data is often presumed to have “trilinear” structure if the profile for each compound does not change shape or position from one sample to the other. By applying this information as a trilinearity constraint in Self Modeling Curve Resolution (SMCR) methods, overlapping peaks related to the pure compounds of interest can be resolved in a unique way. In practice, many systems have non-trilinear behavior due to deviation from ideal response, for example, a sample matrix effect or changes in instrumental response (e.g., shifts or changes in the shape of chromatographic peaks). In such cases, the trilinear model is not valid because every analyte does not have the same peak shape or position in every sample. In such cases, the unique profiles obtained by strictly enforced trilinearity constraints will not necessarily produce true profiles because the data set does not follow the assumed trilinear behavior. In this work, we introduce “soft-trilinearity constraints” to permit peak profiles of given components to have small deviations in their shape and position in different samples. The advantages and disadvantages of this approach are compared to other methods like PARAFAC2. We illustrate the influence of soft-trilinearity constraints on the accuracy of SMCR results for the case of a 3-component simulated system and an experimental data set. The results show that implementing soft-trilinearity constraints reduces the range of possible solutions considerably compared to the application of constraints such as just non-negativity. In addition, we show that the application of hard-trilinearity constraints can lead to solutions that are completely wrong or exclude the opportunity of a possible solution at all.
1. Introduction
The rapid development of analytical instrumentation and data collection tools in recent years has led to the production of multi-way data arrays for a single sample. Experimental measurements generated by analytical instruments are called second-order (i.e., produce three-way data) when there is one matrix per sample (spectra measured over time).1 Instruments that generate second-order data include hyphenated instruments such as high-performance liquid chromatography coupled with diode array detection (HPLC-DAD), gas chromatography-mass spectrometry (GC-MS) and liquid chromatography-mass spectrometry (LC-MS). Under ideal conditions, the data arrays produced by the above-mentioned instruments have a bilinear structure. A trilinear data structure occurs when several samples are run under identical conditions and have one or more constituents in common. Stacking the individual sample data matrices into a data cube produces a second-order data set. Second-order data sets with trilinear structure have a special property known as the “second-order advantage” that can be exploited to perform quantification of known substances and accurately estimate the concentrations of individual components of interest in the presence of unknown interferences. For these reasons, three-way trilinear data analysis methods, especially second-order calibration, is an active area of research that has been gaining widespread acceptance in a variety of scientific fields, such as chemistry, medicine, food and environmental research.2–5A number of different algorithms have already been proposed for the decomposition of three-way data arrays. Some of these methods can be used to decompose a three-way data set, D (m × n × p), based on generalized eigenanalysis such as the generalized rank annihilation method (GRAM),5,6 and direct trilinear decomposition (DTLD).7 There are other decomposition methods for three-way data arrays that are based on iterative procedures, such as parallel factor analysis (PARAFAC)8 and the alternating trilinear decomposition method (ATLD).9 Additionally, the analysis of three-way data can be conducted as a special case of the bilinear factorization method using Multivariate Curve Resolution (MCR). The MCR method can be applied to three-way data arrays that follow the bilinear model for each sample; however, it is not necessary that they follow trilinearity for the whole data set.10 MCR,11,12 is defined as a method to mathematically resolve a measured data matrix of mixtures from hyphenated analytical methods by determining the pure component concentration profiles and the pure component spectral profiles using minimal constraints such as non-negativity. The mathematical solutions of these methods may not be unique because of rotational ambiguity, meaning there is a range of feasible solutions that fulfill the constraints and represent the measured data correctly.13 Therefore, consideration of all feasible solutions can provide useful information about the data set under study.14–21 In order to reduce rotational ambiguity, additional information in the form of constraints can be used. These constraints21–23 represent additional physical–chemical information about the components in the mixture.
Imposing chemically meaningful constraints can lead to a smaller range of feasible solutions. In the case of the analysis of three-way data sets by MCR, trilinearity constraints can be imposed such that the pure component profile of one or more components remains invariant between the different samples. When ideal trilinear behavior is observed, the collection of resolved profiles of the component of interest from each sample gives a rank-one matrix,10 such that the components of interest are mathematically resolved in a unique way. In practice, the analysis is complicated by the fact that there are frequently small changes in peak shape and peak position of the components of interest from sample to sample (e.g., peak shifts or width changes in the chromatogram). Moreover, the sensitivity of the spectral response can change in the presence of different chemical matrix effects in the sample (the so-called matrix effect). For these reasons, a strict trilinear model is often not valid, and every component of interest will not have the same concentration profile in every sample. In such cases, the unique profiles obtained by strictly enforced “hard” trilinearity constraints, are not necessarily the true profiles because the data set does not exhibit ideal trilinear behavior. Some algorithms have been introduced to handle such non-trilinear behavior while retaining a mathematically unique solution, such as PARAFAC2.24–26
“Soft” constraints that allow small deviations from constrained values were introduced by Gemperline.27,28 He introduced a new algorithm using least squares penalty functions to implement constraints during alternating least squares steps. Later, Rahimdoust et al. visualized the effect of soft constraints on the accuracy of self-modeling curve resolution methods.29 They introduced new, improved cost functions to be used during the MCR optimization process to apply non-negativity, unimodality, equality, and closure constraints and compared the results with those calculated by hard constraints. They demonstrated that imposing “hard” constraints when non-ideal behavior is observed can result in mathematical solutions that lie outside the set of feasible solution boundaries. In such cases, the resulting solution may suffer from active constraints due to non-ideal chemical response. Therefore, based on recent studies, applying soft constraints can produce more reliable results when the properties of the two-way data array are non-ideal.
In this work, we introduce “soft-trilinearity constraints” and a new MATLAB program to permit peak profiles of the components of interest to have small deviations in their shape and position from sample to sample. In order to visualize the results, soft-trilinearity constraints were incorporated into a systematic grid search algorithm for the case of a three-component system.30 This algorithm is general and can be applied to any MCR method. Results are provided for noisy simulated data with non-trilinear behavior and one experimental data set. The results show that implementing soft-trilinearity constraints reduces the range of feasible solutions considerably compared to the application of simpler non-negativity constraints. The results of this approach are compared to other methods, including PARAFAC2 and MCR-ALS, with hard-trilinearity31 constraints. It is shown that the methods employing hard-trilinearity constraints lead to incorrect solutions, or produces solutions outside the range of feasible solutions.
2. Theory
Many hyphenated analytical methods (for example, HPLC with VU/Visible diode array detection) produce a bilinear data matrix, D (m × n) of measured responses, where a linear relationship exists between the measured response and the concentrations of the chemical species in a mixture (eqn (1)) where m represents the number of measured spectra (responses) at n wavelengths for nc components.| D(m×n) = C(m×nc)AT(nc×n) + E(m×n) | (1) |
In eqn (1), the matrix C (m × nc) contains the nc concentration profiles in its columns, and the matrix AT (nc × n) contains the nc pure component spectra of those components in its rows. The error matrix, E, comprises residuals (noise) or non-modeled parts of D, which has the same dimension as D.
A frequent first step in MCR is to perform a decomposition of the data matrix by using the singular value decomposition (SVD) or principal component analysis (PCA):
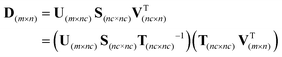 | (2) |
By use of the SVD or PCA, the bilinear data matrix, D, can be decomposed giving left eigenvectors U (m × nc), right eigenvectors V (nc × n) and a diagonal matrix of singular values S (nc × nc), where the orthonormal U and V matrices define the basis vectors of the column and row spaces, respectively. In eqn (2), the matrix T is a nonsingular transformation matrix that transforms the abstract solutions (US and VT) into the concentration profiles and pure spectral response profiles, where TT−1 = I and I is an identity matrix. The rows of matrix T and the columns of matrix T−1 represent the coordinates of the feasible solutions in row and column space, respectively. The dimension of the T and T−1 matrices are nc × nc based on the number of components in the system. There are a number of published procedures to estimate the range of feasible solutions for two-component, three-component, and higher component mixtures.15–21 In this work, a systematic grid search method for three-component systems was modified to include soft-trilinear constraints and used to find the range of possible T(3×3) matrices that define the correct C and AT based on eqn (2) and chemically meaningful constraints. In order to perform this task, the standard simplex algorithm for nonlinear optimization (fminsearch in MATLAB) was used. In the case of three-component systems, the T matrix has nine elements, which can be reduced to six elements in normalized form by dividing each row of the T matrix by its first element. For example, for the first component, the values of t12 and t13 are searched in a 2 × 2 grid for a feasible solution (one that obeys all constraints) while the other coefficients in the sub-matrix F are optimized using fminsearch:
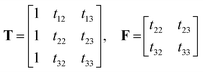 | (3) |
During the calculation of C = UST−1 and AT = TVT, the physical constraints on the calculated concentration and spectral profiles are tested, and feasible solutions at each grid point can be defined as the set of rotation matrices, T, that give feasible solutions which fulfill the applied constraints.
2.1. Soft-trilinearity constraints
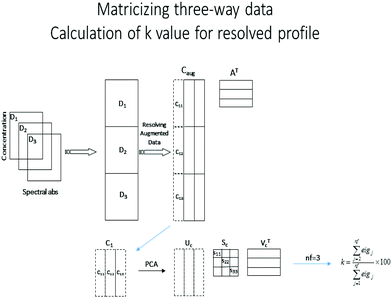
Soft-trilinearity constraints were implemented by defining a constant, α, that determines the degree of softness allowed. The parameter for the evaluation of each component under soft-trilinearity constraints is δα. The procedure for imposing soft-trilinearity constraints is as follows where the coefficient, k, is computed at each iteration according to eqn (4), and nf is the number of augmented or folded matrices.1. For the ith component:
a. Fold the current estimate of the concentration profile of component i into a matrix
2. Apply PCA to the matrix
3. Calculate the value of k, according to eqn (4).
4. If k ≤ α, then
δα = 0
else
r = ci–ci-hat
5. δα = ∑∑(r × rT)
where, ci-hat=|(uc (:,2:nf) sc (2:nf,2:nf) vTc (:,2:nf))|
6. end if
In order to calculate the value of k for the ith component (presented graphically in Scheme 1), the resolved profile with dimension of (m × nf) × 1 for the augmented data set is folded into a new matrix ci (m × nf), where m is the number of rows in each data matrix and nf is the number of augmented data matrices according to the above procedure. This matrix is decomposed by PCA. If the resolved concentration profiles in the different matrices do not have any deviation from trilinearity, they will have the same shape, and only the first principal component will be significant. In the case of non-ideal chemical behavior, the resolved profiles will differ in shape, so additional principal components will be meaningful. In this procedure, the value of k for imposing soft-trilinearity constraints is the percentage of the summation of all eigenvalues except the first one, divided by the summation of all eigenvalues (eigj is j'th eigenvalue obtained by using PCA on the folded concentration profiles).
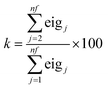 | (4) |
In the case that the estimated profiles fulfill the soft constraint, δα is equal to zero and if not, δα is greater than zero. By increasing the value of α, larger deviations from ideal trilinearity behavior are allowed, causing the area of feasible solutions (AFS) for the analyte under consideration to be expanded. Adjustment of the parameter α is a crucial step, and the application of soft-trilinearity constraints restricts the range of possible T matrices. The parameter α must be chosen for the system under study such that the amount of expected deviation from ideal trilinear behavior is based on prior information about the reproducibility of the analytical method under consideration. If α is too large, then trilinearity constraints are weakly applied, and in the limit, the AFS borders for the analyte of interest would be the same as borders without trilinearity and just non-negativity constraints. In contrast, if α = 0, hard-trilinearity constraints are imposed, and the profile of the compound in different matrices must be exactly the same.
If the calculated k value for component i is less than α, the grid point is accepted as a location with concentration profiles that obey soft-trilinearity behavior; otherwise, it is not a proper solution, and its deviation from trilinearity is more than the accepted level (see ESI†)
3. Data
3.1 Example 1, simulated data
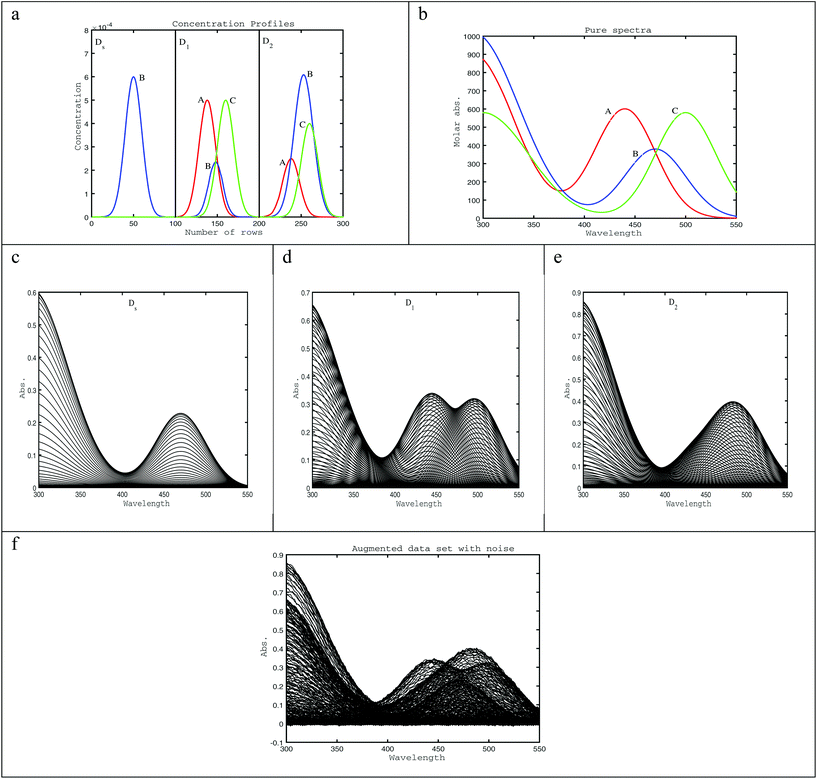
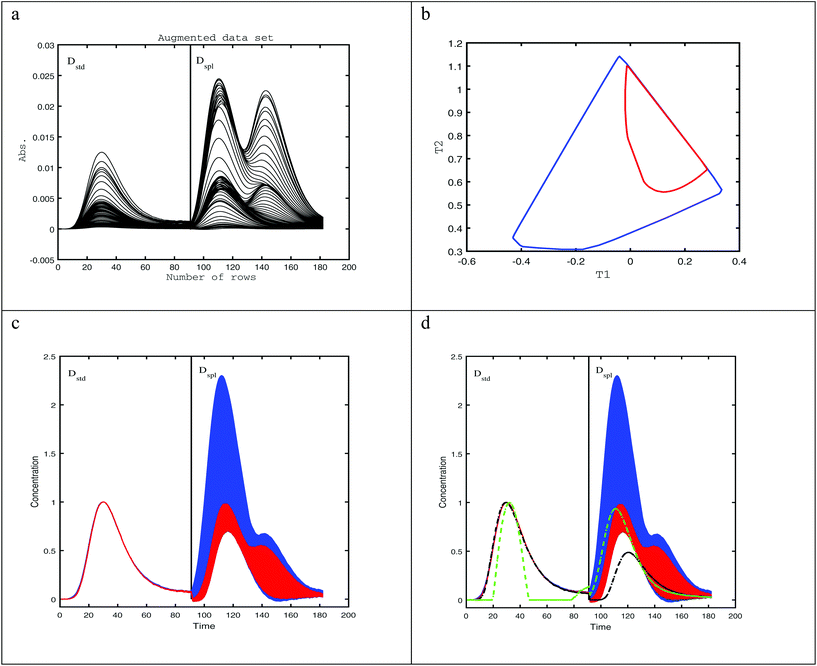
To illustrate the situation where second-order data does not have an ideal trilinear structure, 3 chromatographic based data matrices; Ds, D1, and D2 were simulated. Ds is a standard of one component (B), which is the analyte of interest having a retention time of Rs = 50 and a full-width at half-maximum (Ws = 23.55). D1 and D2 are samples having mixture data matrices, each containing three components, one being the analyte of interest overlapped with two unknown interference peaks. Non-ideal trilinear behavior of the analyte peak is modeled by deviations in retention time, Rt, and peak width, W. The peak maxima (Rt) of the analyte in D1, and D2 is shifted to Rt1 = 48 and Rt2 = 53 respectively, and the peak width of the analyte is changed to W1 = 20.02 and W2 = 27.09 in D1, and D2 in turn. Plots of the simulated elution profiles are shown in Fig. 1a, and the pure component spectra of three components are shown in Fig. 1b. The simulated elution profiles are Gaussian, while spectra are linear combinations of two Gaussians. The individual data matrices have the same dimensions (Fig. 1c–e) of 100 elution times and 126 wavelengths. The augmented data matrix, Daug, is built from the individual data matrices, Ds, D1, and D2, which are augmented column wise [Ds; D1; D2]. The size of this augmented matrix is (3 × 100, 126). Finally, in order to consider the effect of noise that is unavoidable in real data sets, 0.5% of the maximum value of the augmented data is added to Daug (Fig. 1f).3.2 Example 2
A real experimental case is used to illustrate the proposed algorithm in the quantitative analysis of an HPLC-DAD chromatogram of a three-component system with two identified pesticides (azinphos-ethyl and fenitrothion) and one unknown interferent.31,32 In this example, only one analyte was of interest, azinphos-ethyl. A three-way data set was formed by column-wise augmentation of one standard data matrix containing only azinphos-ethyl with one sample data matrix of three compounds (both analytes and one unknown interferent). This data set was downloaded from http://www.cid.csic.es/homes/rtaqam/tmp/WEB_MCR/download_dataHPLC.html. Noisy spectra in the first 8 rows of the data matrix were deleted, so the remaining data matrix had dimensions 91 × 73.4. Results and discussion
In order to evaluate the effect of soft-trilinearity constraints on the area of feasible solutions (AFS), the simulated and experimental data sets described above were analyzed using the new soft-trilinear constraint algorithm described in section 2.1. Both were three-component data sets with non-trilinear behavior. The analysis of the augmented data sets using the systematic grid search method and soft non-negativity constraints for concentration profiles and absorbance profiles produced the range of feasible solutions.4.1 The AFS under soft non-negativity constraints
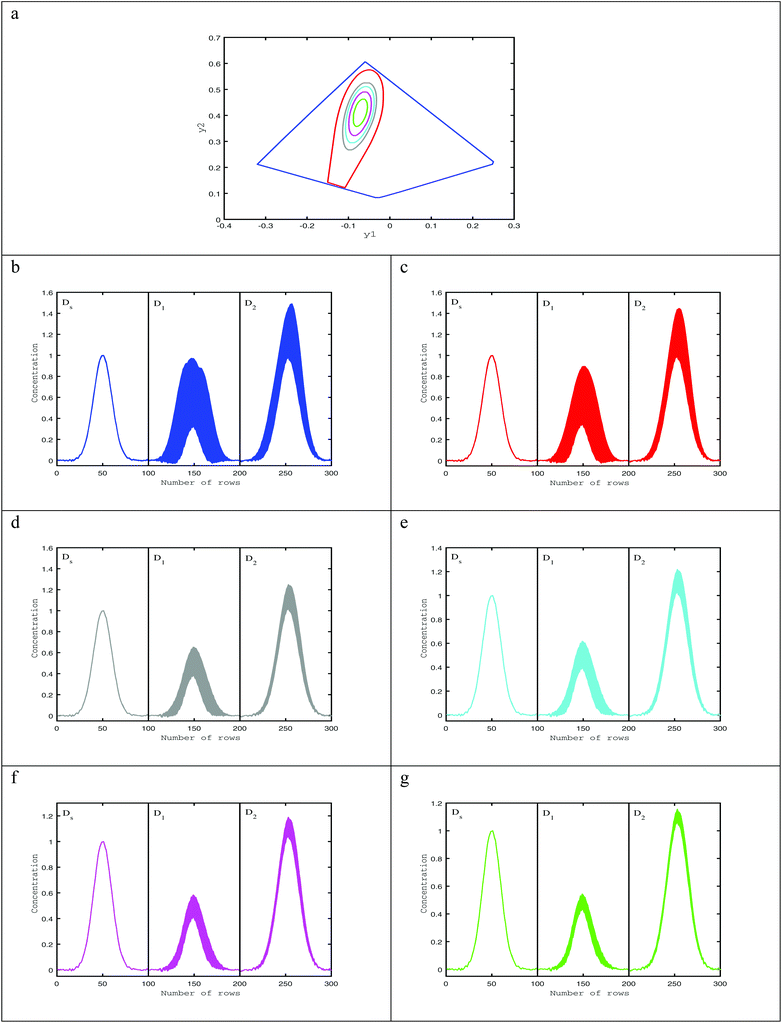
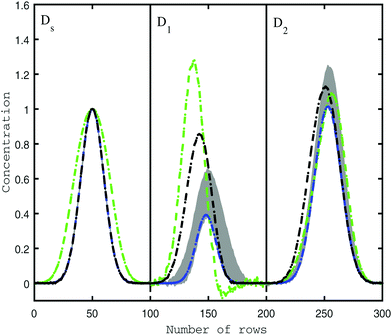
As reported before in the literature,27–29 by using soft non-negativity constraint, the borders of the area of feasible solutions can be calculated, showing bounded regions with no active constraints. In the case of soft non-negativity constraints, small negative deviations that lie within known noise levels of the data sets are accepted. In order to accept small deviations from non-negativity of the C and A matrices, the noise levels in resolved profiles must be estimated. In this way, a defined threshold for accepting the profiles is 6 times the median absolute deviation (MAD) from a double smoothing procedure. For this purpose, the estimated concentration and spectral profiles are smoothed by a three-point binomial filter. The difference between the smoothed and unsmoothed profiles is calculated as the residual. The median absolute deviation of the difference between smoothed residual and unsmoothed residual is set as the noise level for each resolved profile, 6xMAD.17Fig. 2a and b represents the AFS and concentration profiles of the analyte of interest (component B) under soft non-negativity constraint.4.2. The reduction of AFS under soft-trilinearity constraints
| Concentration values in D1 | Concentration values in D2 | |
|---|---|---|
| True values | 2.00 × 10−4 (AU) | 7.00 × 10−4 (AU) |
| Soft non-negativity constraint | 1.20 × 10−4–8.34 × 10−4 | 6.53 × 10−4–1.10 × 10−3 |
| Soft-trilinear constraint α = 1.60 | 1.45 × 10−4–7.46 × 10−4 | 6.67 × 10−4–1.10 × 10−3 |
| Soft-trilinear constraint α = 1.54 | 1.86 × 10−4–4.80 × 10−4 | 6.95 × 10−4–8.97 × 10−4 |
| Soft-trilinear constraint α = 1.52 | 1.99 × 10−4–4.40 × 10−4 | 7.03 × 10−4–8.70 × 10−4 |
| Soft-trilinear constraint α = 1.51 | 2.18 × 10−4–4.03 × 10−4 | 7.16 × 10−4–8.43 × 10−4 |
| Soft-trilinear constraint α = 1.49 | 2.45 × 10−4–3.59 × 10−4 | 7.34 × 10−4–8.13 × 10−4 |
| MCR-ALS | 5.44 × 10−4 | 8.70 × 10−4 |
| PARAFAC2 | 4.66 × 10−4 | 5.78 × 10−4 |
4.3. Hard constraints
| Relative concentration values (AU) | |
|---|---|
| Soft non-negativity constraint | 0.54–2.07 |
| Soft-trilinear constraint using α = 3 | 0.57–1.19 |
| MCR-ALS | 0.49 |
| PARAFAC2 | 1.57 |
4.4. RSM
An experimental design was created using the two simulated data sets in Example 1 to study the main effects and interaction of retention time, peak width, and noise level on the accuracy of concentration profiles produced by soft-trilinear constraints. A three-factor, two-level central composite experimental design was used, where the controlled factors were retention time of the analyte (X), peak width of the analyte (Y), and the measurement noise level (Z). Two matrices Ds and D1 were augmented, the first being the standard matrix containing one component, the analyte of interest, and the second being a mixture of the three components shown in Fig. 1c and d. In order to simulate a non-trilinear data set, the retention times and peak widths of the concentration profile of the analyte in the second data matrix were perturbed by known amounts as dictated by the experimental design. The three controlled factors, retention time (X), peak width (Y), and noise level of the augmented data (Z), were adjusted based on the levels listed in Table 3. By changing these three factors, 15 data sets were generated. After applying soft-trilinearity constraints, the AFS for the concentration profile of the analyte was calculated. The resulting band of transformed concentration profiles was used to calculate the area difference between the upper and lower band for use as the response variable of the experimental design. The responses were fitted to the factors via multiple regression using Quantum XL program downloaded from http://www.sigmazone.com/QuantumXLdownload.htm. The response surface plot (Fig. 5) shows that in this example, the peak-broadening effect has the largest influence on deviation from trilinearity. eqn (1) shows the contributions of individual factors and interactions between factors on the accuracy of results. Looking at the main effects, the regression coefficient for factor Y (peak-broadening) confirms that Y has the most significant influence on the response, while factor X (retention time shifts) has the smallest influence on the response. Also, it is clear that XZ (interaction of retention time and noise) has the biggest influence among the interaction of factors. Note that this result is valid for this particular simulated data set and may not be the same for all cases with different non-ideal situations.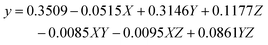 | (5) |
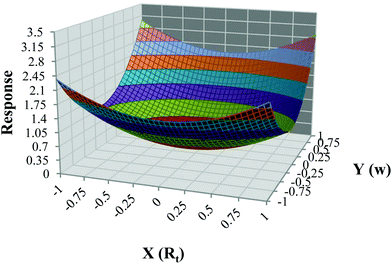 | ||
| Fig. 5 Obtained Response Surface for different non-trilinear behaviors due to changes in retention time (X), peak width (Y) and noise level. | ||
| Factor | Range | Setpoint | |
|---|---|---|---|
| Low | High | ||
| X | −1 (48) | 1 (53) | 0 (50) |
| Y | −1 (8.5) | 1 (11.5) | 0 (10) |
| Z | −1 (0.1% max data) | 1 (1% max data) | 0 (0.5% max data) |
5. Conclusion
Using reliable constraints to narrow the range of possible solutions is an interesting subject in SMCR methods. Some of these constraints are more robust and lead to unique solutions. In this work, trilinearity constraints were studied, which many SMCR methods apply as a hard constraint. By implementing hard constraints and forcing the resolved profiles of all matrices to have the same shape or follow special patterns of variation can lead to incorrect solutions, and it can be expected that many real-world data sets suffer from these kinds of shifts and small changes in the shape of profiles. In this work, we introduced soft-trilinearity constraints and showed its advantages in simulated and experimental data sets. This approach is generally useful in many circumstances and leads to solutions that are more accurate than those that are obtained with hard constraints. Moreover, the use of soft constraints allows for the possibility to tune the AFS boundary based on chemical information about the sample and method reproducibility.Conflicts of interest
There are no conflicts to declare.References
- E. Sanchez and B. Kowalski, J. Chemom., 1988, 2, 247–263 CrossRef CAS.
- K. S. Booksh and B. R. Kowalski, Anal. Chem., 1994, 66, 782A–791A CrossRef CAS.
- V. Gómez and M. P. Callao, Anal. Chim. Acta, 2008, 627, 169–183 CrossRef PubMed.
- H.-L. Wu, J.-F. Nie, Y.-J. Yu and R.-Q. Yu, Anal. Chim. Acta, 2009, 650, 131–142 CrossRef CAS PubMed.
- E. Sanchez and B. R. Kowalski, Anal. Chem., 1986, 58, 496–499 CrossRef CAS.
- B. E. Wilson, E. Sanchez and B. R. Kowalski, J. Chemom., 1989, 3, 493–498 CrossRef CAS.
- E. Sanchez and B. R. Kowalski, J. Chemom., 1990, 4, 29–45 CrossRef CAS.
- R. Bro, Chemom. Intell. Lab. Syst., 1997, 38, 149–171 CrossRef CAS.
- H. L. Wu, M. Shibukawa and K. Oguma, J. Chemom., 1998, 12, 1–26 CrossRef CAS.
- R. Tauler, I. Marqués and E. Casassas, J. Chemom., 1998, 12, 55–75 CrossRef CAS.
- W. H. Lawton and E. A. Sylvestre, Technometrics, 1971, 13, 617–633 CrossRef.
- R. Tauler, B. Kowalski and S. Fleming, Anal. Chem., 1993, 65, 2040–2047 CrossRef CAS.
- H. Abdollahi and R. Tauler, Chemom. Intell. Lab. Syst., 2011, 108, 100–111 CrossRef CAS.
- O. S. Borgen and B. R. Kowalski, Anal. Chim. Acta, 1985, 174, 1–26 CrossRef CAS.
- P. D. Wentzell, J.-H. Wang, L. F. Loucks and K. M. Miller, Can. J. Chem., 1998, 76, 1144–1155 CAS.
- R. Rajkó and K. István, J. Chemom., 2005, 19, 448–463 CrossRef.
- P. J. Gemperline, Anal. Chem., 1999, 71, 5398–5404 CrossRef CAS PubMed.
- M. Sawall and K. Neymeyr, J. Chemom., 2014, 28, 633–644 CrossRef CAS.
- A. Golshan, H. Abdollahi, S. Beyramysoltan, M. Maeder, K. Neymeyr, R. Rajkó, M. Sawall and R. Tauler, Anal. Chim. Acta, 2016, 911, 1–13 CrossRef CAS PubMed.
- R. Tauler, J. Chemom., 2001, 15, 627–646 CrossRef CAS.
- A. Golshan, H. Abdollahi and M. Maeder, Anal. Chim. Acta, 2012, 709, 32–40 CrossRef CAS.
- M. Sawall, C. Fischer, D. Heller and K. Neymeyr, J. Chemom., 2012, 26, 526–537 CrossRef CAS.
- S. Beyramysoltan, H. Abdollahi and R. Rajkó, Anal. Chim. Acta, 2014, 827, 1–14 CrossRef CAS.
- H. A. Kiers, J. M. ten Berge and R. Bro, J. Chemom., 1999, 13, 275–294 CrossRef CAS.
- R. Bro, C. A. Andersson and H. A. Kiers, J. Chemom., 1999, 13, 295–309 CrossRef CAS.
- S. A. Bortolato and A. C. Olivieri, Anal. Chim. Acta, 2014, 842, 11–19 CrossRef CAS.
- P. J. Gemperline and E. Cash, Anal. Chem., 2003, 75, 4236–4243 CrossRef CAS.
- S. Richards, R. Miller and P. Gemperline, Appl. Spectrosc., 2008, 62, 197–206 CrossRef CAS.
- N. Rahimdoust Mojdehi, M. Sawall, K. Neymeyr and H. Abdollahi, J. Chemom., 2016, 30, 252–267 CrossRef CAS.
- A. Golshan, H. Abdollahi and M. Maeder, Anal. Chem., 2011, 83, 836–841 CrossRef CAS.
- A. De Juan and R. Tauler, J. Chemom., 2001, 15, 749–771 CrossRef CAS.
- R. Tauler, S. Lacorte and D. Barcelo, J. Chromatogr., A, 1996, 730, 177–183 CrossRef CAS.
- S. Beyramysoltan, R. Rajkó and H. Abdollahi, Anal. Chim. Acta, 2013, 791, 25–35 CrossRef CAS.
- G. Ahmadi and H. Abdollahi, Current Applications of Chemometrics, 2015, p. 57 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8an00615f |
| This journal is © The Royal Society of Chemistry 2020 |