Ultralow thermal conductivity of Tl₄Ag₁₈Te₁₁

Abstract

Tl₄Ag₁₈Te₁₁ was reported to crystallize in a cubic structure with disordered thallium atoms filling cuboctahedral voids. Our electronic structure calculations of Tl₄Ag₁₈Te₁₁ revealed a zero-band gap, based on an I4mm space group model with ordered Tl atom sites. Utilizing differential scanning calorimetry, we demonstrated that the material melted incongruently at 723 K. Our studies of the thermoelectric properties of hot-pressed Tl₄Ag₁₈Te₁₁ and its nonstoichiometric homologs, revealed an unusual n-type extrinsic semiconducting behavior, combined with an ultralow thermal conductivity. The thermal conductivity of a sample of the nominal composition “Tl_4.05Ag₁₈Te₁₁” reached 0.19 W m⁻¹ K⁻¹ at 500 K, with this value being one of the lowest achieved by crystalline materials to date. This can be attributed to the highly disordered Tl atoms and the large unit cell with its highly complex structure, in accord with the low Debye temperature of 98 K.

---

Introduction

Mankind continues to utilize fossil energy, which results in increased greenhouse gas emissions into the atmosphere. This consequently leads to further depletion of Earth's ozone layer and increases the rate of climate change. Thermoelectric materials offer a prospective solution by harvesting heat from different systems and converting it into useful energy without creating greenhouse gases.

Currently, thermoelectric devices are primarily applied to produce electricity for satellites, aerospace machinery, communication systems, and powering daily life devices, such as wearable watches, fridges, and supplement energy to vehicles with internal combustion engines for fuel-efficient alternatives.^1–3 Thermoelectric materials are evaluated by their figure-of-merit zT, based on the equation: zT = S²σT/κ, where S the Seebeck coefficient, σ the electrical conductivity, κ the thermal conductivity, and T the absolute temperature.^4–7

Thallium chalcogenides have sparked continued interest in the thermoelectrics field because of their often low thermal conductivity,^8,9 which is an important trait for advanced thermoelectric materials. Tl₂Ag₁₂Te₇ was reported to achieve an ultralow thermal conductivity of 0.25 W m⁻¹ K⁻¹ and high zT of 1.1 at 525 K.¹⁰ TlAgTe possesses a low thermal conductivity of 0.36 W m⁻¹ K⁻¹ and zT of 0.6 at 550 K after substituting 40% of Ag with Cu.⁹ Tl_8.1Pb_1.9Te₆ was stated to have a thermal conductivity of 0.45 W m⁻¹ K⁻¹ and a zT_max of 1.5 at 700 K.¹¹ TlAg₉Te₅ demonstrated a thermal conductivity of 0.23 W m⁻¹ K⁻¹ and a high zT of 1.23 at 700 K.¹² However, all of the above are p-type materials. There are only two n-type thallium tellurides reported thus far, namely TlBiTe₂ and Tl₂HgGeTe₄, with only the thermoelectric properties of TlBiTe₂ determined at high temperatures.^13,14 Examples of state-of-the-art n-type thermoelectric materials include bismuth telluride,^15,16 lead telluride,^17,18 filled skutterudites^19,20 and Bi-doped magnesium silicide stannides,^21,22 all with zT values above unity. This paper introduces the hitherto unknown properties of the n-type Tl₄Ag₁₈Te₁₁, which exhibits an ultralow thermal conductivity.

Experimental

The compounds were obtained via solid-state synthesis: stoichiometric amounts of the respective elements (Tl, granules, 6 mm, 99.99%, Alfa Aesar; Ag ingots, 100 mesh, 99.5%, Alfa Aesar; Te, broken ingots, 99.99%) were weighed and placed into a silica tube in an argon filled glove box. The tubes containing the elements were then transferred to a vacuum line and evacuated to 2.4 × 10⁻³ mbar. The tubes were sealed using a hydrogen/oxygen torch and then heated up to 923 K for several hours in a resistance furnace, and then water-quenched to room temperature. The yielded ingots were ground into fine powder and annealed at 573 K for 72 hours. The powder was then hot-pressed under a 5% hydrogen +95% argon atmosphere using the Oxy-Gon FR-210-30T-ASA-160-EVC hot press furnace system in a hardened graphite die with an inner diameter of 12.7 mm. The density of pellets was determined by the Archimedes method: the densities for all the presented samples were higher than 95% of the theoretical density (8.43 g cm⁻³).

The electronic structure of Tl₄Ag₁₈Te₁₁ was computed utilizing the WIEN2k package applying the full-potential linearized augmented plane wave (FP-LAPW) method with the density functional theory (DFT).^23,24 The generalized gradient approximation (GGA) from Perdew, Burke and Ernzerhof (PBE) was utilized for exchange and correlation energies.²⁵ Afterwards, the modified Becke–Johnson (mBJ) potential was applied to obtain a more reliable band gap. For the self-consistent energy calculations, 99 independent k points were selected on a grid of 10 × 10 × 10 points spread out evenly throughout the Brillouin zone. The energy convergence was set to be 10⁻⁴ Ry for the self-consistency.

The phase identification was performed utilizing our INEL X-ray powder diffractometer with a position-sensitive detector and Cu Kα1 radiation. The acceleration voltage and current were 30 kV and 30 mA, respectively. The diffraction patterns were collected at room temperature in the 2θ range from 5° to 120°.

The homogeneity of the samples was analysed by scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDX) using a FEI Quanta Feg 250 ESEM with an acceleration voltage of 25 kV (WATLab, University of Waterloo). The experimental elemental ratios were determined by averaging four analyzed spots, and the standard deviations of the elemental ratios were determined by the population standard deviation method. No impurity elements were detected, and the sample appeared to be homogenous with Tl amounts generally slightly higher and Ag amounts slightly lower than expected based on the theoretical values. SEM images were also obtained on a hot-pressed pellet, showing a homogenous distribution of all elements (Fig. S1 in the ESI†).

Both differential scanning calorimetry (DSC) and thermogravimetry (TG) were performed with the Netzsch STA 409 PC Luxx instrument on an 80 mg powder sample of the nominal stoichiometry of Tl₄Ag₁₈Te₁₁. The measurement was conducted under a constant argon flow with a heating rate of 20 K min⁻¹ up to 773 K utilizing sapphire as the reference.

The thermal diffusivity, D, was measured on hot-pressed pellets with heights approximating 2 mm using the TA-Instruments LASERFLASH DLF-1 system under an ultrapure argon atmosphere. The thermal conductivity was determined via the equation κ = ρC_pD, where ρ is the density of the pellet, and C_p is the specific heat, estimated through the Dulong–Petit law to be 0.198 J g⁻¹ K⁻¹, which is appropriate for high temperature values. The experimental error margin for our thermal conductivity measurements was estimated as ±5%. Low temperature specific heat measurements were performed with a Quantum Design PPMS Dynacool at WATLab. The experimentally determined C_p reached a plateau at 0.192 J g⁻¹ K⁻¹ (Fig. S2, ESI†), supporting the validity of using the Dulong–Petit value.

The Seebeck coefficient and electrical conductivity were determined by using our ULVAC-RIKO ZEM-3 system under ultrapure helium, utilizing a cut rectangular bar from the hot-pressed pellet with approximate dimensions of 10 × 2 × 2 mm. The experimental error for the Seebeck coefficient, electrical conductivity, and figure-of-merit are estimated as ±3%, ±5%, and ±10%.

Results and discussion

In 1992, Moreau et al. determined the crystal structure of Tl₄Ag₁₈Te₁₁.²⁶ This crystal structure consists of AgTe₄ tetrahedra interconnected in three dimensions with Tl cations occupying tunnels of this framework (Fig. 1). The space group of Tl₄Ag₁₈Te₁₁ is F4̄3m, a subgroup of the K₄Ag₁₈Te₁₁ space group Fm3̄m,²⁷ due to the disordered Tl atom positions occupying an additional Wyckoff site. The lattice parameter of Tl₄Ag₁₈Te₁₁ was published to be a = 18.717(8) Å, and the unit cell volume V = 6557.1 ų. The Tl atom positions in the cubic (Tl1 atoms) and antiprismatic (Tl2 atoms) voids are 100% occupied, but disordered within the cuboctahedral (Tl3 atoms) voids. In K₄Ag₁₈Te₁₁, all the potassium atoms were determined to be located in the centers of the respective polyhedra. However, the large anisotropic displacement parameter of the K3 atom (U_eq = 0.067(6) Ų, compared to K1 with 0.016(2) Ų and K2 with 0.013(1) Ų), may indicate a tendency towards disorder in that cage as well.

Fig. 1 Left: Crystal structure of Tl₄Ag₁₈Te₁₁. Blue polyhedra: AgTe₄ tetrahedra; grey circles: disordered Tl3 atoms; right: arrangements of Tl atoms in the chain along the c-axis.

The shortest distance between the Tl2 atom and the disordered Tl3 atom is 3.57 Å as a consequence of its displacement from the center of its polyhedron. Typical homonuclear Tl–Tl distances in thallium chalcogenides, such as Tl₅Te₃,²⁸ Tl₉BiTe₆,²⁹ and Tl₄ZrTe₄,³⁰ are in the range of 3.5 Å to 4.0 Å. While the cuboctahedron cannot accommodate two Tl atoms, two Ag atoms would fit, with an Ag–Ag distance of 3.0 Å, thereby allowing for a cation excess and thus extra electrons causing n-type conduction.

The Tl1–Te distances in the Tl1Te₆ cube are between 3.47 Å and 3.58 Å, and the Tl2–Te distances in the Tl2Te₆ antiprism between 3.62 Å and 3.69 Å. On the other hand, the Tl3 atoms occupy the void in a cuboctahedron, whose center is too far away (5.04 Å) from the surrounding twelve Te atoms for regular Tl3–Te bonds. Consequently, the Tl3 positions were refined to be disordered in that cage, resulting in six sites, each with a 16.7% occupancy. Each of these sites participates in four short Tl3–Te bonds of 3.32 Å, and larger contacts with the next four Te atoms at a distance of 4.42 Å. This situation is reminiscent of the guest atoms in the icosahedral cages of the filled skutterudites^31–33 and in the tetrakaidecahedral holes of the clathrates.^8,34,35

The distances between all the Te atoms are larger than 4 Å, so their oxidation states are assigned as Tl⁺, Ag⁺, and Te²⁻, resulting in a charge balanced formula of (Tl⁺)₄(Ag⁺)₁₈(Te²⁻)₁₁. The Ag atoms in this compound form Ag₁₂ clusters that are three-dimensionally interconnected by Ag₂ dumbbells. d¹⁰–d¹⁰ Ag–Ag interactions of the order of 3 Å are thus present in this structure, which are common in silver chalcogenides, such as Tl₂Ag₁₂Te₇,¹⁰ Tl₂Ag₁₂Se₇,³⁶ K₄Ag₁₈Te₁₁, and TlNdAg₂S₃.³⁷

The PXRD patterns of the synthesized samples are presented in Fig. 2. No significant amount of impurities or side products were detected in any sample. The atomic percentages (at%) obtained by EDX analysis are presented in Table 1. The amount of Te is very close to the nominal percent for all the samples. The at% of Tl are between 0.4–0.7% higher and 0.3–0.5% lower than the theoretical percentages in case of Ag. The two samples with the same nominal formula reveal similar elemental ratios, indicating the samples are reproducible. The standard deviations are 0.1–0.6%, demonstrating that homogeneous samples were obtained.

Fig. 2 PXRD pattern of calculated Tl₄Ag₁₈Te₁₁, experimental Tl₄Ag₁₈Te₁₁, “Tl_4.05Ag₁₈Te₁₁”, “Tl₄Ag₁₈Te_10.95”, and repeat samples of the latter two.

Table 1 Experimental atomic% (standard deviation)/nominal at% of the different elements determined via EDX

	Tl at%	Ag at%	Te at%
Tl4Ag18Te11	12.8(1)/12.1	53.9(2)/54.5	33.3(2)/33.3
“Tl4.05Ag18Te11”	12.7(4)/12.3	54.0(4)/54.5	33.4(2)/33.3
“Tl4.05Ag18Te11”	12.7(2)/12.3	54.1(3)/54.5	33.3(1)/33.3
“Tl4Ag18Te10.95”	12.7(4)/12.1	54.2(6)/54.6	33.1(2)/33.2
“Tl4Ag18Te10.95”	12.5(6)/12.1	54.3(6)/54.6	33.1(2)/33.2

---

The electronic structure was determined based on an I4mm space group model, where one of the six disordered Tl3 sites was treated as 100% occupied, with the other five removed, as shown in Fig. 3(a). The density of states (DOS) of Tl₄Ag₁₈Te₁₁ is shown in Fig. 3(b). From −6.5 eV to −3 eV, the DOS is dominated by Ag-d orbitals, from −2 eV to the Fermi level (E_F), it is mainly composed of Te-p orbitals and Ag-d orbitals and above E_F to 3 eV, the states contain (empty) Ag-s and Ag-p states, with some contributions from covalent mixing with Te-p states. The Tl states have only negligible contributions, partially caused by the small ratio of Tl in this material and the Tl-s states appearing to be below the selected energy range. The band structure (shown in Fig. 3(c)) reveals a zero band gap, with the valence band slightly in contact with the conduction band without any overlapping, notably known as the Dirac-semimetallic band structure. A similar band structure was determined for K₄Ag₁₈Te₁₁, with zero band gap. The flat bands just below the Fermi energy and the steep bands just above the Fermi energy predict that this material could possibly possess a high Seebeck coefficient and a high electrical conductivity.

Fig. 3 (a) I4mm structure model; (b) density of states (DOS); (c) band structure of the I4mm model of Tl₄Ag₁₈Te₁₁.

The thermal behavior of Tl₄Ag₁₈Te₁₁ was investigated by DSC and TG measurements, and the data is plotted in Fig. 4. The curve of TG indicates a weight gain smaller than 1%. The DSC curve reveals that Tl₄Ag₁₈Te₁₁ melts incongruently starting from 723 K. According to the Tl₂Te–Ag₂Te phase diagram published in 1990,³⁸ the melting processes can be interpreted as (with L = liquid):

At 723 K: Tl₄Ag₁₈Te₁₁ → TlAg_5.14Te_3.14 + L

At 729 K: TlAg_5.14Te_3.14 → TlAg₉Te₅ + L′

At 780 K: TlAg₉Te₅ → Ag₂Te + L′′

(At 1228 K: Ag₂Te → L′′′)

Fig. 4 DSC and TG plots of Tl₄Ag₁₈Te₁₁.

However, the last process occurs outside of the temperature range we measured. The small exothermic peak presented at 570 K might correspond to the peritectic point of TlTe.³⁹ The PXRD pattern obtained after this DSC measurement revealed a mixture of phases caused by the fast cooling process going through peritectic points.

All the physical properties obtained during cooling agree with the data obtained during heating, proving the data are reproducible (Fig. S3, ESI†). The Seebeck coefficients, S, of all samples are negative (Fig. 5(a)), which indicates that they are n-type semiconductors. This may be a consequence of a small amount of nonstoichiometric defects, such as two Ag cations replacing one Tl atom in the cuboctahedron of Te atoms, leading to a small amount of excess electrons.

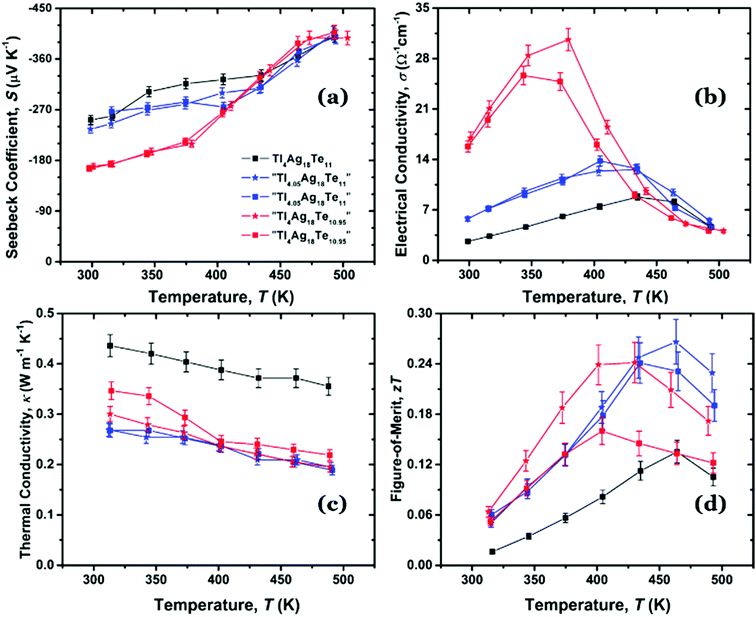Fig. 5 Physical properties of Tl₄Ag₁₈Te₁₁. (a) Seebeck coefficient, (b) electrical conductivity, (c) thermal conductivity, and (d) figure-of-merit versus temperature.

The absolute Seebeck values increase with a slower rate below 400 K, and then with a larger slope above 400 K. S of Tl₄Ag₁₈Te₁₁ ranges from −250 μV K⁻¹ at room temperature to −400 μV K⁻¹ at 500 K. The absolute Seebeck values of “Tl_4.05Ag₁₈Te₁₁” (with S = −240 μV K⁻¹ at 300 K to S = −300 μV K⁻¹ at 420 K) and “Tl₄Ag₁₈Te_10.95” (S = −160 μV K⁻¹ at 300 K to −270 μV K⁻¹ at 420 K) are both lower compared to Tl₄Ag₁₈Te₁₁ up to 420 K. Beyond that, all curves merge to equivalent values within experimental error. The maximum absolute Seebeck value of TlBiTe₂ is much lower than the one of Tl₄Ag₁₈Te₁₁ (with S = −75 μV K⁻¹ at 760 K).¹³ The absolute Seebeck coefficient values of Tl₄Ag₁₈Te₁₁ are also much higher than the values of Mg₂Si_0.325Sn_0.645Bi_0.03 (S = −115 μV K⁻¹ at 300 K to −215 μV K⁻¹ at 773 K),²² and the values of Bi₂Te_2.79Se_0.21 (S = −115 μV K⁻¹ at 300 K to −150 μV K⁻¹ at 540 K).²¹

As displayed in Fig. 5(b), the electrical conductivity of stoichiometric Tl₄Ag₁₈Te₁₁ increases as temperature increases to a maximum of σ = 9 Ω⁻¹ cm⁻¹ at 435 K, and then it starts to rapidly decrease. The four non-stoichiometric materials exhibit higher electrical conductivity at low temperature, indicative of more extrinsic charge carriers, in line with their lower absolute Seebeck values. For “Tl_4.05Ag₁₈Te₁₁”, the electrical conductivity increases to a maximum of σ = 13 Ω⁻¹ cm⁻¹ at 435 K. For “Tl₄Ag₁₈Te_10.95”, the electrical conductivity of the two different samples have some minor differences while generally exhibiting the same slope – the higher one reaches its electrical conductivity maximum value of 31 Ω⁻¹ cm⁻¹ at 380 K, which is almost 30 times lower than in TlBiTe₂,¹³ 40 times lower than in Bi₂Te_2.79Se_0.21,²¹ and 70 times lower than in Mg₂Si_0.325Sn_0.645Bi_0.03.²² The differences between these two samples with the same nominal formula “Tl₄Ag₁₈Te_10.95” may be caused by weighing errors leading to small differences in the actual composition. E.g., an error of 0.5 mg would correspond to 0.09% Tl or 0.05% Te. Above 425 K, the electrical conductivity curves of all materials merge together, because more intrinsic charge carriers are thermally activated, eliminating the differences in the initial carrier concentration.

The samples all possess very low thermal conductivity for the whole temperature range, and their thermal conductivity decreases as temperature increases due to increased phonon Umklapp scattering,⁴⁰ as shown in Fig. 5(c). The thermal conductivity κ of Tl₄Ag₁₈Te₁₁ ranges from 0.44 W m⁻¹ K⁻¹ at 320 K to 0.35 W m⁻¹ K⁻¹ at 500 K. The thermal conductivity of “Tl_4.05Ag₁₈Te₁₁” is the lowest in this series, ranging from 0.27 W m⁻¹ K⁻¹ at 320 K to 0.19 W m⁻¹ K⁻¹ at 500 K. The two sets of thermal conductivity data obtained from the two different samples of “Tl_4.05Ag₁₈Te₁₁” correspond with each other very well.

For comparison, these values are almost ten times lower than the thermal conductivity of TlBiTe₂,¹³ 17 times lower than in Mg₂Si_0.325Sn_0.645Bi_0.03 (κ = 3 W m⁻¹ K⁻¹ at 500 K),²² and nine times lower than in Bi₂Te_2.79Se_0.21 (1.6 W m⁻¹ K⁻¹ at 500 K).²¹ The comparison of total thermal conductivity between “Tl_4.05Ag₁₈Te₁₁” with five other state-of-the-art thermoelectric materials is presented in Fig. 6, demonstrating the thermal conductivity of “Tl_4.05Ag₁₈Te₁₁” is extremely low. The range of thermal conductivity of bulk nanostructured Bi₂Te₃,⁴¹ Pb_0.98Tl_0.02Te,⁴² BiSbTe,⁴³ Cu_1.98Ag_0.02Te,⁴⁴ and Ag_1−xPb₁₈SbTe₂₀⁴⁵ is approximately 0.4–2.2 W m⁻¹ K⁻¹, and their maximum zT values all exceed unity.

Fig. 6 Comparison of the thermal conductivity with other state-of-the-art thermoelectric materials.

The total thermal conductivity (κ_tot) contains both the lattice (κ_l) and electrical contributions (κ_e) to thermal conductivity: κ_tot = κ_l + κ_e, where κ_e can be estimated from the Wiedemann–Franz equation: κ_e= LσT.⁴⁶ The Lorenz number L was calculated from the measured Seebeck coefficient values based on the single Kane band model.⁴⁷ Due to the small electrical conductivity, the electrical thermal conductivity is only a minor contribution (its maximum value reaches 0.008 W m⁻¹ K⁻¹ at 430 K), and the lattice thermal conductivity is about 0.26 W m⁻¹ K⁻¹ at 320 K and 0.18 W m⁻¹ K⁻¹ at 500 K.

This ultralow thermal conductivity correlates nicely with the low Debye temperature of θ_D = 98 K obtained from of fit of the specific heat measurement. For comparison, PbTe has a Debye temperature of 177 K, and the binary thallium tellurides Tl₂Te, Tl₅Te₃, TlTe, and Tl₂Te₃ all comparable values between 107 K and 124 K.⁴⁸ The Debye temperature is directly proportional to the speed of sound:

Therein, ħ is the reduced Planck constant, k_B the Boltzmann constant, n the number density of atoms {number of atoms/cell/(unit cell volume)}, and ν_S the arithmetic average of the speed of sound. ν_S in turn is proportional to the minimum thermal conductivity of both Clarke⁴⁹ and Cahill,⁵⁰ recently compared to the “diffuson thermal conductivity” by Snyder's group:⁵¹

Cahill: κ_glass = 1.21n^2/3k_Bν_S

Clarke: κ_min = 0.93n^2/3k_Bν_S

Snyder: κ_diff = 0.76n^2/3k_Bν_S

To derive the equation for κ_diff, thermal transport was based on diffusons instead of on phonons as used for κ_glass. This results in lower values for all materials, and may well correspond to the lowest possible thermal conductivity. Using ν_S = 1385 m s⁻¹ as calculated from θ_D = 98 K, we obtain κ_glass = 0.27 W m⁻¹ K⁻¹, κ_min = 0.21 W m⁻¹ K⁻¹, and κ_diff = 0.17 W m⁻¹ K⁻¹. These numbers show that “Tl_4.05Ag₁₈Te₁₁” exhibits a thermal conductivity below the so-called glass limit according to Cahill, but not below the diffuson limit.

This extraordinary low thermal conductivity is likely caused by Tl disorders, heavy composing elements, and the large unit cell, which all contribute to reducing the mean free path length of the phonons travelling though the lattice. The disorder effect to lower thermal conductivity was thoroughly discussed in many previously published articles, such as for Tl₂Ag₁₂Te_7+δ,¹⁰ Cu₂Se,⁵² and Ba₃Cu_16−x(S,Te)₁₁.⁵³ The “cage rattling” mechanism, where Tl3 atoms exhibit concerted rattling in a cage of Te atoms, is known to be important as well. Best known examples of this phenomenon are the filled skutterudites^54–56 and clathrates.^8,34,35,57 This concerted rattling phenomenon was also observed in CsAg₅Te₃, which owns an ultralow lattice thermal conductivity of 0.14 W m⁻¹ K⁻¹ at 727 K, and a Debye temperature of 118 K.⁵⁸ Furthermore, heavy elements tend to vibrate with a smaller amplitude because of the inertial resistance provided by the heavy nucleus, and thus cause a lower phonon transfer effect to the neighboring atoms. The principles of how larger unit cells and more complex crystal structures lower the lattice thermal conductivity were reviewed in 2010.⁵⁹

The figure-of-merit curves of the samples are plotted in Fig. 5(d). The stoichiometric Tl₄Ag₁₈Te₁₁ sample achieves a maximum zT value of 0.13 at 470 K; whereas the zT of “Tl_4.05Ag₁₈Te₁₁” is twice as large, reaching a maximum of 0.26 at 465 K. The highest zT of “Tl_4.05Ag₁₈Te₁₁” is higher than the maximum zT of TlBiTe₂ which was achieved at 760 K with a value of 0.15.¹³ However, it is still low in comparison to Mg₂Si_0.325Sn_0.645Bi_0.03, whose maximum zT is 1.35 at 773 K,²² and Bi₂Te_2.79Se_0.21 whose maximum zT is 0.9 at 430 K.²¹ For the two “Tl₄Ag₁₈Te_10.95” samples, the one with higher electrical conductivity exhibits the higher zT of 0.24 between 400 K and 425 K. These relatively low zT values could likely be significantly improved if the carrier concentration could be optimized via doping with heteroelements.

Conclusions

Thallium chalcogenides are known to rarely perform as n-type semiconductors; however, we found that Tl₄Ag₁₈Te₁₁ is an n-type material. The thermal behaviour of Tl₄Ag₁₈Te₁₁ was investigated by DSC, illustrating its incongruent melting at 723 K. The samples prepared and investigated are homogenous, and the physical properties of the samples are reproducible. All the samples have negative Seebeck coefficient values throughout the temperature range of 300–500 K, indicating that the majority of charge carriers are electrons. “Tl_4.05Ag₁₈Te₁₁” has the lowest thermal conductivity of 0.19 W m⁻¹ K⁻¹ at 500 K, which is extraordinary low compared to other thermoelectric materials. This is mainly a consequence of the disordered heavy Tl atoms filling the cuboctahedral cages and the complex crystal structure built by heavy elements.

The highest dimensionless figure-of-merit, zT, is about 0.26 obtained by the sample with the nominal formula of “Tl_4.05Ag₁₈Te₁₁” at 475 K, which is twice as high as the maximum zT of Tl₄Ag₁₈Te₁₁. Doping with other elements in order to optimize the thermoelectric properties, which are at this moment negatively affected by the low electrical conductivity, will be performed in the near future. Overall, Tl₄Ag₁₈Te₁₁ based materials will provide a promising n-type thermoelectric material, if their carrier concentrations can be enhanced.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Natural Sciences and Engineering Research Council of Canada in form of a Discovery Grant (RGPIN-2015-04584) is appreciated.

References

1. J. Yang and F. R. Stabler, Automotive Applications of Thermoelectric Materials, J. Electron. Mater., 2009, 38(7), 1245–1251.
2. L. E. Bell, Cooling, heating, generating power, and recovering waste heat with thermoelectric systems, Science, 2008, 321(5895), 1457–1461.
3. I. Petsagkourakis, K. Tybrandt, X. Crispin, I. Ohkubo, N. Satoh and T. Mori, Thermoelectric materials and applications for energy harvesting power generation, Sci. Technol. Adv. Mater., 2018, 19(1), 836–862.
4. G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7(2), 105–114.
5. Y. Shi, C. Sturm and H. Kleinke, Chalcogenides as thermoelectric materials, J. Solid State Chem., 2019, 270, 273–279.
6. J. He and T. M. Tritt, Advances in thermoelectric materials research: Looking back and moving forward, Science, 2017, 357(6358), eaak9997.
7. T. Mori, Novel Principles and Nanostructuring Methods for Enhanced Thermoelectrics, Small, 2017, 13(45), 1702013.
8. H. Kleinke, New bulk materials for thermoelectric power generation: clathrates and complex antimonides, Chem. Mater., 2010, 22(3), 604–611.
9. K. Kurosaki, K. Goto, H. Muta and S. Yamanaka, Enhancement of thermoelectric figure of merit of AgTlTe by tuning the carrier concentration, J. Appl. Phys., 2007, 102(2), 023707.
10. Y. Shi, A. Assoud, S. Ponou, S. Lidin and H. Kleinke, A New Material with a Composite Crystal Structure Causing Ultralow Thermal Conductivity and Outstanding Thermoelectric Properties: T_l2Ag₁₂Te_7+δ, J. Am. Chem. Soc., 2018, 140(27), 8578–8585.
11. Q. Guo, A. Assoud and H. Kleinke, Improved bulk materials with thermoelectric figure-of-merit greater than 1: Tl_10−xSn_xTe₆ and Tl_10−xPb_xTe₆, Adv. Energy Mater., 2014, 4(14), 1400348.
12. K. Kurosaki, A. Kosuga, H. Muta, M. Uno and S. Yamanaka, Ag₉TlTe₅: A high-performance thermoelectric bulk material with extremely low thermal conductivity, Appl. Phys. Lett., 2005, 87(6), 3–5.
13. K. Kurosaki, A. Kosuga and S. Yamanaka, Thermoelectric properties of TlBiTe2, J. Alloys Compd., 2003, 351(1–2), 279–282.
14. M. A. McGuire, T. J. Scheidemantel, J. V. Badding and F. J. DiSalvo, Tl₂AXTe₄ (A = Cd, Hg, Mn; X = Ge, Sn): Crystal Structure, Electronic Structure, and Thermoelectric Properties, Chem. Mater., 2005, 17(24), 6186–6191.
15. X. Yan, B. Poudel, Y. Ma, W. S. Liu, G. Joshi and H. Wang, et al., Experimental studies on anisotropic thermoelectric properties and structures of n-type Bi₂Te_2.7Se_0.3, Nano Lett., 2010, 10(9), 3373–3378.
16. L. P. Hu, X. H. Liu, H. H. Xie, J. J. Shen, T. J. Zhu and X. B. Zhao, Improving thermoelectric properties of n-type bismuth-telluride-based alloys by deformation-induced lattice defects and texture enhancement, Acta Mater., 2012, 60(11), 4431–74431.
17. L. Yang, Z. G. Chen, M. Hong, L. Wang, D. Kong and L. Huang, et al., n-Type Bi-doped PbTe Nanocubes with Enhanced Thermoelectric Performance, Nano Energy, 2017, 31, 105–112.
18. A. D. Lalonde, Y. Pei and G. J. Snyder, Reevaluation of PbTe1-xIx as high performance n-type thermoelectric material, Energy Environ. Sci., 2011, 4(6), 2090–2096.
19. M. Matsubara and R. Asahi, Optimization of Filler Elements in CoSb3-Based Skutterudites for High-Performance n-Type Thermoelectric Materials, J. Electron. Mater., 2016, 45(3), 1669–1678.
20. G. Rogl, A. Grytsiv, K. Yubuta, S. Puchegger, E. Bauer and C. Raju, et al., In-doped multifilled n-type skutterudites with ZT = 1.8, Acta Mater., 2015, 95, 201–211.
21. L. Hu, H. Wu, T. Zhu, C. Fu, J. He and P. Ying, et al., Tuning Multiscale Microstructures to Enhance Thermoelectric Performance of n-Type Bismuth-Telluride-Based Solid Solutions, Adv. Energy Mater., 2015, 5(17), 1500411.
22. L. R. Macario, X. Cheng, D. Ramirez, T. Mori and H. Kleinke, Thermoelectric Properties of Bi-Doped Magnesium Silicide Stannides, ACS Appl. Mater. Interfaces, 2018, 10, 40585–40591.
23. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, ed. K. Schwarz, Techn. Universität, Wien, Austria, 2001.
24. K. Schwarz, DFT calculations of solids with LAPW and WIEN2k, J. Solid State Chem., 2003, 176, 319–328.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
26. J. Le Roy, J. M. Moreau, G. Brun and B. Liautard, A new phase in the Tl-Ag-Te system: crystal structure of Tl₄Ag_24−xTe_15−y, J. Alloys Compd., 1992, 186(2), 249–254.
27. B. Davaasuren, E. Dashjav and A. Rothenberger, Synthesis and Characterization of the Ternary Telluroargentate K₄[Ag₁₈Te₁₁], Z. Anorg. Allg. Chem., 2014, 640(14), 2939–2944.
28. I. Schewe, P. Böttcher and H. G. von Schnering, The crystal structure of Tl₅Te₃ and its relationship to the Cr₅B₃ type, Z. Kristallogr., 1989, 188, 287–298.
29. Q. Guo, M. Chan, B. A. Kuropatwa and H. Kleinke, Enhanced thermoelectric properties of variants of Tl₉SbTe₆ and Tl₉BiTe₆, Chem. Mater., 2013, 25(20), 4097–4104.
30. C. R. Sankar, S. Bangarigadu-Sanasy, A. Assoud and H. Kleinke, Syntheses, Crystal Structures and Thermoelectric Properties of two new Thallium Tellurides: Tl₄ZrTe₄ and Tl₄HfTe₄, J. Mater. Chem., 2010, 20, 7485–7490.
31. J. Eilertsen, S. Rouvimov and M. A. Subramanian, Rattler-seeded InSb nanoinclusions from metastable indium-filled In_0.1Co₄Sb₁₂ skutterudites for high-performance thermoelectrics, Acta Mater., 2012, 60(5), 2178–2185.
32. C. H. Lee, I. Hase, H. Sugawara, H. Yoshizawa and H. Sato, Low-lying optical phonon modes in the filled skutterudite CeRu₄Sb₁₂, J. Phys. Soc. Jpn., 2006, 75(12), 123602.
33. G. A. Slack, Design concepts for improved thermoelectric materials, Mater. Res. Soc. Symp. Proc., 1997, 478, 47–54.
34. M. Christensen, S. Johnsen and B. B. Iversen, Thermoelectric clathrates of type I, Dalton Trans., 2010, 39(4), 978–992.
35. T. Takabatake, K. Suekuni, T. Nakayama and E. Kaneshita, Phonon-glass electron-crystal thermoelectric clathrates: Experiments and theory, Rev. Mod. Phys., 2014, 86, 669–716.
36. Y. Shi, A. Assoud, C. R. Sankar and H. Kleinke, Tl2Ag12Se7: a new pnp conduction switching material with extraordinarily low thermal conductivity, Chem. Mater., 2017, 29(21), 9565–9571.
37. A. Assoud, Y. Shi, Q. Guo and H. Kleinke, Crystal and electronic structure of the new quaternary sulfides TlLnAg₂S₃ (Ln = Nd, Sm and Gd), J. Solid State Chem., 2017, 256, 6–9.
38. G. Brun, M. Boubali, J. C. Tedenac, R. M. Ayral and B. Legendre, Redetermination of the phase equilibria in the system Tl₂Te-Ag₂Te, Thermochim. Acta, 1990, 165, 93–101.
39. A. A. Toure, G. Kra, R. Eholie, J. Olivier-Fourcade and J. C. Jumas, Mise au point sur le système binaire TlTe et affinement des structures de TlTe et Tl5Te₃, J. Solid State Chem., 1990, 87, 229–236.
40. P. G. Klemens, Thermal resistance due to point defects at high temperatures, Phys. Rev., 1960, 119, 507.
41. M. Saleemi, M. S. Toprak, S. Li and M. Johnsson, Muhammed M. Synthesis, processing, and thermoelectric properties of bulk nanostructured bismuth telluride (Bi2Te3), J. Mater. Chem., 2012, 22(2), 725–730.
42. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki and A. Charoenphakdee, et al., Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States, Science, 2008, 321, 554–557.
43. B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich and B. Yu, et al., High-Thermoelectric Performance of Nanostructured Bismuth Antimony Telluride Bulk Alloys, Science, 2008, 320, 634–638.
44. S. Ballikaya, H. Chi, J. R. Salvador and C. Uher, Thermoelectric properties of Ag-doped Cu₂Se and Cu₂Te, J. Mater. Chem. A, 2013, 1, 12478–12484.
45. K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck and C. Uher, et al., Cubic AgPbmSbTe2+m: Bulk Thermoelectric Materials with High Figure of Merit, Science, 2004, 303(5659), 818–821.
46. G. V. Chester and A. Thellung, The Law of Wiedemann and Franz, Proc. Phys. Soc., 1961, 77, 1005.
47. Y. Pei, A. D. Lalonde, H. Wang and G. J. Snyder, Low effective mass leading to high thermoelectric performance, Energy Environ. Sci., 2012, 5, 7963–7969.
48. H. Matsumoto, K. Kurosaki, H. Muta and S. Yamanaka, Thermoelectric Properties of the Thallium–Tellurium Binary Compounds, Mater. Trans., 2009, 50, 1582–1585.
49. D. R. Clarke, Materials selection guidelines for low thermal conductivity thermal barrier coatings, Surf. Coat. Technol., 2003, 163–164, 67–74.
50. D. G. Cahill, S. K. Watson and R. O. Pohl, Lower limit to the thermal conductivity of disordered crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(10), 6131–6140.
51. M. T. Agne, R. Hanus and G. J. Snyder, Minimum thermal conductivity in the context of diffuson-mediated thermal transport, Energy Environ. Sci., 2018, 11(3), 609–616.
52. B. Yu, W. Liu, S. Chen, H. Wang, H. Wang and G. Chen, et al., Thermoelectric properties of copper selenide with ordered selenium layer and disordered copper layer, Nano Energy, 2012, 1(3), 472–478.
53. P. Jafarzadeh, M. Oudah, A. Assoud, N. Farahi, E. Müller and H. Kleinke, High thermoelectric performance of Ba₃Cu_16−x(S,Te)₁₁, J. Mater. Chem. C, 2018, 6(47), 13043–13048.
54. W. Y. Zhao, C. L. Dong, P. Wei, W. Guan, L. S. Liu and P. C. Zhai, et al., Synthesis and high temperature transport properties of barium and indium double-filled skutterudites BaxInyCo4Sb12-z, J. Appl. Phys., 2007, 102(11), 113708.
55. C. Uher Skutterudites: prospective novel thermoelectrics. Semicond Semimet. 2001;69(Recent Trends in Thermoelectric Materials Research I):139–253.
56. T. He, J. Chen, H. D. Rosenfeld and M. A. Subramanian, Thermoelectric Properties of Indium-Filled Skutterudites, Chem. Mater., 2006, 18, 759–762.
57. V. L. Kuznetsov, L. A. Kuznetsova, A. E. Kaliazin and D. M. Rowe, Preparation and thermoelectric properties of A8IIB16IIIB30IV clathrate compounds, J. Appl. Phys., 2000, 87(11), 7871–7875.
58. H. Lin, G. Tan, J. N. Shen, S. Hao, L. M. Wu and N. Calta, et al., Concerted Rattling in CsAg₅Te₃ Leading to Ultralow Thermal Conductivity and High Thermoelectric Performance, Angew. Chem., Int. Ed., 2016, 55(38), 11431–11436.
59. E. S. Toberer, A. F. May and G. J. Snyder, Zintl chemistry for designing high efficiency thermoelectric materials, Chem. Mater., 2010, 22(3), 624–634.

---

Footnote

† Electronic supplementary information (ESI) available: One figure with SEM images, one figure showing the specific heat, three figures showing the stability of the materials. See DOI: 10.1039/c9tc02029b

---