Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Low thermal conductivity and promising thermoelectric performance in AxCoSb (A = V, Nb or Ta) half-Heuslers with inherent vacancies†
Daniella A.
Ferluccio
 a,
John E.
Halpin
a,
John E.
Halpin
 b,
Kathryn L.
MacIntosh
a,
Robert J.
Quinn
a,
Eric
Don
c,
Ronald I.
Smith
d,
Donald A.
MacLaren
b,
Kathryn L.
MacIntosh
a,
Robert J.
Quinn
a,
Eric
Don
c,
Ronald I.
Smith
d,
Donald A.
MacLaren
 *b and
Jan-Willem G.
Bos
*b and
Jan-Willem G.
Bos
 *a
*a
aInstitute of Chemical Sciences and Centre for Advanced Energy Storage and Recovery, School of Engineering and Physical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. E-mail: j.w.g.bos@hw.ac.uk
bSUPA, School of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, UK. E-mail: dmaclaren@physics.org
cSemiMetrics Ltd, Kings Langley WD4 9WB, UK
dISIS Neutron and Muon Source, Harwell Campus, Didcot OX11 0QX, UK
First published on 13th March 2019
Abstract
Half-Heuslers with vacancies that are stabilised by a semiconducting electron count offer new opportunities for discovering good thermoelectric performance. Here, we present a comparative study of AxCoSb half-Heuslers (A = V, Nb or Ta) with intrinsic vacancies. Structural analysis reveals an increasing vacancy concentration from V (13%) to Nb (15%) to Ta (19%) with evidence for ∼3% V/Co inversion. This decrease in ability to n-type dope these materials is caused by an increase in conduction band dispersion, evident from a decreasing density of states mass from Hall data, leading to a higher cost of populating these antibonding states. V0.87CoSb has an ultralow lattice thermal conductivity, κlat ∼ 2.2 W m−1 K−1, which cannot be explained within the Callaway framework. Coupled to a promising power factor, S2/ρ = 2.25 mW m−1 K−2, this results in ZT = 0.6 at 950 K. Nb0.85CoSb has a power factor of S2/ρ = 2.75 mW m−1 K−2 with κ ∼ 4.75 W m−1 K−1, yielding a similar ZT = 0.5 at 950 K. Ta0.81CoSb has a microstructure consisting of smaller grains than the other samples, impacting both the carrier and thermal transport, yielding a power factor S2/ρ = 0.75 mW m−1 K−2 and ZT = 0.3 at 950 K. The ultralow κlat for V0.87CoSb may be linked to porosity effects that do not strongly impact on the charge transport, thus affording a new route towards improved performance.
Introduction
Thermoelectric waste heat recovery is one of a range of renewable energy strategies that are currently being developed to reduce reliance on fossil fuels and to mitigate climate change.1,2 Half-Heuslers (HHs) are leading candidates for commercialisation due to their unique combination of good thermoelectric performance, abundance of constituent elements, good mechanical properties and thermal stability.3–5 HHs are ternary XYZ compounds typically comprising two transition metals (X and Y) and a main group element (Z) that crystallise in the cubic space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m with the electropositive X metals occupying octahedral sites and the Y metals occupying half the tetrahedral sites in a face centred cubic Z lattice.6 Recently, HH compositions with a nominal 19 valence electron count (VEC), including VCoSb and NbCoSb,7,8 have attracted attention due to their apparent violation of the long-established 18-electron requirement for semiconducting properties.6 This was resolved through studies of NbCoSb that demonstrated the formation of Nb vacancies, leading to NbxCoSb (x ∼ 0.85) compositions with VEC ∼ 18.25.9–11 Varying the nominal Nb content between x = 0.8 (VEC = 18) and x = 1 (VEC = 19) affords a systematic change in carrier concentration (nH) and a means of optimising the thermoelectric power factor, S2/ρ, where S is the Seebeck coefficient and ρ is the electrical resistivity.11 The optimised power factor of S2/ρ = 2.4 mW m−1 K−2 and low thermal conductivity (κ) resulted in a highly promising thermoelectric figure of merit, ZT = (S2/ρκ)T = 0.9 at 1123 K, demonstrating that vacancies are a new, useful route to tune the individual thermoelectric parameters and achieve good performance. Here, κ is the sum of κlat and an electronic component (κel) and T is the absolute temperature. Up to this point optimisation of HHs has been achieved chiefly via doping and alloying,12–14 use of interstitial metals15 or nanostructuring.16–19 The vacancy approach is therefore a new route in the portfolio that is not well explored.
3m with the electropositive X metals occupying octahedral sites and the Y metals occupying half the tetrahedral sites in a face centred cubic Z lattice.6 Recently, HH compositions with a nominal 19 valence electron count (VEC), including VCoSb and NbCoSb,7,8 have attracted attention due to their apparent violation of the long-established 18-electron requirement for semiconducting properties.6 This was resolved through studies of NbCoSb that demonstrated the formation of Nb vacancies, leading to NbxCoSb (x ∼ 0.85) compositions with VEC ∼ 18.25.9–11 Varying the nominal Nb content between x = 0.8 (VEC = 18) and x = 1 (VEC = 19) affords a systematic change in carrier concentration (nH) and a means of optimising the thermoelectric power factor, S2/ρ, where S is the Seebeck coefficient and ρ is the electrical resistivity.11 The optimised power factor of S2/ρ = 2.4 mW m−1 K−2 and low thermal conductivity (κ) resulted in a highly promising thermoelectric figure of merit, ZT = (S2/ρκ)T = 0.9 at 1123 K, demonstrating that vacancies are a new, useful route to tune the individual thermoelectric parameters and achieve good performance. Here, κ is the sum of κlat and an electronic component (κel) and T is the absolute temperature. Up to this point optimisation of HHs has been achieved chiefly via doping and alloying,12–14 use of interstitial metals15 or nanostructuring.16–19 The vacancy approach is therefore a new route in the portfolio that is not well explored.
We have investigated the concentration of X-site vacancies and thermoelectric properties of the AxCoSb (A = V, Nb and Ta) compositions allowing for the impact of the A metal to be assessed. A recent study has investigated the structural stability of a range of vacancy HHs.20 This revealed an increasing cost for filling the X-site from V to Nb to Ta. We confirm the existence of preferred x compositions for the V and Nb compositions and show that A = Ta fits with the proposed trend.20 The thermoelectric properties of stoichiometric VCoSb have been reported (ref. 8) but the properties of the AxCoSb (A = V, Ta) compositions with targeted vacancies remain unexplored.
Experimental
Synthesis
A preliminary series of polycrystalline A0.84CoSb (A = V, Nb and Ta) samples was prepared on a 1 gram scale from powdered elements purchased from Alfa Aesar; V: 325-mesh, 99.5% purity; Nb: 325-mesh, 99.8%; Ta: 325-mesh, 99.9%; Co: 1.6 μm, 99.8% and Sb: 1–5 mm shots, 99.99%. This was followed by a 5 gram scale-up of the optimised compositions (see below) to produce V0.87CoSb, Nb0.85CoSb and Ta0.81CoSb. The initial choice for the A0.84CoSb compositions was based on a survey of the literature for A = Nb, where 0.83 ≤ x ≤ 0.85 based on diffraction results.9,10 In all reactions, stoichiometric amounts of elemental precursors were mixed using an agate pestle and mortar and cold-pressed into 13 mm diameter pellets using a 10 tonne press. Samples were wrapped in Nb (V, Nb samples) or Ta (Ta samples) foil and sintered in vacuum sealed quartz tubes for 24 hours at 1073 K, then cooled at 20 K min−1. The samples were then re-ground, re-sealed and subjected to a further 7 days of sintering at 1123 K before being air-quenched. As a final step, the samples were powdered using mortar and pestle then hot-pressed into two 13 mm disks under an argon atmosphere at 1273 K (Nb and Ta samples) or 1123 K (V sample) and 80 MPa for 30 minutes.Characterisation
Laboratory X-ray powder diffraction (XRD) data was collected using a D8 Bruker Advance diffractometer with monochromated Cu Kα1 radiation. High-quality datasets suitable for Rietveld analysis were collected in the 5° ≤ 2θ ≤ 100° range over seven hours. Time-of-flight neutron powder diffraction (NPD) patterns were collected on the POLARIS instrument at the ISIS neutron and muon source, Rutherford Appleton Laboratory, UK. Data were collected at room temperature for between 200 and 300 μA proton beam current to the ISIS target, with 1–2 g of powdered sample loaded into cylindrical vanadium cans. This corresponds to an exposure of approximately 1.5–2 hours for each sample. Note that a different A = Nb sample was used for the NPD and Hall study, with nominal Nb0.83CoSb composition. This was due to the timings of these experiments, which were not done in-house. All other data in this manuscript were collected on the AxCoSb samples with optimised compositions. Rietveld analysis of both XRD and NPD datasets were done using the GSAS and EXPGUI software programs.21,22Microscopy
Scanning electron microscopy (SEM) employing both secondary electron (SE) and backscattered electron (BSE) imaging was performed on samples that were first cut from a hot-pressed disk with a low speed diamond saw to expose an internal face, then mechanically polished (SiC paper followed by alumina, colloidal silica and diamond paste to achieve a flat surface finish). A Thermo Fischer Helios Dualbeam instrument equipped with a Bruker XFlash 100 mm2 detector was used for energy dispersive X-ray spectroscopy (EDS) analysis of composition and a Bruker eFlash FS Electron back-scattered diffraction (EBSD) detector was used for assessment of crystallography and granularity. EDS analysis was performed using Bruker's Esprit 2.1 software package and a standard-less quantification method to derive compositions that are accurate to 2–3 atomic percent. EBSD images were processed using ATOM,23 whereby EBSD patterns were fitted to HH structures and pixels were false-coloured to indicate the crystallographic orientation, producing vivid mosaic-like images that clearly discriminate grains and which were then used to assess grain size distributions.Thermoelectric property measurements
The Seebeck coefficient (S) and electrical resistivity (ρ) were measured on rectangular bars cut from the hot-pressed disks using a Linseis LSR 3 instrument between 320–970 K. Thermal diffusivities (α) were measured on whole hot-pressed disks (∼2 mm thickness) using a Linseis LFA 1000 Laser Flash instrument. The samples were coated with graphite spray to avoid emissivity errors. The densities (d) of the samples were calculated from the dimensions and mass of the pellets and are given in Table 1. The thermal conductivity κ = αCpd was calculated using experimental α and d values, with heat capacity (Cp) values taken from the literature.8,24 A porosity correction, κm/κ = (1 − φ)/(1 + φ/2), where κm is the uncorrected measured value and ϕ is the porosity taken from the percentage density, was applied for the V sample. Hall measurements were undertaken on 5 × 5 mm2 square slices in applied fields of ±1 T using an AC Field Hall system from SemiMetrics, Ltd. Silver paint was used to achieve good electrical contacts on the corners of the samples.| Sample | x | a (Å) | d (g cm−3) | d% | EDX composition | Rietveld composition |
|---|---|---|---|---|---|---|
| a Compositions from Rietveld analysis of neutron powder diffraction data. | ||||||
| VxCoSb | 0.84 | 5.8039(1) | V0.87(1)CoSb | |||
| 0.87 | 5.8058(1) | 7.2 | 95 | 0.87(1):0.99(1):1.00 | [V0.838(2)Co0.032(2)][Co0.968(2)V0.032(2)]Sba | |
| NbxCoSb | 0.84 | 5.9024(1) | Nb0.85(1)CoSb | |||
| 0.85 | 5.9023(1) | 8.4 | 100 | 0.86(1):0.99(1):1.00 | Nb0.85(1)CoSb | |
| TaxCoSb | 0.84 | 5.8888(1) | Ta0.81(1)CoSb | |||
| 0.81 | 5.8910(1) | 10.7 | 100 | 0.89(2):1.02(1):1.00 | Ta0.83(1)CoSba | |
Results
XRD
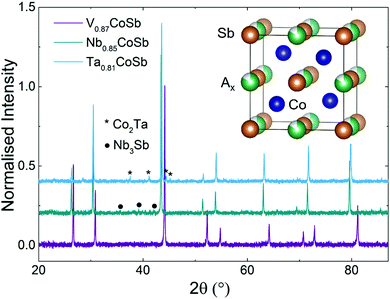
A preliminary series of A0.84CoSb (A = V, Nb, Ta) samples was prepared to check for phase purity and analysis of the crystallographic site occupancies of the HH phase through Rietveld fitting. The XRD patterns for these samples are shown in Fig. S1 in the ESI.† Rietveld analysis of the X-site occupancy suggested a systematic decrease from 0.87(1) for A = V to 0.85(1) for A = Nb and 0.81(1) for A = Ta. In response to these initial results, synthesis of V0.87CoSb, Nb0.85CoSb and Ta0.81CoSb was undertaken on a 5 gram scale so that full structural and thermoelectric characterisation could be undertaken. Rietveld analysis of XRD data collected from these samples (the patterns are shown in Fig. 1) confirmed the targeted X-site occupancies. The V and Nb samples have good purity from XRD with only a small Nb3Sb phase (<1 wt%) observed. The lattice parameter for the Nb0.85CoSb sample (a = 5.902 Å) is in good agreement with the near-constant values reported for NbxCoSb (a = 5.903 Å; 0 ≤ x ≤ 0.2).11 The Ta sample contains a 5.3(1) wt% Co2Ta intermetallic impurity.NPD
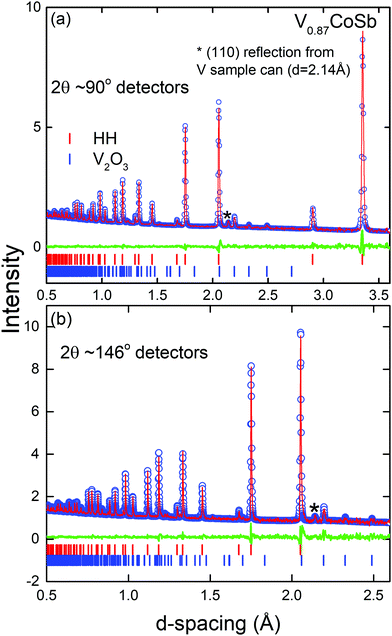
Neutron diffraction is highly complementary to XRD as it offers good scattering contrast between first row transition metals, which is important as V/Co inversion has been suggested to occur.8 The full results of the Rietveld fits are summarised in Table S1 (ESI†) with the experimental HH compositions given in Table 1. The final fits are shown in Fig. 2 (V sample) and Fig. S2 in the ESI† (Nb and Ta samples). The main result is that the V0.87CoSb sample does indeed have a degree of V/Co inversion with an experimental composition of [V0.838(2)Co0.032(2)][Co0.968(2)V0.032(2)]Sb. Free refinement of the X-site occupancy yielded an unrealistic composition of V0.58(1)CoSb, which corresponds to a 17-electron HH. HHs with this valence electron count are predicted to be metallic,6,25 which is not in keeping with the observed semiconducting behaviour. We note that this result is robust against variations in atomic displacement parameter (ADP). For example, fixing the X-site site occupancy at 0.87 leads to ADP values for that site that are unphysically large with respect to those of the other sites. The best way to reconcile the XRD and NPD fits is to assume that the overall V0.87CoSb composition from XRD is maintained and allow for V/Co inversion over the X and Y sites. This yields near identical goodness of fit statistics (see Table S1, ESI†) and indicates the presence of ∼3% V/Co inversion. Analysis of the site occupancies for the Nb and Ta samples confirms the XRD results with refined compositions of Nb0.85(1)CoSb and Ta0.83(1)CoSb that are within 1–2 estimated standard deviations of the starting values. The indexed impurity phases include a small V2O3 phase (1.1(1) wt%) that had not been noted by XRD and the Nb3Sb and Co2Ta phases that were already observed in XRD. The final fits for all samples were compared against a model-less LeBail fit and found to be close to the best possible value for all compositions (Table S1, ESI†).Scanning electron microscopy
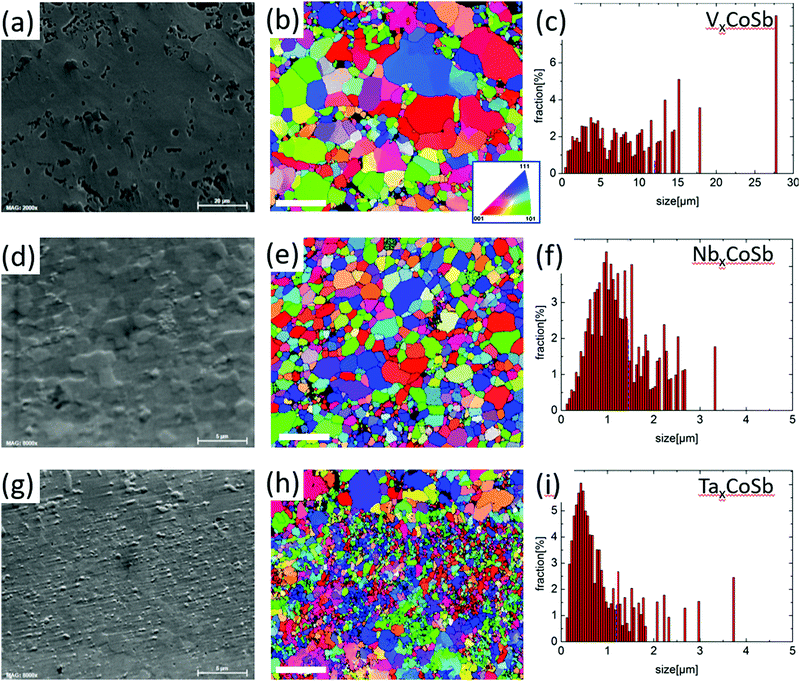
SEM imaging, EBSD and EDX mapping were used to investigate the microstructure and compositions of all three AxCoSb compositions. Large area (>200 × 200 μm2) SEM images are shown in Fig. S3 (ESI†); higher magnification images and EBSD data are presented in Fig. 3 with the EDX maps for these areas given in Fig. S4 (ESI†). Several striking trends are discernible in the SEM and EBSD data. First, the V0.87CoSb sample has notable micron-scale porosity, despite having a gravimetric density of 95%. The Nb and Ta samples by contrast appear fully dense, in keeping with the 100% gravimetric densities (Table 1). Secondly, the EBSD data show a gradual decrease of the average grain size diameter from ∼3.2 μm (V) to ∼0.80 μm (Nb) and ∼0.43 μm (Ta). This trend is in keeping with the increasing refractory nature of the A-elements. The EDS mapping reveals that all AxCoSb samples are largely phase pure HHs with no obvious variation in composition. The elemental maps for V0.87CoSb indicate fractionally more oxide formation than for the other two samples. The obtained HH compositions, averaged across all HH grains measured in the samples, are given in Table 1.Electrical properties
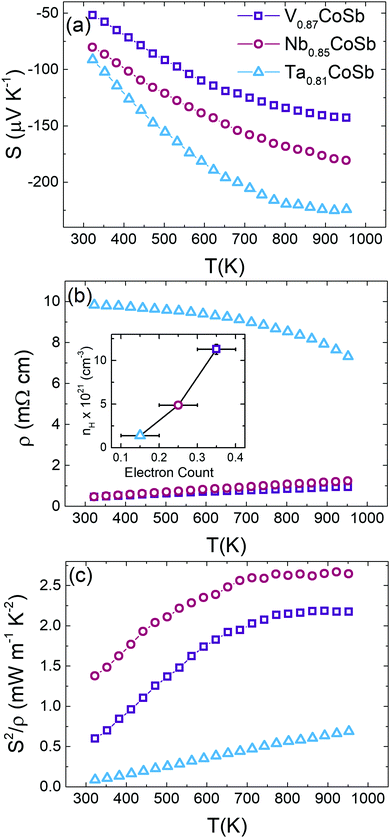
All samples exhibit negative S(T) values, indicating n-type conduction (Fig. 4a). There is a clear increase in S(T) as the A site element becomes heavier; in addition, the Ta sample has a much steeper increase. The V and Nb samples have a similar metal-like ρ(T) that increases across the temperature range whilst the Ta sample, by contrast, is much less conductive and has a gradually decreasing convex temperature dependence. This non-standard temperature dependence is not typical of either degenerate or non-degenerately doped semiconductors and is likely linked to its microstructure, consisting of many nanoscale grains. The highest power factor, S2/ρ = 2.7 mW m−1 K−2, is observed for the Nb0.85CoSb composition, while V0.87CoSb has S2/ρ = 2.2 mW m−1 K−2 (Fig. 4c). Both compositions are characterised by a S2/ρ plateau above ∼800 K (V) and ∼700 K (Nb), reflecting the saturation of S and increasing ρ. Increasing the temperature above 950 K is expected to lead to a reduction in S2/ρ. The Ta sample with its high ρ values has a S2/ρ that increases linearly from ∼0.1 mW m−1 K−2 at 323 K to a maximum ∼0.7 mW m−1 K−2 at 950 K. However, it is worth emphasising that this might not reflect its intrinsic behaviour but instead be a result of microstructure effects.Hall measurements were undertaken to gain further insight in the electrical properties of these materials. The nH, Hall mobilities (μH) and S and ρ for these samples are summarised in Table 2. Significantly, nH has a linear dependence on the nominal free electron count (VEC-18) from the Rietveld compositions (see inset to Fig. 4b), confirming the validity of our structural analysis, and the tendency for a reduced occupation of the X-site from V to Nb to Ta.20 To gain insight into possible changes in the electronic structure of these materials, Single Parabolic Band analysis was undertaken, following approaches outlined in the literature (e.g.ref. 26). This led to a significant result, namely the gradual decrease of the electronic density of states band masses from m* = 12.8me (V), to m* = 9.6me (Nb) and m* = 5.9me (Ta), demonstrating that the A-metal impacts on the electronic bandstructure. The value for the Nb sample is in good agreement with m* = 8–10me from the literature.11,27 The decrease of m* = Nv2/3mb signals either a decrease in valley degeneracy (Nv) or increasingly dispersive electronic bands (reduced mb) for the pockets that contribute the electrical transport. The more diffuse 4d and 5d orbitals for the heavier A elements are known to afford better orbital overlap and increased bandwidths, which is in keeping with the observed trend. The carrier mobility for the Nb sample is largest at μH = 4.2 cm2 V−1 s−1, which is comparable to the highest literature values.11,27 The mobility is lower for the V sample with μH = 1.2 cm2 V−1 s−1, which is partially due to its higher m* and nH but is also likely to be linked to the observed porosity. The magnitude is in keeping with reported data for nominally stoichiometric VCoSb.27 The A = Ta sample has μH = 0.3 cm2 V−1 s−1, despite its lower m* and nH, which reflects its microstructure consisting of many very small grains.
| Composition | Electron count | S (μV K−1) | ρ (mΩ cm) | n H (×1021 cm−3) | μ H (cm2 V−1 s−1) | m*(me) |
|---|---|---|---|---|---|---|
| V0.87CoSb | 0.35(5) | −53 | 0.44 | 11.3 | 1.2 | 12.8 |
| Nb0.85CoSb | 0.25(5) | −68 | 0.31 | 4.9 | 4.2 | 9.6 |
| Ta0.81CoSb | 0.15(5) | −93 | 15.3 | 1.4 | 0.3 | 5.9 |
Thermal conductivity
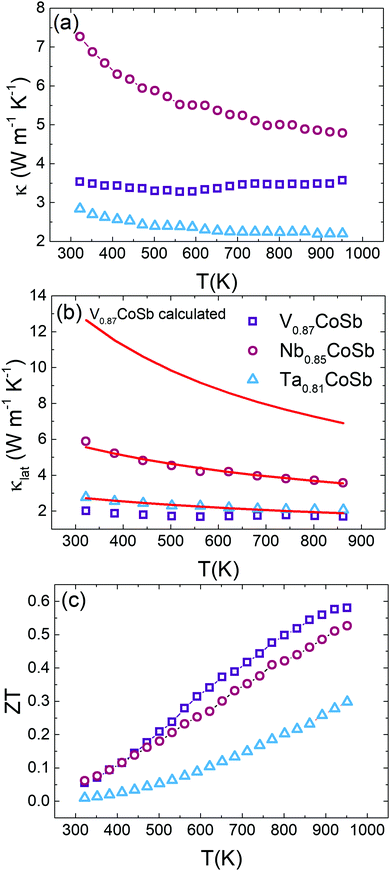
Fig. 5a shows the total thermal conductivity (κ) for all samples. The measured thermal diffusivities (α) and heat capacities (Cp) are shown in Fig. S5 (ESI†). Nb0.85CoSb has the highest κ and the value for Ta0.81CoSb is much reduced by comparison. V0.87CoSb has an unusual, nearly temperature independent, κ(T) between 323–950 K, which is not in line with the observed decreasing κ(T) trends for the Nb and Ta samples. Subtraction of κel using the Wiedemann–Franz law yields the lattice thermal conductivities (κlat) that are plotted in Fig. 5b. The temperature dependence of the Lorenz number (L) and κel are shown in Fig. S6 (ESI†). The κlat(T) values confirm the gradual decreasing temperature dependence for the Nb and Ta samples. κel ∼ 1.5 W m−1 K−1 for the V sample, leading to κlat values of 2.0 W m−1 K−1 at 323 K and 1.8 W m−1 K−1 at 950 K. These values are lower than those for Ta0.81CoSb, and around three times lower than the Nb sample. The ultralow κlat for the V sample goes against the usual dependence on average atomic mass, where lower sound velocities (vs) for heavier elements tend to favour lower κlat.To gain a better understanding of the thermal transport in these three samples, κlat(T) was modelled using the Callaway model. As a first step the Debye temperatures (θD) and vs were estimated from the average room temperature ADPs listed in Table S1 (ESI†) using the procedure from ref. 28 as followed in our earlier work.10 The resulting θD and vs for the AxCoSb samples are listed in Table 3 and follow the expected trends based on increasing average atomic mass. θD values decrease from V (279(6) K) to Nb (221(3) K) and Ta (192(2) K), signalling a softening of the lattice for the heavier A atoms. This is reflected in vs, which gradually reduces. For comparison, θD = 361(3) K for NbCoSn,10 demonstrating that the X-site vacancies lead to a softening of the lattice, as expected when removing a fraction of the chemical bonds in the structure. The low κlat of the V sample is therefore not explained by an anomalous θD or vs value, which both fit in with the behaviour of the Nb and Ta samples.
| Composition | κ lat,322K (W m−1 K−1) | θ D (K) | v s (m s−1) | Γ M | L (μm) | B U,calc (10−18 s K−1) | B U,fit (s K−1) |
|---|---|---|---|---|---|---|---|
| a The Gruneisen parameter was set to 1.0 for all three compositions. | |||||||
| V0.87CoSb | 2.0 | 270(6) | 2339(50) | 0.016 | 3.2 | 1.10 | — |
| Nb0.85CoSb | 5.9 | 221(3) | 1951(25) | 0.044 | 0.80 | 1.65 | 1.45 |
| Ta0.81CoSb | 3.0 | 192(2) | 1696(20) | 0.099 | 0.43 | 2.07 | 2.06 |
The Callaway model is based on the Debye approximation for Cp for a monoatomic cubic lattice and allows for phonon scattering from boundaries between grains, point-defects and other phonons through the Umklapp mechanism. This leads to the following expressions:29–31
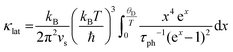 | (1) |
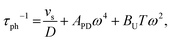 | (2) |
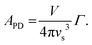 | (3) |
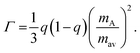 | (4) |
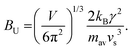 | (5) |
The magnitude of APD was calculated using eqn (3) and (4) and kept fixed through the fitting. D was estimated from the average grain size from the EBSD data and was also kept fixed. Values for the disorder parameter Γ and grain size D are given in Table 3. Starting values of BU were calculated and are compared against the fitted values in Table 3. We find that κlat(T) for the Nb and Ta samples is well described using the Callaway model (see Fig. 5b, full lines), where γ = 1 gives good agreement between predicted and experimental BU values (Table 3). The γ = 1 value is in keeping with the largely harmonic bonding in HHs. The limited temperature dependence of κlat(T) for the Ta sample is linked to the small grains (B = 0.44 μm), leading to substantial boundary scattering. Fits with B > 1 μm could not satisfactorily reproduce the data. In case of the Nb sample, a comparable fit can be obtained with BU at the calculated value and B = 1.8 μm, suggesting that boundary scattering is less important for this composition. The good agreement between experimental and calculated κlat(T) for the Nb and Ta samples, from an essentially parameter-less fit, suggests that the behaviour for “ideal” V0.87CoSb can be predicted using the Callaway model. The calculated κlat(T) for V0.87CoSb using the input parameters as listed in Table 3 (D = 3.2 μm; Γ = 0.016; BU = 1.12 × 10−18 s K−1) is shown in Fig. 5b and yields κlat values that are much greater and with a stronger temperature dependence than the experimental trends. The discrepancy between the predicted and observed values will be discussed below.
Figure of merit
The highest ZT is observed for V0.87CoSb with a maximum of 0.58 at 950 K (Fig. 5c). This value is slightly higher than ZT ∼ 0.5 at 973 K for “stoichiometric” VCoSb, which has a comparable S2/ρ = 2.5 mW m−1 K−2 but slightly larger κ = 4.4 W m−1 K−1 at 973 K.8 Nb0.85CoSb has a maximum ZT = 0.52 at 950 K, which is consistent with previous values from nominally stoichiometric NbCoSb (ref. 7 and 10) and Sn substituted samples (ZT ∼ 0.5 at 950 K for NbCoSb0.8Sn0.2);27 but is ∼33% lower than the best NbxCoSb composition with adjusted stoichiometry (ZT = 0.75 at 950 K for x = 0.82).11 This discrepancy is mostly caused by a lower κlat = 2.25 W m−1 K−1 at 950 K for those samples that were processed via levitation melting. Ta0.81CoSb reaches ZT = 0.3 at 950 K, which is limited by the high ρ values.Discussion
Structural analysis and Hall measurements both confirm the reported tendency for a reduced occupancy of the X-site from V to Nb to Ta, and thereby lower n-type carrier concentrations. We find values of x = 0.87 (V), x = 0.85 (Nb) and x = 0.81 (Ta), which were observed for both the trial series and when specifically targeted, suggesting that these are “preferred” values under the used synthesis conditions. The reduced X-site occupancy has been linked to the cost of filling antibonding conduction band states.20 Our Hall data support this with the reduced m* from V to Nb to Ta signalling an increase in band dispersion. This results in a higher cost for band filling, leading to reduced X-site occupancies. Whilst our data show that each system has a preferred vacancy concentration, this does not mean that it cannot be controlled, as has indeed been done for the NbxCoSb HHs by varying the nominal composition between 0.8 ≤ x ≤ 1.11 The reported nH suggests that the actual variation is between 0.81 ≤ x ≤ 0.87, assuming each Nb beyond x = 0.8 donates 5 electrons. This is in good agreement with the stability window (Δx ∼ 0.05 at 1073 K) reported by Anand et al.20 It is likely that the V and Ta systems have a similar stability window over which the vacancy concentration can be varied and this should be pursued to optimise ZT. Using nH to estimate the X-site occupancy, leads to x = 0.91 (V), x = 0.85 (Nb) and x = 0.81 (Ta), where the slight overestimate for the V sample may be linked to V/Co inversion.The second important result pertains to the microstructure, where both porosity and grain-size variations were discovered between samples. A gradually decreasing average grain size was observed from V to Nb to Ta, a reduction that scales with the increased melting point of the A elements and suggests that much higher sintering and consolidation temperatures are needed for the Ta sample. On the other hand, despite its largest average grain size diameter (∼3.2 μm) and 95% gravimetric density, the V sample has many micron-sized pores that reduce the connectivity of grains.
The other significant result is the unexpectedly low κlat for the V sample. Our results demonstrate a gradual decrease in θD and a softening of the lattice from V to Nb to Ta, consistent with the increased mass of the A atom and the increasing amount of chemical bonds removed from the structure. The observation of the lowest κlat for the V sample is therefore highly surprising. The κlat for the Nb and Ta samples is explained well within the Callaway framework, but this model substantially over-estimates κlat for V0.87CoSb. The two main differences compared to the other samples are the presence of V/Co inversion and the micron-scale porosity and it is tempting to speculate that one of these differences accounts for the failure of the model. The impact of V/Co disordering in terms of mass fluctuations and lattice strain is small and is not expected to explain the low κlat values. Literature on nominally stoichiometric VCoSb with similar ∼95% gravimetric densities, prepared using arc-melting, ball-milling and hot-pressing, reveals a comparable κlat = 3 W m−1 K−1.8 We therefore surmise that the observed ultralow κ is generic and linked to the microstructure of these samples. The microstructure also affects the electrical properties with a reduced μH compared to the Nb sample. However, the observed S2/ρ remain competitive and the electrical transport is therefore less affected than κlat. The surface area porosity based on analysis of Fig. 3a is ∼14%, which is much larger than the ∼5% estimated from density measurements. This pushes this material in the domain where classical porosity corrections no longer hold.33,34 To fully analyse the low κlat, multilength scale modelling considering the nature of the porosity and the phonon spectrum needs to be undertaken.
Finally, the ultralow κ for the V0.87CoSb sample is coupled to a large nH and modest μH = 1.2 cm2 V−1 s−1, enabling S2/ρ = 2.3 mW m−1 K−2 and ZT = 0.6. It may be possible to improve μH through sample processing, while the vacancy concentration could be changed to control nH and optimise ZT. The Nb sample has μH = 4.2 cm2 V−1 s−1 and S2/ρ = 2.7 mW m−1 K−2, which are amongst the largest values in the literature,11,27 demonstrating the viability of the powder-based synthesis route for the Nb samples. The performance of the Ta sample is limited by its low μH and large ρ, which is caused by the nanoscale grain sizes that also affect κlat. For the Ta system, the focus should be on increasing the average grain size, e.g. by higher temperature processing, which will afford increases in S2/ρ, whereas even for B = 5 μm, κlat increases by only ∼0.8 W m−1 K−1 at 323 K from the Callaway analysis. In case of the V system, work should focus on controlling the micron-scale porosity evident in Fig. 3a to explore to what extent it is possible to increase μH and reduce κlat.
Conclusions
To conclude, the topical AxCoSb (X = V, Nb, Ta) HHs form with different “preferred” vacancy concentrations, increasing from 13% (V) to 15% (Nb) and 19% (Ta). This is explained by the increased cost of populating antibonding conduction band states, which limits the maximum achievable n-type carrier concentration. The anomalously low κlat for V0.87CoSb was modelled using the Callaway approximation but cannot be understood within this framework, whilst the Nb and Ta compositions can. Further work is needed to understand the low κlat, which may be linked to porosity, and could offer a route to improved ZT via microstructure control. Competitive maximum figures of merit of ZT = 0.5–0.6 were observed for A = V, Nb at 950 K, whilst A = Ta has ZT = 0.3 at the same temperature, largely due to a higher electrical resistivity linked to smaller grain sizes compared to the other compositions.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The EPSRC is acknowledged for funding the research on half-Heusler thermoelectrics and instrumentation (EP/N01717X/1, EP/N017218/1 and EP/P001483/1) and for a studentship for DAF. The STFC is acknowledged for allocation of neutron scattering beamtime at the ISIS facility (RB1810470 and Xpress 1890125). Raw data upon with this publication is based can be accessed at http://dx.doi.org/10.5525/gla.researchdata.753.References
- CRC Handbook of Thermoelectrics, ed. D. M. Rowe, CRC Press, Boca Raton, 1995 Search PubMed.
- Thermoelectrics and its Energy Harvesting ed. D. M. Rowe, CRC Press, Boca Raton, 2012 Search PubMed.
- L. H. Huang, Q. Y. Zhang, B. Yuan, X. Lai, X. Yan and Z. F. Ren, Mater. Res. Bull., 2016, 76, 107–112 CrossRef CAS.
- J. W. G. Bos and R. A. Downie, J. Phys.: Condens. Matter, 2014, 26, 433201 CrossRef PubMed.
- T. J. Zhu, C. G. Fu, H. H. Xie, Y. T. Liu and X. B. Zhao, Adv. Energy Mater., 2015, 5, 1500588 CrossRef.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- L. Huang, R. He, S. Chen, H. Zhang, K. Dahal, H. Zhou, H. Wang, Q. Zhang and Z. Ren, Mater. Res. Bull., 2015, 70, 773–778 CrossRef CAS.
- H. Zhang, Y. Wang, L. Huang, S. Chen, H. Dahal, D. Wang and Z. Ren, J. Alloys Compd., 2016, 654, 321–326 CrossRef CAS.
- W. G. Zeier, S. Anand, L. Huang, R. He, H. Zhang, Z. Ren, C. Wolverton and G. J. Snyder, Chem. Mater., 2017, 29, 1210–1217 CrossRef CAS.
- D. A. Ferluccio, R. I. Smith, J. Buckman and J. W. G. Bos, Phys. Chem. Chem. Phys., 2018, 20, 3979–3987 RSC.
- K. Xia, Y. Liu, S. Anand, J. G. Snyder, J. Xin, J. Yu, X. Zhao and T. Zhu, Adv. Funct. Mater., 2018, 28, 1705845 CrossRef.
- M. Gurth, G. Rogl, V. Romaka, A. Grytsiv, E. Bauer and P. Rogl, Acta Mater., 2016, 104, 210–222 CrossRef.
- J. J. Yu, C. G. Fu, Y. T. Liu, K. Y. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. B. Zhao and T. J. Zhu, Adv. Energy Mater., 2018, 8, 1701313 CrossRef.
- L. Chen, S. Gao, X. Zeng, A. M. Dehkordi, T. M. Tritt and S. J. Poon, Appl. Phys. Lett., 2015, 107, 041902 CrossRef.
- S. A. Barczak, J. E. Halpin, J. Buckman, R. Decourt, M. Pollet, R. I. Smith, D. A. MacLaren and J. W. G. Bos, ACS Appl. Mater. Interfaces, 2018, 10, 4786–4793 CrossRef CAS PubMed.
- W. J. Xie, Y. G. Yan, S. Zhu, M. Zhou, S. Populoh, K. Galazka, S. J. Poon, A. Weidenkaff, J. He, X. F. Tang and T. M. Tritt, Acta Mater., 2013, 61, 2087–2094 CrossRef CAS.
- J. Makongo, D. Misra, X. Zhou, A. Pant, M. Shabetai, X. Su, C. Uher, K. Stokes and P. Poudeu, J. Am. Chem. Soc., 2011, 133, 18843–18852 CrossRef CAS PubMed.
- R. A. Downie, R. I. Smith, D. A. MacLaren and J. W. G. Bos, Chem. Mater., 2015, 27, 2449–2459 CrossRef CAS.
- X. A. Yan, G. Joshi, W. S. Liu, Y. C. Lan, H. Wang, S. Lee, J. W. Simonson, S. J. Poon, T. M. Tritt, G. Chen and Z. F. Ren, Nano Lett., 2011, 11, 556–560 CrossRef CAS PubMed.
- S. Anand, K. Xia, T. Zhu, C. Wolverton and J. G. Snyder, Adv. Energy Mater., 2018, 1801409 CrossRef.
- B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report LAUR, 2000, pp. 86–748 Search PubMed.
- B. Beausir and J.-J. Fundenberger, ATOM - Analysis Tools for Orientation Maps, Université de Lorraine – Metz, 2015, http://atom-software.eu, software package Search PubMed.
- R. He, L. H. Huang, Y. M. Wang, G. Samsonidze, B. Kozinsky, Q. Y. Zhang and Z. F. Ren, APL Mater., 2016, 4, 104804 CrossRef.
- S. Anand, K. Xia, V. I. Hegde, U. Aydemir, V. Kocevski, T. Zhu, C. Wolverton and J. G. Snyder, Energy Environ. Sci., 2018, 11, 1480–1488 RSC.
- H. H. Xie, H. Wang, Y. Z. Pei, C. G. Fu, X. H. Liu, G. J. Snyder, X. B. Zhao and T. J. Zhu, Adv. Funct. Mater., 2013, 23, 5123–5130 CrossRef CAS.
- L. Huang, Q. Zhang, Y. Wang, R. He, J. Shuai, J. Zhang, C. Wang and Z. Ren, Phys. Chem. Chem. Phys., 2017, 19, 25683–25690 RSC.
- B. C. Sales, B. C. Chakoumakos, D. Mandrus and J. W. Sharp, J. Solid State Chem., 1999, 146, 528–532 CrossRef CAS.
- J. Callaway, Phys. Rev., 1959, 113, 1046–1051 CrossRef CAS.
- A. Petersen, S. Bhattacharya, T. M. Tritt and S. J. Poon, J. Appl. Phys., 2015, 117, 035706 CrossRef.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- J. Yang, G. Meisner and L. Chen, Appl. Phys. Lett., 2004, 85, 1140–1142 CrossRef CAS.
- R. H. Tarkhanyan and D. G. Niarchos, Int. J. Therm. Sci., 2013, 67, 107–112 CrossRef.
- R. H. Tarkhanyan and D. G. Niarchos, APL Mater., 2014, 2, 076107 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Structural parameters and fit statistics from Rietveld analysis of polaris neutron powder diffraction data; XRD data for the preliminary series of samples, Rietveld fits to polaris NPD data for the AxCoSb (A = Nb, Ta) samples; complementary larger area SEM images and EDX elemental maps; temperature dependence of the thermal diffusivity, heat capacity, Lorenz number and electronic thermal conductivity. See DOI: 10.1039/c9tc00743a |
| This journal is © The Royal Society of Chemistry 2019 |