Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Additively manufactured porous metallic biomaterials
Amir A.
Zadpoor

Department of Biomechanical Engineering, Faculty of Mechanical, Maritime, and Materials Engineering, Delft University of Technology (TU Delft), Mekelweg 2, 2628 CD, Delft, The Netherlands. E-mail: a.a.zadpoor@tudelft.nl
First published on 13th May 2019
Abstract
Additively manufactured (AM, =3D printed) porous metallic biomaterials with topologically ordered unit cells have created a lot of excitement and are currently receiving a lot of attention given their great potential for improving bone tissue regeneration and preventing implant-associated infections. This paper presents an overview of the various aspects of design, manufacturing, and bio-functionalization of these materials from a “designer material” viewpoint and discusses how rational design principles could be used to topologically design the underlying lattice structures in such a way that the desired properties including mechanical properties, fatigue behavior, mass transport properties (e.g., permeability, diffusivity), surface area, and geometrical features affecting the rate of tissue regeneration (e.g., surface curvature) are simultaneously optimized. We discuss the different types of topological design including those based on beam-based unit cells, sheet-based unit cells (e.g., triply periodic minimal surfaces), and functional gradients. We also highlight the use of topology optimization algorithms for the rational design of AM porous biomaterials. The topology–property relationships for all of the above-mentioned types of properties are presented as well followed by a discussion of the applicable AM techniques and the pros and cons of different types of base materials (i.e., bioinert and biodegradable metals). Finally, we discuss how the huge (internal) surfaces of AM porous biomaterials and their pore space could be used respectively for surface bio-functionalization and accommodation of drug delivery vehicles so as to enhance their bone tissue regeneration performance and minimize the risk of implant-associated infections. We conclude with a general discussion and by suggesting some possible areas for future research.
1. Introduction
During the last decade, additive manufacturing (AM, =3D printing) has evolved from a mere prototyping technique to a full-fledge fabrication technique capable of producing functional parts from a variety of materials including metals,1–4 polymers,5–11 and ceramics.12–16 AM has multiple advantages to offer for fabrication of medical devices of which two stand out, namely “batch-size-indifference” and “complexity-for-free”.17 While batch-size-indifference directly translates to the feasibility of producing patient-specific biomaterials, implants, and surgical instruments18–22 that exactly match the complex and highly variable anatomy23 of individual patients, complexity-for-free enables designers to use complex geometries that give rise to favorable properties and advanced functionalities.24–29One particularly useful class of geometrically complex biomaterials is the class of topologically ordered porous biomaterials that are designed by repeating one or more regular unit cells in different spatial directions to create a lattice (cellular) structure (Fig. 1). The type and dimensions of the unit cell determine the mechanical,30–34 mass transport (e.g., permeability, diffusivity),35–38 and biological (e.g., rate of tissue regeneration)39–41 properties of AM porous biomaterials.
In this paper, we review the various aspects of topologically ordered AM porous metallic biomaterials particularly those aimed for application in orthopaedic surgery as temporary or permanent bone substitutes (Fig. 1). As opposed to solid metallic biomaterials that are up to 10–15 times stiffer than bone, the elastic modulus of AM porous biomaterials could be adjusted to mimic those of trabecular or cortical bone.35,42,43 Moreover, the topological order and precise control over the fabricated topology ensures a fully interconnected pore space that could enhance integration of the implant in the host bony tissue (osseointegration) and improve bone tissue regeneration performance in the case of temporary bone substitutes. This improved performance is partially due to the increased oxygenation and nutrition of the cells migrating to the inner pore space. In addition, the volume-porous nature of these materials tremendously increases the surface area by up to several orders of magnitude. This increased surface area could then be used for bio-functionalization of biomaterials using either biochemical (e.g., pharmaceutics) or physical (e.g., nanopatterns) means. Finally, the large pore space in highly porous AM metallic biomaterials could be used for accommodation of drug delivery vehicles.44,45
Throughout this review, we will particularly focus on a few major challenges facing orthopaedic surgeons including inadequate bony ingrowth and osseointegration and lack of full regeneration in critical size (segmental) bony defects on the one hand and implant-associated infections on the other. We then discuss how the above-mentioned features of AM porous metallic biomaterials could be used to address both above-mentioned challenges.
Given the fact that the small-scale topological design of AM porous biomaterials determines their large-scale properties, we will start by reviewing the topological design approaches and topology–property relationships. Then, various AM techniques will be briefly discussed followed by a discussion of the effects of material choice on the properties of the resulting materials. We will then discuss the different ways in which surface bio-functionalization approaches as well as drug delivery from the pore space could be used for improving bone tissue regeneration performance and preventing implant-associated infections. We conclude by presenting a general discussion of the current state of technological developments in this active area of research and making some recommendations for future research.
2. Rational topological design of AM porous biomaterials
“Rational design” is an emerging theme in materials science,46–48 where mechanics and physics theories, computational models, analytical solutions, and physical reasoning are used to devise the (topological) design of a material particularly at the “small-scale”. As opposed to other design approaches such as “creative” or “explorative” design processes, the designs originating from such sound methodological approaches are guaranteed to meet the design objective, as long as the underlying methodologies are properly selected and applied. However, the topological designs resulting from rational design approaches may be highly complex and infeasible to fabricate using conventional techniques, which is why the use of AM is required in practically all cases. Fabrication of topologically ordered lattice structures is one of the areas where AM is the only feasible option and where rational design approaches could play an important role in topological design of the materials. It is important to realize that the type and dimensions of the unit cell do not need to remain the same throughout the entire implant, as graded designs could offer additional freedom in meeting the design objectives particularly when one is trying to meet competing objectives. For example, the competing needs for highly porous designs to allow for bony ingrowth and sturdy designs to provide enough mechanical support could be both met by positioning higher porosity unit cells in the regions close to the boundaries of the implant where bony ingrowth is the most important factor while gradually decreasing the porosity towards the internal parts of the implant to provide a solid core that is capable of carrying the applied musculoskeletal loads.49 Many research groups are therefore studying the properties of graded designs and their potential in meeting competing design requirements.24,50–59Regardless of the type of design used, one of the first questions that we need to answer is “what are the design requirements that AM porous biomaterials used as temporary or permanent bone substitutes need to satisfy?” Once the design objectives are well defined, a host of analytical and computational techniques could be used to solve the inverse problem of finding the topological designs that best satisfy the design objectives. There is therefore a need for predictive models that establish the “topology–property relationship” and an optimization procedure that uses the “topology–property relationship” to determine the topological design that satisfies the design requirements. The topology–property relationships may be established using either analytical60–65 or computational models.37,50,66–69
2.1. Unit cell design paradigms: beam-based vs. sheet-based
Several topological design approaches have been used in the literature to establish the topology–property relationships for specific classes of AM porous biomaterials. Generally speaking, two general types of repeating unit cells have used for the design of porous biomaterials, namely beam-based (Fig. 2) and sheet-based (Fig. 3) unit cells.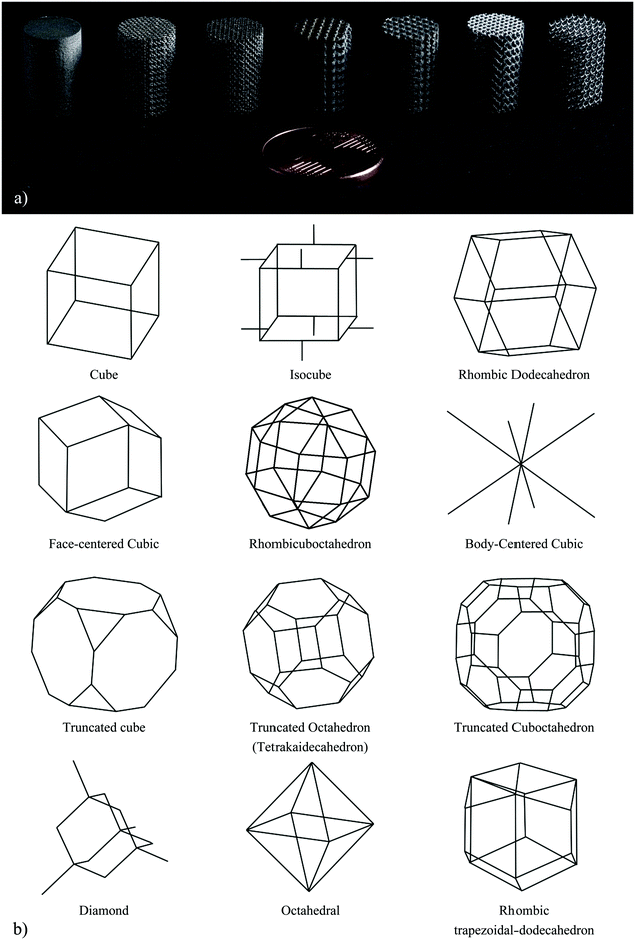 | ||
| Fig. 2 A number of cylindrical specimens designed using different types of beam-based unit cells as well as a solid specimen (reprinted from ref. 101 with permission from Elsevier) (a). The beam-based unit cells could be very different in geometry but are usually some type of polyhedron. Subfigure (b) presents a number of such unit cells particularly the ones for which analytical solutions regarding their elastic properties are available. | ||
 | ||
| Fig. 3 Topological design based on four different types of TPMS (reprinted from ref. 35 with permission from Elsevier) (a) and actual specimens fabricated using those topological designs (reprinted from ref. 35 with permission from Elsevier) (b). A catalogue of different types of minimal surfaces (c). The images were created using the program Surface Evolver.282 | ||
Beam-based unit cells are usually polyhedra whose edges are made from structural elements with relatively large (i.e., ≫1) length to diameter ratios that could carry both bending and axial loads. When only one type of unit cell is used in the design of the porous structure, the unit cell should be able to fully fill the space when repeated in different directions. Such polyhedra are called “space-filling” or “plesiohedron”70,71 and are capable of tessellating the three-dimensional space. From the five platonic solids, only cube is space-filling.71 Among all convex regular polyhdera, there are only four additional space-filling unit cells including triangular prism, hexagonal prism, truncated octahedron, and gyrobifastigium.71–74 However, a number of other convex regular polyhedra could tessellate the space in combination with each other,71 meaning that more than one type of unit cell should be used in the design of the porous structure. Furthermore, a number of slightly less regular unit cells such as rhombic dodecahedron (Fig. 2) are also space-filling (note: regular dodecahedron is not space-filling). Many irregular polyhedra could be designed to be space-filling as well and are often used in the design of AM porous biomaterials. The vast majority of the studies published to date have used beam-based unit cells in the design of their porous structures.
The dimeters of the beam-like elements making up the unit cell are usually assumed to be constant. However, interesting properties such as fluid-like mechanical behavior (i.e., negligible shear resistance and near-incompressibility) or decoupling of the mechanical properties from the relative density could be achieved with carefully designed variations in the shape of the cross-sections of the beam-like elements (e.g., in pentamode metamaterials).75 AM of such type of lattice structures is, however, extremely challenging.
In powder bead fusion AM processes, the different beams constituting the unit cell make different angles with respect to the powder bed. It is known that the build qualities of the beams with different angles with respect to the powder bed is not equal with a higher angle resulting in a higher build quality.76 Horizontal struts are therefore usually of the lowest quality while vertical struts are the easiest ones to fabricate.
Another category of structural elements that could be used for the topological design of AM porous biomaterials is the category of sheet-based unit cells. One advantage of sheet-based designs is that they generally present superior mechanical properties (e.g., fatigue strength) as compared to beam-based designs.35,36 Moreover, the curvature of sheet-based geometries is better defined as compared to beam-based geometries. This is an important point given the fact that surface curvature is a crucial parameter affecting the tissue regeneration performance of AM porous biomaterials (Section 3.4). In the case of biomaterials used for tissue regeneration purposes, the pore space should be fully interconnected to allow for cell nutrition and oxygenation. A relatively small fraction of sheet-based designs satisfies this requirement. Among those, the unit cells based on triply periodic minimal surfaces (TPMS) (Fig. 3) have received increasing attention due to their curvature properties (Section 3.4). There are many types of minimal surfaces that have been studied since several decades ago in certain sub-disciplines of mathematics including differential geometry and computational geometry (Fig. 3c).77–79 However, a relatively small number of minimal surfaces including the gyroid, Schwartz P (primitive), Schwartz D (diamond), and Schoen's I-WP have received the most attention (Fig. 3a and b).35,36,80
While, in principle, it is also possible to combine beam-based designs with sheet-based designs, not much research has been performed in that direction and most AM porous biomaterials studied to date belong to one of the above-mentioned categories.
The other important type of variation in unit cell design is spatially varying the type or the dimensions of the repeating unit cell so as to obtain different properties at different regions of the implant, thereby satisfying competing design requirements or creating new advanced functionalities. These types of designs are called “gradient structures” or “(functionally) graded structures”. The change in the type or dimensions of the unit cell along specific spatial directions is in many (but not all) cases gradual. Among other reasons, a gradual change in the topological design minimizes the stress concentrations caused by sudden geometrical changes.
There are many ways to change the type and dimensions of the unit cell. The easiest way is to keep the type and size of the unit cell constant and only change the diameter of the beam-like elements or the thickness of the sheet-like elements. This allows for creating a gradient in the porosity or pore size of the porous structure through a procedure that is straightforward to implement in design software. Indeed, most software packages available for the design of lattice structures only allow for this type of graded designs. The direction of the change could be either axial or radial (Fig. 4a). The next step in designing complex graded structures is to change the size of the unit cell as well. More complex algorithms are needed for implementing this type of graded designs, as transition from one size of the repeating unit cell to another size is not always possible (certain geometrical constraints need to be satisfied depending on the topology of the unit cell). Two examples in which the sizes of the unit cells are changing in axial and diagonal directions are presented in Fig. 4b. Finally, the most difficult design problem to automate would be to change the type of the repeating unit cell. This is a particularly difficult design problem, as interfacing different types of unit cells is neither straightforward or even generally possible without adding additional interfacing artifacts. This type of designs is relatively rare in the literature (e.g., Fig. 4c) but could be very interesting, as they allow for completely different types of behavior in different locations. For example, a conventional porous structure (i.e., a porous structure with a positive Poisson's ratio) could be combined with an auxetic porous structure (i.e., a porous structure with a negative Poisson's ratio) to improve bone-implant contact and, thus, implant longevity.47 Such changes in the type of the unit cells are usually designed manually and with careful consideration of the constraints imposed by the geometries of the different types of unit cells.
 | ||
| Fig. 4 Different approaches to the design of functionally graded AM porous biomaterials. In the first approach, only the diameter of the struts is changed and the size and type of the unit are kept constant (reprinted from ref. 283 with permission from Elsevier) (a). In the second approach (reprinted by permission from Springer22) (b), the size of the unit cell changes either axially (left) or radially (right) but the type of the unit cell is kept constant. In the third approach47 (c), the type of the unit cell is changed from auxetic (i.e., negative Poisson's ratio) to a convectional (i.e., positive Poisson's ratio) (c). | ||
2.2. Topology optimization
Topology optimization is a systematic way for the rational design of AM porous biomaterials. In this approach, the topological design is optimized in such a way that an objective function is minimized. Traditionally, the objective function used in topology optimization has often been the compliance of the structure. Minimizing the compliance of a structure equals maximizing its stiffness and, thus, load bearing capability. In the case of orthopaedic implants made from metals, maximizing the stiffness is usually not the best approach,49 as the metal itself is already much stiffer than the surrounding bone, leading to the stress shielding phenomenon. One way of formulating the design problem would be to keep the compliance as the objective function but restrict the material budget such that the local density cannot exceed certain pre-determined values. The stiffness of a lattice structure is related to its relative density through a power law relationship.81–84 Limiting the maximum relative density limits the maximum stiffness of the lattice structure to certain limits (i.e., Hashin–Shtrikman limit85). However, such a formulation is not guaranteed to result in the least amount of stress shielding. The least amount of stress shielding is achieved when the change in the stress distribution of the bone before and after implantation is minimized. The optimization problem could therefore be formulated such that the difference between the pre- and post-operative conditions is minimized. However, such a problem does not easily lend itself to a lean implementation in terms of topology optimization algorithms, as it is highly dependent on patient-specific aspects including such as bone shape and musculoskeletal loading as well as the specific design of the implant geometry. Moreover, minimizing the stress shielding is not the only important criterion in the topological design of AM porous biomaterials. Other important criteria such as adjusting the fatigue behavior, mass transport properties, and geometrical cues for tissue regeneration (e.g., curvature) should be considered as well. Simultaneous consideration of all important design criteria requires a multi-physics computational model to establish the topology–property relationships and a multi-objective optimization scheme to satisfy the different requirements that are at times competing with each other. New topology optimization algorithms or alternative approaches may therefore be needed. In addition, the design freedom is limited even in the case of AM, as not every topological design can be printed without the need for elaborate and difficult-to-remove support structures. One may therefore need to implement those manufacturability constraints in the optimization algorithms to make sure the overall shape of the implants and the small-scale design of porous biomaterials can be feasibly manufactured using the currently available techniques and materials. Finally, manufacturing imperfections will cause the actual topology of the implant and the porous biomaterial to deviate from the designed topology both at the micro-scale (due to micro-scale manufacturing imperfections) and, if not properly compensated for during the production stage, at the macro-scale. The rational design approach should take such real-world deviations of the topological design into account when optimizing the design. For example, stochastic finite element models that model the presence of manufacturing imperfections through random processes could be used to obtain better predictions of the properties of the actual material. Several studies (e.g., ref. 86) have shown that considering the manufacturing imperfections help computational models provide more accurate predictions of topology–property relationships.49Similar to what was discussed before (Section 2.1) regarding the interfacing of different types of unit cells in gradient designs, the compatibility of the unit cells resulting from topology optimization algorithms needs to be respected as well. One way of ensuring the computability of neighboring unit cells is to enforce certain geometrical constraints.87 However, there is no guarantee that such a constraint will be optimal from the viewpoint of load transfer. Recently, an algorithm has been proposed that guarantees the optimal interfacing of different unit cells, as the computability conditions is directly implemented in the topology optimization scheme.87 The resulting unit cell connections (Fig. 5a) are therefore also optimal for load transfer and could be used to design and AM functionally graded implants (Fig. 5b and c).87 During the last few years, there has been a surge of interest in the application of different variations of (topology) optimization algorithms to AM in general and to the problem of designing optimal lattice structures in particular.27,28,88–97 As a result of this fundamental research, it is expected that optimal solutions and more mature algorithms will emerge in the near future that could be also benefit the topological design of AM porous biomaterials.
 | ||
| Fig. 5 Topology optimization of lattice structures while respecting the compatibility between neighboring unit cells (a). This approach can be used to design (b) and AM (c) orthopaedic implants with functional gradients (reprinted from ref. 87 with permission from Elsevier). | ||
3. Topology–property relationships
Given the fact that small-scale topological design determines many properties of AM porous biomaterials at the macro-scale, it is important to review the currently available evidence on how topological design and different types of properties are related to each other. Each of the following sub-sections of the current section therefore review a specific type of topology–property relationship.3.1. Relationship between topological design and quasi-static mechanical properties
The relationship between topological design of AM porous biomaterials and their quasi-static mechanical properties have been widely studied in the literature using analytical, computational, and experimental techniques. That is partially due to the fact that such lattice structures are also of value in other domains such as the design of lightweight structures in the aircraft and automotive industries. A number of dedicated review papers have also appeared recently.49,98 We will therefore limit our discussion to a brief description of the most important conclusions.The mechanical properties of porous biomaterials generally decrease as the porosity of the lattice structure increases. In general, there is a power law relationship between the relative density of a porous structure and its elastic modulus (Fig. 6a and b).81–84 The coefficients of the power law are strongly dependent on the topological design of the unit cell.99–102 An important distinction is often made between bending-dominated and stretch-dominated unit cells.82,103–106 For the same value of the relative density, stretch-dominated lattice structures exhibit a much higher stiffness as compared to bending-dominated ones. There is a relatively simple way to determine whether a beam-based unit cell is bending-dominated or stretch-dominated. A unit cell is bending dominated, if the Maxewell's metric, M, defined as M = b − 3j + 6 (in two dimensions: M = b − 2j + 3) is negative.82 Otherwise, the unit cell is bending-dominated. In this definition, b is the number of beams (struts) and j is the number of joints (i.e., strut junctions). Bending-dominated unit cells could be modified to become stretch-dominated by increasing the number of struts making up the unit cell.
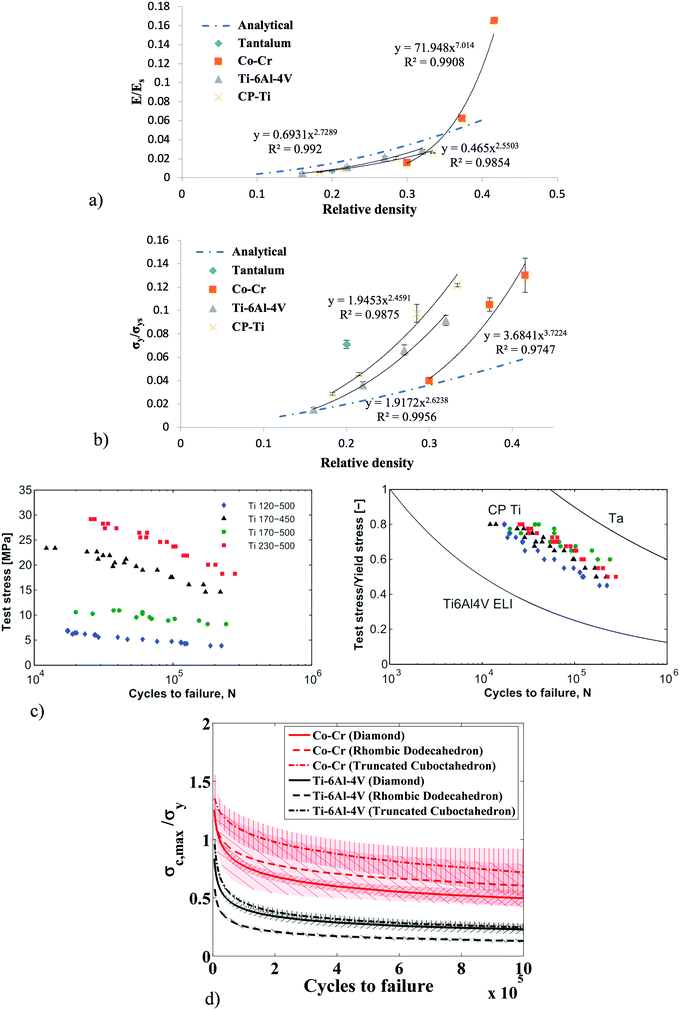 | ||
| Fig. 6 The normalized elastic modulus (a) and yield stress (b) of different AM porous biomaterials made from different types of materials and based on the rhombic dodecahedron unit cell (reprinted from ref. 31 with permission from Elsevier). The absolute S–N curves of AM porous titanium (commercially pure) and its comparison in the normalized format with those of tantalum and a titanium alloy (Ti–6Al–4V) (reprinted from ref. 183 with permission from Elsevier) (c). A comparison between the normalized S–N curves of Co–Cr and Ti–6Al–4V with different types of unit cells (reprinted from ref. 30 with permission from Elsevier) (d). | ||
Most unit cells based on space-filling polyhdera tend to be bending-dominated.82 However, this is not necessarily a major problem in the case of AM porous metallic biomaterials, as one usually tries to lower the stiffness of the bulk metal to the levels comparable to those of the human bone.49 Multiple studies have shown that with proper choice of topological design, porous metallic biomaterials with mechanical properties in the range of those observed for trabecular and cortical bone could be manufactured even when the mechanical properties of the bulk material from which the porous structure is made (e.g., Ti–6Al–4V107) are several orders of magnitude higher than those of the human bone.
It is well established that topological imperfections caused by the AM process could substantially affect the mechanical behavior of the resulting porous structures,86,108 which is why it is important to consider those imperfections when trying to establish topology-elastic modulus and topology-yield stress relationships using computational or analytical models. In general, using idealized topologies (i.e., neglecting the manufacturing imperfections) results in an overestimation of the actual mechanical properties of lattice structures.86
3.2. Relationship between topological design and fatigue behavior
Topological design strongly affects the fatigue life of AM porous biomaterials too. Similar to the case of the elastic modulus and yield stress, a higher porosity results in a lower value of the absolute stress corresponding to the same number of cycles to failure.30,33,34 The S–N curves are otherwise similar to continuous materials with a power-law nature (Fig. 6c and d).59,109–115 It is customary to normalize the level of stress to the yield (or plateau) stress of the porous structure and calculate the so-called normalized S–N curve (Fig. 6c and d).30,33,34 The normalized S–N curves of porous biomaterials with different porosities but the same type of unit cell and base material are generally quite close to each other, although the level of differences is dependent on the type of the unit cell.30,33,34 This is an important conclusion, as it implies that there is no need for separate measurement of the S–N curve corresponding to each porosity.The S–N curves of AM porous metallic biomaterials can be measured in compression–compression, compression–tension, or tension–tension. Given the intended use of these materials as bone substitutes and orthopaedic implants, compression–compression is the most relevant mode of loading, which is why the majority of the studies on the fatigue behavior of AM porous metallic biomaterials use this loading regimen. Continuous materials rarely fail under compression–compression cyclic loading, as purely compressive stresses cause crack closure and arrest further propagation of the initiated cracks. In the case of porous biomaterials, the architected nature of the porous structures means that even when the macro-scale stresses are purely compressive, tensile stresses could develop at the level of individual struts and at strut junctions. Whether or not tensile stresses develop in individual struts and the magnitude of the tensile stresses determine the compressive fatigue life of AM porous metallic biomaterials. For example, the struts of an ideal cubic unit cell do not experience any tensile stresses as long as the porous structure is loaded along its orthogonal directions. In accordance with this theoretical prediction, experimental observations have shown that the compression–compression fatigue life of AM lattice structures based on the cubic unit cell is infinite even for applied stresses amounting to 80% of their yield stress.33 Moreover, the normalized compression–compression S–N curves of porous structures based on different types of unit cells could be very different from each other.30,33 It is worth mentioning that, in addition to topological design, the type of the material from which the porous structure is made could affect the normalized S–N curves to a great extent. For example, porous structures made from a Co–Cr alloy showed much higher fatigue lives as compared to those made from the titanium alloy Ti–6Al–4V.30 As an indication, lattice structures based on beam-based unit cells show a fatigue strength of 20–30% of their yield stress in the case of Ti–6Al–4V but that could increase to 60% of the yield stress when Co–Cr is used.30 Finally, there is growing evidence indicating that sheet-based unit cells particularly those based on TPMS result in fatigue strengths that are 2–3 times higher than those achieved through beam-based unit cells (for the same base material).35
Despite a growing interest in the fatigue behavior of AM porous biomaterials including some studies that try to shed light on the mechanisms of fatigue crack propagation,116,117 the exact mechanisms relating the topological design and the effects of the AM process to crack propagation at the microscale and the S–N curves at the macroscale remain largely elusive. More systematic research is therefore required to better understand the mechanistic aspects.
3.3. Relationship between topological design and mass transport properties
Permeability and diffusivity are two important parameters describing the mass transport through porous biomaterials.118 While the permeability coefficient relates pressure gradient to mass flux (Darcy's law), diffusivity establishes the same kind of relationship between diffusion flux and the concentration gradient (Fick's first law). The ease of mass transport determines how easy it is for the cells residing in the inner space of the porous structures to be oxygenated and nurtured and how easy it is for the metabolic byproducts to be carried away. Permeability and diffusivity are therefore some of the most important parameters strongly influencing the bone regeneration performance of AM porous metallic biomaterials. Topological design determines the permeability and diffusivity of a porous structures. That includes not only the porosity and pore size but also the exact geometry of the pores.35,38 It is clear that both permeability and diffusivity increase with porosity. However, the relationship between the type of the unit cell (pore shape) and mass transport coefficients is less straightforward to predict. Computational modeling and experimental measurements should therefore be used to determine the topology–property relationships in the case of permeability and diffusivity. The design objective is usually taken to be mimicking the mass transport properties of the native bone. However, the mass transport coefficients of bone vary within wide ranges.35 Some studies have shown the permeability of various designs of AM porous biomaterials to be within the range of values reported for the human bone.35 With that said, there is no reason to believe that the mass transport properties in a highly vascularized tissue such as bone is a good indication for the mass transport properties required during the initial stages of bone regeneration where blood vessels have not yet formed and the entire mass transport should happen through diffusion or as a result of local pressure differences. Detailed data regarding the topological design requirements to achieve the best values of permeability and diffusivity coefficients and to optimize the bone tissue regeneration performance of AM porous biomaterials is still lacking and requires further research.3.4. Relationship between topological design and bone tissue regeneration performance
The fact that the topological design of porous structures influences their bone regeneration performance is obvious at least in an indirect way. That is because, as previously discussed, topological design influences the other properties of porous structures including mechanical properties and mass transport properties. It is well established that bone regeneration is dependent on the mechanical stimulus received by the cells (the Wolff's law).119–121 A change in the mechanical properties of a scaffold could change the local distribution of stresses and strains. This will influence the amount and pattern of the regenerated bone.122–125 Moreover, a change in the mechanical properties of a bone substitute could lead to modifications in the amount of mechanical load transferred through the implant. For example, it has been shown that the use of a more stiff implant in a segmental bone defect animal model could result in a higher portion of the load going through the implant instead of the fixation plate.126 Similarly, topological design influences the mass transport in the scaffold and, thus, cell oxygenation, cell nutrition, and, ultimately, cell proliferation and differentiation.41,127 Therefore, some of the parameters characterizing the topological design such as pore size and their relationships with the bone regeneration performance of porous scaffolds have been extensively studied in the literature. A comprehensive review of the existing literature has, for example, found that pore sizes in the range of 300 μm to 1000 μm are optimal for bone tissue regeneration.128 More extensive summaries of such relationships could be found in dedicated review papers appearing in the recent literature.41,127A relatively recent discovery is that geometrical features could influence the tissue regeneration performance of biomaterials in their own right and independently from the changes they cause in the other properties of the scaffolds.41,129–132 In particular, surface curvature has been recently discovered to have profound effects on the cytoskeletal reorganization and stress fiber orientation of the cells and, ultimately, the rate of tissue regeneration.133–139 For example, several studies have found that a concave surface results in a much higher rate of tissue regeneration as compared to convex and planar surfaces.41,129–132 The exact mechanisms through which surface curvature and other geometrical parameters influence cell response and tissue regeneration are of high current interest and are being extensively researched.133–139 Some of those studies suggest a mechanobiological pathway in which surface curvature influences the tensile stresses experienced by the cell and the cytoskeleton,140 which then influences cell processes that regulate the rate of tissue regeneration. Given the fact that surface curvature could have important effects in terms of bone tissue regeneration performance, topological designs with well-defined surface curvatures including the ones based on sheet-like elements are particularly attractive for designing AM porous metallic biomaterials. Interestingly, TPMS geometries have been found to be similar to trabecular bone in terms of their mean surface curvature, which is zero by definition in the case of TPMS and has been found to be close to zero in the case of trabecular bone.141,142 This further highlights the importance of TPMS as promising geometries for the design of AM porous biomaterials. A better understanding of how curvature regulates tissue regeneration could guide topological design approaches such that the bone tissue regeneration performance of AM porous biomaterials is enhanced. This could, for example, be done by identifying the (sheet-based) unit cells that could best harness the advantages of curvature-regulated cellular processes.
3.5. Relationship between topological design and implant-associated infections
There are some possible relationships between topological design and the risk of infection as well as the efficacy of the techniques used for preventing infections. There are two major mechanisms at play both of which are a result of the much larger surface areas of AM volume-porous biomaterials as compared to an equally-sized (and equally-shaped) solid material. The exact value of the surface to volume ratio is dependent on the type of the unit cell but could be up to several orders of magnitude higher in the case of AM porous biomaterials as compared to solid specimens. As a consequence of this increased surface area and the presence of difficult-to-reach internal surfaces, sterilization of the implants made from AM porous biomaterials is more challenging. The number of bacteria surviving the sterilization process or reaching the (internal) surfaces pre-operatively may therefore increase. There is, however, no clear evidence of an increased risk of implant-associated infections in the case of volume-porous biomaterials as compared to solid implants. For one specific type of porous implants (not AM) for which extensive clinical data is available, namely trabecular metal, a few studies suggest even a lower risk of revisions due to septic loosening (e.g., see ref. 143) while one study has found a small (statistically insignificant) increase in the risk of infections.144 Although the currently available data is inconclusive, compounded by the fact that this type of implant (i.e., trabecular metal) is often recommended for more challenging cases, it could be stated that there is no clear evidence supporting an increased risk of infection in the case of volume-porous implants as compared to the other types of implants.The other side of the coin is that the increased surface area of AM porous biomaterials could substantially improve the efficacy of the antibacterial coatings used for prevention of implant-associated infections, as there is simply a much larger surface area available to deliver the antibacterial agents or to otherwise kill (or inhibit the growth of) the bacteria. The above-mentioned mechanisms compete with each other and it is not clear a priori the effects of which mechanism is dominant. However, one in vitro study has found that, for the same type of antibacterial coating, the size of the zone of inhibition (i.e., the zone within which bacteria cannot grow) is a few times larger in the case of AM porous biomaterials as compared to a corresponding solid implant.145 This suggests that the effects of the increased surface area on the efficacy of the antibacterial coatings may be stronger than on the number of the bacteria surviving the sterilization process.
4. Additive manufacturing techniques
Metal and metallic alloys can be processed using different categories of AM methods.4,22,146,147 Three categories of AM techniques have been used most frequently in the literature. That includes direct energy deposition techniques, material extrusion techniques, and powder bed fusion techniques. In direct energy deposition, a moving nozzle ejects metallic powder, which is then sintered with the aid of the energy provided by a moving energy source (e.g., a laser beam). The material extrusion techniques applied to metals usually require mixing the metallic powder with a binder. The mix of the metallic powder and binder is then disposed from a moving nozzle to create the 3D structure. Finally, the binder is removed and the metallic part is sintered. In powder bed fusion processes, the part is built within a powder bed. An energy source is used to selectively sinter the desired areas within the powder bed that make up the final part. The energy source is usually either a laser beam or an electron beam. The process is called selective laser melting (SLM)148–152 in the case of a laser beam, while electron beam melting (EBM)4,32,59,112,115,146,153–158 refers to the processes using an electron beam. Among the three different types of AM processes mentioned above, only powder bed fusion processes are capable of fabricating complex topological designs with fine micro-architectural details, which is why powder bed fusion techniques dominate the literature on AM porous metallic biomaterials.A few important differences are noted when comparing SLM and EBM. The build plate is heated to high temperatures in EBM. This reduces the temperature gradients and the cooling rates controlling the solidification process. The thermal residual stresses therefore tend to be lower in the case of EBM as compared to SLM159 where the temperature of the build plate is much lower. Moreover, a lower cooling rate often translates to a more favorable microstructure.160,161 For example, in the case of the titanium alloy Ti–6Al–4V processed with SLM, a very brittle phase (i.e., α′) is often formed, which reduces the fatigue life of the resulting material.162
Heat treatments alone76,158,163–170 as well as in combination with high pressures (e.g., in hot isostatic pressing157,162,171) and surface treatments162 could be used to both reduce the level of the residual stresses and to improve the microstructural features of the materials processed with EBM and SLM.
On the plus side, the powder size used in SLM is usually smaller than the one used in EBM. That translates to a lower surface roughness as well as the ability to fabricate lattice structures with finer details (e.g., smaller strut thicknesses and unit cell sizes). These aspects are particularly important for realizing the complex topological designs that were discussed before. In the two following sub-sections of this section, we will discuss the practical aspects that are important in AM of porous metallic biomaterials as well as the effects of post-AM heat and surface treatments on the properties of the resulting lattice structures. In both cases, our primary focus is on PBF processes.
4.1. Practical AM aspects
Successful AM of complex lattice structures requires a proper selection of many processing parameters that are briefly discussed here. In particular, the lattice structures should be designed and positioned such that the use of support structures is minimized particularly inside the volume of the porous biomaterial. That is due to the fact that, as opposed to polymeric materials where soluble materials are used for fabricating the support structures, the vast majority of PBF processes used for metallic materials do not allow for soluble support structures. Furthermore, manual removal of support structures from within a lattice structure is very cumbersome, if not impossible.The powder bed filled with metallic powder provides certain levels of support for creating lattice structures, which is somewhat higher than the level of support available in some other AM processes (e.g., vat photopolymerization). The level of the available mechanical support may be even higher, if the powder is compacted by the wiper when a new layer of powder is deposited. However, the compaction force could damage the thin and fragile struts being built, thereby imposing a lower limit on the thickness of the struts. Regardless of the available level of mechanical support, overhangs whose angle with respect to the powder bed is below a certain threshold or whose length is above a certain threshold will require support structures. Although the exact thresholds are dependent on multiple processing parameters including the magnitude of the compaction force and the type of the material, overhangs with angles below 45° usually require support structures.
Given the importance of the angle with respect to the powder bed, it is sometimes possible to avoid the support structures simply by fabricating the lattice structure under a different angle. Regardless of what angle is used for the positioning of the lattice structure, it is important to realize that the microstructure, mechanical properties, and quality of the resulting materials are dependent on the building orientation.49,172–174 This direction-dependency makes the resulting materials highly anisotropic.49,172–174 In addition to being anisotropic, the quality of the different struts within a lattice structure is different and dependent on their angle with respect to the powder bed.76 Generally, vertical struts have a higher quality (i.e., less manufacturing defects) as compared to horizontal struts.76
There are many other important parameters that need to be also considered. In particular, the parameters determining the energy input including the power, scanning speed, and scanning pattern of the energy source (i.e., laser or electron beam) should be chosen such that there is enough energy to fully melt and fuse the metal powder. At the same time, excessive levels of energy will lead to transitioning from the conduction mode to the so-called “keyhole mode” where deep melt pools and evaporation of the processed material lead to large manufacturing defects.175–177 The above-mentioned parameters should therefore be selected such that the size of the melt pool is closely controlled and the amount of the generated heat stays within the desired range.
4.2. Post-AM heat and surface treatments
The microstructure, mechanical properties, and (surface) quality of AM porous metallic biomaterials could be improved through post-AM heat and surface treatments. As far as heat treatments are concerned, an optimized heat treatment process could be used to release residual stresses, transform the microstructure of the resulting materials to a more favorable one, improve the mechanical properties of the lattice structures, and reduce anisotropy in the mechanical properties.49,76,158,163,165,166,168,170 Combining high temperatures with high levels of pressure could be also used in a process called hot isostatic pressing (HIP) to close the pores (i.e., manufacturing defects) created by the AM process, thereby increasing the mechanical properties of the resulting lattice structures.49,157,162,171 The surface properties of the struts constituting the lattice structures could be also improved through surface treatments such as sand blasting and chemical etching aimed at removing the unmolten powder particles and smoothening the surface of AM porous structures.49,162 It is important to realize that these types of surface treatments are different both in protocol and purpose from those used for bio-functionalization of AM porous biomaterials (Section 6). Improving the smoothness of the surface of the struts could, for example, help in reducing the notches that act as crack initiation sites and may lead to premature fatigue failure under repetitive mechanical loading. Both heat and surface treatments may therefore be needed before using AM porous implants in vivo.5. Metals and alloys
AM porous metallic biomaterials have been fabricated from a variety of metals and metallic alloys. In this section, we will discuss two major categories of the materials used to date including both bioinert and biodegradable metals. In particular, we briefly discuss the pros and cons of each material and highlight their potential for application in design and manufacturing of bone substitutes and orthopaedic implants.5.1. Bioinert metals and alloys
Among bioinert metals, the titanium alloy Ti–6Al–4V,109,115,153,158,170,178,179 Co–Cr alloys,180,181 pure titanium,182,183 stainless steel,174,184 NiTi alloys,185–188 and tantalum189 are the most important biomaterials used for fabrication of AM porous structures. Ti–6Al–4V is probably the most extensively studied material given its high mechanical properties, good biocompatibility, relatively low price, and widely available experience regarding its processing with AM. However, the fatigue strength of Ti–6Al–4V is not that as high as CoCr,30 its ductility is not as high as pure titanium,183 and the presence of Al and V create some concerns regarding its cytocompatibility. CoCr alloys exhibit good mechanical properties including an exceptionally high fatigue strength.30 However, their biocompatibility is not as high as titanium.190,191 The mechanical properties of pure titanium are not as high as Ti–6Al–4V or CoCr. However, pure titanium is very ductile. This translates to various benefits including a high normalized fatigue strength.183,189 Furthermore, pure titanium is a very biocompatible material192 with no major concerns regarding its cytocompatibility. The price of pure titanium is also lower than Ti–6Al–4V. Stainless steel shows reasonable biocompatibility193 and is not expensive. However, the elastic modulus of stainless steel is about two times higher than Ti–6Al–4V, which could lead to problems regarding stress shielding. An advantage of stainless steels (e.g., surgical steels) is that they could more easily be processed with SLM to create fine structures with smaller strut thicknesses as compared to some other materials. NiTi alloys (e.g., nitinol) show the special properties of superelasticity and shape memory.185,187,188,194–196 These properties are particularly useful for creating advanced medical devices such as deployable orthopaedic implants.197 However, there are concerns regarding the biocompatibility of NiTi alloys as some studies have reported certain levels of cytotoxicity for NiTi alloys.198 Finally, tantalum is an extremely biocompatible material that stimulates bone regeneration even in absence of surface treatments and coatings and has shown very promising results in vivo.189 However, it is extremely expensive, meaning that fabricating entire implants from tantalum is not feasible in most cases. There has been a recent trend in using alloys of titanium and tantalum to benefit from the best features of both materials.199–201 However, most studies have been limited to solid specimens so far and thorough studies of porous structures made from these alloys are still lacking.5.2. Biodegradable AM porous metallic biomaterials
Topologically-ordered AM porous metallic biomaterials made from biodegradable metals is a very recent topic with the key papers just appearing in the literature (Fig. 7).202,203 There are three main types of materials that are of particular interest in this regard including magnesium, iron, and zinc. While the biodegradation rate of most magnesium alloys is faster than is desired for orthopaedic applications, the opposite holds for iron and zinc.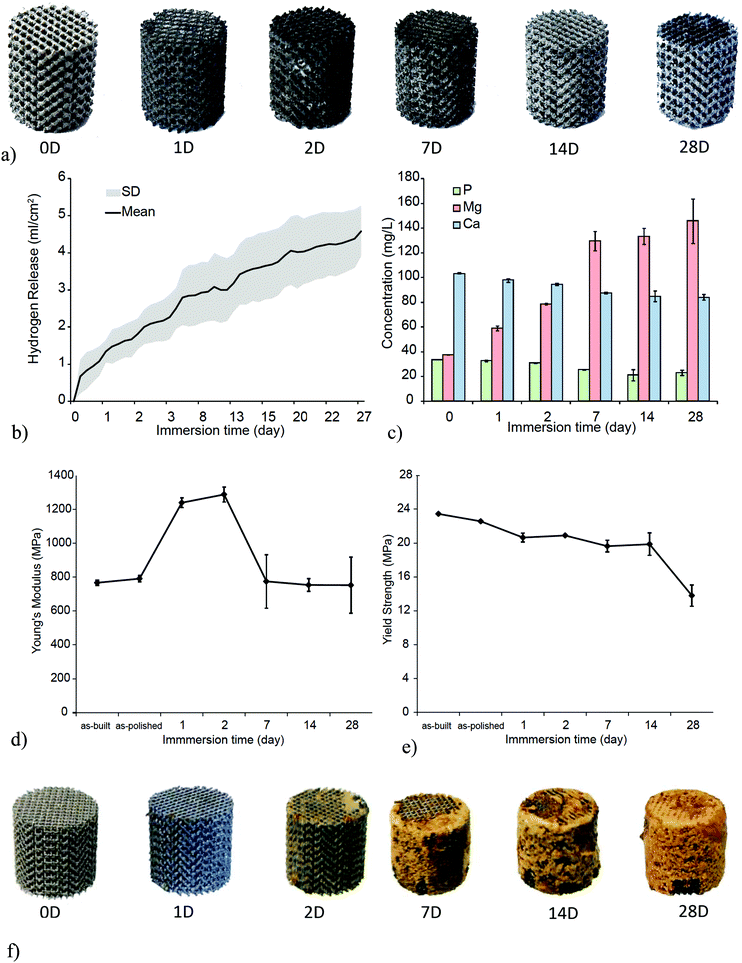 | ||
| Fig. 7 AM porous magnesium scaffolds (WE43) and the evolution of their appearance during 4 weeks of in vitro biodegradation (a). The evolution of the released hydrogen gas (b), the concentration of ions in the solution (c), Young's modulus (d), and yield strength (e) with time (reprinted from ref. 203 with permission from Elsevier). Similar biodegradation experiments were performed on AM porous iron (reprinted from ref. 202 with permission from Elsevier) (f). | ||
The recent emergence of Mg alloys incorporating rare earth elements (e.g., WE43203) has enabled reducing the biodegradation rate of magnesium alloys to reasonable levels suitable for orthopaedic applications. However, porous designs tend to increase the surface area tremendously, thereby increasing the biodegradation rate. The other challenge associated with a high rate of magnesium biodegradation is the rapid buildup of the hydrogen gas. AM of Mg alloys is extremely challenging given its high degree of inflammability,49,203 which is why very few labs have been able to AM topologically ordered porous structures from magnesium alloys (Fig. 7a–e). One of these rare studies has shown that after 4 weeks of biodegradation, there is about 20% mass loss.203 However, the elastic modulus of the porous structure remains within the ranges reported for trabecular bone in the literature.203
As opposed to magnesium alloys, the major challenge in the case of iron and zinc is to speed up the biodegradation process. This is somethings that could potentially be achieved using rational design of the topology of the porous structure. For example, simple measures such as increasing the surface area will likely result in significant increase in the rate of biodegradation. A study on directly printed (i.e., SLM) porous iron structures (Fig. 7f) has shown promising results including favorable mechanical properties up to 4 weeks of biodegradation and signs of substantial increase in the rate of biodegradation.202
Fewer studies on topologically ordered porous zinc structures are currently available. One important concern with most biodegradable metals is certain levels of cytotoxicity that are caused by the biodegradation process. For example, the biodegradation process often results in significant changes in pH that are not well tolerated by some the host cells. However, the apparent cytotoxicity is in some cases a result of highly local phenomena that have limited practical implications in vivo.
6. Bio-functionalization
Even though topological design could help in its own right to improve bone tissue regeneration and prevent implant-associated infections (Sections 3.4 and 3.5), it is often not enough for fully overcoming both challenges. Bio-functionalization of the lattice structures through surface treatments and coatings on the one hand and incorporation of drug delivery vehicles on the other could provide additional ammunition. In the two following sub-sections, we will briefly review the bio-functionalization processes used for both above-mentioned purposes and discuss the results of their in vitro and in vivo evaluations.6.1. Improving bone regeneration performance and osseointegration
The surface treatments and coatings used for improving the bone tissue regeneration performance of biomaterials work through three general mechanisms, namely biological, chemical, and physical. In the biological approach, biomolecules such as osteogenic or angiogenic growth factors are incorporated onto the biomaterial surface. In the chemical approach, the surface chemistry is modified to make it more favorable for bone tissue regeneration. For example, specific surface treatments could improve the apatite forming ability of surfaces or directly incorporate calcium phosphate compounds onto the surface so as to stimulate further apatite formation and to ultimately improve bone regeneration. Finally, the physical approaches provide cues that stimulate the osteogenic behavior. For example, specific types of topographies at the micro- and nanoscale have been found to stimulate the osteogenic differentiation of stem cells through mechanobiological pathways that involves integrin molecules, focal adhesions, and cytoskeletal re-organization.204–208 All above-mentioned mechanisms have been exploited for surface bio-functionalization of AM porous metallic biomaterials.When applying surface treatments and coatings to AM porous biomaterials, it is important to reach their entire internal surface and create uniform surface throughout the specimen. One therefore has to rely on chemical or electrochemical techniques that are capable of reaching the internal surfaces of the porous structure. Therefore, techniques such as dipping,209 chemical surface treatments using acid and alkali solutions,164,210,211 anodizing,169,212 plasma electrolytic oxidation,145,213 and electrophoretic deposition214,215 have been usually used for such purposes.
Considering the three above-mentioned action mechanisms, bone morphogenic protein (BMP) and to a lesser extent other growth factors are the most commonly used biomolecules, although a number of other molecules such as osteostatin216 have been also used in some studies. The results of in vitro and in vivo evaluations of AM porous biomaterials bio-functionalized using biomolecules confirm that the bone tissue regeneration performance significantly improves as a result of these treatments. In the case of in vitro studies, the expression of osteogenic markers is observed to be upregulated.187 Animal studies also show improved bone regeneration performance and partial filling of the pore space with de novo bone.216
Similar results have been found regarding the chemical surface treatments techniques. While a number of surface treatments have been unsuccessful in improving the apatite forming ability of AM porous metallic biomaterials,164 some other surface treatments are shown to improve the apatite forming ability of these materials.211 An important question in this regard is whether the in vitro measurement of apatite forming ability using simulated body fluid (SBF) is a good predictor of an improved bone regeneration performance in vivo. A systematic review217 of the studies where data regarding both the in vitro apatite forming ability and in vivo performance of biomaterials are presented has found that, in the vast majority of cases, materials exhibiting a better apatite forming ability show better in vivo performance as well. In the specific case of AM porous biomaterials, there is relatively limited evidence available as to whether an improved apatite forming ability translates to a better bone tissue regeneration performance. In a few studies that are available,211 the above-mentioned correlation between the apatite forming ability and in vivo bone regeneration performance seems to hold.
In the case of physical mechanisms, specific types of micro- and nanotopography are often used to stimulate osteogenic differentiation of stem cells. There is abundant evidence in the literature that specific ranges of nanopattern sizes particularly in the sub-100 nm range give rise to such effects.205 Some of the surface functionalization techniques such as anodizing could create nanotopographical features that are capable of inducing such effects (e.g., nanotubular surfaces211). A comprehensive study of the in vitro cell culture response, in vivo bone regeneration performance, and the biomechanical stability of anodized AM porous Ti–6Al–4V has shown that anodized surfaces with nanotubular structures upregulate the expression of osteogenic markers in vitro and lead to significantly improved biomechanical stability of the implants used for grafting critical size segmental bone defects (Fig. 8).211
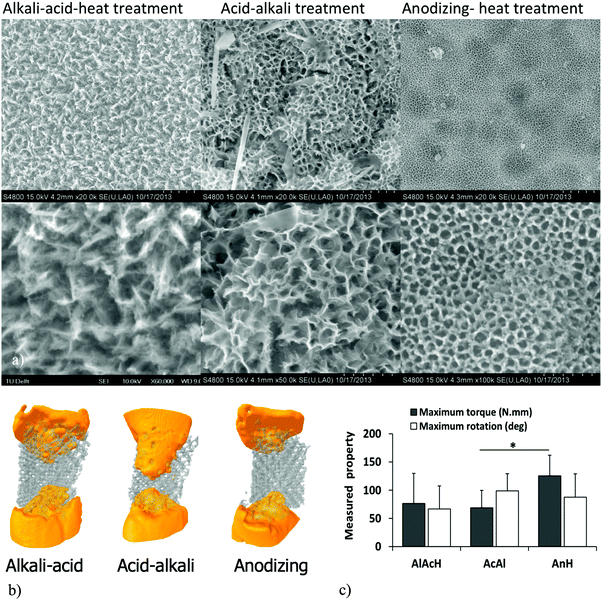 | ||
| Fig. 8 The surface characteristics of AM porous titanium after three different types of surface treatments (a). The surface treatments influence the volume of regenerated bone (b) as well as the biomechanical stability of an implant used to graft a segmental bone defect (reprinted from ref. 211 with permission from Elsevier) (c). | ||
The studies that use the pore space of AM porous biomaterials for incorporation of drug delivery vehicles are relatively small in number. In one such study (Fig. 9a and b),45 colloidal gels were used to deliver two types of growth factors, namely BMP-2 and bFGF, to stimulate osteogenesis and angiogenesis, respectively. The results of the study showed that the delivery of growth factors results in a significantly larger volume of regenerated bone in a critical size segmental bone defect model.45 Another study utilizing fibrin gels for the delivery of BMP-2 from the pore space of similar AM porous titanium has shown even better in vivo results with full regeneration of critical size segmental bone defects and full biomechanical stability with failure loads exceeding those of the native controls (i.e., collateral femora) (Fig. 9d).44 This shows the high potential of bio-functionalized AM porous metallic biomaterials for full regeneration of bone in such challenging problems as critical size segmental defects.
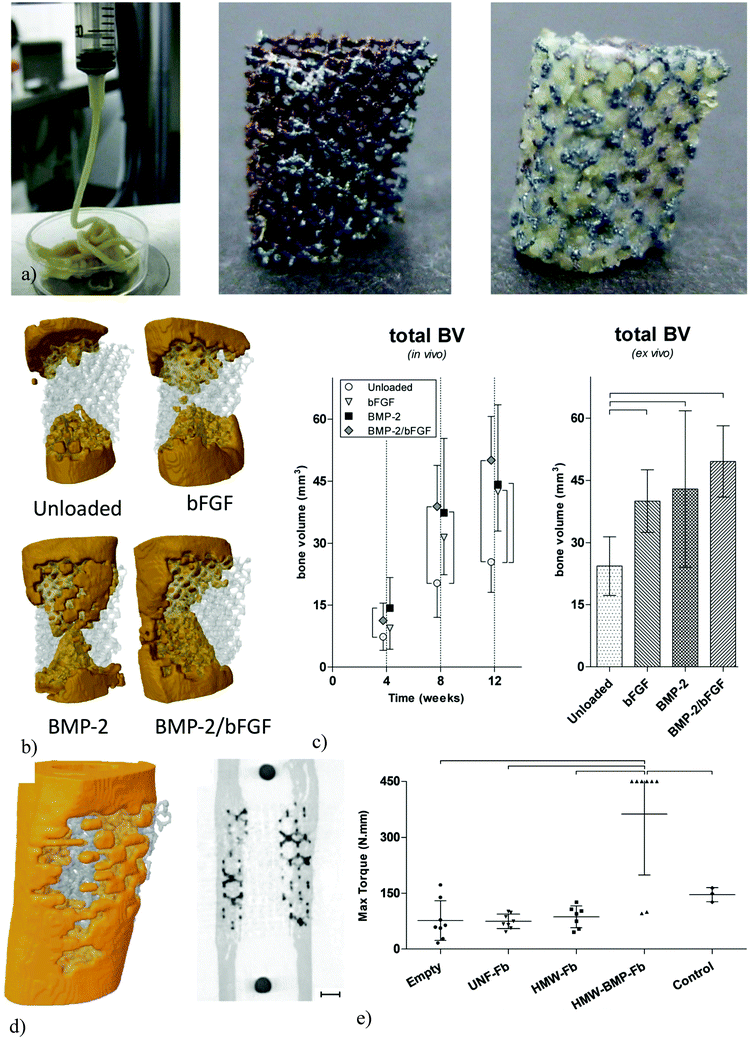 | ||
| Fig. 9 Incorporation of drug delivery vehicles such as a drug-loaded colloidal gel into AM porous titanium45 (a). The release of BMP-2 and bFGF significantly increases the volume of regenerated bone45 (b and c). A different study using fibrin gels for the delivery of BMP-2 from the pore space of AM porous titanium could achieve full regeneration of bone in a critical size segmental bone defect (d) and resulted in full recovery of the biomechanical functionality44 (e). | ||
6.2. Infection prevention
As in the case of bone tissue regeneration performance, there are different mechanisms through which biomaterials could be functionalized to minimize the risk of implant-associated infections, namely biochemical and physical mechanisms.218 In the biochemical approach, one or more antibacterial agents are used to kill bacteria. The antibacterial agent could be antibiotics,219–221 inorganic antibacterial agents (e.g., silver,222–225 zinc,226–228 or copper229,230), antibacterial peptides,219,231,232 or certain types of metal oxides.233–236 As for the physical mechanism, specific types of nanotopographical features are used to kill bacteria through a mechanical process, namely inducing high levels of strain (deformation) that exceed the level of strain bacteria could tolerate.237 It has been found that specific ranges of dimensions (i.e., heights, dimeters, and interspacing) of nanopillars lead to strong bactericidal effects.238–241 The majority of the work performed in terms of surface bio-functionalization of AM porous metallic biomaterials use the first approach, as it is very challenging to cover the entire (internal) surfaces of volume-porous materials with nanotopographical features whose dimensions are precisely controlled. However, a few studies where micro- and nanotopographical features were created on AM porous titanium through anodizing (nanotubes)242 or plasma electrolytic oxidations145 have shown clear antibacterial behavior even in the absence of any antibacterial agents. It is, however, not clear to what extent are these antibacterial effects a result of the topographical features, given the fact that certain forms of titanium oxide could also exhibit antibacterial behavior.233–236 This unclarity regarding the exact antibacterial mechanism holds for many surface treatment techniques, because they simultaneously change the nanotopography and chemistry of the surface.Antibacterial surfaces that work on the basis of antibacterial agents are found more frequently in the literature. Several studies have applied such type of surfaces to AM porous metallic biomaterials and have evaluated their performance against both planktonic and adherent (i.e., biofilm-related bacteria) bacteria. In one such study, anodized surfaces that had been previously shown to improve bone tissue regeneration performance were further treated to create antibacterial surfaces working on the basis of released silver ions.242 The antibacterial surfaces were found to be effective against both planktonic and adherent bacteria.242 However, high levels of cytotoxicity against host cells were observed due to the release of silver ions.242 When silver nanoparticles were firmly attached to the titanium oxide surfaces created using plasma electrolytic oxidation (Fig. 10a),145 very high levels of antibacterial activity against methicillin-resistant Staphylococcus aureus were (MRSA) observed in both in vitro and ex vivo (Fig. 10b) experiments without any signs of cytotoxicity against mesenchymal stromal cells (Fig. 10c).145 In fact, cell proliferation even increased for the groups treated with plasma electrolytic oxidation (with or without silver nanoparticles).145 This was attributed to the formation of a hydroxyapatite phase during the same surface treatment process.145
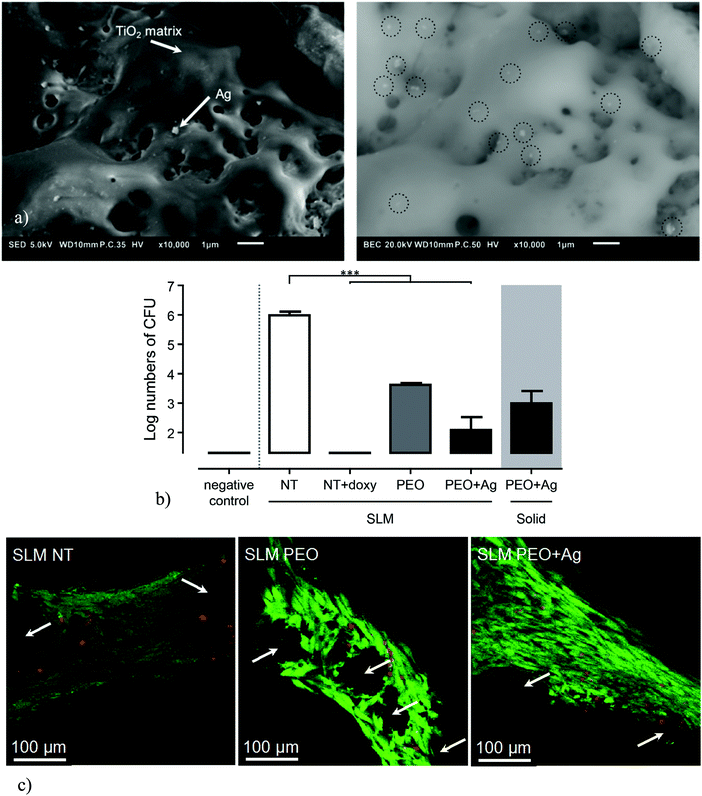 | ||
| Fig. 10 Silver nanoparticles immobilized on the surface of AM porous metallic biomaterials using plasma electrolytic oxidation minimize the risk of implant-associated infections (a). In an ex vivo test, the number of bacteria could be decreased by ≈4 orders of magnitude (b). Interestingly, cell viability even increased in comparison with a non-treated porous specimen145 (c). | ||
Another way to tackle the cytotoxicity of silver is to use the synergistic effects resulting from a combination of silver ions with antibiotics.214 One study has shown that simultaneous delivery of silver ions and vancomycin from an AM porous titanium could be used to fully eradicate both planktonic and adherent Staphylococcus aureus for up to several weeks214 even when the concentration of silver ions drops below the minimum inhibitory level within the first day.
The first in vivo studies that use animal models to evaluate the performance of antibacterial coatings applied to AM porous biomaterials have also started to appear in the literature. A few such studies that are currently available indicate that the effects of the immune response should be also considered when evaluating the efficacy of the applied coatings.243 This aspect (i.e., immune response) requires further attention, as there is very limited information available regarding the modulation of the immune response as a result of the applied bio-functionalizing surface treatments and their relationship with the other performance indicators of AM porous biomaterials that should be studied within the context of osteoimmunomodulation.244–250
7. Discussion and future research directions
We discussed the various aspects pertaining to AM porous metallic biomaterials all the way from the rational design of their topology to the applicable topology–property relationships, AM processes, the different types of base materials, and bio-functionalization processes that could be used to improve their bone regeneration performance and minimize the risk of implant-associated infections. It is clear that AM porous metallic biomaterials hold great promise as they offer a rare combination of suitable mechanical properties (including bone-mimicking elastic modulus, high levels of strength, and extremely long fatigue lives), appropriate ranges of mass transport properties, surface curvatures favorable for tissue regeneration (e.g., in the case of TPMS materials), adjustable biodegradability (e.g., in Mg, Zn, and Fe), huge internal surface areas that could be used for bio-functionalization (e.g., to create osteogenic and antibacterial surfaces), and large pore spaces that can accommodate drug delivery vehicles and adjust their topology-dependent release kinetics (e.g., to create bespoke release profiles for growth factors and antibacterial agents). An ever-present feature in all above-mentioned properties is that they could be adjusted through rational topological design of the biomaterials. This makes AM porous biomaterials highly adjustable and affords them a lot of flexibility to meet the multiple design objectives that are required for proper functioning of bone substitutes and orthopaedic implants.7.1. Relationship with the designer materials paradigm
The study of AM porous biomaterials is a part of a more general emerging research trend called “designer materials”. Designer materials or as they are sometimes referred to “metamaterials” with different types of properties including mechanical46,251–255 and acoustic256–259 have been receiving increasing attention during the last few years. Similar to AM porous biomaterials discussed here, topological design is a major design approach in the study of other types of metamaterials.Given that AM porous biomaterials are part of a bigger designer material paradigm, it is natural to utilize the analogies present with the other types of metamaterials to improve performance of AM porous metallic biomaterials. One of the most important emerging trends in the rational design of the other types of metamaterials is the use of the spatial distribution of material properties to adjust the properties of the designer materials and create novel, advanced functionalities. Many properties of AM porous biomaterials could be further adjusted through spatial distribution of multiple materials. Moreover, combining biodegradable materials with different biodegradation profiles either with each other or with bioinert materials could allow for adjusting the time-evolution of biomaterial properties. The biggest challenge in this regard is the lack of robust multi-material AM techniques for metals. The study into this type of techniques are still relatively rare (e.g., ref. 260 and 261). It is therefore suggested that the development of multi-metal AM techniques should be a priority for future research.
The rational design of AM porous biomaterials requires direct application of physics, mathematics, and mechanics principles. Moreover, more thorough characterization of the human tissues is required to better understand the exact properties that need to be replicated by the designer biomaterials. The natural discipline to use for this purpose is biomechanics where the properties of human tissues are studied using computational262–266 and experimental267–271 techniques and the musculoskeletal loads are estimated using musculoskeletal models272–275 and mass-spring-damper models276–279 of the human body.
7.2. Future research directions
There are many more important areas of research that need more attention from researchers.280,281 Three of those areas have been selected here for further elaboration. The first important area for future research is streamlining the rational design of topologies including widely available software packages that could deal with advanced topological design principles including sheet-based unit cells, advanced functionally graded designs (e.g., the ones with different types of unit cell types), and multi-scale topology optimization algorithms. The second area that would be of high importance is development of a larger number of biodegradable metallic materials. Currently, the number of such materials and studies investigating their properties is extremely limited. Finally, bio-functionalization of AM porous metallic biomaterials needs to be further studied, as the currently available studies are limited both in terms of number and scope. In particular, bio-functionalization techniques should be used for fabricating multi-functional AM porous metallic biomaterials that simultaneously address osteointegration and implant-associated infections, thereby providing innovative solutions for unmet clinical needs.Conflicts of interest
There are no conflicts to declare.References
- S. K. Everton, M. Hirsch, P. Stravroulakis, R. K. Leach and A. T. Clare, Review of in-situ process monitoring and in-situ metrology for metal additive manufacturing, Mater. Des., 2016, 95, 431–445 CrossRef CAS.
- W. E. Frazier, Metal additive manufacturing: a review, J. Mater. Eng. Perform., 2014, 23(6), 1917–1928 CrossRef CAS.
- J. J. Lewandowski and M. Seifi, Metal additive manufacturing: a review of mechanical properties, Annu. Rev. Mater. Res., 2016, 46, 151–186 CrossRef CAS.
- L. E. Murr, S. M. Gaytan, D. A. Ramirez, E. Martinez, J. Hernandez, K. N. Amato, P. W. Shindo, F. R. Medina and R. B. Wicker, Metal fabrication by additive manufacturing using laser and electron beam melting technologies, J. Mater. Sci. Technol., 2012, 28(1), 1–14 CrossRef CAS.
- S. Janbaz, M. McGuinness and A. A. Zadpoor, Multimaterial control of instability in soft mechanical metamaterials, Phys. Rev. Appl., 2018, 9(6), 064013 CrossRef.
- S. C. Ligon, R. Liska, J.r. Stampfl, M. Gurr and R. Mülhaupt, Polymers for 3D printing and customized additive manufacturing, Chem. Rev., 2017, 117(15), 10212–10290 CrossRef CAS PubMed.
- M. Mirzaali, A. Caracciolo, H. Pahlavani, S. Janbaz, L. Vergani and A. Zadpoor, Multi-material 3D printed mechanical metamaterials: rational design of elastic properties through spatial distribution of hard and soft phases, Appl. Phys. Lett., 2018, 113(24), 241903 CrossRef.
- T. van Manen, S. Janbaz and A. A. Zadpoor, Programming 2D/3D shape-shifting with hobbyist 3D printers, Mater. Horiz., 2017, 4(6), 1064–1069 RSC.
- T. Van Manen, S. Janbaz and A. A. Zadpoor, Programming the shape-shifting of flat soft matter, Mater. Today, 2018, 21, 144–163 CrossRef CAS.
- X. Wang, M. Jiang, Z. Zhou, J. Gou and D. Hui, 3D printing of polymer matrix composites: a review and prospective, Composites, Part B, 2017, 110, 442–458 CrossRef CAS.
- Y. Yang, Y. Chen, Y. Wei and Y. Li, 3D printing of shape memory polymer for functional part fabrication, Int. J. Adv. Manuf. Technol., 2016, 84(9–12), 2079–2095 CrossRef.
- U. Gbureck, T. Hölzel, U. Klammert, K. Würzler, F. A. Müller and J. E. Barralet, Resorbable dicalcium phosphate bone substitutes prepared by 3D powder printing, Adv. Funct. Mater., 2007, 17(18), 3940–3945 CrossRef CAS.
- J. A. Inzana, D. Olvera, S. M. Fuller, J. P. Kelly, O. A. Graeve, E. M. Schwarz, S. L. Kates and H. A. Awad, 3D printing of composite calcium phosphate and collagen scaffolds for bone regeneration, Biomaterials, 2014, 35(13), 4026–4034 CrossRef CAS PubMed.
- H. Seitz, W. Rieder, S. Irsen, B. Leukers and C. Tille, Three-dimensional printing of porous ceramic scaffolds for bone tissue engineering, J. Biomed. Mater. Res., Part B, 2005, 74(2), 782–788 CrossRef PubMed.
- E. Vorndran, M. Klarner, U. Klammert, L. M. Grover, S. Patel, J. E. Barralet and U. Gbureck, 3D powder printing of β-tricalcium phosphate ceramics using different strategies, Adv. Eng. Mater., 2008, 10(12), B67–B71 CrossRef CAS.
- P. H. Warnke, H. Seitz, F. Warnke, S. T. Becker, S. Sivananthan, E. Sherry, Q. Liu, J. Wiltfang and T. Douglas, Ceramic scaffolds produced by computer-assisted 3D printing and sintering: characterization and biocompatibility investigations, J. Biomed. Mater. Res., Part B, 2010, 93(1), 212–217 Search PubMed.
- A. A. Zadpoor, Design for additive bio-manufacturing: from patient-specific medical devices to rationally designed meta-biomaterials, Int. J. Mol. Sci., 2017, 18(8), 1607 CrossRef PubMed.
- E. Farré-Guasch, J. Wolff, M. N. Helder, E. A. Schulten, T. Forouzanfar and J. Klein-Nulend, Application of additive manufacturing in oral and maxillofacial surgery, J. Oral Maxillofac. Surg., 2015, 73(12), 2408–2418 CrossRef PubMed.
- A. Khalyfa, S. Vogt, J. Weisser, G. Grimm, A. Rechtenbach, W. Meyer and M. Schnabelrauch, Development of a new calcium phosphate powder-binder system for the 3D printing of patient specific implants, J. Mater. Sci.: Mater. Med., 2007, 18(5), 909–916 CrossRef CAS PubMed.
- M. Salmi, J. Tuomi, K.-S. Paloheimo, R. Björkstrand, M. Paloheimo, J. Salo, R. Kontio, K. Mesimäki and A. A. Mäkitie, Patient-specific reconstruction with 3D modeling and DMLS additive manufacturing, Rapid Prototyp. J., 2012, 18(3), 209–214 CrossRef.
- M. Takemoto, S. Fujibayashi, E. Ota, B. Otsuki, H. Kimura, T. Sakamoto, T. Kawai, T. Futami, K. Sasaki and T. Matsushita, Additive-manufactured patient-specific titanium templates for thoracic pedicle screw placement: novel design with reduced contact area, Eur. Spine J., 2016, 25(6), 1698–1705 CrossRef PubMed.
- A. A. Zadpoor and J. Malda, Additive manufacturing of biomaterials, tissues, and organs, Ann. Biomed. Eng., 2017, 45(1), 1–11 CrossRef PubMed.
- N. Sarkalkan, H. Weinans and A. A. Zadpoor, Statistical shape and appearance models of bones, Bone, 2014, 60, 129–140 CrossRef PubMed.
- G. H. Loh, E. Pei, D. Harrison and M. D. Monzón, An overview of functionally graded additive manufacturing, Addit. Manuf., 2018, 23, 34–44 CrossRef CAS.
- M. Mirzaali, R. Hedayati, P. Vena, L. Vergani, M. Strano and A. Zadpoor, Rational design of soft mechanical metamaterials: independent tailoring of elastic properties with randomness, Appl. Phys. Lett., 2017, 111(5), 051903 CrossRef.
- M. Mirzaali, S. Janbaz, M. Strano, L. Vergani and A. Zadpoor, Shape-matching soft mechanical metamaterials, Sci. Rep., 2018, 8(1), 965 CrossRef CAS PubMed.
- J. Wu, N. Aage, R. Westermann and O. Sigmund, Infill optimization for additive manufacturing—approaching bone-like porous structures, IEEE Trans. Vis. Comput. Graph., 2018, 24(2), 1127–1140 Search PubMed.
- Z. Xiao, Y. Yang, R. Xiao, Y. Bai, C. Song and D. Wang, Evaluation of topology-optimized lattice structures manufactured via selective laser melting, Mater. Des., 2018, 143, 27–37 CrossRef CAS.
- D. J. Yoo, Porous scaffold design using the distance field and triply periodic minimal surface models, Biomaterials, 2011, 32(31), 7741–7754 CrossRef CAS PubMed.
- S. Ahmadi, R. Hedayati, Y. Li, K. Lietaert, N. Tümer, A. Fatemi, C. Rans, B. Pouran, H. Weinans and A. Zadpoor, Fatigue performance of additively manufactured meta-biomaterials: the effects of topology and material type, Acta Biomater., 2018, 65, 292–304 CrossRef CAS PubMed.
- R. Hedayati, S. Ahmadi, K. Lietaert, B. Pouran, Y. Li, H. Weinans, C. Rans and A. Zadpoor, Isolated and modulated effects of topology and material type on the mechanical properties of additively manufactured porous biomaterials, J. Mech. Behav. Biomed. Mater., 2018, 79, 254–263 CrossRef CAS PubMed.
- S. Li, Q. Xu, Z. Wang, W. Hou, Y. Hao, R. Yang and L. Murr, Influence of cell shape on mechanical properties of Ti–6Al–4V meshes fabricated by electron beam melting method, Acta Biomater., 2014, 10(10), 4537–4547 CrossRef CAS PubMed.
- S. A. Yavari, S. Ahmadi, R. Wauthle, B. Pouran, J. Schrooten, H. Weinans and A. Zadpoor, Relationship between unit cell type and porosity and the fatigue behavior of selective laser melted meta-biomaterials, J. Mech. Behav. Biomed. Mater., 2015, 43, 91–100 CrossRef PubMed.
- S. A. Yavari, R. Wauthlé, J. van der Stok, A. Riemslag, M. Janssen, M. Mulier, J.-P. Kruth, J. Schrooten, H. Weinans and A. A. Zadpoor, Fatigue behavior of porous biomaterials manufactured using selective laser melting, Mater. Sci. Eng., C, 2013, 33(8), 4849–4858 CrossRef PubMed.
- F. Bobbert, K. Lietaert, A. A. Eftekhari, B. Pouran, S. Ahmadi, H. Weinans and A. Zadpoor, Additively manufactured metallic porous biomaterials based on minimal surfaces: a unique combination of topological, mechanical, and mass transport properties, Acta Biomater., 2017, 53, 572–584 CrossRef CAS PubMed.
- H. Montazerian, E. Davoodi, M. Asadi-Eydivand, J. Kadkhodapour and M. Solati-Hashjin, Porous scaffold internal architecture design based on minimal surfaces: a compromise between permeability and elastic properties, Mater. Des., 2017, 126, 98–114 CrossRef CAS.
- S. Truscello, G. Kerckhofs, S. Van Bael, G. Pyka, J. Schrooten and H. Van Oosterwyck, Prediction of permeability of regular scaffolds for skeletal tissue engineering: a combined computational and experimental study, Acta Biomater., 2012, 8(4), 1648–1658 CrossRef CAS PubMed.
- S. Van Bael, Y. C. Chai, S. Truscello, M. Moesen, G. Kerckhofs, H. Van Oosterwyck, J.-P. Kruth and J. Schrooten, The effect of pore geometry on the in vitro biological behavior of human periosteum-derived cells seeded on selective laser-melted Ti6Al4V bone scaffolds, Acta Biomater., 2012, 8(7), 2824–2834 CrossRef CAS PubMed.
- N. Taniguchi, S. Fujibayashi, M. Takemoto, K. Sasaki, B. Otsuki, T. Nakamura, T. Matsushita, T. Kokubo and S. Matsuda, Effect of pore size on bone ingrowth into porous titanium implants fabricated by additive manufacturing: an in vivo experiment, Mater. Sci. Eng., C, 2016, 59, 690–701 CrossRef CAS PubMed.
- Z. Wang, C. Wang, C. Li, Y. Qin, L. Zhong, B. Chen, Z. Li, H. Liu, F. Chang and J. Wang, Analysis of factors influencing bone ingrowth into three-dimensional printed porous metal scaffolds: a review, J. Alloys Compd., 2017, 717, 271–285 CrossRef CAS.
- A. A. Zadpoor, Bone tissue regeneration: the role of scaffold geometry, Biomaterials, Science, 2015, 3(2), 231–245 CAS.
- S. M. Ahmadi, S. A. Yavari, R. Wauthle, B. Pouran, J. Schrooten, H. Weinans and A. A. Zadpoor, Additively manufactured open-cell porous biomaterials made from six different space-filling unit cells: the mechanical and morphological properties, Materials, 2015, 8(4), 1871–1896 CrossRef CAS PubMed.
- J. Van der Stok, O. P. Van der Jagt, S. Amin Yavari, M. F. De Haas, J. H. Waarsing, H. Jahr, E. M. Van Lieshout, P. Patka, J. A. Verhaar and A. A. Zadpoor, Selective laser melting-produced porous titanium scaffolds regenerate bone in critical size cortical bone defects, J. Orthop. Res., 2013, 31(5), 792–799 CrossRef CAS PubMed.
- J. Van der Stok, M. Koolen, M. De Maat, S. A. Yavari, J. Alblas, P. Patka, J. Verhaar, E. Van Lieshout, A. A. Zadpoor and H. Weinans, Full regeneration of segmental bone defects using porous titanium implants loaded with BMP-2 containing fibrin gels, Eur. Cells Mater., 2015, 2015(29), 141–154 CrossRef.
- J. Van der Stok, H. Wang, S. Amin Yavari, M. Siebelt, M. Sandker, J. H. Waarsing, J. A. Verhaar, H. Jahr, A. A. Zadpoor, S. C. Leeuwenburgh and H. Weinans, Enhanced bone regeneration of cortical segmental bone defects using porous titanium scaffolds incorporated with colloidal gelatin gels for time-and dose-controlled delivery of dual growth factors, Tissue Eng., Part A, 2013, 19(23–24), 2605–2614 CrossRef CAS PubMed.
- B. Florijn, C. Coulais and M. van Hecke, Programmable mechanical metamaterials, Phys. Rev. Lett., 2014, 113(17), 175503 CrossRef PubMed.
- H. M. Kolken, S. Janbaz, S. M. Leeflang, K. Lietaert, H. H. Weinans and A. A. Zadpoor, Rationally designed meta-implants: a combination of auxetic and conventional meta-biomaterials, Mater. Horiz., 2018, 5(1), 28–35 RSC.
- J. T. Overvelde, J. C. Weaver, C. Hoberman and K. Bertoldi, Rational design of reconfigurable prismatic architected materials, Nature, 2017, 541(7637), 347 CrossRef CAS PubMed.
- A. A. Zadpoor, Mechanical performance of additively manufactured meta-biomaterials, Acta Biomater., 2019, 85, 41–59 CrossRef CAS PubMed.
- M. Afshar, A. P. Anaraki, H. Montazerian and J. Kadkhodapour, Additive manufacturing and mechanical characterization of graded porosity scaffolds designed based on triply periodic minimal surface architectures, J. Mech. Behav. Biomed. Mater., 2016, 62, 481–494 CrossRef CAS PubMed.
- D. S. Al-Saedi, S. Masood, M. Faizan-Ur-Rab, A. Alomarah and P. Ponnusamy, Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM, Mater. Des., 2018, 144, 32–44 CrossRef CAS.
- S. Y. Choy, C.-N. Sun, K. F. Leong and J. Wei, Compressive properties of functionally graded lattice structures manufactured by selective laser melting, Mater. Des., 2017, 131, 112–120 CrossRef CAS.
- C. Han, Y. Li, Q. Wang, S. Wen, Q. Wei, C. Yan, L. Hao, J. Liu and Y. Shi, Continuous functionally graded porous titanium scaffolds manufactured by selective laser melting for bone implants, J. Mech. Behav. Biomed. Mater., 2018, 80, 119–127 CrossRef CAS PubMed.
- S. A. Khanoki and D. Pasini, Multiscale design and multiobjective optimization of orthopedic hip implants with functionally graded cellular material, J. Biomech. Eng., 2012, 134(3), 031004 CrossRef PubMed.
- S. Limmahakhun, A. Oloyede, K. Sitthiseripratip, Y. Xiao and C. Yan, Stiffness and strength tailoring of cobalt chromium graded cellular structures for stress-shielding reduction, Mater. Des., 2017, 114, 633–641 CrossRef CAS.
- I. Maskery, N. Aboulkhair, A. Aremu, C. Tuck, I. Ashcroft, R. D. Wildman and R. J. Hague, A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting, Mater. Sci. Eng., A, 2016, 670, 264–274 CrossRef CAS.
- E. Onal, J. E. Frith, M. Jurg, X. Wu and A. Molotnikov, Mechanical properties and in vitro behavior of additively manufactured and functionally graded Ti6Al4V porous scaffolds, Metals, 2018, 8(4), 200 CrossRef.
- Y. Wang, L. Zhang, S. Daynes, H. Zhang, S. Feih and M. Y. Wang, Design of graded lattice structure with optimized mesostructures for additive manufacturing, Mater. Des., 2018, 142, 114–123 CrossRef CAS.
- S. Zhao, S. Li, S. Wang, W. Hou, Y. Li, L. Zhang, Y. Hao, R. Yang, R. Misra and L. Murr, Compressive and fatigue behavior of functionally graded Ti–6Al–4V meshes fabricated by electron beam melting, Acta Mater., 2018, 150, 1–15 CrossRef CAS.
- R. Hedayati, M. Sadighi, M. Mohammadi Aghdam and A. A. Zadpoor, Mechanical properties of additively manufactured thick honeycombs, Materials, 2016, 9(8), 613 CrossRef PubMed.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Effect of mass multiple counting on the elastic properties of open-cell regular porous biomaterials, Mater. Des., 2016, 89, 9–20 CrossRef.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanical properties of regular porous biomaterials made from truncated cube repeating unit cells: analytical solutions and computational models, Mater. Sci. Eng., C, 2016, 60, 163–183 CrossRef CAS PubMed.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanics of additively manufactured porous biomaterials based on the rhombicuboctahedron unit cell, J. Mech. Behav. Biomed. Mater., 2016, 53, 272–294 CrossRef CAS PubMed.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanical behavior of additively manufactured porous biomaterials made from truncated cuboctahedron unit cells, Int. J. Mech. Sci., 2016, 106, 19–38 CrossRef.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Analytical relationships for the mechanical properties of additively manufactured porous biomaterials based on octahedral unit cells, Appl. Math. Model., 2017, 46, 408–422 CrossRef.
- M. Dumas, P. Terriault and V. Brailovski, Modelling and characterization of a porosity graded lattice structure for additively manufactured biomaterials, Mater. Des., 2017, 121, 383–392 CrossRef CAS.
- R. Hedayati, H. Hosseini-Toudeshky, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Computational prediction of the fatigue behavior of additively manufactured porous metallic biomaterials, Int. J. Fatigue, 2016, 84, 67–79 CrossRef CAS.
- J. Kadkhodapour, H. Montazerian, A. C. Darabi, A. Anaraki, S. Ahmadi, A. Zadpoor and S. Schmauder, Failure mechanisms of additively manufactured porous biomaterials: effects of porosity and type of unit cell, J. Mech. Behav. Biomed. Mater., 2015, 50, 180–191 CrossRef CAS PubMed.
- A. Zargarian, M. Esfahanian, J. Kadkhodapour and S. Ziaei-Rad, Numerical simulation of the fatigue behavior of additive manufactured titanium porous lattice structures, Mater. Sci. Eng., C, 2016, 60, 339–347 CrossRef CAS PubMed.
- B. Grünbaum and G. C. Shephard, Tilings with congruent tiles, Bull. Am. Math. Soc., 1980, 3(3), 951–973 CrossRef.
- E. W. Weisstein, Space-Filling Polyhedron, 2019, http://mathworld.wolfram.com/Space-FillingPolyhedron.html, 2019.
- N. W. Johnson, Uniform Polytopes, Cambridge University Press, Cambridge, England, 2000 Search PubMed.
- H. Steinhaus, Mathematical Snapshots, Dover, New York, 1999 Search PubMed.
- D. Wells, The Penguin Dictionary of Curious and Interesting Geometry, Penguin, London, United Kingdom, 1991 Search PubMed.
- R. Hedayati, A. Leeflang and A. Zadpoor, Additively manufactured metallic pentamode meta-materials, Appl. Phys. Lett., 2017, 110(9), 091905 CrossRef.
- R. Wauthle, B. Vrancken, B. Beynaerts, K. Jorissen, J. Schrooten, J.-P. Kruth and J. Van Humbeeck, Effects of build orientation and heat treatment on the microstructure and mechanical properties of selective laser melted Ti6Al4V lattice structures, Addit. Manuf., 2015, 5, 77–84 CrossRef CAS.
- E. Giusti and G. H. Williams, Minimal Surfaces and Functions of Bounded Variation, Springer, 1984 Search PubMed.
- R. Osserman, A Survey of Minimal Surfaces, Dover, New York, 2002 Search PubMed.
- U. Pinkall and K. Polthier, Computing discrete minimal surfaces and their conjugates, Exper. Math., 1993, 2(1), 15–36 CrossRef.
- D.-J. Yoo, Computer-aided porous scaffold design for tissue engineering using triply periodic minimal surfaces, Int. J. Precis. Eng. Manuf., 2011, 12(1), 61–71 CrossRef.
- M. Ashby, The properties of foams and lattices, Philos. Trans. R. Soc., A, 2006, 364(1838), 15–30 CrossRef CAS PubMed.
- V. Deshpande, M. Ashby and N. Fleck, Foam topology: bending versus stretching dominated architectures, Acta Mater., 2001, 49(6), 1035–1040 CrossRef CAS.
- I. Gibson and M. F. Ashby, The mechanics of three-dimensional cellular materials, Proc. R. Soc. London, Ser. A, 1982, 382(1782), 43–59 CrossRef.
- L. J. Gibson and M. F. Ashby, Cellular Solids: Structure and Properties, Cambridge University Press, 1999 Search PubMed.
- Z. Hashin and S. Shtrikman, A variational approach to the theory of the elastic behaviour of multiphase materials, J. Mech. Phys. Solids, 1963, 11(2), 127–140 CrossRef.
- G. Campoli, M. Borleffs, S. A. Yavari, R. Wauthle, H. Weinans and A. A. Zadpoor, Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing, Mater. Des., 2013, 49, 957–965 CrossRef CAS.
- E. Garner, H. M. Kolken, C. C. Wang, A. A. Zadpoor and J. Wu, Compatibility in microstructural optimization for additive manufacturing, Addit. Manuf., 2019, 26, 65–75 CrossRef.
- A. Asadpoure and L. Valdevit, Topology optimization of lightweight periodic lattices under simultaneous compressive and shear stiffness constraints, Int. J. Solids Struct., 2015, 60, 1–16 CrossRef.
- L. Cheng, J. Liu, X. Liang and A. C. To, Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design, Comput. Methods Appl. Mech. Eng., 2018, 332, 408–439 CrossRef.
- Y. Du, H. Li, Z. Luo and Q. Tian, Topological design optimization of lattice structures to maximize shear stiffness, Adv. Eng. Softw., 2017, 112, 211–221 CrossRef.
- Y.-H. Kuo, C.-C. Cheng, Y.-S. Lin and C.-H. San, Support structure design in additive manufacturing based on topology optimization, Struct. Multidiscipl. Optim., 2018, 57(1), 183–195 CrossRef.
- H. Li, Z. Luo, L. Gao and P. Walker, Topology optimization for functionally graded cellular composites with metamaterials by level sets, Comput. Methods Appl. Mech. Eng., 2018, 328, 340–364 CrossRef.
- M. C. Messner, Optimal lattice-structured materials, J. Mech. Phys. Solids, 2016, 96, 162–183 CrossRef.
- A. Panesar, M. Abdi, D. Hickman and I. Ashcroft, Strategies for functionally graded lattice structures derived using topology optimisation for additive manufacturing, Addit. Manuf., 2018, 19, 81–94 CrossRef.
- P. Vogiatzis, M. Ma, S. Chen and X. D. Gu, Computational design and additive manufacturing of periodic conformal metasurfaces by synthesizing topology optimization with conformal mapping, Comput. Methods Appl. Mech. Eng., 2018, 328, 477–497 CrossRef.
- Y. Wang, H. Xu and D. Pasini, Multiscale isogeometric topology optimization for lattice materials, Comput. Methods Appl. Mech. Eng., 2017, 316, 568–585 CrossRef.
- W. Zhang, J. Song, J. Zhou, Z. Du, Y. Zhu, Z. Sun and X. Guo, Topology optimization with multiple materials via moving morphable component (MMC) method, Int. J. Numer. Meth. Eng., 2018, 113(11), 1653–1675 CrossRef.
- M. Rashed, M. Ashraf, R. Mines and P. J. Hazell, Metallic microlattice materials: a current state of the art on manufacturing, mechanical properties and applications, Mater. Des., 2016, 95, 518–533 CrossRef CAS.
- R. Hedayati, S. Janbaz, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, How does tissue regeneration influence the mechanical behavior of additively manufactured porous biomaterials?, J. Mech. Behav. Biomed. Mater., 2017, 65, 831–841 CrossRef CAS PubMed.
- R. Hedayati, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Mechanical properties of additively manufactured octagonal honeycombs, Mater. Sci. Eng., C, 2016, 69, 1307–1317 CrossRef CAS PubMed.
- A. A. Zadpoor, Mechanics of additively manufactured biomaterials, J. Mech. Behav. Biomed. Mater., 2017, 70, 1–6 CrossRef CAS PubMed.
- A. A. Zadpoor and R. Hedayati, Analytical relationships for prediction of the mechanical properties of additively manufactured porous biomaterials, J. Biomed. Mater. Res., Part A, 2016, 104(12), 3164–3174 CrossRef CAS PubMed.
- M. S. Elsayed and D. Pasini, Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials, Mech. Mater., 2010, 42(7), 709–725 CrossRef.
- L. R. Meza, S. Das and J. R. Greer, Strong, lightweight, and recoverable three-dimensional ceramic nanolattices, Science, 2014, 345(6202), 1322–1326 CrossRef CAS PubMed.
- H. Mitschke, F. Schury, K. Mecke, F. Wein, M. Stingl and G. E. Schröder-Turk, Geometry: the leading parameter for the Poisson's ratio of bending-dominated cellular solids, Int. J. Solids Struct., 2016, 100, 1–10 CrossRef.
- A. Vigliotti and D. Pasini, Linear multiscale analysis and finite element validation of stretching and bending dominated lattice materials, Mech. Mater., 2012, 46, 57–68 CrossRef.
- S. Ahmadi, G. Campoli, S. A. Yavari, B. Sajadi, R. Wauthlé, J. Schrooten, H. Weinans and A. Zadpoor, Mechanical behavior of regular open-cell porous biomaterials made of diamond lattice unit cells, J. Mech. Behav. Biomed. Mater., 2014, 34, 106–115 CrossRef CAS PubMed.
- K. Genovese, S. Leeflang and A. A. Zadpoor, Microscopic full-field three-dimensional strain measurement during the mechanical testing of additively manufactured porous biomaterials, J. Mech. Behav. Biomed. Mater., 2017, 69, 327–341 CrossRef CAS PubMed.
- M. Dallago, V. Fontanari, E. Torresani, M. Leoni, C. Pederzolli, C. Potrich and M. Benedetti, Fatigue and biological properties of Ti–6Al–4V ELI cellular structures with variously arranged cubic cells made by selective laser melting, J. Mech. Behav. Biomed. Mater., 2018, 78, 381–394 CrossRef CAS PubMed.
- J. De Krijger, C. Rans, B. Van Hooreweder, K. Lietaert, B. Pouran and A. A. Zadpoor, Effects of applied stress ratio on the fatigue behavior of additively manufactured porous biomaterials under compressive loading, J. Mech. Behav. Biomed. Mater., 2017, 70, 7–16 CrossRef CAS PubMed.
- N. W. Hrabe, P. Heinl, B. Flinn, C. Körner and R. K. Bordia, Compression-compression fatigue of selective electron beam melted cellular titanium (Ti–6Al–4V), J. Biomed. Mater. Res., Part B, 2011, 99(2), 313–320 CrossRef PubMed.
- S. Li, L. E. Murr, X. Cheng, Z. Zhang, Y. Hao, R. Yang, F. Medina and R. Wicker, Compression fatigue behavior of Ti–6Al–4V mesh arrays fabricated by electron beam melting, Acta Mater., 2012, 60(3), 793–802 CrossRef CAS.
- K. Lietaert, A. Cutolo, D. Boey and B. Van Hooreweder, Fatigue life of additively manufactured Ti6Al4V scaffolds under tension-tension, tension-compression and compression-compression fatigue load, Sci. Rep., 2018, 8(1), 4957 CrossRef PubMed.
- B. Van Hooreweder, Y. Apers, K. Lietaert and J.-P. Kruth, Improving the fatigue performance of porous metallic biomaterials produced by Selective Laser Melting, Acta Biomater., 2017, 47, 193–202 CrossRef CAS PubMed.
- S. Zhao, S. Li, W. Hou, Y. Hao, R. Yang and R. Misra, The influence of cell morphology on the compressive fatigue behavior of Ti–6Al–4V meshes fabricated by electron beam melting, J. Mech. Behav. Biomed. Mater., 2016, 59, 251–264 CrossRef CAS PubMed.
- R. Hedayati, H. Hosseini-Toudeshky, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, Multiscale modeling of fatigue crack propagation in additively manufactured porous biomaterials, Int. J. Fatigue, 2018, 113, 416–427 CrossRef CAS.
- R. Hedayati, S. A. Yavari and A. Zadpoor, Fatigue crack propagation in additively manufactured porous biomaterials, Mater. Sci. Eng., C, 2017, 76, 457–463 CrossRef CAS PubMed.
- S. J. Hollister, Scaffold design and manufacturing: from concept to clinic, Adv. Mater., 2009, 21(32–33), 3330–3342 CrossRef CAS PubMed.
- J.-H. Chen, C. Liu, L. You and C. A. Simmons, Boning up on Wolff's Law: mechanical regulation of the cells that make and maintain bone, J. Biomech., 2010, 43(1), 108–118 CrossRef PubMed.
- P. Christen, K. Ito, F. Galis and B. van Rietbergen, Determination of hip-joint loading patterns of living and extinct mammals using an inverse Wolff's law approach, Biomech. Model. Mechanobiol., 2015, 14(2), 427–432 CrossRef PubMed.
- A. A. Zadpoor, Open forward and inverse problems in theoretical modeling of bone tissue adaptation, J. Mech. Behav. Biomed. Mater., 2013, 27, 249–261 CrossRef PubMed.
- G. Campoli, H. Weinans and A. A. Zadpoor, Computational load estimation of the femur, J. Mech. Behav. Biomed. Mater., 2012, 10, 108–119 CrossRef PubMed.
- R. Huiskes, R. Ruimerman, G. H. Van Lenthe and J. D. Janssen, Effects of mechanical forces on maintenance and adaptation of form in trabecular bone, Nature, 2000, 405(6787), 704 CrossRef CAS PubMed.
- E. Ozcivici, Y. K. Luu, B. Adler, Y.-X. Qin, J. Rubin, S. Judex and C. T. Rubin, Mechanical signals as anabolic agents in bone, Nature Reviews, Rheumatology, 2010, 6(1), 50 CAS.
- A. A. Zadpoor, G. Campoli and H. Weinans, Neural network prediction of load from the morphology of trabecular bone, Appl. Math. Model., 2013, 37(7), 5260–5276 CrossRef.
- S. A. Yavari, J. van der Stok, S. Ahmadi, R. Wauthlé, J. Schrooten, H. Weinans and A. A. Zadpoor, Mechanical analysis of a rodent segmental bone defect model: the effects of internal fixation and implant stiffness on load transfer, J. Biomech., 2014, 47(11), 2700–2708 CrossRef PubMed.
- F. Bobbert and A. Zadpoor, Effects of bone substitute architecture and surface properties on cell response, angiogenesis, and structure of new bone, J. Mater. Chem. B, 2017, 5(31), 6175–6192 RSC.
- V. Karageorgiou and D. Kaplan, Porosity of 3D biomaterial scaffolds and osteogenesis, Biomaterials, 2005, 26(27), 5474–5491 CrossRef CAS PubMed.
- C. M. Bidan, K. P. Kommareddy, M. Rumpler, P. Kollmannsberger, Y. J. Bréchet, P. Fratzl and J. W. Dunlop, How linear tension converts to curvature: geometric control of bone tissue growth, PLoS One, 2012, 7(5), e36336 CrossRef CAS PubMed.
- C. M. Bidan, K. P. Kommareddy, M. Rumpler, P. Kollmannsberger, P. Fratzl and J. W. Dunlop, Geometry as a factor for tissue growth: towards shape optimization of tissue engineering scaffolds, Advanced Healthcare, Materials, 2013, 2(1), 186–194 CAS.
- C. M. Bidan, F. M. Wang and J. W. Dunlop, A three-dimensional model for tissue deposition on complex surfaces, Comput. Methods Biomech. Biomed. Eng., 2013, 16(10), 1056–1070 CrossRef PubMed.
- M. Rumpler, A. Woesz, J. W. Dunlop, J. T. van Dongen and P. Fratzl, The effect of geometry on three-dimensional tissue growth, J. R. Soc., Interface, 2008, 5(27), 1173–1180 CrossRef PubMed.
- N. D. Bade, R. D. Kamien, R. K. Assoian and K. J. Stebe, Curvature and Rho activation differentially control the alignment of cells and stress fibers, Sci. Adv., 2017, 3(9), e1700150 CrossRef PubMed.
- N. D. Bade, T. Xu, R. D. Kamien, R. K. Assoian and K. J. Stebe, Gaussian Curvature Directs Stress Fiber Orientation and Cell Migration, Biophys. J., 2018, 114(6), 1467–1476 CrossRef CAS PubMed.
- R. M. Gouveia, E. Koudouna, J. Jester, F. Figueiredo and C. J. Connon, Template curvature influences cell alignment to create improved human corneal tissue equivalents, Adv. Biosyst., 2017, 1(12), 1700135 CrossRef.
- L. Pieuchot, J. Marteau, A. Guignandon, T. Dos Santos, I. Brigaud, P.-F. Chauvy, T. Cloatre, A. Ponche, T. Petithory and P. Rougerie, Curvotaxis directs cell migration through cell-scale curvature landscapes, Nat. Commun., 2018, 9(1), 3995 CrossRef PubMed.
- J. R. Vetsch, R. Müller and S. Hofmann, The influence of curvature on three-dimensional mineralized matrix formation under static and perfused conditions: an in vitro bioreactor model, J. R. Soc., Interface, 2016, 13(123), 20160425 CrossRef PubMed.
- M. Werner, S. B. Blanquer, S. P. Haimi, G. Korus, J. W. Dunlop, G. N. Duda, D. W. Grijpma and A. Petersen, Surface curvature differentially regulates stem cell migration and differentiation via altered attachment morphology and nuclear deformation, Adv. Sci., 2017, 4(2), 1600347 CrossRef PubMed.
- M. Werner, N. A. Kurniawan, G. Korus, C. V. Bouten and A. Petersen, Mesoscale substrate curvature overrules nanoscale contact guidance to direct bone marrow stromal cell migration, J. R. Soc., Interface, 2018, 15(145), 20180162 CrossRef PubMed.
- E. Gamsjäger, C. Bidan, F. Fischer, P. Fratzl and J. Dunlop, Modelling the role of surface stress on the kinetics of tissue growth in confined geometries, Acta Biomater., 2013, 9(3), 5531–5543 CrossRef PubMed.
- H. Jinnai, Y. Nishikawa, M. Ito, S. D. Smith, D. A. Agard and R. J. Spontak, Topological similarity of sponge-like bicontinuous morphologies differing in length scale, Adv. Mater., 2002, 14(22), 1615–1618 CrossRef CAS.
- H. Jinnai, H. Watashiba, T. Kajihara, Y. Nishikawa, M. Takahashi and M. Ito, Surface curvatures of trabecular bone microarchitecture, Bone, 2002, 30(1), 191–194 CrossRef CAS PubMed.
- G. S. Matharu, A. Judge, D. W. Murray and H. G. Pandit, Trabecular metal acetabular components reduce the risk of revision following primary total hip arthroplasty: a propensity score matched study from the National Joint Registry for England and Wales, J. Arthroplasty, 2018, 33(2), 447–452 CrossRef PubMed.
- I. Laaksonen, M. Lorimer, K. Gromov, A. Eskelinen, O. Rolfson, S. E. Graves, H. Malchau and M. Mohaddes, Trabecular metal acetabular components in primary total hip arthroplasty: higher risk for revision compared with other uncemented cup designs in a collaborative register study including 93,709 hips, Acta Orthop., 2018, 89(3), 259–264 CrossRef PubMed.
- I. A. Van Hengel, M. Riool, L. E. Fratila-Apachitei, J. Witte-Bouma, E. Farrell, A. A. Zadpoor, S. A. Zaat and I. Apachitei, Selective laser melting porous metallic implants with immobilized silver nanoparticles kill and prevent biofilm formation by methicillin-resistant Staphylococcus aureus, Biomaterials, 2017, 140, 1–15 CrossRef CAS PubMed.
- L. Murr, Open-cellular metal implant design and fabrication for biomechanical compatibility with bone using electron beam melting, J. Mech. Behav. Biomed. Mater., 2017, 76, 164–177 CrossRef CAS PubMed.
- L. E. Murr, E. Martinez, K. N. Amato, S. M. Gaytan, J. Hernandez, D. A. Ramirez, P. W. Shindo, F. Medina and R. B. Wicker, Fabrication of metal and alloy components by additive manufacturing: examples of 3D materials science, J. Mater. Res. Technol., 2012, 1(1), 42–54 CrossRef CAS.
- V. Cain, L. Thijs, J. Van Humbeeck, B. Van Hooreweder and R. Knutsen, Crack propagation and fracture toughness of Ti6Al4V alloy produced by selective laser melting, Addit. Manuf., 2015, 5, 68–76 CrossRef CAS.
- Y. Kajima, A. Takaichi, T. Nakamoto, T. Kimura, Y. Yogo, M. Ashida, H. Doi, N. Nomura, H. Takahashi and T. Hanawa, Fatigue strength of Co–Cr–Mo alloy clasps prepared by selective laser melting, J. Mech. Behav. Biomed. Mater., 2016, 59, 446–458 CrossRef CAS PubMed.
- J.-P. Kruth, P. Mercelis, J. Van Vaerenbergh, L. Froyen and M. Rombouts, Binding mechanisms in selective laser sintering and selective laser melting, Rapid Prototyp. J., 2005, 11(1), 26–36 CrossRef.
- P. Lipinski, A. Barbas and A.-S. Bonnet, Fatigue behavior of thin-walled grade 2 titanium samples processed by selective laser melting. Application to life prediction of porous titanium implants, J. Mech. Behav. Biomed. Mater., 2013, 28, 274–290 CrossRef CAS PubMed.
- L. Liu, P. Kamm, F. García-Moreno, J. Banhart and D. Pasini, Elastic and failure response of imperfect three-dimensional metallic lattices: the role of geometric defects induced by Selective Laser Melting, J. Mech. Phys. Solids, 2017, 107, 160–184 CrossRef.
- A. Ataee, Y. Li, D. Fraser, G. Song and C. Wen, Anisotropic Ti–6Al–4V gyroid scaffolds manufactured by electron beam melting (EBM) for bone implant applications, Mater. Des., 2018, 137, 345–354 CrossRef CAS.
- X. Cheng, S. Li, L. Murr, Z. Zhang, Y. Hao, R. Yang, F. Medina and R. Wicker, Compression deformation behavior of Ti–6Al–4V alloy with cellular structures fabricated by electron beam melting, J. Mech. Behav. Biomed. Mater., 2012, 16, 153–162 CrossRef CAS PubMed.
- P. Heinl, A. Rottmair, C. Körner and R. F. Singer, Cellular titanium by selective electron beam melting, Adv. Eng. Mater., 2007, 9(5), 360–364 CrossRef CAS.
- Y. Liu, H. Wang, S. Li, S. Wang, W. Wang, W. Hou, Y. Hao, R. Yang and L. Zhang, Compressive and fatigue behavior of beta-type titanium porous structures fabricated by electron beam melting, Acta Mater., 2017, 126, 58–66 CrossRef CAS.
- S. Tammas-Williams, P. J. Withers, I. Todd and P. B. Prangnell, The effectiveness of hot isostatic pressing for closing porosity in titanium parts manufactured by selective electron beam melting, Metall. Mater. Trans. A, 2016, 47(5), 1939–1946 CrossRef CAS.
- W. Yuan, W. Hou, S. Li, Y. Hao, R. Yang, L.-C. Zhang and Y. Zhu, Heat treatment enhancing the compressive fatigue properties of open-cellular Ti–6Al–4V alloy prototypes fabricated by electron beam melting, J. Mater. Sci. Technol., 2018, 34(7), 1127–1131 CrossRef.
- L. Sochalski-Kolbus, E. A. Payzant, P. A. Cornwell, T. R. Watkins, S. S. Babu, R. R. Dehoff, M. Lorenz, O. Ovchinnikova and C. Duty, Comparison of residual stresses in Inconel 718 simple parts made by electron beam melting and direct laser metal sintering, Metall. Mater. Trans. A, 2015, 46(3), 1419–1432 CrossRef CAS.
- H. Rafi, N. Karthik, H. Gong, T. L. Starr and B. E. Stucker, Microstructures and mechanical properties of Ti6Al4V parts fabricated by selective laser melting and electron beam melting, J. Mater. Eng. Perform., 2013, 22(12), 3872–3883 CrossRef CAS.
- X. Zhao, S. Li, M. Zhang, Y. Liu, T. B. Sercombe, S. Wang, Y. Hao, R. Yang and L. E. Murr, Comparison of the microstructures and mechanical properties of Ti–6Al–4V fabricated by selective laser melting and electron beam melting, Mater. Des., 2016, 95, 21–31 CrossRef CAS.
- S. Ahmadi, R. Kumar, E. Borisov, R. Petrov, S. Leeflang, Y. Li, N. Tümer, R. Huizenga, C. Ayas and A. Zadpoor, From microstructural design to surface engineering: a tailored approach for improving fatigue life of additively manufactured meta-biomaterials, Acta Biomater., 2019, 83, 153–166 CrossRef CAS PubMed.
- E. Brandl and D. Greitemeier, Microstructure of additive layer manufactured Ti–6Al–4V after exceptional post heat treatments, Mater. Lett., 2012, 81, 84–87 CrossRef CAS.
- S. Bsat, S. A. Yavari, M. Munsch, E. R. Valstar and A. A. Zadpoor, Effect of alkali-acid-heat chemical surface treatment on electron beam melted porous titanium and its apatite forming ability, Materials, 2015, 8(4), 1612–1625 CrossRef CAS PubMed.
- A. Guzanová, G. Ižaríková, J. Brezinová, J. Živčák, D. Draganovská and R. Hudák, Influence of build orientation, heat treatment, and laser power on the hardness of Ti6Al4V manufactured using the DMLS process, Metals, 2017, 7(8), 318 CrossRef.
- Q. Huang, X. Liu, X. Yang, R. Zhang, Z. Shen and Q. Feng, Specific heat treatment of selective laser melted Ti–6Al–4V for biomedical applications, Front. Mater. Sci., 2015, 9(4), 373–381 CrossRef.
- Z. Li, C. Liu, B. Wang, C. Wang, Z. Wang, F. Yang, C. Gao, H. Liu, Y. Qin and J. Wang, Heat treatment effect on the mechanical properties, roughness and bone ingrowth capacity of 3D printing porous titanium alloy, RSC Adv., 2018, 8(22), 12471–12483 RSC.
- S. Wu, Y. Lu, Y. Gan, T. Huang, C. Zhao, J. Lin, S. Guo and J. Lin, Microstructural evolution and microhardness of a selective-laser-melted Ti–6Al–4V alloy after post heat treatments, J. Alloys Compd., 2016, 672, 643–652 CrossRef CAS.
- S. A. Yavari, Y. C. Chai, A. J. Böttger, R. Wauthle, J. Schrooten, H. Weinans and A. A. Zadpoor, Effects of anodizing parameters and heat treatment on nanotopographical features, bioactivity, and cell culture response of additively manufactured porous titanium, Mater. Sci. Eng., C, 2015, 51, 132–138 CrossRef PubMed.
- X.-Y. Zhang, G. Fang, S. Leeflang, A. J. Böttger, A. A. Zadpoor and J. Zhou, Effect of subtransus heat treatment on the microstructure and mechanical properties of additively manufactured Ti–6Al–4V alloy, J. Alloys Compd., 2018, 735, 1562–1575 CrossRef CAS.
- M.-W. Wu and P.-H. Lai, The positive effect of hot isostatic pressing on improving the anisotropies of bending and impact properties in selective laser melted Ti–6Al–4V alloy, Mater. Sci. Eng., A, 2016, 658, 429–438 CrossRef CAS.
- O. Cansizoglu, O. Harrysson, D. Cormier, H. West and T. Mahale, Properties of Ti–6Al–4V non-stochastic lattice structures fabricated via electron beam melting, Mater. Sci. Eng., A, 2008, 492(1–2), 468–474 CrossRef.
- L. Thijs, F. Verhaeghe, T. Craeghs, J. Van Humbeeck and J.-P. Kruth, A study of the microstructural evolution during selective laser melting of Ti–6Al–4V, Acta Mater., 2010, 58(9), 3303–3312 CrossRef CAS.
- C. Yan, L. Hao, A. Hussein, P. Young and D. Raymont, Advanced lightweight 316L stainless steel cellular lattice structures fabricated via selective laser melting, Mater. Des., 2014, 55, 533–541 CrossRef CAS.
- D. Dai and D. Gu, Effect of metal vaporization behavior on keyhole-mode surface morphology of selective laser melted composites using different protective atmospheres, Appl. Surf. Sci., 2015, 355, 310–319 CrossRef CAS.
- W. E. King, H. D. Barth, V. M. Castillo, G. F. Gallegos, J. W. Gibbs, D. E. Hahn, C. Kamath and A. M. Rubenchik, Observation of keyhole-mode laser melting in laser powder-bed fusion additive manufacturing, J. Mater. Process. Technol., 2014, 214(12), 2915–2925 CrossRef.
- J. Yang, J. Han, H. Yu, J. Yin, M. Gao, Z. Wang and X. Zeng, Role of molten pool mode on formability, microstructure and mechanical properties of selective laser melted Ti–6Al–4V alloy, Mater. Des., 2016, 110, 558–570 CrossRef CAS.
- M. Benedetti, V. Fontanari, M. Bandini, F. Zanini and S. Carmignato, Low-and high-cycle fatigue resistance of Ti–6Al–4V ELI additively manufactured via selective laser melting: mean stress and defect sensitivity, Int. J. Fatigue, 2018, 107, 96–109 CrossRef CAS.
- C. Yan, L. Hao, A. Hussein, Q. Wei and Y. Shi, Microstructural and surface modifications and hydroxyapatite coating of Ti–6Al–4V triply periodic minimal surface lattices fabricated by selective laser melting, Mater. Sci. Eng., C, 2017, 75, 1515–1524 CrossRef CAS PubMed.
- A. Cutolo, B. Neirinck, K. Lietaert, C. de Formanoir and B. Van Hooreweder, Influence of layer thickness and post-process treatments on the fatigue properties of CoCr scaffolds produced by laser powder bed fusion, Addit. Manuf., 2018, 23, 498–504 CrossRef CAS.
- B. Van Hooreweder, K. Lietaert, B. Neirinck, N. Lippiatt and M. Wevers, CoCr F75 scaffolds produced by additive manufacturing: influence of chemical etching on powder removal and mechanical performance, J. Mech. Behav. Biomed. Mater., 2017, 70, 60–67 CrossRef CAS PubMed.
- S. Roy, N. Khutia, D. Das, M. Das, V. K. Balla, A. Bandyopadhyay and A. R. Chowdhury, Understanding compressive deformation behavior of porous Ti using finite element analysis, Mater. Sci. Eng., C, 2016, 64, 436–443 CrossRef CAS PubMed.
- R. Wauthle, S. M. Ahmadi, S. A. Yavari, M. Mulier, A. A. Zadpoor, H. Weinans, J. Van Humbeeck, J.-P. Kruth and J. Schrooten, Revival of pure titanium for dynamically loaded porous implants using additive manufacturing, Mater. Sci. Eng., C, 2015, 54, 94–100 CrossRef CAS PubMed.
- R. Li, J. Liu, Y. Shi, M. Du and Z. Xie, 316L stainless steel with gradient porosity fabricated by selective laser melting, J. Mater. Eng. Perform., 2010, 19(5), 666–671 CrossRef CAS.
- S. Bernard, V. K. Balla, S. Bose and A. Bandyopadhyay, Compression fatigue behavior of laser processed porous NiTi alloy, J. Mech. Behav. Biomed. Mater., 2012, 13, 62–68 CrossRef CAS PubMed.
- M. H. Elahinia, M. Hashemi, M. Tabesh and S. B. Bhaduri, Manufacturing and processing of NiTi implants: a review, Prog. Mater. Sci., 2012, 57(5), 911–946 CrossRef CAS.
- Z. Gorgin Karaji, M. Speirs, S. Dadbakhsh, J.-P. Kruth, H. Weinans, A. Zadpoor and S. Amin Yavari, Additively manufactured and surface biofunctionalized porous nitinol, ACS Appl. Mater. Interfaces, 2017, 9(2), 1293–1304 CrossRef CAS PubMed.
- M. Speirs, B. Van Hooreweder, J. Van Humbeeck and J.-P. Kruth, Fatigue behaviour of NiTi shape memory alloy scaffolds produced by SLM, a unit cell design comparison, J. Mech. Behav. Biomed. Mater., 2017, 70, 53–59 CrossRef CAS PubMed.
- R. Wauthle, J. Van Der Stok, S. A. Yavari, J. Van Humbeeck, J.-P. Kruth, A. A. Zadpoor, H. Weinans, M. Mulier and J. Schrooten, Additively manufactured porous tantalum implants, Acta Biomater., 2015, 14, 217–225 CrossRef CAS PubMed.
- L. Baldwin and J. Hunt, Host inflammatory response to NiCr, CoCr, and Ti in a soft tissue implantation model, J. Biomed. Mater. Res., Part A, 2006, 79(3), 574–581 CrossRef CAS PubMed.
- S. S. Jakobsen, J. Baas, T. Jakobsen and K. Soballe, Biomechanical implant fixation of CoCrMo coating inferior to titanium coating in a canine implant model, J. Biomed. Mater. Res., Part A, 2010, 94(1), 180–186 CrossRef PubMed.
- Y.-J. Park, Y.-H. Song, J.-H. An, H.-J. Song and K. J. Anusavice, Cytocompatibility of pure metals and experimental binary titanium alloys for implant materials, J. Dent., 2013, 41(12), 1251–1258 CrossRef CAS PubMed.
- A. Yamamoto, Y. Kohyama, D. Kuroda and T. Hanawa, Cytocompatibility evaluation of Ni-free stainless steel manufactured by nitrogen adsorption treatment, Mater. Sci. Eng., C, 2004, 24(6–8), 737–743 CrossRef.
- A. Bagheri, M. J. Mahtabi and N. Shamsaei, Fatigue behavior and cyclic deformation of additive manufactured NiTi, J. Mater. Process. Technol., 2018, 252, 440–453 CrossRef CAS.
- M. J. Mahtabi and N. Shamsaei, Fatigue modeling for superelastic niti considering cyclic deformation and load ratio effects, Shape Mem. Superelasticity, 2017, 3(3), 250–263 CrossRef.
- M. J. Mahtabi, T. W. Stone and N. Shamsaei, Load sequence effects and variable amplitude fatigue of superelastic NiTi, Int. J. Mech. Sci., 2018, 148, 307–315 CrossRef.
- F. S. L. Bobbert, S. Janbaz and A. A. Zadpoor, Towards deployable meta-implants, J. Mater. Chem. B, 2018, 6(21), 3449–3455 RSC.
- R. E. McMahon, J. Ma, S. V. Verkhoturov, D. Munoz-Pinto, I. Karaman, F. Rubitschek, H. J. Maier and M. S. Hahn, A comparative study of the cytotoxicity and corrosion resistance of nickel–titanium and titanium–niobium shape memory alloys, Acta Biomater., 2012, 8(7), 2863–2870 CrossRef CAS PubMed.
- J. Fuerst, D. Medlin, M. Carter, J. Sears and G. Vander Voort, LASER additive manufacturing of titanium-tantalum alloy structured interfaces for modular orthopedic devices, JOM, 2015, 67(4), 775–780 CrossRef CAS.
- S. L. Sing, F. E. Wiria and W. Y. Yeong, Selective laser melting of titanium alloy with 50 wt% tantalum: effect of laser process parameters on part quality, Int. J. Refract. Met. Hard Mater., 2018, 77, 120–127 CrossRef CAS.
- S. L. Sing, W. Y. Yeong and F. E. Wiria, Selective laser melting of titanium alloy with 50 wt% tantalum: microstructure and mechanical properties, J. Alloys Compd., 2016, 660, 461–470 CrossRef CAS.
- Y. Li, H. Jahr, K. Lietaert, P. Pavanram, A. Yilmaz, L. Fockaert, M. Leeflang, B. Pouran, Y. Gonzalez-Garcia, H. Weinans, J. Mol, J. Zhou and A. A. Zadpoor, Additively manufactured biodegradable porous iron, Acta Biomater., 2018, 77, 380–393 CrossRef CAS PubMed.
- Y. Li, J. Zhou, P. Pavanram, M. Leeflang, L. Fockaert, B. Pouran, N. Tümer, K.-U. Schröder, J. Mol, H. Weinans, H. Jahr and A. A. Zadpoor, Additively manufactured biodegradable porous magnesium, Acta Biomater., 2018, 67, 378–392 CrossRef CAS PubMed.
- M. J. Dalby, N. Gadegaard and R. O. Oreffo, Harnessing nanotopography and integrin–matrix interactions to influence stem cell fate, Nat. Mater., 2014, 13(6), 558 CrossRef CAS PubMed.
- S. Dobbenga, L. E. Fratila-Apachitei and A. A. Zadpoor, Nanopattern-induced osteogenic differentiation of stem cells–A systematic review, Acta Biomater., 2016, 46, 3–14 CrossRef CAS PubMed.
- B. K. K. Teo, S. T. Wong, C. K. Lim, T. Y. Kung, C. H. Yap, Y. Ramagopal, L. H. Romer and E. K. Yim, Nanotopography modulates mechanotransduction of stem cells and induces differentiation through focal adhesion kinase, ACS Nano, 2013, 7(6), 4785–4798 CrossRef CAS PubMed.
- K. Yang, K. Jung, E. Ko, J. Kim, K. I. Park, J. Kim and S.-W. Cho, Nanotopographical manipulation of focal adhesion formation for enhanced differentiation of human neural stem cells, ACS Appl. Mater. Interfaces, 2013, 5(21), 10529–10540 CrossRef CAS PubMed.
- E. K. Yim, E. M. Darling, K. Kulangara, F. Guilak and K. W. Leong, Nanotopography-induced changes in focal adhesions, cytoskeletal organization, and mechanical properties of human mesenchymal stem cells, Biomaterials, 2010, 31(6), 1299–1306 CrossRef CAS PubMed.
- Y. Li, W. Yang, X. Li, X. Zhang, C. Wang, X. Meng, Y. Pei, X. Fan, P. Lan and C. Wang, Improving osteointegration and osteogenesis of three-dimensional porous Ti6Al4V scaffolds by polydopamine-assisted biomimetic hydroxyapatite coating, ACS Appl. Mater. Interfaces, 2015, 7(10), 5715–5724 CrossRef CAS PubMed.
- S. A. Yavari, S. Ahmadi, J. van der Stok, R. Wauthlé, A. Riemslag, M. Janssen, J. Schrooten, H. Weinans and A. A. Zadpoor, Effects of bio-functionalizing surface treatments on the mechanical behavior of open porous titanium biomaterials, J. Mech. Behav. Biomed. Mater., 2014, 36, 109–119 CrossRef PubMed.
- S. A. Yavari, J. van der Stok, Y. C. Chai, R. Wauthle, Z. T. Birgani, P. Habibovic, M. Mulier, J. Schrooten, H. Weinans and A. A. Zadpoor, Bone regeneration performance of surface-treated porous titanium, Biomaterials, 2014, 35(24), 6172–6181 CrossRef PubMed.
- S. A. Yavari, R. Wauthlé, A. J. Böttger, J. Schrooten, H. Weinans and A. A. Zadpoor, Crystal structure and nanotopographical features on the surface of heat-treated and anodized porous titanium biomaterials produced using selective laser melting, Appl. Surf. Sci., 2014, 290, 287–294 CrossRef.
- Z. G. Karaji, R. Hedayati, B. Pouran, I. Apachitei and A. A. Zadpoor, Effects of plasma electrolytic oxidation process on the mechanical properties of additively manufactured porous biomaterials, Mater. Sci. Eng., C, 2017, 76, 406–416 CrossRef PubMed.
- S. Bakhshandeh, Z. Gorgin Karaji, K. Lietaert, A. C. Fluit, C. E. Boel, H. C. Vogely, T. Vermonden, W. E. Hennink, H. Weinans and A. A. Zadpoor, Simultaneous Delivery of Multiple Antibacterial Agents from Additively Manufactured Porous Biomaterials to Fully Eradicate Planktonic and Adherent Staphylococcus aureus, ACS Appl. Mater. Interfaces, 2017, 9(31), 25691–25699 CrossRef CAS PubMed.
- S. Bakhshandeh and S. A. Yavari, Electrophoretic deposition: a versatile tool against biomaterial associated infections, J. Mater. Chem. B, 2018, 6(8), 1128–1148 RSC.
- J. Van Der Stok, D. Lozano, Y. C. Chai, S. Amin Yavari, A. P. Bastidas Coral, J. A. Verhaar, E. Gómez-Barrena, J. Schrooten, H. Jahr and A. A. Zadpoor, Osteostatin-coated porous titanium can improve early bone regeneration of cortical bone defects in rats, Tissue Eng., Part A, 2015, 21(9–10), 1495–1506 CrossRef CAS PubMed.
- A. A. Zadpoor, Relationship between in vitro apatite-forming ability measured using simulated body fluid and in vivo bioactivity of biomaterials, Mater. Sci. Eng., C, 2014, 35, 134–143 CrossRef CAS PubMed.
- D. Campoccia, L. Montanaro and C. R. Arciola, A review of the biomaterials technologies for infection-resistant surfaces, Biomaterials, 2013, 34(34), 8533–8554 CrossRef CAS PubMed.
- J. Hasan, R. J. Crawford and E. P. Ivanova, Antibacterial surfaces: the quest for a new generation of biomaterials, Trends Biotechnol., 2013, 31(5), 295–304 CrossRef CAS PubMed.
- J. A. Inzana, E. M. Schwarz, S. L. Kates and H. A. Awad, Biomaterials approaches to treating implant-associated osteomyelitis, Biomaterials, 2016, 81, 58–71 CrossRef CAS PubMed.
- T. H. Niepa, L. M. Snepenger, H. Wang, S. Sivan, J. L. Gilbert, M. B. Jones and D. Ren, Sensitizing Pseudomonas aeruginosa to antibiotics by electrochemical disruption of membrane functions, Biomaterials, 2016, 74, 267–279 CrossRef CAS PubMed.
- M. Fang, J.-H. Chen, X.-L. Xu, P.-H. Yang and H. F. Hildebrand, Antibacterial activities of inorganic agents on six bacteria associated with oral infections by two susceptibility tests, Int. J. Antimicrob. Agents, 2006, 27(6), 513–517 CrossRef CAS PubMed.
- Q. L. Feng, J. Wu, G. Chen, F. Cui, T. Kim and J. Kim, A mechanistic study of the antibacterial effect of silver ions on Escherichia coli and Staphylococcus aureus, J. Biomed. Mater. Res., 2000, 52(4), 662–668 CrossRef CAS PubMed.
- C. Marambio-Jones and E. M. Hoek, A review of the antibacterial effects of silver nanomaterials and potential implications for human health and the environment, J. Nanopart. Res., 2010, 12(5), 1531–1551 CrossRef CAS.
- Z.-m. Xiu, Q.-b. Zhang, H. L. Puppala, V. L. Colvin and P. J. Alvarez, Negligible particle-specific antibacterial activity of silver nanoparticles, Nano Lett., 2012, 12(8), 4271–4275 CrossRef CAS PubMed.
- K. R. Raghupathi, R. T. Koodali and A. C. Manna, Size-dependent bacterial growth inhibition and mechanism of antibacterial activity of zinc oxide nanoparticles, Langmuir, 2011, 27(7), 4020–4028 CrossRef CAS PubMed.
- A. Sirelkhatim, S. Mahmud, A. Seeni, N. H. M. Kaus, L. C. Ann, S. K. M. Bakhori, H. Hasan and D. Mohamad, Review on zinc oxide nanoparticles: antibacterial activity and toxicity mechanism, Nano-Micro Lett., 2015, 7(3), 219–242 CrossRef CAS PubMed.
- O. Yamamoto, Influence of particle size on the antibacterial activity of zinc oxide, Int. J. Inorg. Mater., 2001, 3(7), 643–646 CrossRef CAS.
- A. Esteban-Cubillo, C. Pecharromán, E. Aguilar, J. Santarén and J. S. Moya, Antibacterial activity of copper monodispersed nanoparticles into sepiolite, J. Mater. Sci., 2006, 41(16), 5208–5212 CrossRef CAS.
- M. Raffi, S. Mehrwan, T. M. Bhatti, J. I. Akhter, A. Hameed, W. Yawar and M. M. ul Hasan, Investigations into the antibacterial behavior of copper nanoparticles against Escherichia coli, Ann. Microbiol., 2010, 60(1), 75–80 CrossRef CAS.
- F. Costa, I. F. Carvalho, R. C. Montelaro, P. Gomes and M. C. L. Martins, Covalent immobilization of antimicrobial peptides (AMPs) onto biomaterial surfaces, Acta Biomater., 2011, 7(4), 1431–1440 CrossRef CAS PubMed.
- A. S. Veiga, C. Sinthuvanich, D. Gaspar, H. G. Franquelim, M. A. Castanho and J. P. Schneider, Arginine-rich self-assembling peptides as potent antibacterial gels, Biomaterials, 2012, 33(35), 8907–8916 CrossRef CAS PubMed.
- J. Forsgren, F. Svahn, T. Jarmar and H. Engqvist, Formation and adhesion of biomimetic hydroxyapatite deposited on titanium substrates, Acta Biomater., 2007, 3(6), 980–984 CrossRef CAS PubMed.
- H. Li, Q. Cui, B. Feng, J. Wang, X. Lu and J. Weng, Antibacterial activity of TiO2 nanotubes: influence of crystal phase, morphology and Ag deposition, Appl. Surf. Sci., 2013, 284, 179–183 CrossRef CAS.
- S. Wu, Z. Weng, X. Liu, K. Yeung and P. K. Chu, Functionalized TiO2 based nanomaterials for biomedical applications, Adv. Funct. Mater., 2014, 24(35), 5464–5481 CrossRef CAS.
- T. Yuranova, A. Rincon, C. Pulgarin, D. Laub, N. Xantopoulos, H.-J. Mathieu and J. Kiwi, Performance and characterization of Ag–cotton and Ag/TiO2 loaded textiles during the abatement of E. coli, J. Photochem. Photobiol., A, 2006, 181(2–3), 363–369 CrossRef CAS.
- M. Mirzaali, I. Van Dongen, N. Tümer, H. Weinans, S. A. Yavari and A. Zadpoor, In-silico quest for bactericidal but non-cytotoxic nanopatterns, Nanotechnology, 2018, 29(43), 43LT02 CrossRef CAS PubMed.
- C. D. Bandara, S. Singh, I. O. Afara, A. Wolff, T. Tesfamichael, K. Ostrikov and A. Oloyede, Bactericidal effects of natural nanotopography of dragonfly wing on Escherichia coli, ACS Appl. Mater. Interfaces, 2017, 9(8), 6746–6760 CrossRef CAS PubMed.
- A. Elbourne, R. J. Crawford and E. P. Ivanova, Nano-structured antimicrobial surfaces: from nature to synthetic analogues, J. Colloid Interface Sci., 2017, 508, 603–616 CrossRef CAS PubMed.
- K. Modaresifar, S. Azizian, M. Ganjian, L. E. Fratila-Apachitei and A. A. Zadpoor, Bactericidal effects of nanopatterns: a systematic review, Acta Biomater., 2019, 83, 29–36 CrossRef CAS PubMed.
- A. Tripathy, P. Sen, B. Su and W. H. Briscoe, Natural and bioinspired nanostructured bactericidal surfaces, Adv. Colloid Interface Sci., 2017, 248, 85–104 CrossRef CAS PubMed.
- S. Amin Yavari, L. Loozen, F. L. Paganelli, S. Bakhshandeh, K. Lietaert, J. A. Groot, A. C. Fluit, C. Boel, J. Alblas and H. C. Vogely, Antibacterial behavior of additively manufactured porous titanium with nanotubular surfaces releasing silver ions, ACS Appl. Mater. Interfaces, 2016, 8(27), 17080–17089 CrossRef CAS PubMed.
- M. Croes, S. Bakhshandeh, I. van Hengel, K. Lietaert, K. van Kessel, B. Pouran, B. van der Wal, H. Vogely, W. Van Hecke and A. Fluit, Antibacterial and immunogenic behavior of silver coatings on additively manufactured porous titanium, Acta Biomater., 2018, 81, 315–327 CrossRef CAS PubMed.
- L. Bai, Z. Du, J. Du, W. Yao, J. Zhang, Z. Weng, S. Liu, Y. Zhao, Y. Liu and X. Zhang, A multifaceted coating on titanium dictates osteoimmunomodulation and osteo/angio-genesis towards ameliorative osseointegration, Biomaterials, 2018, 162, 154–169 CrossRef CAS PubMed.
- Z. Chen, A. Bachhuka, F. Wei, X. Wang, G. Liu, K. Vasilev and Y. Xiao, Nanotopography-based strategy for the precise manipulation of osteoimmunomodulation in bone regeneration, Nanoscale, 2017, 9(46), 18129–18152 RSC.
- Z. Chen, T. Klein, R. Z. Murray, R. Crawford, J. Chang, C. Wu and Y. Xiao, Osteoimmunomodulation for the development of advanced bone biomaterials, Mater. Today, 2016, 19(6), 304–321 CrossRef CAS.
- Z. Chen, X. Mao, L. Tan, T. Friis, C. Wu, R. Crawford and Y. Xiao, Osteoimmunomodulatory properties of magnesium scaffolds coated with β-tricalcium phosphate, Biomaterials, 2014, 35(30), 8553–8565 CrossRef CAS PubMed.
- Z. Chen, J. Yuen, R. Crawford, J. Chang, C. Wu and Y. Xiao, The effect of osteoimmunomodulation on the osteogenic effects of cobalt incorporated β-tricalcium phosphate, Biomaterials, 2015, 61, 126–138 CrossRef CAS PubMed.
- B. Li, P. Gao, H. Zhang, Z. Guo, Y. Zheng and Y. Han, Osteoimmunomodulation, osseointegration, and in vivo mechanical integrity of pure Mg coated with HA nanorod/pore-sealed MgO bilayer, Biomaterials, Science, 2018, 6(12), 3202–3218 CAS.
- J. M. Sadowska, F. Wei, J. Guo, J. Guillem-Marti, M.-P. Ginebra and Y. Xiao, Effect of nano-structural properties of biomimetic hydroxyapatite on osteoimmunomodulation, Biomaterials, 2018, 181, 318–332 CrossRef CAS PubMed.
- J. Berger, H. Wadley and R. McMeeking, Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness, Nature, 2017, 543(7646), 533 CrossRef CAS PubMed.
- J. Christensen, M. Kadic, O. Kraft and M. Wegener, Vibrant times for mechanical metamaterials, MRS Commun., 2015, 5(3), 453–462 CrossRef CAS.
- J. H. Lee, J. P. Singer and E. L. Thomas, Micro-/nanostructured mechanical metamaterials, Adv. Mater., 2012, 24(36), 4782–4810 CrossRef CAS PubMed.
- Q. Wang, J. A. Jackson, Q. Ge, J. B. Hopkins, C. M. Spadaccini and N. X. Fang, Lightweight mechanical metamaterials with tunable negative thermal expansion, Phys. Rev. Lett., 2016, 117(17), 175901 CrossRef PubMed.
- X. Zheng, H. Lee, T. H. Weisgraber, M. Shusteff, J. DeOtte, E. B. Duoss, J. D. Kuntz, M. M. Biener, Q. Ge and J. A. Jackson, Ultralight, ultrastiff mechanical metamaterials, Science, 2014, 344(6190), 1373–1377 CrossRef CAS PubMed.
- H. Chen and C. Chan, Acoustic cloaking in three dimensions using acoustic metamaterials, Appl. Phys. Lett., 2007, 91(18), 183518 CrossRef.
- S. A. Cummer, J. Christensen and A. Alù, Controlling sound with acoustic metamaterials, Nature Reviews, Materials, 2016, 1(3), 16001 Search PubMed.
- J. Mei, G. Ma, M. Yang, Z. Yang, W. Wen and P. Sheng, Dark acoustic metamaterials as super absorbers for low-frequency sound, Nat. Commun., 2012, 3, 756 CrossRef PubMed.
- L. Zigoneanu, B.-I. Popa and S. A. Cummer, Three-dimensional broadband omnidirectional acoustic ground cloak, Nat. Mater., 2014, 13(4), 352 CrossRef CAS PubMed.
- Z. Liu, D. Zhang, S. Sing, C. Chua and L. Loh, Interfacial characterization of SLM parts in multi-material processing: metallurgical diffusion between 316L stainless steel and C18400 copper alloy, Mater. Charact., 2014, 94, 116–125 CrossRef CAS.
- S. Sing, L. Lam, D. Zhang, Z. Liu and C. Chua, Interfacial characterization of SLM parts in multi-material processing: intermetallic phase formation between AlSi10Mg and C18400 copper alloy, Mater. Charact., 2015, 107, 220–227 CrossRef CAS.
- Y. Chang, N. Kim and S. Stenfelt, The development of a whole-head human finite-element model for simulation of the transmission of bone-conducted sound, J. Acoust. Soc. Am., 2016, 140(3), 1635–1651 CrossRef PubMed.
- Y. Chen, E. Dall, E. Sales, K. Manda, R. Wallace, P. Pankaj and M. Viceconti, Micro-CT based finite element models of cancellous bone predict accurately displacement once the boundary condition is well replicated: a validation study, J. Mech. Behav. Biomed. Mater., 2017, 65, 644–651 CrossRef PubMed.
- M. Goff, F. Lambers, R. Sorna, T. Keaveny and C. Hernandez, Finite element models predict the location of microdamage in cancellous bone following uniaxial loading, J. Biomech., 2015, 48(15), 4142–4148 CrossRef CAS PubMed.
- L. Grassi, S. P. Väänänen, S. A. Yavari, H. Weinans, J. S. Jurvelin, A. A. Zadpoor and H. Isaksson, Experimental validation of finite element model for proximal composite femur using optical measurements, J. Mech. Behav. Biomed. Mater., 2013, 21, 86–94 CrossRef PubMed.
- L. Lin, J. Samuel, X. Zeng and X. Wang, Contribution of extrafibrillar matrix to the mechanical behavior of bone using a novel cohesive finite element model, J. Mech. Behav. Biomed. Mater., 2017, 65, 224–235 CrossRef CAS PubMed.
- A. Ali, S. Newman, P. Hooper, C. Davies and J. Cobb, The effect of implant position on bone strain following lateral unicompartmental knee arthroplasty: a biomechanical model using digital image correlation, Bone Joint Res., 2017, 6(8), 522–529 CrossRef CAS PubMed.
- M.-T. Nguyen, J.-M. Allain, H. Gharbi, C. Desceliers and C. Soize, Experimental multiscale measurements for the mechanical identification of a cortical bone by digital image correlation, J. Mech. Behav. Biomed. Mater., 2016, 63, 125–133 CrossRef PubMed.
- M. Peña Fernández, A. Barber, G. W. Blunn and G. Tozzi, Optimization of digital volume correlation computation in SR-microCT images of trabecular bone and bone-biomaterial systems, J. Microsc., 2018, 272(3), 213–228 CrossRef PubMed.
- G. Tozzi, E. Dall’Ara, M. Palanca, M. Curto, F. Innocente and L. Cristofolini, Strain uncertainties from two digital volume correlation approaches in prophylactically augmented vertebrae: local analysis on bone and cement-bone microstructures, J. Mech. Behav. Biomed. Mater., 2017, 67, 117–126 CrossRef PubMed.
- S. P. Väänänen, S. A. Yavari, H. Weinans, A. A. Zadpoor, J. S. Jurvelin and H. Isaksson, Repeatability of digital image correlation for measurement of surface strains in composite long bones, J. Biomech., 2013, 46(11), 1928–1932 CrossRef PubMed.
- F. Azari, N. Arjmand, A. Shirazi-Adl and T. Rahimi-Moghaddam, A combined passive and active musculoskeletal model study to estimate L4-L5 load sharing, J. Biomech., 2018, 70, 157–165 CrossRef CAS PubMed.
- D. Cazzola, T. P. Holsgrove, E. Preatoni, H. S. Gill and G. Trewartha, Cervical spine injuries: a whole-body musculoskeletal model for the analysis of spinal loading, PLoS One, 2017, 12(1), e0169329 CrossRef PubMed.
- D. L. Crouch, L. Pan, W. Filer, J. W. Stallings and H. Huang, Comparing Surface and Intramuscular Electromyography for Simultaneous and Proportional Control Based on a Musculoskeletal Model: A Pilot Study, IEEE Trans. Neural Syst. Rehabil. Eng., 2018, 26(9), 1735–1744 Search PubMed.
- E. Montefiori, B. Kalkman, A. Clarke, M. Paggiosi, E. McCloskey and C. Mazzà, A subject-specific musculoskeletal model to estimate joint loading at different walking speeds, Gait & Posture, Elsevier, 2018, p. S28 Search PubMed.
- A. A. Nikooyan and A. A. Zadpoor, An improved cost function for modeling of muscle activity during running, J. Biomech., 2011, 44(5), 984–987 CrossRef PubMed.
- A. A. Nikooyan and A. A. Zadpoor, Effects of muscle fatigue on the ground reaction force and soft-tissue vibrations during running: a model study, IEEE Trans. Biomed. Eng., 2012, 59(3), 797–804 Search PubMed.
- A. A. Zadpoor and A. A. Nikooyan, Modeling muscle activity to study the effects of footwear on the impact forces and vibrations of the human body during running, J. Biomech., 2010, 43(2), 186–193 CrossRef PubMed.
- A. A. Zadpoor, A. A. Nikooyan and A. R. Arshi, A model-based parametric study of impact force during running, J. Biomech., 2007, 40(9), 2012–2021 CrossRef PubMed.
- A. A. Zadpoor, Current trends in metallic orthopedic biomaterials: from additive manufacturing to bio-functionalization, infection prevention, and beyond, Int. J. Mol. Sci., 2018, 19(9), 2684 CrossRef PubMed.
- A. A. Zadpoor, Frontiers of additively manufactured metallic materials, Materials, 2018, 11(9), 1566 CrossRef PubMed.
- K. A. Brakke, The surface evolver, Exper. Math., 1992, 1(2), 141–165 CrossRef.
- X.-Y. Zhang, G. Fang, S. Leeflang, A. A. Zadpoor and J. Zhou, Topological design, permeability and mechanical behavior of additively manufactured functionally graded porous metallic biomaterials, Acta Biomater., 2019, 84, 437–452 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |