Mapping the frontiers of quinone stability in aqueous media: implications for organic aqueous redox flow batteries†
Daniel P.
Tabor‡
 a,
Rafael
Gómez-Bombarelli‡§
a,
Rafael
Gómez-Bombarelli‡§
 a,
Liuchuan
Tong
a,
Liuchuan
Tong
 a,
Roy G.
Gordon
a,
Roy G.
Gordon
 ab,
Michael J.
Aziz
ab,
Michael J.
Aziz
 b and
Alán
Aspuru-Guzik
b and
Alán
Aspuru-Guzik
 *acd
*acd
aDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA. E-mail: alan@aspuru.com
bHarvard John A. Paulson School of Engineering and Applied Sciences, Cambridge, Massachusetts 02138, USA
cDepartment of Chemistry and Department of Computer Science, University of Toronto, Toronto, Ontario M5S 3H6, Canada
dVector Institute, Toronto, ON M5G 1M1, Canada
First published on 3rd May 2019
Abstract
Quinone–hydroquinone pairs have been proposed as biologically-inspired, low-cost redox couples for organic electrolytes for electrical energy storage, particularly in aqueous redox flow batteries. In their oxidized form, quinones are electrophiles that can react with the nucleophilic water solvent resulting in loss of active electrolyte. Here we study two mechanisms of nucleophilic addition of water, one reversible and one irreversible, that limit quinone performance in practical flow batteries. Using a combination of density functional theory and semi-empirical calculations, we have quantified the source of the instability of quinones in water, and explored the relationships between chemical structure, electrochemical reduction potential, and decomposition or instability mechanisms. The importance of these mechanisms was further verified through experimental characterization of a family of alizarin-derived quinones. Finally, ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 prospective quinone pairs (over 1
000 prospective quinone pairs (over 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 calculations including decomposition products) were analyzed in a virtual screening using the learned design principles. Our conclusions suggest that numerous low reduction potential molecules are stable with respect to nucleophilic addition, but promising high reduction potential molecules are much rarer. This latter fact suggests the existence of a stability cliff for this family of quinone-based organic molecules, which challenges the development of all-quinone aqueous redox flow batteries.
000 calculations including decomposition products) were analyzed in a virtual screening using the learned design principles. Our conclusions suggest that numerous low reduction potential molecules are stable with respect to nucleophilic addition, but promising high reduction potential molecules are much rarer. This latter fact suggests the existence of a stability cliff for this family of quinone-based organic molecules, which challenges the development of all-quinone aqueous redox flow batteries.
1 Introduction
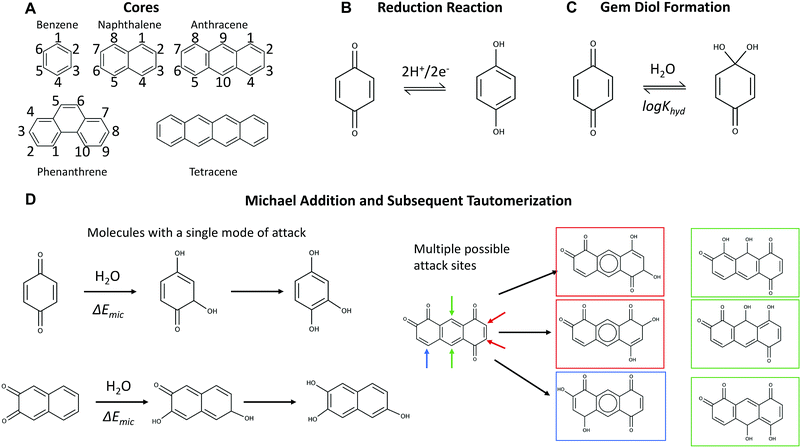
Flow batteries could help solve the intermittency problem of wind and solar renewable sources by storing electrical energy in fluids in scalable external storage tanks. Research into low-cost alternatives to current-standard vanadium electrolytes has exploded in the past five years, with organic, inorganic, and organometallic electrolytes developed for both aqueous and non-aqueous systems.1–19 For aqueous flow batteries, the vast majority of developments have been new molecules for the low reduction potential electrolyte (the negolyte), with the molecule for the high-potential electrolyte (the posolyte) serving as a greater challenge. Some success has been found using single-electron couples at neutral and high-pH.3–5,9,10 Initial work in acidic aqueous metal-free flow batteries used bromine as the posolyte active species2 and two recent studies used benzoquinone-based molecules.6,8 However, the maximum standard reduction potential for an acidic organic posolyte that has lasted even a few cycles (3,6-dihydroxy-2,4-dimethylbenzene sulfonic acid or DHDMBS) is only 0.85 V vs. the standard hydrogen electrode (SHE)—this is almost 0.4 V below the thermodynamic threshold for evolving oxygen.8 In addition to the need to develop high potential molecules, there is also interest in developing single molecules with three distinct, well separated (>1.0 V) redox states, that could potentially serve in both posolyte and negolyte. Discovering molecules with this property could enable flow batteries that replace the ion-selective membrane with an inexpensive porous separator.20–22 One potential three-redox-state molecule is a fused quinone, which contains four total ketone groups.A primary concern in developing flow battery electrolytes is their chemical and electrochemical stability. Organic molecules are subject to a variety of decomposition reactions, which vary across different backbones, functionalizations, and environments. Reactions involving quinones, as both reactants and catalysts, have long been of interest to chemists for both fundamental and industrial reasons.23 Researchers interested in employing quinones in aqueous flow batteries have investigated the susceptibility of low potential quinones to reactions with bromine in acid24 and anthrone formation in base.25 A Michael-addition mechanism has been proposed for their reactions with water.6,8,20
Here, we present a virtual screening of quinone space to quantify the thermodynamic susceptibility of quinones to decomposition reactions with water. We constructed a comprehensive library of quinone-derived molecules (with backbones shown in Fig. 1A), containing 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 hydroquinone pairs and associated products from reactions.4,26,27 The targets are high reduction potential and high thermodynamic stability with respect to water attack. Some high potential molecules, such as tiron, have been previously shown to undergo a Michael reaction in the literature and the calculated susceptibility can serve as a rough cutoff to use in screening. For this work, we experimentally characterized a family of alizarin derivatives (structures shown Table S3†) with high reduction potential to verify that these mechanisms transfer from benzoquinones to anthraquinones and gain some further information on what thermodynamic cutoffs to use in our virtual screening. These results, taken together, show the tradeoffs between achieving a high reduction potential quinone and maintaining long-term stability.
857 hydroquinone pairs and associated products from reactions.4,26,27 The targets are high reduction potential and high thermodynamic stability with respect to water attack. Some high potential molecules, such as tiron, have been previously shown to undergo a Michael reaction in the literature and the calculated susceptibility can serve as a rough cutoff to use in screening. For this work, we experimentally characterized a family of alizarin derivatives (structures shown Table S3†) with high reduction potential to verify that these mechanisms transfer from benzoquinones to anthraquinones and gain some further information on what thermodynamic cutoffs to use in our virtual screening. These results, taken together, show the tradeoffs between achieving a high reduction potential quinone and maintaining long-term stability.
2 Results and discussion
The molecular backbones and mechanisms of decomposition reactions that we considered are summarized in Fig. 1. The two-proton two-electron redox activity of a molecule (Fig. 1B) can be kinetically inhibited by the formation of a gem-diol (Fig. 1C) and the molecule can undergo chemical degradation through a Michael addition or substitution reaction (Fig. 1D).2.1 Reduction potential structure–property relationships
The choice of candidate quinone pool was based on previous reports,26 where molecular motifs more likely to give high reduction potentials and high solubility have been identified. The molecules were generated as fully reduced parts of redox pairs and subject to two-proton, two-electron oxidation reactions. The reduction potentials are calculated at the calibrated PM7 COSMO level of theory.28,29 Details on the calibration procedure and the calibration results for higher levels of theory are given at the end of the manuscript and in the ESI (Fig. S1†). The parity between the DFT and PM7 COSMO results on the calibration set enabled the computation of all of the properties of the molecules within this large chemical space. For hydroquinones with multiple potential oxidation patterns, all mechanisms have been considered, and results are reported for the reaction with the highest thermodynamic driving force.Fig. 2 plots the distribution of the calculated reduction potentials vs. SHE at pH = 0 for the benzoquinones, naphthoquinones, anthraquinones, and phenanthrene-functionalized quinones across the three main functional groups considered in this study: carboxylic acids, sulfonic acids, and phosphonic acids. Within each distribution, there are variations in the hydroxyl substitutions for the non redox-active parts of the molecules and the number and positioning of the other functional groups. In general, the redox pattern, also referred to as the relative positions of the redox-active hydroxyl groups, has the strongest influence over reduction potential; this is most easily seen by examining the median values in Fig. 2. The choice of electron withdrawing group has a slightly weaker effect, particularly for the larger backbones. Also of note is that essentially every redox pattern and functional group combination is capable of producing quinones with both high potentials (near ∼1.00 V) and low potentials (∼0.1 V). Overall, the theoretical methods predict that carboxylic acid and sulfonic acid functionalizations lead to higher reduction potentials within a given redox-active pattern.
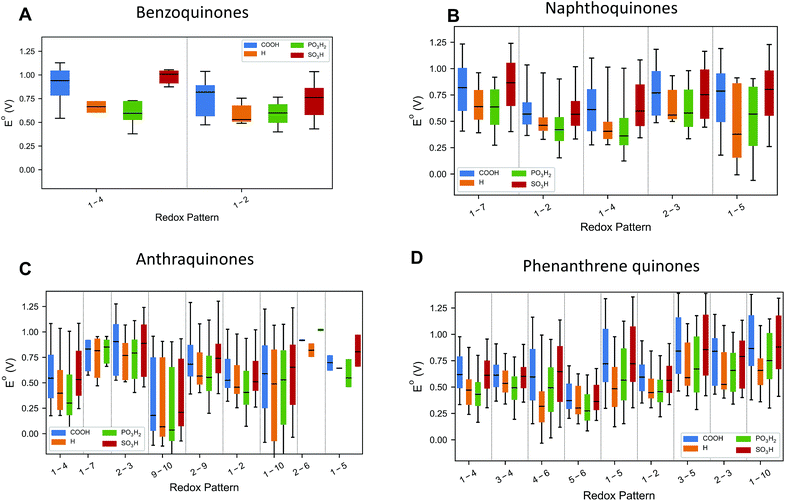 | ||
| Fig. 2 Reduction potential dependence on both relative ketone positions and functional groups. The numbers refer to the topology of the redox-active ketones and correspond to the labels in Fig. 1. The median of each set of data is indicated with a black line. The regions bounded by the colors indicate the range of the 5th and 95th percentile of reduction potentials. The lines extend out to the maximum and minimum reduction potential for each substitution and ketone topology. | ||
For the benzoquinones (Fig. 2A) and naphthoquinones (Fig. 2B), there is not as large of a difference between the medians of the different redox-active patterns as there are for the anthraquinones (Fig. 2C) and phenanthrene-functionalized quinones (Fig. 2D). In the former two cases, the functional groups are much more likely to be close to the redox-active sites of the molecules and thus appear to have a more pronounced effect on the reduction potential. For the two three-ring families of molecules, we see that certain reduction patterns consistently produce higher distributions with 1-7 and 2-3 for anthraquinones and 3-5, 2-3, and 1-10 for the phenanthrene-functionalized quinones.
2.2 Relationship between reduction potential and water stability: computational results
Having established the structure–property relationships between the quinone functionalization and reduction potential, the relationship between the reduction potential and thermodynamic stability criteria was explored. Two metrics of susceptibility related to the addition of water were considered: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd (the calculated base-10 logarithm) and ΔEmic for a reversible gem-diol formation (Fig. 1C) and irreversible Michael addition/substitution (Fig. 1D), respectively. The calibration results for the calculation of log
Khyd (the calculated base-10 logarithm) and ΔEmic for a reversible gem-diol formation (Fig. 1C) and irreversible Michael addition/substitution (Fig. 1D), respectively. The calibration results for the calculation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd are in Fig. S2.† The thermodynamic susceptibility to Michael addition is calculated from the initial reaction in Fig. 1D to form a high-energy tetrahedral intermediate that breaks aromaticity, which according to Hammond's postulate, should most bear the most similarity to the transition state associated with this reaction across the library of quinones. Though we do not have a calibration set for these Michael addition energies, we can compare molecules within the library to each other for relative fitness. Chemical principles suggest that as molecules become more electron-deficient, both the reduction potential would increase and so would the electrophilicity, thus increasing the susceptibility to nucleophilic attack from a species like water.
Khyd are in Fig. S2.† The thermodynamic susceptibility to Michael addition is calculated from the initial reaction in Fig. 1D to form a high-energy tetrahedral intermediate that breaks aromaticity, which according to Hammond's postulate, should most bear the most similarity to the transition state associated with this reaction across the library of quinones. Though we do not have a calibration set for these Michael addition energies, we can compare molecules within the library to each other for relative fitness. Chemical principles suggest that as molecules become more electron-deficient, both the reduction potential would increase and so would the electrophilicity, thus increasing the susceptibility to nucleophilic attack from a species like water.
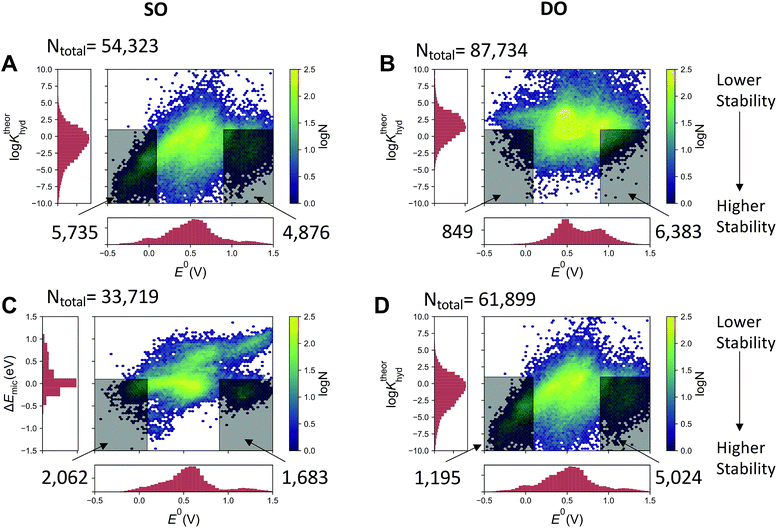
The quinone molecules were divided into two groups, motivated by the possibility of discovering a fused-quinone with three separated redox states. Note that in all cases, the fully reduced hydroquinone, which has no ketone groups, is subject to neither gem-diol formation nor the Michael addition. The first group includes quinones that have only a single two-proton two-electron oxidation (referred to in shorthand as SO – single oxidation) from its fully reduced form. The second group involves quinones that are the products of a subsequent second oxidation (referred to as DO – double oxidation), which means that the oxidized products have four ketone groups. Fig. 3A and B show the calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd of the SO and DO oxidized forms of the pairs, respectively, and Fig. 3C and D show the same for the Michael addition/substitution energy. We define Michael addition/substitution energy as
Khyd of the SO and DO oxidized forms of the pairs, respectively, and Fig. 3C and D show the same for the Michael addition/substitution energy. We define Michael addition/substitution energy as
| ΔEmic = (E(oxidized) + E(H2O) − E(Michael product)) | (1) |
For the first oxidation (SO group), the thermodynamic favorability of nucleophilic attack by water increases with the reduction potential of the molecule (Fig. 3A and C). This is consistent with the chemical principles argument outlined above that the more electron deficient core will have both a higher reduction potential and be more susceptible to Michael addition. However, for the second two-proton two-electron oxidations, the correlation between both log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd and ΔEmic and the reduction potential is substantially less pronounced, indicating that all fused quinones in their fully oxidized state are relatively electron deficient, or at least have an electron deficient spatial region, in terms of having a vulnerable site for water attack. This implies that the development of a fused quinone that is stable is more challenging than a high reduction potential molecule with the same reduction potential.
Khyd and ΔEmic and the reduction potential is substantially less pronounced, indicating that all fused quinones in their fully oxidized state are relatively electron deficient, or at least have an electron deficient spatial region, in terms of having a vulnerable site for water attack. This implies that the development of a fused quinone that is stable is more challenging than a high reduction potential molecule with the same reduction potential.
2.3 Experimental investigation of fused quinone stability
A family of fused quinones was investigated experimentally to both test the validity of the computational studies and also provide guidance for what cutoff criteria should be used for various properties in a virtual screening. The full list of molecules investigated is provided in Table S3 of the ESI.† The molecules in this family in general have a stable, reversible cyclic voltammetry (CV) signal at low potential (∼ 0.1–0.2 V), but do not have a reversible peak at high potential (∼1.0 V). The CVs are provided in Fig. S3–S5 in the ESI.† We focus on alizarin red S (molecule indicated in Fig. S6A†), which was subject to a single charging cycle in a flow cell. At 50% state of charge, an aliquot was taken and separated with high-performance liquid chromatography. The separated components were detected with mass spectrometry (MS), which allowed for assignment of the molecules present at 50% state of charge.Molecules were detected in two mass channels. The first detected molecule is the starting material (Fig. S6A†) with evidence of a small amount of impurity that corresponds to a sulfonate functionalization at a different position. The second detected mass (Fig. S6B†) has a mass consistent with two products: (1) Michael addition to the fully oxidized form of alizarin red S at the 4 position and subsequent tautomerization or (2) gem-diol formation on the fully oxidized form of alizarin red S, which theoretical calculations predict to be most thermodynamically favored at the 1 position (a smaller third peak is also detected, which is most likely the product of one of these processes on the impurity). When the mode of nucleophilic attack is Michael addition, it is effectively a reduction of the system (Fig. 1D) after tautomerization.
The LC-MS results raise the question on the extent of the vulnerability of the fully-oxidized molecule to Michael attack in the presence of water. It is possible to chemically synthesize the oxidized form of quinizarin (Fig. S7 of the ESI†) and leave it in solution overnight. In the presence of H2SO4, the molecule decomposes to some extent, but not completely, which implies that the oxidized form is at least stable on a measurable timescale.
For reference, the PM7 COSMO-calculated Michael addition energy to alizarin red S is 0.03 eV (lower susceptibility than predicted for tiron: 0.25 eV), which we use as an upper cutoff for the virtual screening criteria below.
2.4 Effects of Michael addition on reduction potential
Given the theoretical and experimental evidence for the susceptibility of high reduction potential quinones to Michael addition/substitution, the next important question to address is the ultimate effects of Michael addition on battery performance. To investigate this, we found ∼1700 molecules in our database that had been generated through combinatorics that are also Michael addition/substitution products of other molecules in our database and evaluated the reduction potential of these Michael products. The effects of Michael addition/substitution on the reduction potential show a bimodal distribution (Fig. 4A). The first of these modes clustered around a −0.15 to −0.2 V shift in reduction potential upon Michael addition. This cluster consists of molecules that maintain the same redox-active topology as before Michael addition and the decrease in the reduction potential simply comes from the increased electron density on the quinone core, due to the electron-donating tendencies of hydroxyl groups. The second cluster of molecules is centered around a −0.5 V shift in reduction potential. These correspond to molecules where the redox pattern is changed, for instance a 1-2 quinone becomes a 1-4 quinone. In both cases, Michael addition will substantially decrease the OCV of any battery that uses the Michael-susceptible molecule as a posolyte, as has been seen in tiron.6 In addition, the first Michael addition product may also be susceptible to further reactions with water; this would further decrease performance. Thus, it is most reasonable to search for molecules lacking thermodynamic susceptibility to Michael addition to begin with.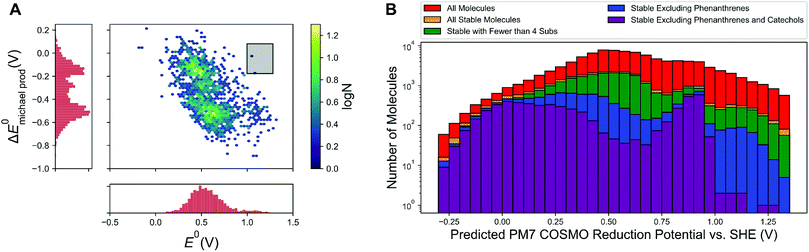 | ||
Fig. 4 (A) Change in the reduction potential of a molecule upon Michael addition, 1763 molecules pictured. The desired region, high potential molecules that show almost no change in reduction potential upon Michael addition, is shaded in the black box and contains only two molecules (sulfonated 1-4 benzoquinones), which are shown in Fig. S8.† (B) Plot of the redox potential distributions of various sets of molecules, as indicated in the legend. Molecules are defined as “stable” if they have the following criteria (1) PM7 COSMO Michael addition energy <0.03 eV and (2) log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd < 1.0. Khyd < 1.0. | ||
2.5 Number of promising candidates at all reduction potentials
Fig. 4B shows the number of molecules of particular categories with a Michael addition site that satisfy stability criteria, on a logarithmic scale. The stability criteria that were employed are:(1) Calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd < 1.0, this corresponds the gem-diol form of a molecule being less than 10 times more abundant, in equilibrium, than the oxidized form of the molecule. Although gem-diol formation is still more favored when Khyd is between 1 and 10, the redox-active ketone form may be present in sufficient quantity to give satisfactory battery performance.
Khyd < 1.0, this corresponds the gem-diol form of a molecule being less than 10 times more abundant, in equilibrium, than the oxidized form of the molecule. Although gem-diol formation is still more favored when Khyd is between 1 and 10, the redox-active ketone form may be present in sufficient quantity to give satisfactory battery performance.
(2) ΔEmic < 0.03 eV, this cutoff means that the molecule is less susceptible to Michael addition than alizarin red S, which we showed via LC-MS undergoes Michael addition.
At the low reduction potentials (<0.2 V), hundreds of molecules are calculated to be thermodynamically stable, even though our library was biased towards discovering high-reduction-potential molecules by employing electron withdrawing groups. However, at high reduction potentials (>0.95 V vs. SHE), the number of stable molecules drops off precipitously, especially if exotic phenanthrene-functionalized molecules or oxidized catechols (which may be vulnerable to kelation reactions) are excluded. The surviving molecules are enormously rare, numbering in the tens (and are shown in Fig. S9 and S10,† with estimated solubility computed using ChemAxon,30 in the ESI†). Given that there is a mean absolute error associated with the PM7 COSMO calculations of about 0.07 V for reduction potentials and 1.3 log units for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd from our calibrated results, it is possible that the molecules that are passing the stability screening are the molecules with larger calculations errors and thus are false positives. Ideally, the strongest candidates from a virtual screening will pass the screening criteria by several multiples of the error bars associated with the calculations; the absence of said molecules suggests that molecules with the desired properties are especially rare for “traditional” quinones with straightforward modifications. Making the criteria more stringent (log
Khyd from our calibrated results, it is possible that the molecules that are passing the stability screening are the molecules with larger calculations errors and thus are false positives. Ideally, the strongest candidates from a virtual screening will pass the screening criteria by several multiples of the error bars associated with the calculations; the absence of said molecules suggests that molecules with the desired properties are especially rare for “traditional” quinones with straightforward modifications. Making the criteria more stringent (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd < 0.0 and ΔEmic < 0.00 eV) dramatically reduces the number of viable molecules (Fig. S11†). It should be noted that there is a population of about 40
Khyd < 0.0 and ΔEmic < 0.00 eV) dramatically reduces the number of viable molecules (Fig. S11†). It should be noted that there is a population of about 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 pairs, containing mostly exotic phenanthrene-functionalized quinones, with oxidized forms lacking a valid Michael addition site according to the substitution rules we formulated. These are potentially viable, resulting in about 1500 pairs whose oxidized form has a predicted reduction potential > 0.95 V vs. SHE. A sampling of these is enumerated in Fig. S12 in the ESI† and the full list is provided in a computer-readable format. These molecules are expected to be challenging to synthesize and it is possible that they are subject to other decomposition mechanisms not considered in this work, but they constitute a substantial fraction of the most promising molecules at this juncture.
000 pairs, containing mostly exotic phenanthrene-functionalized quinones, with oxidized forms lacking a valid Michael addition site according to the substitution rules we formulated. These are potentially viable, resulting in about 1500 pairs whose oxidized form has a predicted reduction potential > 0.95 V vs. SHE. A sampling of these is enumerated in Fig. S12 in the ESI† and the full list is provided in a computer-readable format. These molecules are expected to be challenging to synthesize and it is possible that they are subject to other decomposition mechanisms not considered in this work, but they constitute a substantial fraction of the most promising molecules at this juncture.
3 Conclusion
Taking the computational screening and the experimental results together, it is not surprising that the highest reduction potential quinone that has been demonstrated with any full cell cycling in acid reported to date has a reduction potential at 0.85 V vs. SHE (DHDMBS).8 This lies very close to the stability cliff that we observed in our library, which is between 0.90 and 0.95 V. These results have several implications for the future development of an all-organic redox flow battery. We found almost no quinones that are based on currently used backbones with currently employed functional groups that are both high in reduction potential (leading to >1.0 V OCV when paired against another quinone) and thermodynamically protected from Michael addition and/or gem-diol formation. Going forward, two pathways for exploration that do not involve fused quinones are apparent: (1) attempt to synthesize the exotic phenanthrene-based quinones (which may be susceptible to other not-yet-observed decomposition mechanisms, see Scheme S1 in the ESI† for another potential mechanism), or (2) employ strategies to mitigate the Michael addition from a kinetics perspective. Our calculations indicate that the thermodynamic susceptibility to Michael substitution is about 0.13 eV less than the thermodynamic susceptibility to Michael addition between potentials of 1.00 and 1.05 V after averaging over all of the R-groups considered in this study. This can be taken a step further, by developing molecules which, while thermodynamically susceptible to Michael addition, may not be kinetically susceptible, through protection with bulky groups. This strategy has the drawback of adding molecular weight and potentially increasing synthetic cost and decreasing the solubility of the molecules. It would also be desirable to screen for this computationally (as opposed to here, where we investigated the highest energy intermediate along the nucleophilic addition pathway), though transition state searches are expensive. While introducing a bulky functional group to block the Michael addition/substitution site makes sense from a kinetics perspective, it is not clear what strategy might be employed to mitigate the effects of gem-diol formation. The groups could also lead to the stabilization of tertiary carbocations if the molecule is protonated in acidic solution. The formation of these carbocations was recently reported as a key step in the capacity fade mechanism for DHDMBS.31 Another potential strategy could be to modulate the pKas of the redox-active sites of the reduced form of these couples. This would lead to a “flattening out” of the potential on the Pourbaix diagram at lower pH and could lead to otherwise unpromising molecules at pH = 0 becoming viable at higher values of pH. Additionally, it may be necessary to investigate other organic molecule or low-cost metal complex9,10 motifs to find molecules that are less susceptible to water attack, while still providing the high reduction potential and energy density. Finally, although aqueous redox flow batteries have large advantages in terms of solvent cost and conductivity over non-aqueous systems, the absence of these water-driven instability mechanisms explored here in the latter makes further research and development intriguing.4 Experimental methods
Flow cells were constructed similar to previous reports.3,18 Pyrosealed POCO graphite flow plates were used for both electrodes. Each electrode comprised a 5 cm2 geometric surface area covered by a stack of three sheets of Sigracet SGL 39AA porous carbon paper pre-baked in air overnight at 400 °C. The membrane used was Nafion 117. The pumping rate was 60 mL min−1. The positive electrolyte used was 7 mL 0.1 M alizarin red S dissolved in 1 M sulfuric acid. The negative electrolyte used was 30 mL 0.2 M 2,7-anthraquinone-disulfonic acid dissolved in 1 M sulfuric acid. Aliquots were taken out at 50% state-of-charge in the first charging cycle as calculated by coulometry.High-resolution LC-MS analysis of alizarin red S decomposition products was performed in the Small Molecule Mass Spectrometry Facility at Harvard on a Bruker Impact II q-TOF with internal calibration by sodium formate clusters. Liquid chromatography was performed on an Agilent 1290 Infinity HPLC using a Allure PFPP column (5 μm particle size, 150 × 2.1 mm) at a flow rate of 0.4 mL min−1 and the following elution conditions were applied (solvent A = 0.1% v/v formic acid in water; solvent B = 0.1% v/v formic acid in acetonitrile): 100% solvent A for 2 min, a gradient increasing from 0% to 15% solvent B in solvent A over 13 min, a gradient increasing to 100% solvent B over 5 min, a gradient decreasing to 0% solvent B in solvent A over 0.1 min, and 100% solvent A for 4.9 min. The ESI mass spectra were recorded in negative ionization mode.
5 Computational methods
5.1 Library generation
Molecular libraries were generated programmatically, using several aromatic backbones (benzene, naphthalene, and anthracene from a previous study26 and phenanthrene and tetracene, which are new for this work; see Fig. 1) using the open-source cheminformatics suite RDKit.32 The previous study26 showed that the two-proton, two-electron redox processes in benzo-, naphtho-, and anthraquinones can be modulated by changing the number and position of various substituents along with the positions of the redox-active ketones. The results from that work, using single and full substitution patterns, match organic chemistry principles. This suggests that electron-donating groups (EDG) such as –OH and electron-withdrawing groups (EWG) such as –COOH, –SO3H, –PO3H2 can tune E0 while maintaining high aqueous solubility and synthetic accessibility.For this work, molecules were generated using all possible substitution patterns for each of the three electron withdrawing groups alone and in combination with hydroxyls. In addition, the quinone dataset was expanded via intuition-driven suggestions from experimental collaborators. The molecules generated were used as the reduced parts of redox pairs and subject to two-proton, two-electron oxidation reactions. The R-groups that were included for all backbones were carboxylic, hydroxyl, phosphonic, and sulfonic. In addition, for benzoquinones methylimidazolium, methylpyridinium, and tetramethylimidazolium groups were included on benzoquinones based on feedback from experimentalists.
The presence of multiple hydroxyl R-groups implies multiple oxidation patterns for a given molecule, but only one isomer will be thermodynamically predominant at virtually any given redox potential. Redox pairs were stored in a database as objects with pointers to reduced and oxidized molecules, allowing us to build reactivity graphs. The ability to create and track molecular linkages allowed us to book-keep the relationships between the species and to calculate pairwise properties, such as reaction free energies.
The presence of multiple substitutions also expands the idea of blocking of Michael addition. This blockage was less likely to happen in the previous one-substitution studies. However, these substituents are also good leaving groups, so the important quantity to examine is the relative energy of the tetrahedral intermediate of the Michael substitution. If this step in the proposed mechanism is thermodynamically favored, then we assume that substitution is favored overall.
Whereas some of the patterns may appear rare and are thermodynamically unfavorable if alternative oxidations exist, it is important to include them. Otherwise a fraction of the molecules in a reaction graph could be outside the library, and thus completely ignored. In total, 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 857 quinone/hydroquinone pairs were generated. Corresponding gem-diols for each oxidized molecule were also included in the database. We also included decomposition products associated with irreversible Michael addition of water onto α-β unsaturated carbonyls (or α-γ, α-δ, etc. when available). Depending on the substitution of the β site, two potential pathways are possible:
857 quinone/hydroquinone pairs were generated. Corresponding gem-diols for each oxidized molecule were also included in the database. We also included decomposition products associated with irreversible Michael addition of water onto α-β unsaturated carbonyls (or α-γ, α-δ, etc. when available). Depending on the substitution of the β site, two potential pathways are possible:
(1) For hydrogen-substituted sites, this reaction results in an intermediate enol, which isomerizes to a reduced, hydroxylated hydroquinone (Fig. 1C). Thus, the final product of this reaction is an electrochemically active quinone, although it is in the reduced state, so it needs to be oxidized again to recover the stored charge. However, this molecule can have significantly different electrochemical behavior than the original electrolyte with a much lower potential.
(2) For functionalized β sites and depending on the nature of the substituent, the addition can be followed by loss of the R-group and isomerization to hydroquinone. Bulky substituents will have a significant steric effect, increasing the barrier for water addition.
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043 Michael addition products were generated from these pairs, based on the allowed patterns considered above. Both Michael substitution and Michael addition were allowed. We originally explored other avenues for exploring reactivity. Fukui functions33 are known to be good qualitative descriptors for broad classes of reactivity,34 but for our application here where we seek a quantitative assessment of known, well-defined mechanisms, direct computation of the landscape of products and intermediates is more appropriate.35,36
043 Michael addition products were generated from these pairs, based on the allowed patterns considered above. Both Michael substitution and Michael addition were allowed. We originally explored other avenues for exploring reactivity. Fukui functions33 are known to be good qualitative descriptors for broad classes of reactivity,34 but for our application here where we seek a quantitative assessment of known, well-defined mechanisms, direct computation of the landscape of products and intermediates is more appropriate.35,36
5.2 Electronic structure methods
Quantum chemistry is the bottleneck of this virtual screening study. In the previous study on a select group of singly and fully-substituted quinones (totaling 1710 quinone molecules), plane wave DFT calculations were employed.26 Here, on a molecular screening study with ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules (considering all of the potential decomposition products that are also considered), lower cost electronic structure methods are needed that also maintain accuracy similar to the previous study. Other recent studies have also demonstrated capability of different levels of DFT (with and without calibration and/or explicit solvation) to estimate the reduction potentials of organic molecules, including quinones.4,27,37,38
000 molecules (considering all of the potential decomposition products that are also considered), lower cost electronic structure methods are needed that also maintain accuracy similar to the previous study. Other recent studies have also demonstrated capability of different levels of DFT (with and without calibration and/or explicit solvation) to estimate the reduction potentials of organic molecules, including quinones.4,27,37,38
The calculated reaction energies for both reduction and gem-diol reactions were benchmarked against experimental reduction potentials and gem-diol hydration equilibrium constants (Tables S1 and S2 of the ESI†) at several different levels of electronic structure theory. Benchmarking studies have been performed at the following levels of theory: PBE/6-31G(d) optimization and B3LYP/6-31G(d) optimization, B3LYP/6-311+G(d,p) gas-phase single point (at PBE/6-31G(d) gas-phase geometries), and B3LYP/6-311+G(d,p) PCM single point energies using the CPCM as implemented in QChem 4.0 with water as the solvent.39 The PBE/6-31G(d) optimizations were implemented using TeraChem.40,41 Semi-empirical methods were also benchmarked; the energies were computed at both the PM7 and PM7 with the COSMO solvation model with water as a solvent (referred to as PM7 and PM7 COSMO, respectively).
We have performed a benchmark study of these cheaper methods and compared their ability to predict the reduction potential and hydration equilibrium constant.
Using a well-characterized experimental set of reduction potential measurements, we tested the calibration scheme by comparing the zero-temperature reaction electronic energy for the reduction (Ered) with experimentally-determined quinone reduction potentials (E0) in aqueous solution (pH = 0) at 298 K.26 Notwithstanding computational affordability, all the methods are close in the accuracy of their predictions (see ESI Fig. S1†).
Similarly, we carried out carried out a calibration of the hydration equilibrium constant by mapping zero-temperature energy differences for the carbonyl hydration reaction (Ehyd) with experimentally determined equilibrium constants42 (Khyd) in water at 298 K.
When considering both the accuracy and computational cost of the various methods, the PM7 COSMO optimization has the best balance. B3LYP/6-311+G(d,p) (PCM) gives a marginally lower deviation on the calibration set, but does not justify the extra cost here.
As stated above, for computing the vulnerability to Michael addition/substitution, we did not have a body of data against which to calibrate. However, we can use the results of tiron and alizarin red S to gain a sense of scale. At the PM7 COSMO level of theory, the Michael addition free energy for water addition to tiron is 0.25 eV and that of alizarin red S is 0.03 eV. We expect the Khyd and Michael addition energy calculations to be of the most utility in acidic and neutral pH—the regime where water (and not hydroxide) is the primary nucleophilic species present.
Conflicts of interest
L. T., R. G. G., M. J. A., and A. A.-G. are inventors on a patent application “Quinone and Hydroquinone Based Flow Battery.” Patent Application US20160248114A1. Filed by Harvard University.Acknowledgements
Research at Harvard was supported by the Innovation Fund Denmark via the Grand Solutions project “ORBATS” file nr. 7046-00018B, U.S. DOE ARPA-E award DE-AR0000767, and the Massachusetts Clean Energy Technology Center. This work was also supported by the National Science Foundation through grant No. CBET-1509041. A. A.-G. is very thankful to the Canadian Institute for Advanced Research (CIFAR) for their generous support and collaborations. A. A.-G. thanks Anders G. Frøseth for the generous support of his work. A. A.-G. acknowledges support from the Canada 150 Research Chairs Program.References
- F. R. Brushett, J. T. Vaughey and A. N. Jansen, Adv. Energy Mater., 2012, 2, 1390–1396 CrossRef CAS.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198 CrossRef CAS PubMed.
- K. Lin, Q. Chen, M. R. Gerhardt, L. Tong, S. B. Kim, L. Eisenach, A. W. Valle, D. Hardee, R. G. Gordon, M. J. Aziz and M. P. Marshak, Science, 2015, 349, 1529–1532 CrossRef CAS PubMed.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 1, 16102 CrossRef CAS.
- T. Liu, X. Wei, Z. Nie, V. Sprenkle and W. Wang, Adv. Energy Mater., 2016, 6, 1501449 CrossRef.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. K.S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2014, 161, A1371–A1380 CrossRef CAS.
- T. Janoschka, N. Martin, M. D. Hager and U. S. Schubert, Angew. Chem., Int. Ed., 2016, 55, 14427–14430 CrossRef CAS PubMed.
- L. Hoober-Burkhardt, S. Krishnamoorthy, B. Yang, A. Murali, A. Nirmalchandar, G. K. S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2017, 164, A600–A607 CrossRef CAS.
- B. Hu, C. DeBruler, Z. Rhodes and T. L. Liu, J. Am. Chem. Soc., 2017, 139, 1207–1214 CrossRef CAS PubMed.
- E. S. Beh, D. De Porcellinis, R. L. Gracia, K. T. Xia, R. G. Gordon and M. J. Aziz, ACS Energy Lett., 2017, 2, 639–644 CrossRef CAS.
- J. A. Kowalski, M. D. Casselman, A. P. Kaur, J. D. Milshtein, C. F. Elliott, S. Modekrutti, N. H. Attanayake, N. Zhang, S. R. Parkin, C. Risko, F. R. Brushett and S. A. Odom, J. Mater. Chem. A, 2017, 5, 24371–24379 RSC.
- W. Duan, J. Huang, J. A. Kowalski, I. A. Shkrob, M. Vijayakumar, E. Walter, B. Pan, Z. Yang, J. D. Milshtein, B. Li, C. Liao, Z. Zhang, W. Wang, J. Liu, J. S. Moore, F. R. Brushett, L. Zhang and X. Wei, ACS Energy Lett., 2017, 2, 1156–1161 CrossRef.
- T. Quan, R. D. Milton, S. Abdellaoui and S. D. Minteer, Chem. Commun., 2017, 53, 8411–8414 RSC.
- C. S. Sevov, K. H. Hendriks and M. S. Sanford, J. Phys. Chem. C, 2017, 121, 24376–24380 CrossRef CAS.
- Z. Yang, L. Tong, D. P. Tabor, E. S. Beh, M.-A. Goulet, D. De Porcellinis, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2018, 8, 1702056 CrossRef.
- G. Kwon, S. Lee, J. Hwang, H.-S. Shim, B. Lee, M. H. Lee, Y. Ko, S.-K. Jung, K. Ku, J. Hong and K. Kang, Joule, 2018, 2, 1771–1782 CrossRef CAS.
- A. Hollas, X. Wei, V. Murugesan, Z. Nie, B. Li, D. Reed, J. Liu, V. Sprenkle and W. Wang, Nat. Energy, 2018, 3, 508–514 CrossRef CAS.
- D. G. Kwabi, K. Lin, Y. Ji, E. F. Kerr, M.-A. Goulet, D. De Porcellinis, D. P. Tabor, D. A. Pollack, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Joule, 2018, 2, 1894–1906 CrossRef CAS.
- Y. Ji, M.-A. Goulet, D. A. Pollack, D. G. Kwabi, S. Jin, D. De Porcellinis, E. F. Kerr, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2019, 1900039 CrossRef.
- K. Wedege, E. Dražević, D. Konya and A. Bentien, Sci. Rep., 2016, 6, 39101 CrossRef CAS PubMed.
- J. Carretero-Gonzalez, E. Castillo-Martinez and M. Armand, Energy Environ. Sci., 2016, 9, 3521–3530 RSC.
- B. Huskinson, M. Marshak, M. J. Aziz, R. G. Gordon, A. Aspuru-Guzik, S. Er, C. Suh, L. Tong and K. Lin, Quinone and Hydroquinone Based Flow Battery, Patent Application US20160248114A1, 2016.
- A. E. Wendlandt and S. S. Stahl, in Quinones in Hydrogen Peroxide Synthesis and Catalytic Aerobic Oxidation Reactions, John Wiley & Sons, Ltd, 2016, ch. 14, pp. 219–237 Search PubMed.
- M. R. Gerhardt, L. Tong, R. Gómez-Bombarelli, Q. Chen, M. P. Marshak, C. J. Galvin, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2017, 7, 1601488 CrossRef.
- M.-A. Goulet, L. Tong, D. A. Pollack, D. P. Tabor, S. A. Odom, A. Aspuru-Guzik, E. E. Kwan, R. G. Gordon and M. J. Aziz, J. Am. Chem. Soc., 2019 DOI:10.1021/jacs.8b13295.
- S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Chem. Sci., 2015, 6, 885–893 RSC.
- S. D. Pineda Flores, G. C. Martin-Noble, R. L. Phillips and J. Schrier, J. Phys. Chem. C, 2015, 119, 21800–21809 CrossRef CAS.
- James J. P. Stewart, MOPAC2016, Stewart Computational Chemistry, Colorado Springs, CO, USA, 2016, http://OpenMOPAC.net Search PubMed.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- Marvin 18.1.0, 2018, ChemAxon, http://www.chemaxon.com Search PubMed.
- A. Murali, A. Nirmalchandar, S. Krishnamoorthy, L. Hoober-Burkhardt, B. Yang, G. Soloveichik, G. K. S. Prakash and S. R. Narayanan, J. Electrochem. Soc., 2018, 165, A1193–A1203 CrossRef CAS.
- G. Landrum, RDKit: Open-source cheminformatics, http://www.rdkit.org Search PubMed.
- Y. Li and J. N. S. Evans, J. Am. Chem. Soc., 1995, 117, 7756–7759 CrossRef CAS.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Molecules, 2016, 748 CrossRef PubMed.
- F. Méndez and J. L. Gázquez, J. Am. Chem. Soc., 1994, 116, 9298–9301 CrossRef.
- J. L. Gázquez and F. Méndez, J. Phys. Chem., 1994, 98, 4591–4593 CrossRef.
- M. T. Huynh, C. W. Anson, A. C. Cavell, S. S. Stahl and S. Hammes-Schiffer, J. Am. Chem. Soc., 2016, 138, 15903–15910 CrossRef CAS PubMed.
- H. Kim, T. Goodson and P. M. Zimmerman, J. Phys. Chem. C, 2016, 120, 22235–22247 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- TeraChem v 1.9, PetaChem, LLC, 2009, 2015, see http://www.petachem.com Search PubMed.
- I. S. Ufimtsev and T. J. Martinez, J. Chem. Theory Comput., 2009, 5, 2619–2628 CrossRef CAS PubMed.
- R. Gómez-Bombarelli, M. González-Pérez, M. T. Pérez-Prior, E. Calle and J. Casado, J. Phys. Chem. A, 2009, 113, 11423–11428 CrossRef PubMed.
Footnotes |
† Electronic supplementary information (ESI) available: The ESI contains plots showing the calibration of the reduction potential and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd at different levels of electronic structure theory, the raw data that are used to calibrate the reduction potential and log Khyd at different levels of electronic structure theory, the raw data that are used to calibrate the reduction potential and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Khyd, CVs and the calculated thermodynamic stability of the alizarin family, the synthesis and NMR stability study of quinizarin, lists of high-potential molecules that pass various stability criteria, results of screening from stricter stability criteria, and a scheme for a potential ring-opening mechanism not fully explored in this paper. See DOI: 10.1039/c9ta03219c Khyd, CVs and the calculated thermodynamic stability of the alizarin family, the synthesis and NMR stability study of quinizarin, lists of high-potential molecules that pass various stability criteria, results of screening from stricter stability criteria, and a scheme for a potential ring-opening mechanism not fully explored in this paper. See DOI: 10.1039/c9ta03219c |
| ‡ These authors contributed equally to this work. |
| § Present address: Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. |
| This journal is © The Royal Society of Chemistry 2019 |