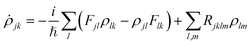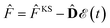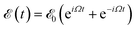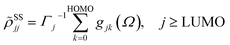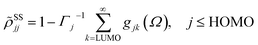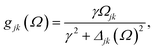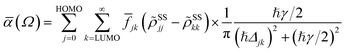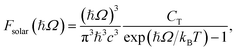Increasing the optical response of TiO₂ and extending it into the visible region through surface activation with highly stable Cu₅ clusters

Abstract

The decoration of semiconductors with subnanometer-sized clusters of metal atoms can have a strong impact on the optical properties of the support. The changes induced differ greatly from effects known for their well-studied, metallic counterparts in the nanometer range. In this work, we study the deposition of Cu₅ clusters on a TiO₂ surface and investigate their influence on the photon-absorption properties of TiO₂ nanoparticles via the computational modeling of a decorated rutile TiO₂ (110) surface. Our findings are further supported by selected experiments using diffuse reflectance and X-ray absorption spectroscopy. The Cu₅ cluster donates an electron to TiO₂, leading to the formation of a small polaron Ti³⁺ 3d¹ state and depopulation of Cu(3d) orbitals, successfully explaining the absorption spectroscopy measurements at the K-edge of copper. A monolayer of highly stable and well fixated Cu₅ clusters is formed, which not only enhances the overall absorption, but also extends the absorption profile into the visible region of the solar spectrum via direct photo-induced electron transfer and formation of a charge-separated state.

---

1 Introduction

Titanium dioxide is one of the most popular materials for photocatalytic applications and solar energy conversion due to its abundance, non-toxicity, biological inertness, and chemical stability. However, a large band-gap of 3.2 eV and 3.0 eV for the most common forms rutile and anatase, respectively, enables the absorption of ultraviolet irradiation to trigger photoinduced reactions. This undesired feature severely limits the usability of TiO₂ for solar energy conversion as the UV part comprises only 5–8% of the total energy of solar light. As a consequence, the rate of formation of reaction products divided by the incident photon flow is typically under 10% in TiO₂-based photocatalysts.^1,2

Several methods are known to extend the photoactivity of TiO₂ to the visible region, e.g. the insertion of transition metals or rare earth elements to modify its electronic structure,^3,4 the sensitization of TiO₂ photoelectrodes via copper phthalocyanine,⁵ or the biosynthesis of transition metal-doped TiO₂ nanoparticles.^6,7 Standard techniques for doping include wet impregnation,⁸ sol–gel spin coating,⁹ and hydrothermal^10,11 and oxidative pyrolysis.¹²

Due to quantum confinement, small clusters of metal atoms (with sizes below approx. 1.5 nm, i.e. approximately 150 atoms) behave very different from the corresponding bulk material or nanoparticles. For example, due to their small size, atomic clusters do not retain their metallicity and do not show plasmonic behavior, which is very characteristic of Au, Ag and Cu nanoparticles in the visible region.¹³ Instead, the presence of a molecule-like HOMO–LUMO gap has a strong impact on their chemical and physical properties with potential applications including luminescence,¹⁴ sensing,¹⁵ therapeutics,¹⁶ energy conversion,¹⁷ and catalysis.¹⁸ Although some results were reported before for the use of metal clusters as photosensitizers of solar cells¹⁹ and to extend the photoactivity of TiO₂,²⁰ the increase in activity was only moderate. This is mainly due to the use of large, strongly bonding ligands which are usually introduced to synthesize and to protect the clusters (mostly thiolated organic molecules). The use of small and weak protecting ligands (tetrabutylammonium) leads to a dramatic increase of the photocatalytic quantum efficiencies up to three orders of magnitude in comparison to standard SCs, as has been shown in recent experiments.²¹ Therefore, the use of ligand-free clusters, which can directly interact with the substrate, should be preferred. This can be achieved by kinetic control using electrochemical methods. Such techniques open the possibility for numerous applications ranging from cancer therapeutic drugs¹⁶ to efficient hydrogen photoproduction.²²

Except for the sensitization strategy with copper phthalocyanine molecules, all techniques mentioned above imply a direct modification of the electronic structure of the bulk material in order to increase the activity of TiO₂. As an alternative, we study the impact of deposition of a single monolayer of Cu₅ clusters (i.e. planar decoration with non-interacting, isolated Cu₅ clusters) onto the surface of TiO₂ (see Fig. 1), taking advantage of the slightly different electronic structure at the Cu₅–TiO₂ layer and the ability to create electron–hole pairs in the direct vicinity of the surface. These two features bear the potential to boost the quantum efficiency of charge transfer processes onto surface-mounted photocatalysts, making such a material superior to standard semiconductors (SCs). In the latter, photogenerated charge carriers have to travel large distances to reach the surface, which increases their probability of recombination and quenches the total charge transfer significantly.

Fig. 1 Decoration of TiO₂ with a Cu₅ cluster (global minimum configuration). Bridging oxygen atoms O_b, five-fold coordinated titanium atoms Ti_5f, and in-plane oxygen atoms O_p are indicated for later reference in the text.

Previously reported experimental measurements indicate an exceptional chemical stability of Cu₅ clusters against irreversible oxidation through the formation of CuO_x oxides,²³ which are stable in solution in the whole pH range (1–14). This stability of ‘atomic’ or sub-nanometer-sized Cu clusters is in stark contrast with the irreversible oxidation observed for larger Cu clusters or plasmonic nanoparticles (≈2 nm), as recently reported by Corma's group.²⁴ Moreover, we have also observed that Cu₅ clusters deposited onto TiO₂ are stable against irreversible oxidation via the formation of CuO_x oxides at temperatures higher than 700 °C,²⁵ and display very interesting properties for electrochemical applications.^26,27 In this article, we study the impact of the deposition of Cu₅ atomic clusters on the optical properties of titanium oxide, providing a thorough theoretical analysis followed by its experimental validation.

First, we address the stability of Cu₅ clusters deposited on the rutile TiO₂ (110) surface and simulate their impact on the optical response of the support material through computational modelling. Density functional theory (DFT) is applied to shed light on the charge transfer processes and band structure changes triggered by the adsorption. Furthermore, a mechanism is identified which explains how the deposition of Cu₅ onto TiO₂ can extend the photon absorption of the material into the visible region of the solar spectrum. Finally, diffuse reflectance and X-ray absorption spectroscopy measurements are presented which confirm our theoretical predictions.

DFT allows accurate characterization of molecular adsorption onto solid surfaces if special care is taken of dispersion interaction. In this work, we have chosen a DFT-D3 ansatz^28,29 on the basis of its excellent performance in describing the adsorption of small silver clusters on the same surface.³⁰ Structural optimizations and the calculation of interaction energies are performed with the Perdew–Burke–Ernzerhof (PBE) density functional and the Becke–Johnson (BJ) damping²⁸ for the D3 dispersion correction. We will refer to this combination as the PBE-D3(BJ) scheme. The Hubbard DFT + U term³¹ was added in PBE-D3(BJ) minimizations of all atoms of the Cu₅/TiO₂ system to describe localized 3d-electrons on Ti cations.

In order to calculate the theoretical absorption spectra, we employ reduced density matrix (RDM) theory within the Redfield approximation,³² combined with DFT calculations using the HSE06 hybrid functional of Heyd, Scuseria and Ernzerhof,^33,34 a well-established tool for the band gap analysis of semiconductors including TiO₂.³⁵ Moreover, the RDM treatment has been successfully applied to atomic silver clusters adsorbed on semiconductor TiO₂ and silicon surfaces.^30,36–39

On the experimental side, we have chosen diffuse reflectance spectroscopy (DRS) as a suitable technique to measure the optical absorption spectra of TiO₂ nanoparticles (NPs) with and without additional surface coating with Cu₅ clusters. Additionally, X-ray absorption spectroscopy (XAS) measurements in the XANES (X-ray absorption near edge structure) region at the K-edge of copper have been performed, mainly to probe the modification in the electronic structure of Cu atoms in Cu₅ clusters upon surface adsorption.

2 Results and discussion

2.1 Adsorption energies of the Cu₅ cluster on TiO₂

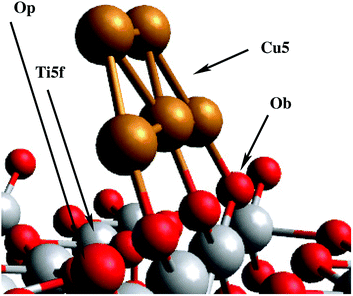
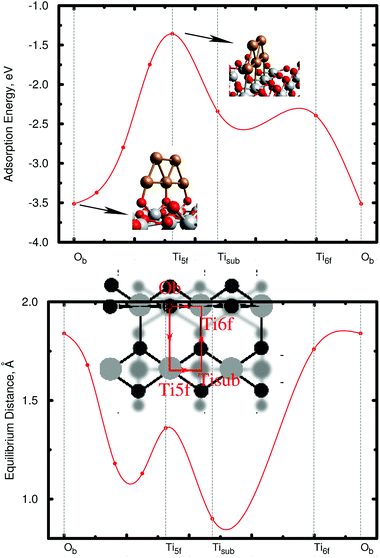
As a first step, the geometry of the bare cluster Cu₅ is optimized with the PBE-D3(BJ) method, resulting in a planar trapezoidal structure. Keeping this geometry fixed, we then insert the Cu₅ cluster into our slab model and perform a series of periodic PBE-D3 calculations in order to characterize the energy landscape for cluster adsorption. The copper cluster is displaced along four straight trajectories as shown in the small subgraphics of Fig. 2, but allowed to relax with respect to its distance from the surface at each point. The planar, trapezoidal cluster is kept perpendicular to the TiO₂ surface at all times, with its Cu–Cu–Cu axis parallel to the rows of surface oxygen atoms. This way, the one-dimensional surface scan runs through the previously determined minimum energy configuration (fully optimized without constraints) which corresponds to a position where the Cu–Cu–Cu axis is exactly above a row of bridging oxygen atoms O_b as shown in the inset of Fig. 2. Although performed on constrained pathways, this series of scans provides a useful impression of the energy landscape, which is illustrated in the upper graphics of Fig. 2. The lower graphics shows the corresponding minimum energy distance between the cluster and the TiO₂ (110) surface at each point on the pathway.

Fig. 2 Illustration of the stability of the Cu₅ cluster upon deposition on the rutile TiO₂ (110) surface. Adsorption energies (upper graphics) and optimized vertical distances (lower graphics) – from the central Cu atom to the surface plane where the bridging oxygen atoms O_b are located – along the pathway connecting four reference adsorption sites on the TiO₂ (110) surface: O_b atoms; atop fivefold coordinated titanium atoms (Ti_5f); hollow site atop the titanium atoms on the 2^nd-molecular-layer (Ti_sub); atop sixfold coordinated titanium atoms (Ti_6f).

The first thing to notice from Fig. 2 is that supported Cu₅ clusters are very stable. Adsorption energies are very large (up to −3.5 eV), but so are the energy barriers for diffusion. This indicates that cluster diffusion is highly unlikely at room temperature, at which the experiments were carried out. Therefore, any diffusion of clusters deposited on TiO₂ can be neglected in the given case. In fact, as stated in the introduction, the diffusion of Cu₅ clusters (and with it their agglomeration to larger, more easily oxidized nanoparticles) is observed only at temperatures as high as ≈700 °C.²⁵ Moreover, at the adsorbed global minimum configuration shown in Fig. 1, the structure of the Cu₅ cluster changes very little from its gas-phase geometry: the Cu–Cu distances are minimally elongated by 0.06 Å and the adsorption energy increases by just 0.21 eV, with the cluster getting slightly tilted towards the Ti_5f site. As can be observed from Fig. 1, three copper atoms are above three bridging oxygen atoms. Note that the Cu₅ cluster is stable in that configuration even without including the dispersion contribution (see the ESI†). Contrarily, when the Cu₅ cluster shifts in space so that three Cu atoms become aligned along the row of Ti_5f atoms, the resulting structure (referred to as an “atop Ti_5f” structure) is 2 eV higher in energy (see Fig. 2). The binding energy of Cu₅ in the atop Ti_5f configuration is significant only if dispersion is included.

2.2 Electronic structure in the ground state: copper cluster oxidation state, XANES spectra, frontier orbitals, and electronic density of states

For appropriate determination of the electronic structure, we have applied the HSE06 method.^35,40–42 This treatment has been the preferred approach in previous studies of optical and other electronic properties of TiO₂.^40–42 The hybrid HF/DFT HSE06 treatment provides a direct band gap of 3.26 eV for the (rutile) TiO₂ (110) surface in this work. Moreover, as shown in ref. 35, this method also describes localized midgap states in TiO₂ modifications, as those associated with excess electrons in reduced TiO₂ (ref. 43) which are capable of introducing localized Ti³⁺ 3d¹ states below the conduction band.⁴⁴ An obvious first question then is whether Cu₅ clusters are capable of introducing excess electrons in TiO₂. All our theoretical evidence indicates that the cluster indeed acts as an electron donor essentially transferring its unpaired electron. For example, for the structure shown in Fig. 1, Bader decomposition⁴⁵ shows that each of the three Cu atoms closest to the surface donates about 0.3|e| of electronic charge on average. Hence, the estimated net charge donation from the copper cluster to the support is 0.9|e|.

Experimental input to further analyze the electronic changes on the Cu atoms of the clusters upon adsorption is provided by XANES measurements at the Cu K-edge. Fig. 3 shows the XANES spectra of Cu₅ clusters supported on highly oriented pyrolytic graphite (HOPG) and on TiO₂. With HOPG being an inert substrate, we do not expect strong interaction with the support and consider the results as effectively unbiased XANES spectra of the copper clusters. The minimal impact of inert support materials, such as gold or HOPG, on the XANES spectrum of Cu₅ clusters is a known fact, which allows us to interpret that the changes observed in the XANES spectrum of Cu₅ clusters supported on TiO₂ are exclusively related to the interaction between Cu atoms and TiO₂. Moreover, using the PBE-D3(BJ) method with the computational approach reported in ref. 46 and 47 to describe the Cu₅/graphene interaction, we have found from a Bader decomposition⁴⁵ that the net charge donation from the copper cluster to the support is in fact insignificant (less than 0.02|e|). As can be observed in Fig. 3, a splitting of the main absorption line is present in both spectra (denoted as A and B). This effect has been explained considering the contribution of both 3d⁹ and 3d¹⁰L (L denoting a hole from the O ligand) electronic configurations in the final state.^48–50 Because of the presence of the core hole in the final state, the 3d¹⁰L electronic configuration shifts to a lower energy than the 3d⁹ state. In our case, a strong increase of the B resonance is observed when Cu₅ clusters interact with TiO₂, indicating a final state with a dominant 3d⁹ character, which can be associated with a lower Cu electron density due to charge transfer from the cluster to TiO₂. Therefore, the experiment also suggests that copper acts as an electron donor. Previous work has shown that Ag₅ and Au₅ clusters also act as electron donors on the TiO₂ (110) surface,^30,51 similar to Cu₅. However, the Au₅ cluster donates less charge⁵¹ (0.6|e|) than the Cu₅ and Ag₅ counterparts, which can be explained by the very different ionization potential of Au (about 9.23 eV) compared to that of Cu and Ag (ca. 7.73 and 7.58 eV, respectively). Hence, our results demonstrate that the copper cluster acts as an electron donor. However, it is not oxidized through the formation of CuO_x oxides at temperatures lower than 700 °C.²⁵

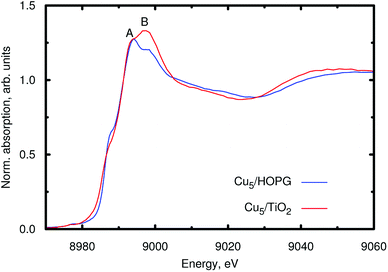Fig. 3 XANES spectra at the Cu K-edge of the Cu₅ clusters supported either on HOPG (blue line) or on TiO₂ nanoparticles (red line).

The second question is whether the excess electron from copper introduce a localized Ti³⁺ 3d¹ state. As shown by Selloni and collaborators,⁴⁴ a correct description of these localized defect states is achieved when a proper geometry relaxation is accounted for using hybrid exchange functionals. For this purpose, all atoms of the Cu₅/TiO₂ system were allowed to relax in a PBE-D3 minimization with a Hubbard DFT + U term³¹ added (see later section on Computational methods). Using the resulting wavefunction as an initial guess in a follow-up HSE06 calculation at the relaxed geometry, we find that the excess electron is localized in a Ti³⁺ 3d¹ state. As can be observed in the iso-density surface of the frontier singly-occupied molecular orbital (referred to as SOMO, see Fig. 4), the electron occupies the 3d orbital of the Ti(5f) ion right below the cluster, bearing a magnetic moment of 0.94 μ_B. As expected, the electron localization is accompanied by the typical geometric lattice distortion found in polaron problems. Thus, basal O atoms (indicated as O_p in Fig. 1) depart from the Ti(5f) ion by moving 0.16 Å in a direction normal to the surface and 0.09 Å in the surface plane. This solution was found to be −1.18 eV more stable than that obtained without surface relaxation (see Section S6 of the ESI† for the solution without accounting for surface relaxation). Of course, alternative locations for small polarons besides the Ti(5f) ion must exist with similar energies, as previously found in hydroxylated and reduced TiO₂ (110) surfaces.^52,53 Trapping energy differences between several Ti sites were estimated to be within 0.2 by Deskins et al.⁵² while Chrétien and Metiu⁵³ found that states with unpaired electrons located on Ti(5f) atoms are very close to those with the electrons on Ti atoms below the surface.

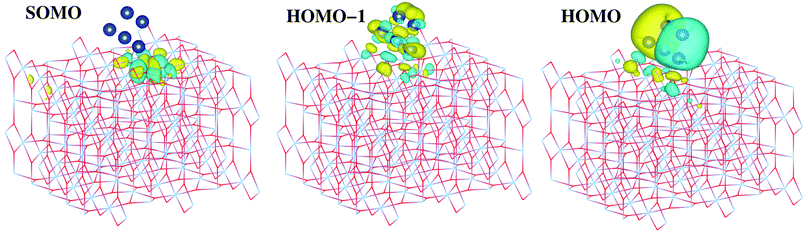Fig. 4 Picture showing isosurfaces of the frontier “singly-occupied” (or occupied only by a single spin component) molecular orbital (referred to as SOMO) as well as the highest-energy and second “doubly-occupied” (or occupied by two spin components) molecular orbitals (referred to as HOMO and HOMO − 1). The energy positions of the SOMO, HOMO, and HOMO − 1 are indicated in the upper panel of Fig. 5.

The enhanced catalytic performance of reduced TiO₂ surfaces upon formation of small Ti³⁺ polarons has been experimentally demonstrated in several reactions such as heterogeneous CO₂ reduction upon electron attachment⁵⁴ (for a recent review see, e.g., ref. 55). Earlier theoretical studies on the interaction of O₂ with surface Ti³⁺ sites^56–59 had also showed that a superoxo O₂⁻ species can be formed due to the electron transfer from Ti³⁺ to (gas-phase) O₂, thus illustrating its well-known role as an electron scavenger.

As can be observed in the projected electronic density of states (dotted pink lines in the upper panel of Fig. 5), the localized Ti³⁺ state appears about 1 eV below the conduction band as found by Di Valentin et al. in hydroxylated and reduced rutile TiO₂ (110) surfaces.⁴⁴ Importantly, localized Ti³⁺ states have been previously found by Seriani et al.⁶⁰ for Cu_n (n < 5) clusters adsorbed on TiO₂ anatase surfaces. As can also be noticed from Fig. 5, the midgap Ti³⁺ state (i.e., the SOMO) is almost resonant to the HOMO − 1 state. The iso-density surface of the HOMO − 1 (see Fig. 4) clearly shows the mixing of Cu(3d) with contributions from O(2p) orbitals (4.3%, see Table S9 of the ESI†) resulting in the evidently covalent nature of the Cu–O binding, but the mixing with Ti(3d) orbitals is also apparent (6.4%, see Table S9 of the ESI†). Cu₅ shares electrons localized in 3d orbitals with O ions rather than its unpaired electron which occupies a molecular orbital dominated by 4s contributions in the gas-phase (see also model cluster calculations in Section S7 of the ESI†). Instead, the highest-energy orbital dominated by 4s contributions (referred to as HOMO in Fig. 4) is doubly-occupied, also bearing 3p and 3d components and having energy very close to the bottom of the conduction band (see Fig. 5). The SOMO, being dominated by the Ti(5f) 3d contribution (ca. 87%, see Table S9†), also shows some mixing with 3d(Cu) but not with 4s(Cu) atomic components. Hence, ignoring the deviation of the Cu atoms in the Cu₅ cluster from the unperturbed atomic [Ar]3d¹⁰4s¹ configuration, the enhancement of the 3d⁹(Cu) signature in the XANES spectra can be interpreted as the transfer of a single 3d electron from Cu₅ to the nearest Ti(5f) ion.

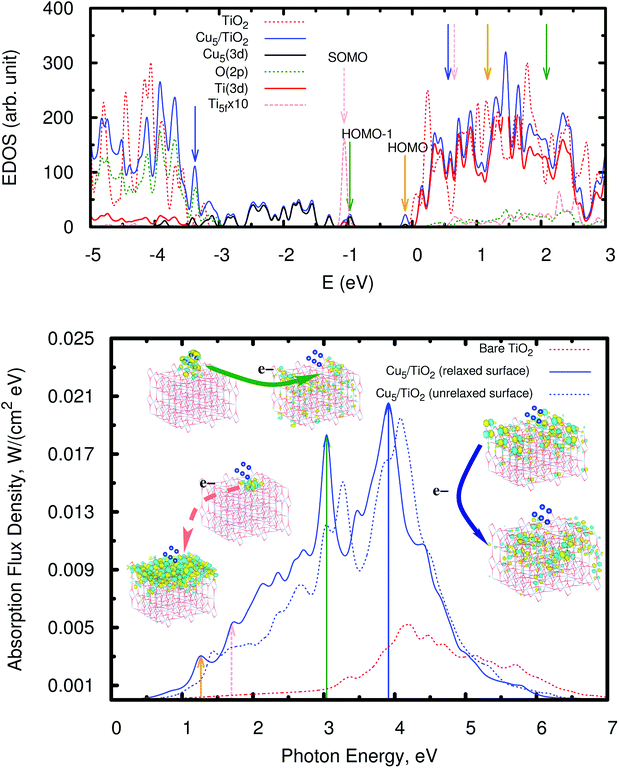Fig. 5 Upper panel: electronic density of states (EDOS) of the bare rutile TiO₂ (110) surface and the Cu₅–TiO₂ (110) system. The positions of the SOMO, HOMO − 1, and HOMO are also indicated (also see orbital pictures in Fig. 4). The zero of energy is set to the energy of the lowest unoccupied molecular orbital (LUMO). The projected density of states onto O(2p), Ti(3d), and Cu(3d) orbitals is also shown as well as that projected on the 3d orbitals from the nearest Ti(5f) ion (dotted pink lines). Orange, forest-green, and blue arrows indicate the bands responsible for the most intense peaks in the spectrum (bottom panel). Bottom panel: photo-absorption spectra of the TiO₂ (110) surface, without adsorbates (dotted red lines) and with the adsorbed Cu₅ cluster in the trapezoidal-shaped configuration shown in Fig. 1, including (blue lines) and without including (dotted blue lines) relaxation. Orange, forest-green, and blue arrows indicate the position of the most intense peaks as well as those arising from the excitation of the SOMO (dotted pink lines). The insets present the orbitals involved in the photo-excitation processes.

To get further insights into the binding mechanism and the 3d⁹(Cu) signature, model cluster calculations were also performed (see Section S9 of the ESI†). The comparison with the gas-phase Cu₅ case clearly shows that the 3d(Cu) orbitals lose their population upon adsorption while the opposite holds for the 4s(Cu) orbitals, particularly those centered on the two Cu atoms lying farthest from the surface. The analysis of Löwdin charges⁶¹ using the cluster model also indicates that the copper cluster acts as an electron donor but with the net donation being smaller than that estimated using the Bader decomposition and the periodic model (0.5 vs. 0.9|e|), with the charge transferred from 3d(Cu) orbitals to the support (Ti atoms) being about three times larger than that received by 4s(Cu) orbitals from TiO₂. In a slightly simplified picture, the electrons of the 3d orbitals centered at the two terminal Cu atoms, each connected by a bridging oxygen ion, are paired in the free Cu₅ cluster. However, upon adsorption, they unpair and arrange themselves in an antiferromagnetic configuration, as favored by the superexchange interaction with the oxygen ion. One unpaired electron is transferred to the Ti(3d) orbitals (mainly the Ti(5f) ion), with a net donation of charge to the TiO₂ system, while the second unpaired electron becomes paired in the s-type HOMO. This way, the Cu₅ cluster, originally magnetic in the gas phase due to its singly-occupied highest energy orbital, loses its magnetic moment when adsorbed on TiO₂.

As can also be seen in the EDOS presented in Fig. 5 (upper panel), the presence of Cu₅ clusters leads to a very pronounced modification at the bottom of the valence band extending it by about 1.5 eV as compared to the bare TiO₂ surface. The orbitals responsible for this extension have a similar composition to the HOMO − 1 and show a clear mixing of the dominant 3d(Cu) components with contributions from the 2p orbitals of the closest bridging oxygen ions (see Fig. S8 of the ESI†). Our frontier orbital analysis of the Cu₅–TiO₂ system differs significantly from that reported for the Au₅–TiO₂ counterpart,⁶² where a small mixing degree between Au(5d) and O(2p) orbitals was found to be responsible for the weakness of the Au–O bond. A very recent study of the closely related Au₂₀–TiO₂ system⁶³ highlighted the noncovalent nature of the interaction, as opposed to the Cu₅–TiO₂ system in our work.

Additional calculations were performed considering a rectangular-shaped Cu₅ configuration with the plane of the rectangle lying parallel to the surface plane (see Section S8 of the ESI†). This structure is 0.31 eV higher in energy than the trapezoidal gas-phase structure. When the surface atoms are allowed to relax, the formation of a small polaron Ti³⁺ 3d¹ state was also found but it was located at a Ti(6f) site adjacent to the Ti(5f) atom lying right below the center of the copper cluster. The polaronic solution was found to be 0.23 eV more stable than the non-polaronic counterpart. The Bader decomposition revealed that the net charge donation is very similar for the copper cluster in trapezoidal and rectangular-shaped configurations (0.9 vs. 1.1|e|).

2.3 Photoabsorption spectra

Having analyzed the Cu₅-decorated surface system in the ground electronic state we focus now on its optical excitation. Fig. 5 (bottom panel) illustrates how the photo-absorption spectra of a thin slab of TiO₂ are modified by the Cu₅ cluster: the absorption is strongly enhanced and extended into the visible region. The projected electronic density of states (PDOS) onto the O(2p), Ti(3d), and Cu(3d) orbitals indicates that the main peak at the end of the visible region (marked with a forest-green arrow at about 3.0 eV) mainly arises from the direct photo-induced transfer of electrons from the frontier orbital HOMO − 1, bearing chemical mixing of Cu(3d) orbitals with O(2p) and Ti(3d) states, to surface Ti(3d) orbitals and, to a much lesser extent, sub-surface Ti ions (see also the pictures of the orbital densities in the insets of Fig. 5). The Cu₅ influence on the dynamics of photo-generated charge carriers which need to reach the surface to be catalytically active is very relevant in TiO₂-based photocatalysis.^64,65 A similar electron transfer process takes place from the HOMO − 2 and from frontier orbitals of lower energy (HOMO − x) so that the photo-absorption extends from 3.0 to lower energies covering the entire visible region. This is in fact the fundamental difference when compared to a decoration with Ag₅,³⁰ where the intense absorption peaks are related to electron transfer from ‘isolated’ midgap states with a dominant Ag(5s) atomic contribution to acceptor Ti(3d) states in the TiO₂ conduction band. In the case of the Cu₅–TiO₂ system, there is also photo-induced electron transfer from the HOMO midgap states with a dominant Cu(4s) atomic composition (see Fig. 4) but the associated absorption peak is much less intense, being located in the infrared region (indicated by an orange arrow in Fig. 5).

In summary, the main mechanism of enhanced photoabsorption in the visible region can be described as a single electron ‘jumping’ from the 3d orbitals of the Cu₅ atomic cluster to the conduction band, leaving behind a long-lived ‘hole’ located at the Cu₅ cluster. As can be clearly seen in the orbital pictures, the Cu₅ cluster induces spatial separation of photogenerated holes and electrons. In particular, notice that the orbital for the acceptor state bears a depleted region of charge (empty region) at the Cu₅–TiO₂ layer that hinders electron–hole recombination. Since hole–electron recombination is a key factor limiting the photocatalyst efficiency of unmodified TiO₂ (see, e.g., ref. 64), the Cu₅-induced ability to promote separation of charge carriers is expected to have a pronounced influence on the visible light photocatalytic activity of the modified TiO₂ material.

Interestingly, a novel mechanism for charge separation has been recently reported for the Au₂₀–TiO₂ system,⁶³ where an electron appears inside TiO₂ immediately upon photoexcitation. The Au₂₀ cluster is also small enough to bear a band-gap due to quantum confinement but, as a variation from the Cu₅ case, the excitation also generates electron–hole pairs in the gold cluster itself with a 50% probability. Both the Cu₅ and Au₂₀ cases illustrate very different photo-excitation scenarios than those more typically occurring in plasmonic metal nanoparticle–TiO₂ interfaces, involving collective excitations of the nanoparticle and dephasing of electron–hole pairs before the electrons are injected into TiO₂.

As can also be observed in Fig. 5 (orbitals connected by dotted pink arrows), a second photo-excitation mechanism can be identified at the low-energy end of the visible region (at about 1.7 eV), which can be described as the delocalization of a single electron, originally characterizing the localized Ti³⁺ 3d¹ state, over all Ti surface ions. Remarkably, previous experimental measurements have shown that visible light excitation of Ti³⁺ centers on reduced TiO₂ nanoparticles is associated with transfer of the localized 3d¹ electrons into the conduction band of TiO,² with the electron spin resonance (ESR) signal disappearing when exposed to sub-bandgap light.⁶⁶

An interesting aspect in the context of photo-chemistry is the ability to also photo-generate or better ‘recover’ a localized Ti³⁺ 3d¹ state after such delocalization as described above. In order to investigate this feature, we depopulate the SOMO artificially by promoting its electron into the LUMO and perform a separate spectral analysis. The photo-excitation of such a non-equilibrium state shows indeed intense absorption peaks, also in the visible region, which corresponds to the recovery of an unpaired electron, localized at the Ti(5f) site, i.e. the former SOMO. This shows that the recovery of the localized Ti³⁺ 3d¹ state by absorption of a solar photon is possible in principle but needs to be studied in much greater detail for an actual catalytic reaction of interest, i.e. in the presence of adsorbed reactants.

By comparing the spectrum to that obtained without surface relaxation (and, then, localized Ti³⁺ 3d¹ state formation), an absorbance enhancement as well as a shift of the main peaks towards the visible region can be noticed due to the relaxation of the surface ions. As discussed above (see Section 2.2), we have also considered a rectangular-shaped isomer of higher energy (see Section S8 of the ESI†), for which the formation of a small polaron state has also been found. The corresponding absorption spectrum (see Fig. S11 of the ESI†) is similar in the UV region to that of the trapezoidal-shaped isomer (see bottom panel of Fig. 5). However, the substantial re-arrangement of the Cu₅ cluster gives rise to a significant shift of the energy position of the frontier orbitals responsible for the absorption in the visible region (see the EDOS in Fig. S12 of the ESI†). As a result, the main peak in the visible region is shifted to much lower energies (ca. 2.4 vs. 3.0 eV). The experimental DRS spectra are already well described assuming only a minimum energy structure (see Fig. 6), being significantly different to those associated to the higher-energy rectangular-shaped structure (see Fig. S13 of the ESI†). Once again, this indicates that the Cu₅ cluster might conserve its gas-phase trapezoidal structure upon deposition.

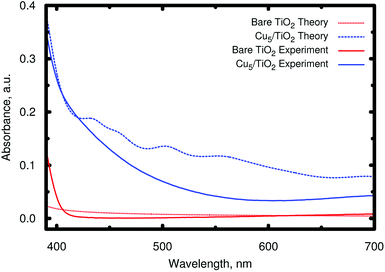Fig. 6 Comparison of the theoretical and experimental absorbance in the visible region. The experimental absorbance A has been calculated via diffuse reflectance spectroscopy (DRS) measurements from the diffuse reflectance signal R_d as A = log₁₀(1/R_d) (see Section S1 of the ESI† for the details of the diffuse reflectance spectrum measurements).

It is also important to highlight that Cu₅ decoration of TiO₂ also allows for the enhancement of the absorbance in the UV region. The mechanism responsible for the main absorption peak at 3.9 eV (illustrated by the orbitals connected by blue arrows) is the electron transfer from electrons located in the 2p orbitals of bridging and subsurface O atoms to (mainly) surface Ti(3d) orbitals but also subsurface Ti ions. Also, in this case, a depleted region of charge develops in the Cu₅–TiO₂ “molecule”-semiconductor layer, hindering electron–hole recombination.

Moreover, the theoretical photo-absorption spectra shown in Fig. 5 are consistent with the experimental spectra recorded using diffuse reflectance measurements (see Section S1 of the ESI†). This is clearly demonstrated in Fig. 6, which compares the theoretical and experimental absorbance in the visible region starting from 700 to about 390 nm. It should be noted that the units of absorbance are arbitrary units, so that we can only make qualitative conclusions on comparing the theoretical and experimental optical absorption. Thus, after depositing Cu₅ clusters on TiO₂ nanoparticles, the experimental spectrum presents absorption in the visible region. Note that the observed increase in the absorption is only due to the surface of the titanium dioxide, which is in direct contact with clusters. As documented in Fig. S2 of the ESI,† X-ray fluorescence measurements of the Cu/Ti ratio provide a value of 0.018(4), from which a molar Cu₅/Ti ratio of 3.6 × 10⁻³ can be obtained. It also indicates that for the titanium dioxide used in the experiments (nanoparticles of ≈20 nm, see Fig. S4 of the ESI†), only a minor part is in direct contact with the copper clusters. This is further confirmed by XANES spectra at the Ti K-edge as explained in Section S3 of the ESI.† Therefore, one can expect a further increase of the optical absorption by a factor of ≈20–30 if the TiO₂ nanoparticle size is reduced to only a few nanometers, which would greatly decrease the ratio of the TiO₂ bulk volume to the decorated surface. Note further that the new absorption band is very different from that of isolated Cu₅ clusters, and starts, as reported in ref. 23, below 300 nm.

3 Conclusions

Most of the methods developed to extend the absorption of TiO₂ to the visible region are based on doping,^67,68 but in volume-based strategies the problem of charge recombination in the bulk remains. In order to solve this, some strategies have been recently reported based on the surface modification by a disordered surface shell, forming the so-called black TiO₂ (i.e. a disordered Ti₂O₃ shell⁶⁹). The problem with this strategy is the limited stability of the resulting core–shell structures. In this work, we have computationally and experimentally proven the effectivity of an alternative, simple strategy, which utilizes surface-deposited, highly stable⁷⁰ Cu₅ clusters to alter the absorption properties of the bulk.

We showed that the clusters are stable and immobilized due to high barriers for isomerization and surface migration, respectively. Upon surface adsorption, a Cu₅ cluster transfers its unpaired electron to the TiO₂ surface, with the excess electron becoming localized in the nearest Ti(5f) ion, giving rise to a localized Ti³⁺ 3d¹ state. The presence of such a small polaron state near the surface, formed by the interaction with Cu₅, and the possibility of adjusting the amount of such surface polarons by a simple change of the concentration of clusters, opens a new way of nanomaterial tuning. It could become highly relevant for the adjustment of material properties in which polarons play a decisive role, such as electron transport, chemical reactivity, or photochemistry.⁷¹ We identify one main process triggered by the follow-up adsorption of a photon in the visible region by Cu₅-decorated TiO₂: the direct electron transfer from frontier cluster-orbitals into surface Ti(3d) orbitals with the acceptor state bearing a depleted region of charge (empty region) hindering electron–hole recombination. This effect explains the desired extension and enhancement of the photo-absorbance towards the visible region. We note that TiO₂ and Cu₅ as separate systems are both semiconductors absorbing in the UV region. However, in combination, with a single layer of Cu₅ clusters adsorbed onto a TiO₂ substrate, they are capable of absorbing across both the visible and UV regions.

Moreover, we could reveal that, upon irradiation with visible light, the Cu₅ cluster induces an effective separation of photo-generated charge carriers. This effect is known to have a strong influence on the photocatalytic activity of a material. Spatial separation increases the lifetime of ‘electrons’ and ‘holes’ to take part in follow-up surface reactions such as the reduction of carbon dioxide, a particularly challenging task in the context of greenhouse gas reduction.¹¹ The extension of the optical response of the material to the visible region has been confirmed by the experimental DRS measurements discussed in this work. Since the visible part in the range between 400 and 700 nm represents about 40% of the solar spectrum radiation, this outcome indicates a very promising route towards the development of a new class of highly efficient photocatalysts.

4 Materials and methods

4.1 Materials

Highly monodisperse samples of Cu₅ clusters without any surfactant or protective agent were synthesized according to the procedure previously reported and were characterized by UV-Vis and fluorescence spectroscopies, AFM, XPS, XANES, EXAFS and ESI-TOF mass spectrometry.²³ As can be seen in ref. 23, all these techniques clearly indicate the presence of clusters with only 5 atoms. As an example, the presence of a single and very narrow emission peak (FWHM ≈ 70 nm) at 305 nm corresponding to a single narrow excitation peak (FWHM ≈ 40 nm) at 224 nm, indicates the existence of clusters with only one concrete size, because it is well-known that the emission of clusters depends on the number of atoms, N. Using a simple spherical Jellium model, which is a good approximation for ligand-free clusters, the emission peak of clusters (≈E_G = HOMO–LUMO gap of the clusters) can be predicted by the equation, E_G = E_FN^−1/3, where E_F is the Fermi level of the bulk metal (≈7 eV for Cu), giving a value of E_G = 4.09 eV, which agrees nicely with the experimental value (4.07 eV). TiO₂ nanoparticles (NP) were purchased from Aldrich, P25, in form of nanopowder, which according to the supplier are composed of particles of 21 nm of primary particle size determined by transmission electron microscopy (TEM).

4.2 Experimental methods

X-ray Absorption Spectroscopy (XAS) measurements in the XANES (X-ray absorption near edge structure) regions were performed at the XAFS2 beamline⁷² of the Laboratorio Nacional de Luz Síncrotron (LNLS), Campinas, Brazil. The measurements were performed in transmission mode using a Si(111) crystal monochromator near the Cu K-edge (8979 eV) and Ti K-edge (4966 eV) at ambient temperature with three ion chambers as detectors. Harmonics were attenuated by detuning to 50% of the peak intensity. The absorption of the sample was determined between the first two chambers and the third one was used to measure the corresponding metallic reference, placed between the last two chambers, simultaneously with the sample. The optimum amount of material for the XAS measurements was calculated in order to obtain an edge-step close to 1. The powdered samples were dispersed in 10 ml of isopropyl alcohol and then filtered through a 0.45 μm pore size MF-Millipore™ membrane filter. The XANES data were normalized by standard methods using the ATHENA software which is part of the IFEFFIT package.⁷³

Optical absorption spectra have been extensively used as one of the most significant tools for probing the energy gaps (E_g) and band structures of semiconductors. There are several methods for measuring them and, in the particular case of semiconductor nanoparticles, diffuse reflectance spectroscopy (DRS) becomes one of the more suitable options due to its convenience and low experimental requirements. The measurements were carried out on a Shimadzu ISR-2600 Plus spectrophotometer equipped with an integrating sphere with two detectors, a photomultiplier and an InGaAs detector. DRS spectra were collected at room temperature in the range of 200 to 700 nm with a 1.0 nm step and the lamp change was set at 350 nm, recording in the mode of exclusion of specular reflectance. Standard BaSO₄ (Nacalai Tesque) was used as a reference. The spectrum of diffuse reflectance was obtained by determining the ratio of intensities of diffusely reflected radiation from the sample and from the standard, respectively.

The Cu/Ti ratio in the modified sample was determined via XRF (X-ray fluorescence) measurements using a tunable X-ray source from an X-ray absorption spectrometer (Rigaku Looper) together with an X-ray silicon drift detector (Amptek XR-100SDD). Fig. S2 of the ESI† shows the XRF spectra obtained using an excitation energy of 10.5 keV to excite the Cu K-edge and the Ti K-edge. By quantification, using a PyMca X-ray Fluorescence Toolkit,⁷⁴ of the emission line intensity of Ti and Cu (Ti-Kα and Cu-Kα), and taking into account every correction factor (cross section, thickness, filters, etc.), it was possible to determine that the Cu/Ti atomic ratio in the modified TiO₂ NP sample was 0.018(4).

4.3 Computational methods

4.3.1 Periodic calculations. Periodic electronic structure calculations are performed with the Vienna Ab initio Simulation Package (VASP 5.4.4)^75,76 following a similar computational approach to that reported in previous work on He– and Ag₅–TiO₂ (110) interactions.^30,77

Electron–ion interactions are described by the projector augmented-wave method,^76,78 using PAW–PBE pseudopotentials as implemented in the program. The electrons of the O(2s, 2p), Ti(3s, 4s, 3p, 3d) and Cu(3d, 4s) orbitals are treated explicitly as valence electrons. A plane wave basis set with a kinetic energy cutoff of 700 eV is used. A Gaussian smearing of 0.05 eV is employed to account for partial occupancies, and the Brillouin zone was sampled at the Γ point.⁷⁹ The convergence criterion was 10⁻⁵ eV for the self-consistent electronic minimization. Geometries were relaxed with a force threshold of 0.02 eV Å⁻¹.

The decorated surface is modelled via periodic slabs, using a 4 × 2 supercell (four TiO₂ trilayers giving ca. 13 Å slab width). Cu₅ adsorption is assumed on one side of the slab, with 38 Å of vacuum above it. This large vacuum region allows the description of long-range tails of the cluster–surface interaction potentials while avoiding unphysical overlaps of electronic densities.

Interaction energies are derived via

E_int = E_{Cu5/TiO2(110)} − E_Cu5 − E_TiO2(110)

where E_{Cu5/TiO2(110)} is the total energy of the system, E_TiO2(110) is the energy of the substrate, and E_Cu5 denotes the energy of the bare copper cluster.

Adsorption energies are calculated with the PBE-D3(BJ) scheme. They were found to agree within 10% with reference values obtained with the domain-based local pair natural orbital correlation approach DLPNO-CCSD(T)⁸⁰ as well as the Symmetry-Adapted Perturbation Theory [SAPT(DFT)] method^81,82 (see ref. 30).

Due to the known underestimation of the band gap with the PBE functional, the density of states and photo-absorption spectra are calculated with the HSE06 exchange–correlation functional instead, which uses a screened Coulomb potential for increased efficiency of metallic systems.^33,34 This approach was applied using a HF/GGA mixing ratio of 25 : 75 and a screening parameter of 0.2 Å⁻¹.

In the first set of spin-polarized HSE06 calculations, the O and Ti atoms of the TiO₂ (110) rutile surface were kept frozen at the positions determined by Busayaporn et al.⁸³ using X-ray Diffraction (XRD). Next, all the surface ions and Cu atoms were relaxed using the PBE-D3 method but with the Hubbard term (DFT + U) added. The values of U reported in a previous study of Cu_n clusters (n ≤ 4) on the (101) and (100) surfaces of anatase⁶⁰ were used (4.2 eV for titanium and 5.2 eV for copper). Finally, the optimized geometries, obtained at the PBE + U/D3 level, were used in follow-up HSE06 calculations of the electronic structures, resulting in the identification of “polaronic” states.

4.3.2 Reduced density matrix treatment. The photo-absorption spectrum has been calculated using the computational approach previously applied to the Ag₅/TiO₂ system in ref. 30. Specifically, we model the involved relaxation processes by means of the reduced density matrix (RDM) approach in the Redfield approximation,³² using the orbitals generated from the HSE06 calculations as a basis set as in ref. 30. 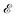This combined RDM–DFT treatment proposed by Micha and collaborators^84,85 has been successfully applied to silver clusters on semiconductor surfaces.^30,37–39 When the monochromatic electromagnetic field of frequency Ω is applied, the evolution equation for the reduced density ρ in the Schrödinger picture reads as follows:


where F̂^KS is the effective Kohn–Sham Hamiltonian with its indices referring to the Kohn–Sham basis set, D̂ is the electric dipole moment operator and R_jklm represents the Kohn–Sham components of the relaxation tensor (Redfield coefficients). The Redfield coefficients are defined as in ref. 32 and are implemented as described in ref. 84. This approximation is valid for long relaxation times in comparison to the duration of a transient energy exchange between the adsorbate and its medium.

Within the Redfield approximation, the relaxation tensor not only describes the effect of the fast electronic dissipation due to electronic fluctuations in the medium, but also the relatively slow relaxation owing to the atomic lattice vibrations. It is convenient to change to a rotating frame accounting for the electromagnetic field oscillation,

[small rho, Greek, tilde]_ij(t) = ρ_ij(t)exp(iΩt), ε_i > ε_j

[small rho, Greek, tilde]_ij(t) = ρ_ij(t)exp(−iΩt), ε_i < ε_j

[small rho, Greek, tilde]_ii(t) = ρ_ii(t)

where ε_i is the energy of the i-th Kohn–Sham orbital. After time averaging over the fast terms in the equation of motion for the RDM; its stationary-state solution for the diagonal elements reads as follows:⁸⁴

with the lowest unoccupied and the highest occupied molecular orbital denoted as LUMO and HOMO, respectively. Γ_j is the depopulation rate, and the sum terms g_jk are given by
where γ denotes the decoherence rate, Ω_jk is the Rabi frequency given by 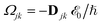, and Δ_jk (Ω) = Ω − (ε_j − ε_k) is the detuning. The diagonal elements provide the populations of the KS orbitals. The population relaxation rate ℏΓ and the decoherence rate ℏγ were not computed but fixed to values of 0.15 meV and 150 meV (27 ps and 27 fs) and have been chosen to be of the order of rates for semiconductors following decay of phonons and electronic density excitations (see, e.g., ref. 86).

In terms of the stationary populations, the absorbance is given by^30,38,39,87

where f̄_jk is oscillator strength per active electron. This is a purely dissipative contribution to the absorbance. We are assuming a thin slab, neglecting any dispersive effects, i.e., assuming a refractive index of ca. 1. The solar flux absorption spectrum is then given by

F(ℏΩ) = [small alpha, Greek, macron](Ω)F_solar(ℏΩ)ℏΩ,

where the solar flux is approximated by the black body flux distribution, normalized to an incident photon flux of 1 kW m⁻²,
where C_T is the flux normalization constant and the temperature T is set to 5800 K.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) and the Fondo Europeo de Desarrollo Regional (FEDER, UE) under Grant No. MAT2016-75354-P, the Austrian Science Fund (FWF) under Grant P29893-N36, the COST Action CM1405 “Molecules in Motion” (MOLIM), La Caixa Foundation (LCF/PR/PR12/11070003), the Ramon Areces Foundation (Project CIVP18A3940), European Union's Horizon 2020 Research and Innovation Programme (Grant Agreement No. Bac-To-Fuel 825999), the MINECO, Spain (MAT2015-67458-P – cofinanced with FEDER Funds – and CTQ2013-44762-R), the Xunta de Galicia, Spain (GRC ED431C2017/22), and the ANPCyT (PICT 2015-2285) and UNLP (Project 11/X790), Argentina. The CESGA Supercomputing Center (Spain) is acknowledged for having provided the computational resources used in this work. The partial support by the Laboratório Nacional de Luz Síncrotron (LNLS) under proposals 20170352 and 20180123 is also acknowledged. D. B. expresses gratitude for a postdoctoral grant from the Xunta de Galicia, Spain (ED481D 2017/021). M. P. de. L. C. is greatly thankful to Alexander Mitrushchenkov and Carlos Cabrillo for very helpful discussions, and to David A. Micha and Tijo Vazhappilly for having shared their Fortran code to calculate absorption coefficients.

References

1. Q. Guo, C. Zhou, Z. Ma, Z. Ren, H. Fan and X. Yang, Chem. Soc. Rev., 2016, 45, 3701–3730.
2. P. Salvador and C. Gutierrez, J. Phys. Chem., 1984, 88, 3696–3698.
3. D. Tobaldi, A. S. Skapin, R. Pullar, M. Seabra and J. Labrincha, Ceram. Int., 2013, 39, 2619–2629.
4. L. Yoong, F. Chong and B. K. Dutta, Energy, 2009, 34, 1652–1661.
5. A. Realpe, D. Núnez, I. Carbal and M. Acevedo, Int. J. Eng. Technol., 2015, 7, 1189–1193.
6. R. Álvaro, D. Núnez and M. Acevedo, Contemp. Eng. Sci., 2017, 10, 1539–1549.
7. C. Wang, Z. Chen, H. Jin, C. Cao, J. Li and Z. Mi, J. Mater. Chem. A, 2014, 2, 17820–17827.
8. M. S. Nahar, K. Hasegawa, S. Kagaya and S. Kuroda, Sci. Technol. Adv. Mater., 2007, 8, 286–291.
9. N. T. Ly, T. H. Dao, L. H. H. To, D. L. Vu and V. H. Le, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2014, 5, 035009.
10. M. A. Khan, S. I. Woo and O.-B. Yang, Int. J. Hydrogen Energy, 2008, 33, 5345–5351.
11. R. Camarillo, S. Tostón, F. Martínez, C. Jiménez and J. Rincón, J. Chem. Technol. Biotechnol., 2018, 93, 1237–1248.
12. R. Alexandrescu, I. Morjan, M. Scarisoreanu, R. Birjega, E. Popovici, I. Soare, L. Gavrila-Florescu, I. Voicu, I. Sandu, F. Dumitrache, G. Prodan, E. Vasile and E. Figgemeier, Thin Solid Films, 2007, 515, 8438–8445.
13. M. Zhou, C. Zeng, Y. Chen, S. Zhao, M. Y. Sfeir, M. Zhu and R. Jin, Nat. Commun., 2016, 7, 13240.
14. B. S. González and M. A. López-Quintela, Functional Nanometer-Sized Clusters of Transition Metals: Synthesis, Properties and Applications, The Royal Society of Chemistry, 2014, pp. 25–50.
15. S. M. Copp, A. Gorovits, S. M. Swasey, S. Gudibandi, P. Bogdanov and E. G. Gwinn, ACS Nano, 2018, 12, 8240–8247.
16. V. Porto, E. Borrajo, D. Buceta, C. Carneiro, S. Huseyinova, B. Domínguez, K. J. E. Borgman, M. Lakadamyali, M. F. Garcia-Parajo, J. Neissa, T. García-Caballero, G. Barone, M. C. Blanco, N. Busto, B. García, J. M. Leal, J. Blanco, J. Rivas, M. A. López-Quintela and F. Domínguez, Adv. Mater., 2018, 30, 1801317.
17. M. A. Abbas, P. V. Kamat and J. H. Bang, ACS Energy Lett., 2018, 3, 840–854.
18. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
19. M. A. Abbas, T.-Y. Kim, S. U. Lee, Y. S. Kang and J. H. Bang, J. Am. Chem. Soc., 2016, 138, 390–401.
20. Y. Negishi, C. Sakamoto, T. Ohyama and T. Tsukuda, J. Phys. Chem. Lett., 2012, 3, 1624–1628.
21. N. Vilar-Vidal, J. R. Rey and M. A. López Quintela, Small, 2014, 10, 3632–3636.
22. Y. A. Attia, D. Buceta, C. Blanco-Varela, M. B. Mohamed, G. Barone and M. A. López-Quintela, J. Am. Chem. Soc., 2014, 136, 1182–1185.
23. S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908.
24. P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568.
25. A. Zanchet, A. O. Mitrushchenkov, D. Buceta, A. M. López-Quintela, A. W. Hauser and M. P. de Lara-Castells, manuscript in preparation.
26. R. Passalacqua, S. Parathoner, G. Centi, A. Halder, E. C. Tyo, B. Yang, S. Seifert and S. Vajda, Catal. Sci. Technol., 2016, 6, 6977–6985.
27. A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901.
28. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
30. M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119.
31. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
32. V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, 2011.
33. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
34. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
35. P. Deák, B. Aradi and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155207.
36. T. Vazhappilly, M. P. de Lara-Castells and D. A. Micha, Mol. Phys., 2019 DOI:10.1080/00268976.2018.1533651.
37. D. S. Kilin and D. A. Micha, J. Phys. Chem. Lett., 2010, 1, 1073–1077.
38. T. Vazhappilly, D. S. Kilin and D. A. Micha, J. Phys. Chem. C, 2012, 116, 25525–25536.
39. R. H. Hembree, T. Vazhappilly and D. A. Micha, J. Chem. Phys., 2017, 147, 224703.
40. J. Anderson and C. G. V. de Walle, Phys. Status Solidi B, 2010, 248, 799–804.
41. A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212.
42. V. Francesc, L. Oriol, C. K. Kyoung, Y. L. Jin and I. Francesc, J. Comput. Chem., 2017, 38, 781–789.
43. W.-J. Yin, B. Wen, C. Zhou, A. Selloni and L.-M. Liu, Surf. Sci. Rep., 2018, 73, 58–82.
44. C. Di Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803.
45. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
46. M. P. de Lara-Castells, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 102804.
47. M. P. de Lara-Castells, M. Bartolomei, A. O. Mitrushchenkov and H. Stoll, J. Chem. Phys., 2015, 143, 194701.
48. C. Li, M. Pompa, A. C. Castellano, S. D. Longa and A. Bianconi, Phys. C, 1991, 175, 369–380.
49. J. Chaboy, A. Muñoz Páez, F. Carrera, P. Merkling and E. S. Marcos, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 134208.
50. J. Chaboy, A. Muñoz-Páez and E. Sánchez Marcos, J. Synchrotron Radiat., 2006, 13, 471–476.
51. S. Chrétien and H. Metiu, J. Chem. Phys., 2007, 127, 084704.
52. N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2009, 113, 14583–14586.
53. S. Chrétien and H. Metiu, J. Phys. Chem. C, 2011, 115, 4696–4705.
54. L. Liu, C. Zhao and Y. Li, J. Phys. Chem. C, 2012, 116, 7904–7912.
55. S. Xu and E. A. Carter, Chem. Rev., 2019 DOI:10.1021/acs.chemrev.8b00481.
56. M. P. de Lara-Castells and J. L. Krause, J. Chem. Phys., 2001, 115, 4798–4810.
57. M. P. de Lara-Castells and J. L. Krause, Chem. Phys. Lett., 2002, 354, 483–490.
58. M. P. de Lara-Castells and J. L. Krause, J. Chem. Phys., 2003, 118, 5098–5105.
59. M. P. de Lara-Castells, A. O. Mitrushchenkov, O. Roncero and J. L. Krause, Isr. J. Chem., 2005, 45, 59–76.
60. N. Seriani, C. Pinilla and Y. Crespo, J. Phys. Chem. C, 2015, 119, 6696–6702.
61. P.-O. Löwdin, Phys. Rev., 1955, 97, 1474–1489.
62. R.-L. Ding, J. Jia and H.-S. Wu, Appl. Surf. Sci., 2015, 359, 729–735.
63. R. Long and O. V. Prezhdo, J. Am. Chem. Soc., 2014, 136, 4343–4354.
64. Z. Zhang and J. T. Yates Jr, Chem. Rev., 2012, 112, 5520–5551.
65. M. A. Henderson, Surf. Sci. Rep., 2011, 66, 185–197.
66. K. Komaguchi, T. Maruoka, H. Nakano, I. Imae, Y. Ooyama and Y. Harima, J. Phys. Chem. C, 2010, 114, 1240–1245.
67. R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271.
68. B. Liu, H. M. Chen, C. Liu, S. C. Andrews, C. Hahn and P. Yang, J. Am. Chem. Soc., 2013, 135, 9995–9998.
69. M. Tian, M. Mahjouri-Samani, G. Eres, R. Sachan, M. Yoon, M. F. Chisholm, K. Wang, A. A. Puretzky, C. M. Rouleau, D. B. Geohegan and G. Duscher, ACS Nano, 2015, 9, 10482–10488.
70. D. Buceta, N. Busto, G. Barone, J. M. Leal, F. Domínguez, L. J. Giovanetti, F. G. Requejo, B. García and M. A. López-Quintela, Angew. Chem., Int. Ed., 2015, 54, 7612–7616.
71. M. Reticcioli, M. Setvin, M. Schmid, U. Diebold and C. Franchini, Phys. Rev. B, 2018, 98, 045306.
72. S. J. A. Figueroa, J. C. Mauricio, J. Murari, D. B. Beniz, J. R. Piton, H. H. Slepicka, M. F. de Sousa, A. M. Espíndola and A. P. S. Levinsky, J. Phys.: Conf. Ser., 2016, 712, 012022.
73. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
74. V. Solé, E. Papillon, M. Cotte, P. Walter and J. Susini, Spectrochim. Acta, Part B, 2007, 62, 63–68.
75. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
76. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
77. N. F. Aguirre, D. Mateo, A. O. Mitrushchenkov, M. Pi and M. P. de Lara-Castells, J. Chem. Phys., 2012, 136, 124703.
78. P. E. Blöch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
79. Test calculations showed that interaction energies at the potential minimum, using a 5 × 5 × 1 Monkhorst–Pack⁸⁸k-point mesh, are similar (within ca. 0.01 eV) to those calculated at the Γ point.
80. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
81. A. J. Misquitta, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2003, 91, 033201.
82. A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2003, 367, 778–784.
83. W. Busayaporn, X. Torrelles, A. Wander, S. Tomić, A. Ernst, B. Montanari, N. M. Harrison, O. Bikondoa, I. Jourmard and J. Zegenhagen, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153404.
84. D. S. Kilin and D. A. Micha, J. Phys. Chem. C, 2009, 113, 3530–3542.
85. D. A. Micha, Adv. Quantum Chem., 2015, 71, 195–220.
86. K. Ozawa, S. Yamamoto, R. Yukawa, R.-Y. Liu, N. Terashima, Y. Natsui, H. Kato, K. Mase and I. Matsuda, J. Phys. Chem. C, 2018, 122, 9562–9569.
87. T. Vazhappilly and D. A. Micha, J. Phys. Chem. C, 2014, 118, 4429–4436.
88. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.

---

Footnote

† Electronic supplementary information (ESI) available: Details on diffuse reflectance, X-ray fluorescence, and X-ray absorption spectroscopy measurements and transmission electron microscopy images of TiO₂ nanoparticles as well as complementary computational periodic and model cluster structures. See DOI: 10.1039/c9ta00994a

---