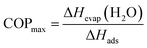Insights into the water adsorption mechanism in the chemically stable zirconium-based MOF DUT-67 – a prospective material for adsorption-driven heat transformations

Abstract

A chemically and thermally stable MOF with composition Zr₆O₄(OH)₄(tdc)₄(CH₃COO)₄ (tdc, 2,5-thiophenedicarboxylate), also known as DUT-67(Zr), was synthesised at the multigram scale using a green synthesis protocol as a potential material for adsorption heat pumps. A series of vapour physisorption experiments at 298 K identified water as the most promising working fluid, showing the desired S-shaped reversible physisorption isotherms with adsorption steps within the desired relative pressure range of p/p₀ = 0.1–0.4. An enhanced long-term chemical stability of the MOF was proved in liquid water and mineral acid and thermal stability was confirmed in temperature dependent PXRD experiments. Stable performance of the material under working conditions was confirmed in 20 adsorption/desorption cycles under conditions typical for an adsorption pump. The mechanism of water adsorption was further studied by neutron powder diffraction, suggesting that the preferable adsorption sites for water are near the μ₃-O and μ₃-OH groups of the Zr₆O₈ cluster and the triangular window of the octahedral micropore, and the order of pore filling starts from the smallest pore, progressing to the middle and largest pore.

---

Introduction

The climate agreement, signed in Paris in 2015 by 185 countries, aimed to pursue efforts to limit the temperature increase to 1.5 °C above pre-industrial levels.¹ Achieving this target is only possible if the use of fossil fuels and natural gas as energy sources in industry, transportation and household will be significantly reduced. Therefore, a major challenge facing human society is the development of renewable energy sources as well as development of environmentally friendly energy carriers. One of the many approaches to save or transform heat in a sustainable way is development of adsorption heat pumps and chillers, which allow reversibly storing thermal energy in porous materials.^2,3 Currently such devices are available on the market as stationary systems for heating and cooling, and also as energy-saving household appliances. Usually well-established porous materials like zeolites, porous silica and activated carbons are used as adsorbents and water is most often used as a working fluid. However, the main drawback of these materials is a low working capacity, caused by low porosity and polarity of the inner surface, which is extremely hydrophilic in the case of zeolites or hydrophobic in the case of active carbons. Therefore, material scientists are actively searching for alternative materials with desired adsorption properties.^4–7 Various working fluids are considered ranging from ammonia, hydrocarbons, fluorinated hydrocarbons, alcohols to water.^8,9 Their coefficient of performance is strongly dependent on their critical temperature and density. The desired material should feature high adsorption capacity with adsorption steps at desired relative pressure, which is hard to achieve with established classical porous materials.

Metal–organic frameworks (MOFs) belong to an advanced class of crystalline porous materials, constructed from metal clusters and organic ligands by a modular principle,¹⁰ which unifies a high surface area and pore volume,¹¹ various functionalisation possibilities¹² and a strictly defined pore system.¹³ These properties predesignate their application potential in gas storage,^14,15 capture,¹⁶ separation¹⁷ and heterogeneous catalysis.¹⁸ Due to the fine tunability of the pore system and polarity of the inner surface, MOFs were recently recognised as potential working materials for adsorption-driven heat pumps.¹⁹ In the case of water as a working fluid, Kapteijn and co-authors defined a set of criteria for materials to be used for such applications: (a) S-shape of the water adsorption isotherm at 298 K; (b) high pore volume is desirable for improved performance; (c) adsorption steps should be located in the pressure range 0.1 < p/p₀ < 0.4, which not only increases the temperature lift, but also decreases the desorption temperature; (d) hysteresis between adsorption and desorption branches should be avoided if possible; and (e) the material should show a stable adsorption/desorption performance over thousands of cycles. The latter was nicely reviewed by Walton and co-workers, where authors classified existing MOFs in terms of water stability and proposed a defined procedure for characterising the water stability of MOFs.²⁰ Farrusseng and co-workers summarized the water adsorption properties of more than 60 MOFs considering the aspects of pore filling and application potential.²¹ Currently, several water-stable MOF materials are considered the most promising for this type of application. Henninger and co-workers extensively studied the water adsorption behaviour of CAU-10-H²² (CAU stands for Christian-Albrechts-Universität zu Kiel), aluminium fumarate⁶ and MIL-100(Al)²³ (MIL stands for Materials of Institute Lavoisier) for heat exchanger applications. Furthermore, authors developed a full-scale heat exchanger, coated with an aluminium fumarate framework.⁶ Yaghi and co-workers proposed the use of MOF-841 with a defined and steep step in the water adsorption isotherm at p/p₀ = 0.25 as a working material for adsorption heat storage.²⁴ Serre and co-workers recently designed a CAU-10-H analogue with 2,5-furandicarboxylic acid, denoted as MIL-160, which shows steep adsorption of water at p/p₀ < 0.2 and can be easily regenerated at temperatures lower than 373 K, thus outperforming the commercial SAPO-34 material.²⁵ However, the recently reported AlPO₄-LTA material slightly outperforms MIL-160 in terms of heat storage capacity.²⁶ Recently even mesoporous MOFs with exceptionally high working capacities were reported.^27,28 However, fluorinated hydrocarbons with extremely high greenhouse effect are used as working fluids in both cases. More recently, Yaghi and co-workers highlighted the promising performance of MOFs in water harvesting devices.^29,30

However, synthesis of most of these materials requires large amounts of volatile organic solvents or valuable or even not commercially available organic ligands. This makes them either too expensive or environmentally unfriendly, and therefore prevents their use in commercial applications.³¹ Fortunately, Reinsch and co-authors recently reported the “green” water-based and scalable synthesis of a number of water-stable Zr-based materials based on commercially available ligand molecules.^32–34 One of these materials, DUT-67(Zr) (DUT stands for Dresden University of Technology), was initially developed by our group,³⁵ and shows excellent water stability, a hierarchical pore system and, as a consequence, a multistep water adsorption isotherm with two of three steps within the desired pressure range 0.1 < p/p₀ < 0.4. With a total pore volume of 0.47 cm³ g⁻¹, derived from the water adsorption isotherm, DUT-67(Zr) is ranked amongst the best performing MOF materials in this branch, fulfilling all criteria defined in the review article by Kapteijn and co-workers.¹⁹ This prompted us to investigate the water adsorption mechanism and the thermal and chemical stability of the material, as well as the cycle stability under similar conditions to the real application.

Here, we synthesise DUT-67(Zr) in the multigram scale using the recently developed “green” synthesis, and then extensively test it to confirm its chemical and thermal stability. In parallel to this study, Janiak and co-workers reported a promising material for heat transformations namely MIL-53(Al)-TDC,³⁶ which is a structural analogue of a well-known MIL-53(Al), but synthesized using the H₂tdc ligand.³⁷ This material shows surface area and pore volume very similar to those of DUT-67(Zr) and despite of completely different pore system shows water adsorption isotherm, which is very similar to those of DUT-67(Zr). However, investigations of the water adsorption mechanism were not reported in this case, and the synthesis procedure requires toxic DMF, and is therefore less environmentally friendly.

Insights into the water adsorption mechanism from neutron powder diffraction of pre-loaded samples will be presented. Enhanced chemical stability of DUT-67(Zr) in water and mineral acid was confirmed in a series of stability tests. Cycle stability of the material over 20 adsorption/desorption cycles is proven using optical infrared calorimetry.

Results and discussion

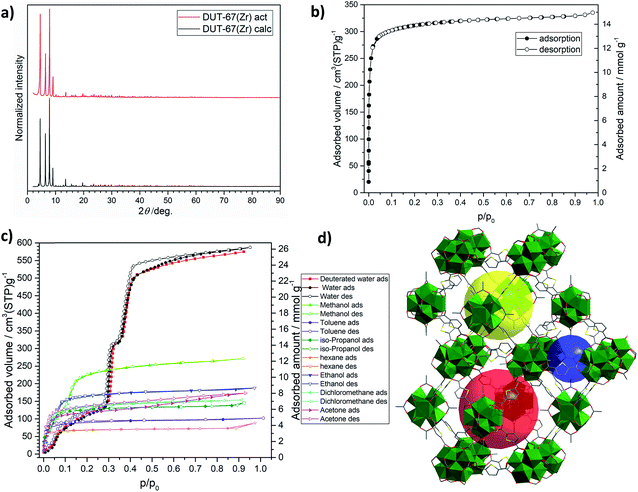
Since the report of chemically stable UiO-66 in 2008, Zr-based MOFs have revolutionised MOF chemistry, demonstrating the diversity of frameworks with various connectivity and topological types. For the first time, these materials combined ultra-high porosity with chemical and thermal stability, which could not be achieved in any other porous material.^38–49 Recently, a novel Zr-based MOF with composition Zr₆O₆(OH)₂(tdc)₄(DMF)₆(CH₃COO)₂ (determined from DMF-based synthesis), further denoted as DUT-67(Zr), was synthesised by our group.³⁵ The chemically stable framework is constructed from commercially available reagents and, following development of the “green” synthesis route by Reinsch and co-workers,³² the material has a high chance for future commercialisation.

DUT-67(Zr) crystallises in the cubic space group Fm3̄m and consists of Zr₆O₈ in organic bricks, which are interconnected by eight equally oriented tdc linkers forming a uninodal framework with reo underlying topology (Fig. 3). The remaining four positions of the Zr SBU are usually occupied by terminal ligands, namely solvent molecules and modulators, which can be exchanged post-synthetically by other molecules to adjust the polarity of the inner surface. In the case of the recently developed “green” synthesis, TG data suggest that the composition of the product is Zr₆O₄(OH)₄(tdc)₄(CH₃COO)₄ (see ESI, Fig. S2†), involving cluster protonation, similar to that observed in UiO-type frameworks but with lower connectivity. The combination of the reo topology and bent tdc linker results in the formation of three different pores: one octahedral and two cuboctahedral (Fig. 1d). The smallest octahedral pore is centred at the 8c Wyckoff position, which possesses 4̄3m symmetry. Centres of cuboctahedral pores surface are located at 4a and 4b Wyckoff positions, both having m3̄m symmetry. In the crystal structure, these pores are in the ratio of 2 : 1 : 1. From a structural point of view, the polarity of the pores should be different because all μ₃-O atoms and terminal ligands face on to the pores centred at 8c and 4a Wyckoff positions.

Fig. 1 Characterisation data for DUT-67(Zr): (a) theoretical DUT-67(Zr) calc. and experimental DUT-67(Zr) act. PXRD patterns; (b) nitrogen physisorption isotherm at 77 K; (c) vapour physisorption isotherms of water and selected organic solvents at 298 K; (d) pore system of DUT-67(Zr).

Upscaling of the “green” synthesis and textural properties of DUT-67(Zr)

The recently published “green” synthesis procedure of DUT-67(Zr) was successfully upscaled by a factor of 40 and shows an excellent yield of 82% of activated MOF. The material was degassed at 368 K under dynamic vacuum, and shows high crystallinity and phase purity in the powder X-ray diffraction (PXRD) pattern (Fig. 1a). SEM images show crystallite sizes in the range of 500–1000 nm, which is suitable for shaping using a binder (Fig. S14, ESI†). The TG data of the activated material suggest the composition Zr₆O₄(OH)₄(tdc)₄(CH₃COO)₄, which is slightly different from the DMF-based synthesis and contains no coordinated solvent molecules on the cluster. The pore accessibility was tested by a nitrogen physisorption experiment, showing a typical type Ia isotherm with a saturation uptake of 335 cm³ g⁻¹ at p/p₀ = 0.97 (Fig. 1b). It corresponds to a pore volume (V_p) of 0.52 cm³ g⁻¹, which was not reached if DMF was used as the solvent in the synthesis. As the theoretically calculated pore volume is only slightly higher (V_p = 0.67 cm³ g⁻¹), the achieved capacity can be considered as a realistic value, which approaches the theoretically calculated value for the structure with acetate anions on the cluster. As reported previously,⁵⁰ DUT-67(Zr) synthesised from DMF shows an S-shaped water adsorption isotherm with three separate steps, reflecting the filling of the three different pores of the MOF. In order to prove this finding for the MOF, synthesized using a “green” synthesis procedure, a series of vapour physisorption experiments were performed on DUT-67(Zr) at 298 K using solvents with various kinetic diameters and polarity.

Solvent vapour adsorption on DUT-67(Zr)

In the case of water vapour adsorption, we were able to reproduce the S-shaped isotherm involving three steps and steep adsorption branch in the range p/p₀ = 0.2–0.4 reported previously. As expected, deuterated water adsorption follows the water isotherm, reproducing three well-resolved steps. Both isotherms show the same water uptake of 510 cm³ g⁻¹ at p/p₀ = 0.43, which corresponds to the pore volume of 0.41 cm³ g⁻¹. The hydrophilicity of each pore was evaluated using the α coefficient or p/p₀ at which half of the total pore capacity is reached.²¹ For the smallest octahedral pore we obtained a value of α = 0.09, while both cuboctahedral pores fill later at α = 0.30 and 0.39.

Beside water, further solvent vapours with various polarity and kinetic diameters, namely methanol, ethanol, 2-propanol, acetone, dichloromethane, toluene and n-hexane, were adsorbed on DUT-67(Zr) because some of them can also be used as working fluids in adsorption-based heat exchangers. In the case of alcohol vapours, the step in the adsorption isotherm is gradually shifted to a lower relative pressure with increasing length of the alkyl chain. In the case of methanol, one can still define two distinct steps in the range p/p₀ = 0.001–0.2. For ethanol and 2-propanol, type I isotherms with uniform pore filling at low relative pressures are observed. All other measured solvent vapours behave in the same manner, reaching the saturation uptake at p/p₀ = 0.1. Nevertheless, in terms of hydrophilicity, a general trend could be derived: the isotherms of hydrophobic adsorptives reach saturation at a lower relative pressure, pointing to the hydrophobic interior of DUT-67 pores. In terms of the pore filling, all adsorptives perform nearly equally, reaching pore volumes of 0.43–0.49 cm³ g⁻¹ at p/p₀ = 0.9 except for acetone, which outperformed all others, reaching a pore volume comparable to the value deduced from nitrogen physisorption.

Analysis of the vapour adsorption data shows that only water and, to some extent, methanol meet the criteria for application in adsorption heat transformation. In terms of gravimetric water uptake, DUT-67(Zr) adsorbs 0.44 g g⁻¹ water at p/p₀ = 0.6 and ranks amongst the best MOFs, surpassed only by Co₂Cl₂(BTDD), MOF-74(Mg) and MOF-74(Ni) frameworks.²⁹ In the same relative pressure range, only deuterated water and DCM show higher gravimetric capacities of 0.48 and 0.56 g g⁻¹ (Fig. S13, ESI†).

Characterisation of the D₂O-loaded samples

To gain a better understanding of the structure–property relationships and the water adsorption mechanism, preferred adsorption sites were investigated by neutron powder diffraction (NPD). NPD is an ideal tool for such studies due to large coherent scattering lengths for both deuterium (²H) and oxygen (¹⁶O), allowing precise determination of the position of adsorbed water molecules in the pores. However, direct in situ NPD studies during deuterated water vapour adsorption are difficult because of slow adsorption kinetic and large amount of sample needed.

Therefore, controlled amounts of deuterated water were pre-adsorbed on DUT-67(Zr) samples ex situ prior to the diffraction experiments. Adsorption was performed using a volumetric adsorption instrument by manual dosing of D₂O vapour until the desired pressure and full equilibration were reached. The loaded amount was estimated from the D₂O adsorption isotherm, measured under the same conditions.

The adsorbed amount was also proved gravimetrically by weighing the cell before and after loading with D₂O, as well as by TG analysis. The TG curves show an expected loss of mass at approximately 373 K, corresponding to the removal of D₂O from the pores of DUT-67(Zr) (see ESI, Fig. S2†).

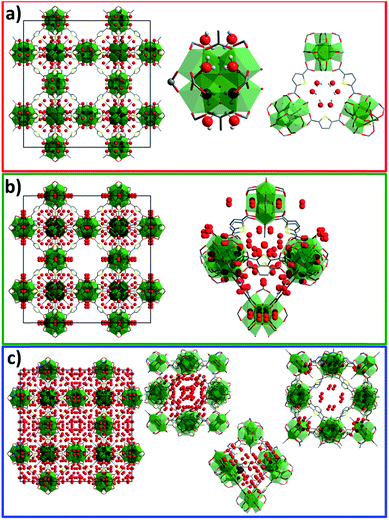
Analysis of the DRIFT spectra of the desolvated and D₂O-loaded samples shows the same absorption bands in the fingerprint area, but significant differences in the large wavenumber region (3000–3500 cm⁻¹) corresponding to the stretching vibrations of O–D bonds. As expected, stronger absorbance is observed for samples with higher D₂O loadings (see ESI, Fig. S3†). According to the analytical data, the following loadings were achieved: Sample 1 was loaded with 34 D₂O molecules per unit cell, corresponding to an equilibrium pressure of 64 Pa. This pressure should facilitate determination of the most attractive adsorption sites in the framework (Fig. 2). Loading of sample 2 corresponds to the second adsorption step with 375 molecules adsorbed per unit cell, corresponding to 855 Pa of equilibrium pressure. Sample 3 was loaded with 735 D₂O molecules per unit cell, positioned within the third adsorption step of the isotherm with an equilibrium pressure of 1068 Pa.

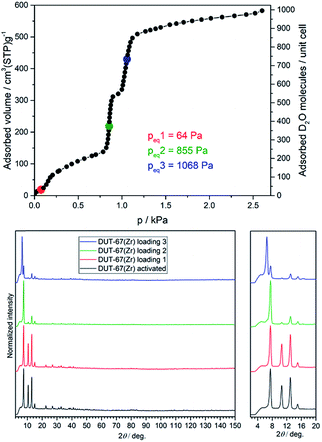Fig. 2 (Top) D₂O vapour adsorption isotherm at 298 K showing loadings for samples 1 (red), 2 (green) and 3 (blue); (bottom) NPD patterns at 180 K (λ = 2.536 Å) for corresponding loadings.

Water adsorption mechanism of DUT-67(Zr) by neutron powder diffraction

Neutron powder diffraction patterns for all samples were measured at 180 K, showing significant differences in the reflection intensities especially for samples with higher loadings (Fig. 2). The NPD patterns were further subjected to Rietveld analysis (see ESI, Fig. S9–S12, Table S1†) to localise the preferable adsorption sites for D₂O in the framework.

The initial model for the desolvated framework was built using the composition Zr₆O₄(OH)₄(tdc)₄(CH₃COO)₄, suggested by the TG data. The obtained framework structure was then used to refine the D₂O-loaded structures.

The NPD patterns collected on desolvated and D₂O-loaded DUT-67(Zr) samples show no changes in crystal symmetry. Rietveld analysis of the NPD pattern of sample 1 suggests two preferable adsorption sites for D₂O (Fig. 3a, ESI animation 1†). The first D₂O molecule with a site occupancy of 0.39 is located close to the μ₃-O atom of the Zr-cluster, and the second is located within the perimeter of the triangular pore window and is present with an occupancy of 0.23. The driving force for the adsorption on the first adsorption site could be attributed to the formation of the O–D⋯O hydrogen bonds with μ₃-O(H) atoms of the Zr-cluster. Since triangular windows can be considered as the smallest pores in the structure (see ESI, Fig. S1†), the preferable adsorption site can be explained by the high Lennard-Jones potential of the water in the triangular cavity. Refinement of the overall occupancy of both positions can lead to overestimation of the overall amount of water when compared to the de facto adsorbed D₂O amount.

Fig. 3 Crystal structures of D₂O-loaded DUT-67: (a) loading 1 with depicted preferred adsorption sites at the Zr-cluster and pore window, (b) loading 2 with depicted adsorption sites around the Zr-cluster and within the octahedral pore, and (c) loading 3 shows adsorption sites within each separate pore (red spheres are the oxygen atoms of the adsorbed water in the pores. Hydrogen and deuterium atoms have been omitted for clarity).

In sample 2, five independent positions were localised for adsorbed D₂O molecules within the pores of DUT-67(Zr) (Fig. 3b, ESI animation 2†). In this case, two positions with occupancies of 0.62 and 0.25 are located within two symmetrically independent triangular windows of the octahedral pore. Similar to sample 1, D₂O molecules with an occupancy of 0.55 were localised close to the μ₃-O atom of the Zr-cluster. The next position with an occupancy of 0.3, which was not present in sample 1, is located within the octahedral pore (Fig. 3b). The last position with an occupancy of 0.37 was found within the cuboctahedral pore (centred at Wyckoff 4a) close to the Zr-cluster, which is in good agreement with the second isotherm step in the isotherm (Fig. 2). In contrast to sample 1, the overall D₂O occupancy of 401 molecules per unit cell, refined from the neutron data, fits with the loading, derived from the D₂O isotherm, and is equal to 380 molecules per unit cell.

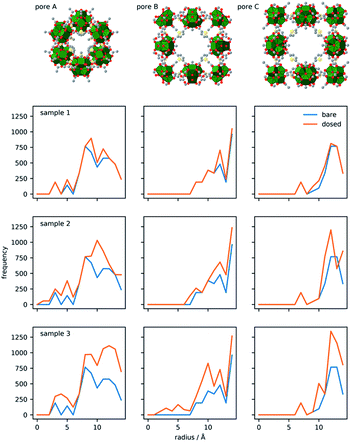Fig. 4 Pore system of DUT-67 (top) and corresponding spherical atomic distribution for bare (blue lines) and D₂O-loaded (orange lines) frameworks at three different loadings.

The loading for sample 3 corresponds to the second step of the isotherm with 735 D₂O molecules per unit cell. Refinement of the NPD patterns suggests nine independent adsorption sites in the crystal structure. The overall occupancy, recalculated to the unit cell, amounts to 743 molecules, which exactly matches the introduced amount of water. As expected from the adsorption isotherm, the adsorption sites are mainly located within the octahedral and cuboctahedral pores, correspondingly centred at 8c and 4a Wyckoff positions. Three positions of D₂O could be found within the largest cuboctahedral pore (centred at Wyckoff position 4b), which corresponds to the third step in the isotherm (Fig. 3c, ESI animation 3†).

In order to visualise and quantify the distribution of the water molecules in the pores for loadings 1–3, the resulting crystal structures were subjected to computational analysis, using a spherical model, in which the radial distributions of atoms were calculated for each pore and corresponding D₂O loading (Fig. 4). Differences between the corresponding distributions give differences in the atomic distribution for bare and water-loaded structures. Indeed, for loading 1, there is only a slight difference between the octahedral pore A and small cuboctahedral pore B, which corresponds to preferred adsorption sites within the triangular windows and near Zr-clusters. Loading 2 is characterised by differences in all three distributions, confirming adsorption of water within the octahedral pore and on the surface of cuboctahedral pores centred at 4a and 4b, respectively. In the case of loading 3, the difference between the graphs of bare and loaded frameworks indicates the filling of the cuboctahedral pore 4a, while in pore 4b water molecules are still 7 Å away from the pore centre, indicating additional spare capacity.

Cycling and thermodynamic stability and adsorption kinetics of H₂O@DUT-67(Zr) by optical calorimetry

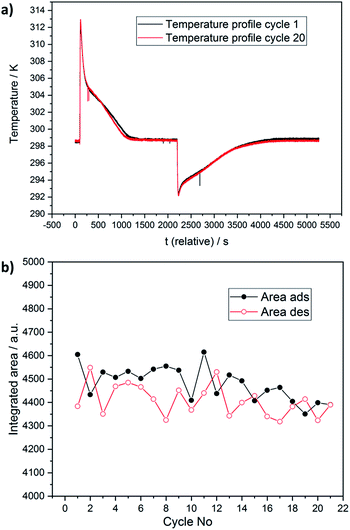
Thermal and chemical stabilities are both crucial criteria for materials to be applied in adsorption heat pumps. For this purpose Janiak and co-workers used TGA/DSC coupled with a humidity generator, thus working on a similar principle.⁵¹ We prove the cycle performance of “water-born” DUT-67(Zr) by optical calorimetry or so-called InfraSORP technology.^52,53 Here, the adsorption heat released is optically recorded by the resulting temperature change. There is a temperature increase by water adsorption and a decrease by desorption with pure nitrogen. During the 20 adsorption/desorption cycles, we did not observe changes in the temperature profile (see Fig. 6a, ESI S6†). Analysis of the integrated peak areas, and hence the water uptake,³⁹ shows only minor fluctuations in the range of 4450 ± 150 (Fig. 6b), which is within the uncertainty range of the technique.^52,54 As previously reported, the peak area is directly correlated with the adsorption capacity and integral enthalpy. During adsorption, a temperature maximum was observed at 313 ± 1 K, and desorption showed endothermal cooling of the sample to 292 ± 1 K. More in-depth analysis of the profile for both adsorption and desorption peaks indicates two distinct steps corresponding to pore filling of the octahedral and two cuboctahedral pores. As the last two steps are located in a quite narrow pressure range of the isotherm (855–1068 Pa), they cannot be distinguished in the temperature profile. While the first step of the temperature profile corresponds to the filling of octahedral pores, the shoulder of the temperature signal is caused by further heat release by filling of both cuboctahedral pores. Detailed adsorption enthalpy studies are discussed in the following paragraph. In addition, analysis of the temperature profile allowed us to estimate the kinetics of water adsorption, which is rarely explored.⁵⁵ Analysis of adsorption peaks shows that under the current experimental conditions, the temperature curve reaches a base temperature after 1400 s, while complete desorption of water from the pores occurs after 2100 s of purging with dry nitrogen gas (Fig. 6a).⁵⁵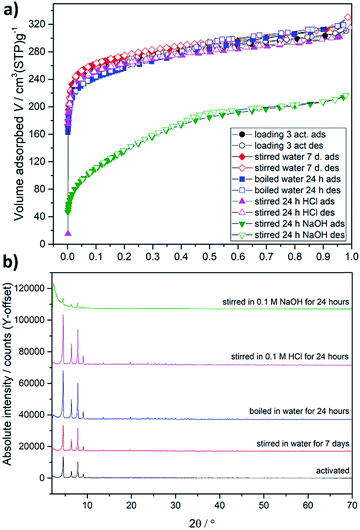

Fig. 5 Nitrogen physisorption isotherms at 77 K (a) and PXRD patterns (b) on samples exposed to liquid water, 0.1 M HCl and 0.1 M NaOH.

Fig. 6 Adsorption/desorption cycling data: (a) temperature profile during water vapour adsorption and desorption at cycles 1 and 20 and (b) plot of the peak area during the adsorption and desorption of water vapour.

Multiple exposure of the adsorbent to a working fluid during the lifetime of the device requires an enhanced chemical stability of the material. In previous studies, DUT-67(Zr), synthesized in DMF, was claimed as a MOF with reduced chemical stability against water and acids,²⁴ and therefore, we performed a comprehensive stability study on the MOF, synthesized using a “green” synthesis procedure, under normal working conditions, but also under harsh conditions, which are rather not typical for adsorption heat pumps. In these experiments we used sample 3, which was stored under ambient conditions for 2 years. After activation we obtained the type Ia isotherm with an uptake of 304 cm³ (STP) g⁻¹ at p/p₀ = 0.9, which is 91% of the initial capacity (Fig. 5a). Stirring the MOF in liquid water at room temperature for 7 days does not influence the capacity at all, while boiling of the material in water for 24 h leads to negligible degradation, which is reflected in the slightly decreasing micropore volume and appearance of the narrow hysteresis in the range p/p₀ = 0.4–0.7. Stirring of the MOF in 0.1 M HCl does not significantly influence textural properties. As expected, exposure of DUT-67(Zr) to 0.1 M aqueous solution of sodium hydroxide for 24 hours leads to decomposition of the MOF. Nitrogen uptake decreases from 304 to 207 cm³ (STP) g⁻¹, showing that one-third of the capacity is lost. PXRD patterns measured on all samples confirm these observations, except the sample exposed to NaOH, where a significant decrease of peak intensities and increase of amorphous background is observed (Fig. 5b). The thermal stability of the DUT-67(Zr) was determined by a temperature-dependent PXRD study for which the desolvated MOF and sample 3 were used. PXRD patterns measured in the range of 298–723 K show the stability of both samples at least up to 473 K (ESI, Fig. S4 and S5†).

As the material undergoes significant temperature fluctuations during the performance of the adsorption heat pump, water physisorption experiments were carried out at 318 K to prove the hydrothermal stability of the material in a working environment. The isotherm showed no significant changes compared to the isotherm, measured at 298 K, in neither adsorption capacity nor relative pressure steps (see ESI, Fig. S7†). The adsorption enthalpy, derived from these isotherms using the Clausius–Clapeyron equation, was calculated as 58 kJ mol⁻¹ at very low loadings, with a further drop to 38 kJ mol⁻¹ at 100 cm³ g⁻¹ (ESI, Fig. S8†). Filling of both cuboctahedral pores leads to an increase in enthalpy to 45–47 kJ mol⁻¹ up to when saturation is reached at nearly 500 cm³ g⁻¹. This value is comparable to those of the best performing MOFs from the CAU-10 family.²⁹

Since nitrogen gas with 80% relative humidity was used for the adsorption/desorption cycling study, the capacity of w_ads = 0.462 g g⁻¹ was extracted from the adsorption isotherm at p/p₀ = 0.8. The peak area in the temperature profile is proportional to adsorption capacity, the working capacity can be derived as follows:

Δw = A_des/A_ads × w_ads

where A_des and A_ads are peak areas of adsorption and desorption cycles. Subsequently we calculate an average working capacity over 20 cycles as 0.455 g g⁻¹ and working capacity in the first cycle as 0.440 g g⁻¹, which indicates nearly complete desorption of water from the MOF in a nitrogen flow at 298 K. If conditions of 80% r.h. for adsorption and 20% r.h. for desorption are considered, the working capacity, calculated from the isotherm, amounts to 0.375 g g⁻¹. The maximal theoretical efficiency or coefficient of performance (COP) is described by the equation:

If complete desorption of water from the pores is assumed, the COP_max (DUT-67) = 78%, which is among the highest reported values in the literature.^56,57

Experimental

Materials

All chemicals were purchased from commercial sources and used without further purification. Zirconyl chloride octahydrate ZrOCl₂·8H₂O (99.99% trace metal basis) and 2,5-thiophenedicarboxylic acid (H₂tdc) (99%) were purchased from Sigma Aldrich. Glacial acetic acid (100% extra pure) for the synthesis was purchased from Carl Roth GmbH. Deuterated water (99.9 at% deuteration degree) for the neutron powder diffraction experiments was purchased from Sigma Aldrich.

MOF synthesis

For the synthesis of the MOF material, the green synthesis procedure, reported by Reinsch et al. was up-scaled by a factor of 40. A mixture of ZrOCl₂·8H₂O (51.6 g, 160.15 mmol) and H₂tdc (18.4 g, 106.98 mmol) was dissolved in a mixture of 400 mL deionized water and 400 mL glacial acetic acid while heating and mixing. The mixture was stirred at 368 K under reflux for 1 h. The resulting precipitate was centrifuged, filtered, and washed two times with 0.1 M sodium acetate solution and water. The material was then activated under dynamic vacuum at 368 K. The yield was 31.2 g (82.2%) based on H₂tdc.

Chemical stability tests

For stability tests, sample 3 loaded with deuterated water two years before the test and stored under ambient conditions was used. After thermal activation, 20 adsorption/desorption cycles on Infrasorp, the sample was exposed to the following conditions: (1) stirring for 7 days at room temperature; (2) stirring for 24 hours in boiling water; (3) stirring for 24 hours in 0.1 M HCl (pH = 1); (4) stirring for 24 hours in 0.1 M NaOH (pH = 13). Further, the MOF powder was washed with an excess amount of water, filtered and dried in an oven at 100 °C. Subsequently, the powder was degassed in dynamic vacuum at 120 °C for 12 hours. Physisorption experiments were performed on a Quadrasorb (Quantachrome) volumetric instrument using 80–100 mg of the activated powder for each measurement.

Physical measurements

Powder X-ray diffraction (PXRD) patterns were collected in transmission geometry on a STOE STADI P diffractometer operated at 40 kV and 40 mA with monochromatic Cu Kα1 (λ = 0.15405 nm) radiation at room temperature (RT), equipped with a 0D gas filled detector. The samples were prepared in boron-silicon glass capillaries 0.3 mm in diameter. All measurements were performed in the 2θ range from 2 to 90°, with an exposure time of 30 s per step and step width of 0.02°. Temperature dependent PXRD patterns in the range of 298–748 K with 30 K steps were measured on the same instrument, which was equipped with a high-temperature oven and capillary setup in transmission geometry in the 2θ range of 2–70° with 30 s exposition time per step. Nitrogen physisorption experiments were carried out in a pressure range of 10⁻⁴–1 bar at 77 K using a BELSORP-max instrument (Microtrac BEL, Japan). Water vapour adsorption experiments were performed at 298 and 318 K on the same sample using the Hydrosorb instrument (Quantachrome). FT-IR spectra were measured on a Bruker VERTEX 70 using the DRIFT technique in the range of 4000–400 cm⁻¹. Thermogravimetric analysis was performed under synthetic air flow in a temperature range of 298–1273 K with a heating rate of 5 K min⁻¹ using STA 409 PC (NETZSCH). SEM images were taken with secondary electrons in a HITACHI SU8020 microscope using 1.0 kV acceleration voltage and 10.8 mm working distance.

Pre-loading of the samples for NPD experiments

Samples for the neutron powder diffraction experiments were pre-loaded with the deuterated water at 298 K on the BELSORP-max instrument. The needle valve and span adjustment procedures were first performed to calibrate needle valves and pressure transducers of the instrument. 7 g of the activated sample was divided over three measurement cells and additionally degassed on the instrument ports for 12 h at room temperature under ultra-high vacuum. The reservoir with the liquid adsorptive was filled with D₂O and the corresponding degassing procedure for the liquid adsorptive was performed. The manifold of the instrument was then exposed to an ultra-high vacuum for another 2 h. Then, the D₂O vapour was dosed using a fine needle valve to all three cells at the same time. After reaching the targeted pressure, the valve to the cell with the adsorptive was closed and the pressure in all three cells (connected to each other) was monitored until the adsorption equilibrium was reached. After the last dose, the cells were additionally equilibrated for 12 h. All cells were filled with dry nitrogen and weighed. In such a way, the correct loading could be extracted from the water adsorption isotherm and measured gravimetrically by weighing the adsorption cell before and after the loading procedure. In such a way, three samples with an equilibrium pressure of 64 Pa (sample 1), 855 Pa (sample 2) and 1068 Pa (sample 3) were prepared. The D₂O loadings estimated from the isotherm and obtained gravimetrically were in good agreement.

Neutron powder diffraction experiments

Four samples were prepared for the neutron diffraction experiments: (1) DUT-67(Zr) activated; (2) DUT-67(Zr) loading 1; (3) DUT-67(Zr) loading 2; and (4) DUT-67(Zr) loading 3. The samples for NPD experiments were placed into vanadium sample cans with 15.5 mm inner diameter and 40 mm filling height. The sample cans were sealed with indium in an argon atmosphere. The high-resolution NPD measurements were performed at the Heinz Meier-Leibnitz (FRM II) research reactor on the high-resolution powder diffractometer SPODI (Structure Powder Diffractometer). The monochromatic neutron flux with λ = 2.536 Å was used for all experiments. The measurement temperature of 180 K (water is frozen in the micropores of the MOF) was ensured by the closed cycle helium cryostat. NPD patterns were measured in the 2θ range of 1–152°.

Rietveld refinement of DUT-67(Zr) structures from NPD data

Rietveld refinement of desolvated and pre-loaded DUT-67(Zr) structures against NPD data was performed using the reflex module of Materials Studio 5.0 software. The NPD profile was fitted using the Thompson-Cox-Hastings function. The asymmetry of the peaks was modelled using the Berar–Baldinozzi function. The background was refined as a polynomial function with 12 components (see ESI,†Table 1). The source model for the desolvated DUT-67(Zr) structure was constructed using single crystal X-ray diffraction data, published elsewhere.³⁵ Four acetate anions were introduced into the structure by coordination in a bidentate manner to the eight oxygen atoms, located in the equatorial plane of the Zr₆O₈ cluster. Further, eight 8 hydrogen atoms, each with an occupancy of 0.5, were introduced to the μ₃-O-atoms of Zr₆O₈ bricks. The geometry of the obtained model was then optimised using the UFF force field, incorporated in Material Studio 5.0. The motion groups were defined as follows: two independent Zr-atoms of Zr₆O₈ SBU, two μ₃-O atoms, two acetate carboxylates, two acetate methyl groups, one carboxylate of the tdc²⁻ linker and one thiophene of the tdc²⁻ linker. These motion groups were used for a rigid body Rietveld refinement with energy (UFF, energy contribution 1%). The final experimental data for the refinement are given in Table S1 (ESI†). In the case of D₂O-loaded structures, the refined desolvated structure was used as the initial model and was not refined further. An amount of D₂O calculated from the isotherm was added randomly into the pores of the framework. The positions of the D₂O molecules (as rigid body groups) and their occupancies were refined freely using Rietveld refinement. The final experimental data are given in Table S1 (ESI†). CCDC 1891266–1891269 contains the structural data on desolvated and D₂O-loaded samples.†

Table 1 Total pore volumes calculated at p/p₀ = 0.9

	N2	H2O	CH3OH	C2H5OH	Iso-C3H7OH	DCM	Acetone	Toluene	Hexane
V p, cm^3 g^−1 (p/p0 = 0.9)	0.52	0.47	0.46	0.48	0.49	0.44	0.56	0.47	0.43

---

Multiple adsorption/desorption cyclisation of water

Before the experiment, a desolvated sample of DUT-67(Zr) was degassed in dynamic vacuum at 393 K for 12 h. The cyclisation measurement was performed using a version of the optical calorimeter InfraSORP, adapted for water vapour adsorption measurements. The measurement was performed at 298 K using 140 cm³ min⁻¹ flow. The nitrogen gas with a relative humidity of 80% was used during adsorption and dry nitrogen gas was used for desorption. Adsorption and desorption were recorded until complete equilibrium adjustment under these conditions. The adsorption time was 1800 s, while desorption was performed for 5000 s. The adsorption and desorption kinetics were extracted from the temperature profile and correspondingly amounted to 1500 and 2500 s.

Conclusions

Upscaling of environmentally friendly “green” synthesis of DUT-67(Zr) to a multigram scale makes this a promising material for adsorptive heat transformation processes. The comprehensive characterisation of the synthesised batch shows outstanding chemical and thermal stabilities, which are required for working materials in adsorptive heat pumps. The test to determine the best working fluid identified water as the most promising for the desired application because of the S-shaped isotherm with two steps below of p/p₀ = 0.4. The mechanism of pore filling, derived experimentally from neutron powder diffraction on the D₂O-loaded samples, suggests two strong adsorption sites within the framework, the first located near the Zr-cluster and showing a strong O–D⋯O interaction with the μ₃-O(H) groups of the cluster, while the second is located within the triangular pore window of the octahedral pore. The sequence of pore filling correlates well with the pore sizes, showing alternate filling of the octahedral and cuboctahedral pores centred at 4a and 4b Wyckoff positions. The long-term stability of water-loaded DUT-67(Zr) was confirmed. It shows 91% of its initial adsorption capacity in the nitrogen physisorption experiment. After two years storage at ambient conditions, stability of DUT-67(Zr) under the harsh conditions, such as liquid water and mineral acid was also proved. Multiple adsorption/desorption cycling experiments using optical calorimetry confirmed the stable performance of DUT-67(Zr) under working conditions of adsorption heat exchangers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the German Federal Ministry of Education and Research (BMBF) within “EnerMOF” Project No 05K16D1. The authors gratefully acknowledge FRM II for beamtime on neutron powder diffractometer SPODI and financial support provided by Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. The authors also thank Dr Philipp Schlender for assistance with temperature dependent PXRD measurements and M.Sc. Sebastian Ehrling for SEM images.

Notes and references

1. A. Hsu, A. S. Moffat, A. J. Weinfurter and J. D. Schwartz, Nat. Clim. Change, 2015, 5, 501.
2. Y. I. Aristov, Heat Transfer Eng., 2014, 35, 1014–1027.
3. S. Vasta, V. Brancato, D. La Rosa, V. Palomba, G. Restuccia, A. Sapienza and A. Frazzica, Nanomaterials, 2018, 8, 522.
4. F. Stallmach, T. Splith, C. Chmelik, G. Füldner, S. K. Henninger, P. T. Kolokathis, E. Pantatosaki and G. K. Papadopoulos, Chem. Ing. Tech., 2016, 88, 372–378.
5. L. Garzón-Tovar, J. Pérez-Carvajal, I. Imaz and D. Maspoch, Adv. Funct. Mater., 2017, 27, 1606424.
6. H. Kummer, F. Jeremias, A. Warlo, G. Füldner, D. Fröhlich, C. Janiak, R. Gläser and S. K. Henninger, Ind. Eng. Chem. Res., 2017, 56, 8393–8398.
7. O. Ola, Y. Chen and Y. Zhu, Sol. Energy Mater. Sol. Cells, 2019, 191, 297–305.
8. F. Jeremias, D. Frohlich, C. Janiak and S. K. Henninger, New J. Chem., 2014, 38, 1846–1852.
9. G. Santori and C. Di Santis, Sustainable Mater. Technol., 2017, 12, 52–61.
10. M. Eddaoudi, D. B. Moler, H. Li, B. Chen, T. M. Reineke, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2001, 34, 319–330.
11. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428.
12. X. Kong, H. Deng, F. Yan, J. Kim, J. A. Swisher, B. Smit, O. M. Yaghi and J. A. Reimer, Science, 2013, 341, 882–885.
13. M. Li, D. Li, M. O'Keeffe and O. M. Yaghi, Chem. Rev., 2014, 114, 1343–1370.
14. L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314.
15. Y. He, W. Zhou, G. Qian and B. Chen, Chem. Soc. Rev., 2014, 43, 5657–5678.
16. K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781.
17. B. Li, H. Wang and B. Chen, Chem.–Asian J., 2014, 9, 1474–1498.
18. L. Zhu, X.-Q. Liu, H.-L. Jiang and L.-B. Sun, Chem. Rev., 2017, 117, 8129–8176.
19. M. F. de Lange, K. J. F. M. Verouden, T. J. H. Vlugt, J. Gascon and F. Kapteijn, Chem. Rev., 2015, 115, 12205–12250.
20. N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575–10612.
21. J. Canivet, A. Fateeva, Y. Guo, B. Coasne and D. Farrusseng, Chem. Soc. Rev., 2014, 43, 5594–5617.
22. D. Frohlich, E. Pantatosaki, P. D. Kolokathis, K. Markey, H. Reinsch, M. Baumgartner, M. A. van der Veen, D. E. De Vos, N. Stock, G. K. Papadopoulos, S. K. Henninger and C. Janiak, J. Mater. Chem. A, 2016, 4, 11859–11869.
23. T. Splith, E. Pantatosaki, P. D. Kolokathis, D. Fröhlich, K. Zhang, G. Füldner, C. Chmelik, J. Jiang, S. K. Henninger, F. Stallmach and G. K. Papadopoulos, J. Phys. Chem. C, 2017, 121, 18065–18074.
24. H. Furukawa, F. Gándara, Y.-B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381.
25. A. Cadiau, J. S. Lee, D. Damasceno Borges, P. Fabry, T. Devic, M. T. Wharmby, C. Martineau, D. Foucher, F. Taulelle, C.-H. Jun, Y. K. Hwang, N. Stock, M. F. De Lange, F. Kapteijn, J. Gascon, G. Maurin, J.-S. Chang and C. Serre, Adv. Mater., 2015, 27, 4803.
26. A. Krajnc, J. Varlec, M. Mazaj, A. Ristić, N. Z. Logar and G. Mali, Adv. Energy Mater., 2017, 7, 1601815.
27. J. Zheng, D. Barpaga, O. Y. Gutiérrez, N. D. Browning, B. L. Mehdi, O. K. Farha, J. A. Lercher, B. P. McGrail and R. K. Motkuri, ACS Appl. Energy Mater., 2018, 1, 5853–5858.
28. Z.-W. Mo, H.-L. Zhou, D.-D. Zhou, R.-B. Lin, P.-Q. Liao, C.-T. He, W.-X. Zhang, X.-M. Chen and J.-P. Zhang, Adv. Mater., 2018, 30, 1704350.
29. M. J. Kalmutzki, C. S. Diercks and O. M. Yaghi, Adv. Mater., 2018, 30, 1704304.
30. H. Kim, S. Yang, S. R. Rao, S. Narayanan, E. A. Kapustin, H. Furukawa, A. S. Umans, O. M. Yaghi and E. N. Wang, Science, 2017, 356, 430–434.
31. P. Silva, S. M. F. Vilela, J. P. C. Tome and F. A. Almeida Paz, Chem. Soc. Rev., 2015, 44, 6774–6803.
32. H. Reinsch, S. Waitschat, S. M. Chavan, K. P. Lillerud and N. Stock, Eur. J. Inorg. Chem., 2016, 2016, 4490–4498.
33. H. Reinsch, B. Bueken, F. Vermoortele, I. Stassen, A. Lieb, K.-P. Lillerud and D. De Vos, CrystEngComm, 2015, 17, 4070–4074.
34. H. Reinsch, Eur. J. Inorg. Chem., 2016, 2016, 4290–4299.
35. V. Bon, I. Senkovska, I. A. Baburin and S. Kaskel, Cryst. Growth Des., 2013, 13, 1231–1237.
36. N. Tannert, S.-J. Ernst, C. Jansen, H.-J. Bart, S. K. Henninger and C. Janiak, J. Mater. Chem. A, 2018, 6, 17706–17712.
37. C. B. L. Tschense, N. Reimer, C.-W. Hsu, H. Reinsch, R. Siegel, W.-J. Chen, C.-H. Lin, A. Cadiau, C. Serre, J. Senker and N. Stock, Z. Anorg. Allg. Chem., 2017, 643, 1600–1608.
38. Y. Bai, Y. Dou, L.-H. Xie, W. Rutledge, J.-R. Li and H.-C. Zhou, Chem. Soc. Rev., 2016, 45, 2327–2367.
39. S. B. Kalidindi, S. Nayak, M. E. Briggs, S. Jansat, A. P. Katsoulidis, G. J. Miller, J. E. Warren, D. Antypov, F. Corà, B. Slater, M. R. Prestly, C. Martí-Gastaldo and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2015, 54, 221–226.
40. V. Guillerm, F. Ragon, M. Dan-Hardi, T. Devic, M. Vishnuvarthan, B. Campo, A. Vimont, G. Clet, Q. Yang, G. Maurin, G. Férey, A. Vittadini, S. Gross and C. Serre, Angew. Chem., 2012, 124, 9401–9405.
41. S. Yuan, Y.-P. Chen, J.-S. Qin, W. Lu, L. Zou, Q. Zhang, X. Wang, X. Sun and H.-C. Zhou, J. Am. Chem. Soc., 2016, 138, 8912–8919.
42. B. Wang, X.-L. Lv, D. Feng, L.-H. Xie, J. Zhang, M. Li, Y. Xie, J.-R. Li and H.-C. Zhou, J. Am. Chem. Soc., 2016, 138, 6204–6216.
43. T.-F. Liu, D. Feng, Y.-P. Chen, L. Zou, M. Bosch, S. Yuan, Z. Wei, S. Fordham, K. Wang and H.-C. Zhou, J. Am. Chem. Soc., 2015, 137, 413–419.
44. A. E. Platero-Prats, A. B. League, V. Bernales, J. Ye, L. C. Gallington, A. Vjunov, N. M. Schweitzer, Z. Li, J. Zheng, B. L. Mehdi, A. J. Stevens, A. Dohnalkova, M. Balasubramanian, O. K. Farha, J. T. Hupp, N. D. Browning, J. L. Fulton, D. M. Camaioni, J. A. Lercher, D. G. Truhlar, L. Gagliardi, C. J. Cramer and K. W. Chapman, J. Am. Chem. Soc., 2017, 139, 10410–10418.
45. M. H. Teplensky, M. Fantham, P. Li, T. C. Wang, J. P. Mehta, L. J. Young, P. Z. Moghadam, J. T. Hupp, O. K. Farha, C. F. Kaminski and D. Fairen-Jimenez, J. Am. Chem. Soc., 2017, 139, 7522–7532.
46. D. A. Gómez-Gualdrón, T. C. Wang, P. García-Holley, R. M. Sawelewa, E. Argueta, R. Q. Snurr, J. T. Hupp, T. Yildirim and O. K. Farha, ACS Appl. Mater. Interfaces, 2017, 33419–33428,  DOI:10.1021/acsami.7b01190.
47. T. C. Wang, N. A. Vermeulen, I. S. Kim, A. B. F. Martinson, J. F. Stoddart, J. T. Hupp and O. K. Farha, Nat. Protoc., 2016, 11, 149–162.
48. J. E. Mondloch, M. J. Katz, W. C. Isley, P. Ghosh, P. Liao, W. Bury, G. W. Wagner, M. G. Hall, J. B. DeCoste, G. W. Peterson, R. Q. Snurr, C. J. Cramer, J. T. Hupp and O. K. Farha, Nat. Mater., 2015, 14, 512–516.
49. T. C. Wang, W. Bury, D. A. Gómez-Gualdrón, N. A. Vermeulen, J. E. Mondloch, P. Deria, K. Zhang, P. Z. Moghadam, A. A. Sarjeant, R. Q. Snurr, J. F. Stoddart, J. T. Hupp and O. K. Farha, J. Am. Chem. Soc., 2015, 137, 3585–3591.
50. F. Drache, V. Bon, I. Senkovska, C. Marschelke, A. Synytska and S. Kaskel, Inorg. Chem., 2016, 55, 7206–7213.
51. A. Khutia, H. U. Rammelberg, T. Schmidt, S. Henninger and C. Janiak, Chem. Mater., 2013, 25, 790–798.
52. P. Wollmann, M. Leistner, W. Grählert, O. Throl, F. Dreisbach and S. Kaskel, Microporous Mesoporous Mater., 2012, 149, 86–94.
53. M. Wöllner, N. Klein and S. Kaskel, Microporous Mesoporous Mater., 2019, 278, 206–211.
54. M. Wöllner, M. Leistner, M. Benusch, P. Wollmann, W. Grählert and S. Kaskel, Adv. Powder Technol., 2017, 28, 1065–1068.
55. J. Dai, M. L. McKee and A. Samokhvalov, J. Phys. Chem. C, 2015, 119, 2491–2502.
56. L. G. Gordeeva, M. V. Solovyeva and Y. I. Aristov, Energy, 2016, 100, 18–24.
57. A. A. Askalany, M. Salem, I. M. Ismael, A. H. H. Ali, M. G. Morsy and B. B. Saha, Renewable Sustainable Energy Rev., 2013, 19, 565–572.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1891266–1891269. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ta00825j

---