Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Band vs. polaron: vibrational motion and chemical expansion of hydride ions as signatures for the electronic character in oxyhydride barium titanate
Erik Jedvik
Granhed
 a,
Anders
Lindman
a,
Anders
Lindman
 a,
Carin
Eklöf-Österberg
b,
Maths
Karlsson
a,
Carin
Eklöf-Österberg
b,
Maths
Karlsson
 b,
Stewart F.
Parker
b,
Stewart F.
Parker
 c and
Göran
Wahnström
c and
Göran
Wahnström
 *a
*a
aDepartment of Physics, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden. E-mail: goran.wahnstrom@chalmers.se
bDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden
cISIS Facility, STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxon OX11 0QX, UK
First published on 18th June 2019
Abstract
The oxyhydride phase of barium titanate, BaTiO3−xHx, is a mixed hydride ion and electron conductor. The substitution of oxygen with hydrogen to form a hydride ion is accompanied by donation of an electron to the initially empty titanium 3d conduction band. It is not clear, however, whether the electron forms a delocalized state where it is shared among all titanium ions forming a bandstate, or if it localizes on a titanium ion and forms a bound electron polaron. Here, we investigate polaron formation in this material using density-functional theory (DFT) calculations, where the self-interaction error has been corrected by the DFT + U method and the HSE hybrid functional. While calculated formation energies do not provide a conclusive description of the electronic state, a comparison of the results from first-principles phonon calculations with vibrational spectra measured with inelastic neutron scattering (INS) suggests that the electrons form bandstates in bulk BaTiO3−xHx. This is further supported by comparison of the computed chemical expansion of the involved defect species with experimental data of the lattice expansion in the oxyhydride formation. The oxyhydride phase of barium titanate, BaTiO3−xHx, should thus exhibit metallic-like conductivity.
1 Introduction
Oxyhydrides, where a hydride ion (H−) is substituted on an oxygen site, are rare in nature and the oxyhydride phases (Ca,Sr,Ba)TiO3−xHx, which can form under strongly reducing conditions,1,2 were the first ones discovered based on the simple perovskite structure ABO3. Among them, BaTiO3−xHx exhibits the largest number of hydride ions with a concentration up to about x = 0.6 and the material exhibits both hydride ion mobility and electronic conductivity.1,3 Understanding the transport is of great importance in developing electrochemical devices but neither the ionic or the electronic transport mechanisms are fully understood.4 Here we focus on the electronic part.The substitutional hydride ion ( in Kröger–Vink notation) acts as a donor, contributing to n-type conductivity in the initially empty titanium 3d band,5–7 and measurements confirm that BaTiO3−xHx is electrically conducting.1,8,9 Kobayashi et al.1 reported a semiconducting behaviour for the bulk phase of BaTiO3−xHx (with x = 0.3 and x = 0.6). However, as the conductivity measurement was performed on a powder sample pressed into a pellet without sintering, the reported values may not reflect the true bulk properties of the material.1 More recent studies on epitaxial thin films showed that at high hydride concentrations (x ≳ 0.2) BaTiO3−xHx exhibits metallic-like conductivity, while at lower concentrations (x ≲ 0.2) the conductivity is semiconductor-like.9
in Kröger–Vink notation) acts as a donor, contributing to n-type conductivity in the initially empty titanium 3d band,5–7 and measurements confirm that BaTiO3−xHx is electrically conducting.1,8,9 Kobayashi et al.1 reported a semiconducting behaviour for the bulk phase of BaTiO3−xHx (with x = 0.3 and x = 0.6). However, as the conductivity measurement was performed on a powder sample pressed into a pellet without sintering, the reported values may not reflect the true bulk properties of the material.1 More recent studies on epitaxial thin films showed that at high hydride concentrations (x ≳ 0.2) BaTiO3−xHx exhibits metallic-like conductivity, while at lower concentrations (x ≲ 0.2) the conductivity is semiconductor-like.9
Based on first-principles calculations it has been suggested that electron polarons, which form localized electronic states in the band gap, are responsible for the experimentally observed semiconductor-like conductivity in bulk BaTiO3−xHx.7 A polaron is a quasiparticle consisting of a charge localization in association with a local lattice distortion. In the present case this refers to a localized electron on a titanium ion that resides next to a hydride ion, thereby changing the valence of the titanium ion from +4 to +3. The concomitant distortion of the lattice influences the local atomic environment and thereby the vibrational properties of the hydride ion. In pristine BaTiO3, (self-trapped) electron polarons have been found to be unstable,7 but bound polarons have been discussed in connection to n-type doping such as Nb5+ substitution10,11 and oxygen vacancies.12,13 The question naturally arises whether the H− substitution also can form bound polarons in BaTiO3. In addition, electron polarons have been found in TiO2,14–19 which, similar to BaTiO3, has valence and conduction bands that are dominated by oxygen 2p states and titanium 3d states, respectively.
The aim of the present study is to investigate the possibility of polaron formation in bulk BaTiO3−xHx. We use two complementary techniques: first-principles calculations based on density-functional theory (DFT) and inelastic neutron scattering (INS) experiments. We focus on: (i) the formation energy of the polaron, (ii) the chemical expansion of the lattice due to the polaronic defect, and (iii) the effect of the polaron on the hydride ion vibrational motion.
Modelling of polarons using DFT requires additional considerations due to the self-interaction error of the standard local and semi-local exchange–correlation (XC) functionals, which favour charge delocalization. The self-interaction error can be remedied by using the DFT + U method,20 where the U-parameter should correct for the self-interaction error. Here we use DFT + U to study the polaronic distortion and the associated formation energy. To obtain an appropriate value of the U-parameter we determine U by restoring the piecewise linearity of the total energy as a function of fractional occupancy of the polaron level, a known property of the exact density functional.21–23
Inelastic neutron scattering (INS) is used to study the vibrational motion of the hydride ion. This experimental technique provides a straightforward way to investigate the vibrational properties of hydride ions because of the large neutron cross section of hydrogen relative to the other atomic species in BaTiO3−xHx. The vibrational spectrum is also computed and to obtain accurate frequencies we make use of the hybrid functional HSE,24,25 which is known to reproduce the experimental frequencies for BaTiO3 accurately.26
We find that the electrons in bulk BaTiO3−xHx form delocalized bandstates, in contrast to ref. 7, and thus bulk BaTiO3−xHx should exhibit metallic-like conductivity.
2 Theoretical approach
2.1 Computational details
Density-functional theory (DFT) calculations were performed using the projector augmented wave (PAW) method27,28 as implemented in the Vienna ab initio simulation package (VASP).29 The semi-local functional PBE30 and the hybrid functional HSE24 were used to model exchange and correlation (XC) effects. For the latter we consider the conventional mixing and screening (α = 0.25 and ω = 0.2 Å−1), which is often referred to as HSE06.25 The DFT + U method was considered in its rotationally invariant form,31 where the U-parameter was applied to the Ti-3d orbitals. The choice of U was based on the concept of piecewise linearity23,32 and is further described in Section 2.3.Unless otherwise stated, calculations were carried out using supercells containing 2 × 2 × 2 unit cells (40 atoms). For this supercell size the sampling of the Brillouin zone was performed using 6 × 6 × 6 Monkhorst–Pack grids for PBE and PBE + U calculations while 4 × 4 × 4 grids were used for HSE. k-point meshes for calculations with larger supercells were reduced accordingly. The rather high k-point density is necessary in order to accurately describe the delocalized electronic states. All calculations were performed spin polarized using a Gaussian smearing of width σ = 10−5 eV in order to properly populate the localized polaronic defect level. A plane wave cut-off energy of 500 eV was used. The calculations were converged to energies within 10−7 eV for the electronic structure and the ionic relaxations to forces within 10−4 eV Å−1.
2.2 Pristine BaTiO3
In order to assess the validity of our calculations we begin by investigating the bulk properties of the cubic phase of pristine BaTiO3 using PBE, PBE + U (U = 3.3 eV, see Section 2.3 for details) and HSE. The results of PBE and HSE (Table 1) agree very well with the previous calculations in ref. 26. Relative to PBE, PBE + U predicts both a slightly larger lattice constant and band gap. A more striking difference between the two methods is connected to the unstable vibrational mode, where the magnitude of the imaginary frequency is reduced substantially with PBE + U. The smaller magnitude indicates that the addition of a U-parameter increases the stability of the cubic phase, although the tetragonal phase remains favorable with the present choice of U. The real frequencies, on the other hand, are very similar for PBE and PBE + U, which shows that the addition of U does not alter the vibrational properties of pristine BaTiO3 in any significant way. PBE + U can therefore be expected to perform similarly to PBE also when defects are introduced.| This work | Wahl et al.26 | Exp. | ||||
|---|---|---|---|---|---|---|
| PBE | PBE + Ua | HSEb | PBE | HSEc | ||
| a U = 3.3 eV. b α = 0.25 and ω = 0.2 Å−1. c α = 0.25 and ω = 0.3 Å−1. | ||||||
| a 0 | 4.032 | 4.052 | 3.989 | 4.035 | 3.995 | 3.9975 (ref. 33) |
| Eg | 1.71 | 2.12 | 3.10 | 1.70 | 2.92 | 3.22 (ref. 34) |
| T1u(TO1) | 247i | 57i | 257i | 239i | 241i | Soft (ref. 35) |
| T1u(TO2) | 170 | 167 | 185 | 169 | 185 | 181 (ref. 35) |
| T2u | 286 | 283 | 312 | 286 | 310 | 306 (ref. 35) |
| T1u(TO3) | 452 | 461 | 478 | 453 | 480 | 487 (ref. 35) |
When compared with experimental data35 we notice that PBE and PBE + U underestimate the vibrational frequencies while HSE gives excellent results (see Table 1). The PBE error is partly due to the overestimated lattice constant but the improved performance of HSE also depends on the inclusion of exact exchange, which produces a more accurate electron density that leads to stiffening of the bonds.26,36,37 The T1u-modes all contain a component of stretching character in the Ti–O bonds, which make these modes pressure dependent. Wahl et al. showed that using a semi-local XC functional (PBEsol) with a more accurate lattice constant increases the frequencies by about 3–5% and inclusion of exact exchange (HSE) further increases the frequencies by 3–4%.26 The T2u-mode has more of a bending character, which makes it rather insensitive to variations of the lattice constant.38 The inclusion of exact exchange, however, increases the vibrational frequencies of this mode by about 8–9%. To summarize, the use of HSE improves on the PBE description substantially as it increases the frequencies by about 5–10% and enables a very accurate description of the vibrational modes compared with experimental data (Table 1).26
2.3 Polaron calculations
The choice of U in the DFT + U method is of significant importance. The method is a parametric correction of standard DFT and the value of U is not transferable but will depend on the physical quantity under consideration as well as the underlying functional. Here we determine the value of U by enforcing the piecewise linearity constraint, which is a known property of the exact XC functional.21 We follow the same approach as in ref. 23 and 32, and tune U so that the energy depends linearly on the charge during the population of the polaronic level.The addition of a U-parameter on Ti introduces a pressure in the system, which increases with increasing U. Consequently, for each value of U a different equilibrium lattice constant is obtained. We chose to release this pressure by relaxing the lattice constant for each considered U-value.
The lattice distortion consistent with polaron formation cannot be known a priori and we chose to prepare an archetype polaron configuration by displacing the atoms randomly and performing ionic relaxations in the confinement of a cubic supercell at a large value of U. The obtained structure was confirmed to be stable through a phonon calculation, which displayed no imaginary modes. The ionic positions were then further relaxed within a cubic supercell for the respective U values at the corresponding equilibrium lattice constants.
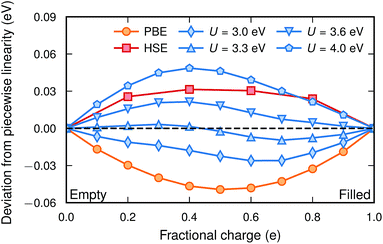
Fig. 1 shows the deviation from a piecewise linear behaviour for four different values of U together with PBE and HSE for a polaronic  configuration in a 2 × 2 × 2 supercell. As expected, PBE yields a convex behaviour consistent with delocalization, while the HSE calculation results in a slightly concave behaviour consistent with over-localization. The PBE + U method, with the appropriate U, performs reasonably well although a slight sinusoidal shape can be seen. The residual, defined as the root mean square of the deviation from piecewise linearity, was minimized at a value of U = 3.3 eV, for which the lattice constant is 4.0520 Å. The value of U is not completely transferable between different supercell sizes and for a 3 × 3 × 3 supercell a smaller value of U was found to yield piecewise linearity. The residual for this system was minimized at a value of U = 3.1 eV with the corresponding lattice constant of 4.0507 Å.
configuration in a 2 × 2 × 2 supercell. As expected, PBE yields a convex behaviour consistent with delocalization, while the HSE calculation results in a slightly concave behaviour consistent with over-localization. The PBE + U method, with the appropriate U, performs reasonably well although a slight sinusoidal shape can be seen. The residual, defined as the root mean square of the deviation from piecewise linearity, was minimized at a value of U = 3.3 eV, for which the lattice constant is 4.0520 Å. The value of U is not completely transferable between different supercell sizes and for a 3 × 3 × 3 supercell a smaller value of U was found to yield piecewise linearity. The residual for this system was minimized at a value of U = 3.1 eV with the corresponding lattice constant of 4.0507 Å.
In a previous theoretical study of BaTiO3−xHx where polaron formation was found to be favourable, the PBE + U method with U = 4.49 eV was used.7 That value was determined for the LSDA functional.6 However, the value of U for correcting the self-interaction error is not transferable between different XC functionals, different projection radii (PAW potentials)39 and, as shown here, different supercell sizes. As indicated by Fig. 1, such a high value of U would lead to over-localization and erroneously favor polaron formation in these systems.
2.4 Vibrational calculations
Vibrational calculations were conducted following two different approaches. The full phonon spectra were calculated within the harmonic approximation using the frozen phonon approach with finite displacements and phonopy40 software. Forces were computed with a 2 × 2 × 2 augmented supercell consisting of 320 atoms for the defect-containing configurations, which allows for a zone folding scheme with interpolation between high symmetry points. Due to the computational cost the electronic k-point mesh was reduced to 2 × 2 × 2 for the augmented supercell. In computing the vibrational density of states, a Monkhorst–Pack q-point mesh of 10 × 10 × 10 was used.When using the computationally more costly HSE functional, a simplified approach was used for determining the hydride ion frequencies. These oscillations are very localized (which was confirmed by the full phonon calculations, see Fig. 4) and can be well described by a 3D oscillator in a potential well provided by the relaxed positions of the surrounding atoms. The 3D potential is mapped out through displacements of the hydride ion by ±0.1 Å and ±0.2 Å along the three different directions, where the energy is calculated at each displacement. Second order polynomials are then used to fit the energy landscape and to obtain the vibrational frequencies. We denote this approach as the one particle harmonic potential (OPHP) method, and its validity is demonstrated in Section 4.4.1.
3 Materials and experimental technique
3.1 Sample preparation
The oxyhydride powder sample was prepared by mixing CaH2 powder with BaTiO3 powder and subsequently pelletizing inside an Ar filled glove box. The pellet was placed in a custom made stainless steel autoclave and heated inside a tube furnace to a temperature of 700 °C for a period of three days. Finally, the pellet was washed and subsequently dried under dynamic vacuum at 120 °C for about 1 day. The details of the sample preparation can be found in ref. 41 and the present work makes use of the sample denoted as CA1 in ref. 41.Powder X-ray diffraction (PXRD) measurements confirmed a simple cubic structure for the sample with lattice parameter a = 4.0055 Å at ambient temperature.41 Thermogravimetric analysis (TGA) of the sample showed that the total defect concentration x, as in BaTiO3−xHy□x−y, was x = 0.18,41 where □ denotes oxygen vacancies in the oxyhydride. The hydride ion concentration was determined to be y = 0.10 using nuclear magnetic resonance (NMR) spectroscopy,41 which implies an oxygen vacancy concentration of (x − y) = 0.08.
3.2 Inelastic neutron scattering
The INS experiment was performed on TOSCA at the ISIS Facility,42 with the sample loaded into a aluminum sachet and the sachet into indium wire sealed thin-walled aluminum can. The measurement was performed at 10 K with a measuring time of approximately 6 h per sample. The INS spectra were analyzed with Mantid43 and DAVE44 software.To theoretically analyze the spectrum from the multi-component poly-crystalline sample the incoherent approximation was employed.45 The emission part of the one-phonon contribution to the INS law can then be written as46
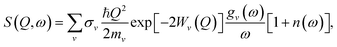 | (1) |
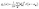 | (2) |
A key aspect of TOSCA42 is that the momentum of the scattered neutrons is very small. The momentum transfer ℏQ and the energy transfer ℏω in the scattering event are therefore related approximately as (ℏ2Q2)/(2mn) = ℏω, where mn is the neutron mass.47 The measured intensity S(Q,ω) at low temperatures can then be written as
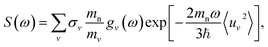 | (3) |
4 Results and discussion
The substitutional hydrogen on an oxygen site acts as a donor contributing one electron to the empty Ti 3d band. Here we investigate two possible states for this electron. The first option is the delocalized state, where the electron is shared among all titanium ions forming a bandstate. In the second option the electron localizes on a titanium ion that is the nearest neighbour to the hydride ion. The consequent formation of a bound polaron will be referred to as the polaron state.
acts as a donor contributing one electron to the empty Ti 3d band. Here we investigate two possible states for this electron. The first option is the delocalized state, where the electron is shared among all titanium ions forming a bandstate. In the second option the electron localizes on a titanium ion that is the nearest neighbour to the hydride ion. The consequent formation of a bound polaron will be referred to as the polaron state.
4.1 Electronic and atomic structures
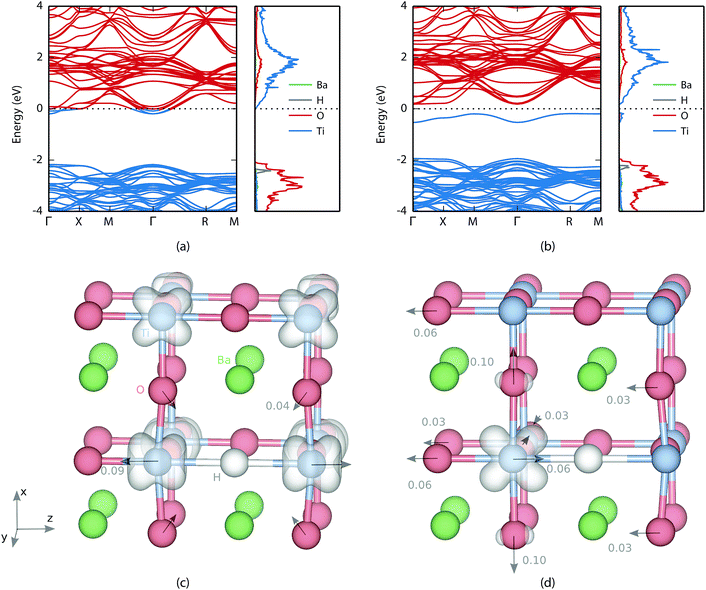
The valence and conduction bands of BaTiO3 consist of oxygen 2p states and titanium 3d states, respectively (see Fig. 2). In the oxyhydride phase the hydrogen level is found in the valence band with a peak at about 0.3 eV below the valence band edge. Bader analysis49,50 shows an electron excess of 0.6, which confirms electron transfer to the hydrogen atom. Similar values were found by Iwazaki et al. for the substitutional hydrogen ion in BaTiO3 (ref. 5) as well as in SrTiO3.51For the bandstate the Fermi level is found inside the conduction band making the material effectively metallic [Fig. 2(a)]. The charge is delocalized and shared between all titanium atoms [see Fig. 2(c)]. The formation of a H− defect also causes lattice distortions. The atomic displacements for the bandstate relative to pristine BaTiO3 are indicated with arrows in Fig. 2(c). The largest displacement is found for the nearest neighbour Ti, which move away from H by a distance of 0.09 Å. The nearest neighbour O moves 0.04 Å towards the hydride ion.
For the polaron state a defect level is formed in the band gap 0.37 eV below the conduction band edge [see Fig. 2(b)]. In real space the electron is localized on one of the neighbouring Ti atoms. While the bandstate maintains a principal axis of fourfold rotational symmetry, the symmetry of the polaron state is reduced to twofold rotational symmetry and the degeneracy of the perpendicular axes is removed. This can be seen in Fig. 2(d) where the electron density of the polaron is located in the xz-plane.
The atomic displacements due to polaron formation can be described relative to the hydride ion in the bandstate, by placing the origin on the hydrogen. Almost all major displacements are found in the vicinity of the polaron, which is not surprising since the Ti ion needs more space to accommodate the additional electron. The nearest neighbour oxygen atoms are all displaced away from the polaron along the Cartesian coordinate axes by a distance of 0.10 Å, 0.06 Å and 0.03 Å, respectively [see Fig. 2(d)]. The polaronic titanium itself is displaced by 0.06 Å towards the hydrogen, which decreases the distance between the two from 2.12 Å in the bandstate to only 2.06 Å. It is, however, still 0.04 Å larger than the oxygen-titanium distance in pristine BaTiO3 (as computed with PBE + U). Finally, there is a shift of the entire oxygen-barium plane in the direction opposite to the titanium distortion that increases the distance between every second oxygen and titanium, which is similar to a ferroelectric transition.
4.2 Formation energy
In order to determine the stability of the polaron we first turn to the formation energy. For it has been calculated according to52
it has been calculated according to52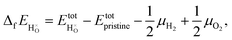 | (4) |
 and Etotpristine are the total energies of the oxyhydride and pristine BaTiO3, respectively. The chemical potentials for the gas phases of O2 and H2 (μO2 and μH2, respectively) were calculated as twice the total energy of the atom plus the experimental cohesive energy for the molecule, where the latter was obtained from ref. 53. Calculations were performed with 2 × 2 × 2 and 3 × 3 × 3 supercells, which correspond to hydrogen concentrations of x = 0.125 and x = 0.037. PBE, PBE + U and HSE all predict rather similar formation energies that are somewhat lower in the larger supercell (see Table 2), indicating that the hydrogen concentration may influence the formation energy.
and Etotpristine are the total energies of the oxyhydride and pristine BaTiO3, respectively. The chemical potentials for the gas phases of O2 and H2 (μO2 and μH2, respectively) were calculated as twice the total energy of the atom plus the experimental cohesive energy for the molecule, where the latter was obtained from ref. 53. Calculations were performed with 2 × 2 × 2 and 3 × 3 × 3 supercells, which correspond to hydrogen concentrations of x = 0.125 and x = 0.037. PBE, PBE + U and HSE all predict rather similar formation energies that are somewhat lower in the larger supercell (see Table 2), indicating that the hydrogen concentration may influence the formation energy.
We define the polaron formation energy as the formation energy difference between the localized polaron state and the delocalized bandstate:
 | (5) |
With this definition a negative value indicates that the polaron is more stable than the bandstate. The polaron formation energy is found to depend not only on the value of U but also on the system size (see Fig. 3 and Table 2). The polaron formation energy is about 150 meV more negative for a 2 × 2 × 2 compared to a 3 × 3 × 3 supercell. Thus, in the smaller supercell a value of U = 3.2 eV is sufficient to favour polaron formation while in the larger supercell a value of 3.7 eV is necessary. Furthermore, the U-value that fulfils piecewise linearity (see Section 2.3) is larger for a 2 × 2 × 2 supercell (U = 3.3 eV) than for a 3 × 3 × 3 supercell (U = 3.1 eV). This suggests that a polaron is stable (ΔEpol = −57 meV) in the smaller supercell but unstable (ΔEpol = 124 meV) in the larger supercell. In addition, the zero point energy is about 6 meV higher for the polaron compared to the bandstate making the polaron less stable.
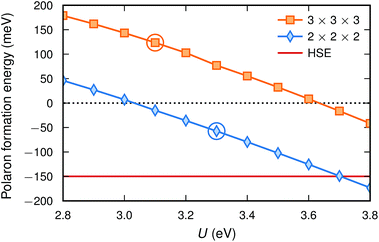 | ||
| Fig. 3 Polaron formation energy [eqn (5)] calculated with PBE + U for the two supercell sizes. The circles indicate the U-values fulfilling piecewise linearity. The formation energy as calculated with HSE is also included for comparison. | ||
Calculations with HSE suggest an even more stable polaron, which is in agreement with the trend in Fig. 1. Such an agreement between piecewise linearity and formation energy has previously been found for both electron and hole polarons in perovskites and other oxides.32,39
4.3 Chemical expansion
When a defect is introduced into the material it can induce an expansion (or contraction) of the material, a chemical expansion. In analogy with thermal expansion the chemical expansion coefficient β is defined as54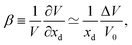 | (6) |
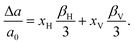 | (7) |
The induced strain from a single defect is generally not isotropic. It is described by the defect induced strain tensor λ, and β is then given by the trace of λ, β = Tr(λ).55 The tensor λ can be computed by performing full relaxations, i.e., relaxation of both ionic positions and cell parameters. The defect induced strain tensor is then obtained as55
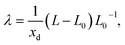 | (8) |
We have determined the chemical expansion for both the bandstate and the polaron state of  using a 2 × 2 × 2 supercell. Our sample also contains oxygen vacancies (see Section 3.1). This type of cubic O-deficient oxyhydride is found to be quite common.56 In BaTiO3 these vacancies act as shallow donors and we have therefore also considered the neutral vacancy
using a 2 × 2 × 2 supercell. Our sample also contains oxygen vacancies (see Section 3.1). This type of cubic O-deficient oxyhydride is found to be quite common.56 In BaTiO3 these vacancies act as shallow donors and we have therefore also considered the neutral vacancy  .57,58 We find that the lattice expands along the principal axis (z) for all three defects and that the degeneracy of the perpendicular axes (x and y) is lifted for the polaron (see Table 3), in agreement with the symmetries described above. The expansion of the lattice along the principal direction is largest for the neutral vacancy. For the bandstate there is a small contraction along the perpendicular axes, but the chemical expansion is still positive with β = 0.030. For the polaron state there is also a contraction along the y direction but an expansion along the x direction causing an overall chemical expansion of β = 0.056, which is nearly twice as large as that of the bandstate. For the oxygen vacancy there is also a small contraction along the perpendicular axes, and the resulting chemical expansion is β = 0.049, nearly as large as for the polaron state.
.57,58 We find that the lattice expands along the principal axis (z) for all three defects and that the degeneracy of the perpendicular axes (x and y) is lifted for the polaron (see Table 3), in agreement with the symmetries described above. The expansion of the lattice along the principal direction is largest for the neutral vacancy. For the bandstate there is a small contraction along the perpendicular axes, but the chemical expansion is still positive with β = 0.030. For the polaron state there is also a contraction along the y direction but an expansion along the x direction causing an overall chemical expansion of β = 0.056, which is nearly twice as large as that of the bandstate. For the oxygen vacancy there is also a small contraction along the perpendicular axes, and the resulting chemical expansion is β = 0.049, nearly as large as for the polaron state.
 as well as for the neutral oxygen vacancy
as well as for the neutral oxygen vacancy  calculated with PBE + U (U = 3.3 eV) in a 2 × 2 × 2 supercell
calculated with PBE + U (U = 3.3 eV) in a 2 × 2 × 2 supercell
| λ xx | λ yy | λ zz | β | |
|---|---|---|---|---|
| Bandstate | −0.0045 | −0.0045 | 0.0392 | 0.030 |
| Polaron state | 0.0283 | −0.0179 | 0.0456 | 0.056 |
| Oxygen vacancy | −0.0059 | −0.0059 | 0.0608 | 0.049 |
The magnitude of the chemical expansion for the bandstate and the polaron state is quite different and depending on which state is present the lattice expansion will be different. The measured composition is BaTiO2.82H0.1□0.08 and the expanded lattice constant a = 4.0055 Å. To obtain the change of the lattice constant we need an experimental value for a0 at 20 °C. By extrapolating the data for cubic BaTiO3 in ref. 59 to 20 °C, a0 = 3.9975 Å is obtained. This implies that experimentally Δa/a0 = 0.0020. We can also compute the lattice expansion using the data in Table 3. By assuming a bandstate and polaron state, respectively, we obtain the lattice expansions Δa/a0 = 0.0023 and Δa/a0 = 0.0032 (see Table 4). Clearly, by assuming a bandstate the theoretical lattice expansion becomes much closer to the experimental value compared with assuming the polaron state.
It is also interesting to compare with the experimental data by Kobayashi et al.1 They synthesized a sample with the composition BaTiO2.38H0.62. It was stated that the number of oxygen vacancies was small. The expanded lattice constant was a = 4.0236 Å, which then corresponds to an expansion of Δa/a0 = 0.0065. Again, we find that by assuming a bandstate the theoretical lattice expansion becomes much closer to the experimental value (see Table 4).
4.4 Vibrational spectra
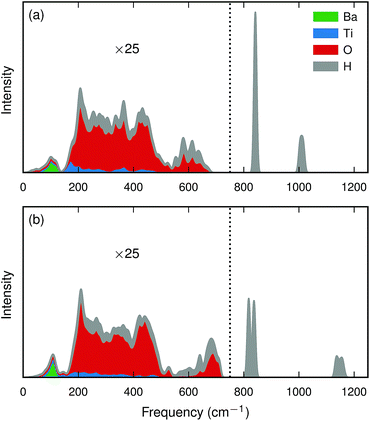 | ||
| Fig. 4 Calculated partial (cumulative) intensity [eqn (3)] for a hydride ion in a 2 × 2 × 2 BaTiO3 supercell for (a) the bandstate and (b) the polaron state. Intensities below 750 cm−1 (marked with a dotted line) have been magnified by a factor of 25. | ||
The hydrogen motion for the bandstate can be seen as two sharp peaks around 843 cm−1 and 1018 cm−1 [see Fig. 4(a)] and the assignment of these modes is illustrated in Fig. 5. The higher frequency mode is the stretching mode of A2u symmetry along the principal axis, which is denoted as ω∥. The lower mode frequency is the doubly degenerate bending mode of Eu symmetry in the mirror plane perpendicular to the principal axis and is denoted as ω⊥. The vibrational frequencies of the hydride ion motion for the bandstate configuration of  have been studied previously by Iwazaki et al.5 using a method similar to our OPHP method (see Section 2.4) with the PBE functional and the results from their investigation are in good agreement with our results.
have been studied previously by Iwazaki et al.5 using a method similar to our OPHP method (see Section 2.4) with the PBE functional and the results from their investigation are in good agreement with our results.
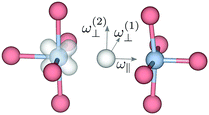 | ||
| Fig. 5 Illustration of the vibrational modes for the substitutional hydride ion in oxyhydride BaTiO3 in the polaronic state. For the bandstate ω(1)⊥ and ω(2)⊥ are degenerate. | ||
The lattice distortion associated with polaron formation breaks the mirror-plane symmetry as well as the symmetry of fourfold rotation into a two-fold rotation symmetry. The Eu bending mode is split into two modes of B1 and B2 symmetry, for which the separation is about 20 cm−1 [see Fig. 4(b)]. In addition, the displacement of the polaronic Ti towards the hydrogen causes a substantial upward shift of the stretching mode frequency from 1006 cm−1 to 1133 cm−1.
Due to the small mass of the hydride ion its vibrational eigenmodes are localized and show little dispersion. Table 5 shows the maximum and minimum frequencies together with the Γ-point frequency for the bandstate, where it can be seen that the dispersion is small. For the stretching mode, the width of the band is only 16 cm−1 and the dispersion is negligible for the bending mode. These modes should therefore be well described by the OPHP method. By symmetry, the eigenmodes must lie along the lattice vectors: the principal axis and the two perpendicular axes, which can be considered independently. The frequencies obtained with the OPHP method show good agreement with the frequencies obtained from the full phonon calculation using phonopy40 software (see Table 5). This implies that the vibrational modes for the hydride ion are accurately described using the OPHP method.
 computed using phonopy with a 4 × 4 × 4 augmented supercell (Γ, max, min) and the OPHP method. PBE + U calculations were performed using U = 3.3 eV. The data that are used in the comparison with the INS spectra are highlighted in bold
computed using phonopy with a 4 × 4 × 4 augmented supercell (Γ, max, min) and the OPHP method. PBE + U calculations were performed using U = 3.3 eV. The data that are used in the comparison with the INS spectra are highlighted in bold
| Mode | PBE + U | HSE | ||||
|---|---|---|---|---|---|---|
| Γ | Max | Min | OPHP | OPHP | ||
| Bandstate | ω ∥ | 1018 | 1018 | 1002 | 998 | 1033 |
| ω ⊥ | 843 | 843 | 841 | 849 | 899 | |
| Polaron state | ω ∥ | 1133 | 1168 | 1133 | 1142 | 1160 |
| ω (1)⊥ | 835 | 835 | 840 | 831 | 894 | |
| ω (2)⊥ | 818 | 815 | 818 | 814 | 874 | |
As discussed in Section 2.2, the HSE functional predicts accurate frequencies for pristine BaTiO3. The stretching mode for the hydride ion is similar to the T1u modes of pristine BaTiO3 and the bending mode is similar to the T2u mode. It is therefore desirable to use HSE also for the vibrational motion of the hydride ion. However, a full phonon calculation with HSE is computationally very demanding but as we have shown here that the computationally less expensive OPHP method can be used to obtain accurate frequencies. We have therefore restricted the HSE calculations to the OPHP method.
Let us first consider the bandstate. A relaxed HSE configuration at the HSE lattice constant is used to obtain the 3D potential as described in Section 2.4, from which the harmonic frequencies are determined. Compared with PBE + U the HSE functional shifts the stretching frequency upwards by 35 cm−1, while the shift for the bending mode is even larger, 50 cm−1 (see Table 5).
Let us now consider the polaron state. The atomic relaxation with the HSE functional was conducted only for the ions along the Ti–H–Ti–O axis and its nearest neighbour oxygen ions, i.e., the ions depicted in Fig. 5. The largest displacements are found along the principal axis, where the hydrogen and oxygen atoms are both displaced in the negative z-direction, while the non-polaronic titanium is displaced in the positive z-direction (see Fig. 2 for the definition of the coordinate system). The polaronic Ti itself is displaced only marginally relative to the lattice. This causes the distance between the polaronic Ti and the hydrogen to decrease by 0.04 Å, from 2.06 Å to 2.02 Å, and increase between the polaronic Ti and the oxygen by 0.02 Å. Displacements of similar magnitudes were also found for the nearest neighbour oxygen ions relative to the polaronic Ti. In the x-direction the distance increases by 0.02 Å and in the y-direction by 0.03 Å. The relaxed configuration was used to create a 3D potential from which the harmonic frequencies are determined using the OPHP method. The HSE functional shifts the frequencies of the polaron state in a similar way to that for the bandstate. The stretching mode frequency is shifted upwards by 18 cm−1 and the bending mode frequencies by 63 cm−1 and 60 cm−1, respectively (see Table 5). Compared with the PBE + U values the frequencies are shifted upwards by about 3–4% and 7% for the stretching mode and the bending mode, respectively. These relative shifts are quite similar to the shifts for pristine BaTiO3 (see Section 2.2).
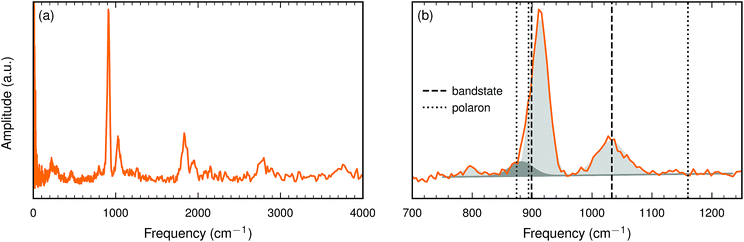 | ||
| Fig. 6 (a) The INS spectrum of the BaTiO2.82H0.10□0.08 sample at 10 K. (b) Close up of the spectrum in the interval 700–1250 cm−1. Frequencies calculated with HSE (see Table 5) are marked with dashed (bandstate) and dotted (polaron) lines. Gaussian fits are indicated by shaded areas (see Table 6). | ||
For a more quantitative analysis we have fitted the peaks in the interval between 750 and 1250 cm−1. Four Gaussians were required to obtain a good fit. The fit parameters are listed in Table 6 and the corresponding Gaussians are plotted in Fig. 6(b).
| ω (cm−1) | Area (a.u.) | FWHM (cm−1) | |
|---|---|---|---|
| 799 | 0.3 | 33.5 | |
| 882 | 0.7 | 44.8 | |
| 913 | 6.2 | 33.9 | |
| 1031 | 2.3 | 56.8 |
The present oxyhydride sample contains about an equal number of hydride ions and oxygen vacancies. The interaction between these two defects is repulsive and hence we do not expect any pronounced hydride ion–oxygen vacancy association. We have computed the hydride ion frequency spectrum for a few systems with an equal number of hydride ions and oxygen vacancies, with about 10% each. We find that when the hydride ion and the oxygen vacancy are nearest neighbors the degeneracy of the bending mode is removed and one of these modes is downshifted by about 100 cm−1. The other two modes are essentially unaffected. It is tempting to identify the weak experimental peak around 800 cm−1 with this defect configuration. For other defect configurations, where the hydride ion and the oxygen vacancy are not nearest neighbors, we find only small changes of the computed vibrational frequencies.
This comparison between measured and computed vibrational frequencies strongly suggests that electrons form bandstates in this O-deficient cubic oxyhydride.
5 Summary and conclusion
In the present contribution we have investigated the character of conduction electrons in cubic BaTiO3−xHx, where an electron can form either a delocalized bandstate or localize as a small electron polaron on titanium bound next to a hydride ion. The polaron formation energy has been determined with density-functional theory (DFT) calculations using both the DFT + U method and the hybrid functional HSE, where U in the former case was carefully chosen such that piecewise linearity was obtained and the self-interaction error was minimized. The formation energy was found to be small, on the order of thermal energy, and this result alone does not provide a conclusive description of the electronic state.The formation of a polaron causes a local lattice distortion where the Ti–H distance is reduced, which affects the localized hydride ion vibrational modes. These vibrational frequencies have been determined using HSE and we find that the stretching mode frequency shifts up from 1033 cm−1 to 1160 cm−1 upon polaron formation. At the same time the degenerate bending mode is split into two modes that are slightly downshifted by up to 30 cm−1. A comparison of these frequencies with data from inelastic neutron scattering (INS) experiments strongly suggests that electrons form bandstates in the present bulk material.
Furthermore, the chemical expansion has been determined, showing that the lattice expansion of the polaron state is about twice as large as that for the bandstate. By comparing the calculated data with our experimental data as well as with the experimental data for a fully hydride-ion substituted sample by Kageyama and coworkers1 we conclude that the expansion due to the bandstate fits much better than the polaron state, which further supports the presence of delocalized electrons in the oxyhydride.
The delocalized nature of the electrons is in line with metallic conductivity. For thin films of BaTiO3−xHx, Kageyama and co-workers have reported metallic conductivity at high hydride concentration,8,9 while at lower concentration a semiconducting behaviour was observed.9 It is possible that strain in epitaxial thin films could favour polaron formation and the small formation energies found here suggest that a rather small perturbation of the structure is sufficient for changing the relative stability of the two electronic states. Indeed, in ref. 9 it is found that the lattice structure of the thin film is not cubic but tetragonal. The semiconducting behaviour observed in bulk BaTiO3−xHx as reported in ref. 1 is, however, most likely due to grain boundaries in the powder sample.8
To conclude, we find that the electrons form delocalized bandstates in bulk BaTiO3−xHx, which implies a metallic conduction mechanism in this material. Furthermore, we have shown that first-principles calculations in combination with INS experiments are excellent tools to study the vibrational motion of the hydride ions and relate this to the character of the conduction electrons in oxyhydrides, and that chemical expansion can be used to discriminate between formation of delocalized bandstates and localized small polaron configurations in these materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Prof. Ulrich Häaussermann for useful information on the sample preparation and Laura Mazzei for information on neutron scattering measurements. This research was primarily funded by the Swedish Energy Agency (grant No. 36645-1 and No. 45410-1) and the Swedish Research Council (grant No. 2014-3980). Computational resources have been provided by the Swedish National Infrastructure for Computing (SNIC) at PDC (Stockholm), C3SE (Gothenburg) and NSC (Linköping). The STFC Rutherford Appleton Laboratory is thanked for access to neutron beam facilities.References
- Y. Kobayashi, O. J. Hernandez, T. Sakaguchi, T. Yajima, T. Roisnel, Y. Tsujimoto, M. Morita, Y. Noda, Y. Mogami, A. Kitada, M. Ohkura, S. Hosokawa, Z. Li, K. Hayashi, Y. Kusano, J. eun Kim, N. Tsuji, A. Fujiwara, Y. Matsushita, K. Yoshimura, K. Takegoshi, M. Inoue, M. Takano and H. Kageyama, Nat. Mater., 2012, 11, 507–511 CrossRef CAS PubMed.
- T. Sakaguchi, Y. Kobayashi, T. Yajima, M. Ohkura, C. Tassel, F. Takeiri, S. Mitsuoka, H. Ohkubo, T. Yamamoto, J. eun Kim, N. Tsuji, A. Fujihara, Y. Matsushita, J. Hester, M. Avdeev, K. Ohoyama and H. Kageyama, Inorg. Chem., 2012, 51, 11371–11376 CrossRef CAS PubMed.
- Y. Tang, Y. Kobayashi, K. Shitara, A. Konishi, A. Kuwabara, T. Nakashima, C. Tassel, T. Yamamoto and H. Kageyama, Chem. Mater., 2017, 29, 8187–8194 CrossRef CAS.
- Y. Kobayashi, Y. Tsujimoto and H. Kageyama, Annu. Rev. Mater. Res., 2018, 48, 303–326 CrossRef CAS.
- Y. Iwazaki, T. Suzuki and S. Tsuneyuki, J. Appl. Phys., 2010, 108, 1–8 CrossRef.
- J. Zhang, G. Gou and B. Pan, J. Phys. Chem. C, 2014, 118, 17254–17259 CrossRef CAS.
- X. Liu, T. S. Bjørheim and R. Haugsrud, J. Mater. Chem. A, 2017, 5, 1050–1056 RSC.
- T. Yajima, A. Kitada, Y. Kobayashi, T. Sakaguchi, G. Bouilly, S. Kasahara, T. Terashima, M. Takano and H. Kageyama, J. Am. Chem. Soc., 2012, 134, 8782–8785 CrossRef CAS PubMed.
- G. Bouilly, T. Yajima, T. Terashima, W. Yoshimune, K. Nakano, C. Tassel, Y. Kususe, K. Fujita, K. Tanaka, T. Yamamoto, Y. Kobayashi and H. Kageyama, Chem. Mater., 2015, 27, 6354–6359 CrossRef CAS.
- E. Possenriede, H. Kröse, T. Varnhorst, R. Scharfschwerdt and O. F. Schirmer, Ferroelectrics, 1994, 151, 199–204 CrossRef CAS.
- K. Page, T. Kolodiazhnyi, T. Proffen, A. K. Cheetham and R. Seshadri, Phys. Rev. Lett., 2008, 101, 205502 CrossRef PubMed.
- R. Scharfschwerdt, A. Mazur, O. F. Schirmer, H. Hesse and S. Mendricks, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 15284–15290 CrossRef CAS PubMed.
- M. Schrader, D. Mienert, T.-S. Oh, H.-I. Yoo and K. D. Becker, Solid State Sci., 2008, 10, 768–775 CrossRef CAS.
- V. M. Khomenko, K. Langer, H. Rager and A. Fett, Phys. Chem. Miner., 1998, 25, 338–346 CrossRef CAS.
- B. J. Morgan and G. W. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 233102 CrossRef.
- N. A. Deskins and M. Dupuis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195212 CrossRef.
- P. Deák, B. Aradi and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195206 CrossRef.
- S. Yang, A. T. Brant, N. C. Giles and L. E. Halliburton, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 125201 CrossRef.
- M. Setvin, C. Franchini, X. Hao, M. Schmid, A. Janotti, M. Kaltak, C. Van de Walle, G. Kresse and U. Diebold, Phys. Rev. Lett., 2014, 113, 086402 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 085202 CrossRef.
- P. Erhart, A. Klein, D. Åberg and B. Sadigh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035204 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- R. Wahl, D. Vogtenhuber and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104116 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comp. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- A. Lindman, P. Erhart and G. Wahnström, Phys. Rev. B, 2016, 94, 075204 CrossRef.
- H. D. Megaw, P. Roy. Soc. A, 1947, 189, 261–283 CrossRef CAS.
- S. H. Wemple, Phys. Rev. B: Solid State, 1970, 2, 2679–2689 CrossRef.
- T. Nakamura, Ferroelectrics, 1992, 137, 65–88 CrossRef CAS.
- D. I. Bilc, R. Orlando, R. Shaltaf, G.-M. Rignanese, J. Íñiguez and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165107 CrossRef.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- Y.-S. Seo and J. S. Ahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014114 CrossRef.
- Z. Wang, C. Brock, A. Matt and K. H. Bevan, Phys. Rev. B, 2017, 96, 125150 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- C. Eklöf-Österberg, R. Nedumkandathil, U. Häussermann, A. Jaworski, A. J. Pell, M. Tyagi, N. H. Jalarvo, B. Frick, A. Faraone and M. Karlsson, J. Phys. Chem. C, 2019, 123(4), 2019–2030 CrossRef.
- S. F. Parker, F. Fernandez-Alonso, A. J. Ramirez-Cuesta, J. Tomkinson, S. Rudic, R. S. Pinna, G. Gorini and J. F. Castañon, J. Phys.: Conf. Ser., 2014, 554, 012003 CrossRef.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Meth. A, 2014, 764, 156–166 CrossRef CAS.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- G. L. Squires, Introduction to the Theory of Thermal Neutron Scattering, Cambridge University Press, Cambridge, 2012 Search PubMed.
- R. Osborn, E. A. Goremychkin, A. I. Kolesnikov and D. G. Hinks, Phys. Rev. Lett., 2001, 87, 017005 CrossRef CAS PubMed.
- P. C. H. Mitchell, S. F. Parker, A. J. Ramirez-Cuesta and J. Tomkinson, Vibrational Spectroscopy with Neutrons, World Scientific Publishing Co. Pte. Ltd., Singapore, 2005 Search PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef.
- R. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- Y. Iwazaki, Y. Gohda and S. Tsuneyuki, APL Mater., 2014, 2, 012103 CrossRef.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- NIST JANAF thermochemical tables, ed. M. W. Chase Jr, 1985, http://kinetics.nist.gov/janaf Search PubMed.
- S. B. Adler, J. Am. Ceram. Soc., 2001, 84, 2117–2119 CrossRef CAS.
- E. Jedvik, A. Lindman, M. T. Benediktsson and G. Wahnström, Solid State Ionics, 2015, 275, 2–8 CrossRef CAS.
- R. Nedumkandathil, A. Jaworski, J. Grins, D. Bernin, M. Karlsson, C. Eklöf-Österberg, A. Neagu, C.-W. Tai, A. J. Pell and U. Häussermann, ACS Omega, 2018, 3, 11426–11438 CrossRef CAS.
- M. Choi, F. Oba and I. Tanaka, Appl. Phys. Lett., 2011, 98, 172901 CrossRef.
- C. Linderälv, A. Lindman and P. Erhart, J. Phys. Chem. Lett., 2018, 9, 222–228 CrossRef PubMed.
- S. F. Parker and D. Lennon, J. Phys.: Conf. Ser., 2016, 746, 012066 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |