Mechanism for spontaneous oxygen and hydrogen evolution reactions on CoO nanoparticles

Abstract

Overall photocatalytic water splitting with a high efficiency of ∼5% has recently been observed for CoO nanoparticle suspensions in the absence of an applied bias or co-catalyst. Although experimental measurements indicate that the overall photocatalytic water splitting is caused by optimal band edge alignments with respect to the redox potentials of water, the mechanism by which H₂ and O₂ simultaneously evolve on these nanoparticles is unknown. In this study, we used first-principles density functional theory (DFT) calculations to elucidate the mechanisms for the charge separation and H₂ and O₂ evolution on CoO nanoparticles under illumination in aqueous solution. We demonstrated that electrons are driven to the CoO(100) facet and holes are driven to the hydroxylated CoO(111) facet (OH*–CoO(111)) as a result of the built-in potential arising from the difference in the band edge positions on the two facets. Furthermore, based on a set of criteria, depending on if the photoexcited electrons and holes have sufficient energy to overcome the kinetic barrier along the H₂ and O₂ evolution reaction pathways, respectively, on the relevant surface facet, we show that H₂ evolution preferentially occurs on the CoO(100) facet, while O₂ evolution occurs on the OH*–CoO(111) surface. Our understanding of the overall water splitting mechanism on CoO nanoparticles provides a general explanation for the experimentally observed overall water splitting phenomena on a variety of self-standing photocatalysts, including γ-Ga₂O₃, Cu₂O, and KTaO₃, without an external driving potential or co-catalyst. In addition, we provide a new strategy for designing novel photocatalysts with high efficiency by controlling their surface configurations and morphologies.

---

Introduction

For decades, photocatalysts have been actively studied both experimentally and computationally because solar light harvesting is very attractive for the development of renewable and clean energy. However, for photocatalytic water splitting to become economically feasible, it is crucial to decrease both the cost and energetic cost (i.e., overpotential) of materials for the two half-reactions, the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER). Therefore, photocatalysts composed of non-noble materials and splitting water without an external bias or a co-catalyst are promising.

Nano-sized photocatalysts are known to present a high electron–hole recombination rate due to their confined space, which significantly reduces the photocatalytic efficiency, despite the many advantages of nano-sized photocatalysts (such as inexpensive fabrication cost, high specific surface area, and short carrier diffusion lengths to reach the surface reaction area). Thus, it is difficult to imagine economical nanoparticle photocatalysts where overall water splitting occurs without the application of external energy and/or a co-catalyst. Interestingly, self-standing nanoparticles of various single materials, including γ-Ga₂O₃,¹ Cu₂O,² ZrO₂,³ KTaO₃,⁴ Zn₂GeO₄,^5,6 p-GO : N/n-GO : N,⁷ BiVO₄,^8,9 and CoO,¹⁰ have been reported to create stoichiometric H₂ and O₂ in aqueous solution under light illumination even without an externally applied bias or co-catalyst. Among them, spherical CoO nanoparticles have been observed to create stoichiometric H₂ and O₂ with the highest solar-to-hydrogen photocatalytic efficiency (∼5%), in contrast to bulk CoO, which is photocatalytically inactive for water splitting. A previous experimental work reported that CoO nanoparticles with sizes less than 10 nm have optimal band edge positions for overall water splitting;¹⁰ whereas bulk CoO or CoO micropowder does not.¹⁰ Therefore, it is believed that the different photocatalytic behaviors are related to particle size. However, very recently, it was reported that sub-micrometer CoO octahedra also conducted overall water splitting without an external bias or co-catalyst (but with much lower efficiency compared to spherical CoO nanoparticles),¹¹ suggesting that a critical factor controlling the photocatalytic water splitting behavior is not particle size.

Our previous density functional theory (DFT) study of the CoO/water interface demonstrated that the optimal band alignments of spherical CoO nanoparticles originate from the presence of fully hydroxylated CoO(111) facets (OH*–CoO(111)).¹² The OH*–CoO(111) facet is also predicted to be present on the CoO octahedra, which indicates that overall water splitting on CoO spherical nanoparticles¹¹ and octahedra¹² is due the presence of the OH*–CoO(111) facet. However, despite these experimental¹⁰ and computational¹² works, a clear picture of how the HER and OER occur on CoO nanoparticles with high efficiency is still missing.

In this work, to elucidate the origin of the overall water splitting on CoO nanoparticle photocatalysts without an external bias or co-catalyst, we investigated the mechanisms for charge separation and spontaneous HER and OER under light illumination using first-principles density functional theory (DFT) calculations. By determining the built-in potential between the two facets based on their relative band edges and computing the relative charge accumulation on each, we show that electrons are driven to the CoO(100) facet and holes to the hydroxylated CoO(111) facet (OH*–CoO(111)). We also determine the feasibility of the HER and OER on the two facets based on whether the photogenerated electrons and holes have sufficient energy to overcome the kinetic barrier along the H₂ and O₂ evolution reaction pathways, respectively. Using this feasibility, we demonstrated that H₂ evolution preferentially occurs on the CoO(100) facet, while O₂ evolution occurs on the OH*–CoO(111) surface in the absence of an overpotential or co-catalyst, even though only the band edges of the OH*–CoO(111) facet satisfy the conventional condition for overall water splitting, while that of the CoO(100) facet do not. We believe that this suggested mechanism provides a general framework for understanding the experimental observations of photocatalytic overall water splitting on other self-standing photocatalysts.

Methods

CoO(100) slabs with the rock salt (RS) structure were modeled with a symmetric 2 × 2 in-plane supercell containing 7 atomic layers. The outer 2 layers on both sides were fully structurally relaxed, while the central 3 layers were fixed in the RS-structure of bulk CoO (lattice constant = 4.26 Å).¹² The Co-terminated CoO(111) surface was modeled with a 2 × 2 supercell containing 13 atomic layers, with the central 5 layers fixed in the bulk positions and the outer 4 layers on both surfaces fully relaxed.¹² O-terminated CoO(111) slabs were not considered based on experimental observations and their higher surface free energy.^12,13 All slab structures included a vacuum of ∼15 Å separating periodic copies perpendicular to the surface. The type-II antiferromagnetic (AFM) configuration was applied to all slab structures.^12,14,15 DFT + U calculations were performed using VASP^16,17 with PAW pseudopotentials provided in the VASP database and the PBE-generalized gradient approximation (GGA)¹⁸ exchange-correlation functional. A U value of 4.1 eV was applied to the Co d-states, as described in ref. 12. An energy cutoff of 800 eV was used in the plane-wave expansion. Self-consistent total-energy iterations were accelerated using Gaussian smearing with a width of 0.05 eV, with Pulay mixing to ensure fast convergence of the self-consistent electron density. Atom positions were relaxed until the forces on all atoms were less than 0.005 eV Å⁻¹. All slab structures were modeled with a converged 6 × 6 × 1 Monkhorst–Pack k-point mesh unless otherwise noted.

Possible adsorbates (intermediates created during the water dissociation process), including H, O, and OH, were placed on both sides of the optimized CoO(100) and Co-terminated CoO(111) slabs with various surface coverages, and then relaxed. The adsorbates were initially positioned at a distance of ∼2 Å from both surfaces then relaxed to find the thermodynamically favored adsorption site and configuration.¹² The Hubbard U correction to DFT was also included during the relaxation because it is reported that it is essential for the description of experimentally observed trends in the activity of the strongly correlated cobalt oxides.¹⁹ All computation parameters employed for the relaxation were identical to that used for the bare surfaces.¹²

The free energy changes for the intermediates at P_H2 = 1 bar were calculated using the approach reported in ref. 20 as follows:

ΔG(U,pH,T) = ΔE + ΔZPE − TΔS + ΔG_U + ΔG_pH, (1)

where, ΔE is the reaction energy determined from DFT and ΔZPE is the difference in zero-point energies due to the reaction between the adsorbed and gas phase species by setting H₂O and H₂ in the gas phase as reference states.²⁰ The ΔZPE of various surfaces was calculated using DFT calculations. ΔS is the change in entropy, which was computed using DFT calculations of the vibrational frequencies and standard tables for gas phase molecules, ΔG_U = −eU is the free energy change due to electrode potential U, and ΔG_pH = kT ln[H⁺] = −kT ln 10pHis the free energy change due to the change in pH. All values of ΔG were computed at T = 298 K and pH = 0. Additional details and the computed values of ΔZPE and TΔS are reported in Tables S1 and S2 in the ESI.†

The charge states of the CoO(100) and OH*–CoO(111) surfaces were evaluated by examining how the atomic charge density deviates from the reference value in each layer, i.e., the charge density difference, which is defined as:¹²

Δρ = ρ(z) − [small rho, Greek, macron](CoO(111)), (2)

For the reference of the surface charge density, the average charge density of the bare Co-terminated CoO(111) surface was chosen because the charge density did not vary significantly with respect to the position along the film thickness (z-axis) even at the outmost surface layer, as shown in Fig. 6 in ref. 12.

To investigate whether charge separation occurs in actual CoO nanoparticles, we also constructed a supercell describing a nanorod composed of CoO(100) and OH*–CoO(111) facets, as shown in Fig. 2. The initial atomic configuration was built so that only the OH*–CoO(111) and bare CoO(100) surfaces existed and were in contact with each other. The initial supercell was relaxed with the same parameters as the CoO slabs, but with a 6 × 1 × 1 Monkhorst–Pack k-point mesh. All atoms in the nanorod were relaxed. An initial type-II AFM configuration was constructed with up and down spin polarization on the Co atoms in alternate (111) planes.

Results and discussion

Catalysis on semiconducting photocatalysts generally involves three steps: (i) solar light absorption, which generates electron–hole (e–h) pairs if the energy of the incident light is larger than the band gap of the photocatalyst; (ii) separation of the photogenerated charge carriers (e–h) and their transportation to the surface of the photocatalyst; and (iii) reaction of adsorbed reactants at the surface via use of the transferred electrons/holes. Photogenerated holes are used to generate oxygen at the photoanode (4h⁺ + H₂O(l) → O₂(g) + 4H⁺), while photogenerated electrons generate hydrogen at the photocathode (4H⁺ + 4e⁻ → 2H₂(g)). Consequently, the two half-reactions lead to the stoichiometric generation of hydrogen and oxygen from water (2H₂O(l) → O₂(g) + 2H₂(g)).

In a previous study,¹² we demonstrated the thermodynamic feasibility of photocatalytic overall water splitting on CoO nanoparticles with diameters of ∼10 nm (ref. 10) by elucidating their surface-dependent band edge positions relative to the water redox potentials (step (i)). We showed that the thermodynamically preferred morphology of CoO nanoparticles is a truncated octahedron consisting of two facets: OH*–CoO(111) and bare CoO(100) facets. These two facets have very different band edge positions relative to the redox potentials of water.¹² In particular, the band edge positions of the OH*–CoO(111) facet are shifted significantly upwards compared to that of the CoO(100) facet. As a result, the conduction band edge is located at a more negative potential than the water reduction potential level (H⁺/H₂), and the valence band edge is more positive than the water oxidation potential level (H₂O/O₂); thereby, allowing the possibility of overall water splitting. Once CoO nanoparticles in water are exposed to light, the OH*–CoO(111) surface absorbs light of energy greater than 2.6 eV and generates e–h pairs that have sufficiently high energy for both the HER and OER to occur. However, how both reactions take place on the facets of CoO nanoparticles is not yet understood. Therefore, in this study we investigated the separation process of the photogenerated charge carriers (step (ii)) and the HER and OER feasibilities of the two facets (step (iii)).

Charge separation

Charge separation can occur when there is a driving force for photogenerated electrons and holes to move in different directions or spaces. This implies that charge separation can occur if facets with different electron affinities exist in a nanoparticle. As determined in our previous study,¹² the two types of facets predicted to be present in CoO nanoparticles in water have very different surface properties. Specifically, the CoO(100) surface is likely to be positively charged, while the OH*–CoO(111) surface is negatively charged. Thus, photogenerated electrons are expected to move to the CoO(100) surface; whereas, holes migrate to the OH*–CoO(111) surface. In addition to the charge density difference, the conduction and valence band edge diagram of a CoO nanoparticle in an aqueous environment (Fig. 1) suggests that charges will be rapidly separated between the two facets due to the large potential difference (∼2.19 V) between them. This creates a large electric field throughout the entire nanoparticle due to its small dimensions relative to the typical length scale of band bending in CoO.²¹ This electric field drives photogenerated electrons towards the CoO(100) facet and holes towards the OH*–CoO(111) facet.

Fig. 1 Conduction and valence band edge diagram with respect to an arbitrary position from the CoO(100) surface to the OH*–CoO(111) surface of a nanoparticle in contact with water. The bands are plotted with respect to NHE. The conduction and valence bands (blue lines) linking two facets are considered to be linear because they are unlikely to have a bulk-like structure in the central region considering that the CoO nanoparticles used for the overall water splitting is ∼10 nm in diameter, which is smaller than the general width of the space charge layer (∼10 nm to several μm (ref. 21)).

However, it is unclear whether charge separation still occurs when the two facets exist in conjunction with each other since the charge density distributions studied in the previous work were obtained for isolated supercells.¹² Thus, to confirm whether the charge separation indeed occurs in realistic CoO nanoparticles, we considered a nanorod composed of CoO(100) and OH*–CoO(111) facets, as illustrated in Fig. 2. In the supercell, we investigated how much the charge density of the surface in the nanorod deviates from the average value of the CoO(111) surface, as described in the Methods section and ref. 12. The results are summarized in Table 1. We found that excess electrons are collected on the OH*–CoO(111) surface of the nanorod, as observed for the isolated slab with OH*–CoO(111) surfaces.¹² We also observed a decrease in the electron charge density on the Co atoms in the outermost surface layer of the CoO(100) surface of the nanorod, similar to that observed for the isolated CoO(100) slab. This confirmed our expectation that the charges will be separated between the two facets in actual CoO nanoparticles.

Fig. 2 (a) Atomic configuration of a CoO supercell constructed with OH*–CoO(111) (yellow shade) and CoO(100) (green shade) facets. (b) Side-view of the prepared supercell. (c) Atomic configuration of a CoO nanorod constructed when the periodicity is applied to the prepared supercell along the x-axis.

Table 1 Deviation of charge density relative to the average charge density of the CoO(111) surface, Δρ (refer to Methods), in the OH*–CoO(111) and CoO(100) facets in the supercell shown in Fig. 2. The charge density difference was investigated for each atom and their average values are summarized. The charge density differences calculated in the isolated OH*–CoO(111) and CoO(100) slabs (Δρ in isolated slab) are shown together for reference

Facet	Element in the outermost layer	Δρ	Δρ in isolated slab
In the OH*–CoO(111) facet, the higher value for hydrogen than for oxygen in the hydroxyl group means that the charge in the hydrogen atom largely deviated from neutral hydrogen than the charge in oxygen. This indicates that the charge in the hydroxyl group is highly polarized at the outermost position going from the surface to the end of the hydroxyl group.
OH*–CoO(111)	O	0.124	0.114
	H	0.210	0.207
CoO(100)	Co	−0.023	−0.043
	O	−0.019	−0.017

---

However, we do not think that CoO nanoparticles can sustain the huge electric field for a long time. The previous experimental study¹⁰ demonstrated that the photocatalysis on the CoO nanoparticles became deactivated soon after the photocatalytic water splitting test started (within ∼1 hour of the reaction). The deactivated nanoparticles remained as CoO single crystals, but became aggregated and did not exhibit the initial sharp facets, showing a deviated XPS spectrum from that of the fresh CoO nanoparticles.¹⁰ Considering that a huge built-in potential is generated in the CoO nanoparticles, as shown in Fig. 1, the structural change at the surface is considered to be caused by the high electric field inside the nanoparticle, which explains the poor sustainability of the CoO nanoparticles. Nevertheless, this needs to be confirmed by a further experimental study to determine the origin of the short lifetime of the CoO nanoparticle photocatalyst.

Theoretical HER/OER overpotentials

For the separated charge carriers to overcome the kinetic barriers for the formation of reaction intermediates on the surface of the electrode and to induce the HER and OER, a certain amount of excess energy, i.e., overpotential (η), is required. The magnitude of η determines how easily the reaction can occur, i.e., resulting in HER or OER activity. The theoretical electrochemical overpotential for the HER (OER) is defined as the difference between the energy level of the transition state of the limiting step in the reaction relative to H⁺/H₂ (H₂O/O₂).²² Therefore, the relative HER (OER) activity of the CoO(100) and OH*–CoO(111) surfaces can be roughly estimated by the conduction (valence) band edge position relative to H⁺/H₂ (H₂O/O₂), as marked in Fig. 3.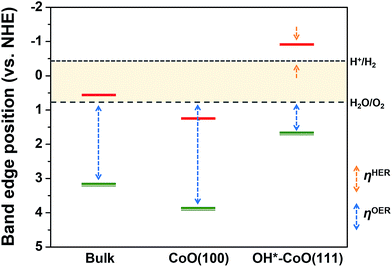

Fig. 3 Band edge positions of bulk CoO and the CoO(100) and OH*–CoO(111) facets relative to the water reduction/oxidation potential levels, which were calculated with an explicit solvation approach.¹² The red horizontal single line denotes the conduction band edge, while the green double line indicates the valence band edge. The relative HER overpotential is shown with an orange dashed line (η^HER) and the relative OER overpotential with a blue dashed line (η^OER).

From the band edge position point of view, both the HER and OER overpotentials are lower on the OH*–CoO(111) surface compared to on the CoO(100) surface, and neither reaction should occur on the CoO(100) surface. However, it is difficult to conceive a mechanism in which both O₂ and H₂ are simultaneously generated on the same facet (without immediately undergoing the back reaction to water). Furthermore, the photoexcited electrons are expected to move to the CoO(100) facet due to the potential difference between the facets, and therefore would not be available for the HER on the OH*–CoO(111) facet of the CoO nanoparticles. On the other hand, if the photoexcited carriers are not separated to different facets as predicted, then we expect high recombination rates and little to no O₂ or H₂ evolution. This suggests that the band edge positions with respect to the water redox levels may not be the most important metric for predicting photocatalytic activity. Instead, we hypothesize that the key property that determines whether photocatalytic HER or OER can occur on a given surface is the difference between the potential of the photoexcited electron or hole and the energy level of the transition state of the relevant rate limiting HER or OER step. Below, we investigated this hypothesis using DFT to compute the free energies of the reaction steps for the HER and OER on both the CoO(100) and OH*–CoO(111) surfaces.

HER/OER activities under equilibrium potential

Initially, we determined the relative HER activities of the CoO(100) and OH*–CoO(111) surfaces by determining the free energy change for H adsorption (ΔG_H*), which has been shown to be a good descriptor for the HER exchange current density (j₀) for a wide variety of surfaces.^23,24 The value of ΔG_H* can be computed by modeling the possible intermediates formed during the hydrogen adsorption-reduction-desorption processes at the cathode, given by 2H⁺ + 2e⁻ → H* + H⁺ + e⁻ → H₂. Using this approach,^23–26 both ΔG_H* values and calculated HER activity trends have been shown to agree well with experimental results.²⁷

According to the Sabatier principle,^28,29 a good HER catalyst should form a sufficiently strong bond with adsorbed H* to facilitate the proton–electron-transfer process, yet be weak enough for facile bond breaking and release of H₂ gas. We used the convention that a negative ΔG_H* indicates strong binding of hydrogen atoms to the surface, which blocks potential active sites and retards hydrogen generation, while a positive ΔG_H* indicates weak bonding of hydrogen atoms to the surface, which fails to stabilize intermediates and prevents any reaction from taking place. Thus, the highest HER activity is given by ΔG_H* close to 0, i.e., at the summit of the volcano plot of j₀versus ΔG_H*.²⁵

Fig. 4(a) shows the calculated free energy change along the HER coordinate on the bare CoO(100) and CoO(111) surfaces with a range of OH coverage at the equilibrium potential (U = 0 V). Since the CoO(100) facet energetically prefers to maintain a clean surface and the CoO(111) facet to be hydroxylated,¹² we assumed that the CoO(100) facet has clean surface sites, while the CoO(111) facet is hydroxylated during the HER and OER except for the adsorption of the intermediates. Indeed, the ab initio MD calculation of the supercell shown in Fig. 2 in contact with the explicit water at 298 K shows that one H dissociated from an H₂O molecule is adsorbed on the CoO(100) surface, suggesting that the CoO(100) surface keeps the clean state with 1/8 coverage of intermediates. As shown in Fig. 4(a), ΔG_H* is positive for the bare CoO(100) surface, but negative for all the CoO(111) surfaces independent of OH coverage, showing that the CoO(100) or OH*–CoO(111) facet binds weakly or strongly with hydrogen, respectively. The figure also shows that the absolute value of ΔG_H*, i.e., η^HER, increases with an increase in OH coverage, indicating that the desorption of hydrogen from the surface becomes increasingly difficult with an increase in OH coverage, thus inhibiting the HER under standard conditions. Interestingly, our results also show that the sign of ΔG_H* is determined by whether the conduction band edge of the surface is at a positive or negative potential relative to the standard water reduction potential, the H⁺/H₂ level. For example, we found that ΔG_H* > 0 on the CoO(100) surfaces, which have a conduction band edge below the H⁺/H₂ level (i.e., at a positive potential relative to the H⁺/H₂ level), while ΔG_H* < 0 for the OH*–CoO(111) surfaces, which have a conduction band edge above the H⁺/H₂ level (i.e., at a negative potential relative to the H⁺/H₂ level). This indicates that a surface with a conduction band edge at a more negative (positive) potential relative to the H⁺/H₂ level will attract hydrogen to its surface more strongly (weakly) due to its negatively (positive) charged surface state.¹² We also found that the HER overpotential is smaller on the CoO(100) surface than on the OH*–CoO(111) surface, in contrast to the theoretical HER overpotentials estimated from the band edge positions (Fig. 3). We will discuss the meaning of the difference between the theoretical overpotential and the overpotential calculated from the intermediate state in the following section.

Fig. 4 (a) Free energy change for hydrogen adsorption on bare CoO(100) and CoO(111) surfaces with various OH coverage along the HER coordinate at the standard potential (U = 0 V). (b) Free energy change along the OER coordinate for the CoO(100), CoO(111) and OH*(3/4)–CoO(111) surfaces at the equilibrium potential (U = 1.23 V). All calculations were conducted with 1/4 coverage of the relevant adsorbates unless otherwise noted. In the legend, the number in parenthesis is the OH coverage on the surface and 1/8 (or 1/2) at the right side of ‘CoO(100)’ (or ‘CoO(111)’) denotes that the energy change was calculated with the 1/8 (or 1/2) H coverage.

Similarly to HER, the OER overpotential of a material can be estimated based on the binding energies of the intermediates on its surface relative to H₂O and H₂ in the gas phase. The proposed OER mechanism consists of four consecutive proton and electron transfer steps with the intermediates OH*, O*, OOH* and OO*(O₂).^27,30 The largest difference in the free energy change of the intermediates along the reaction path, i.e., max[ΔG_OH*, ΔG_O*, ΔG_OOH*],^31,32 is taken to be the theoretical OER overpotential. Previous work has shown that a volcano relationship exists between the OER overpotential (−η^OER) and the descriptor on oxide surfaces.^20,31,32

Fig. 4(b) shows the free energy diagram of the calculated free energies of the intermediates along the overall OER pathway, ΔG_OH*, ΔG_O*, and ΔG_OOH*, of the bare CoO(100), bare CoO(111) and OH*(3/4)–CoO(111) surfaces at the equilibrium potential (U = 1.23 V). The CoO(100) surface has positive values for ΔG_OH*, ΔG_O*, and ΔG_OOH*, implying that none of these adsorbates bind easily to the CoO(100) surface. However, the bare CoO(111) and OH*(3/4)–CoO(111) surfaces stabilize both the O* and OH* adsorbates. Furthermore, they have OER overpotentials (2.17 V for bare CoO(111) and 1.18 V for OH*(3/4)–CoO(111)) much lower than that of the CoO(100) facet (3.67 V). As a result, we expect that the OER preferentially occurs on the OH*–CoO(111) facet.

HER and OER at the photo-induced potential

The HER and OER overpotentials estimated from the binding energies of the reaction intermediates were shown to agree with experimental electrochemical measurements. This is obvious in the case of an electrochemical cell because a certain amount of energy should be supplied to an electrochemical catalyst to induce the reaction. The energy greatly depends on the intermediate state, which is given by the electrode potential required for the initiation of the reaction.

In the same way, previous studies have employed the calculated overpotentials to interpret photocatalytic behavior since the reactions are expected to occur via the same mechanism. However, unlike the electrochemical cell, since the energy source for the HER and OER reactions on photocatalysts is light (photon energy), the feasibility of the photocatalytic HER or OER cannot be determined only by the kinetic barriers for the half reactions without determining the energy state of the photogenerated charge carriers. In addition, the optimal band edge positions for photocatalytic overall water splitting do not always determine H₂ and O₂ creation from water splitting considering that several systems including CdS,^33–37 MoS₂,^38–40 TiO₂,^41,42 SrTiO₃,^43,44 CdSe,^45,46 ZnO,^47,48 Nb₂O₅,⁴ SiC,⁴⁹ and Sn₂TiO₄,⁵⁰ have the required band alignment yet only evolve H₂ or O₂.

To resolve this conundrum, we employed criteria for screening the feasibility of the HER/OER on a specific surface, as Valdés et al.⁵¹ and Montoya et al.⁵² introduced. Specifically, the energy state of the charge carriers provided by light absorption should be sufficient to overcome the kinetic barrier of the reaction of the HER or OER, i.e., the free energy of the transition state of the rate-limiting step relative to that of the initial state. In a semiconducting photocatalyst, the energy state of the photogenerated charge carriers is determined by its band edge positions, which is critical for light absorption. Therefore, the feasibility of the reaction is determined such that HER occurs when the conduction band edge (U(CB)) is more negative than η^HER (=|ΔG_H*|) and the OER proceeds when the valence band edge (U(VB)) is more positive than η^OER.

Fig. 5(a) shows the conduction and valence band edges that determine the potential levels of electrons and holes generated by photon absorption at the interface of the OH*–CoO(111) surface and water. On the OH*–CoO(111) surface, the photogenerated electrons are at a potential 0.55 V more negative than the water reduction potential (H⁺/H₂), while the photogenerated holes are at a potential 2.05 V more positive than the H⁺/H₂. Specifically, the electrons have 0.55 eV extra energy for the HER, while the holes have 0.82 extra energy for the OER relative to an ideal photocatalyst. To determine the feasibility of the HER/OER under the potential given by the photon absorption, we evaluated the HER and OER overpotentials, as shown in Fig. 5(b) and (c), respectively.

Fig. 5 (a) Band edge positions at the OH*–CoO(111) surface and potential levels of photogenerated electrons and holes with respect to the water reduction potential level. (b) Free energy change of OH, O, and H adsorbed CoO(111) surfaces along the OER coordinate under 2.05 V. (c) HER overpotential (η^HER) on CoO(111) surfaces with a range of OH, O, and H coverage under 0 V and −0.55 V. The legend in (b) and vertical axis in (c) denote the initial surface configuration prior to the adsorption of the intermediate species. The number in parenthesis next to ‘*’ indicates the coverage of the species. The (O) in the vertical axis of (c) indicates that H adsorption (or desorption) was conducted by binding on the O site, as illustrated in the inset, rather than adsorbing at the clean surface site. The band edge positions (vs. NHE) and the HER and OER overpotentials are shown at pH = 0. Since the band edge positions (vs. NHE) change as a function of pH, same as the changes in the HER and OER overpotentials with respect to pH, −kT ln 10pH, the photocatalytic reaction activity estimated at pH = 0 by comparing the relative positions of the band edge and the half reaction overpotential is consistent with that at pH = 7.

From the calculated thermodynamic stability¹² and experimental observations with XPS,^11,53,54 the CoO(111) surface is expected to be hydroxylated after equilibration in water, although the exact OH coverage is not known experimentally. However, performing ab initio molecular dynamics (MD) calculations of CoO(111) and OH*–CoO(111) facets in water (Fig. S1†), we found that complex surface configurations can be formed during the actual water splitting reactions, which in turn can significantly alter the HER and OER overpotentials, as shown in Fig. 5(c), S2 and S3.†

Fig. 5(b) shows the free energy changes of the OER intermediates along the reaction pathway under U = 2.05 V, the potential of the photogenerated holes. Our results predict that the photogenerated holes are able to trigger the OER on the CoO(111) surface with half a monolayer of OH (OH*(1/2)–CoO(111)) without a reaction barrier, as indicated by the downhill free energy change for each step along the reaction pathway (dark green line). The OH*(1/2)–CoO(111) surface is the only configuration considered here that is able to induce the OER without an additional applied potential. This means that the transition state of the OH*(1/2)–CoO(111) surface exists at a slightly negative potential relative to the valence band edge at the surface (2.05 V), and therefore the potential for holes obtained from light absorption is sufficient to drive the spontaneous OER. On the other hand, the transition states on the other surface configurations with various OH, O, and H coverage are at positive potentials relative to the valence band edge at the surfaces. On these surfaces, an additional potential (overpotential) corresponding to the energy difference between the transition state and the valence band edge, U(TS) − U(VB), is required to overcome the kinetic barrier for the OER under the light-induced potential.

We also investigated the feasibility of the HER on the OH*–CoO(111) surface via photogenerated electrons by considering the η^HER change under U = −0.55 V (Fig. 5(c)). Since the overpotential depends strongly on the coverage of different species at the surface,⁵⁵ we considered a range of possible surface configurations (Fig. S3†). Under U = −0.55 V, the η^HER values for all the surface configurations are shifted by −0.55 V from that obtained under the standard potential due to η^HER(U) = η^HER(U = 0 V) + U. Among the considered surface configurations, we found that η^HER goes from positive to negative when going from the standard potential to the potential of the photogenerated electrons (−0.55 V) for the OH*(1/4)–O(1/4)–CoO(111)(O) and O*(1/2)–CoO(111) surfaces. This means that the kinetic barriers for the HER do not exist on the surfaces under the electron energy of −0.55 eV vs. H⁺/H₂ level. However, since the main adsorbate is a hydroxyl group on the CoO(111) surface in aqueous solution, the O*–CoO(111) surface is neither stable nor representative in water. Also, the HER feasibility determined in Table 2 indicates that the O*–CoO(111) surface cannot induce the HER because of its higher η^HER than the electron energy obtained by light absorption. Hence, we consider that the OH*(1/4)–O(1/4)–CoO(111)(O) surface is the most probable surface configuration for hydrogen evolution on the CoO(111) facet.

Table 2 Calculated conduction and valence band edge positions (U(CB) and U(VB)) of the CoO(111) surfaces with various initial surface configurations, HER and OER overpotentials (η^HER and η^OER) under U = 0 V, feasibility of the HER and OER (f(HER) and f(OER)) determined based on the comparison of the band edge and the overpotential. Feasible reactions are marked with ‘O’ and unfeasible reactions with ‘X’

Initial surface configurations	U(CB)	U(VB)	η ^HER	η ^OER	f(HER)	f(OER)
The band edge position during the reaction (along the HER and OER pathways) changes slightly (Fig. S4); therefore, the feasibility of the reaction is expected to be essentially constant during the reaction.a Since U(CB) is similar to the HER overpotential of the surface, the HER may be possible given the errors inherent to DFT. However, we expect the actual reaction rate will be negligible due to the high back reaction probability in the confined space of the nanoparticle as well as the low electron concentration at the surface.
CoO(111)	0.048	2.648	−1.406	3.400	X	X
CoO(111)-1/2	0.048	2.648	−1.081	3.310	X	X
CoO(111)-1	0.048	2.648	−0.939	—	X	—
OH*(1/4)–CoO(111)	−0.685	1.915	1.791	4.640	X	X
OH*(1/2)–CoO(111)	−0.608	1.992	1.586	2.000	X	O
OH*(1/2)–CoO(111)-1/2	−0.608	1.992	1.353	—	X	—
OH*(3/4)–CoO(111)	−0.706	1.894	2.252	2.410	X	X
O*(1/2)–CoO(111)	0.680	3.280	0.378	—	X	—
O*(1/2)–CoO(111)-1/2	0.680	3.280	0.150	3.654	X	X
OH*(1/4)–O*(1/4)–CoO(111)	−0.303	2.297	0.716	4.564	X	X
OH*(1/4)–O*(1/4)–CoO(111)(O)	−0.303	2.297	0.381	—	O^a	—
OH*(1/2)–O*(1/4)–CoO(111)	−0.646	1.954	1.954	3.088	X	X
OH*(1/2)–O*(1/4)–CoO(111)(O)	−0.646	1.954	1.214	—	X	—
OH*(3/4)–O*(1/4)–CoO(111)(O)	−0.600	2.000	1.940	—	X	—
OH*(1/2)–H*(1/4)–CoO(111)	−0.267	2.333	1.121	3.688	X	X
H*(1/4)–CoO(111)	1.560	4.160	0.756	—	X	—
H*(1/2)–CoO(111)-1/2	0.656	3.256	0.797	—	X	—

---

The disappearance of the kinetic barrier for the HER on the OH*(1/4)–O(1/4)–CoO(111)(O) surface under U = −0.55 V, indicates that one hydrogen of the hydroxyl group on the OH*(1/2)–CoO(111) surface is readily desorbed from the surface under the potential of the photogenerated electrons (inset of Fig. 5(c)), spontaneously creating H₂. The other surface configurations with η^HER > 0.55 V slightly relieve the strong binding (for an initially negative ΔG_H*) or stabilize the surface with hydrogen (for an initially positive ΔG_H*). However, they still need an additional potential to reach η^HER = ∼0 to trigger spontaneous HER.

From Fig. 5, we find that the CoO(111) surface with 1/2 OH coverage energetically favors both the HER and OER. It is interesting to note that, in principle, this surface can therefore simultaneously oxidize and reduce water with photogenerated carriers without an external bias, as predicted from the band edge positions (Fig. 3).^10,12 This result supports our point insisted in ref. 12 that the origin of the photocatalytic overall water splitting on both the CoO nanoparticle¹⁰ and sub-micrometer CoO octahedra¹¹ is the presence of the OH*–CoO(111) facet (the reason for the lower efficiency of the CoO octahedra compared to the spherical CoO nanoparticles is explained in section ‘Electron transport and HER on CoO(100)’). However, as noted in the ‘Charge separation’ section and Fig. 1, we expect that the relative populations of photoexcited electrons and holes at the surfaces of CoO nanoparticles will favor the OER at the OH*–CoO(111) surface.

It is possible that the potential level of charge carriers given by light absorption deviates from that of the OH*–CoO(111) facet due to the different surface coverage, although the dominant surface configuration of the CoO(111) facet in a water environment is considered to be hydroxylated. Thus, to more accurately assess the feasibility of the HER and OER on various surface configurations, we computed the conduction and valence band edges of all the surfaces and the results are summarized in Table 2. Based on the calculated band edge energies and the HER/OER overpotentials, the feasibility of the reaction is determined such that the HER occurs when η^HER + eU(CB) ≤ 0 and the OER proceeds when η^OER − eU(VB) ≤ 0, screening the photocatalytically active surface. In accordance with the evaluation in Fig. 5, both the HER and OER are energetically feasible on the CoO(111) surface with a hydroxyl coverage of one half.

Unlike the CoO(111) surface, the bare CoO(100) surface is predicted to maintain an ideal surface (no adsorbates) in an aqueous environment. Therefore, we assumed that CoO(100) has clean surface sites during the HER and OER except for the adsorption of intermediates (1/8 coverage). Fig. 6(a) shows the conduction and valence band edges of the bare CoO(100) surface. From the band edge positions, it can be seen that the potential level of electron–hole pairs given by photon absorption at the CoO(100)/water interface is +1.64 V for electrons and +4.25 V for holes with respect to the H⁺/H₂ level.

Fig. 6 (a) Band edge position of the bare CoO(100) surface and potential levels of photogenerated electrons and holes with respect to the water reduction potential level. Free energy change of the bare CoO(100) surface along (b) OER coordinate under U = 4.25 V and (c) HER coordinate under U = 0 V and −0.55 V. All energy calculations were performed with the adsorption of the reaction intermediate of 1/8 surface sites concentration.

Fig. 6(b) shows the free energy change along the OER coordinate under U = 4.25 V. Even though the CoO(100) surface is under a very large positive potential, an additional energy of ∼0.65 eV is required to overcome the reaction barrier for the reaction step going from OH* to O*; therefore, the photogenerated potential is not sufficient to induce the OER on this surface. For hydrogen evolution, the positive E_C relative to the H⁺/H₂ level of the CoO(100) facet (+1.64 V) indicates that the electrons photogenerated on the surface are unable to induce the HER according to the thermodynamic relation ΔG_U = eU for the HER. Consequently, both the HER and OER seem to be infeasible on the CoO(100) surface, as expected from the band edge positions relative to the water redox potentials in Fig. 3.

Electron transport and HER on CoO(100)

As discussed in the ‘Charge separation’ section, the photogenerated electrons and holes are expected to be efficiently separated between the CoO(100) and OH*–CoO(111) facets due to the small dimension of the CoO nanoparticles (∼10 nm) and huge built-in potential in the nanoparticles. The efficient charge separation is regarded as the origin of the prominent conversion efficiency observed in a CoO nanoparticle suspension.¹⁰ In contrast, CoO octahedra composed of only the OH*–CoO(111) facet¹² are hardly able to separate the photogenerated charge carriers, resulting in much lower photocatalytic efficiency.^11,12 These two different results suggest that the high photocatalytic efficiency in the CoO nanoparticles originated from the HER and OER occurring on different facets, i.e., CoO(100) and OH*–CoO(111) surfaces without recombination of the separated charge carriers. Therefore, we reasonably speculate that the HER predominantly occurs on the CoO(100) facet, even though the CoO(100) facet has no photocatalytic capability to spontaneously trigger the HER under illumination, as interpreted in the ‘HER and OER at the photoinduced potential’ section.

Therefore, we investigated whether the electrons photogenerated on the OH*–CoO(111) facet can induce the HER on the CoO(100) facet. Since the U(CB) on the OH*–CoO(111) facet is located at −0.55 V vs. H⁺/H₂ level, the electrons photogenerated at the surface can be provoked to evolve hydrogen on the CoO(100) facet if the electrons can transport to the CoO(100) facet without energy loss (before electron–phonon coupling occurs), as shown in Fig. 6(c) (satisfies the condition for photocatalytic HER; η^HER_CoO(100) + eU(CB) (at OH*–CoO(111)) < 0).

From the numerical calculation of the time required for the electron transportation in the CoO nanoparticles (page 10 in ESI†), we find that the electrons in the CoO nanoparticles can spontaneously move within ∼1 fs from the OH*–CoO(111) to the CoO(100) facets in the absence of an external bias. Considering that relaxation time for electron–phonon coupling (generally greater than 10 fs (ref. 56–59)) is longer than the electron transportation time in the nanoparticles, the electrons generated on the OH*–CoO(111) facet can be carried without energy loss and successfully trigger the HER on the CoO(100) facet. This short transportation time in the CoO nanoparticles is possible due to the high built-in potential and the small size (page 10 in ESI†) of the nanoparticles. As a result, it is anticipated in real CoO nanoparticles that the HER (or OER) occurs on the CoO(100) (or OH*–CoO(111)) facet even without an external bias or a co-catalyst, resulting in high photocatalytic efficiency.¹⁰

Furthermore, at near neutral-pH conditions, the kinetic effect may also be another major reason for the spontaneous overall water splitting with high efficiency, rather than the thermodynamic effects. Therefore, even though CoO(100) facet cannot induce H₂ generation thermodynamically, the HER may be kinetically possible on the CoO(100) facet. However, the kinetic effect has not been proven experimentally and computationally in the field of photocatalysts because the band edge position is known to be the primary factor for determining whether photogenerated electrons can trigger the HER. Therefore, a further study on the kinetic effect is necessary by investigating the transition states on the CoO nanoparticles. We can also validate the kinetic effect on other semiconducting or insulating photocatalysts that conducted spontaneous overall water splitting in a neutral pH environment.

Overall water splitting on CoO nanoparticles

As mentioned in the ‘Charge separation’ section, we predict that in CoO nanoparticles in water, photogenerated charge carriers are separated by a built-in potential, with electrons driven to the CoO(100) surface facets and holes driven to the OH*–CoO(111) surface facets due to the difference in the band edge positions at these surfaces. On the OH*–CoO(111) surface (Fig. 5), our results suggest that the photogenerated holes will serve the OER on a half hydroxylated region, while photogenerated electrons can enable the HER by desorbing hydrogen from a half hydroxylated region. However, we expect the population of photogenerated electrons on the OH*–CoO(111) surface to be very low due to the built-in potential, which will quickly sweep electrons away from the OH*–CoO(111) facet to the CoO(100) facet. Even if the HER can be realized on the half hydroxylated CoO(111) surface before the photogenerated electrons are separated to the CoO(100) surface, the fraction of hydrogen formed on the former facet in the total HER will be very small considering the high probability of back reaction owing to the confined space of the CoO nanoparticles. On the CoO(100) surface, which strongly attracts photogenerated electrons, both the HER and OER are unlikely to occur due to the significant energy barriers, which cannot be overcome by the electrons and holes photogenerated on the CoO(100) facet. However, the HER is available on the CoO(100) facet by the electrons photogenerated on the OH*–CoO(111) facet, but transferred to the CoO(100) facet before electron–phonon coupling without loss of energy after the generation. Thus, we expect the OER to primarily occur on the OH*–CoO(111) facet and the HER to occur on the CoO(100) facet in CoO nanoparticles.

Photocatalytic overall water splitting on CoO nanoparticles is thought to take place without a co-catalyst or an external bias because the nanoparticle functions as either a co-catalyst-integrated nanoparticle or a p–n junction photocatalyst, in which the CoO(100) facet is a p-type semiconductor and the OH*–CoO(111) facet is an n-type semiconductor. In addition, the spontaneous charge separation taking place in the CoO nanoparticles can largely improve the photocatalytic efficiency, which supports the experimentally measured high photocatalytic efficiency (5%) of CoO nanoparticles.¹⁰ Even though the nanoparticle is made of a homogeneous material, the different surface configurations with different charge densities¹² and electron affinities on the nanoparticle enable advanced heterogeneous functions. Unlike spherical CoO nanoparticles of high efficiency,¹⁰ sub-micrometer CoO octahedra covered with OH*–CoO(111) facets cannot separate photogenerated e–h pairs because there is only one type of facet. Thus, even though the OH*–CoO(111) facet can conduct photocatalytic overall water splitting, the efficiency will be significantly reduced compared to that of spherical CoO nanoparticles, as observed experimentally.¹¹ This understanding of overall photocatalytic water splitting on CoO nanoparticles may also explain how other single-material nanoparticles can perform as photocatalysts for overall water splitting without a co-catalyst or an external potential. Furthermore, it emphasizes that understanding photocatalytic water splitting requires the knowledge of three key properties: (i) the morphology of the nanoparticle and its thermodynamically stable surface configurations in an aqueous environment, (ii) the energy state of the photogenerated charge carriers from the calculation of the band edge positions and (iii) the relative energy of the transition state of the reaction under the photoinduced potential.

Conclusions

This study represents the first study to elucidate the mechanism by which overall water splitting can occur on a self-standing CoO nanoparticle photocatalyst with high photocatalytic efficiency and without a co-catalyst or an external bias. We demonstrated that photogenerated charge carriers are separated onto different facets of the nanoparticle due to a strong electric field, which is formed between the two facets due to their very different surface properties: electrons are driven to the CoO(100) facet and holes to the OH*–CoO(111) facet. Furthermore, we showed that the electrons transferred to the CoO(100) facet from the OH*–CoO(111) facet without energy loss can be used for the HER on the CoO(100) surface, while the holes on the OH*–CoO(111) facet can induce the OER under the photogenerated potential on the facet without an external bias because the photogenerated charge carriers have energies sufficient to overcome the kinetic barriers of the relevant reactions. This thorough understanding of the overall photocatalytic water splitting mechanism for all three steps of photocatalysis, including the generation of charge carriers under illumination,¹² separation of photoexcited carriers, and surface H₂ and O₂ evolution reactions, provides insight into the photocatalytic mechanism on a variety of single material photocatalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the MRSEC Program of the National Science Foundation (award number DMR – 1419807), and the Skolkovo Institute of Science and Technology (Skoltech) through the “Center for Research, Education and Innovation for Electrochemical Energy Storage” (contract number 186-MRA). This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, resources of the Texas Advanced Computing Center (TACC) at The University of Texas at Austin that have contributed to the research results reported within this paper. URL: http://www.tacc.utexas.edu.

References

1. X. Zhang, Z. Zhang, J. Liang, Y. Zhou, Y. Tong, Y. Wang and X. Wang, J. Mater. Chem. A, 2017, 5, 9702–9708.
2. M. Hara, T. Kondo, M. Komoda, S. Ikeda, K. Shinohara, A. Tanaka, J. N. Kondo and K. Domen, Chem. Commun., 1998, 357–358.
3. K. Sayama and H. Arakawa, J. Phys. Chem., 1993, 97, 531–533.
4. H. Kato and A. Kudo, Chem. Phys. Lett., 1998, 295, 487–492.
5. S. Yan, L. Wan, Z. Li and Z. Zou, Chem. Commun., 2011, 47, 5632–5634.
6. B. J. Ma, F. Y. Wen, H. F. Jiang, J. H. Yang, P. L. Ying and C. Li, Catal. Lett., 2010, 134, 78–86.
7. T. F. Yeh, C. Y. Teng, S. J. Chen and H. Teng, Adv. Mater., 2014, 26, 3297–3303.
8. S. Sun, W. Wang, D. Li, L. Zhang and D. Jiang, ACS Catal., 2014, 4, 3498–3503.
9. W. Fang, J. Liu, D. Yang, Z. Wei, Z. Jiang and W. Shangguan, ACS Sustainable Chem. Eng., 2017, 5, 6578–6584.
10. L. Liao, Q. Zhang, Z. Su, Z. Zhao, Y. Wang, Y. Li, X. Lu, D. Wei, G. Feng, Q. Yu, X. Cai, J. Zhao, Z. Ren, H. Fang, F. Robles-Hernandez, S. Baldelli and J. Bao, Nat. Nanotechnol., 2014, 9, 69–73.
11. W. Shi, F. Guo, H. Wang, S. Guo, H. Li, Y. Zhou, C. Zhu, Y. Liu, H. Huang, B. Mao, Y. Liu and Z. Kang, ACS Appl. Mater. Interfaces, 2017, 9, 20585–20593.
12. K. W. Park and A. M. Kolpak, J. Catal., 2018, 365, 115–124.
13. M. Schönnenbeck, D. Cappus, J. Klinkmann, H.-J. Freund, L. G. M. Petterson and P. S. Bagus, Surf. Sci., 1996, 347, 337–345.
14. W. Luo and A. Asthagiri, Catal. Sci. Technol., 2014, 4, 3379–3389.
15. H.-X. Deng, J. Li, S.-S. Li, J.-B. Xia, A. Walsh and S.-H. Wei, Appl. Phys. Lett., 2010, 96, 162508.
16. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
17. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
18. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
19. M. García-Mota, M. Bajdich, V. Viswanathan, A. Vojvodic, A. T. Bell and J. K. Nørskov, J. Phys. Chem. C, 2012, 116, 21077–21082.
20. J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89.
21. D. Prendergast, J. C. Grossman and G. Galli, J. Chem. Phys., 2005, 123, 014501.
22. F. Osterloh and B. Parkinson, MRS Bull., 2011, 36, 17–22.
23. B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, J. Am. Chem. Soc., 2005, 127, 5308–5309.
24. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913.
25. J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26.
26. W. I. Choi, B. C. Wood, E. Schwegler and T. Ogitsu, J. Phys. Chem. C, 2013, 117, 21772–21777.
27. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46.
28. P. Sabatier, La catalyse en chimie organique, Librairie Polytechnique, Paris et Liège, 1920.
29. M. Che, Catal. Today, 2013, 218–219, 162–171.
30. J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184.
31. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
32. I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
33. X. Chen, C. Li, M. Grätzel, R. Kostechi and S. S. Mao, Chem. Soc. Rev., 2012, 41, 7909–7937.
34. S. Chen and L. Wang, Chem. Mater., 2012, 24, 3659–3666.
35. D. E. Aspnes and A. Heller, J. Phys. Chem., 1983, 87, 4919–4929.
36. J. R. Darwent, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1703–1709.
37. X. Chen and W. Shangguan, Front. Energy, 2013, 7, 111–118.
38. N. Singh, G. Jabbour and U. Schwingenschlőgl, Eur. Phys. J. B, 2012, 85, 392.
39. T. F. Jaramillo, K. P. Jorgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Science, 2007, 317, 100–102.
40. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
41. M. Grätzel, Photocatalysis with colloidal semiconductors and polycrystalline films, in Photocatalysis and Environment, ed. M. Schiavello, 1988, pp. 367–398.
42. M. Grätzel, Heterogeneous photochemical electron transfer, CRC Press, 1988.
43. Y. Oosawa, R. Takahashi, M. Yonemura, T. Sekine and Y. Goto, New J. Chem., 1989, 13, 435–440.
44. Y. Liu, L. Xiea, Y. Li, R. Yang, J. Qu, Y. Li and X. Li, J. Power Sources, 2008, 183, 701–707.
45. F. A. Frame, E. C. Carroll, D. S. Larsen, M. Sarahan, N. D. Browning and F. E. Osterloh, Chem. Commun., 2008, 2206–2208.
46. M. A. Holmes, T. K. Townsend and F. E. Osterloh, Chem. Commun., 2012, 48, 371–373.
47. S. B. A. Hamid, S. J. Teh and C. W. Lai, Catalysts, 2017, 7, 93.
48. A. M. A. E. Naggar, I. M. Nassar and H. M. Gobara, Nanoscale, 2013, 5, 9994–9999.
49. J.-Y. Hao, Y.-Y. Wang, X.-L. Tong, G.-Q. Jin and X.-Y. Guo, Catal. Today, 2013, 212, 220–224.
50. J. Boltersdorf, I. Sullivan, T. L. Shelton, Z. Wu, M. Gray, B. Zoellner, F. E. Osterloh and P. A. Maggard, Chem. Mater., 2016, 28, 8876–8889.
51. Á. Valdés, Z.-W. Qu, G.-J. Kroes, J. Rossmeisl and J. K. Nørskov, J. Phys. Chem. C, 2008, 112, 9872–9879.
52. J. H. Montoya, M. García-Mota, J. K. Nørskov and A. Vojvodic, Phys. Chem. Chem. Phys., 2015, 17, 2634–2640.
53. M. Hassel and H.-J. Freund, Surf. Sci., 1995, 325, 163–168.
54. X. Liu, C. Dong, W. Dong, X. Wang, X. Yuan and F. Huang, RSC Adv., 2016, 6, 38515–39520.
55. H. A. Hansen, I. C. Man, F. Studt, F. Abild-Pedersen, T. Bligaard and J. Rossmeisl, Phys. Chem. Chem. Phys., 2010, 12, 283–290.
56. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
57. N. P. Blake, S. Latturner, J. D. Bryan, G. D. Stucky and H. Metiu, J. Chem. Phys., 2001, 115, 8060–8073.
58. T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B, 2003, 68, 125210.
59. G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140–12146.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta11087e

---