Water desalination through rim functionalized carbon nanotubes

Abstract

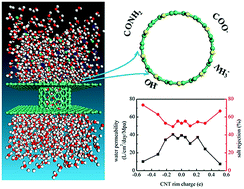
Carbon nanotubes (CNTs) are promising media for seawater desalination due to their high water flow rate. Currently, narrow CNT membranes cannot be mass-produced for salt rejection purposes. Hence, introducing chemical functional groups at the rims of comparatively wider CNTs is an alternative strategy to enhance the ion exclusion performance. Although the dipole moment between the CNT rim and locally anchored functional groups is expected to have an important impact on desalination performance, its specific effects have not been systematically investigated. Herein, we present a comprehensive study of the water permeability and salt rejection of CNTs with various dipole moments anchored at their rims using classic molecular dynamics (MD) simulations. Compared to their bare CNT counterparts, CNTs with a low dipole moment at the rim can slightly increase the water flow and salt rejection rate, and CNTs with a high dipole moment can significantly improve the salt rejection efficiency, although water passage is slowed. In general, introducing functional groups with a high dipole moment on wider CNT rims can filter more than 95% of salt ions while maintaining a high water permeability of 10.2 L cm⁻² day⁻¹ MPa⁻¹. The calculated potential of mean force for water molecule and salt ion passage through the CNTs, oxygen and hydrogen density maps, radial distribution functions, and snapshots of water molecules and salt ions in the CNTs offer in-depth insights into the mechanism of seawater desalination by CNTs. Our study offers guidelines for an alternative design of CNTs to achieve both high salt rejection and fast water flow.