Electronic structure of aqueous-phase anatase titanium dioxide nanoparticles probed by liquid jet photoelectron spectroscopy

Abstract

We report on the nature of water interactions with anatase TiO₂ surfaces. TiO₂ nanoparticles (NPs), 3, 6, 10, and 20 nm in diameter, dispersed in different aqueous solutions, were investigated by soft-X-ray photoemission spectroscopy from liquid microjets. One central aspect of this study is the characterization of the electronic structure and identification of the molecular species that exist at the NP–aqueous solution interface as a function of solution pH. Valence and core-level electron binding energies are determined by the respective non-resonant photoelectron spectra. In addition, we report resonant photoemission spectra at the Ti 2p and the O 1s edges, which considerably increases the detection sensitivity of the interfacial species. This also allows us to distinguish between titanium at the surface and inside the aqueous-phase NPs. Furthermore, from the Ti 2p resonant photoelectron spectra, we obtain the so-called partial electron yield X-ray absorption (PEY-XA) spectra, which help here to rule out an anatase-phase transformation or the occurrence of Ti³⁺ sites due to oxygen defects. However, a more direct spectral feature that allows us to distinguish between molecularly and dissociatively adsorbed water is provided by the actual O 1s resonant photoelectron spectra. This is then exploited to show that water adsorbs molecularly at low pH, and dissociative adsorption at the TiO₂ NP (aq) surface is observed at basic pH. Based on our results, we propose a mechanism of the anatase TiO₂–H₂O interaction that explicitly accounts for the local solution chemical environment. Here, H₂O and OH⁻ adsorb at the Ti sites, and no oxygen defects exist.

---

Introduction

Titanium dioxide, TiO₂, with its three phases in nature, anatase, rutile and brookite, is one of the most important transition metal oxides.¹ It offers wide-ranging properties for science and industry applications, and furthermore, it is a chemically stable, abundant and cheap material.² Exhibiting a large bandgap of 3.2 eV, TiO₂ absorbs light in the UV region,^3,4 which explains the extensive study of this material in photoelectric and photochemical research.^5,6 In 1972, Fujishima and Honda studied water photolysis on the TiO₂ electrode surface, which can be described by the reaction H₂O + 2hν → 1/2O₂ + H₂.⁷ This photochemical reaction thus provides a clean and sustainable way for hydrogen fuel production from solar energy. Many subsequent works have focused on water electrolysis to develop efficient photoelectrochemical cells (PECs) for solar hydrogen generation by immersing two electrodes (TiO₂ photoanode and a cathode).^3,8–14 The challenge in these studies is to minimize the unwanted back-reaction, i.e., the recombination or non-separation of hydrogen and oxygen atoms, which reduces the PEC's efficiency. An ideally performing device, minimally suffering from electric current losses, would assure that the initial charge separation is very fast (on the femtosecond timescale) to slow down the back-reaction.¹⁵ Despite active research, the conversion efficiency from solar to electric power with current PECs is still low, reaching up to 17%,^15,16 and prevents this path for solar hydrogen generation from being economically and commercially viable.^17,18

As the TiO₂ electrode is immersed in an aqueous environment, it is essential to gain a detailed understanding of the electronic properties of the TiO₂–water interface, and this has motivated many investigations of the water adsorption behavior on single crystals, in the rutile as well as anatase phase.^3,19–25 Likewise, the present study aims at determining the electronic structure of this interfacial layer. The novel approach here is to access the interface by soft X-ray photoelectron (PE) spectroscopy, which has not been accomplished previously for a TiO₂ surface fully contained in liquid water. The reason for this is that the detection of photoelectrons in a high-vapor pressure environment has only recently become possible with the introduction of the liquid microjet technique^26–29 and of ambient pressure photoelectron spectroscopy (AP-PES).^21,30–33 Liquid jets are ideally suited to study NPs dispersed in aqueous solutions,^26–29 while the latter technique typically refers to condensation of a few monolayers (MLs) of liquid water on a solid substrate at a suitable relative humidity.^21,30–33 Also, photoelectrons have been detected from liquid cells equipped with a few-nanometer thick graphene membrane to separate the liquid from a vacuum.^34–36

The TiO₂ anatase phase has been found to exhibit higher photocatalytic activity³⁷ and higher efficiency in photo-electrochemistry applications,^38,39 and it is also more stable in the nanometer regime.^40,41 However, on the macroscopic size scale, rutile is the most stable phase,^1,42 and it has been studied more intensively, both theoretically^3,19 and experimentally.^21,43,44 Yet, the nature of water adsorption on TiO₂ surfaces remains unclear; depending on the specific study, water has been concluded to adsorb (1) dissociatively, (2) molecularly, or (3) mixed at the TiO₂ interface.^{3,19–23,45–49} Furthermore, the adsorption mechanisms for these different cases were proposed to depend on whether or not the (vacuum) surface is defect-free. A defect surface site refers to a missing oxygen atom in the crystal structure (oxygen vacancy), and it is easily created by electron bombardment, ion sputtering, or thermal annealing.⁵⁰ In the aqueous phase, the situation is quite different; defects on the titania surface will be healed upon interaction with the water molecules.^21,51 Oxygen vacancies are accompanied by a change of the titanium charge state (Ti⁴⁺ → Ti³⁺) and the occurrence of color centers,⁵⁰ which are the most active surface sites for water dissociation (mechanism (1)).^50,52,53 Defects on the TiO₂ surface are conveniently detected by the Ti³⁺ signal,^20,21 a procedure also adapted here. For the interpretation of the results obtained in the present work, it is useful to briefly review the different adsorption mechanisms.

Dissociative adsorption (mechanism (1) of the TiO₂–water interaction) depends entirely on the existence of surface defects; water molecules dissociate only at oxygen vacancy defects. The thus generated hydroxyl species fills the oxygen vacancies (denoted OH_t), leaving the hydrogen to bond to a neighbor lattice oxygen atom (OH_b) and forming what is termed paired hydroxyl groups.⁴⁴ Ketteler et al.²¹ observed this paired OH for 0.25 ML coverage on rutile (110) using AP-PES. In addition, the authors detected an O 1s photoelectron signal from adsorbed molecular water at less than 1 ML coverage, with an approximately 0.5 eV lower binding energy (BE) as compared to bulk water. This PE peak could correspond to hydroxyl or to molecularly adsorbed water; pseudo-dissociated water has also been suggested.²¹ In the latter process, the paired hydroxyl groups re-form a water molecule by back-reaction. At higher coverage, water has been shown to adsorb molecularly, bonding to the OH groups that act as hydrogen-donors.²¹ A similar conclusion has been drawn from PE spectroscopy measurements of TiO₂ nanoparticles (NPs) exposed to water vapor; experiments were conducted using an aerosol generator.⁵⁴ Mechanism (1) can hence be represented as H₂O + O_b ↔ OH_b + OH_t.^55,56 The interconversion energy of the dissociated hydroxyl pair relative to the water molecule (back-reaction) has been estimated as ΔE = 0.035 ± 0.003 eV, based on a combination of supersonic molecular-beam experiments, scanning tunneling microscopy, and ab initio molecular dynamics.⁵⁵ Given this very small energy difference between the two states, the re-formation of an adsorbed water molecule is slightly more likely over the paired hydroxyl configuration, but not dominating.⁵⁶ In this mechanism, OH_t was assumed to form a covalent bond with the TiO₂ surface.²¹ This interpretation is based on the detected energy of the O 1s and Ti 2p peak positions, both being different for the hydrated TiO₂ rutile crystal surface compared to the bulk crystal.⁴³

In the second proposed mechanism (2) of the TiO₂–water interaction, water is molecularly adsorbed on the surface at very specific geometries where the water oxygen atom binds to Ti⁴⁺ sites and its hydrogens bind to two neighboring lattice oxygen atoms.⁵⁷ This raises the question whether water dissociates exclusively at oxygen vacancies or whether dissociation can also occur at Ti⁴⁺ sites. Here, the third mechanism (3) of TiO₂–water interaction comes into play, and it has been legitimated by experiments on defect-free surfaces of rutile^46,58 and anatase,^20,22,45 both showing a mixed adsorption behavior, with the OH signal being small relative to the signal from molecularly adsorbed water. Specifically, Walle et al.²⁰ reported that the first water layer is composed of 0.47 ± 0.05 ML OH and 0.77 ± 0.55 ML molecular water for the anatase TiO₂ (101) defect-free surface; the OH coverage stays nearly constant for higher water exposure. In a theoretical work, Zheng et al. studied the stability of the dissociated OH species on titanium sites using density function theory (DFT) on a rutile (110) surface edge.⁵⁹ The authors report that its lifetime is highly dependent on the location of the hydrogen species (the second product of the water dissociation) and that the recombination/reformation of the water molecule is possible.⁵⁹ This mechanism is the most related one to the present study, as detailed later in the Results section.

Here, we present PE measurements from anatase-phase TiO₂ NPs dispersed in liquid water, which we refer to as the “all-in-solution” surface-study approach. This is complicated, though, by the fact that NPs are not soluble in water due to the large surface potential. They tend to aggregate and sediment out near the point of zero charge (PZC), which is at pH ∼6.4 for the anatase surface.⁶⁰ That is, when the surface is neutral, NPs reduce their surface energy by aggregating and thereby reducing their surface area. Such unwanted effects are avoided by adding stabilizers to the aqueous solutions, which inevitably leads to a change of pH. In this study, we use three different stabilizers, Cl⁻ and NO₃⁻, resulting in a positive surface zeta potential of the TiO₂ NP (the potential between the TiO₂ surface and the surrounding aqueous solution), and NH₄⁺, yielding a negative surface zeta potential. Under these conditions, the NPs are stable in aqueous solution, and stable liquid microjets for the photoemission experiments can be obtained. Evidently, we are mostly interested in conditions where the stabilizer concentration is low enough such that a sufficiently large fraction of free NP surface sites is available for water adsorption. This fraction can be estimated from the adsorbed ML density on TiO₂ (110) (5.2 nm⁻²).^20,21 Then, one of our major questions is whether water adsorbs molecularly or dissociatively on the anatase TiO₂ NP defect-free surface where no Ti³⁺ sites are present. The other, equally important question is how the adsorption nature depends on pH, explored here for basic and acidic pH. This latter aspect has not been addressed experimentally before. We are aware of a single density functional theory (DFT) molecular dynamic work studying the acidity of the surface groups relevant in the water interaction with a rutile (110) surface.⁶¹ It was predicted that the fraction of terminal water molecules (TiOH₂) is small at neutral pH, and the surface pK_a for this site has been estimated to be 9. In contrast, a pK_a value of −1 was estimated for the surface hydroxide bridge groups (Ti₂OH⁺). Most interesting for the present work is the TiOH₂ case. Deprotonation of TiOH₂ to TiOH⁻, which is coupled with the protonation of H₂O in the liquid water, is paralleled by the reverse reaction where the solution proton is transferred to a TiOH⁻ surface group⁶¹ (TiOH⁻ + H₃O⁺ → TiOH₂ + H₂O). We can hence expect that in a basic solution environment, this reverse reaction is insignificant. Qualitatively, such a behavior is supported by our combined resonant and non-resonant PE spectroscopy, as well as partial-electron yield X-ray absorption (PEY-XA) measurements from TiO₂ NPs (aq) at different pH values.

Experimental

Photoelectron measurements of TiO₂ NP solutions (i.e., colloidal dispersions) were conducted using the SOL³PES setup at the U49/2-PGM-1 soft X-ray beamline, at the synchrotron radiation facility BESSY II, Berlin. The experimental details of SOL³PES have been described recently.⁶² Briefly, synchrotron light, the liquid jet and the photoelectron detection are orthogonal to each other. The X-ray light at this beamline is linearly polarized in the floor plane, which is the plane spanned by jet propagation and light propagation. Focal size is approximately 60 × 20 μm². Solutions were injected into the interaction vacuum chamber through a 25 μm glass capillary. Liquid flow rate was 0.7 ml min⁻¹ using a backing pressure of 10 bars. The liquid jet hits the X-ray beam at 0.5 mm distance from the capillary tip, and this interaction point is at 500 μm distance from the detector orifice. The pressure in this chamber was kept at approximately 3.0 × 10⁻⁴ mbar by using a turbo molecular pump (1600 l s⁻¹) and two liquid nitrogen cold traps. At 500 eV photon energy, using the 80 μm beamline exit slit, the energy resolution in our measurement is higher than 130 meV.

Four sets of anatase TiO₂ NP solutions were studied. The NP sizes used in this study were given by the samples that were commercially available. In addition to different NP sizes, the different vendors also use different stabilizers as well as different stabilizer concentrations. Then, together with the finding that anatase-phase TiO₂ NPs, of 2–200 nm diameter, have been demonstrated to exhibit no noticeable size effects on the electronic structure,⁶³ it is possible to solely vary the ratio of free-to-stabilizer covered surface sites as a single parameter.

Dry NPs: 20 nm diameter, 99.5% anatase TiO₂ NP sample purchased from Io-Li-Tec, Germany. This sample was used for the total electron yield measurements of the Ti L-edge XA and the O K-edge XA spectra for examining the similarity between the XA spectra of the anatase-phase TiO₂ NPs in a dry environment and the TiO₂ single crystal reported in the literature.

TiO₂ NPs in HCl aqueous solution: (acidic solutions without free surface sites) 10 nm, 99.9% pure anatase TiO₂ NPs coated with Cl⁻, purchased from Mknano, Canada, were used to prepare 20 wt% TiO₂ NPs in 0.5 M HCl aqueous solution (yielding pH 1.2) and in 1 M HCl aqueous solution (yielding pH 0.7). In both samples, the NPs are fully covered by Cl⁻ ions with ratios of NP surface sites relative to stabilizer ions of [1 : 1]^Cl− and [1 : 2]^Cl−, respectively. In all these cases, water cannot interact with the actual TiO₂ NP. Our measurements from the HCl-stabilized NP solutions thus provide valuable reference O 1s non-resonant, resonant XPS and PEY-XAS spectra of the TiO₂ NPs, in the absence of interfacial oxygen species.

TiO₂ NPs in HNO₃ aqueous solution: (acidic solutions with free/no free surface sites) 20 wt%, 6 nm TiO₂ NPs in 0.5 M HNO₃ aqueous solution (yielding pH 1.2) and in 0.25 M HNO₃ aqueous solution (pH 0.9), purchased from PlasmaChem, Germany, which have ratios of TiO₂ surface sites relative to the stabilizer of [1 : 1]^NO₃− and [2 : 1]^NO₃−, respectively. Furthermore, in order to increase the [x : y]^NO₃− ratio, a 20 wt%, 3 nm TiO₂ NPs in 0.6 M HNO₃ aqueous solution (pH 0.7) yielding [4 : 1]^NO₃− was used; this ready-to-use solution was purchased from NYACOL, USA.

TiO₂ NPs in NH₄OH aqueous solution: (basic solutions with free surface sites) 20 wt%, 20 nm TiO₂ NPs in 0.3 M NH₄OH aqueous solution (pH 7.8; slightly above the neutral water pH) were obtained from NYACOL, USA. In addition, we added 0.5 M NH₄OH to this NP (aq) solution to obtain 20 wt%, 20 nm TiO₂ NPs in 0.8 M NH₄OH aqueous solution (pH 9.8). This leads to ratios of [2 : 1]^NH₄+ and [1 : 1.5]^NH₄+, respectively. The latter sample was used to support our proposed TiO₂–water interaction mechanism, as discussed in the Results section. It is interesting to mention that the estimated [2 : 1]^NH₄+ ratio is in good agreement with measurements of the surface zeta potential. It is −16.9 mV for the [2 : 1]^NH₄+ solution (measured with a “Zetasizer Nano ZS” spectrometer) and can be compared with a value of +30 mV⁶⁴ for a fully covered anatase TiO₂ NP surface in aqueous solution.

Results and discussion

Ti L-edge PEY-XA spectra

We start by exploring the X-ray absorption (XA) spectra of aqueous-phase TiO₂ NPs measured at the Ti⁴⁺ 2p → valence 3d⁰ resonance. We note that an electron-yield absorption spectrum essentially captures electrons that are emitted in an electronic relaxation process, which is mostly Auger decay. One typically assumes that the Auger-electron yield is proportional to the actual XA.^65,66 In the present work, we detect the partial electron yield corresponding to the refilling of a Ti 2p hole by a 3p electron and subsequent ejection of another 3p electron (Ti LMM Auger channel); this (resonant) Auger signal appears in the 360–420 eV kinetic energy range. More specifically, by integrating the signal intensity over this energy range as a function of the excitation energy, we obtain the so-called partial electron yield XA (PEY-XA) spectrum. For the questions addressed here, the small difference that may occur between PEY and total electron yield (TEY) detection⁶⁵ is irrelevant; the important point here is that we can experimentally track the electronic structure changes that lead to the measured XA spectra. In Fig. 1, we show the Ti L-edge PEY-XA spectra of several NP solutions, [1 : 1]^Cl− [1 : 1]^NO₃−, [4 : 1]^NO₃− and [2 : 1]^NH₄+. We present one sample from each set described in the Experimental section. For the NO₃⁻ sample set only, two samples provided from different companies are shown ([4 : 1]^NO₃− and [1 : 1]^NO₃−). In addition, the dry NP (shown in the bottom of Fig. 1) XA spectrum was measured by detecting the drain current while sweeping the photon energies over the Ti L-edge. This is one way to obtain the total electron yields, and throughout the text, we will refer to the TEY-XA spectrum, serving as the reference.

Fig. 1 (Top): Ti L-edge PEY-XA spectra of anatase TiO₂ NPs dissolved in different aqueous solutions. Here, [x : y]^ion indicates the stabilizer ion that has been used, and inside the bracket, the ratio of available NP surface sites to surface sites covered by the stabilizer ion is shown. Labels A–D refer to the most prominent absorption bands. The splitting of the L₃ edge feature, 10 Dq, is indicated. (Bottom): Ti L-edge TEY-XA spectra of dry anatase TiO₂ NPs.

The measured L-edge XA spectra, presented in Fig. 1, can be divided into two regions, L₂ (2p_1/2) and L₃ (2p_3/2) edges, due to the 2p spin orbital coupling splitting. Results are shown for the NP solutions [1 : 1]^Cl−, [1 : 1]^NO₃− [4 : 1]^NO₃−, and [2 : 1]^NH₄+. Here, we largely focus on the L₃ region. Our first observation is that the spectra of all solutions are nearly identical. The first prominent absorption band A results from the Ti 2p_3/2 → 3d t_2g transition, and band B relates to the Ti 2p_3/2 → 3d e_g transition. The energy difference between A and B, which quantifies the crystal field splitting, 10 Dq, of the empty 3d orbital hybridized with the surrounding oxygen atoms, is indicated. Since 10 Dq is sensitive to the Ti–O distance⁶⁷ its value is an indicator of changes in the Ti local environment. Arguably more important is the overall shape of the L-edge XA spectrum, the details of which are characteristic for a given TiO₂ phase (anatase, rutile, or brookite). We see that the NP spectra in Fig. 1 match well the TEY-XA spectrum of the dry 20 nm NPs, which is also presented at the bottom of Fig. 1; and the latter spectrum perfectly reproduces the XA spectrum of anatase-phase TiO₂ crystal.^68–70 We particularly point out that the broadening of the e_g L₂ edge (as well as the sub-splitting of the e_g L₃ edge), which is very sensitive to the crystal phase, is the same in all spectra and reproduces the shape and width reported in the literature.^68–70 We can thus rule out any NP phase transition in the aqueous solutions, and also, oxygen defects are not detected, which would manifest in contributions from the Ti³⁺ signal.

To further confirm the non-existence of Ti³⁺, we have also recorded the valence spectra at the various resonances A, B, C, and D identified in Fig. 1. The results are exemplarily shown for the [2 : 1]^NH₄+ solution in Fig SI-1 of the ESI,† where we also present an off-resonant spectrum measured slightly below the resonance, at 457 eV photon energy. None of the spectra display any signature of the 2p–3d3d (LVV) Ti³⁺ Auger decay, as judged from comparison with our previous study of atomic Ti³⁺ in TiCl₃ aqueous solution.⁷¹ Our conclusion is also supported by reported valence spectra of pure crystalline anatase TiO₂ (containing no Ti³⁺) and Li⁺-doped TiO₂, in which Ti³⁺ forms.⁷² Hence, the spectra in Fig SI-1† prove that the Ti 3d orbital is empty, and the aqueous-phase NPs are indeed purely anatase-phase TiO₂. Adsorption mechanism (1), described in the introduction, is thus irrelevant for the TiO₂ NP–aqueous solution interface. One further observation from Fig. 1 that is worth mentioning is that 10 Dq appears to be slightly larger for the [2 : 1]^NH₄+ solution than for all other solutions. In Fig SI-2 of the ESI,† we have averaged the [4 : 1]^NO₃−, [1 : 1]^Cl−, and [1 : 1]^NO₃− solution spectra for better visualization of this pH-dependent effect. Arguably, this is an indication that NH₄⁺, unlike the other stabilizing ions, has some specific effect on the interfacial structure. Indeed, a distinct adsorption behavior of H₂O occurs in the NH₄⁺-stabilized NP solutions as we will show below.

O 1s off-resonant photoemission spectra

Fig. 2 presents the (regular) oxygen 1s core-level photoelectron spectra measured at 1200 eV photon energy for all our NP solutions. Here, we have included the reference spectrum of the O 1s spectrum of the 0.05 M NaCl aqueous solution, representative of neat liquid water. We find that all PE spectra (Fig. 2A), again with the one exception of NH₄⁺ (Fig. 2B), are almost identical, exhibiting the main bulk water peak at 538.1 eV BE,⁷³ relative to the vacuum level, the water gas-phase (a shoulder) at 540.0 eV, and an additional small peak at 534.9 eV BE from the lattice oxygen of the TiO₂ NPs, in agreement with the reported value for the TiO₂ rutile crystal with a few layers of water prepared at a suitable relative humidity.²¹ Similar to our previous study of aqueous-phase hematite NPs stabilized with NO₃⁻,²⁶ the PE signal from the NO₃⁻ cannot be observed (at 538.1 eV binding energy⁷⁴) at such a low concentration because of overlap with the large signal intensity from bulk water.^51,74 The OH⁻ signal, on the other hand, gives rise to a peak at 536.0 eV BE (determined in the aforementioned ambient-pressure PE study on rutile TiO₂ single crystal²¹), which is distinguishable from NO₃⁻ and water. But, there is no indication of adsorbed OH⁻ despite available free adsorption sites for interaction with water, for instance in the case of [4 : 1]^NO₃− and [2 : 1]^NO₃−. We thus conclude (and will later corroborate) that water does not dissociate on the TiO₂ NP surface but rather adsorbs molecularly; yet, a small but negligible amount of dissociated water may exist at the NP surface. This is opposite to α-Fe₂O₃ NPs, where water dissociates when the NPs are stabilized by NO₃⁻.²⁶ Note also that adsorbed water, similar to NO₃⁻, has an O 1s BE strongly overlapping with bulk water (0.5 eV lower BE than bulk water²¹), which makes the detection of this contribution impossible in a liquid-jet experiment.

Fig. 2 Oxygen 1s photoelectron spectra of the different anatase TiO₂ NP aqueous solutions, measured at 1200 eV photon energy. As in Fig. 1, [x : y]^ion indicates the stabilizer ion that has been used, and inside the bracket, the ratio of free NP surface sites to surface sites covered by the stabilizer ion is shown. NP size is given in the Experimental section. (A) Acidic NP solutions: [1 : 1]^Cl− (pH 1.2), [1 : 2]^Cl− (pH 0.7), [1 : 1]^NO₃− (pH 1.2), [2 : 1]^NO₃− (pH 0.9), and [4 : 1]^NO₃− (pH 0.7). Also shown is the spectrum of 0.05 M NaCl. (B) Basic solution: [1 : 1]^NH₄+ (pH 7.8). Also shown are the O 1s spectra of the 0.05 M NaCl and 0.5 M NH₄OH aqueous solutions.

We now turn to the [2 : 1]^NH₄+ NP solution (Fig. 2B), where we observe a small intensity signal at 536.0 eV BE, which identifies the adsorbed OH⁻ species. This energy is in agreement with the previously reported value for adsorbed hydroxyl species on a TiO₂ surface under near ambient pressure conditions.^21,31,49 Comparing with the reference O 1s PE spectra of the 0.5 M NH₄OH aqueous solution (pH 11.7) and 0.05 M NaCl aqueous solution, containing no NPs, the OH⁻ signal is seen to vanish. This implies that it is not produced by the NH₄⁺ interaction with bulk water. Notice that the higher-concentration solution, 0.5 M NH₄OH (compared to 0.3 M NH₄OH), does not even show the slightest evidence of OH⁻ signal. Hence, the 536.0 eV BE signal must result from water interaction with the TiO₂ free surface sites. Since the pH of the [2 : 1]^NH₄+ NP solution is 7.8, i.e., the concentration of free OH⁻ in the solution is roughly 10⁻⁷ mol L⁻¹, the detected OH⁻ species must be immobilized within the TiO₂ NP–solution interface rather than being free in the solution. One can also infer from Fig. 2 that dissociation of water on the TiO₂ NP surface depends on solution pH, a hypothesis that we will verify with the help of oxygen K-edge PEY-XA spectra. In the present case of approximately 650 eV O 1s photoelectrons, the top-most layers of the NPs, including their adsorbed molecular layer, are probed. The relatively large OH⁻ signal intensity compared to the lattice oxide signal in Fig. 2B is attributed to the exponentially decreasing electron signal contribution as a function of distance from the (covered) NP surface–aqueous solution interface.

O K-edge photoemission and PEY-XA spectra

Analogous to the Ti L-edge PEY-XA measurements, we also studied the valence photoemission signal (detected in the 510–525 eV kinetic energy range), sweeping the photon energy across the O 1s resonance. Fig. 3A presents the O 1s PEY-XA spectra of five selected NP solutions, [1 : 1]^Cl− [1 : 2]^Cl−, [4 : 1]^NO₃− [2 : 1]^NH₄+, and [1 : 1.5]^NH₄+. In Fig. 3B, we show the respective spectra of four relevant reference salt aqueous solutions, 0.5 M HNO₃ (pH −0.2), 0.5 M NH₄OH (pH 11.7), 0.5 M NaOH (pH 13.7), and 0.05 M NaCl (pH 7). Fig. 3C shows the TEY-XA spectrum of the dry TiO₂ NPs, which was, however, recorded by measuring the resulting electric current through the sample.

Fig. 3 (A) O 1s PEY-XA spectra of different anatase TiO₂ NP aqueous solutions; see caption of Fig. 2 for the solution labels. Intensities are normalized at the water pre-peak band at 535.0 eV. (B) O 1s PEY-XA spectra of reference solutions, as labeled. (C) TEY-XA spectra of dry anatase TiO₂ NPs. Assignment of absorption bands: a and d (TiO₂ lattice oxide), b (NO₃⁻), and c (OH⁻).

In Fig. 3A and B, the large peak at 535 eV photon energy is due to the liquid water absorption pre-peak (O 1s → 4a₁ transition⁷⁵), which is used here for energy calibration and intensity normalization. The shoulder at 534.5 eV photon energy is the respective H₂O gas-phase absorption. This contribution is seen to vary among different solutions, which is due to a combination of changing vapor pressure upon pH variation and perhaps a slight misalignment of the liquid jet when switching solutions. In addition to the water absorption bands, several smaller peaks, a (near 531.2 eV), b (532.3 eV), c (532.8), and d (533.8), can be seen in both Fig. 3A and B. More specifically, and starting with the TEY-XA spectrum of the dry NPs (Fig. 3C), the two main bands, a (531.2 eV) and d (533.8 eV), are the absorptions O 1s → O 2p–Ti 3d (t_2g and e_g); these metal orbitals are hybridized with lattice O 2p.^63,76–79 We next consider the solutions [1 : 1]^Cl− and [1 : 2]^Cl− for which no free adsorption sites on the NP surfaces are available. The respective spectra thus serve as a reference, representative of an O 1s XA spectrum in the absence of interfacial oxygen-containing species, and they are also useful to quantify the stabilizer ion and concentration effects on the detected signal intensities. Not surprisingly, these spectra exhibit just absorption a, corresponding to the TiO₂ NP bulk, and band d stays undetected, hidden under the water pre-edge peak. A small energy shift of band a with respect to the dry NPs is likely caused by the Cl⁻ decoration. Turning now to the [4 : 1]^NO₃− NP solution – where we expect molecular water adsorption (as concluded from Fig. 2A) – an additional band b (at 532.3 eV photon energy) is observed. The same band occurs in the XA spectrum of the 0.5 M HNO₃ aqueous solution (Fig. 3B), and we can unequivocally assign band b to interfacial NO₃⁻ species. For the [2 : 1]^NH₄+ and [1 : 1.5]^NH₄+ NP solutions, we find an intense band c (at 532.8 eV photon energy), i.e., at a slightly larger absorption than b, and the intensity of band a is now very small. Comparing with the XA spectrum of the 0.5 M NaOH aqueous solution (pH ∼13.7) in Fig. 3B, where we also find an absorption band (although small) at position c, shows that this band is due to free OH⁻ (also in agreement with ref. 80 and 81). The comparison with NaOH solution was necessary here because the OH⁻ signal from the 0.5 M NH₄OH solution (our reference discussed along with Fig. 2) is below our detection limit. Note that NaOH is a stronger base than NH₄OH. As a further remark, we point out that the intensities of interfacial OH⁻ in the NP (aq) solutions are much larger than the signal of the free OH⁻ in the reference solutions (particularly 0.5 M NaOH). This result would seem non-intuitive given the NP solution pH of 7.8. We attribute the large OH⁻ signal to immobilized dissociated H₂O at or near the TiO₂ surface; alternatively, this effect might be a consequence of the NP position relative to the solution–vacuum interface to be detailed below. Complementary resonant X-ray scattering (RIXS) studies are underway to clarify the origin of this large signal from TiO₂ NPs in aqueous solution, at basic pH.

In order to explore the water–NP interaction mechanism, we performed O 1s RPE spectroscopy measurements at three selected excitation energies, the t_2g lattice oxide (absorption a), the interfacial NO₃⁻ (b) and OH⁻ (c). Our initial focus is to identify the spectral contributions from the lattice oxide as this will guide us in singling out contributions from interfacial species. In Fig. 4, we present the RPE spectra of all our NP solutions measured at a (531.2 eV), and in addition, we show the off-resonance spectrum of the [2 : 1]^NH₄+ NP solution. All spectra are displayed with a Shirley background subtracted. The off-resonance spectrum reproduces the water valence spectrum (in blue),⁸² and the solute signal is below our detection limit. The most relevant feature in this comparison is the electron signal near 22.5 eV (grey-shaded), which results from Auger electron emission. It is specifically the spectator Auger decay, O²⁻ 1s–1t_2g–1t_2g, occurring at 508.7 eV kinetic energy (equivalent to 22.5 eV BE), and has been assigned with the help of the TiO₆⁸⁻ molecular orbital diagram from ref. 83. The other spectral features at approximately 18.0 and 24.5 eV BE are also due to spectator Auger decay but are not further considered here as their intensities are too small for a quantitative analysis of the interfacial species.

Fig. 4 Valence resonant photoelectron (RPE) spectra of different anatase TiO₂ NP aqueous solutions measured at the O₂⁻ resonance, a (531.2 eV photon energy; compare with Fig. 3). Also presented is the off resonance spectrum of the [2 : 1]^NH₄+ NP solution, measured at 530.0 eV photon energy. Solutions are labeled as explained in the caption of Fig. 1. Here, we have added the NP diameters. The grey-shaded area highlights the contributions from the spectator Auger electrons originating from the TiO₂ lattice oxide.

The next observation from Fig. 4 is the considerable intensity variation of the lattice oxide absorption band among the different solutions. At the applied 531.2 eV photon energy (resonance a in Fig. 3), the electron inelastic mean free path can be assumed to be less than 3 nm,⁸⁴ implying that the NPs are located within this range of the solution–vacuum interface. Arguably, there are several parameters that have direct influence on the exact position of a nanoparticle in the measured solutions, including particle size, stabilizer ion and concentration. The current experiment was not designed to systematically study such effects since the different solutions in this work usually differ by more than one parameter. However, the lattice signal contributions tend to be larger for the smaller NPs, which might be an indication of smaller NPs having a larger affinity for the solution interface. On the other hand, the comparison between the 10 nm [1 : 1]^Cl− and the 6 nm [1 : 1]^NO₃− NP solutions would suggest the opposite, indicating that the distance of the NPs from the solution surface depends on the complex interplay between size, charge, and adsorbate, and specifically on the respective nature of the so-called diffusive layer.⁸⁵ It should be stated here that electronic-structure size effects (see Experimental section) in the NP size range considered here can be expected to be negligible.

Having analyzed the oxygen signal from the NPs, based on the O 1s RPE spectra at the lattice oxide resonance, a, we now turn to exploring the contribution from oxygen-containing molecular species at the NP–water interface. We start with the acidic solution. Fig. 5 shows RPE spectra measured at the NO₃⁻ resonance, b, for the [1 : 1]^NO₃−, [2 : 1]^NO₃−, and [4 : 1]^NO₃− NP aqueous solutions. For comparison, we also include a spectrum of the 0.5 M HNO₃ aqueous solution. All spectra are displayed with a Shirley background subtracted. As in Fig. 4, the signal near 30 eV (2a₁) and 11 eV (1b₁) is due to water,⁸⁶ and the latter was used for signal intensity normalization. The interesting features are the broad electron emissions in the 13–24 eV BE range due to NO₃⁻. As in our previous work on hematite NPs,²⁶ the same four main photoemission bands are observed, at approximately 16.0, 18.0, 22.5, and 24.5 eV BE (all within the red-shaded area), assigned to various Auger-electron decays upon O 1s → valence excitation at 532.2 eV photon energy.²⁶ The 24.5 eV peak strongly overlaps with the lattice oxide peak (black-shaded area); compare with Fig. 4. This peak can be most clearly observed for the [4 : 1]^NO₃− NP solution, in which case, the NO₃⁻ contribution is the lowest; see the Experimental section. On the other hand, the NO₃⁻ signal increasingly dominates when going from [4 : 1]^NO₃− to [1 : 1]^NO₃− solutions. In fact, relative intensities (red-shaded area) almost quantitatively track our estimated NP surface sites-to-stabilizer ratios. Most important for the present study are, however, the [2 : 1]^NO₃− and [4 : 1]^NO₃− solutions, which provide free surface sites for water to interact with the TiO₂ surface. If this interaction were dissociative, Auger signal from adsorbed OH⁻ should appear in the 25–32 eV binding energy finger-print region (blue-shaded area) analogous to the hematite NP (aq) study;²⁶ this is because of the considerable spectral overlap between resonances b and c (of adsorbed NO₃⁻ and OH⁻, respectively) seen in Fig. 3A. Obviously, no signal of adsorbed OH⁻ is observed here, corroborating our above finding (from the O1s non-resonant spectra, Fig. 2A, and O K-edge XAS, Fig. 3) that water adsorbs molecularly on the surface of TiO₂ in an acidic environment. In the next paragraph, we discuss the interaction in basic solution.

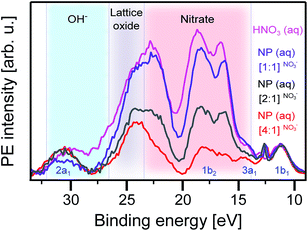Fig. 5 Valence resonant photoelectron (RPE) spectra of different anatase TiO₂ NP aqueous solutions measured at the NO₃⁻ resonance, b (523.2 eV photon energy; compare Fig. 3). Also presented is the spectrum of the 0.5 M HNO₃ aqueous solution. Different shades indicate the regions of Auger-electron emission from different species: NO₃⁻ (red-shaded), lattice oxide (grey-shaded), and OH⁻ (blue-shaded).

Fig. 6 shows the respective O 1s RPE spectra of the basic [2 : 1]^NH₄+ and [1 : 1.5]^NH₄+ NP solutions. Measurements were performed right at the OH⁻ resonance (peak c, 532.8 eV photon energy), rather than at resonance b, which increases the spectral sensitivity to adsorbed OH⁻. The figure also includes an off-resonance spectrum of the [2 : 1]^NH₄+ NP solution measured at 530 eV photon energy as well as a reference spectrum of the 0.5 M NaOH aqueous solution. All the spectra are Shirley-background subtracted. Again, the off-resonance spectrum (in dark blue) reproduces the water valence peaks.⁸² The NaOH spectrum (light blue) exhibits the resonantly enhanced OH⁻ signal, dominated by Auger-electron emission, in the 15–25 eV BE range (corresponding to 505–514 eV kinetic energy range).⁸⁰ This signal contribution is found to be much larger in the spectra of the NP solutions, with an intensity being an order of magnitude larger than the signal from the water valence band. We note, though, that near the 25 eV BE position (grey-shaded area), the OH⁻ signal considerably overlaps with the electron emission from lattice oxide (see also Fig. 4 and 5). The remarkably large OH⁻ signal for the NP solutions, with pH 7.8 ([2 : 1]^NH₄+) and 9.7 ([1 : 1.5]^NH₄+), is a clear indication that this signal cannot be due to free OH⁻ in aqueous solution and rather arises from OH⁻ bound to the aqueous-phase NP surface. It is useful to recall our observation from Fig. 1 that in the case of the [2 : 1]^NH₄+ NP solution, 10 Dq is larger than for all other NP solutions. Together with our findings in Fig. 6, this corroborates that the split can be associated with the different specific interactions between a H₂O molecule and a Ti site at the anatase surface. Our final observation from Fig. 6 is the slight increase of the OH⁻ signal when increasing the NH₄⁺ concentration from 0.3 M ([2 : 1]^NH₄+) to 0.8 M ([1 : 1.5]^NH₄+), which is paralleled by an increase of the OH⁻ XA-band intensity, as was shown in Fig. 3A. This effect will be discussed next.

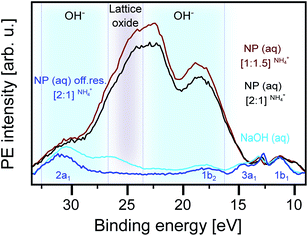Fig. 6 Valence resonant photoelectron (RPE) spectra of different anatase TiO₂ NP aqueous solutions measured at the OH⁻ resonance, c (532.8 eV photon energy; compare Fig. 3). Also presented is the spectrum of the 0.5 M NaOH aqueous solution, and in addition, the off-resonance spectrum measured at 530 eV photon energy of the [2 : 1]^NH₄+ NP solution is shown. Different shades indicate the regions of Auger-electron emission from different species: lattice oxide (grey-shaded) and OH⁻ (blue-shaded).

Our observations from Fig. 1–6 lead us to propose the following pH-dependent adsorption mechanisms for water on the anatase NP surface, as illustrated in Fig. 7. Here, we depict the interaction in the acidic environment in the top tier, and in basic solution in the bottom tier. Our starting point is the hypothetical (prepared) adsorption of a water molecule for both cases. This is followed by the dissociation of H₂O at the defect-free anatase surface, forming a hydroxyl/H⁺ pair similar to the processes discussed in ref. 20 and explained in the introduction. Above, we have inferred from the changes of 10 Dq that water dissociates at the Ti surface sites of the TiO₂ NP. One crucial difference between the acidic and basic environment is then the probability of stabilizing the (paired) proton in the vicinity of OH⁻ at the surface. In fact, the aforementioned simulation of the dissociative/associative water adsorption on rutile TiO₂ using DFT calculations⁵⁹ concludes that the stability of the hydroxylated configuration is largely dependent on the locations of the H⁺ species, and the recombination of water molecules from hydroxyls is observed under the fully hydroxylated condition. We argue that this is what our data show. Under acidic conditions, the free proton is locally rather confined due to hydronium molecules, and recombination to form water is likely. This is illustrated in the acidic-environment model (top tier of the second step) in Fig. 7. Possibly, also the surrounding hydronium in water may transfer a proton to a surface OH⁻ molecule (center tier of the second step). In any case, our experiments suggest that the lifetime of hydroxyl is very short, and this species can thus not be detected here. In contrast, such recombination is less likely in basic solution where H⁺ quickly diffuses away from the surface, and the OH⁻ lifetime is sufficiently large. This situation is illustrated at the right side of the bottom tier of Fig. 7. Our model mechanism would also account for the increase of OH⁻ signal suggested by the spectrum of the [1 : 1.5]^NH₄+ NP solution in Fig. 6. Here, due to the larger pH, the proton delocalization is even larger, which leads to the stabilization of more hydroxyl groups at the TiO₂ surface.

Fig. 7 Illustration of the proposed TiO₂–water interaction in acidic (top tier) and basic (bottom tier) aqueous solutions. TiO₂ NPs are represented by the large white spheres. Water and hydronium oxygens are shown in red, bonded hydrogen atoms are shown in white, and a single free hydrogen (proton) in solution is shown in light-grey. The hydroxyl stability on the NP surface depends on its probability of forming a water molecule by capturing a free H⁺ or via proton transfer from a surrounding hydronium. This probability is largest in the acidic environment, either by recombination of the dissociated H⁺ and OH⁻ pairs (top panel in the acidic model second step) or by proton transfer from the surrounding hydronium (bottom tier in the acidic model second step). Such recombination and proton transfer processes do not occur in a basic or above neutral chemical environment; the basic–pH interaction model is illustrated in the bottom-most tier of the figure.

Conclusion

We have examined the solid–liquid interface of titania NPs in aqueous solutions of different pH. By measuring the Ti L-edge XA spectra, we confirmed that in all solutions studied here, the NPs exhibit an anatase TiO₂ phase. Molecularly adsorbed H₂O molecules were found on the NP surface in the acidic solution. However, a dissociative water interaction, leading to OH⁻ species at the TiO₂ surface, is observed for the near-neutral solutions. This behavior is inferred from the oxygen 1s core level non-resonant PE spectra, and corroborated by the O K edge XA as well as the resonant PE spectra. Specifically, the RPE spectra are a sensitive probe of the NP lattice oxide, and of the existence or absence of NO₃⁻ and OH⁻ interfacial species. The detailed spectral analysis of the 10 Dq value suggests that water interacts with the Ti sites of the NP surface. Our results lead us to propose that at acidic pH, the protonation of adsorbed OH⁻ at the Ti-site of the defect-free anatase NP surface is fast, leading to molecularly adsorbed water as the dominant species. This occurs either by recombination of the proton, which stays rather localized at the site where it was born, with surface OH⁻, or by proton transfer from a hydronium to a surface OH⁻. On the other hand, at basic pH, the proton can easily diffuse away from the surface, which makes the reformation of adsorbed H₂O unlikely. An interesting aspect of these findings is that the pH variation provides a means to control the molecular versus dissociative water interaction with anatase surfaces. This finding is in agreement with previous theoretical studies on the stability of hydroxylated configurations⁵⁹ and on the proton transfer between a TiO₂ surface and hydronium in solution.⁶¹

We would also like to stress that the liquid-jet PE technique is truly complementary to ambient-pressure PE spectroscopy, with the latter ideally suited for investigation of crystalline surfaces covered by several water or aqueous solution monolayers at neutral pH. As shown here, investigation of the respective nanoparticles (TiO₂) fully dispersed in an aqueous solution enables unique access to the study of the TiO₂–water interface as a function of pH. Moreover, application of the multiple aspects of photoemission (beyond the mere measurement of photoelectron spectra) in ambient-pressure studies remains challenging. And yet, future investigations of catalytically-relevant NPs (aq), including also hybrid systems like core–shell nanoparticles,⁸⁷ or tailored nanoparticle properties in material research would benefit from measurements in the soft or even hard X-ray regime in order to better characterize the distribution of NPs at the aqueous solution–vacuum interface.

Author contributions

H. A., R. S. and B. W. planned the experiments and selected the samples. All authors conducted the experiments during multiple beamtimes at BESSY II. H. A., R. S. and B. W. analyzed the data and wrote the article. All authors have given approval to the final version of the manuscript.

Funding sources

H. A. thanks the Egyptian Ministry of Higher Education and Ain Shams University for her PhD grant, and the Egyptian Culture Office in Berlin for support. R. S. and B. W. gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) within the Collaborative Research Center 1109 ‘Understanding of metal oxide/water systems at the molecular scale: structural evolution, interfaces, and dissolution’. R. S. also gratefully acknowledges an Emmy Noether Young Investigator stipend through the DFG (project SE 2253/3-1).

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We thank Hans-Joachim Freund for fruitful discussions, Marvin N. Pohl and Ronny Golnak for participation in some of the experiments, and Fedutik Yirij for preparation of some of the NP samples. The authors thank the staff at the Helmholtz-Zentrum Berlin and BESSY II for assistance during measurements. Open Access funding provided by the Max Planck Society.

References

1. D. A. Hanaor and C. C. Sorrell, J. Mater. Sci., 2011, 46, 855–874.
2. S. Hamad, C. Catlow, S. Woodley, S. Lago and J. Mejias, J. Phys. Chem. B, 2005, 109, 15741–15748.
3. U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229.
4. C. Dette, M. A. Pérez-Osorio, C. S. Kley, P. Punke, C. E. Patrick, P. Jacobson, F. Giustino, S. J. Jung and K. Kern, Nano Lett., 2014, 14, 6533–6538.
5. J. Schneider, M. Matsuoka, M. Takeuchi, J. Zhang, Y. Horiuchi, M. Anpo and D. W. Bahnemann, Chem. Rev., 2014, 114, 9919–9986.
6. S. El-Sherbiny, F. Morsy, M. Samir and O. A. Fouad, Appl. Nanosci., 2014, 4, 305–313.
7. A. Fujishima and K. Honda, Bull. Chem. Soc. Jpn., 1971, 44, 1148–1150.
8. J. Nowotny, T. Bak, M. Nowotny and L. Sheppard, J. Phys. Chem. B, 2006, 110, 18492–18495.
9. J. Nowotny, T. Bak, M. Nowotny and L. Sheppard, Int. J. Hydrogen Energy, 2007, 32, 2651–2659.
10. M. G. Walter, E. L. Warren, J. R. McKone, S. W. Boettcher, Q. Mi, E. A. Santori and N. S. Lewis, Chem. Rev., 2010, 110, 6446–6473.
11. H. Kazuhito, I. Hiroshi and F. Akira, Jpn. J. Appl. Phys., 2005, 44, 8269.
12. R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271.
13. S. U. Khan, M. Al-Shahry and W. B. Ingler, Science, 2002, 297, 2243–2245.
14. J. Nowotny, C. Sorrell, T. Bak and L. Sheppard, Sol. Energy, 2005, 78, 593–602.
15. M. Grätzel, Nature, 2001, 414, 338.
16. J. L. Young, M. A. Steiner, H. Döscher, R. M. France, J. A. Turner and T. G. Deutsch, Nat. Energy, 2017, 2, 17028.
17. M. Ni, M. K. Leung, D. Y. Leung and K. Sumathy, Renewable Sustainable Energy Rev., 2007, 11, 401–425.
18. X. Lu, S. Xie, H. Yang, Y. Tong and H. Ji, Chem. Soc. Rev., 2014, 43, 7581–7593.
19. C. Sun, L.-M. Liu, A. Selloni, G. Q. M. Lu and S. C. Smith, J. Mater. Chem., 2010, 20, 10319–10334.
20. L. Walle, A. Borg, E. Johansson, S. Plogmaker, H. Rensmo, P. Uvdal and A. Sandell, J. Phys. Chem. C, 2011, 115, 9545–9550.
21. G. Ketteler, S. Yamamoto, H. Bluhm, K. Andersson, D. E. Starr, D. F. Ogletree, H. Ogasawara, A. Nilsson and M. Salmeron, J. Phys. Chem. C, 2007, 111, 8278–8282.
22. C. Dette, M. A. Pérez-Osorio, S. Mangel, F. Giustino, S. J. Jung and K. Kern, J. Phys. Chem. C, 2018, 11954–11960.
23. I. M. Nadeem, J. P. W. Treacy, S. Selcuk, X. Torrelles, H. Hussain, A. Wilson, D. C. Grinter, G. Cabailh, O. Bikondoa, C. Nicklin, A. Selloni, J. Zegenhagen, R. Lindsay and G. Thornton, J. Phys. Chem. Lett., 2018, 9, 3131–3136.
24. H. Perron, J. Vandenborre, C. Domain, R. Drot, J. Roques, E. Simoni, J.-J. Ehrhardt and H. Catalette, Surf. Sci., 2007, 601, 518–527.
25. M. B. Hugenschmidt, L. Gamble and C. T. Campbell, Surf. Sci., 1994, 302, 329–340.
26. H. Ali, R. Seidel, M. N. Pohl and B. Winter, Chem. Sci., 2018, 9, 4511–4523.
27. M. A. Brown, A. Beloqui Redondo, M. Sterrer, B. Winter, G. Pacchioni, Z. Abbas and J. A. van Bokhoven, Nano Lett., 2013, 13, 5403–5407.
28. M. A. Brown, I. Jordan, A. B. Redondo, A. Kleibert, H. J. Wörner and J. A. van Bokhoven, Surf. Sci., 2013, 610, 1–6.
29. M. A. Brown, R. Seidel, S. Thürmer, M. Faubel, J. C. Hemminger, J. A. van Bokhoven, B. Winter and M. Sterrer, Phys. Chem. Chem. Phys., 2011, 13, 12720–12723.
30. K. Andersson, G. Ketteler, H. Bluhm, S. Yamamoto, H. Ogasawara, L. G. Pettersson, M. Salmeron and A. Nilsson, J. Am. Chem. Soc., 2008, 130, 2793–2797.
31. S. Yamamoto, H. Bluhm, K. Andersson, G. Ketteler, H. Ogasawara, M. Salmeron and A. Nilsson, J. Phys.: Condens. Matter, 2008, 20, 184025.
32. S. Yamamoto, T. Kendelewicz, J. T. Newberg, G. Ketteler, D. E. Starr, E. R. Mysak, K. J. Andersson, H. Ogasawara, H. Bluhm and M. Salmeron, J. Phys. Chem. C, 2010, 114, 2256–2266.
33. S. Axnanda, E. J. Crumlin, B. Mao, S. Rani, R. Chang, P. G. Karlsson, M. O. Edwards, M. Lundqvist, R. Moberg and P. Ross, Sci. Rep., 2015, 5, 9788.
34. A. Kolmakov, D. A. Dikin, L. J. Cote, J. Huang, M. K. Abyaneh, M. Amati, L. Gregoratti, S. Günther and M. Kiskinova, Nat. Nanotechnol., 2011, 6, 651–657.
35. J. Kraus, R. Reichelt, S. Günther, L. Gregoratti, M. Amati, M. Kiskinova, A. Yulaev, I. Vlassiouk and A. Kolmakov, Nanoscale, 2014, 6, 14394–14403.
36. T. Petit, J. Ren, S. Choudhury, R. Golnak, S. S. Lalithambika, M. F. Tesch, J. Xiao and E. F. Aziz, Adv. Mater. Interfaces, 2017, 4, 1700755.
37. T. Luttrell, S. Halpegamage, J. Tao, A. Kramer, E. Sutter and M. Batzill, Sci. Rep., 2014, 4, 4043.
38. K. I. Hadjiivanov and D. G. Klissurski, Chem. Soc. Rev., 1996, 25, 61–69.
39. L. Kavan, M. Grätzel, S. Gilbert, C. Klemenz and H. Scheel, J. Am. Chem. Soc., 1996, 118, 6716–6723.
40. A. Barnard and L. Curtiss, Nano Lett., 2005, 5, 1261–1266.
41. A. Vittadini, A. Selloni, F. Rotzinger and M. Grätzel, Phys. Rev. Lett., 1998, 81, 2954.
42. Z.-H. Cui, F. Wu and H. Jiang, Phys. Chem. Chem. Phys., 2016, 18, 29914–29922.
43. T. Sham and M. Lazarus, Chem. Phys. Lett., 1979, 68, 426–432.
44. S. Wendt, J. Matthiesen, R. Schaub, E. K. Vestergaard, E. Lægsgaard, F. Besenbacher and B. Hammer, Phys. Rev. Lett., 2006, 96, 066107.
45. J. Blomquist, L. E. Walle, P. Uvdal, A. Borg and A. Sandell, J. Phys. Chem. C, 2008, 112, 16616–16621.
46. L. Walle, A. Borg, P. Uvdal and A. Sandell, Phys. Rev. B, 2009, 80, 235436.
47. J. Balajka, M. A. Hines, W. J. DeBenedetti, M. Komora, J. Pavelec, M. Schmid and U. Diebold, Science, 2018, 361, 786–789.
48. J. Balajka, U. Aschauer, S. F. Mertens, A. Selloni, M. Schmid and U. Diebold, J. Phys. Chem. C, 2017, 121, 26424–26431.
49. M. J. Jackman, A. G. Thomas and C. Muryn, J. Phys. Chem. C, 2015, 119, 13682–13690.
50. T. L. Thompson and J. T. Yates, Top. Catal., 2005, 35, 197–210.
51. M. J. Makowski, R. P. Galhenage, J. Langford and J. C. Hemminger, J. Phys. Chem. Lett., 2016, 7, 1732–1735.
52. F. Hossain, G. Murch, L. Sheppard and J. Nowotny, Adv. Appl. Ceram., 2007, 106, 95–100.
53. H. Zhao, F. Pan and Y. Li, Journal of Materiomics, 2017, 3, 17–32.
54. S. Benkoula, O. Sublemontier, M. Patanen, C. Nicolas, F. Sirotti, A. Naitabdi, F. Gaie-Levrel, E. Antonsson, D. Aureau and F.-X. Ouf, Sci. Rep., 2015, 5, 15088.
55. Z.-T. Wang, Y.-G. Wang, R. Mu, Y. Yoon, A. Dahal, G. K. Schenter, V.-A. Glezakou, R. Rousseau, I. Lyubinetsky and Z. Dohnálek, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1801–1805.
56. U. Diebold, J. Chem. Phys., 2017, 147, 040901.
57. Y. He, A. Tilocca, O. Dulub, A. Selloni and U. Diebold, Nat. Mater., 2009, 8, 585.
58. D. Duncan, F. Allegretti and D. Woodruff, Phys. Rev. B, 2012, 86, 045411.
59. T. Zheng, C. Wu, M. Chen, Y. Zhang and P. T. Cummings, J. Chem. Phys., 2016, 145, 044702.
60. P. Schindler and H. Gamsjäger, Colloid Polym. Sci., 1972, 250, 759–763.
61. J. Cheng and M. Sprik, J. Chem. Theory Comput., 2010, 6, 880–889.
62. R. Seidel, M. N. Pohl, H. Ali, B. Winter and E. F. Aziz, Rev. Sci. Instrum., 2017, 88, 073107.
63. L. Vayssieres, C. Persson and J.-H. Guo, Appl. Phys. Lett., 2011, 99, 183101.
64. C. Sentein, B. Guizard, S. Giraud, C. Yé and F. Ténégal, J. Phys.: Conf. Ser., 2009, 170, 012013.
65. R. Golnak, J. Xiao, K. Atak, I. Unger, R. Seidel, B. Winter and E. F. Aziz, J. Phys. Chem. A, 2016, 120, 2808–2814.
66. R. Golnak, S. I. Bokarev, R. Seidel, J. Xiao, G. Grell, K. Atak, I. Unger, S. Thürmer, S. G. Aziz and O. Kühn, Sci. Rep., 2016, 6, 2808–2814.
67. R. G. Burns and R. G. Burns, Mineralogical applications of crystal field theory, Cambridge University Press, 1993.
68. J. Crocombette and F. Jollet, J. Phys.: Condens. Matter, 1994, 6, 10811.
69. F. De Groot, M. Figueiredo, M. Basto, M. Abbate, H. Petersen and J. Fuggle, Phys. Chem. Miner., 1992, 19, 140–147.
70. G. S. Henderson, F. M. De Groot and B. J. Moulton, Rev. Mineral. Geochem., 2014, 78, 75–138.
71. R. Seidel, K. Atak, S. Thürmer, E. F. Aziz and B. Winter, J. Phys. Chem. B, 2015, 119, 10607–10615.
72. A. Henningsson, H. Rensmo, A. Sandell, H. Siegbahn, S. Södergren, H. Lindström and A. Hagfeldt, J. Chem. Phys., 2003, 118, 5607–5612.
73. B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 139–150.
74. M. A. Brown, B. Winter, M. Faubel and J. C. Hemminger, J. Am. Chem. Soc., 2009, 131, 8354–8355.
75. T. Fransson, Y. Harada, N. Kosugi, N. A. Besley, B. Winter, J. J. Rehr, L. G. M. Pettersson and A. Nilsson, Chem. Rev., 2016, 116, 7551–7569.
76. A. Thomas, W. Flavell, A. Mallick, A. Kumarasinghe, D. Tsoutsou, N. Khan, C. Chatwin, S. Rayner, G. Smith and R. Stockbauer, Phys. Rev. B, 2007, 75, 035105.
77. A. A. Mosquera, J. L. Endrino and J. M. Albella, J. Anal. At. Spectrom., 2014, 29, 736–742.
78. R. Ruus, A. Kikas, A. Saar, A. Ausmees, E. Nommiste, J. Aarik, A. Aidla, T. Uustare and I. Martinson, Solid State Commun., 1997, 104, 199–203.
79. F. M. F. de Groot, M. Grioni, J. C. Fuggle, J. Ghijsen, G. A. Sawatzky and H. Petersen, Phys. Rev. B, 1989, 40, 5715–5723.
80. E. F. Aziz, N. Ottosson, M. Faubel, I. V. Hertel and B. Winter, Nature, 2008, 455, 89–91.
81. C. D. Cappa, J. D. Smith, B. M. Messer, R. C. Cohen and R. J. Saykally, J. Phys. Chem. A, 2007, 111, 4776–4785.
82. B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. Hertel, J. Phys. Chem. A, 2004, 108, 2625–2632.
83. J. Tossell, D. Vaughan and K. Johnson, Am. Mineral., 1974, 59, 319–334.
84. R. Seidel, B. Winter and S. E. Bradforth, Annu. Rev. Phys. Chem., 2016, 67, 283–305.
85. P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206.
86. N. Kurahashi, S. Karashima, Y. Tang, T. Horio, B. Abulimiti, Y.-I. Suzuki, Y. Ogi, M. Oura and T. Suzuki, J. Chem. Phys., 2014, 140, 174506.
87. N. Moustakas, A. Kontos, V. Likodimos, F. Katsaros, N. Boukos, D. Tsoutsou, A. Dimoulas, G. E. Romanos, D. Dionysiou and P. Falaras, Appl. Catal., B, 2013, 130, 14–24.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ta09414d

‡ Present address: Fritz-Haber-Institut der Max-Planck-Gesellschaft, Department of Interface Science, Faradayweg 4-6, D-14195 Berlin, Germany.

---