Open Access Article
Open Access ArticleDolomite: a low cost thermochemical energy storage material†
Terry D.
Humphries
 a,
Kasper T.
Møller
a,
Kasper T.
Møller
 a,
William D. A.
Rickard
a,
William D. A.
Rickard
 b,
M. Veronica
Sofianos
b,
M. Veronica
Sofianos
 a,
Shaomin
Liu
a,
Shaomin
Liu
 c,
Craig E.
Buckley
c,
Craig E.
Buckley
 a and
Mark
Paskevicius
a and
Mark
Paskevicius
 *a
*a
aPhysics and Astronomy, Fuels and Energy Technology Institute, Curtin University, GPO Box U1987, Perth, WA 6845, Australia. E-mail: mark.paskevicius@gmail.com
bJohn De Laeter Centre, Curtin University, GPO Box U1987, Perth, WA 6845, Australia
cDepartment of Chemical Engineering, Curtin University, Perth, 6102, Western Australia, Australia
First published on 13th December 2018
Abstract
The thermal energy storage properties of dolomite, CaMg(CO3)2, from three sources (commercial, mined, and synthetic) are investigated as a potential solid–gas thermochemical energy store for concentrating solar thermal power (CSP) plants. The reversible carbon dioxide release/absorption cycle can be used to store and release large quantities of thermal energy that can be harnessed near 550 °C. To enable carbon dioxide absorption, a novel molten salt eutectic NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 mixture was added to the dolomite, which proved effective. Curiously, the mined (unrefined) sample proved to have the best calcination/carbonation properties with a stable cyclic stability of ∼50 mol% CO2 over 10 cycles. A morphological investigation by scanning electron microscopy reveals the mined sample contains impurities (e.g. quartz) that prevent detrimental agglomeration of dolomite and its reaction products (CaCO3 and MgO). High levels of porosity in the mined dolomite also provide short gas–solid reaction pathways during carbonation. A commercial dolomite source contained too many impurities, resulting in the formation of high levels of Ca2SiO4 that acted as a Ca-sink, lowering CO2 capacity. Finally, a high purity synthetic dolomite sample displayed high levels of agglomeration and phase segregation, lowering reversible CO2 capacity, which was attributed to a lack of impurities that restrict agglomeration.
MgCl2 mixture was added to the dolomite, which proved effective. Curiously, the mined (unrefined) sample proved to have the best calcination/carbonation properties with a stable cyclic stability of ∼50 mol% CO2 over 10 cycles. A morphological investigation by scanning electron microscopy reveals the mined sample contains impurities (e.g. quartz) that prevent detrimental agglomeration of dolomite and its reaction products (CaCO3 and MgO). High levels of porosity in the mined dolomite also provide short gas–solid reaction pathways during carbonation. A commercial dolomite source contained too many impurities, resulting in the formation of high levels of Ca2SiO4 that acted as a Ca-sink, lowering CO2 capacity. Finally, a high purity synthetic dolomite sample displayed high levels of agglomeration and phase segregation, lowering reversible CO2 capacity, which was attributed to a lack of impurities that restrict agglomeration.
Introduction
Renewable energy sources are becoming cheaper and cost-competitive with fossil fuels. However, most renewable energy supplies still lack an energy storage solution, restricting them to intermittent operation based on variable energy fluxes (e.g. wind and solar).1 Concentrating solar thermal power (CSP) plants utilise solar power in a technologically simple manner to generate and store thermal energy, which is used to heat water and run a steam turbine based electrical generator.2 Currently, a number of 1st generation CSP plants utilise molten salt technology to store thermal energy via the specific heat of the liquid when heating from 290–565 °C.2,3 However, the specific heat capacity (150 kJ kg−1 per 100 °C) of state-of-the-art molten nitrate salts (40NaNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60KNO3) is low compared to other phase change or thermochemical energy storage options (Table 1). Most importantly, the low energy density requires large quantities of salt to store large amounts of energy, resulting in high overall energy storage costs despite its relatively low cost per kg (Fig. 1a). Thus, 2nd generation energy storage systems with higher energy density and operational temperature will offer lower overall CSP plant costs and higher technology uptake by industrial and commercial sectors.3
60KNO3) is low compared to other phase change or thermochemical energy storage options (Table 1). Most importantly, the low energy density requires large quantities of salt to store large amounts of energy, resulting in high overall energy storage costs despite its relatively low cost per kg (Fig. 1a). Thus, 2nd generation energy storage systems with higher energy density and operational temperature will offer lower overall CSP plant costs and higher technology uptake by industrial and commercial sectors.3
Molten salt (40NaNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 KNO3) 60 KNO3) |
MgH2 ⇄ Mg + H2 | CaH2 ⇄ Ca + H2 | MgCO3 ⇄ MgO + CO2 | CaCO3 ⇄ CaO + CO2 | CaMg(CO3)2 ⇄ MgO + CaCO3 + CO2 | |
|---|---|---|---|---|---|---|
| a Lower temperature. b To generate 1 TJ of electrical energy, parameters for pure material only. c Based on crystalline density. | ||||||
| Enthalpy ΔH (kJ mol−1 CO2 or H2) | 39.0 | 74.1 | 162.4 | 96.7 | 165.8 | 125.8 |
| Molar mass (g mol−1) | 94.60 | 26.33 | 42.10 | 84.31 | 100.09 | 184.40 |
| Density (g cm−3) | 2.17 | 1.42 | 1.7 | 2.96 | 2.71 | 2.85 |
| Capacity (wt% CO2 or H2) | — | 7.66 | 4.79 | 52.2 | 44.0 | 23.9 |
| Gravimetric energy density (kJ kg−1) | 413 | 2811 | 3857 | 1147 | 1657 | 682 |
| Volumetric energy densityc (MJ m−3) | 895 | 3995 | 6557 | 3396 | 4489 | 1944 |
| Operating temperature range (°C) | 290–565 | 300–400 | >1020 | ∼450 | >880 | ∼590 |
| Carnot efficiencya (%) | 46 | 47 | 77 | 58 | 74 | 65 |
| Estimated practical efficiency (%) | 27 | 27 | 52 | 35 | 49 | 41 |
| Mass requiredb (tonnes) | 5250 | 755 | 339 | 1500 | 819 | 2260 |
| Volume requiredb (m3) | 2420 | 532 | 199 | 507 | 302 | 793 |
| Materials cost ($ per tonne)13 | 630 | 3000 | 6000 | 500 | 60 | 60 |
| Total materials cost requiredb ($) | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 030![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
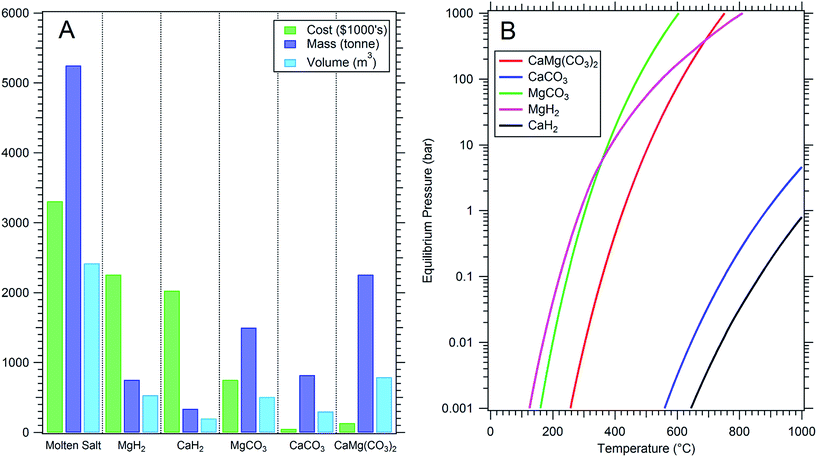 | ||
| Fig. 1 (A) Comparison of thermal energy storage options to generate 1 TJ of electrical energy (see legend for y axis labels). (B) Equilibrium pressure of thermochemical energy storage materials based on thermodynamics of reaction.11 | ||
There are a wide selection of chemicals available to replace molten salts as thermal energy storage materials, including: latent heat storage materials (phase change materials, PCMs) such as inorganic salts/salt eutectics and metals/metal alloys; solid sensible storage media such as concrete and ceramics, where the heat transfer fluid is circulated around the media; and also thermochemical materials such as metal hydrides and metal carbonates.3 Metal hydrides have been identified as promising thermochemical heat storage options for concentrating solar thermal power because of their impressive energy densities.4–7 Although metal hydrides have high material costs, it is offset by the low quantity of material necessary (Table 1, Fig. 1a).8 Therefore, metal hydrides offer potential cost savings over current generation molten salt technology.9 Despite the benefits of metal hydrides, they remain difficult to handle in air due to their sensitivity to oxygen and moisture. Significant cost savings for 2nd generation CSP plants may also be realised when considering much cheaper materials, including directly minable minerals such as metal carbonates (Table 1 and Fig. 1a). A recent techno-economic assessment determined the cost of various oxide and carbonates as thermal energy storage materials including dolomite.10 It noted that despite the low cost of the material, parasitic energy losses, including employing a gas compressor to store the CO2, would consume 82% of the energy produced, leading to a total capital cost of $82 per MJ. Cheaper storage of CO2 without compression must be considered including: operating at higher temperatures to promote gas operating pressures of above 64 bar (promoting liquefaction of CO2);14 or the use of low-temperature CO2 storage in another carbonate material.
A host of research has been conducted to investigate the mineral sequestration of carbon dioxide into metal oxides, forming metal carbonates.15 The process is reversible, where CO2 can be cycled in an out of the metal oxide, in highly exothermic and endothermic reactions. This process embodies the thermochemical process that can be harvested for thermal energy storage applications.4,9,16 In a CSP application, solar energy would heat a metal carbonate in the daytime, which absorbs energy (endothermic process) and releases CO2 forming a metal oxide. The CO2 would be stored in pressure vessels within this closed system. At night, when solar energy fades, CO2 would reabsorb into the metal oxide in an exothermic process, generating heat. In fact, the entire process is self-limiting, governed by the thermodynamics of the solid–gas reactions, which define a temperature dependent equilibrium pressure (Fig. 1b).
Carbonate rocks such as magnesite (MgCO3), calcite (CaCO3) and dolomite (CaMg(CO3)2) form approximately 20% of the sedimentary crust on the Earth.17 The abundance and basic processing requirements result in extremely low materials costs. Crushed limestone (mostly CaCO3) was sold on the gigatonne scale in the USA in 2001 at $5.19 per tonne on average, whereas dolomite had a value of $5.64 per tonne.18 Calcined products, high-calcium quicklime (CaO) and dolomitic quicklime (CaO, MgO) are produced at moderate purity (>95%) with a value of approximately $60 per tonne, whereas magnesia (MgO) is more expensive, ranging from $90–500 per tonne, varying based on purity and source. The thermodynamics of calcination and carbonation are well-known:11
| MgCO3 ⇄ MgO + CO2 | (1) |
| ΔH1bar = 98.9 kJ mol−1 CO2, ΔS1bar = 171.3 J mol−1 CO2/K |
| CaCO3 ⇄ CaO + CO2 | (2) |
| ΔH1bar = 165.8 kJ mol−1 CO2, ΔS1bar = 143.0 J mol−1 CO2/K |
| CaMg(CO3)2 ⇄ MgO + CaCO3 + CO2 | (3) |
| ΔH1bar = 126.2 kJ mol−1 CO2, ΔS1bar = 180.6 J mol−1 CO2/K. |
Here, the bimetallic carbonate, dolomite, CaMg(CO3)2, only releases one unit of CO2, before forming more stable CaCO3, which will not decompose until temperatures >800 °C.
Dolomite offers a thermodynamic stabilisation in comparison to MgCO3, where the carbon dioxide is released at a higher temperature from the bimetallic material. Conveniently, once carbon dioxide is released, only stable metal oxides or carbonates remain in the solid-phase, reducing problems seen in other thermochemical heat storage materials at high temperatures due to kinetically hindering agglomeration and metallic vaporisation.8,9
During the carbonation of metal oxides an impervious (or diffusion limiting) metal carbonate layer can form that restricts further CO2 absorption.19,20 As such, the reaction kinetics of carbonation are governed by particle size, pore structure and surface area. A major problem is the cyclic stability, or reversibility, of carbonation and calcination reactions, as ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles are required over the 30 year operating lifetime of a CSP plant.2 An example is CaO/CaCO3, which only retains 7–8 wt% CO2 capacity after 500 cycles.21 Natural CaO–MgO sorbents (20–40 μm) derived from dolomite have previously been investigated for CO2 capture, but displayed no carbonation of MgO and poor cycling capacity in the CaO/CaCO3 component of the sample (∼60% reversible carbonation after 50 cycles).22 In general, very poor carbonation rates are observed for MgO (<25%),19 which have been shown to improve in the presence of high pressure steam, but cycling studies have yet to be conducted.
000 cycles are required over the 30 year operating lifetime of a CSP plant.2 An example is CaO/CaCO3, which only retains 7–8 wt% CO2 capacity after 500 cycles.21 Natural CaO–MgO sorbents (20–40 μm) derived from dolomite have previously been investigated for CO2 capture, but displayed no carbonation of MgO and poor cycling capacity in the CaO/CaCO3 component of the sample (∼60% reversible carbonation after 50 cycles).22 In general, very poor carbonation rates are observed for MgO (<25%),19 which have been shown to improve in the presence of high pressure steam, but cycling studies have yet to be conducted.
Sodium nitrate (NaNO3) has been heralded as a molten-salt based catalyst for dolomite and other MgO-containing CO2 absorbents.23,24 Zhang et al. studied its effect in detail and provided an illustrative schematic of the process.23 In general, the mechanism promoting CO2 absorption relies on the low melting point of NaNO3 (306.5 °C), where CO2 absorption correlates with the presence of a liquid phase, even below the melting point in the presence of “pre-melting” or “surface melting”.23 Carbon dioxide adsorbs onto the surface of an MgO particle and then migrates to the phase boundary between solid MgO and liquid NaNO3, where the molten salt promotes reactivity and the formation of a metal carbonate. Here, the catalytic effect is assigned to the slight solubility of MgO,25,26 CO2,27 and other carbonate components (such as CaCO3) in the molten salt surface layer, where they gain enhanced mobility and can precipitate out as a double-salt, e.g. dolomite. Note that NaNO3 decomposes above 570 °C.28,29 Therefore, in the present work the performance of a new, higher temperature molten salt system (NaCl/MgCl2) is studied as an alternative. It is noted that the addition of 20 wt% salt additive will decrease the reported energy density (546 kJ kg−1 instead of 682 kJ kg−1) in Table 1 and will also affect the system cost.
Experimental
Mined dolomite, CaMg(CO3)2, was supplied from commercial supplier Richgro and mine site Watheroo Dolomitic Lime, WA, Australia (samples: Rich-A, Wath-A). Subsequently, these dolomite samples were heated from RT to 1000 °C at a rate of 6.5 °C min−1 and held isothermal for 1 h under an Ar flow of 2 L min−1 to form predominantly CaO and MgO (calcined samples: Rich-B, Wath-B). As a reference, a high purity synthetic sample was prepared: metal nitrate precursors were supplied from Sigma-Aldrich, Mg(NO3)2·6H2O (99%) and Ca(NO3)2·4H2O (99%). A 1 M aqueous solution of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Mg(NO3)2 and Ca(NO3)2 was heated to 115 °C in vacuo, while stirring, to uniformly co-crystallise the reagents. The resulting white powder was subsequently heated from RT to 650 °C at a rate of 5 °C min−1 and held isothermal for 3 h under an Ar flow of 2 L min−1, to form the corresponding metal oxides (MgO and CaO; sample: Synth-B). A eutectic mixture of 0.438MgCl2
1 Mg(NO3)2 and Ca(NO3)2 was heated to 115 °C in vacuo, while stirring, to uniformly co-crystallise the reagents. The resulting white powder was subsequently heated from RT to 650 °C at a rate of 5 °C min−1 and held isothermal for 3 h under an Ar flow of 2 L min−1, to form the corresponding metal oxides (MgO and CaO; sample: Synth-B). A eutectic mixture of 0.438MgCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.562NaCl (m.p. 442 °C)30 was ground within an argon glovebox (mBraun < 1 ppm H2O, O2) and mixed in a mortar and pestle with samples Synth-B and Wath-B in a 20 wt% loading. An overview of samples and preparation/treatment methods is given in Table 2.
0.562NaCl (m.p. 442 °C)30 was ground within an argon glovebox (mBraun < 1 ppm H2O, O2) and mixed in a mortar and pestle with samples Synth-B and Wath-B in a 20 wt% loading. An overview of samples and preparation/treatment methods is given in Table 2.
| Sample | Sample name | Primary content | Temperature | Time | Gas | Catalyst |
|---|---|---|---|---|---|---|
| As supplied | ||||||
| Richgro dolomite | Rich-A | CaMg(CO3)2 | — | — | — | — |
| Watheroo dolomite | Wath-A | CaMg(CO3)2 | — | — | — | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Thermally outgassed | ||||||
| Synthetic CaO/MgO | Synth-B | MgO/CaO | 650 °C | 3 h | — | — |
| Synthetic CaO/MgO (with catalyst) | Synth-B-cat | MgO/CaO | 650 °C | 3 h | — | NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 MgCl2 |
| Calcined Richgro (from Rich-A) | Rich-B | MgO/CaO | 1000 °C | 1 h | — | — |
| Calcined Watheroo (from Wath-A) | Wath-B | MgO/CaO | 1000 °C | 1 h | — | — |
| Calcined Watheroo (from Wath-A, with catalyst) | Wath-B-cat | MgO/CaO | 1000 °C | 1 h | — | NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 MgCl2 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Carbonated (single-step 50 bar CO 2 ) | ||||||
| Carbonated synthetic (from Synth-B) | Synth-C | MgO/CaCO3 | 500 °C | 54 h | CO2 | — |
| Carbonated synthetic (from Synth-B, with catalyst) | Synth-C-cat | CaMg(CO3)2 | 500 °C | 8 h | CO2 | NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 MgCl2 |
| Re-carbonated Watheroo (from Wath-B) | Wath-C | MgO/CaCO3 | 500 °C | 18 h | CO2 | — |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| CO 2 cycled | ||||||
| 11-Times cycled Watheroo (from Wath-B-cat in the absorbed state) | Wath-D-cat | CaMg(CO3)2/MgO/CaCO3 | 450–550 °C | 110 h | CO2 | NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 MgCl2 |
| 14-Times cycled synthetic (from Synth-B-cat in the absorbed state) | Synth-D-cat | CaMg(CO3)2/MgO/CaCO3 | 550 °C | 450 h | CO2 | NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 MgCl2 |
X-Ray diffraction (XRD) was performed using a Bruker D8 Advance diffractometer equipped with a CuKα1,2 source in flat-plate geometry mode. Salt-containing samples were analysed in an argon-filled poly(methyl methacrylate) dome, which results in a broad hump in the diffraction background around 2θ = 20°. Data were collected using a Lynxeye PSD detector from 5–80° 2θ at 0.04° s−1. In situ synchrotron powder X-ray diffraction (SR-XRD) was performed at the Powder Diffraction (PD) beamline at the Australian Synchrotron in Melbourne, Australia.31 The annealed powder was loaded in a quartz capillary (outer diameter 0.7 mm, wall thickness 0.01 mm) while inside a glove box, and mounted to a sample holder constructed from Swagelok tube fittings using a graphite ferrule. The sample holder was then connected to a vacuum manifold and the capillary heated with a hot air blower with a heating rate of 6 °C min−1 under a static argon environment. One-dimensional SR-XRD patterns (monochromatic X-rays with λ = 0.8263076 Å) were continuously collected using a Mythen microstrip detector32 with an exposure time of 30 s for each of two detector positions. The capillary was continuously oscillated through 100° during exposure to improve the powder averaging and ensure even heating. Diffraction patterns were quantitatively analysed with the Rietveld method33 using TOPAS (Bruker-AXS).
Scanning Electron Microscopy (SEM) was undertaken on a Tescan Lyra3 field emission microscope coupled with secondary electron (SE) and backscattered electron (BSE) detectors, and an Oxford Instruments Energy Dispersive Spectroscopy (EDS) detector. Samples were sputter coated with 5 nm of Pt and were either dispersed as a powder or embedded in epoxy resin and mechanically polished using an ethanol working fluid before imaging.
Nitrogen (N2) adsorption/desorption measurements were performed at 77 K using a Micromeritics ASAP 3020 system (Micromeritics, Nor-cross, GA, USA) to determine the specific surface area and the porosity of the samples. N2 adsorption data, at relative pressures (P/P0) between 0.05 and 0.30, were used to calculate the specific surface area by employing the Brunauer–Emmett–Teller (BET) multi-point method.34 The Barrett–Joyner–Halenda (BJH) method from the absorption branch of the isotherm35 was used to calculate the pore size distributions and volumes in the macro- (>50 nm) and meso-ranges (2–50 nm).
Simultaneous Differential Scanning Calorimetry-Thermogravimetric Analysis (DSC-TGA) was performed on a Mettler Toledo DSC 1 instrument using sample masses of ∼10 mg. Samples were measured at a heating rate of 10 °C min−1 under an argon flow of 20 mL min−1. The temperature accuracy of this instrument is ±0.2 °C, while the balance has an accuracy of ±20 μg.
Cyclic measurements of CO2 absorption/desorption were performed on a High Energy PCTpro E&E at 450–550 °C for >10 cycles. Desorption was carried out under an initial back pressure of 2 bar CO2 into a reservoir volume of 165 cm3. Absorption was carried out under an initial pressure of 30 bar CO2 in a reservoir volume of 12.3 cm3. The digital pressure transducer (Rosemount 3051S) had a precision and accuracy of 14 mbar. Room temperature measurements were recorded using a 4-wire platinum resistance temperature detector (RTD) while sample temperatures were measured using a K-type thermocouple.
Results and discussion
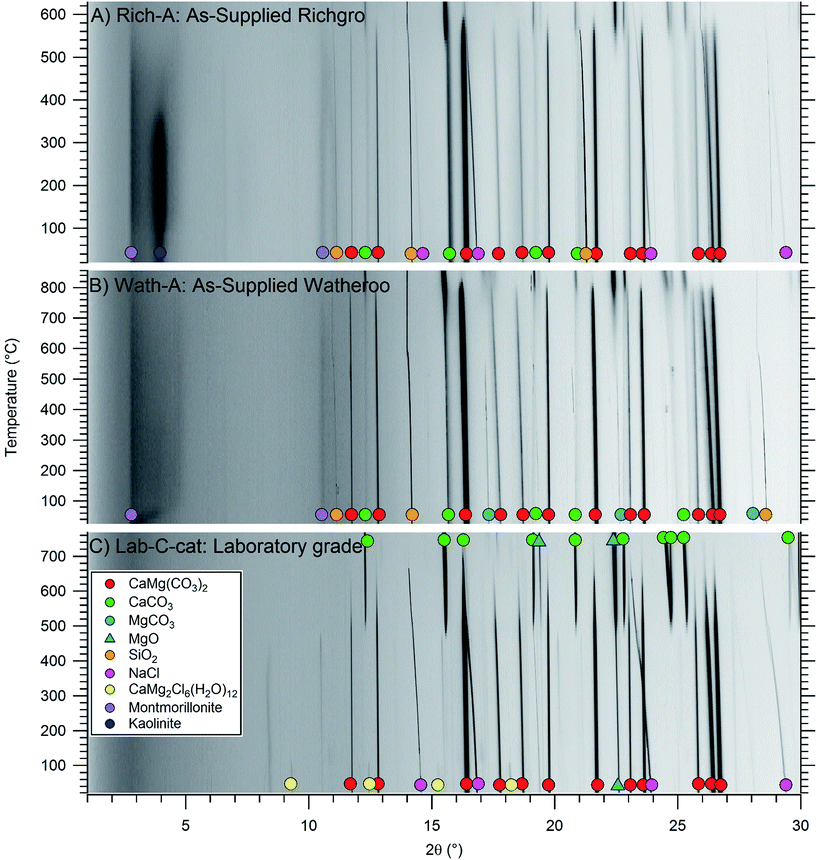
Mined dolomite samples (Rich-A and Wath-A) were analysed, as calcite (CaCO3), magnesite (MgCO3), quartz (SiO2), and additional silicates. Analysis of the crystalline component of the samples showed high purity dolomite for the Watheroo batch (91.8 wt%), but lower purity for the Richgro batch (70.8 wt%). The problem with impurities, especially silicates, becomes apparent when the dolomite samples are calcined at 1000 °C (Rich-B and Wath-B) where silicates react with the calcium-rich components to form larnite (Ca2SiO4) and/or tricalcium aluminate (Ca3Al2O6). Here, calcium is effectively leached from the active carbonate/oxide component of the samples and trapped in a thermodynamic sink (Fig. S2†). Table 3 shows that sample Rich-B only contains 5.1 wt% CaO and Wath-B contains 27.8 wt% CaO, compared to an ideal 58.2 wt% CaO content. In contrast, the Synth-B sample has a 57.7 wt% CaO, close to the theoretical quantity. Irreversible containment of CaO in silicates obviously makes it impossible to carbonate (with CO2 gas) the samples back to their original dolomite content.| Carbonates and oxides | Silicates and aluminates | Salts | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dolomite CaMg(CO3)2 | Calcite CaCO3 | Magnesite MgCO3 | Lime CaO | Magnesia MgO | Montmorillonitea | Gehlenitea | Andraditea | Ca3Al2O6 | Quartz SiO2 | Kaolinite Al2Si2O5(OH)4 | Larnite Ca2SiO4 | Halite NaCl | CaCl2 | CaMg2Cl6(H2O)12 | |
| a Montmorillonite is (Na,Ca)0.33(Al,Mg)2(Si4O10)(OH)2·nH2O, gehlenite is Ca2Al2SiO7, andradite is Ca3Fe2Si3O12. | |||||||||||||||
| As supplied | |||||||||||||||
| Rich-A: Richgro dolomite | 70.8(6) | 9.8(2) | — | — | — | 4.5(4) | — | — | — | 5.2(2) | 8.3(6) | — | 1.31(5) | — | |
| Wath-A: Watheroo dolomite | 91.8(6) | 2.37(9) | 3.0(1) | — | — | 1.1(2) | — | — | — | 1.70(7) | — | — | — | — | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| Thermally outgassed | |||||||||||||||
| Rich-B: Richgro (Rich-A: 1000 °C, Ar) | — | — | — | 5.1(1) | 33.6(3) | — | 5.0(5) | 4.1(2) | — | 3.87(9) | — | 47.8(4) | 0.7(1) | — | |
| Wath-B: Watheroo (Wath-A: 1000 °C, Ar) | — | — | — | 27.8(3) | 34.8(4) | — | — | — | 6.7(4) | 1.31(4) | — | 29.4(6) | — | — | |
| Synth-B: synthetic (650 °C, Ar) | — | — | — | 57.7(2) | 42.3(2) | — | — | — | — | — | — | — | — | — | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| Carbonated (500 °C, single-step 50 bar CO 2 ) | |||||||||||||||
| Wath-C: Watheroo (Wath-B, no catalyst) | — | 47.0(3) | — | — | 28.9(2) | — | — | — | 1.3(2) | 1.62(6) | — | 21.2(3) | — | — | |
| Synth-C: synthetic (Synth-B, no catalyst) | — | 57.6(5) | — | 11.4(1) | 31.0(3) | — | — | — | — | — | — | — | — | — | |
Synth-C-cat: synthetic + catalyst (Synth-B, NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2) MgCl2) |
93.0(1) | — | — | — | 2.07(6) | — | — | — | — | — | — | — | 3.09(7) | 1.9(1) | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||
| CO 2 cycled | |||||||||||||||
| Wath-D-cat | 31.0(2) | 33.0(9) | 19.1(6) | 8.7(5) | 0.4(1) | 6.4(4) | 1.5(4) | — | |||||||
| Synth-D-cat | 14.3(2) | 49.3(2) | 26.8(2) | — | — | — | — | — | — | 6.2(1) | 3.4(2) | — | |||
A single-step carbonation of thermally outgassed samples (Wath-B, Synth-B) was attempted at 500 °C and 50 bar CO2 (18–54 h). X-Ray diffraction results of the carbonated samples (Wath-C, Synth-C), presented in Table 3 and Fig. S3,† demonstrate that carbonation was successful, but only for the CaO portion of the sample, where MgO proved to be unreactive under these conditions. From a thermodynamic viewpoint, the reaction between CO2 and pure MgO should not occur at 500 °C and 50 bar CO2 (173 bar CO2 is required, Fig. 1b and reaction (1)).11 This has previously been shown in the literature for MgO, as discussed in the introduction. However, the formation of dolomite from CaO, MgO, and CO2 only requires 8 bar of CO2 at 500 °C (Fig. 1b and reaction (3)).11 Hence, the dolomite formation reaction is a thermodynamically destabilised pathway. Unfortunately, it is apparent that dolomite is not formed at 500 °C and 50 bar CO2 due to a kinetic barrier, despite favourable thermodynamics.
The addition of a novel molten salt catalyst (NaCl/MgCl2) to the synthetic batch (Synth-C-cat) allows for near complete conversion to dolomite (Table 3, Fig. S4†). The (0 1 5) Bragg ordering reflection for dolomite is present at ∼18.8° 2θ in the synthetic dolomite diffraction data displayed in Fig. 2, which would not be present for magnesium-rich calcite, thus proving the formation of crystallographically ordered dolomite.36 The molten salt acts as a catalyst to dolomite formation, overcoming the kinetic barrier to CO2 absorption, presumably due to its capability of dissolving reactants. Thus, the metal halide eutectic salt mixture is an effective carbonation catalyst for dolomite.
Fig. 2 illustrates in situ powder XRD patterns obtained during thermolysis of the dolomite samples Rich-A, Wath-A, and Synth-C-cat, heated to 850 °C under argon. During thermal treatment the dolomite gradually decomposes to form MgO and CaCO3. The commercial dolomite samples begin decomposition at higher temperatures (Rich-A: 550 °C, Wath-A: 800 °C) than the synthetic dolomite (Synth-C-cat: 500 °C), which also decomposes more gradually. Interestingly, both larnite (Ca2SiO4) and Ca3Al2O6 are not observed at these temperatures, in contrast to their large crystalline fraction after heat treatment at 1000 °C (in Rich-B and Wath-B). This is advantageous as calcium is still present as CaCO3 and can still react to form dolomite upon re-carbonation. The synthetic sample Synth-C-cat is shown in Fig. 2c, with the RT diffraction pattern illustrating the high dolomite content, with traces of received, by X-ray diffraction (Fig. S1,†Table 3), primarily showing dolomite, CaMg(CO3)2, but also a minor content of MgO and the salt-based catalyst. One of the salt phases is hydrated after air exposure, but more interestingly it has the composition CaMg2Cl6(H2O)12. The originally added catalytic salt was a mixture of NaCl and MgCl2, but CaCl2 forms during calcination, likely through a known metathesis reaction between MgCl2 and CaO.37 The NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 eutectic has a melting point of 442 °C (0.562
MgCl2 eutectic has a melting point of 442 °C (0.562![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.438), but there is also an eutectic in the NaCl
0.438), but there is also an eutectic in the NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaCl2 system at 504 °C (0.479
CaCl2 system at 504 °C (0.479![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.521),38 which may also act as an active carbonation catalyst.
0.521),38 which may also act as an active carbonation catalyst.
Fig. 3 illustrates TGA data collected for each of the dolomite samples from the in situ powder XRD study (Rich-A, Wath-A, Synth-C-cat). Each of the samples indicate a lower temperature of decomposition than previously observed for natural dolomite (typically 700–850 °C) under argon flow.39,40 This is most likely due to the heating rate, the quantity of impurities, and the particle size variation between various batches of dolomite. This variation has been well documented in previous studies.39,40 The mass losses measured during heating are consistent with the expected mass losses calculated from Rietveld analysis (Table 3) assuming full decomposition of dolomite. The synthetic sample (Synth-C-cat) loses 36 wt%, compared to the theoretically expected 38 wt% (considering the 20 wt% catalyst). The Richgro and Watheroo samples also show mass losses close to their expected content (Rich-A: 35 wt% loss when expecting 34 wt%, and Wath-A: 44 wt% loss when expecting 44 wt%). The decomposition kinetics of all three samples differ dramatically. The Watheroo batch (Wath-A) exhibits a rapid single-step decomposition near 700 °C, with a minor mass loss at 550 °C. Whereas, the Richgro batch (Rich-A) exhibits a slow single-step mass loss from 500–700 °C. The synthetic catalysed dolomite (Synth-C-cat) exhibits a two-step decomposition (at 475 and 650 °C) before a slight mass loss at high temperature (>800 °C), which is likely due to vaporisation of the molten salt. It is clear that complete calcination is observed in all samples by 800 °C.
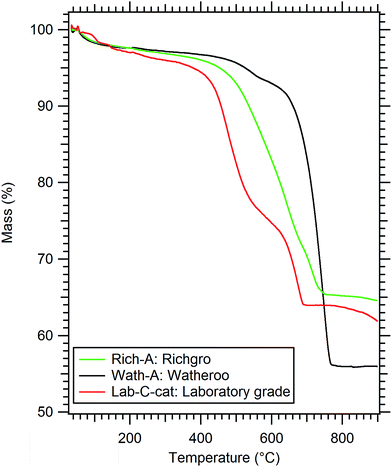 | ||
| Fig. 3 Thermogravimetric analysis (TGA) of dolomite materials under 1 bar Ar flow, heated at 10 °C min−1. | ||
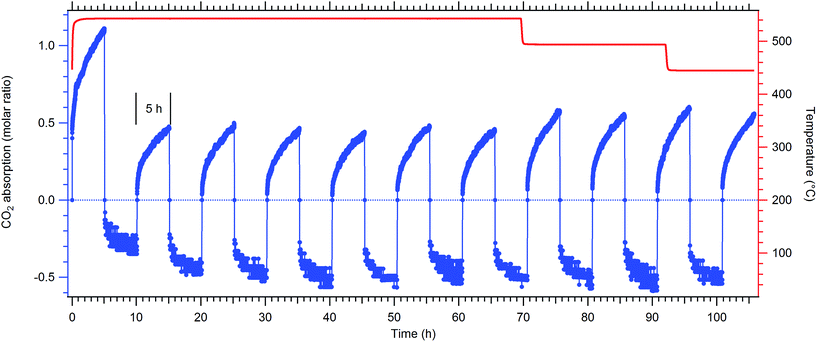
To assess the cyclic CO2 capacity and thermochemical reversibility of the samples, cyclic pressure measurements were performed (Fig. 4, S5 and Table S1†). Since the reformation of dolomite only occurs with the addition of 20 wt% NaCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MgCl2 as a catalyst, cycling tests were performed on catalysed versions of calcined samples, starting from the oxide-rich/CO2 depleted state (Synth-B-cat and Wath-B-cat). The Richgro sample (Rich-B) was omitted due to its very low content of CaO (5.1 wt%, see Table 3).
MgCl2 as a catalyst, cycling tests were performed on catalysed versions of calcined samples, starting from the oxide-rich/CO2 depleted state (Synth-B-cat and Wath-B-cat). The Richgro sample (Rich-B) was omitted due to its very low content of CaO (5.1 wt%, see Table 3).
Absorption of CO2 in the Watheroo sample (Wath-B-cat, Fig. 4 and Table S1†) reveals that more CO2 is absorbed on the first cycle compared to the following 10 cycles. The first cycle involves carbonation of CaO, which is not formed again during CO2 cycling at these pressures and temperatures, where instead CaCO3 is the more thermodynamically stable compound. The quantity of CO2 absorbed and desorbed during subsequent cycles is consistently ∼50% of the theoretical capacity (of reaction (3)) over 5 h. For the eighth absorption, the temperature was reduced to 500 °C and again on the tenth cycle to 450 °C, for which a slight increase in cyclic capacity is observed (∼60% of theoretical capacity). For each of the 11 cycles, the kinetics of absorption and desorption are both slow, with an absorption plateau not being reached within the five hours of data collection, likely due to a diffusion limited process.
After cycling, XRD of the sample in the absorbed state (Wath-D-cat, Table 3, Fig. S6†) indicates that it contains 31.0 wt% dolomite, 19.1 wt% MgO, 33.0 wt% CaCO3, along with 8.7 wt% andradite, 0.4 wt% quartz, 6.4 wt% halite and 1.5 wt% CaCl2. These results illustrate that the catalyst enables dolomite formation, similar to the synthetic sample (Synth-C-cat), in contrast to the single-step carbonation at 500 °C (Wath-C, Table 3).
The synthetic sample (Synth-B-cat) was cycled 14 times at 550 °C (Synth-D-cat, Fig. S5 and Table S1†). The initial carbonation under 35 bar CO2 showed ∼1.75 mol. equivalent absorption (87.5% theoretical capacity, including the carbonation of CaO) although subsequent absorptions only allowed for ∼0.25 mol equivalent of CO2 uptake (25% theoretical capacity). Complete carbonation was again not observed, even after 12–24 h, showing that the reaction kinetics are very slow. XRD of the sample after the final CO2 absorption cycle revealed it contained CaCO3 (49.3 wt%), MgO (26.8 wt%), dolomite (14.3 wt%), NaCl (6.2 wt%) and CaCl2 (3.4 wt%) (Fig. S6†).
Carbon dioxide cycling of dolomite is therefore possible for both mined and synthetically synthesised materials with the aid of a catalyst, but in this study the commercial material (Watheroo) has a larger cycling capacity of ∼50% compared to ∼25% of theoretical capacity for the synthetic material. The better cyclability could be due to the additional impurities contained in the commercial material (quartz, kaolinite and montmorillonite), which also resulted in reasonable carbonation over a 5 h window at 450–500 °C. The geological process of dolomitisation is known to form dolomite when Mg2+ replaces Ca2+ in calcite.41 This process has been studied in detail with many researchers attempting to form dolomite in the direct crystallisation from an aqueous solution at temperatures between 60–220 °C.41 This crystallisation process has been shown to occur on a much longer timescale (hours to days), via an Ostwald-ripening mechanism.
To further understand the difference in cyclic capacity between synthetic and mined dolomite samples microscopy investigations were undertaken on CO2 cycled samples (Synth-D-cat and Wath-D-cat). SEM analysis reveal that the two samples are morphologically different (Fig. 5). Watheroo powders were found to be porous aggregates of fine particles (Fig. 5a and b), displaying higher surface area and better gas migration pathways than synthetic samples (Fig. 5e and f), which were less porous, and more monolithic. However, the drastic differences in phase segregation observed in both samples is most important. The Watheroo sample, as shown by XRD, contains a high SiO2 content that may be present as quartz, silicates or aluminosilicates, whereas the synthetic sample has greater purity and is Si-free (Table 3). Imaging and chemical analysis of particle cross-sections (Fig. 5c, d and g, h) reveal that the Watheroo samples have intermixed Ca- and Mg-rich components in sub-micron domains, which also include Si-rich compounds. Whereas, the synthetic sample shows larger discrete Ca- or Mg-rich domains indicating a much higher degree of phase segregation (>5 μm). Intermixing of Si-rich compounds with MgO and CaO may act to arrest sintering, agglomeration, and segregation of CaO and MgO. Addition of unreactive phases has previously been shown to act as particle refinement agents in gas-sorption materials, which increases their overall cyclability.42 It is feasible that the Si-rich impurities act as grain size refinement agents and reduce the path length between CaO and MgO reaction sites during dolomite formation, while also retaining a porous morphology, which allows CO2 migration through the sample.
Nitrogen (N2) adsorption/desorption measurements (Table S2†) are consistent with the SEM observations that the synthetic and mined dolomite samples are morphologically different. The synthetic dolomite (Synth-B) has 0.98 m2 g−1 specific surface area and 0.0014 cm3 g−1 cumulative pore volume. Mined dolomite samples, Rich-A and Wath-A, have a specific surface area of 16.90 and 16.78 m2 g−1, respectively, which is >16 times higher than the synthetic sample (Synth-B). Their cumulative pore volume is also ∼10 times higher than the synthetic dolomite sample, 0.0155 and 0.0146 cm3 g−1.
Conclusions
This study has illustrated the reversible carbonation of dolomite, demonstrating its potential as a 2nd generation concentrating solar thermal power (CSP) thermochemical energy storage material. This was achieved through the use of a novel molten salt catalyst. Three different dolomite sources were assessed for thermochemical energy storage for CSP applications. Catalysed dolomite samples were shown to cycle (∼50% capacity) over >10 + cycles from 450–550 °C without additional loss in capacity. This operational temperature range is the same as existing molten nitrate salt energy storage systems but with over an order of magnitude in raw material cost reduction, even when considering partial CO2 uptake capacity. These promising results demonstrate that thermochemical energy storage should be targeted for 2nd-generation CSP plants. In fact, metal carbonates offer an incredibly low cost for energy stored per dollar, especially when considering that refining of mined dolomite (and their associated cost) may not be required. Herein, it is shown that impurities within dolomite improve their thermochemical cycling performance, and unrefined mined samples show the most promising results once catalysed by inexpensive salts. Essentially, dolomite could be extracted from the ground and directly deposited into a thermochemical reactor.Future research should be directed towards improving the cyclic capacity of dolomite, investigating other promising metal carbonate systems, and investigating the design/cost of high temperature reactors to house the powder bed. In addition, low cost volumetric storage options must be identified. This would include liquefying the CO2 at pressures above 64 bar or the use of low-temperature CO2 storage in another carbonate material.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Terri Manns from Watheroo Dolomitic Lime for providing dolomite samples. KTM thanks The Independent Research Fund Denmark for International Postdoctoral grant 8028-00009B. MP acknowledges the financial support of ARC Future Fellowship FT160100303. The project utilised the EM and XRD facilities (ARC LE0775551) of the John de Laeter Centre at Curtin University that were partly supported by the Science and Industry Endowment Fund. CEB, TDH and MVS acknowledge the financial support of the Australian Research Council for ARC Linkage grant LP150100730. Part of this research was undertaken on the Powder Diffraction beamline at the Australian Synchrotron, Victoria, Australia.Notes and references
- D. Abbott, Proc. IEEE, 2010, 98, 42–66 CAS.
- SunShot Vision Study, Concentrating Solar Power: Technologies, Cost, and Performance, US Department of Energy, 2012, ch. 5 Search PubMed.
- M. Liu, N. H. Steven Tay, S. Bell, M. Belusko, R. Jacob, G. Will, W. Saman and F. Bruno, Renewable Sustainable Energy Rev., 2016, 53, 1411–1432 CrossRef CAS.
- D. N. Harries, M. Paskevicius, D. A. Sheppard, T. Price and C. E. Buckley, Proc. IEEE, 2012, 100, 539–549 CAS.
- M. Fellet, C. E. Buckley, M. Paskevicius and D. A. Sheppard, MRS Bull., 2013, 38, 1012–1013 CrossRef CAS.
- Q. Lai, M. Paskevicius, D. A. Sheppard, C. E. Buckley, A. W. Thornton, M. R. Hill, Q. Gu, J. Mao, Z. Huang, H. K. Liu, Z. Guo, A. Banerjee, S. Chakraborty, R. Ahuja and K.-F. Aguey-Zinsou, ChemSusChem, 2015, 8, 2789–2825 CrossRef CAS PubMed.
- K. Møller, D. Sheppard, D. Ravnsbæk, C. E. Buckley, E. Akiba, H.-W. Li and T. Jensen, Energies, 2017, 10, 1645 CrossRef.
- D. A. Sheppard, C. Corgnale, B. Hardy, T. Motyka, R. Zidan, M. Paskevicius and C. E. Buckley, RSC Adv., 2014, 4, 26552–26562 RSC.
- D. A. Sheppard, M. Paskevicius, T. D. Humphries, M. Felderhoff, G. Capurso, J. Bellosta von Colbe, M. Dornheim, T. Klassen, P. A. Ward, J. A. Teprovich, C. Corgnale, R. Zidan, D. M. Grant and C. E. Buckley, Appl. Phys. A, 2016, 122, 395 CrossRef.
- A. Bayon, R. Bader, M. Jafarian, L. Fedunik-Hofman, Y. Sun, J. Hinkley, S. Miller and W. Lipiński, Energy, 2018, 149, 473–484 CrossRef CAS.
- Outukumpu, Chemistry Software, Houston, HSC Chemistry, 6.1 edn, 2006 Search PubMed.
- M. Paskevicius, D. A. Sheppard and C. E. Buckley, J. Am. Chem. Soc., 2010, 132, 5077–5083 CrossRef CAS PubMed.
- C. Y. Zhao, Y. Ji and Z. Xu, Sol. Energy Mater. Sol. Cells, 2015, 140, 281–288 CrossRef CAS.
- P. G. Jessop and W. Leitner, in Chemical Synthesis Using Supercritical Fluids, Wiley-VCH Verlag GmbH, 2007, pp. 1–36 Search PubMed.
- V. Romanov, Y. Soong, C. Carney, G. E. Rush, B. Nielsen and W. O'Connor, ChemBioEng Rev., 2015, 2, 231–256 CrossRef CAS.
- D. A. Sheppard, T. D. Humphries and C. E. Buckley, Mater. Today, 2015, 18, 414–415 CrossRef.
- H. J. Bissell and G. V. Chilingar, in Developments in Sedimentology, ed. G. V. Chilingar, H. J. Bissell and R. W. Fairbridge, Elsevier, 1967, vol. 9, pp. 87–168 Search PubMed.
- R. C. Freas, J. S. Hayden and C. A. Pryor Jr, in Industrial Minerals & Rocks, ed. J. E. Kogel, N. C. Trivedi, J. M. Barker and S. T. Krukowski, Society for Mining, Metallurgy, and Exploration, Inc., 7th edn, 2009 Search PubMed.
- S. Kumar and S. K. Saxena, Mater. Renew. Sustain. Energy, 2014, 3, 30 CrossRef.
- V. Manovic and E. J. Anthony, Energy Fuels, 2010, 24, 5790–5796 CrossRef CAS.
- G. S. Grasa and J. C. Abanades, Ind. Eng. Chem. Res., 2006, 45, 8846–8851 CrossRef CAS.
- X. Yang, L. Zhao, S. Yang and Y. Xiao, Asia-Pac. J. Chem. Eng., 2013, 8, 906–915 CrossRef CAS.
- K. Zhang, X. S. Li, H. Chen, P. Singh and D. L. King, J. Phys. Chem. C, 2016, 120, 1089–1096 CrossRef CAS.
- X. Yang, L. Zhao and Y. Xiao, Energy Fuels, 2013, 27, 7645–7653 CrossRef CAS.
- R. L. Martin and J. B. West, J. Inorg. Nucl. Chem., 1962, 24, 105–111 CrossRef CAS.
- M. Ito and K. Morita, Mater. Trans., 2004, 45, 2712–2718 CrossRef CAS.
- E. Sada, S. Katoh, H. Beniko, H. Yoshii and M. Kayano, J. Chem. Eng. Data, 1980, 25, 45–47 CrossRef CAS.
- B. D. Bond and P. W. M. Jacobs, J. Chem. Soc. A, 1966, 1265–1268 RSC.
- S. Yuvaraj, L. Fan-Yuan, C. Tsong-Huei and Y. Chuin-Tih, J. Phys. Chem. B, 2003, 107, 1044–1047 CrossRef CAS.
- G. J. Janz, C. B. Allen, J. R. Downey Jr and R. P. T. Tomkins, National Bureau of Standards, 1978, SRDS-NBS 61, part I Search PubMed.
- K. S. Wallwork, B. J. Kennedy and D. Wang, Synchrotron Radiation Instrumentation: Ninth International Conference on Synchrotron Radiation Instrumentation, 2007, vol. 879, pp. 879–882 Search PubMed.
- B. Schmitt, C. Brönnimann, E. Eikenberry, F. Gozzo, C. Hörmann, R. Horisberger and B. Patterson, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 501, 267–272 CrossRef CAS.
- R. A. Young and R. A. Young, The Rietveld Method, Oxford University Press, 1995 Search PubMed.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- E. P. Barrett, L. G. Joyner and P. P. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef CAS.
- M. Gregg Jay, L. Bish David, E. Kaczmarek Stephen and G. Machel Hans, Sedimentology, 2015, 62, 1749–1769 CrossRef.
- K. L. Strelets and N. Bondarenko, Zh. Neorg. Khim., 1963, 8, 1706–1709 CAS.
- FactSage FTsalt salt database – List of systems and phases, http://www.factsage.cn/fact/documentation/ftsalt/ftsalt_list.htm, accessed June 12, 2018.
- S. Gunasekaran and G. Anbalagan, Bull. Mater. Sci., 2007, 30, 339–344 CrossRef CAS.
- A. I. Rat'ko, A. I. Ivanets, A. I. Kulak, E. A. Morozov and I. O. Sakhar, Inorg. Mater., 2011, 47, 1372–1377 CrossRef.
- J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Am. Mineral., 2015, 100, 1172–1181 CrossRef.
- M. P. Pitt, M. Paskevicius, C. J. Webb, D. A. Sheppard, C. E. Buckley and E. M. Gray, Int. J. Hydrogen Energy, 2012, 37, 4227–4237 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Quantitative analysis of XRD data; CO2 pressure cycling data of synthetic dolomite; BET analysis. See DOI: 10.1039/c8ta07254j |
| This journal is © The Royal Society of Chemistry 2019 |