View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence
DOI: 10.1039/C9SM90224D (Correction) Soft Matter, 2019, 15, 9157-9158

Correction: Transfer matrix theory of polymer complex coacervation

Tyler K. Lytle a and Charles E. Sing *b
aDepartment of Chemistry, University of Illinois at Urbana-Champaign, 505 S. Mathews, Urbana, IL 61801, USA. E-mail: cesing@illinois.edu
bDepartment of Chemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, 600 S. Mathews, Urbana, IL 61801, USA

Received 24th October 2019 , Accepted 24th October 2019

First published on 1st November 2019

Abstract

Correction for ‘Transfer matrix theory of polymer complex coacervation’ by Tyler K. Lytle et al., Soft Matter, 2017, 13, 7001–7012.

The authors regret that there is an incorrect equation in ref. 1. Eqn (18) in the manuscript, and the subsequent example, are intended to compute the conditional probability p(si|si−1) of observing a state si at monomer i given a state si−1 at the previous monomer i − 1.1 The correct expression requires a similar calculation using the frequency n of the transitions from si−1 to si:
 
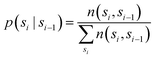image file: c9sm90224d-t1.tif(1)

In the original manuscript,1 the matrix elements M are taken to be the frequencies, but this is incorrect. Instead, these values of n require that a term be added to the calculation of the partition via a factor ζ added to the transfer matrix element of interest (i.e., M(si,si−1) → M(si,si−1) × ζ for si,si−1). The frequency can then be calculated via the expression:

 
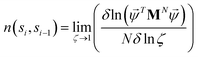image file: c9sm90224d-t2.tif(2)
We numerically calculate the new quantities for these conditional probabilities, as a correction to Fig. 3 of the original manuscript,1 and plot them below against the original simulation values. The same parameters are used here as in the original manuscript. We note that, while possessing quantitative differences from the original (incorrect) values, these theoretical predictions still exhibit similar agreement with simulation values. We thus consider that the original parameters are still appropriate, and therefore the remainder of the manuscript remains quantitatively unchanged and the original conclusions are still valid.


image file: c9sm90224d-f1.tif
Fig. 3 Simulation (points) and theory (curves) describing the adsorption sequence statistics in various coacervate-forming systems at a number of values of ϕP and ϕS. (a) The conditional probabilities p(X|Y) of having a monomer with adsorbed state of type X immediately following a monomer with adsorbed state of type Y. p(C|C), p(C|P′), p(P′|P), and p(P′|P′) as a function of salt concentration ϕS at constant ϕP = 0.06. (b) The same conditional probabilities as a function of polymer concentration ϕP for constant ϕS = 0.06. For both (a and b) there is near-quantitative fitting between theory and simulation, indicating that this formalism describes the environment surrounding a test chain.

Acknowledgements

We acknowledge Jason J. Madinya for bringing this error to our attention.

The Royal Society of Chemistry apologises for these errors and any consequent inconvenience to authors and readers.

References

  1. T. K. Lytle and C. E. Sing, Soft Matter, 2017, 13, 7001–7012 RSC.
This journal is © The Royal Society of Chemistry 2019