Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microgels as viscosity modifiers influence lubrication performance of continuum†
Efren
Andablo-Reyes
a,
Demetra
Yerani
a,
Ming
Fu
a,
Evangelos
Liamas
 a,
Simon
Connell
b,
Ophelie
Torres
a and
Anwesha
Sarkar
a,
Simon
Connell
b,
Ophelie
Torres
a and
Anwesha
Sarkar
 *a
*a
aFood Colloids and Bioprocessing Group, School of Food Science and Nutrition, University of Leeds, UK. E-mail: A.Sarkar@leeds.ac.uk
bMolecular and Nanoscale Physics Group, School of Physics and Astronomy, University of Leeds, UK
First published on 11th October 2019
Abstract
Biocompatible microgels have been demonstrated to act as excellent lubricants, however, the influence of the continuum on their overall mechanical performance has been neglected so far. In this work, the mechanical performance of colloidal whey protein microgels (hydrodynamic diameter ∼100 nm measured using dynamic light scattering and atomic force microscopy) of different rigidity dispersed in Newtonian (buffer and corn syrup) or complex non-Newtonian fluids (xanthan gum) is investigated for the first time via rheology and soft tribology. Dispersions of both soft microgels (G′ ∼ 100.0 Pa) and hard microgels (G′ ∼ 10.0 kPa) were observed to act as thickeners in buffer as well as in low viscosity corn syrup and correspondingly reduced the friction, latter decreased as a function of the increased rigidity of the microgels. Differently, in high viscosity continuum, the microgels acted as thinning agents and increased the friction. In the lubrication limit, microgels in buffer or corn syrup behaved as Newtonian fluids with effective viscosity corresponding to their second Newtonian plateau value (η∞). However, the lubrication performance of the microgels dispersed in the complex fluid (xanthan gum) could not be described quantitatively by η∞. For the low viscosity xanthan gum, the microgels had no influence on friction. Nevertheless, for the high viscosity counterparts, the soft microgels acted as thinning agents whilst the hard microgels accelerated the onset of elastohydrodynamic regime. This study demonstrates that microgels act as viscosity modifiers directly influencing the tribological performance, depending upon a subtle interplay of rheological properties of the particles and continuum.
1. Introduction
Microgels are soft colloids made of cross-linked polymers that are capable of entrapping significant proportions of solvent or water. Their composition and size, which ranges from tens of nanometers to hundreds of microns, can be tailored in order to provide desirable chemical and physical characteristics to target different applications.1 Recently, biocompatible microgels, such as those made up of proteins have shown remarkable properties in highly demanding biological applications, such as drug delivery,2,3 altering interfacial digestion kinetics4 and lubrication of biological contacts.5 For instance, submicron-sized whey protein microgels have been used to stabilise Pickering emulsion, providing a transient barrier against enzymatic diffusion by lipase.6 Another example of microgel performance is lubrication, which is essential in the development of physiological processes involved in mechanical contacts, such as highly loaded synovial joints as well as delicate rubbing surfaces like eyelids.7 Sensory properties related to skin or oral processing are also examples where lubrication is of paramount importance. For instance, recent studies have demonstrated correlation between the tribological performance of edible hydrogels in soft silicon contacts with oral perception attributes, such as pastiness and slipperiness8 and effects of such unique lubrication on satiety responses.9Aqueous lubrication has been recognized as one of the main mechanisms for bio-lubrication due to the abundance of water in complex living organisms.10 Aqueous lubrication is attributed to the capacity of biopolymers to electrostatically bind water molecules while being tethered to the bio-surfaces. Hydrated layers formed near the surfaces by this mechanism are capable of supporting high pressure such as those developed in synovial joints.11 The aqueous lubrication performance of colloidal microgels has recently attracted research attention, such as in the case of particles made of thermo-responsive hydrogels12 or biopolymers including starch,13 whey protein14,15 as well as non-starch polysaccharides (alginate,16 agarose,17 κ-carrageenan18). The capacity of these soft particles to reduce friction in soft mechanical contacts has been attributed to their action as surface separators in combination to a roll bearing mechanism, the latter phenomenon is still under debate.13
An important aspect which has been as-of-yet neglected in the literature, whilst possibly having an exceptional relevance in the mechanical performance of the colloidal dispersions, is the role of the continuous phase i.e., the continuum in which the microgels are dispersed.19 Farres et al. carried out an elegant study where the role of co-solutes, such as glucose and glycerol on the lubrication properties of agar fluid gels was investigated.20 The authors proposed that altering both the rate of ordering transition and the degree of solvation of the gel particles by the co-solutes present in the continuum could influence the lubricating behaviour of fluid gels. Nevertheless, many, if not most studies conducted on microgel or fluid gel lubrication have focused on simple aqueous dispersions. Complex fluids are, in general terms, a combination of a variety of microscopic components with different microstructures, such as colloidal particles and polymers. The self and collective dynamics and configuration of these components contribute in different manner to the macroscopic behaviour of the material.21 For instance, the response of complex fluids to mechanical deformation is dominated by a wide spectrum of relaxation times associated with different levels of component level reorganisation, such as chain segments decorrelation22 or colloidal mesostructures breakage under shear.23 The understanding of the mechanical behaviour of microgel dispersions in complex continuum might also be relevant as simple aqueous media are often altered with the addition of rheology modifiers in real-life applications. Particularly such fundamental knowledge will open up possibilities for templating new soft microgel + complex continuum combinations with optimized performance, such as shear-thinning with ultra-low friction coefficients, and will pave the way towards the development of novel functional biomedical, personal care and nutritional applications.
In this work, colloidal whey protein particles are investigated as models of soft microgels dispersed in continuums of different rheological behaviours. Whey protein microgels have been recently regarded as important biocompatible lubricants.14,15 Two different types of well-characterised fluids are used as continuum in this study. On the one hand, corn syrup solutions with different viscosities are used as Newtonian continuum to serve as a comparison with various literature. On the other hand, xanthan gum solutions are investigated as examples of complex non-Newtonian continuum. While the lubrication performance of corn syrup has been found to be controlled by the viscosity24 of the Newtonian fluid, the lubrication capacity of xanthan gum has also been largely attributed to aqueous lubrication.25,26 In addition to the changes in the continuum properties, the role of the particle softness was also investigated by synthesising microgels of different whey protein content to influence the corresponding protein-crosslinking densities. Variation of mechanical characteristics of microgels and continuum allowed establishing a relationship between the high shear rheology of the dispersions and their lubrication properties, which to the best of our knowledge has never been reported for this kind of complex continuum before.
2. Experimental
2.1 Materials
Whey protein isolate (WPI) powder containing 96.3 wt% protein was kindly donated by Fonterra Limited (Auckland, New-Zealand). Xanthan gum was purchased from Sigma Aldrich, Dorset, UK and used as received. Corn syrup was purchased from Special Ingredients Ltd (Chesterfield, UK). Monosodium phosphate (NaH2PO4) and disodium phosphate (Na2HPO4) were purchased from VWR Chemicals, UK. Milli-Q water (resistivity of 18 M Ω cm by Milli-Q apparatus, Millipore Corp., Bedford, MA, USA) was used for preparation of 20 mM phosphate buffer at pH 7.0.2.2 Methods
The previously crosslinked whey protein gels (10.0 wt% or 15.0 wt%) were mixed with either phosphate buffer or corn syrup solutions at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w ratio and subsequently sheared with a hand blender (HB711M, Kenwood, UK) for 1 minute. The whey protein gel dispersed in either the phosphate buffer or the corn syrup was then placed under vacuum for 30 minutes in order to remove the excess air introduced during blending. The system was finally homogenized via the Leeds Jet Homogenizer (University of Leeds, UK), with two passes at 300 ± 20 bars.14,27 The final concentration of microgels in either the buffer or the two corn syrup solutions was 50.0 vol%, although the protein content in the microgels was either 10.0 or 15.0 wt%. Volume fraction calculation was based on gravimetric measurement based on previous literature,14 however future work should consider calculating volume fraction of the particles based on theoretical models on soft-hairy colloidal spheres.28
1 w/w ratio and subsequently sheared with a hand blender (HB711M, Kenwood, UK) for 1 minute. The whey protein gel dispersed in either the phosphate buffer or the corn syrup was then placed under vacuum for 30 minutes in order to remove the excess air introduced during blending. The system was finally homogenized via the Leeds Jet Homogenizer (University of Leeds, UK), with two passes at 300 ± 20 bars.14,27 The final concentration of microgels in either the buffer or the two corn syrup solutions was 50.0 vol%, although the protein content in the microgels was either 10.0 or 15.0 wt%. Volume fraction calculation was based on gravimetric measurement based on previous literature,14 however future work should consider calculating volume fraction of the particles based on theoretical models on soft-hairy colloidal spheres.28
In order to ease the discussion of results, labels are given to the different samples according to the content of protein in microgels and the type of continuum (i.e., buffer, corn syrup or xanthan gum solution) as described in Table 1.
| Sample name | Microgel protein content (wt%) | Corn syrup content (wt%) | Xanthan gum content (wt%) |
|---|---|---|---|
| Buffer | No particles | 0.0 | 0.0 |
| Buffer10 | 10.0 | 0.0 | 0.0 |
| Buffer15 | 15.0 | 0.0 | 0.0 |
| 50CS | No particles | 50.0 | 0.0 |
| 50CS10 | 10.0 | 50.0 | 0.0 |
| 50CS15 | 15.0 | 50.0 | 0.0 |
| 75CS | No particles | 75.0 | 0.0 |
| 75CS10 | 10.0 | 75.0 | 0.0 |
| 75CS15 | 15.0 | 75.0 | 0.0 |
| 0p5XG | No particles | 0.0 | 0.5 |
| 0p5XG10 | 10.0 | 0.0 | 0.5 |
| 0p5XG15 | 15.0 | 0.0 | 0.5 |
| 1XG | No particles | 0.0 | 1.0 |
| 1XG10 | 10.0 | 0.0 | 1.0 |
| 1XG15 | 15.0 | 0.0 | 1.0 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 v/v ratio and placed in a disposable micro plastic cuvette (ZEN 0040). Measurements were performed using a detection angle of 173°. Time dependent correlation functions were fitted using a cumulant analysis satisfying standard criteria to obtain representative particle size distributions. Analysis was performed assuming refractive index of 1.54 and 1.33 for particles and fluid, respectively. The dispersant viscosity was assumed to be the viscosity of water (i.e., 8.9 × 10−4 Pa s).
500 v/v ratio and placed in a disposable micro plastic cuvette (ZEN 0040). Measurements were performed using a detection angle of 173°. Time dependent correlation functions were fitted using a cumulant analysis satisfying standard criteria to obtain representative particle size distributions. Analysis was performed assuming refractive index of 1.54 and 1.33 for particles and fluid, respectively. The dispersant viscosity was assumed to be the viscosity of water (i.e., 8.9 × 10−4 Pa s).
Topographic images were acquired using a Bruker Multimode 8 AFM equipped with a Bruker Nanoscope V controller. Silicon nitride AFM cantilevers (model MLCT-DC-BIO) with a nominal spring constant of 0.01 N m−1 were purchased from Bruker AFM probes (Camarillo, CA). These cantilevers are thermally stable despite the low spring constant, so it was possible to maintain the force set-point at extremely small values, typically <100 pN producing the most defined images, whilst at 150 pN sample deformation was clearly observed. Slow line rates of 0.5–0.8 Hz and gains at the very upper limits of stability were necessary to track the microgels with minimum disturbance. The measurements were performed at room temperature, using a fluid cell loaded with 20 mM phosphate buffer solution (pH = 7). Images were acquired at 768 pixel resolution and processed using Bruker Nanoscope Analysis v1.9. To our knowledge, this is the first study that has carried out AFM imaging of whey protein microgels.
3. Results
3.1 Particle size
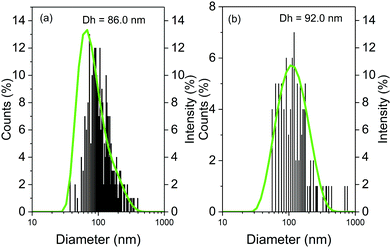
Atomic force microscopy (AFM) allowed structural characterisation of the submicron-sized whey protein microgels. The extremely soft and adherent nature of the microgels led to large instabilities when using Peak Force Tapping mode (even with its fine and absolute force control) and standard Tapping Mode, hence contact mode was used. Topographical images of the microgels Buffer10 (Fig. 1) deposited on a silicon surface revealed a homogenous distribution of single spherical particles of microgels as well as small clusters that contained between two to six individual particles. The surface of the microgels appeared to be relatively smooth also seen in other polymeric microgels.30 Using dynamic light scattering, the average hydrodynamic diameter (Dh) of the microgels produced at 10.0 wt% or 15.0 wt% protein content was estimated to be 86.0 (Fig. 2a) and 92.0 nm (Fig. 2b), respectively. Such values are in close range of previous protein microgels reported in literature that are designed using top down approach of heat-set crosslinking and controlled shearing.27,31Particle size distribution was also calculated by processing the topographic AFM image with Nanoscope Analysis v1.9 and represented as histograms for microgels containing 10.0 (Fig. 2a) or 15.0 wt% (Fig. 2b) protein. Size distributions obtained by AFM are in good agreement with DLS measurements regarding the hydrodynamic radii of the microgels. The particle size distributions of microgels with 10.0 wt% and 15.0 wt% protein content dispersed either in buffer or 75.0 wt% corn syrup solution are presented in the Fig. S1 (ESI†). The viscosity of the continuum that has been used during microgel formation did not influence the particle size significantly.
3.2 Rheology
In this study, microgels were suspended in Newtonian and non-Newtonian fluids, referred as continuum hereafter. Fig. 3 shows the shear viscosity of the different continuums, i.e., phosphate buffer at pH 7.0, corn syrup and xanthan gum solutions without any added microgels. Phosphate buffer (Buffer), 50.0 wt% (50CS) and 75.0 wt% (75CS) corn syrup solutions were observed to be Newtonian fluids with viscosities of 0.7, 8.0 and 60.0 mPa s, respectively. Viscosity values found here for corn syrup solution are in agreement with values previously reported in literature.25 Xanthan gum solutions are well known shear-thinning fluids,25,32 quality that can be appreciated in Fig. 3 where viscosities of 0p5XG and 1XG decrease at least two orders of magnitude in the shear rate experimental window covering a range from 0.1 to 1000 s−1. At 0.3 s−1, 0p5XG and 1XG had values of shear viscosity of approximately 1.5 and 30.0 Pa s, respectively. However, at the highest shear rate (1000 s−1), viscosity values observed for 0p5XG and 1XG approximated the Newtonian viscosities of 50CS and 75CS, respectively. One of the aims of this study was to establish the mechanisms dominating the lubrication capacity of soft colloidal microgel dispersions in complex media using a macroscopic approach. The lubrication performance of some polysaccharide solutions has been successfully explained in terms of hydrodynamics.25 In this approach, the strength of hydrodynamic forces are approximated using the fluid viscosity in the high shear rate limit. Hence, in order to obtain an estimate for the high shear rate viscosity plateau η∞, experimental data were fitted using the cross model33 presented in eqn (1).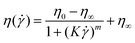 | (1) |
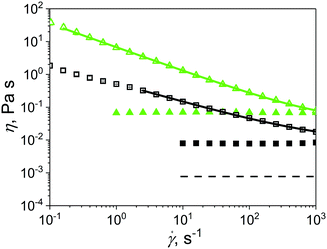 | ||
Fig. 3 Shear viscosity of Newtonian and non-Newtonian fluids used as continuum in microgel dispersions. Buffer (dashed line), 50CS (filled square) and 75CS (filled triangle) are Newtonian fluids with shear viscosity independent to the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . 0p5XG (open square) and 1XG (open triangle) are shear thinning non-Newtonian fluids. The continuous lines correspond to fittings using eqn (1). . 0p5XG (open square) and 1XG (open triangle) are shear thinning non-Newtonian fluids. The continuous lines correspond to fittings using eqn (1). | ||
| Sample | η ∞ (Pa) | μ (U = 0.005 m s−1, boundary*/mixed lubrication) | μ (U = 0.04 m s−1, mixed lubrication) |
|---|---|---|---|
| Buffer | 0.0007 | 0.67 ± 0.08* | 0.41 ± 0.06 |
| Buffer10 | 0.004 | 0.48 ± 0.1* | 0.20 ± 0.05 |
| Buffer15 | 0.010 | 0.23 ± 0.06 | 0.09 ± 0.01 |
| 50CS | 0.008 | 0.89 ± 0.18 | 0.18 ± 0.03 |
| 50CS10 | 0.010 | 0.36 ± 0.09* | 0.09 ± 0.02 |
| 50CS15 | 0.022 | 0.14 ± 0.07 | 0.023 ± 0.005 |
| 75CS | 0.070 | 0.07 ± 0.05 | 0.0049 ± 0.006 |
| 75CS10 | 0.022 | 0.26 ± 0.05 | 0.04 ± 0.02 |
| 75CS15 | 0.041 | 0.07 ± 0.02 | 0.009 ± 0.001 |
| 0p5XG | 0.008 | 0.22 ± 0.08* | 0.09 ± 0.03 |
| 0p5XG10 | No data | 0.31 ± 0.04 | 0.14 ± 0.03 |
| 0p5XG15 | 0.12 ± 0.05 | 0.05 ± 0.01 | |
| 1XG | 0.034 | 0.08 ± 0.03 | 0.020 ± 0.008 |
| 1XG10 | No data | 0.17 ± 0.03 | 0.080 ± 0.004 |
| 1XG15 | 0.06 ± 0.01 | 0.032 ± 0.004 |
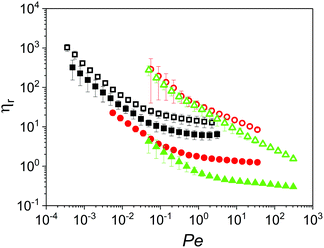
In order to appreciate the impact of microgel inclusions on the overall properties of the dispersions, their relative viscosity (ηr) was plotted as function of the Peclet number (Pe) as defined in eqn (2) and (3), respectively.
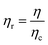 | (2) |
Pe = 6π![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ηca3/KBT ηca3/KBT | (3) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1) and Brownian diffusion time of the microgels. Fig. 4 shows the ηr for microgel dispersions in Newtonian continuum. In this representation, dispersions containing microgels with 10.0 wt% protein content (Buffer10, 50CS10 and 75CS10) show similar shear thinning behaviour, however, this region extends to higher values of Pe as the particle Brownian diffusion is slowed down on increasing the continuum viscosity. Although influence of particle size is not explored here, in agreement to eqn (3), increasing particle size should also extend the shear thinning region. For instance, shear viscosity reported elsewhere14 for dispersions of microgels with diameter of 300.0 nm (three times larger than reported here) showed a shear thinning region that extended beyond the shear rate (larger than 100.0 s−1). In Fig. 4, at the end of the shear thinning region, the second Newtonian plateau is observed, where the values of ηr decrease on increasing the continuum viscosity. For instance, microgels in Buffer10 and 50CS10 have an incremental effect on the high shear rate viscosity showing values of relative viscosity of about 5.7 and 1.3, respectively. However, it is clear that increasing continuum viscosity has a detrimental effect on the second plateau viscosity. This is more evident in the case of 75CS10, having the highest viscosity continuum (0.07 Pa s), where the relative plateau viscosity drops about 0.4, i.e., absolute viscosity of the microgel dispersion is less than half in comparison to the continuum.
−1) and Brownian diffusion time of the microgels. Fig. 4 shows the ηr for microgel dispersions in Newtonian continuum. In this representation, dispersions containing microgels with 10.0 wt% protein content (Buffer10, 50CS10 and 75CS10) show similar shear thinning behaviour, however, this region extends to higher values of Pe as the particle Brownian diffusion is slowed down on increasing the continuum viscosity. Although influence of particle size is not explored here, in agreement to eqn (3), increasing particle size should also extend the shear thinning region. For instance, shear viscosity reported elsewhere14 for dispersions of microgels with diameter of 300.0 nm (three times larger than reported here) showed a shear thinning region that extended beyond the shear rate (larger than 100.0 s−1). In Fig. 4, at the end of the shear thinning region, the second Newtonian plateau is observed, where the values of ηr decrease on increasing the continuum viscosity. For instance, microgels in Buffer10 and 50CS10 have an incremental effect on the high shear rate viscosity showing values of relative viscosity of about 5.7 and 1.3, respectively. However, it is clear that increasing continuum viscosity has a detrimental effect on the second plateau viscosity. This is more evident in the case of 75CS10, having the highest viscosity continuum (0.07 Pa s), where the relative plateau viscosity drops about 0.4, i.e., absolute viscosity of the microgel dispersion is less than half in comparison to the continuum.
The role of the microgel properties is further explored by increasing their whey protein content to 15.0 wt%. Viscoelasticity of the parent whey protein gels was studied before shearing them into microgels in order to have an estimate of the mechanical properties of microgels. The Fig. S2 (ESI†) shows the linear elasticity of the parent whey protein gels. The elastic shear modulus of the whey protein gels at 10.0 wt% and 15.0 wt% protein content were about 0.1 and 10.0 kPa, respectively. Therefore, the microgels containing 10.0 and 15.0 wt% protein in this study have been referred to as soft and hard microgels, respectively. Dispersions of microgels with 15.0 wt% protein content show differences in the shear thinning region. Sample Buffer15 exhibits similar thinning in comparison to Buffer10 with second Newtonian plateau starting at similar value of Pe ∼ 0.5. Interestingly, relative viscosity of Buffer15 shows a twofold increase in comparison to the Buffer10 in the plateau region. The increase in viscosity can be associated to relatively higher elastic modulus of microgels with higher protein content. Here again microgels in Buffer15 appears to act as thickening agents increasing the viscosity relative to the continuum. Samples 50CS15 and 75CS15 show a similar thinning region between them extending towards Pe values higher than the experimental window. However, values of relative viscosity exhibited by these two fluids are considerably higher in comparison to the rest of the experimental fluids in the shear thinning region with Pe < 2.0. Thus, their response in the shear thinning region at low Pe numbers splits the microgel dispersions studied here into two groups depending on both, particle rigidity and continuum viscosity. This might be because the definition of Pe does not consider particle deformability during flow. Fitted curves to the experimental data are shown in the Fig. S3 (ESI†), where absolute viscosity is presented as function of shear rate.
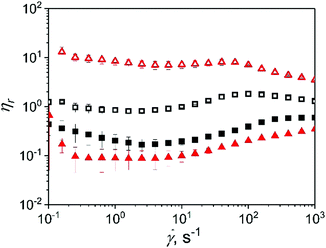
Fig. 5 shows the relative shear viscosity of microgel dispersions in xanthan gum as a function of shear rate. Due to the non-Newtonian nature of the continuum, it is not possible to define a single Brownian diffusion time, thus the use of Pe was not suitable to describe the balance between the hydrodynamic and Brownian relaxation. Fig. 5 shows a detrimental effect of microgel with 10.0 wt% (0p5XG10 and 1XG10) protein content on the shear viscosity relative to the continuum in the whole range of shear rates studied here. The decrease in viscosity is higher in sample 1XG10 in comparison to 0p5XG10 due to the higher viscosity of the continuum in the former. Both samples started to show an onset of a plateau region at shear rates above 200.0 s−1 with ηr about 0.4 and 0.6 for 0p5XG10 and 1XG10, respectively. Differently, microgels with 15.0 wt% protein content exhibit either neutral or active role in the dispersion viscosity depending on the shear conditions and continuum properties.
Relative viscosity of 0p5XG15 is about 1.0 up to shear rates of 1.0 s−1, increasing afterwards to reach value of about 2.0 at 100.0 s−1. Interestingly, 1XG15 shows values of ηr as high as 10.0 for shear rates up to 100 s−1. After this point, ηr decreases monotonically reaching a value of about 4.0 at the shear rate of 1000.0 s−1. In comparison to the rest of the dispersions, the behaviour of 1XG15 is counterintuitive since the higher viscosity of the continuum should contribute to decrease ηr values. This behaviour is evidence of a synergistic effect between microgels with 15.0 wt% protein content and the 1.0 wt% xanthan gum mesh. Further studies are necessary to understand this inversion. In the case of dispersion in xanthan gum continuum, shear viscosity do not show the onset of the second Newtonian plateau making it not possible to fit eqn (1) to the experimental data.
It is important to mention that all rheological discussion has been carried out under the assumption of stick conditions where the macroscopic deformation (imposed at the sample-rheometer surface interface) is representative of the deformation at any point of the fluid bulk. However, wall slip is known to be an artefact present when studying highly concentrated dispersions of Brownian solid and soft particles.34 Noteworthy, that microgel dispersions studied here exhibit a fluid-like behaviour, where transmission of strain/stress from the rheological surfaces to the fluid bulk is mostly performed through the continuum making the chances of slippage to be highly unlikely. Furthermore, stress curves are shown in the Fig. S4 and S5 (ESI†) for microgel dispersions in Newtonian and non-Newtonian continuum, respectively. As it can be observed, shear stress increases monotonically showing no signs of discontinuities suggesting no obvious wall slippage. Overall, the rheological analyses are intended to provide an explanation to the tribological performance of the microgels presented in the next section.
3.3 Soft tribology
Dispersions of whey protein microgels in aqueous media have demonstrated the capability to reduce friction in soft contacts. For example, Sarkar et al. studied the lubrication properties of 300 nm diameter whey protein (10.0 wt%) microgels dispersed in aqueous media.14 They demonstrated the capability of colloidal whey protein microgels to reduce friction in compliant sliding/rolling contacts. In this study, the microgels were three-times smaller (Fig. 1 and 2) and also prepared with different protein content resulting in different degree of protein crosslinking and elasticity (Fig. S2, ESI†) and thus expected to have different lubrication performance in absence or presence of the complex continuum. Fig. 6 shows the lubrication performance of microgel dispersions in comparison to their respective continuum (black squares) in the form of Stribeck curves, where the friction coefficients are shown as a function of entrainment speed. Stribeck curves in Fig. 6a show the boundary and mixed lubrication regimes. The boundary regime is identified as the region where friction coefficient is independent of the entrainment speed. On the other hand, in the mixed lubrication regime, the friction coefficient decreases monotonically on increasing the speed. The presence of microgels helped decreasing the contact friction in the mixed lubrication regime, in comparison to the continuous phase alone (Buffer), however no significant differences are found in the boundary region. For example, at entrainment speed U = 0.005 m s−1 corresponding to the boundary regime, friction coefficient show no significant difference between Buffer and Buffer10 (p > 0.05). At the same speed, sample Buffer15 was found to be performing in the mixed lubrication regime as evident in the decrease of friction coefficient on increasing entrainment speed. Thus, at U = 0.005 m s−1, friction coefficient for Buffer15 was about 0.23, significantly lower (p < 0.05) than values obtained for Buffer and Buffer10. At U = 0.04 m s−1, Buffer, Buffer10 and Buffer15 were found to be working in the mixed lubrication regime. Friction coefficient of buffer was about three to five times higher with respect to the friction coefficient values for Buffer10 and Buffer15, respectively (p < 0.05). These observations show the influence of the microgel mechanical properties (i.e., elastic modulus) on their lubrication performance, the higher the particle elastic modulus (i.e., higher protein content) the lower was the contact friction, at least in the mixed lubrication regime. Friction coefficient Buffer10 is similar to friction measurements (using the same set-up) reported elsewhere14 for similar whey protein microgels (10.0 wt%) with average diameter three times larger. Thus, increasing particle size of the microgels might have no influence on the tribological performance of the final dispersion. A systematic study on impact of average microgel size on lubrication properties is required; however, this is out of scope of the present study. All values of friction are summarised in Table 2 with the corresponding values of η∞ obtained using eqn (1) except for microgels in xanthan gum solutions.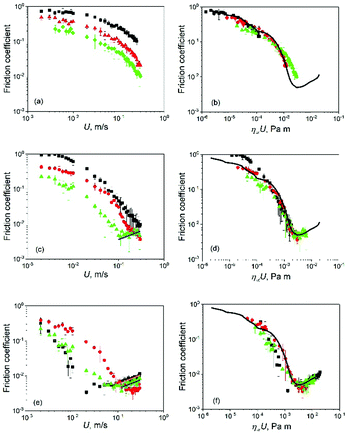 | ||
| Fig. 6 Friction coefficient as a function of U (a, c and e) or η∞U (b, d and f) for microgel dispersions in Newtonian continuum. (a and b) Buffer (squares), Buffer10 (circles) and Buffer15 (triangles). (c and d) 50CS (squares), 50CS10 (circles) and 50CS15 (triangles). (e and f) 75CS (squares), 75CS10 (circles) and 75CS15 (triangles). The particle volume fraction of microgels is fixed at 50.0 vol% in all systems. Continuous line in b, d and e represents an average Stribeck curve of Newtonian fluids (buffer and corn syrups) used in this study. Continuous lines in c and d are fittings to the hydrodynamic lubrication regime using eqn (4). Error bars represent standard deviations. | ||
Fig. 6c presents the Stribeck curves obtained for microgels in 50 wt% syrup solutions (50CS10 and 50CS15) as well as the continuum alone (50CS). Stribeck curves for 50CS and 50CS10 showed the boundary and mixed lubrication regimes. Sample 50CS15 showed the mixed lubrication regime and the onset of the elastohydrodynamic lubrication regime. The latter is observed as an upturn of the Stribeck curve with friction coefficients increasing with the entrainment speeds above 0.1 m s−1. At U = 0.005 m s−1, friction coefficient obtained for 50CS10 is about 0.36, twice as low in comparison to CS50 (plain continuum) at the same entrainment speed. While at U = 0.005 m s−1, 50CS is found to be working in the boundary regime (friction coefficient independent of speed), 50CS10 is working in the mixed lubrication regime showing a subtle decrease in friction on increasing entrainment speed. 50CS75 is also found to be working in the mixed lubrication regime with friction coefficient about 0.14, approximately four and two times lower in comparison to 50CS and 50CS10, respectively. This confirms the positive influence of increasing whey protein in microgels, decreasing the friction coefficient as observed also for microgels dispersed in buffer (Fig. 6a). In Fig. 6b, at entrainment speed U = 0.04 m s−1, 50CS, 50CS10 and 50CS15 performed in the mixed lubrication regime. While values of friction coefficients for 50CS and 50CS10 are not significantly different (p > 0.05), the friction coefficient measured for 50CS15 was significantly lower in comparison to both, 50CS and 50CS10. Moreover, at approximately U = 0.1 m s−1, the onset of the hydrodynamic lubrication can be clearly appreciated only in the curve corresponding to 50CS15.
In the case of simple Newtonian fluids, increasing lubricant viscosity decreases the speed at which the elastohydrodynamic lubrication regime starts.24 This can be clearly observed comparing 50CS (Fig. 6c) and 75CS (Fig. 6e), both Newtonian fluids having viscosities of 0.008 and 0.07 Pa s, respectively. Due to its larger viscosity, 75CS displays the elastohydrodynamic lubrication, while in the same range of speeds 50CS shows only the mixed regime. Applying this reasoning to dispersions 50CS10 and 50CS15 in Fig. 6c, the appearance of an elastohydrodynamic regime for the latter indicates larger viscosity in comparison to the former.
In Fig. 6e, Stribeck curves correspond to 75CS and microgels dispersions 75CS10 and 75CS15. Opposite to the observations in dispersion in lower viscosity continuum (i.e., Buffer10, 50CS10), microgels in 75CS10 increased friction in the mixed lubrication regime in comparison to the continuum alone (75CS). For instance, at U = 0.005 m s−1, friction coefficient found for 75CS10 is about 0.26, representing more than a three-fold increase with respect to 75CS. 75CS and 75CS15 show similar lubrication, however the onset of elastohydrodynamic lubrication reveals differences in viscosity. Onset of elastohydrodynamic lubrication of 75CS appears at the lowest speed at about 0.03 m s−1, followed by 75CS15 at 0.07 m s−1 and finally 75CS10 shows the end of mixed lubrication (and start of elastohydrodynamic regime) at a higher speed of about 0.2 m s−1. Thus, in agreement to discussion presented above, viscosity values of the lubricants follow the same order from highest to lowest, i.e., 75CS > 75CS15 > 75CS10. This is also in line with values of viscosity obtained by means of steady shear rheological experiments as shown in Table 2. The appearance of the hydrodynamic lubrication regime in friction curves for samples 50CS15, 75CS and 75CS15 makes it possible to have an estimation of effective viscosity from a tribological perspective. de Vicente et al.,35 provided an arithmetic expression for the soft-hydrodynamic lubrication regime of a rolling/sliding ball on plate contact as introduced in eqn (4):
μ = 1.46Ū0.65![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) −0.70 + SRR(3.8Ū0.71 −0.70 + SRR(3.8Ū0.71![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) −0.76 + 0.96Ū0.36 −0.76 + 0.96Ū0.36![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) −0.11) −0.11) | (4) |
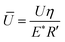 and
and 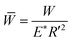 , where E′ and R′ are the reduced Young modulus and the ball radius, respectively. Eqn (4) was successfully fitted to the experimental data using viscosity as the only fitting parameter. Fittings are presented as lines in Fig. 6. Values of viscosity estimated for 50CS15, 75CS and 75CS15 using eqn (4) are 0.017, 0.05 and 0.025 Pa s, respectively. Although in comparisons to values presented in Table 2, values obtained using eqn (4) are slightly lower, the trend obtained in rheology is replicated. Thus, when dispersed in the highest viscosity continuum CS75 (0.07 Pa s), microgels have a detrimental effect on both, rheological and lubrication properties.
, where E′ and R′ are the reduced Young modulus and the ball radius, respectively. Eqn (4) was successfully fitted to the experimental data using viscosity as the only fitting parameter. Fittings are presented as lines in Fig. 6. Values of viscosity estimated for 50CS15, 75CS and 75CS15 using eqn (4) are 0.017, 0.05 and 0.025 Pa s, respectively. Although in comparisons to values presented in Table 2, values obtained using eqn (4) are slightly lower, the trend obtained in rheology is replicated. Thus, when dispersed in the highest viscosity continuum CS75 (0.07 Pa s), microgels have a detrimental effect on both, rheological and lubrication properties.
A common procedure to compare the tribological performance of different fluids is accomplished by using their rheological properties representing friction coefficient as function of the product of viscosity and entrainment speed. In the case of Newtonian fluids, this procedure is well known to deliver master curves (overlapping of curves representing different lubricants) that covers at least the mixed and hydrodynamic lubrication regimes, where fluid dynamics plays an important role in the lubrication.35 Although for most non-Newtonian lubricants the viscosity is a function of working conditions (i.e., shear rate), a similar representation is commonly found where the Newtonian viscosity is replaced by a value of viscosity at a high shear rate (above 1000.0 s−1).25 This approximation relies on the fact that the tribological limit imposes high shear rates on the lubricant due to the proximity between contact surfaces involving submicron separations. Here, the relation between lubrication performance of non-Newtonian microgel dispersions and their rheology is carried out by representing the friction coefficient as function of the product of entrainment speed and η∞. In fact, the successful fitting of eqn (4) in the elastohydrodynamic lubrication regime is a clear indication that this procedure is adequate at least for microgels in Newtonian continuum. In the case of lubricants 75CS10 and 75CS15, the plateau was not observed in the experimental window and values for η∞ were estimated by extrapolation using eqn (1). Fig. 6b, d and e show friction coefficient as function of the product U·η∞ for microgel dispersion with Buffer, 50CS and 75CS as continuum, respectively. A Stribeck curve representing the average lubrication performance of Newtonian lubricants is also presented for comparison purposes. There is a reasonable overlap of Stribeck curves for dispersions regardless of their continuum and protein content in the microgels. Hence, lubrication performance of colloidal microgel dispersions in media with different viscosity (covering three orders of magnitude) can be approximated by considering them as Newtonian fluids having viscosity η∞. In other words, tribological deformation corresponds to the rheological shear rates in the second Newtonian plateau of the microgel dispersions, which has been seldom reported in literature. It is worth noticing that lubricants 50CS15 in Fig. 6d, 75CS10 and 75CS15 in Fig. 6f, show a clear overlap in the onset of the transition between the mixed and hydrodynamic lubrication regime. This is an important indication that hydrodynamic forces acting on the microgel dispersions in the soft tribological limit are still dominated by the rheological response in the equivalent shear rate range, i.e., high shear rate limit.
Having established the influence of microgels in Newtonian continuum of different viscosities in the rheological and tribological limit, a similar study was also conducted for the non-Newtonian continuum, i.e., xanthan gum solutions. Fig. 7a shows the Stribeck curves obtained for microgels dispersions 0p5XG10 and 0p5XG15 in comparison to their continuum alone (0p5XG). Stribeck curves for all lubricants shown in Fig. 7a show only the mixed lubrication regime. In Fig. 7a, only 0p5XG15 shows significant differences. For instance, at entrainment speed 0.005 and 0.04 m s−1, friction coefficient values for 0p5XG15 are about half the values found for 0p5XG and 0p5XG10 at the same speeds. Fig. 7b shows the Stribeck curves for microgels dispersed in the highest viscosity non-Newtonian continuum (1XG). While Stribeck curves for 1XG and 1XG15 show no relative differences, friction coefficients obtained for 1XG10 are significantly higher in comparison to the other two curves up to U = 0.1 m s−1, where a minimum for the friction coefficient is reached. The appearance of a hydrodynamic lubrication regime is only evident in the case of 1XG15, where fitting of eqn 4 generates a value of viscosity of about 0.2 Pa s. Using this calculation, a comparison between rheological and tribological performance can be carried out for 1XG and 1XG15. Effective viscosity of 1XG15 in the elastohydrodynamic regime (eqn (4)) represents a six-fold increase in comparison to the high shear viscosity value extrapolated for 1XG (Table 2). However, in the mixed lubrication regime, no significant differences are found between friction coefficients of 1XG and 1XG15. Thus, it is clear that a single value of viscosity η∞ cannot be used to explain the lubrication performance of microgels in non-Newtonian continuum (xanthan gum). In addition, in the non-Newtonian continuum, microgels in the lowest viscosity continuum (0p5XG) can improve the lubrication with respect to the continuum and the same microgels can cause a detrimental effect when dispersed in the higher viscosity continuum (1XG). Regardless of the continuum properties, lubrication performance of the microgel dispersion is better for the higher protein content particles.
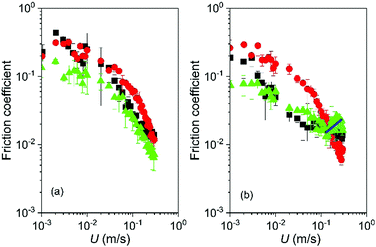 | ||
| Fig. 7 Friction coefficient as a function of U for the microgel dispersions non-Newtonian continuum. (a) 0p5XG (squares), 0p5XG10 (circles) and 0p5XG15 (triangles). (b) 1XG (squares), 1XG10 (circles) and 1XG15 (triangles). The particle volume fraction of microgels is fixed at 50 vol% in all fluids. Continuous lines in b represent fitting to the hydrodynamic lubrication regime using eqn (4). Error bars represent standard deviations. | ||
4. Discussion
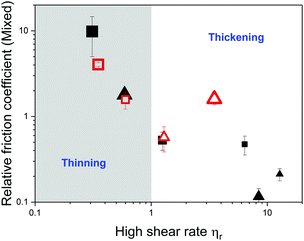
Fig. 8 summarizes the role of microgels on the high shear rheology and lubrication performance of all the microgel dispersions studied. To do so, the relative friction coefficient, defined as the ratio of the friction coefficient of the dispersions to the value of the plain continuum, is represented as function relative viscosity in the high shear rate limit. Friction coefficient values used here correspond to an entrainment speed of 0.04 m s−1, which lies in the mixed lubrication regime for all dispersions. Choice of relative viscosity differs between dispersions in Newtonian and non-Newtonian continuum. For dispersions in buffer or corn syrup solutions, the viscosity corresponds to the extrapolated values η∞ using eqn (1). Since extrapolation was not suitable for dispersions in non-Newtonian continuum, viscosity used in Fig. 8 corresponds to values at the highest shear rate accessible (1000.0 s−1). It is evident that lubrication and high shear rate viscosity are closely related, with friction coefficients decreasing as the dispersion viscosity increases for both, Newtonian and non-Newtonian continuum.Using the definition of relative viscosity, data presented in Fig. 8 is divided in two regions representing the influence of microgels as thickening or thinning agents. In the thinning region, relative high shear rate viscosity is lower than 1.0, with microgels decreasing the viscosity with respect to the continuum. Whether a dispersions falls in either regime depends on both, continuum viscosity and the mechanical properties of the microgel particles.
This is true for both, Newtonian and non-Newtonian continuum. Based on a balance between stored (in soft elastic particles) and dissipated (by Newtonian continuum) energy during shear flow, Avazmohammadi and Castaneda36 estimated the viscosity of soft particles dispersions in Newtonian continuum as function of the dimensionless parameter Ca defined in eqn (5), as shown below:
Ca = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ηc/G ηc/G | (5) |
Finally, a rough estimation of the shear rates in the elastohydrodynamic lubrication regime is possible by using the expression provided by de Vicente et al.35 for the central film thickness as shown in eqn (6).
hc = 3.3R′Ū0.6![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) −0.14 −0.14 | (6) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = SRRU/hc. Samples showing elastohydrodynamic regime in the range of entrainment speeds studied here are 50CS15, 75CS, 75CS15 and 1XG15. Table 3 shows estimation of central film thickness and shear rate together with values of viscosity and speed used to evaluate eqn (6). Entrainment speed values used for calculations correspond to the onset of elastohydrodynamic lubrication. Viscosity corresponds to values obtained from fitting eqn (4) to the elastohydrodynamic lubrication regime of the different dispersions. Values of hc for all microgels in Newtonian continuum are about 7.0 × 10−6 m, whilst for dispersion in xanthan gum solution thickness is one order of magnitude higher i.e., about 3.0 × 10−5 m. Nevertheless, in all cases, shear rate is above 1000.0 s−1. This provides further justification to the use of second Newtonian plateau viscosity to represent the tribological performance of microgels in Newtonian continuum. In the case of microgels in non-Newtonian continuum (xanthan gum solution), their tribological performance is not simply represented by one viscosity value. However, their elastohydrodynamic lubrication regime might be well approximated by their bulk viscosity.
= SRRU/hc. Samples showing elastohydrodynamic regime in the range of entrainment speeds studied here are 50CS15, 75CS, 75CS15 and 1XG15. Table 3 shows estimation of central film thickness and shear rate together with values of viscosity and speed used to evaluate eqn (6). Entrainment speed values used for calculations correspond to the onset of elastohydrodynamic lubrication. Viscosity corresponds to values obtained from fitting eqn (4) to the elastohydrodynamic lubrication regime of the different dispersions. Values of hc for all microgels in Newtonian continuum are about 7.0 × 10−6 m, whilst for dispersion in xanthan gum solution thickness is one order of magnitude higher i.e., about 3.0 × 10−5 m. Nevertheless, in all cases, shear rate is above 1000.0 s−1. This provides further justification to the use of second Newtonian plateau viscosity to represent the tribological performance of microgels in Newtonian continuum. In the case of microgels in non-Newtonian continuum (xanthan gum solution), their tribological performance is not simply represented by one viscosity value. However, their elastohydrodynamic lubrication regime might be well approximated by their bulk viscosity.
| Dispersion | Viscosity (Pa) | U (m s−1) | h c (m) | Shear rate (s−1) |
|---|---|---|---|---|
| 50CS10 | 0.017 | 0.10 | 7.4 × 10−6 | 6764.0 |
| 75CS | 0.050 | 0.03 | 6.9 × 10−6 | 2187.0 |
| 75CS15 | 0.025 | 0.07 | 7.5 × 10−6 | 4653.0 |
| 1XG15 | 0.200 | 0.10 | 3.2 × 10−5 | 1541.0 |
5. Conclusions
Soft whey protein microgels with average size of about 100.0 nm (determined by AFM and DLS) dispersed in Newtonian and non-Newtonian continuum were investigated by means of rheology and soft tribology. Steady shear rheology and soft tribology experiments showed that the lubrication performance of microgels dispersed in either Newtonian or non-Newtonian continuum (xanthan gum solution) is related to their hydrodynamics. On the one hand, the tribological performance of microgels dispersed in Newtonian continuum can be quantitatively explained in terms of their second Newtonian plateau bulk viscosity. On the other hand, for microgels dispersed in xanthan gum solutions, the relation between bulk rheology and soft tribological performance is qualitative.Microgels enhanced the rheological and tribological performance when dispersed in continuum with relatively low viscosity, increasing the viscosity i.e., acting as thickeners, thus lowering the friction coefficient. However in high viscosity continuum, microgels caused a detrimental effect in mechanical performance, decreasing the viscosity and increasing the friction coefficients. Regardless of being dispersed in Newtonian or non-Newtonian continuum, increasing the elastic modulus of the microgels (higher protein content) showed benefits by increasing the high shear rate viscosity of the final dispersion. This consequently improved their tribological performance, i.e., decreased the friction coefficients. Thus, in order to obtain a benefit from microgels on the tribology performance of a dispersion, it is necessary to have harder particles when the continuum viscosity is increased. However, further studies are necessary to determine when microgels become too hard that they can increase the abrasiveness in biological contacts. Future work should look into a more thorough calculation of the effective volume fraction of the soft microgel particles in order to compare with theoretical models.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no 757993).References
- J. K. Oh, R. Drumright, D. J. Siegwart and K. Matyjaszewski, Prog. Polym. Sci., 2008, 33, 448–477 CrossRef CAS.
- N. Murthy, M. C. Xu, S. Schuck, J. Kunisawa, N. Shastri and J. M. J. Frechet, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 4995–5000 CrossRef CAS.
- S. V. Vinogradov, Curr. Pharm. Des., 2006, 12, 4703–4712 CrossRef CAS.
- A. Sarkar, S. N. Zhang, M. Holmes and R. Ettelaie, Adv. Colloid Interface Sci., 2019, 263, 195–211 CrossRef CAS PubMed.
- G. Q. Liu, Z. L. Liu, N. Li, X. L. Wang, F. Zhou and W. M. Liu, ACS Appl. Mater. Interfaces, 2014, 6, 20452–20463 CrossRef CAS.
- A. Sarkar, B. Murray, M. Holmes, R. Ettelaie, A. Abdalla and X. Y. Yang, Soft Matter, 2016, 12, 3558–3569 RSC.
- O. Sterner, C. Karageorgaki, M. Zurcher, S. Zurcher, C. W. Scales, Z. Fadli, N. D. Spencer and S. G. P. Tosatti, ACS Appl. Mater. Interfaces, 2017, 9, 20150–20160 CrossRef CAS.
- E. M. Krop, M. M. Hetherington, M. Holmes, S. Miquel and A. Sarkar, Food Hydrocolloids, 2019, 88, 101–113 CrossRef CAS.
- E. M. Krop, M. M. Hetherington, S. Miquel and A. Sarkar, Food Qual. Prefer., 2019, 74, 118–124 CrossRef.
- S. Jahn and J. Klein, Macromolecules, 2015, 48, 5059–5075 CrossRef CAS.
- M. Wathier, B. A. Lakin, P. N. Bansal, S. S. Stoddart, B. D. Snyder and M. W. Grinstaff, J. Am. Chem. Soc., 2013, 135, 4930–4933 CrossRef CAS PubMed.
- G. Q. Liu, X. L. Wang, F. Zhou and W. M. Liu, ACS Appl. Mater. Interfaces, 2013, 5, 10842–10852 CrossRef CAS PubMed.
- O. Torres, E. Andablo-Reyes, B. S. Murray and A. Sarkar, ACS Appl. Mater. Interfaces, 2018, 10, 26893–26905 CrossRef CAS PubMed.
- A. Sarkar, F. Kanti, A. Gulotta, B. S. Murray and S. Y. Zhang, Langmuir, 2017, 33, 14699–14708 CrossRef CAS PubMed.
- M. L. Olivares, K. Shahrivar and J. de Vicente, J. Food Eng., 2019, 245, 157–165 CrossRef CAS.
- I. F. Farres, M. Douaire and I. T. Norton, Food Hydrocolloids, 2013, 32, 115–122 CrossRef.
- A. Gabriele, F. Spyropoulos and I. T. Norton, Soft Matter, 2010, 6, 4205–4213 RSC.
- D. A. Garrec and I. T. Norton, Food Hydrocolloids, 2013, 33, 160–167 CrossRef CAS.
- J. de Vicente, H. A. Spikes and J. R. Stokes, J. Tribol., 2006, 128, 795–800 CrossRef CAS.
- I. F. Farres and I. T. Norton, Food Hydrocolloids, 2015, 45, 186–195 CrossRef.
- T. Kairn, P. J. Daivis, I. Ivanov and S. N. Bhattacharya, J. Chem. Phys., 2005, 123, 194905 CrossRef CAS PubMed.
- R. G. Larson and P. S. Desai, Annu. Rev. Fluid Mech., 2015, 47, 47–65 CrossRef.
- S. Adams, W. J. Frith and J. R. Stokes, J. Rheol., 2004, 48, 1195–1213 CrossRef CAS.
- J. de Vicente, J. R. Stokes and H. A. Spikes, Proc. Inst. Mech. Eng., Part J, 2006, 220, 55–63 CrossRef.
- J. de Vicente, J. R. Stokes and H. A. Spikes, Food Hydrocolloids, 2006, 20, 483–491 CrossRef CAS.
- J. R. Stokes, L. Macakova, A. Chojnicka-Paszun, C. G. de Kruif and H. H. J. de Jongh, Langmuir, 2011, 27, 3474–3484 CrossRef CAS PubMed.
- A. Araiza-Calahorra and A. Sarkar, Food Struct., 2019, 21, 100113 CrossRef.
- W. C. K. Poon, E. R. Weeks and C. P. Royall, Soft Matter, 2012, 8, 21–30 RSC.
- A. Sarkar, E. Andablo-Reyes, M. Bryant, D. Dowson and A. Neville, Curr. Opin. Colloid Interface Sci., 2019, 39, 61–75 CrossRef CAS.
- A. Aufderhorst-Roberts, D. Baker, R. J. Foster, O. Cayre, J. Mattsson and S. D. Connell, Nanoscale, 2018, 10, 16050–16061 RSC.
- A. Sarkar, V. Ademuyiwa, S. Stubley, N. H. Esa, F. M. Goycoolea, X. F. Qin, F. Gonzalez and C. Olvera, Food Hydrocolloids, 2018, 84, 282–291 CrossRef CAS.
- O. Torres, A. Yamadaa, N. M. Rigby, T. Hanawab, Y. Kawano and A. Sarkar, Biotribology, 2019, 17, 8–18 CrossRef.
- J. Xie and Y. C. Jin, Eng. Appl. Comp. Fluid, 2016, 10, 111–129 Search PubMed.
- S. P. Meeker, R. T. Bonnecaze and M. Cloitre, J. Rheol., 2004, 48, 1295–1320 CrossRef CAS.
- J. de Vicente, J. R. Stokes and H. A. Spikes, Tribol. Lett., 2005, 20, 273–286 CrossRef.
- R. Avazmohammadi and P. P. Castaneda, J. Fluid Mech., 2015, 763, 386–432 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01802f |
| This journal is © The Royal Society of Chemistry 2019 |