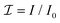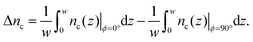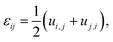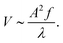Open Access Article
Open Access ArticleTravelling waves on photo-switchable patterned liquid crystal polymer films directed by rotating polarized light†
Ling
Liu
 a,
Dirk J.
Broer
a,
Dirk J.
Broer
 b and
Patrick R.
Onck
b and
Patrick R.
Onck
 *a
*a
aMicromechanics of Materials, Zernike Institute for Advanced Materials, University of Groningen, 9747 AG Groningen, The Netherlands. E-mail: p.r.onck@rug.nl
bDepartment of Chemical Engineering and Chemistry & Institute for Complex Molecular Systems (ICMS), Technology University of Eindhoven, 5600 MB Eindhoven, The Netherlands
First published on 1st October 2019
Abstract
Nature employs travelling waves to generate propulsion of fluids, cells and organisms. This has inspired the development of responsive material systems based on different external triggers. Especially light-actuation is suitable because of its remote control and scalability, but often complex, moving light sources are required. Here, we developed a method that only requires flood exposure by rotating the linear polarization of light to generate propagating surface waves on azobenzene-modified liquid crystalline polymer films. We built a photomechanical computational model that accounts for the attenuation of polarized light and trans-to-cis isomerization of azobenzene. A non-uniform in-plane distribution of the liquid crystal molecules allows for the generation of travelling surface waves whose amplitude, speed and direction can be controlled through the intensity, rotation direction and rotation speed of the linear polarization of a light source. Our method opens new avenues for motion control based on light-responsive topographical transformations for application in microfluidic lab-on-chip systems and soft robotics.
Introduction
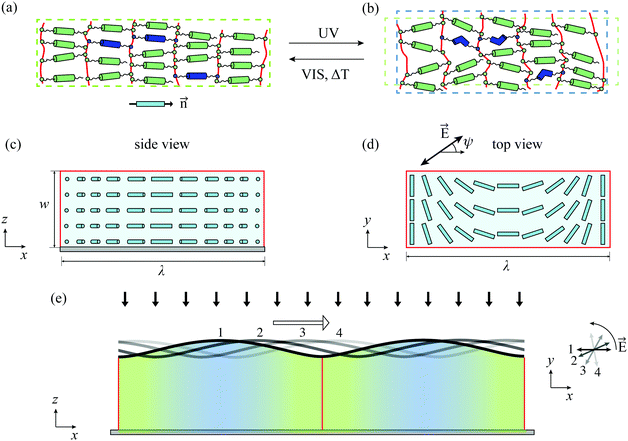
Swimming and fluid propulsion in nature occurs predominantly by the generation of traveling waves, such as the peristalsis of annelids and the human intestines, the swimming of fish, spermatozoa and synechococcus, and the metachronal waves of ciliates. This has formed the inspiration for many man-made propulsive systems for different applications, e.g., cargo transportation,1 fluid propulsion,2–4 robotics,5,6 autonomous swimming7–12 and caterpillar locomotion.13–15 A range of responsive material systems has been used, such as, gels,1,16 and liquid crystal polymers,2,10,13–15,17 that respond to various external triggers, like heating,1,14 electric18,19 and magnetic4,7,9 fields and light.2,8,10,13,15 By taking advantage of its remote, scalable and precise spatial-temporal control, light often is the most attractive actuation source and compares favorably with electric, magnetic and thermal actuation. However, the currently-available systems require complex matrix-like structured lenses, masks and mirrors and often requires a moving light source.2,8,10,13,20,21 In the current work, we demonstrate that travelling waves can be generated under uniform light exposure by rotating the linear polarization of light, representing a drastic reduction in complexity.We use liquid crystal (LC) glassy polymers networks as obtained by in situ polymerization of polyfunctional reactive mesogens, with embedded photo-responsive azobenzene chromophores, that undergo dimensional changes in response to ultra-violet (UV) light.22–29 Compared to LC elastomer systems, these glassy polymers feature a higher crosslink density.22 The azobenzene molecules are embedded in the polymer network as crosslinker and upon UV exposure transition from a rod-like trans state to a bent-like cis state (see Fig. 1(a and b)). This process decreases the orientational order of the neighbouring liquid crystal molecules, leading to an anisotropic mechanical response: a contraction along the average direction of the LC molecules (denoted by the director ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ) together with an expansion in the plane perpendicular to the director. Based on this mechanism, we have developed various surface topographical transformations that are reversibly controlled by light for substrate-constrained glassy LC films.25,30,31 The high-resolution imprinting of the internal molecular order using photo-alignment command layers provides the possibility to design complex director distributions and material anisotropies,32–34 and allows for miniaturization into the micrometer regime.26,27,35
) together with an expansion in the plane perpendicular to the director. Based on this mechanism, we have developed various surface topographical transformations that are reversibly controlled by light for substrate-constrained glassy LC films.25,30,31 The high-resolution imprinting of the internal molecular order using photo-alignment command layers provides the possibility to design complex director distributions and material anisotropies,32–34 and allows for miniaturization into the micrometer regime.26,27,35
In this study, we use a recently-developed optomechanical model25 to design travelling surface waves under a uniform continuous polarized light source that rotates in time. We take advantage of the selective absorption of the azobenzenes when oriented parallel to the electric field of the polarized light.24,36–38 As schematically shown in Fig. 1(c and d), the directors are all confined in the plane parallel to the substrate and feature a continuous rotation in the direction of the x axis, see Fig. 1(d). This periodic splay-bend pattern has been experimentally realized in liquid crystal elastomers.39 When the film is exposed to a uniform polarized light source, different regions have different trans-to-cis conversion levels due to the fact that the isomerization depends on the angle between the local director and the electric field of the polarized light. As a result, a periodic distribution of cis concentration is generated in the plane of the film and thus a surface undulation is formed. Upon rotation of the electric field in the x–y plane, a continuous change of the cis concentration field ensues leading to a travelling wave (see Fig. 1(e)). The propagating direction and speed of the wave can be tuned by inverting the rotation direction of the polarized light and by changing the rotation speed, respectively.
Results
Optimal wave amplitude at small and large film thicknesses
Under the illumination of a polarized light source, different regions absorb the incoming UV light differently due to the non-uniform director distribution resulting in varying angles ϕ between the local director![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) and the electric field
and the electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) . As given by the opto-mechanical constitutive equation (see eqn (8) in the Methods section), the cis volume fraction determines the photo-induced spontaneous deformation.
. As given by the opto-mechanical constitutive equation (see eqn (8) in the Methods section), the cis volume fraction determines the photo-induced spontaneous deformation.
Fig. 2(a and b) show the nc distribution and the normalized light intensity through the film depth for two combinations of the dimensionless light parameters α and β with α/β = 10 for various angles ϕ. The larger α and β values, which correspond to larger input intensities, feature a higher trans-to-cis conversion level, as expected. For both intensity levels, the cis generation is highest at the top surface when ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ‖
‖![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (ϕ = 0°). For ϕ = 0°, the light intensity is heavily attenuated (see Fig. 2(b)) leading to a sharp drop in cis fraction nc (Fig. 2(a)). For larger values of ϕ the light is less strongly absorbed so that it can penetrate deeper, leading to a more uniform distribution of the cis concentration with increasing ϕ (Fig. 2(a)). Note that for the extreme case ϕ = 90°, when
(ϕ = 0°). For ϕ = 0°, the light intensity is heavily attenuated (see Fig. 2(b)) leading to a sharp drop in cis fraction nc (Fig. 2(a)). For larger values of ϕ the light is less strongly absorbed so that it can penetrate deeper, leading to a more uniform distribution of the cis concentration with increasing ϕ (Fig. 2(a)). Note that for the extreme case ϕ = 90°, when ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ⊥
⊥![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) , the polarization coefficient ζ (see eqn (4), Method section) is minimal but not zero, since the azobenzene molecules are not perfectly aligned with the director (order parameter S = 0.8), so that still light is attenuated.
, the polarization coefficient ζ (see eqn (4), Method section) is minimal but not zero, since the azobenzene molecules are not perfectly aligned with the director (order parameter S = 0.8), so that still light is attenuated.
Next we ask the question which combination of incoming light intensity α and film thickness w should be selected for optimal wave amplitudes. These optimal amplitudes are generated when the average through thickness strain for ϕ = 0° is maximally different from that at ϕ = 90°. To quantify this, we define Δnc to be the difference in the cis volume fraction (averaged through the thickness) between ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ‖
‖![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) and
and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ⊥
⊥![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ,
,
Fig. 2(c) shows the variation of Δnc as a function of α and w/dt. For positive values of Δnc, the maximum (Δnc = 0.45) occurs at α ≈ 5 for thin films, which can be verified from Fig. 2(a). For this situation, the region where the director is parallel to the electric field has a higher cis conversion level, leading to surface protrusions at the ϕ = 0° regions. For negative values of Δnc, however, the situation is notably different. Here the maximum Δnc occurs at high intensities and thick films, which can be understood from the α = 40 case in Fig. 2(a). For that situation the cis distribution through the thickness for ϕ = 90° is much more uniform than for ϕ = 0°, leading to larger integrated nc levels and thus to surface protrusions at the ϕ = 90° regions.
Two distinct scenarios are explored in this work to illustrate the generation of travelling-wave-like topographical transformations controlled by rotating the linear polarization of a light source: thin films at a low level of input intensity and thick films at high intensity.
Thin films at low light intensity
Based on the maximum shown in Fig. 2(c), we select a light intensity of α = 5 and β = 0.5 and a thickness of w = 2dt. As shown in our previous work, the characteristic in-plane dimension relative to the film thickness is crucial for the surface topography of LC films with non-uniform director distributions25,40 and determines the mechanical interactions between the neighbouring regions with different director alignments. We start the analysis by taking the length of the unit cell λ (see Fig. 1(c and d)) to be 4 times the thickness, i.e., λ/w = 4. The top surface of the original film is assumed to be perfectly flat. Although we did not consider it here, possible minor surface reliefs during the photo-polymerization process25,31 can be readily incorporated.When the film is exposed to the polarized light, gradients in the cis volume fractions are formed both through the thickness and along the in-plane dimension (the x axis), see Fig. 3(a). Upon rotation of the polarized light, the locations of the maximal and minimal cis concentration change along the x-axis according to the electric field orientation, ψ = 0°, 30°, 60° and 90° (Fig. 3(a), see other orientations in Movies S1 and S2 in the ESI†). The resulting topographical transformations are shown in Fig. 3(b) for various ψ in the range from 0° to 180° (half a period of the rotating polarization, see Movie S2 in ESI†), during which the surface wave travels one wavelength λ. All the regions undergo expansion (the horizontal axis presents the original surface), due to the non-zero cis fraction everywhere and due to the fact that all the directors are in the x–y plane. For the situation with ψ = 0°, a surface protrusion is formed at the central region, in accordance with the cis generation in Fig. 3(a). Upon rotation of the polarized light, the peak of the protrusion moves in a direction that is guided by the rotation direction of the light and the distribution of the director in the plane of the film (Fig. 1(d)). As a result, the protrusion moves to the right under anti-clockwise rotation of the light in the plane of the film, see Fig. 1(e) and Movie S1 (ESI†). Note that a reversal of the rotation direction of the polarized light results in a reversal of the travelling wave direction, featuring great flexibility for a range of practical applications.
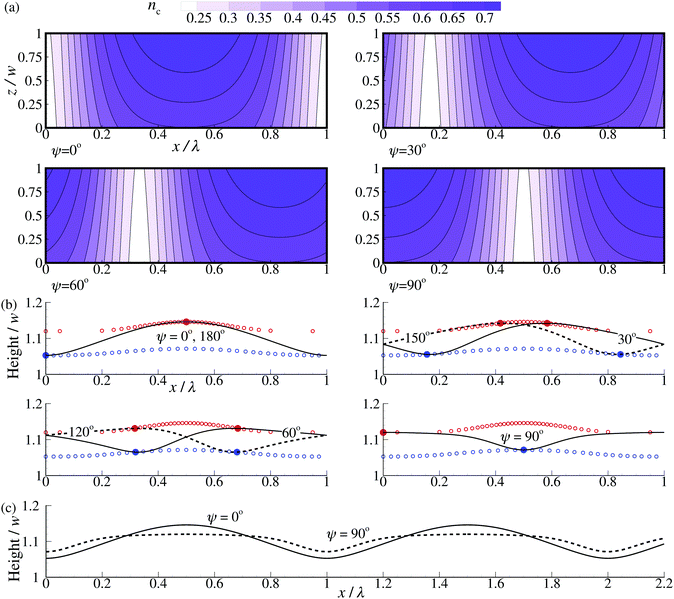 | ||
| Fig. 3 (a) Evolution of the trans-to-cis conversion by rotating the linear polarization of a light source at four different electric field directions: ψ = 0°, 30°, 60° and 90° for a thickness w/dt = 2, light intensity α = 5 and β = 0.5 and RVE size λ/w = 4. (b) The normalized surface profiles under various ψ. The red and blue open circles record the highest and lowest points for each tested electric field direction. (c) Two snapshots of the wave profile for ψ = 0° (solid line) and ψ = 90° (dash line). The waves are two unit cells long and the ψ = 90° curve is shifted over a distance λ/2. Movies of the simulations are added as ESI† (Movies S1 and S2). | ||
The amplitude of the surface wave is slightly changing during the movement. The red and blue open circles in Fig. 3(b) record the highest and lowest points, respectively, at every x-position along the film during one cycle (ψ ranging from 0° to 180° with an increment dψ = 5°). The wave amplitude is largest for ψ = 0° and smallest for ψ = 90° (see the red and blue circles in Fig. 3(b)). This is due to the anisotropy of the stiffness tensor. Another observation is that the specific surface profile is a function of the polarization angle ψ, see Fig. 3(c), with the peaks for ψ = 90° being wider than for ψ = 0°. This effect is also reflected by the non-uniform distribution of the red circles.
In order to quantify these surface profiles and how they change with ψ, we introduce two roughness parameters: the modulation and the root mean square (RMS) gradient, Sdq. The modulation is defined as the vertical distance between the highest and lowest points along the surface profile and the Sdq is a measure of the slope of the profiles (see the Methods section for their exact definition).
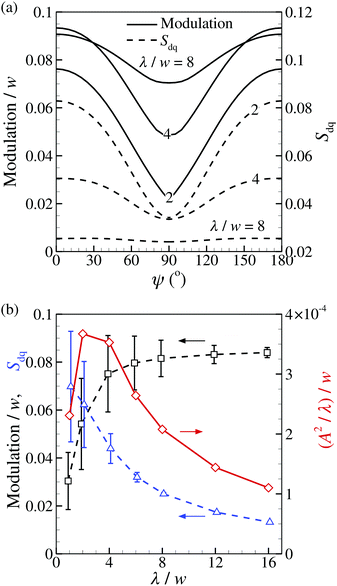
Fig. 4(a) plots the variation of the modulation, normalized by the thickness, and the Sdq as a function of the electric field direction, ψ. Both roughness parameters follow the same trend, reaching the highest value when the central part of the unit cell (see Fig. 1(d)) is most strongly actuated (ψ = 0°) and the lowest value when the electric field is rotated by 90 (ψ = 90°).
Next we study the effect of the in-plane dimension, λ. Simulations were conducted with a fixed thickness w = 2dt and a varying λ, showing that the modulation increases and the Sdq decreases with increasing λ, until they reach a ψ-independent roughness profile at large λ-values (see Fig. 4(a) and Fig. S1, ESI†). Since the roughness parameters themselves are dependent on the electric field direction, the average values are plotted in Fig. 4(b) with the corresponding error bars representing the standard deviation of the roughness parameters in the range 0° ≤ ψ ≤ 180°. Consistent with Fig. 4(a), the normalized modulation increases with λ/w until it reaches a plateau of 0.08 for λ/w ≥ 8. For small in-plane dimensions, the mechanical interactions between different regions are strong due to the large gradient in director orientations and the anisotropy in the photo-induced strains and the elastic constants (see for larger in-plane dimensions, these mechanical constraints are relaxed, resulting in larger expansions in the out-of-plane direction). The ψ-dependent standard deviation of the modulation is largest for the intermediate in-plane sizes (i.e., 2 ≤ λ/w ≤ 4) and decreases with a further increase of λ/w beyond 4 in Fig. 4(b). Fig. S1 (see ESI†) plots the evolution of the normalized surface profiles for λ/w = 16. The effect of the mechanical interaction is much lower than for λ/w = 4 so that at ψ = 90° the surface profile is similar to that at ψ = 0°, leading to the highest averaged modulation featuring a small variation (Fig. 4(b)). Thus, for larger λ/w, the amplitude of the surface wave is stable under the rotation of the polarized light, mimicking a peristaltic wave that moves at a constant velocity.41
In contrast to the modulation, Sdq decreases with increasing λ/w, due to the fact that the slope considers both the height change and the in-plane dimensions of the surface profiles. An increase of λ both increases the out-of-plane expansion (due to the relaxed mechanical constraints) as well as the in-plane dimensions, the competition of which results in a decreasing Sdq. The ψ-dependent standard deviation of Sdq is observed to continuously decrease with λ/w.
In order to illustrate the applicability of the travelling-surface-wave developed here for practical applications, such as, free-standing swimming10 and peristaltic fluid propulsion in microchannels,42,43 we introduce a Taylor index, A2/λ, with A the wave amplitude and λ the wavelength which is equal to the unit-cell length in our case; see the Methods section. Fig. 4(b) shows the Taylor index normalized by w, as a function of λ/w. We found that it first increases when λ < 2, then reaches a maximal value in the range 2 ≤ λ ≤ 4, which is followed by a sharp decrease for λ > 4. The results clearly show that the Taylor index is a convolution (e.g., a multiplication) of the modulation and the Sdq value, reaching an optimal free-swimming speed or fluid-propulsion velocity for an intermediate value of λ/w in the range between 2 and 4.
Thick films
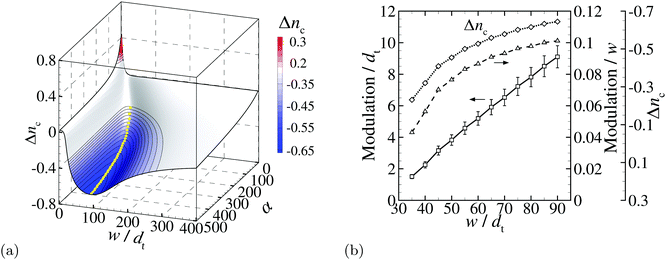
As illustrated in Fig. 2, in addition to the positive Δnc achieved using a low input intensity and a small thickness, one also can explore the negative Δnc regime using a large film thickness and a high intensity. An expanded study of the dependence of Δnc on w/dt and α is shown in Fig. 5(a), in which the regime with Δnc < −0.3 is highlighted by the blue contour plot. There is a trench (yellow dots) depicting the minimal Δnc. In contrast to the maximal positive Δnc of 0.45 for the thin film scenario, the minimal negative Δnc is continuously decreasing for increasing α and w/dt, even beyond the range shown in Fig. 5(a).We take w/dt = 40, α = 40 and β = 4 to demonstrate wave propagation for the thick film regime. The in-plane wavelength is selected to be λ/w = 4 to allow a direct comparison with Fig. 3. The evolution of the cis generation is shown in Fig. 6(a) for ψ = 0°, 30°, 60° and 90° (for the other orientations see Movie S5, ESI†). A large portion of the film remains fully in the trans (nc = 0) state, since the incoming light is strongly attenuated for these thick films, especially in regions with small ϕ values (see Fig. 2(a and b)). The only exception is the region where the director is more-or-less perpendicular to the electric field (80° < ϕ < 90°). In these regions, the cis conversion level at the surface of the film is lower than in other regions, but the attenuation is much lower, resulting in a further penetration of the light, resulting in larger uniform cis levels through the thickness. The surface profile evolution is plotted in Fig. 6(b) and shown in Movie S6 (ESI†). Here, a striking difference is observed with the travelling waves on the thin films (Fig. 3(b)). In Fig. 6, an input with ψ = 0 results in the largest expansion at x/λ = 0 and 1 for the thick films scheme where ϕ = 90°, while for the thin films this occurs at the center (x/λ = 0.5) where ϕ = 0°. The total out-of-plane deformation of the thick film is smaller, despite the increased light input energy, which is attributed to the large film thickness resulting in broad passive regions (Fig. 6(a)). In addition, the normalized wave amplitude is smaller than that of the thin films, due to the fact that Δnc = −0.32 in Fig. 6 and +0.45 in Fig. 3. However, while Δnc = +0.45 is maximal for the thin films, for the thick films Δnc can be further lowered by increasing α and w (see yellow dots in Fig. 5(a)), leading to values of the modulation/w (Fig. 5(b)) that are larger than the maximal value of 0.085 for the thin films (Fig. 4(b)). Here, the remarkable advantage of thick films comes about, since not only a larger thickness-normalized modulation can be reached, the absolute modulation values that can be generated are almost two orders of magnitude larger than these of the thin films (see the dt-normalized modulation in Fig. 5(b)).
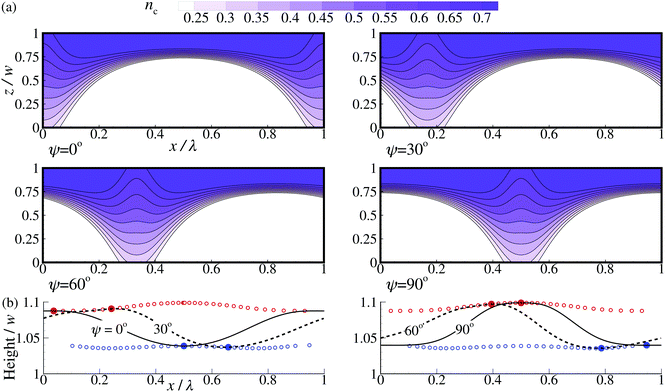 | ||
| Fig. 6 Evolution of the cis generation (a) and the surface profiles (b) under the rotating linear polarization of light with ψ = 0°, 30°, 60° and 90° for a film with the thickness w/dt = 40 and the light input α = 40. A movie of the simulation is added as ESI† (Movies S5 and S6). | ||
Discussion
We have developed a model that simulates travelling surface waves on azobenzene-modified liquid crystal polymeric systems induced by rotating the linear polarization of light. Both thin films with intermediate light intensities and thick films with high intensities are presented that demonstrate the feasibility of creating peristaltic surface motions, but with very different underlying photo-mechanical behaviour (compare Fig. 3 and 6).For application in miniaturized microfluidic devices,8 our method is able to generate well-controlled, peristaltic waves with small modulations on the order of 0.1 μm and wavelengths of several micrometers (take dt ≈ 1 μm for LC mixtures with 5 wt% azo-dosage25 in combination with Fig. 4). On the other hand our system can also generate travelling waves with modulations on the order of 10 μm (take dt ≈ 1 μm (ref. 25) in combination with modulation/dt = 10 for thick films in Fig. 5(b)). These modulations are a factor of 10 larger than in our previous work25 and are comparable with other light-controlled liquid crystal elastomer systems.10 Although it is not straightforward to make films with uniform directors through the depth of the film, considerable progress has recently been made in accurately controlling the director distribution in both thin44 and thick26 LC polymeric films. It should be noted that the absolute modulation can be further enhanced by increasing the film thickness and light intensity (Fig. 5).
To estimate the speed of the travelling waves, we can use the actuation frequency from a recent experimental study using a similar material system,38f = 0.014 s−1 (the light rotation speed is 2.5 s−1), leading to wave speeds U = λf of 0.11 μm s−1 and larger for films with λ/w = 4 and higher (cf.Fig. 3(b) taking dt = 1 μm). The wave speed can be further enhanced by an increase in actuation frequency, which has been observed for a glassy azobenzene-embedded LC polymer by a slight addition of visible light and temperature increase,38 attributed to a boosted cis-to-trans isomerization. Furthermore, a moderate addition of visible light is found to enhance the total light-induced strains due to the additional effect of continuous trans-cis-trans isomerization cycles,29,45,46 leading to wave amplitudes that can be a factor of 4 higher. Thus, we expect that the modulation and frequency can be further enhanced leading to larger wave speeds and amplitudes and thus a higher flow efficiency for peristaltic microfluidic propulsion.
Exposing azobenzene-doped LC samples to high intensity light (required for the thick films, e.g., ∼1.1 W cm−2 for α = 100 in Fig. 5 according to the light parameter calibration in ref. 25) is reported to soften the material,47 which is not considered in the current work. To estimate the effect of photo-softening, we have performed additional simulations by accounting for a reduction of the Young's modulus along the director, E11, and perpendicular to it, E22, by a factor that is larger than that experimentally reported (a reduction by a factor of 3 for UV intensity I0 = 300 mW cm−2 (ref. 47)). Only a negligible difference was found compared with the non-softening results (see Fig. S2 for details, ESI†).
The specific shape and speed of the surface waves can be controlled by the film thickness and light intensity. For intermediate film thicknesses, for which both positive and negative Δnc can be reached by tuning the light intensity (cf.Fig. 2(c)), the amplitude of the wave can be controlled and even reduced to zero (Δnc ≈ 0), while keeping the rotation speed of the polarizer unaffected. In addition, the direction of the waves is guided by the rotation direction of the polarizer. Thus, the wave amplitude, wave speed and wave direction can be tuned through the light intensity, rotation speed and rotation direction of the polarized light source. This versatility allows application of this system for microfluidic propulsion in lab-on-chip devices,2,39,48 light-driven swimming and locomotion10,15,49 and integrated soft robotics.5,11,50
Methods
Light attenuation model
Upon UV exposure, the driving mechanism of the spontaneous deformation of azobenzene-modified liquid crystal polymeric networks is the conversion of azobenzene from the trans to the cis state, as shown in Fig. 1(c and d). The conversion depends on the wavelength and the local light intensity. The nonlinear light attenuation model, developed by Corbett and Warner.51–53 We assume the incoming light to propagate in the negative z-direction from the top surface (z = w) to the bottom (z = 0), where w is the thickness of the film (see Fig. 1(c)). The local light intensity at location z and time t is denoted by I(z,t) and the corresponding input intensity is I0. The evolution of the isomerization process consists of three contributions: (i) the photo-induced trans-to-cis forward reaction, (ii) the photo-induced cis-to-trans backward reaction, and (iii) the thermally-driven spontaneous cis-to-trans backward reaction. The governing equations for the light penetration are:25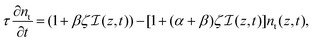 | (1) |
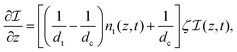 | (2) |
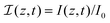 is the reduced local light intensity. The dimensionless parameter α captures the ability of the incoming light to trigger the forward trans-to-cis conversion with respect to the thermally-driven back reaction. The coefficient β has a similar meaning for the cis-to-trans conversion. The parameters dt and dc are the attenuation lengths of the trans and cis azobenzenes, respectively, and they are related to the ratio of the quantum efficiencies η = ηt/ηc by
is the reduced local light intensity. The dimensionless parameter α captures the ability of the incoming light to trigger the forward trans-to-cis conversion with respect to the thermally-driven back reaction. The coefficient β has a similar meaning for the cis-to-trans conversion. The parameters dt and dc are the attenuation lengths of the trans and cis azobenzenes, respectively, and they are related to the ratio of the quantum efficiencies η = ηt/ηc by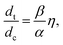 | (3) |
The parameter ζ is the polarization coefficient and is defined for polarized light illumination as54
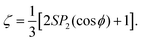 | (4) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) and the electric field of the incoming light
and the electric field of the incoming light ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) . The S is the order parameter, describing the average orientational order of the local liquid crystal molecules with respect to the director
. The S is the order parameter, describing the average orientational order of the local liquid crystal molecules with respect to the director ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) .22 If the electric field is parallel to the director,
.22 If the electric field is parallel to the director, ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ‖
‖![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) , the polarization coefficient ζ equals 1 when the order parameter S = 1, indicating that the embedded azobenzenes, which follow the orientational order of the LC molecules, can fully absorb the UV light and thus the isomerization is maximized. On the other hand, if
, the polarization coefficient ζ equals 1 when the order parameter S = 1, indicating that the embedded azobenzenes, which follow the orientational order of the LC molecules, can fully absorb the UV light and thus the isomerization is maximized. On the other hand, if ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ⊥
⊥![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) , the probability of the azobenzenes to undergo isomerization is low (i.e., ζ = 0 when S = 1), leading to a minimal effective absorption. Since the azobenzenes are covalently bonded to the polymer network, they return to their original orientation when falling back from the cis to the trans state during cyclic isomerization. Typical values of the order parameter S of nematic glassy liquid crystal polymer networks range from 0.5 to 0.8.22,56 Here, we assume the order parameter to be constant (S = 0.8), since the loss of order in heavily-crosslinked glassy LC polymers is usually found to be small.22,25,37
, the probability of the azobenzenes to undergo isomerization is low (i.e., ζ = 0 when S = 1), leading to a minimal effective absorption. Since the azobenzenes are covalently bonded to the polymer network, they return to their original orientation when falling back from the cis to the trans state during cyclic isomerization. Typical values of the order parameter S of nematic glassy liquid crystal polymer networks range from 0.5 to 0.8.22,56 Here, we assume the order parameter to be constant (S = 0.8), since the loss of order in heavily-crosslinked glassy LC polymers is usually found to be small.22,25,37
One can get the temporal evolution of the trans and cis fractions and the local intensity by solving the coupled partial differential eqn (1) and (2) subject to the boundary condition 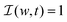 and the initial condition nt(z,0) = 1. The time needed to reach an equilibrium (photo-stationary) state for the deformation is observed to be fast for glassy LC polymers, typically in the range of a few seconds.15,25,31,45,57 Here we assume this time to be smaller than the period of rotation of the polarized light,38 so that we only focus on the photo-stationary state. We thus apply ∂nt/∂t = 0 in eqn (1), leading to
and the initial condition nt(z,0) = 1. The time needed to reach an equilibrium (photo-stationary) state for the deformation is observed to be fast for glassy LC polymers, typically in the range of a few seconds.15,25,31,45,57 Here we assume this time to be smaller than the period of rotation of the polarized light,38 so that we only focus on the photo-stationary state. We thus apply ∂nt/∂t = 0 in eqn (1), leading to
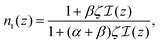 | (5) |
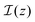 .
.
The values of the dimensionless light coefficients α and β depend on the wavelength and scale with the intensity of the incoming light, I0. The attenuation lengths, dt and dc, are dependent on the concentration of the azobenzene as well as the wavelength of the light source. These parameters can be obtained by fitting the results of the light attenuation equations to the measured transmitted intensities through a reference sample, which were found to be in excellent agreement with experimental data.25 In the current study, however, we explore their effect on the generation of travelling waves. The attenuation length dt is inversely proportional to the concentration of the azobenzene added to the LC polymer and falls typically in the sub-micrometer range for heavily-dozed polymers,24 and in the range from a few micrometers25,29,58 to a few tens of micrometers59 for systems with relatively low azo-dosages. Thicknesses of LC films fall in the range from a few to tens of micrometers.22,60 Here, we fix dt to 1 μm and vary the thickness of the film w. The quantum efficiency ratio η is taken to be equal to 3.25,59 We vary the light input intensity α and keep α/β = 10, which fixes dc through eqn (3).
It should be noted that the polarization can change when the light travels through the film due to the birefringence effect of the liquid crystal. This is not the case when the electric field is parallel or perpendicular to the director, but it will develop in intermediate cases where the polarization changes cyclically from a linear, to elliptical to orthogonal linear. As a result, the actual through-thickness distribution of nc will be affected for these intermediate cases. In the current paper, however, these effects are not accounted for. Eqn (4) is used to capture the general probability of the UV light absorption by the embedded azobenzenes. In a similar experimental implementation,38 in which the uniaxially-aligned liquid crystal film is exposed to a rotating linear polarization of light, the surface features a continuously undulatory height change.
Optomechanical equations
A local coordinate framework is defined in which the local x1 axis is parallel to the director![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ‖
‖![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) (see Fig. 1(a)). The components of the total strain tensor with respect to this local reference frame can be written as
(see Fig. 1(a)). The components of the total strain tensor with respect to this local reference frame can be written as| εij = εeij + εphij, | (6) |
| σij = Cijklεekl = Cijkl(εkl − εphkl), | (7) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) when an extension is applied along the director, the Poisson's ratio inside the isotropic plane μ23 and the shear moduli parallel to the director G12 = G13. For all simulations, we adopt Young's moduli that are close the measured data,25E11 = 1 GPa and E22 = E33 = 0.5 GPa. In contrast to the incompressibility of rubber-like elastomeric LC systems,61 typical elastic Poisson's ratios are in the range 0.3–0.4,57 which means that elastic stresses can result in changes in volume. Here we take μ12 = μ13 = μ23 = 0.3. The shear modulus along the director is set as G12 = G13 = E11/(2(1 + μ12)) = 384.6 MPa. We assume all the elastic properties to be uniform throughout the film and constant during the deformations.
when an extension is applied along the director, the Poisson's ratio inside the isotropic plane μ23 and the shear moduli parallel to the director G12 = G13. For all simulations, we adopt Young's moduli that are close the measured data,25E11 = 1 GPa and E22 = E33 = 0.5 GPa. In contrast to the incompressibility of rubber-like elastomeric LC systems,61 typical elastic Poisson's ratios are in the range 0.3–0.4,57 which means that elastic stresses can result in changes in volume. Here we take μ12 = μ13 = μ23 = 0.3. The shear modulus along the director is set as G12 = G13 = E11/(2(1 + μ12)) = 384.6 MPa. We assume all the elastic properties to be uniform throughout the film and constant during the deformations.
The anisotropic spontaneous response resulting from the azobenzene isomerization is captured by the photo-induced eigenstrains εphij. These strains are assumed to be linearly proportional to the volume fraction of the cis molecules,25,58,59
| εphij = Pijnc. | (8) |
To complete the mechanical framework, the stress equilibrium equations and the kinematic equations are adopted to supplement the constitutive equations (eqn (7)),
| σij,j = 0, |
where the operator (
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ),j denotes differentiation with respect to the coordinate j, i.e., ∂()/∂xj, and the Einstein summation convention is used in case of repeated indices. Since the liquid crystal alignment is continuously changing inside the film (see the director distribution in Fig. 1(c and d)), the director-guided photo-induced deformations are non-uniform throughout the film. As a result, stresses build up due to the mismatch of these deformations, the anisotropy of the material and the constraints imposed by the rigid substrate.
),j denotes differentiation with respect to the coordinate j, i.e., ∂()/∂xj, and the Einstein summation convention is used in case of repeated indices. Since the liquid crystal alignment is continuously changing inside the film (see the director distribution in Fig. 1(c and d)), the director-guided photo-induced deformations are non-uniform throughout the film. As a result, stresses build up due to the mismatch of these deformations, the anisotropy of the material and the constraints imposed by the rigid substrate.
In this study, periodic boundary conditions are employed on the lateral surfaces of the unit cell (see the red box in Fig. 1), in which the director rotates a full 180° in a span of λ. All displacements at the bottom surface are zero due to the perfect bonding to the rigid substrate and the top surface is traction free. The above framework is implemented numerically in the finite element package Abaqus/Standard.
Roughness parameters
Roughness parameters are introduced to quantify the surface waves. We take the discretized point set of the top surface before the light exposure to be defined by the points (i,j) with coordinates (x(i,j),y(i,j),z0), where i = 1, 2,…M, j = 1, 2,…N and z0 = w. Upon actuation, the points undergo the displacements (ux(i,j),uy(i,j),uz(i,j)). The first roughness parameter used here is the modulation depth,30,40 defined as the vertical distance between the highest and lowest points along the surface profile,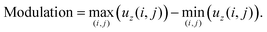 | (9) |
We also adopt a roughness parameter that is able to incorporate the slope of the different profiles. Here, the root mean square (RMS) gradient,68Sdq, is employed to characterize the slope of the corrugated surfaces,
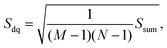 | (10) |
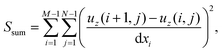 | (11) |
To analyze the applicability of the controllable travelling-wave developed here, we focus on the swimming speed V of a free-standing sheet featuring travelling waves with a speed of U = λf on its surface,7,10,43 or the propulsion speed V of fluid through a channel whose surfaces generate a peristaltic wave,69,70 to be
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research forms a part of the research programme of the Dutch Polymer Institute (DPI), project #775 TOPSWITCH. D. J. Broer acknowledges funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement 669991. The authors would like to thank Prof. Jaap den Toonder, Dr Danqing Liu, Edwin De Jong and Matthew Hendrikx for useful discussions.References
- V. Nistor, J. Cannell, J. Gregory and L. Yeghiazarian, Stimuli-responsive cylindrical hydrogels mimic intestinal peristalsis to propel a solid object, Soft Matter, 2016, 12, 3582–3588 RSC.
- J. Lv, Y. Liu, J. Wei, E. Chen, L. Qin and Y. Yu, Photocontrol of fluid slugs in liquid crystal polymer microactuators, Nature, 2016, 537, 179–184 CrossRef CAS PubMed.
- S. Khaderi, J. den Toonder and P. Onck, Microfluidic propulsion by the metachronal beating of magnetic artificial cilia: a numerical analysis, J. Fluid Mech., 2011, 688, 44–65 CrossRef.
- S. Khaderi, C. Craus, J. Hussong, N. Schorr, J. Belardi and J. Westerweel, et al., Magnetically-actuated artificial cilia for microfluidic propulsion, Lab Chip, 2011, 11(12), 2002–2010 RSC.
- A. J. Ijspeert, Biorobotics: Using robots to emulate and investigate agile locomotion, Science, 2014, 346(6206), 196–203 CrossRef CAS.
- B. J. Gemmell, S. P. Colin, J. H. Costello and J. O. Dabiri, Suction-based propulsion as a basis for efficient animal swimming, Nat. Commun., 2015, 6, 8790 CrossRef CAS PubMed.
- E. Diller, J. Zhuang, G. Z. Lum, M. R. Edwards and M. Sitti, Continuously distributed magnetization profile for millimeter-scale elastomeric undulatory swimming, Appl. Phys. Lett., 2014, 104, 174101 CrossRef.
- C. Huang, J. Lv, X. Tian, Y. Wang, Y. Yu and J. Liu, Miniaturized swimming soft robot with complex movement actuated and controlled by remote light signals, Sci. Rep., 2015, 5, 17414 CrossRef CAS PubMed.
- T. Li, J. Li, H. Zhang, X. Chang, W. Song and Y. Hu, et al., Magnetically Propelled Fish-Like Nanoswimmers, Small, 2016, 12, 6098–6105 CrossRef CAS PubMed.
- S. Palagi, A. G. Mark, S. Y. Reigh, K. Melde, T. Qiu and H. Zeng, et al., Structured light enables biomimetic swimming and versatile locomotion of photoresponsive soft microrobots, Nat. Mater., 2016, 15, 647–653 CrossRef CAS PubMed.
- S. J. Park, M. Gazzola, K. S. Park, S. Park, V. Di Santo and E. L. Blevins, et al., Phototactic guidance of a tissue-engineered soft-robotic ray, Science, 2016, 353(6295), 158–162 CrossRef CAS.
- S. Namdeo, S. Khaderi, J. den Toonder and P. Onck, Swimming direction reversal of flagella through ciliary motion of mastigonemes a, Biomicrofluidics, 2011, 5(3), 034108 CrossRef CAS.
- M. Rogóż, H. Zeng, C. Xuan, D. S. Wiersma and P. Wasylczyk, Light-Driven Soft Robot Mimics Caterpillar Locomotion in Natural Scale, Adv. Opt. Mater., 2016, 4, 1689–1694 CrossRef.
- X. Liu, S. K. Kim and X. Wang, Thermomechanical Liquid Crystalline Elastomer Capillary with Biomimetic Peristaltic Crawling Function, J. Mater. Chem. B, 2016, 4, 7293–7302 RSC.
- A. H. Gelebart, D. J. Mulder, M. Varga, A. Konya, G. Vantomme and E. Meijer, et al., Making waves in a photoactive polymer film, Nature, 2017, 546(7660), 632–636 CrossRef CAS PubMed.
- Y. Murase, S. Maeda, S. Hashimoto and R. Yoshida, Design of a mass transport surface utilizing peristaltic motion of a self-oscillating gel, Langmuir, 2008, 25(1), 483–489 CrossRef PubMed.
- H. Zeng, P. Wasylczyk, C. Parmeggiani, D. Martella, M. Burresi and D. S. Wiersma, Light-Fueled Microscopic Walkers, Adv. Mater., 2015, 27, 3883–3887 CrossRef CAS PubMed.
- N. T. Jafferis, H. A. Stone and J. C. Sturm, Traveling wave-induced aerodynamic propulsive forces using piezoelectrically deformed substrates, Appl. Phys. Lett., 2011, 99(11), 114102 CrossRef.
- K. Nakahara, M. Yamamoto, Y. Okayama, K. Yoshimura, K. Fukagata and N. Miki, A peristaltic micropump using traveling waves on a polymer membrane, J. Micromech. Microeng., 2013, 23(8), 085024 CrossRef.
- J. H. Na, N. P. Bende, J. Bae, C. D. Santangelo and R. C. Hayward, Grayscale gel lithography for programmed buckling of non-Euclidean hydrogel plates, Soft Matter, 2016, 12(22), 4985–4990 RSC.
- D. Liu, C. W. M. Bastiaansen, J. M. J. den Toonder and D. J. Broer, Light-Induced Formation of Dynamic and Permanent Surface Topologies in Chiral-Nematic Polymer Networks, Macromolecules, 2012, 45, 8005–8012, DOI:10.1021/ma301628h.
- T. J. White and D. J. Broer, Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS PubMed.
- L. Hines, K. Petersen, G. Z. Lum and M. Sitti, Soft Actuators for Small-Scale Robotics, Adv. Mater., 2017, 29, 1603483 CrossRef PubMed.
- Y. Yu, M. Nakano and T. Ikeda, Photomechanics: directed bending of a polymer film by light, Nature, 2003, 425, 145 CrossRef CAS PubMed.
- D. Liu, L. Liu, P. R. Onck and D. J. Broer, Reverse switching of surface roughness in a self-organized polydomain liquid crystal coating, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3880–3885 CrossRef CAS PubMed . Available from: http://www.pnas.org/content/112/13/3880.abstract.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Voxelated liquid crystal elastomers, Science, 2015, 347, 982–984 CrossRef CAS.
- C. L. van Oosten, C. W. Bastiaansen and D. J. Broer, Printed artificial cilia from liquid-crystal network actuators modularly driven by light, Nat. Mater., 2009, 8, 677–682 CrossRef CAS.
- S. Iamsaard, S. J. Aßhoff, B. Matt, T. Kudernac, J. J. Cornelissen and S. P. Fletcher, et al., Conversion of light into macroscopic helical motion, Nat. Chem., 2014, 6, 229 CrossRef CAS.
- L. Liu and P. R. Onck, Enhanced deformation of azobenzene-modified liquid crystal polymers under dual wavelength exposure: A photophysical model, Phys. Rev. Lett., 2017, 119(5), 057801 CrossRef.
- D. Liu, C. W. M. Bastiaansen, J. M. J. den Toonder and D. J. Broer, Photo-Switchable Surface Topologies in Chiral Nematic Coatings, Angew. Chem., Int. Ed., 2012, 51, 892–896, DOI:10.1002/anie.201105101.
- D. Liu and D. J. Broer, Self-assembled Dynamic 3D Fingerprints in Liquid-Crystal Coatings Towards Controllable Friction and Adhesion, Angew. Chem., Int. Ed., 2014, 126, 4630–4634, DOI:10.1002/ange.201400370.
- L. T. de Haan, C. Sánchez-Somolinos, C. M. Bastiaansen, A. P. Schenning and D. J. Broer, Engineering of complex order and the macroscopic deformation of liquid crystal polymer networks, Angew. Chem., Int. Ed., 2012, 51, 12469–12472 CrossRef CAS PubMed.
- C. Mostajeran, M. Warner, T. H. Ware and T. J. White, The Royal Society. Encoding Gaussian curvature in glassy and elastomeric liquid crystal solids, Proc. R. Soc. A, 2016, 472, 20160112 CrossRef PubMed.
- C. Modes, M. Warner, C. Sanchez-Somolinos, L. de Haan and D. J. Broer, The Royal Society. Angular deficits in flat space: remotely controllable apertures in nematic solid sheets, Proc. R. Soc. A, 2013, 469, 20120631 CrossRef.
- H. Zeng, D. Martella, P. Wasylczyk, G. Cerretti, J. C. G. Lavocat and C. H. Ho, et al., High-resolution 3D direct laser writing for liquid-crystalline elastomer microstructures, Adv. Mater., 2014, 26, 2319–2322 CrossRef CAS PubMed.
- T. J. White, N. V. Tabiryan, S. V. Serak, U. A. Hrozhyk, V. P. Tondiglia and H. Koerner, et al., A high frequency photodriven polymer oscillator, Soft Matter, 2008, 4, 1796–1798 RSC.
- C. C. Li, C. W. Chen, C. K. Yu, H. C. Jau, J. A. Lv and X. Qing, et al., Arbitrary Beam Steering Enabled by Photomechanically Bendable Cholesteric Liquid Crystal Polymers, Adv. Opt. Mater., 2017, 5(4), 1600824, DOI:10.1002/adom.201600824.
- M. Hendrikx, A. P. H. J. Schenning and D. J. Broer, Patterned oscillating topographical changes in photoresponsive polymer coatings, Soft Matter, 2017, 13, 4321–4327, 10.1039/C7SM00699C.
- G. Babakhanova, H. Yu, I. Chaganava, Q. H. Wei, P. Shiller and O. D. Lavrentovich, Controlled Placement of Microparticles at the Water-Liquid Crystal Elastomer Interface, ACS Appl. Mater. Interfaces, 2019, 11(16), 15007–15013 CrossRef CAS PubMed.
- L. Liu and P. R. Onck, Computational Modelling of Light-triggered Topography Changes of Azobenzene-modified Liquid Crystal Polymer Coatings, in Responsive Polymer Surfaces-Dynamics in Surface Topographies and Properties, ed. D. Liu and D. J. Broer, Wiley, 2017 Search PubMed.
- S. Maeda, Y. Hara, R. Yoshida and S. Hashimoto, Peristaltic motion of polymer gels, Angew. Chem., 2008, 120(35), 6792–6795 CrossRef.
- N. T. Nguyen, X. Huang and T. K. Chuan, MEMS-micropumps: a review, J. Fluids Eng., 2002, 124(2), 384–392 CrossRef.
- G. Taylor, The Royal Society. Analysis of the swimming of microscopic organisms, Proc. R. Soc. A, 1951, 209, 447–461 CrossRef.
- K. Nickmans, J. N. Murphy, B. de Waal, P. Leclère, J. Doise and R. Gronheid, et al., Sub-5 nm Patterning by Directed Self-Assembly of Oligo (Dimethylsiloxane) Liquid Crystal Thin Films, Adv. Mater., 2016, 28(45), 10068–10072 CrossRef CAS PubMed.
- D. Liu and D. J. Broer, New insights into photoactivated volume generation boost surface morphing in liquid crystal coatings, Nat. Commun., 2015, 6, 8334 CrossRef CAS PubMed.
- D. Liu, N. B. Tito and D. J. Broer, Protruding organic surfaces triggered by in-plane electric fields, Nat. Commun., 2017, 8(1), 1526 CrossRef PubMed.
- K. Kumar, A. P. Schenning, D. J. Broer and D. Liu, Regulating the modulus of a chiral liquid crystal polymer network by light, Soft Matter, 2016, 12, 3196–3201 RSC.
- M. M. Teymoori and E. Abbaspour-Sani, Design and simulation of a novel electrostatic peristaltic micromachined pump for drug delivery applications, Sens. Actuators, A, 2005, 117(2), 222–229 CrossRef CAS.
- M. Camacho-Lopez, H. Finkelmann, P. Palffy-Muhoray and M. Shelley, Fast liquid-crystal elastomer swims into the dark, Nat. Mater., 2004, 3, 307–310 CrossRef CAS PubMed.
- L. Ricotti, B. Trimmer, A. W. Feinberg, R. Raman, K. K. Parker and R. Bashir, et al., Biohybrid actuators for robotics: A review of devices actuated by living cells, Sci. Robot., 2017, 2(12), eaaq0495 CrossRef.
- D. Corbett and M. Warner, Linear and Nonlinear Photoinduced Deformations of Cantilevers, Phys. Rev. Lett., 2007, 99, 174302, DOI:10.1103/PhysRevLett.99.174302.
- D. Corbett, C. L. van Oosten and M. Warner, Nonlinear dynamics of optical absorption of intense beams, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 013823, DOI:10.1103/PhysRevA.78.013823.
- D. Corbett and M. Warner, Bleaching and stimulated recovery of dyes and of photocantilevers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051710, DOI:10.1103/PhysRevE.77.051710.
- D. Corbett and M. Warner, Polarization dependence of optically driven polydomain elastomer mechanics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061701, DOI:10.1103/PhysRevE.78.061701..
- D. Statman and I. Janossy, Study of photoisomerization of azo dyes in liquid crystals, J. Chem. Phys., 2003, 118, 3222 CrossRef CAS.
- I. Heynderickx, D. Broer, H. Van Den Boom and W. Teesselink, Liquid-crystalline ordering in polymeric networks as studied by polarized Raman scattering, J. Polym. Sci., Part B: Polym. Phys., 1992, 30, 215–220 CrossRef CAS.
- C. L. van Oosten, K. Harris, C. Bastiaansen and D. J. Broer, Glassy photomechanical liquid-crystal network actuators for microscale devices, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 329–336 CrossRef CAS PubMed.
- C. L. van Oosten, D. Corbett, D. Davies, M. Warner, C. W. Bastiaansen and D. J. Broer, Bending dynamics and directionality reversal in liquid crystal network photoactuators, Macromolecules, 2008, 41, 8592–8596 CrossRef CAS.
- M. Knežević, M. Warner, M. Čopič and A. Sánchez-Ferrer, Photodynamics of stress in clamped nematic elastomers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062503 CrossRef PubMed.
- D. Liu and D. J. Broer, Liquid crystal polymer networks: switchable surface topographies, Liq. Cryst. Rev., 2013, 1, 20–28, DOI:10.1080/21680396.2013.766410.
- M. Warner and E. M. Terentjev, Liquid crystal elastomers, Oxford University Press, 2003, vol. 120 Search PubMed.
- M. Warner, C. Modes and D. Corbett, Curvature in nematic elastica responding to light and heat, Proc. R. Soc. A, 2010, 466, 2975–2989 CrossRef.
- K. D. Harris, R. Cuypers, P. Scheibe, C. L. van Oosten, C. W. M. Bastiaansen and J. Lub, et al., Large amplitude light-induced motion in high elastic modulus polymer actuators, J. Mater. Chem., 2005, 15, 5043–5048, 10.1039/B512655J.
- A. Elias, K. Harris, C. Bastiaansen, D. Broer and M. Brett, Photopatterned liquid crystalline polymers for microactuators, J. Mater. Chem., 2006, 16(28), 2903–2912 RSC.
- G. N. Mol, K. D. Harris, C. W. Bastiaansen and D. J. Broer, Thermo-Mechanical Responses of Liquid-Crystal Networks with a Splayed Molecular Organization, Adv. Funct. Mater., 2005, 15, 1155–1159 CrossRef CAS.
- M. L. Smith, K. M. Lee, T. J. White and R. A. Vaia, Design of polarization-dependent, flexural-torsional deformation in photo responsive liquid crystalline polymer networks, Soft Matter, 2014, 10, 1400–1410, 10.1039/C3SM51865E.
- Y. You, C. Xu, S. Ding and Y. Huo, Coupled effects of director orientations and boundary conditions on light induced bending of monodomain nematic liquid crystalline polymer plates, Smart Mater. Struct., 2012, 21, 125012 CrossRef . Available from: http://stacks.iop.org/0964-1726/21/i=12/a=125012.
- E. S. Gadelmawla, M. M. Koura, T. M. A. Maksoud, I. M. Elewa and H. H. Soliman, Roughness parameters, J. Mater. Process. Technol., 2002, 123, 133–145 CrossRef . Available from: http://www.sciencedirect.com/science/article/pii/S0924013602000602.
- B. Felderhof, Swimming and peristaltic pumping between two plane parallel walls, J. Phys.: Condens. Matter, 2009, 21(20), 204106 CrossRef CAS PubMed.
- E. Lauga and T. R. Powers, The hydrodynamics of swimming microorganisms, Rep. Prog. Phys., 2009, 72(9), 096601 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01594a |
| This journal is © The Royal Society of Chemistry 2019 |