Self-assembly and adsorption of cetyltrimethylammonium bromide and didodecyldimethylammonium bromide surfactants at the mica–water interface

Abstract

The self-assembly and adsorption of the surfactants cetyltrimethylammonium bromide (CTAB) and didodecyldimethylammonium bromide (DDAB) at the muscovite mica–water interface are studied using molecular-dynamics simulations. Adsorption takes place by an ion-exchange mechanism, in which K⁺ ions are replaced by the organic alkylammonium cations from the solution. Simulations are performed with and without the surface K⁺ ions, with pure water, and with the surfactants in aqueous solution. CTAB and DDAB form micellar structures in bulk solution, and in the absence of the surface K⁺ ions, they quickly adsorb and form bilayer structures. The bilayer ordering of CTAB is not perfect, and there is a competition with the formation of cylindrical micelles. DDAB, on the other hand, forms a well-ordered bilayer structure, with the innermost layer showing strong orientational ordering, and the outermost layer being more disordered. The simulations with pure water highlight the molecular ordering and strong electrostatic interactions with the mica-surface atoms. Using simulated scattering length density profiles, the results are compared directly and critically with existing neutron reflectivity measurements. The simulation results are generally consistent with experiments, and yield new insights on the molecular-scale ordering at the mica–water interface.

---

1 Introduction

Surface active agents (surfactants) are amphiphilic molecules with a broad range of applications, such as detergents, emulsifiers, wetting agents, dispersants, and solubilisers, due to their ability to undergo self-assembly and adsorption at interfaces. They consist of a hydrophobic part, which is usually a hydrocarbon backbone, and a polar, hydrophilic part, known as the head group, which may also be charged. The most significant property of surfactants is the ability to adsorb at interfaces,^1–11 which can dramatically change the properties of the interface. The adsorption pathway and associated dynamics are very important, and the structures of the adsorbed layers can change significantly with time. Below the critical micelle concentration (CMC), adsorption is a sequential molecular process. Above the CMC, adsorption can also involve self-assembled aggregates, and the surface reorganisation of these objects can be slow,¹² or may not happen at all. One example that is germane to the current work, and which will be detailed below, is the adsorption of a surfactant at a solid-water interface. At low surfactant concentration, an adsorbed monolayer may be formed. At high surfactant concentration, above the CMC, the surfactant can form cylindrical micelles, which may adsorb at the interface. Over time these micelles reorganise to form a bilayer structure.¹²

The surfactants studied in this work are hexadecyltrimethylammonium bromide [or cetyltrimethylammonium bromide (CTAB)] and didodecyldimethylammonium bromide (DDAB). CTAB is an antiseptic agent, and a surfactant used in DNA extraction. DDAB is a phase-transfer catalyst, often used in biological applications. The molecular structures are shown in Fig. 1. The focus of this work is the adsorption of these surfactants at the mica–water interface. Common mica [KAl₃Si₃O₁₀(OH)₂] is a form of aluminium potassium silicate mineral with easily cleaved, atomically smooth surfaces, making it a convenient substrate for adsorption studies. During cleaving, mica surfaces can become charged, attract oppositely charged particles, and participate in adsorption and ion-exchange mechanisms, and these have long been studied in the case of simple inorganic ions.^13–19 When immersed in an aqueous solution of an ionic surfactant, the external potassium layer of the slab can be exchanged with large organic cations.^16,20 The specific literature on CTAB and DDAB is discussed below.

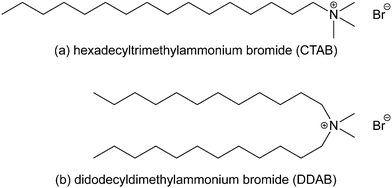Fig. 1 The molecular structures of (a) hexadecyltrimethylammonium bromide (or cetyltrimethylammonium bromide, CTAB) and (b) didodecyldimethylammonium bromide (DDAB).

There has been a lot of experimental and simulation work on CTAB in aqueous solutions, with varying results. CTAB is known to form micelles of various shapes in water and other solvents.^21–23 The CMC is estimated to be about 9 × 10⁻⁴ mol L⁻¹,^21,24 equivalent to about 0.03 wt%. Sun et al.²⁵ performed molecular-dynamics (MD) simulations of prepared CTAB monolayers at the mica–water interface, and noticed the growth of a water channel penetrating the monolayer and transforming it into disordered aggregates. Other simulations have shown cylindrical CTAB micelles on Au(100) surfaces in aqueous solutions,²⁶ various CTAB aggregate shapes in water solutions,²⁷ and different shapes of CTAB and anionic sodium octyl sulfate (SOS) aggregates, which depend strongly on the surfactant composition.²⁸

Modern experimental techniques such as surface force apparatus (SFA), neutron reflectivity (NR), X-ray reflectometry (XRR), and atomic force microscopy (AFM) have been used to explore the structural aspects of the micellisation and adsorption of CTAB. CTAB forms a monolayer structure at about 5% of the CMC,²⁹ and a bilayer structure at about 50% of the CMC.³⁰ SFA measurements show that the bilayer thickness is in the range 31–36 Å.^29,31–34 AFM imaging by Ducker and Wanless showed that, initially, CTAB formed flattened cylinders parallel with the mica surface, and then transformed over 24 hours to form a flat bilayer.³⁵ This was put down to the time for the exchange of K⁺ ions in the mica surface, which appears to be a slow process in the case of ammonium ions.¹⁸ Speranza et al.³⁶ used XRR to explore a series of quaternary alkylammonium bromides (C_nTABs with n = 16 corresponding to CTAB) adsorbed at the mica–water interface. It was found that under quiescient conditions, the XRR data were consistent with a disordered and interdigitated bilayer structure below and above the CMC, and with a more densely packed, ordered, and separated bilayer structure at the CMC. The discrepancy between AFM and XRR measurements could be put down to the influence of the scanning microscopy tip, and the long time for structural reorganisation to recover the bilayer. NR studies show that the surface coverage of the CTAB bilayer is incomplete, suggesting that adsorption is in the form of aggregates.³⁷ Howard and Craig proposed that surface-adsorbed aggregates are the cause of slow adsorption in the case of CTAB, and that this may also apply to other surfactants.¹² Clarke and co-workers used NR to study the aggregation of CTAB³⁸ and DDAB^39–41 at the mica–water interface, and observed bilayer formation of the surfactants in both cases.

The aim of this work is to gain some insights on the adsorption and self-assembly of CTAB and DDAB at the mica–water interface using MD simulations. By preparing an initial ‘bulk’ solution of the surfactants and putting it in contact with the mica surfaces, and letting the system reach equilibrium (or at least a steady state) without external bias, it should be possible to determine what kinds of structures are formed first at the interface. It is essential that the simulated structure is compared with experimental measurements. The adsorbed-layer thickness is an insensitive measure, as it reflects the molecular-scale ordering at the interface only indirectly, and relies on assumptions about the molecular geometry and the internal structure of the bilayer. In this work, the neutron scattering length density (SLD) profile is extracted from atomic-density profiles calculated in MD simulations, and the neutron reflectivity is computed for direct comparison with the results presented in ref. 38–41, including the effects of substrate, etc. that influence the experimental measurements. If the simulated and experimental reflectivities are in good agreement, then robust atom-level information can be inferred.

The properties of water near the mica surface are also of great interest. It has been shown with X-ray scattering,⁴² SFA measurements,^15,43 and molecular simulations^44–46 that the water layers near the interface are well ordered and separated by 2.5–2.7 Å, which is approximately equal to the van der Waals diameter of a water molecule. Although this is not the main focus of the current work, it does provide an opportunity to show that the MD simulations are consistent with earlier findings, and in particular, that the NR profiles for the mica–water interface presented in ref. 38–41 can be reproduced reliably.

The rest of this article is organised as follows. The simulation model, protocols, and analysis are described in Section 2. The results are presented in Section 3, and divided into three parts: the mica–water interface (Section 3.1); CTAB adsorption at the mica–water interface (Section 3.2); and DDAB adsorption at the mica–water interface (Section 3.3). Section 4 concludes the article.

2 Model and methods

2.1 Molecular dynamics simulations

In a first tranche of MD simulations, three systems were studied with 44.7 wt% CTAB in water, 39.1 wt% DDAB in water, and pure water, each confined between two muscovite mica slabs. These concentrations are well above the CMC, because the focus is on the structure of the solid–liquid interface, and it would be completely infeasible to do all-atom simulations near the CMC. (The CMC of DDAB is 8 × 10⁻⁵ mol L⁻¹,^39–41 equivalent to about 0.004 wt%.) The compositions of these systems are summarised in Table 1. The mica structure was taken from the Interface Force Field toolkit,^47–51 with the unit-cell dimensions being 5.1918 Å × 9.0153 Å × 10.0228 Å. A 10 × 6 × 1 surface slab was formed from the unit cell.⁵² Each slab had lateral (xy) dimensions of 52 Å × 54 Å, a thickness (z) of 10 Å, and contained 2520 atoms. Simulations were carried out with and without the 60 K⁺ ions in the top layer of each mica slab; there is one K⁺ ion per unit cell.

Table 1 Compositions of systems simulated at P = 1 atm and T = 298.15 K. N_CTAB is the number of CTAB molecules, N_DDAB is the number of DDAB molecules, N_w is the number of water molecules, and N_atom is the total number of atoms in the liquid layer

wt% CTAB	wt% DDAB	N CTAB	N DDAB	N w	N atom
44.7	—	240	—	6000	33 120
32.7	—	240	—	10 000	45 120
—	39.1	—	200	8000	40 800
—	—	—	—	8000	24 000

---

LAMMPS^53,54 was used to perform all-atom MD simulations. All interactions and topology parameters were taken from the PCFF-INTERFACE force field.⁵¹ The non-bonded Lennard-Jones (9,6) and electrostatic interaction parameters are given in Table 2. Periodic boundary conditions were applied in the x and y directions. The Ewald particle–particle particle-mesh method was used to calculate all long-range electrostatic interactions, and the equations of motion were integrated with the velocity-Verlet algorithm and a time step of 1 fs.

Table 2 Non-bonded interaction parameters from the PCFF-INTERFACE force field.⁵¹ Atom type is according to the naming convention used to define the mineral structures and interactions in the Interface Force Field. The mica atoms are ay1-sy2, the water atoms are hw and o*, and the surfactant atoms are br-n. For instance, in the surfactants, ‘c2’ is an aliphatic CH₂ carbon, ‘c3’ is an aliphatic CH₃ carbon, ‘c2n’ and ‘c3n’ are the corresponding carbons bonded to the ammonium nitrogen, ‘hc’ is an aliphatic hydrogen, and ‘n’ is the ammonium nitrogen. ε and σ are the Lennard-Jones (9,6) energy and distance paramters, respectively. q is the charge on the atom

Element	Atom type	ε/kcal mol^−1	σ/Å	q/e
Al	ay1	0.0350	4.500	+1.4490
Al	ay2	0.0350	4.500	+1.4480
Al	ayt1, ayt2	0.0350	4.500	+0.8000
H	hoy	0.0130	1.098	+0.2000
K	k+	0.2000	4.100	+1.0000
O(–Si)	oy1, oy2, oy3	0.0150	3.800	−0.5500
O(–Al)	oy1, oy2, oy3	0.0150	3.800	−0.7830
O	oy4, oy5, oy7, oy8	0.0150	3.800	−0.7580
O	oy6, oy9	0.0150	3.800	−0.6830
Si	sy1, sy2	0.0350	4.200	+1.1000
H	hw	0.0130	1.098	+0.4100
O	o*	0.2740	3.608	−0.8200
Br	br	0.3489	4.300	−1.0000
C	c2	0.0540	4.010	−0.1060
C	c3	0.0540	4.010	−0.1590
C	c2n	0.0540	4.010	+0.3011
C	c3n	0.0540	4.010	+0.2481
H	hc	0.0200	2.995	+0.0530
N	n	0.0650	3.262	−0.6284

---

The simulations were carried out according to the following protocol. First, the surfactant and water were randomly mixed to generate an initial disordered configuration. The energy of the system was minimised, and then NVE dynamics were run for 0.2 ns to relax the system. To compress the solution layer, a fixed load corresponding to P = 1 atm was applied to the outermost layer of atoms in the top mica surface, while the bottom surface was held fixed, and the system was held at T = 298 K. The simulation was then switched to the NVT ensemble with T = 298 K. The temperature was controlled by a Nosé–Hoover thermostat.

For the CTAB system, runs of 60 ns were required to reach equilibrium. Then, an additional 4000 water molecules were inserted into the centre of the solution layer, to further separate the slabs and ensure there that there were no interactions between the adsorbed structures. The composition of the solution layer was then 32.7 wt% CTAB (see Table 1). The larger system was simulated under NVT conditions for 30 ns. For the DDAB and pure-water systems, 50 ns runs were sufficient to reach equilibrium.

For each liquid layer, simulations were carried out both with and without the K⁺ ions on the innermost surface of each slab. The ion-exchange mechanism occurs on timescales that are inaccessible to MD simulations, and so to mimic the process, K⁺ ions were simply removed from the surfaces. In the real system, the resulting concentration of K⁺ (aq) is very low because of the volume of the solution, and so in the surfactant simulations, 120 ions were simply deleted from the system. To preserve the charge neutrality, 120 Br⁻ ions from CTAB and DDAB were also deleted. Stripping the K⁺ ions from the surface exposes the surfactant cations to surface anions, and leads to rapid and strong adsorption. For the pure-water system, the K⁺ ions were moved from the surface into solution, resulting in a concentration of approximately 0.83 mol kg⁻¹.

The structures of the adsorbed films were characterised by calculating the density profiles ρ(z) (atoms Å⁻³) for each atom type, where z is the distance from a surface. A resolution of 1 Å was sufficient in all cases. The density profiles for each surface were combined and averaged over the last 20 ns of the simulation. The neutron SLD profile was calculated from the individual atomic-density profiles using the scattering lengths collated by Sears.⁵⁵ The SLD (m⁻²) of each atom type at a distance z is simply the local concentration (m⁻³) multiplied by the scattering length (m).

2.2 Comparison with NR measurements

An essential feature of this work is the comparison of simulated and experimental structures using NR. Clarke and co-workers have measured the NR profiles of CTAB and DDAB solutions in water, and pure water, in contact with mica surfaces.^{38–41,56,57} In connection with the NR and SLD profiles, ‘water’ means D₂O. The surfactant concentration was fixed at or near the CMC. The NR is a function of the SLD profile, which is fitted to the experimental measurements, including the effects of the substrate as well as the adsorbed layer at the mica-solution interface. Because of the available range of the scattering wave vector Q, the resolution of the NR measurements is limited. In simulations, the atomic-density and SLD profiles can be determined with sub-ångström resolution. Hence, the simulations should be able to give more detailed insights on the structures of the adsorbed layers.

The multi-layered nature of the NR substrates used experimentally required a complex fitting routine, where ‘thick’ and ‘thin’ layers are accounted for differently due to the loss of phase information in the ‘thick’ layers. I-CALC, a custom fitting routine, was used to fit data from these substrates, and generate the SLD and corresponding NR profiles. The specifics of the fitting routine are described in detail elsewhere.³⁹ The NR profile corresponding to the fitted SLD is used in comparisons with simulations, but this is very close to the raw NR data obtained in experiments.

The NR corresponding to the MD simulations was obtained from the SLD profile computed as described at the end of Section 2.1. To make sure that the solution-mica interface was described accurately, and to avoid any issues of how to match the two up, the simulated SLD profile was extended into the mica substrate by replicating the mica SLD profile nine more times. This resulted in a mica substrate ten layers thick, plus the solution layer. The composite profile was then extended further to the experimental substrate thickness by adding a uniform SLD corresponding to the average for mica, which is 3.67 × 10⁻⁶ Å⁻². The resulting NR profile was calculated using other necessary parameters taken from a prior experiment on a bare mica surface, with a silica/silicon/glue multi-layered substrate. The details are given in ref. 41.

For consistency, the NR profiles from both the experimental and simulated SLDs were computed using the same bare-substrate parameters.

3 Results

3.1 Mica–water interface

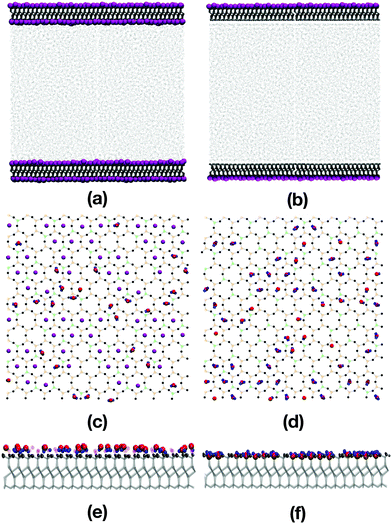
Fig. 2(a)–(f) show various snapshots of the pure water system, with and without the inner layer of potassium ions.

Fig. 2 Snapshots of pure water confined between mica slabs: (a, c and e) are for mica slabs with potassium; (b, d and f) are for mica slabs without potassium. (a and b) Show side-on views of the systems. K⁺ ions are shown in purple, water bonds are shown as light grey sticks, and mica bonds are shown as dark grey bonds. Two periodic replicas are shown. (c and d) Show top-down views of the surfaces, and (e and f) show side-on views of the surface. Water oxygens are shown in red, and water hydrogens are shown in blue. In the mica surfaces, oxygen atoms are shown in black, aluminium atoms in green, and silicon atoms in orange.

The water molecules adsorb onto the mica surfaces with potassium by occupying positions adjacent to the potassium ions [Fig. 2(a), (c), and (e)]. The atomic-density profiles are shown in Fig. 3(a). The hydrogen density is higher than the oxygen density near the potassium layer, suggesting that the water molecules adsorb with the hydrogen atoms pointing towards the surface. One would expect that the positively charged potassium ions on the mica surface would attract the negatively charged oxygen atoms of the water. However, the underlying layer on the mica surface is an oxygen layer, also negatively charged. Thus, the water molecules adsorb so that both the hydrogens are close to the sub-surface oxygen layer, and the oxygen atoms are close to the potassium layer. Steric interactions between potassium and water prevent the latter from penetrating any further into the mica surface.

Fig. 3 Atomic-density profiles (a–d) and radial distribution functions (e and f) for pure water confined between mica slabs: (a, c and e) are for mica slabs with potassium; (b, d and f) are for mica slabs without potassium. (a and b) Show atomic-density profiles for both mica and water. (c and d) Show the atomic-density profiles of the water oxygen atoms on an expanded scale. In (a–d), z = 9 Å corresponds to the position of the first layer of Al/Si atoms, and the horizontal dashed lines are the H_w-atom and O_w-atom densities at the experimental bulk-water density. (e and f) Show the radial distribution functions, in the xy plane, for the oxygen atoms of the water molecules in three adjacent layers closest to each surface.

The opposite effect is observed when the potassium ions are moved from the mica surface; now the water molecules point towards the surface oxygen-first. The atomic-density profile in Fig. 3(b) shows that oxygen atoms now occupy positions among the outermost oxygen atoms of the mica surface. The layer below the oxygen layer of the mica is formed from Al and Si cations. So now, the water oxygens coordinate to Al/Si, and the water hydrogens coordinate to the mica oxygen. The absence of the potassium ions, and the low concentration of the mica oxygen atoms, mean that the water molecules can penetrate the surface cavities of the mica and form strong electrostatic interactions.

Fig. 2(c) and (d) show snapshots of the innermost surfaces of the mica slabs with and without potassium, and display all solvent atoms within 2 Å of the surface. The water molecules in both cases are positioned in the ditrigonal cavities among the K⁺ ions. This is in agreement with the structures described by Arai et al.,⁵⁸ who used atomic force microscopy to investigate the ions on muscovite surfaces in bulk water, and the hydration layers at the solid-water interface. Fig. 2(e) and (f) show side-on views of the mica surfaces and the neighbouring solvent atoms. From this perspective, the positions of the adsorbed water molecules are easy to see, with greater penetration of the mica slab without potassium than with potassium. As shown in Fig. 2(e), in the presence of potassium, the hydrogen atoms of the water molecules are pointing towards the surface, and are aligned with the K⁺ ions. As shown in Fig. 2(f), in the absence of the K⁺ ions, the oxygens are pointing towards the surface and are settled among the oxygen atoms of the mica surface.

The layering of the water molecules at the interface is shown by plotting the atomic-density profile of the oxygen atoms on an expanded scale; see Fig. 3(c) and (d). The ordering of the oxygen atoms is more pronounced near the surface without potassium than near the surface with potassium. In Fig. 3(d), the peak labelled P₁ has been reported in other work as the ‘adsorption layer’, while the peak labelled P₂ is referred to as the ‘hydration layer’.^42,44,59 The distance between the two peaks is 2.8 Å, which is larger than the value of 1.2 Å estimated in previous work using high-resolution specular X-ray reflectivity, and Monte Carlo and MD simulations.^42,44,59 The layering extends to about 10 Å into the liquid, which is in excellent agreement with that seen in earlier work.^42,44,59Fig. 3(c) shows that the water adjacent to the surface with potassium is less well ordered, but the weak layering extends a similar distance into the liquid. Note that the H-atom and O-atom densities at large values of z are very slightly lower than the experimental values for bulk water, especially for the water containing desorbed K⁺ ions; in the experiments, the water is essentially pure, but the deviations of the simulated densities (arising from the dissolved ions and/or force field) are insignificant.

Fig. 3(e) and (f) show the in-layer ordering of the water, represented by the two-dimensional radial distribution function g(r), where r is the O–O distance in the xy plane. The water was separated into layers, as indicated by the labels P₁–P₃ in Fig. 3(c) and (d). In the presence of potassium [Fig. 3(e)], the water layer nearest the mica surface is slightly more ordered than the next two layers, but fundamentally, the structure is the same. The water layer nearest the mica surface without potassium [Fig. 3(f)] is much more strongly ordered than the next two layers, and this is due to the pinning of the water molecules to the charged sites on the mica surface. In fact, this is visible from the simulation snapshots in Fig. 2(a) and (b). In (a) (with potassium) no strong layering is visible, while in (b) (without potassium) there is a continuous band adjacent to the surface, corresponding to a well-ordered layer of water molecules, but no second or third bands.

Fig. 4 shows the NRs and SLD profiles for water near mica surfaces; simulation results for mica surfaces with and without potassium are compared to the same set of fits to the experimental data.³⁸ The simulated NR profile for the system without the K⁺ ions is slightly closer to the experimental NR, but both systems exhibit good overall agreement with experiment. Each SLD profile shows the solution layer and ten replicas of the mica layer with atomic resolution, which is extended in the −z direction with the uniform value for mica. Note that even though the resolution of the simulated SLD profiles is much higher than that which can be extracted by fitting to the experimental NR, the fine details of the simulated SLDs are smeared out in the calculation of the NR at low wave vectors. Nonetheless, the SLD profile for the surface without potassium shows two pronounced peaks near the solid–liquid interface, which are absent from the profile for the surface with potassium. These peaks correspond to the alignment of the water molecules with the mica-oxygen layer, therefore generating a high scattering-length density at that position. As shown, these peaks do not have an observable effect on the NR profile. Away from the interface, the water SLD profiles level off at about 6.21 × 10⁻⁶ Å⁻² (with potassium ions) and 6.05 × 10⁻⁶ Å⁻² (without potassium ions). These values are 2–4% smaller than the fitted experimental value of 6.30 × 10⁻⁶ Å⁻².³⁸ This is simply because the simulated water density is slightly too low, as noted above.

Fig. 4 NR (a and b) and SLD profiles (c and d) for pure water confined between mica slabs: (a) and (c) are for mica slabs with potassium; (b) and (d) are for mica slabs without potassium. The MD simulation results are shown as solid black lines, and the fits to the experimental results are shown as dashed red lines.³⁸ In (a) and (b), the same fits to the experimental data are shown for comparison.

3.2 CTAB adsorption at the mica–water interface

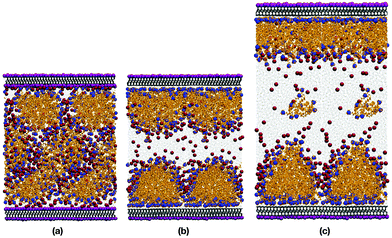
Fig. 5(a) and (b) show snapshots of 44.7 wt% CTAB in water, with and without the innermost potassium layer on each mica surface. Fig. 5(c) shows a snapshot of 32.7 wt% CTAB in water, without the K⁺ ions. It is obvious that removing the K⁺ ions (and the Br⁻ ions for charge balance) is essential for the CTAB aggregates to adsorb onto the surface. In both cases, the CTAB self-assembles because the concentration is well above the CMC.

Fig. 5 Snapshots of CTAB in water confined between mica slabs at P = 1 atm and T = 298.15 K: (a) 44.7 wt% CTAB between mica slabs with potassium; (b) 44.7 wt% CTAB between mica slabs without potassium; (c) 32.7 wt% CTAB between mica slabs without potassium. Two periodic replicas are shown. CTA⁺ molecules are shown as orange chains, with the nitrogen atoms shown as blue spheres. Br⁻ ions are shown as dark-red spheres, and K⁺ ions on the mica surfaces are shown as purple spheres.

In the presence of the K⁺ ions, CTAB forms extended aggregates in solution. Table 3 shows the composition and size of the structures formed in all three systems examined. The top and bottom layers refer to the two mica surfaces. The structures in the CTAB systems are micellar, and their sizes are estimated using the radius of gyration, R_g, defined by

where n is the number of atoms in the aggregate, m_i is the mass of atom i, r_i is the distance of atom i from the centre of mass (taking into account the periodic boundary conditions), and is the mass of the aggregate. R_g was calculated and averaged during the production run where there is no change in the number of molecules involved. The micelles reported in Table 3 in the CTAB systems have sizes of 35 Å and 28 Å. Griffin et al. described the formed CTAB structures as bilayers, and estimated their thickness as 31 Å, with a roughness at the bilayer/water interface of 3 Å.³⁸ Even though the aggregates described in Table 3 are micelles, their average sizes are in good agreement with the bilayer size estimated by Griffin et al.

Table 3 Composition and structural properties of micellar and bilayer structures in CTAB and DDAB in water confined between mica slabs without potassium. The micelles are described by the radius of gyration R_g and the bilayers by their thickness L. ‘Top’ and ‘bottom’ refer to the position in the simulation cell. ‘Inner’ and ‘outer’ refer to the simulated surfactant layers in contact with solution and mica, respectively. Experimental values for the adsorbed-layer thickness are included for comparison^38–41

Surfactant concentration	Layer	N surfactant	L or Rg	Value/Å
44.7 wt% CTAB	Top	118	R g	34.8 ± 3.5
	Bottom	122	R g	27.6 ± 4.6
32.7 wt% CTAB	Top	108	R g	34.6 ± 2.6
	Bottom	122	R g	27.4 ± 4.4
1.0 CMC CTAB	Ref. 38		L	31 ± 1
39.1 wt% DDAB	Top	74	L	23.5 ± 1.0
	Top/outer	60	L	16.8 ± 1.0
	Top/inner	14	L	6.5 ± 1.8
	Bottom	82	L	22.9 ± 1.0
	Bottom/inner	23	L	5.81 ± 1.6
	Bottom/outer	59	L	17.1 ± 1.0
0.5 CMC DDAB	Ref. 40		L	23 ± 2
1.0 CMC DDAB	Ref. 40		L	23 ± 2
1.0 CMC DDAB	Ref. 41		L	22.1 ± 0.1
2.0 CMC DDAB	Ref. 39		L	24 ± 2

---

In the absence of the K⁺ ions, the CTAB is instantly adsorbed onto the surfaces, creating something in between a bilayer structure and flattened hemispherical aggregates, both of which have been reported in previous studies.^{2,12,25,35,36,60} Adding additional water was intended to eliminate any strong interactions between the two adsorbed layers. Indeed, the two sets of simulation results given in Table 3 show that the effect of increasing the water content was small, inasmuch as the apparent thicknesses of the top and bottom adsorbed layers were virtually unchanged. This suggests that there was enough water between the adsorbed layers to remove finite-size effects. On one of the surfaces, the hemispherical aggregates had merged to form a well-defined bilayer structure. This shows that there is not one structure which is strongly thermodynamically favoured, and it is not claimed here that one or other should dominate. But it is possible that relatively minor variations in surface composition and charge could tip the balance one way or the other. The adsorbed structures on both surfaces contain a small but significant amount of water. This is detailed in the atomic density profiles, shown in Fig. 6(a). There are peaks in the water hydrogen and oxygen profiles about 2 Å from the first Al/Si layer in the mica surfaces, and the tails of those peaks extend about 10 Å into the CTAB layer.

Fig. 6 Atomic density profiles for (a) 32.7 wt% CTAB in water and (b) 39.1 wt% DDAB in water confined between mica surfaces without potassium.

The essential test is to compare the simulation results with the NR experiments performed by Griffin et al.³⁸Fig. 7(a) and (b) show the NR and SLD profiles, respectively, from experiment and simulation. The NR profile from simulation is broadly in agreement with that from experiment, although the features in the experimental profile are more pronounced in the wave vector range 0.03 Å⁻¹ ≤ Q ≤ 0.2 Å⁻¹. To put that in context, Fig. 7(a) also shows the NR profile for the bare mica surface in contact with pure water, as determined experimentally. The deviation between the simulated and experimental NR profiles for the CTAB solution is smaller than that between the experimental profiles for the CTAB solution and pure water.

Fig. 7 NR (a) and SLD (b) profiles for 32.7 wt% CTAB in water confined between mica surfaces without potassium. The MD simulation results are shown as solid black lines, and the fits to the experimental results are shown as dashed red lines.³⁸ In (a), the dotted blue line shows the experimental fit for the bare mica surface in contact with pure water.

The SLD profile shows that the reason for the discrepancy is the larger dip in the fitted function through the bilayer as compared to simulation. The decrease of the SLD in the range 0 Å ≤ z ≤ 50 Å signifies the existence of a thick, organic-rich layer, because the SLD of CTAB is lower than that of mica or water. But while the simulation results show an adsorbed, hydrated structure in the shape of a disordered bilayer or a hemimicelle – see Fig. 5(b) and (c) – the experiment indicates a perfect bilayer with no signs of contained water. The presence of water in the simulated layer increases the SLD, and reduces the contrast between mica and water. Therefore, the reflectivity profile shows a weaker hump in the aforementioned wave-vector range. Essentially, the bilayer is not as well resolved in simulations as in the SLD profile fitted to experiment. Note that the atomic-level resolution of the SLD in the mica slab does not have any influence on the reflectivity profile, as shown in Section 3.1. Atomic resolution is used down to z = −80 Å, and the mica is treated as a uniform substrate beyond that.

3.3 DDAB adsorption at the mica–water interface

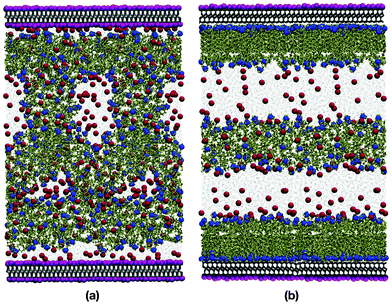
Fig. 8(a) and (b) show snapshots of 39.1 wt% DDAB in water, with and without the innermost potassium layer on each mica surface. Due to its two backbone chains, and the resulting higher packing parameter, DDAB forms very well defined, compact bilayer structures on both surfaces, which contain relatively little water, as shown in Fig. 6(b). The water is mainly confined to a 5 Å region near the surface. Table 3 contains information about the content and structure of the bilayers. The width L of the bilayers was calculated by averaging the z coordinates of all the nitrogen atoms that belong to the headgroup near the surface (in the ‘outer’ layer), and then the positions of the nitrogen atoms that are facing the bulk (in the ‘inner’ layer). The height difference between the nitrogen positions was then averaged for the production run, and this represents the width of the bilayer.

Fig. 8 Snapshots of 39.1 wt% DDAB in water confined between mica slabs at P = 1 atm and T = 298.15 K: (a) mica slabs with potassium; (b) mica slabs without potassium. Two periodic replicas are shown. DDA⁺ molecules are shown as green chains, with the nitrogen atoms shown as blue spheres. Br⁻ ions are shown as dark-red spheres, and K⁺ ions on the mica surfaces are shown as purple spheres.

Close inspection shows that the two components of the bilayer are quite distinct: a highly ordered monolayer directly on the mica surface (outer layer); and a much thinner, disordered layer on the side of the bulk solution (inner layer). Because of the high chain density in the outermost adsorbed layer (in contact with the mica surface), the molecules in the innermost layer cannot penetrate it, which results in the DDAB molecules laying flat on top of the outermost layer. These two parts are distinct, and this is shown in the snapshots as a faint white line which is where the monolayer part ends and the disordered DDAB molecules lie in various orientations. The approximate thickness of, and number of molecules in, in each of the inner and outer layers are given in Table 3. With this in mind, it is expected that the total thickness of the bilayer structure would be more than the length of a single DDAB molecule (17 Å), but less than the length of two DDAB molecules lying end-to-end.⁶¹ As shown in Table 3, the total thicknesses of the two adsorbed bilayer structures are 23.5 Å and 22.9 Å, which are in excellent agreement with the values of 24.0 Å, 23.0 Å, and 22.1 Å reported by Browning et al.,³⁹ Griffin et al.,⁴⁰ and Allen et al.,⁴¹ respectively. The DDAB molecules that were not adsorbed on the surfaces formed a lamellar aggregate in the middle of the bulk solution, because the concentration was well above the CMC. This aggregate was far from the adsorbed structures, and so any interactions between adsorbed layers and self-assembled aggregates were largely eliminated.

The simulated reflectivity and SLD profiles of the system are plotted with the corresponding experimental results in Fig. 9(a) and (b), respectively. The reflectivity profiles are in excellent agreement. The simulated SLD shows a dip at z ≃ 25 Å, which corresponds to a well-ordered layer of terminal hydrogen atoms at the ends of the hydrocarbon tails of the DDAB molecules that belong to the outermost adsorbed layer. This clearly indicates the innermost edge of the outermost adsorbed layer, and that there is almost no interdigitation between the layers. As before, the simulated SLD profile captures more fine details than the fitted profile, but there is little impact on the reflectivity profile. Nonetheless, the overall thickness and definition of the bilayer region of the SLD profile is captured extremely well by the simulations. Overall, there is very good agreement with the experiment, and this supports the existence of a bilayer with the reported dimensions.

Fig. 9 NR (a) and SLD (b) profiles for 39.1 wt% DDAB in water confined between mica surfaces without potassium. The MD simulation results are shown as solid black lines, and the fits to the experimental results are shown as dashed red lines.^39–41 In (a), the dotted blue line shows the experimental fit for the bare mica surface in contact with pure water.

The orientational structure of the outermost and innermost layers can be characterised by calculating the distribution of the molecular angle cosine (cos θ) with respect to the laboratory z axis (normal to the mica surfaces). A unit orientation vector was defined as pointing from the terminal N atom in the ammonium head group to the terminal methyl C atom at the end of the hydrocarbon chain. DDAB molecules have two chains, and so both of the vectors emanating from the same N atom were included. To separate the two surfaces, the angle cosine was defined with respect to the bottom surface: cos θ = +1 means that the molecular vector is pointing away from the surface; cos θ = −1 means that the molecular vector is pointing towards the surface. The results are shown in Fig. 10. It is observed that most molecules are parallel to the z axis with |cos θ| ≥ 0.8, corresponding to the outermost layers on each surface, which contain more molecules than the innermost layers.

Fig. 10 Histogram of molecular orientations in 39.1 wt% DDAB in water confined between mica slabs without potassium. The orientation is defined as cos θ, where θ is the angle between a molecule and the laboratory z axis.

4 Conclusions

In this work, MD simulations were performed to explore the self assembly and adsorption of the surfactant molecules CTAB and DDAB in water, confined between common mica surfaces. An additional study of pure water on mica surfaces was conducted to investigate the structural properties of water at the solid–liquid interface. The role of the computational work is to complement previous experimental work on those systems, and to provide atomistic details on the underlying adsorption mechanisms and resulting structures.

It was observed that the innermost potassium layer on the mica surface plays a significant role when it comes to the shape of the aggregate structures of the two surfactants. The presence of that ion layer prevents the surfactants from adsorbing onto the surface; CTAB forms compact micelles in the bulk solution, while DDAB aggregates into disordered clusters, which remain unchanged throughout the simulation. By removing the potassium-ion layer (and some counterions), and thereby introducing a surface charge, the two surfactants quickly adsorbed onto the surface. In the case of CTAB, the structure was intermediate between a bilayer and flattened, adsorbed hemi-micelles. DDAB, on the other hand, formed a well-defined bilayer. Using the simulated atomic density profiles, the results from the simulations were compared to experimental NR and SLD profiles. The results for the CTAB system were in moderately good agreement, with small deviations coming from the simulated adsorbed structures being not as well defined as in experiments, and the presence of small concentrations of water localised within the surfactant film. The match between simulated and experimental profiles was excellent in the case of DDAB. In all cases, the apparent thicknesses of the adsorbed films were in excellent agreement with experimental estimates.

In the DDAB system, the two components of the bilayer showed markedly different structures. The DDAB molecules in contact with the mica surface formed a dense, orientationally ordered monolayer. The second layer exhibited a thin and disordered structure, with almost no interdigitation, but with the polar head groups in contact with the aqueous solution. Overall, the thickness of the bilayer structure was in between one and two times the length of a DDAB molecule.

The results for the pure-water system showed that the potassium layer prevents the water molecules from penetrating the mica surface, which affects the orientation of the molecules at the interface. This manifests itself in rather different atomic-scale ordering at the surface. The simulated NR and SLD profiles were in good agreement with experimental results with or without the potassium ions, although the agreement was marginally better without the ions.

Overall, this study shows the extent to which MD simulations can be used to complement experimental reflectivity studies of surface-adsorbed structures. The apparent structures extracted from reflectivity measurements are naturally limited in terms of resolution, while molecular simulations can resolve atomic-level structures. Nonetheless, before any conclusions can be drawn from the simulations, it must be confirmed that the results are, as far as possible, consistent with experiment. The examples studied in this work show that it is possible to combine experiment and simulation in order to get an almost complete picture of the structures of surface-adsorbed films.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

G. T. was supported by a PhD studentship from BP Castrol [Research Agreement GPTL/92534(2)]. Access to the BP High Performance Computing Facility in Houston, Texas is gratefully acknowledged. F. J. A. was supported by EPSRC (Project Reference 1799423) and BP plc (RG8620). F. J. A. and S. M. C. also thank the beamtime committees and instruments scientists that made the initial experiments possible.^56,57

References

1. B.-Y. Zhu and T. Gu, Adv. Colloid Interface Sci., 1991, 37, 1–32.
2. R. Sharma, Surfactant Adsorption and Surface Solubilization, American Chemical Society, Washington, DC, 1996.
3. P. Somasundaran and S. Krishnakumar, Colloids Surf., A, 1997, 123–124, 491–513.
4. J. Brinck, B. Jönsson and F. Tiberg, Langmuir, 1998, 14, 5863–5876.
5. K. L. Mittal and D. O. Shah, Adsorption and Aggregation of Surfactants in Solution, CRC Press, New York, 2002, vol. 109.
6. S. Paria and K. C. Khilar, Adv. Colloid Interface Sci., 2004, 110, 75–95.
7. D. M. Colegate and C. D. Bain, Phys. Rev. Lett., 2005, 95, 198302.
8. H. Mohrbach, J. Chem. Phys., 2005, 123, 126101.
9. A. V. Sineva, A. M. Parfenova and A. A. Fedorova, Colloids Surf., A, 2007, 306, 68–74.
10. H. Yunfei, S. Yazhuo, L. Honglai, L. Dominique and S. Anniina, Langmuir, 2012, 28, 3146–3151.
11. Z. Chang, X. Chen and Y. Peng, Miner. Eng., 2018, 121, 66–76.
12. S. C. Howard and V. S. J. Craig, Soft Matter, 2009, 5, 3061–3069.
13. G. L. Gaines, J. Phys. Chem., 1957, 61, 1408–1413.
14. G. L. Gaines, Nature, 1959, 183, 1109–1110.
15. R. M. Pashley and J. N. Israelachvili, J. Colloid Interface Sci., 1984, 101, 511–523.
16. R. M. Pashley, Clays Clay Miner., 1985, 33, 193–199.
17. M. A. Osman, C. Moor, W. R. Caseri and U. W. Suter, J. Colloid Interface Sci., 1999, 209, 232–239.
18. M. A. Osman and U. W. Suter, J. Colloid Interface Sci., 2000, 224, 112–115.
19. W. de Poel, S. L. Vaessen, J. Drnec, A. H. J. Engwerda, E. R. Townsend, S. Pintea, A. E. F. de Jong, M. Jankowski, F. Carlà, R. Felici, J. A. A. W. Elemans, W. J. P. van Enckevort, A. E. Rowan and E. Vlieg, Surf. Sci., 2017, 665, 56–61.
20. R. A. Shelden, W. R. Caseri and U. W. Suter, J. Colloid Interface Sci., 1993, 157, 318–327.
21. W. Li, M. Zhang, J. Zhang and Y. Han, Front. Chem. China, 2006, 1, 438–442.
22. A. Desai, D. Varade, J. Mata, V. Aswal and P. Bahadur, Colloids Surf., A, 2005, 259, 111–115.
23. V. Farafonov and A. Lebed, Kharkov Univ. Bull., 2016, 27, 25–30.
24. A. Domínguez, A. Fernández, N. González, E. Iglesias and L. Montenegro, J. Chem. Educ., 1997, 74, 1227–1231.
25. J. Sun, J. Shi, P. Zhang and S. Yuan, Mol. Simul., 2018, 44, 396–404.
26. J. A. da Silva, R. P. Dias, G. C. A. da Hora, T. A. Soares and M. R. Meneghetti, J. Braz. Chem. Soc., 2018, 29, 191–199.
27. G. F. Catá, H. C. Rojas, A. P. Gramatges, C. M. Zicovich-Wilson, L. J. Alvarez and C. Searle, Soft Matter, 2011, 7, 8508–8515.
28. J. Chen and J. Hao, Phys. Chem. Chem. Phys., 2013, 15, 5563–5571.
29. R. M. Pashley and J. N. Israelachvili, Colloids Surf., 1981, 2, 169–187.
30. P. Kékicheff, H. K. Christenson and B. W. Ninham, Colloids Surf., 1989, 40, 31–41.
31. J. N. Israelachvili and R. M. Pashley, J. Colloid Interface Sci., 1984, 98, 500–514.
32. R. M. Pashley and B. W. Ninham, J. Phys. Chem., 1987, 91, 2902–2904.
33. R. M. Pashley, P. M. McGuiggan, R. G. Horn and B. W. Ninham, J. Colloid Interface Sci., 1988, 126, 569–578.
34. C. A. Helm, J. N. Israelachvili and P. M. McGuiggan, Science, 1989, 246, 919–922.
35. W. A. Ducker and E. J. Wanless, Langmuir, 1999, 15, 160–168.
36. F. Speranza, G. A. Pilkington, T. G. Dane, P. T. Cresswell, P. Li, R. M. J. Jacobs, T. Arnold, L. Bouchenoire, R. K. Thomas and W. H. Briscoe, Soft Matter, 2013, 9, 7028–7041.
37. G. Fragneto, R. K. Thomas, A. R. Rennie and J. Penfold, Langmuir, 1996, 12, 6036–6043.
38. L. R. Griffin, K. L. Browning, C. L. Truscott and S. M. Clarke, J. Phys. Chem. B, 2015, 21, 6457–6461.
39. K. L. Browning, L. R. Griffin, P. Gutfreund, R. D. Barker, L. A. Clifton, A. Hughes and S. M. Clarke, J. Appl. Crystallogr., 2014, 47, 1638–1646.
40. L. R. Griffin, K. L. Browning, C. L. Truscott, L. A. Clifton, J. Webster and S. M. Clarke, J. Colloid Interface Sci., 2016, 478, 365–373.
41. F. J. Allen, C. L. Truscott, R. J. L. Welbourn and S. M. Clarke, Appl. Clay Sci., 2018, 160, 276–281.
42. L. Cheng, P. Fenter, K. L. Nagy, M. L. Schlegel and N. C. Sturchio, Phys. Rev. Lett., 2001, 87, 156103.
43. G. Zhao, Q. Tan, L. Xiang, D. Cai, H. Zeng, H. Yi, Z. Ni and Y. Chen, J. Chem. Phys., 2015, 143, 104705.
44. S.-H. Park and G. Sposito, Phys. Rev. Lett., 2002, 89, 085501.
45. Y. S. Leng and P. T. Cummings, Phys. Rev. Lett., 2005, 94, 026101.
46. Y. S. Leng and P. T. Cummings, J. Chem. Phys., 2006, 124, 074711.
47. H. Heinz, H. J. Castelijns and U. W. Suter, J. Am. Chem. Soc., 2003, 125, 9500–9510.
48. H. Heinz and U. W. Suter, Angew. Chem., Int. Ed., 2004, 116, 2289–2293.
49. H. Heinz, H. Koerner, K. L. Anderson, R. A. Vaia and B. L. Farmer, Chem. Mater., 2005, 17, 5658–5669.
50. H. Heinz, T.-J. Lin, R. K. Mishra and F. S. Emami, Langmuir, 2013, 29, 1754–1765.
51. Interface Force Field, https://bionanostructures.com/interface-md, 2019.
52. J. L. Bradley-Shaw, P. J. Camp, P. J. Dowding and K. Lewtas, Langmuir, 2016, 32, 7707–7718.
53. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
54. LAMMPS Molecular Dynamics Simulator, http://lammps.sandia.gov, 1995.
55. V. F. Sears, Neutron News, 1992, 3, 29–37.
56. S. Clarke, B. Howe, L. Griffin and C. Truscott, Neutron Reflection of Cetyltrimethylammonium Bromide (C16TAB) at the Mica Water Interface, STFC ISIS Neutron and Muon Source, 2017 DOI:10.5286/ISIS.E.42589983.
57. S. Clarke and L. Griffin, Neutron Reflection of Didodecyldimethylammonium Bromide at the Mica Water Interface, STFC ISIS Neutron and Muon Source, 2017 DOI:10.5286/ISIS.E.59893619.
58. T. Arai, K. Sato, A. Iida and M. Tomitori, Sci. Rep., 2017, 7, 4054.
59. S. Adapa and A. Malani, Sci. Rep., 2018, 8, 12198.
60. F. Zhao, Y. Du, P. Y. X. Li and J. Tang, Sci. China, Ser. B: Chem., 2005, 48, 101–106.
61. Y. Lvov and H. Möhwald, Protein Architecture: Interfacing Molecular Assemblies and Immobilization Biotechnology, CRC Press, New York, 1999.

---