Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using optical tweezing to control phase separation and nucleation near a liquid–liquid critical point†
Finlay
Walton
 and
Klaas
Wynne
and
Klaas
Wynne
 *
*
School of Chemistry, University of Glasgow, UK. E-mail: klaas.wynne@glasgow.ac.uk
First published on 4th October 2019
Abstract
About 20 years ago, it was shown that lasers can nucleate crystals in super-saturated solutions and might even be able to select the polymorph that crystallises. However, no theoretical model was found explaining the results and progress was slowed down. Here we show that laser-induced nucleation may be understood in terms of the harnessing of concentration fluctuations near a liquid–liquid critical point using optical tweezing in a process called laser-induced phase separation (LIPS) and LIPS and nucleation (LIPSaN). A theoretical model is presented based on the regular solution model with an added term representing optical tweezing while the dynamics are modelled using a Kramers diffusion equation, and the roles of heat diffusion and thermophoresis are evaluated. LIPS and LIPSaN experiments were carried out on a range of liquid mixtures and the results compared to theory.
Introduction
In the late 1990s and early 2000s, it was shown that a nanosecond laser can be used to induce nucleation of crystals in a supersaturated solution through a non-photochemical process.1 Most excitingly, it was reported that the laser polarisation could be used to control which polymorph would nucleate, promising an unprecedented degree of control.2,3 Subsequent work showed that laser pulses can induce nucleation of various crystals,4–8 liquid crystals9,10 and bubbles.11 However, these nanosecond-laser nucleation experiments defied all explanation.12–14A series of publications has shown that optical tweezing can be used to nucleate crystals from super-saturated15–18 and strangely even from under-saturated solutions.19 Optical tweezing is a technique used widely in physics and biology and involves the trapping of a high-refractive-index particle through optical forces.20 Thus, it was assumed that in these experiments the laser was tweezing pre-existing clusters or pre-nuclei.16 However, these optical tweezing nucleation experiments were only shown to work on a liquid–gas interface. This strongly suggests that heating, evaporation, convection, and Marangoni effects play critical roles,21 which would also explain why the method works in under-saturated solutions. However, very excitingly, these experiments also demonstrated polymorph selection.15–19 As in the case of non-photochemical laser-induced nucleation, no sensible theory is available to describe the physics of these results. Thus, it is fair to say that a physical understanding of all of these phenomena is still sorely lacking.
A possible explanation for these laser-induced nucleation experiments might come from thermodynamics. According to classical Gibbs nucleation theory, nucleation is impeded by the fact that a growing nucleus has an energetically-unfavourable interface that results in a barrier on the way to the crystalline state.22,23 This means that in a supersaturated solution or supercooled liquid, the crystal is the thermodynamically most stable state but—in the absence of heterogeneous nucleation sites—can only be accessed through random fluctuations leading to a nucleus exceeding a critical size. A number of recent experiments have called into question the validity of classical Gibbs nucleation theory and invoked the presence of so-called pre-nucleation clusters.24–26 Although there have been experimental studies reporting pre-nucleation clusters, they are still considered controversial.27,28
However, an older paper by Frenkel on protein crystallisation showed that nucleation is sped up, not simply by increasing the concentration, but by choosing a concentration that is near a (hidden) liquid–liquid demixing critical point.29–31 This is because critical concentration fluctuations give rise to liquid-like protein droplets (with a very high protein concentration) that increase the probability of the formation of a critical nucleus. The metastable critical point idea found some traction in the chemical engineering community where it was related to the phenomenon of “oiling out” without too much detailed theoretical analysis.23,32–34 Could liquid–liquid phase separation, oiling out, pre-nucleation clusters, and laser-induced nucleation all be aspects of the same phenomenon?26,35,36
On approaching a liquid–liquid demixing critical point, concentration fluctuations increase. As a result, it should be easier for an external “force”, such as optical tweezing, to manipulate the concentration locally.37–39 Optical tweezing normally involves the trapping of a high-refractive-index particle by the small forces exerted by a focused laser beam. However, a chemist's view of nucleation is like a chemical reaction where the supersaturated solution is the reactant state and the crystal (nucleus) the product state. Switching on an optical tweezing laser will lower the free energy of the product state (even if the crystal nucleus does not exist yet), will therefore increase the driving force and lower the barrier for the nucleation process, and increase the “reaction rate”. This simple but novel idea was first tested by us on liquid mixtures.40,41
Here we will present a simple theoretical model of a liquid mixture based on the regular solution model42 including an extra term representing the stored electromagnetic energy of a tweezing laser. This model shows that the concentration-dependent free energy is indeed more easily perturbed near a critical point.40,41 Experiments were carried out on a number of mixtures—exhibiting an upper consolute point near room temperature—using a simple continuous wave (CW) diode laser that showed that the optical tweezer can pull the high refractive-index liquid out of the mixture in a process named laser-induced phase separation (LIPS).40,41 Near the liquid–liquid binodal the laser can trigger the formation of phase-separated droplets through LIPS and nucleation (LIPSaN).
Theory
Regular solution model of mixing
In order to model the free energy associated with the mixing (and demixing) of two liquids, the widely used regular solution model will be employed.42 Define a liquid mixture with mole fractions of molecule A and B given by x0 and xB, such that xB = 1 − x0. The regular solution model defines the strength of the energetic interaction between A and B relative to their self-interaction by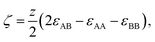 | (1) |
Fmix(x0,T,ζ) = RT(x0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x0 + xB x0 + xB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) xB) + ζx0xB. xB) + ζx0xB. | (2) |
The coexistence curve (binodal) is at dFmix/dx = 0 and the spinodal at d2Fmix/dx2 = 0, which are easily solved for T as
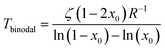 | (3) |
| Tspinodal = 2x0ζ(1 − x0)R−1 | (4) |
Before considering the effect of optical tweezing, one should first consider the free-energy changes in a small volume due to spontaneous concentration fluctuations. Define V0 as the volume of the sample container and x0 as the initial mole fraction of A in the mixture. Now consider a small volume Vlaser, which will contain the focal volume of the tweezing laser that will cause LIPS. If the mole fraction of A in this volume changes to xlaser and the mole fraction in the remaining volume to xrest, conserving the total amount of A and B implies
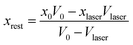 | (5) |
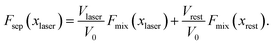 | (6) |
Adding in the effect of optical tweezing
It is reasonable to assume that the refractive index in a mixture is approximately given by the concentration-weighted refractive indices of the component liquids A and B, that is,| n(x) = xnA + (1 − x)nB, | (7) |
| Ulaser = −ε0n2(xlaser)E2Vlaser. | (8) |
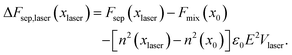 | (9) |
| I = ε0E2 = Ulaser,ext/Ac, | (10) |
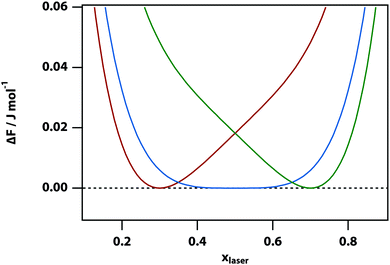
The change of the free-energy potential by the optical tweezing effect is illustrated in Fig. 2 under the assumption that liquid B has the higher refractive index. Switching on the optical-tweezing potential biases the potential towards the right and therefore the laser volume is expected to become enriched with the high refractive index liquid. This process we will refer to as laser-induced phase separation (LIPS).40,41 In the metastable case, switching on the laser causes the system to tip from metastable (two minima separated by a barrier) to unstable (single minimum determined by the tweezing laser) at sufficient laser power, thereby triggering phase separation.
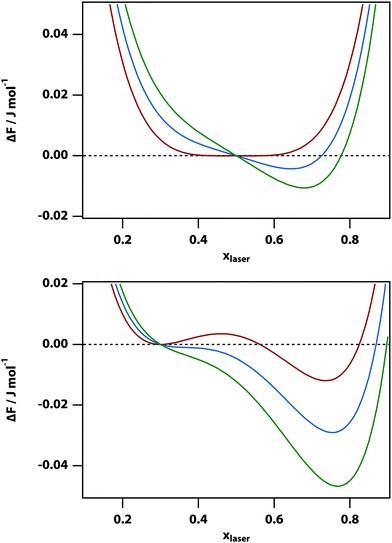
In the high temperature regime, the free-energy difference curve, eqn (9), has only a single minimum. Thus, in principle, one could find this stable minimum by determining dΔFsep,laser/dx = 0, however, this does not have a simple analytical solution. Therefore, instead we determined the minimum of the free energy difference using a numerical algorithm. In the low temperature limit (below the spinodal), the free energy difference also has single minimum. However, for temperatures between the binodal and spinodal, the free energy difference has two minima. Our numerical approach implies that the metastable minimum will be missed and only the stable minimum will be found.
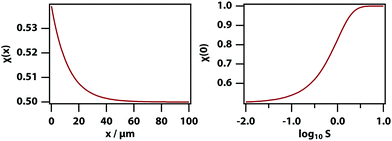
The experiments described below are carried out by using phase-contrast microscopy, which is sensitive to changes in refractive index. Since the refractive index is linearly proportional to the volume fraction in our model (as per eqn (7)), the volume fraction can be used as a proxy for the signal measured in the experiments. Fig. 3 shows the predicted phase-contrast signal calculated by finding the x that minimises the free-energy difference numerically and subtracting off the original volume fraction x0, as a function of temperature, laser intensity, and initial mole fraction. At sufficiently high temperature all of these curves follow the power law (T − T0)−1 but deviate from this behaviour very near the binodal.
The Kramers equation for diffusion
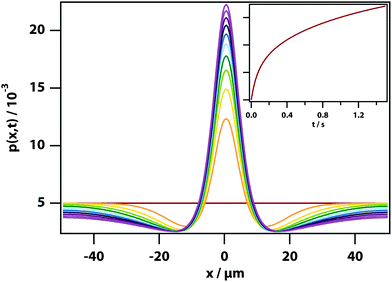
The free-energy change induced by the laser (eqn (9)) gives rise to an optical trap that will draw in the liquid with the highest refractive index giving rise to LIPS kinetics. The liquid diffusion can be modelled by a Fokker–Planck equation, describing the evolution of the probability distribution function p(x,t) of a random variable x as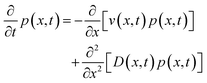 | (11) |
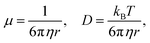 | (12) |
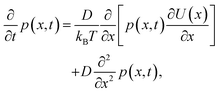 | (13) |
When the potential U(x) is set to zero everywhere, one can easily derive the Green's function of this Fokker–Planck equation, which is given by
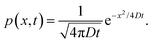 | (14) |
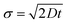 . The diffusion coefficient D can be approximated using the Stokes–Einstein expression eqn (12). If this equation is applied to nitrobenzene (molar mass 123.06 g mol−1, density 1.199 g cm−3, therefore r = 3.44 nm, and η = 2.03 cP) one finds Dtrans = 3.1 × 10−10 m2 s−1.
. The diffusion coefficient D can be approximated using the Stokes–Einstein expression eqn (12). If this equation is applied to nitrobenzene (molar mass 123.06 g mol−1, density 1.199 g cm−3, therefore r = 3.44 nm, and η = 2.03 cP) one finds Dtrans = 3.1 × 10−10 m2 s−1.
In the case of a focussed laser with a Gaussian beam profile of width w, the trapping potential is simply
| U(x) ∝ e−x2/2w2 | (15) |
Heat diffusion
The trapping laser can also be partially absorbed by vibrational overtones resulting in a rise in temperature, which would counteract the optical-trapping effect. The one-dimensional heat equation is46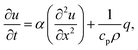 | (16) |
As heat transport is rapid, it is reasonable to assume that the heat source is a delta function in space, which allows a stationary solution to be found if it is taken that heat is lost by cooling (for example, to the cooling stage used in our experiments). The stationary heat equation then becomes
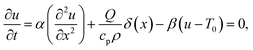 | (17) |
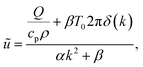 | (18) |
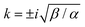 . The inverse Fourier transform is solved by contour integration to yield
. The inverse Fourier transform is solved by contour integration to yield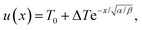 | (19) |
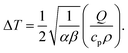 | (20) |
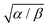 . The parameter β can be calculated using Fourier's law of heat flow yielding
. The parameter β can be calculated using Fourier's law of heat flow yielding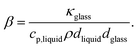 | (21) |
Thermophoresis
In this work, we argue that LIPS is achieved through an optical-tweezing effect. However, phase separation could potentially also be caused by a temperature gradient (such as that generated by the laser, see eqn (19)) through thermophoresis. The one-dimensional thermophoresis equation in equilibrium is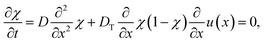 | (22) |
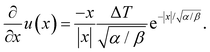 | (23) |
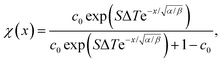 | (24) |
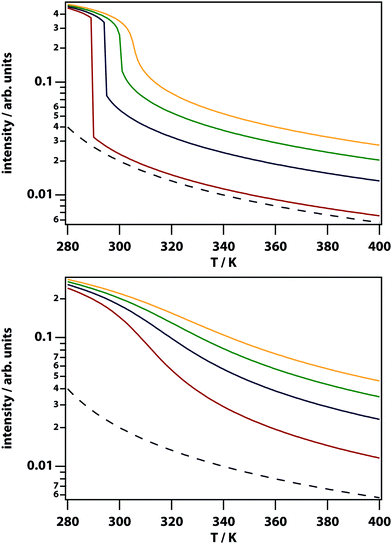
Fig. 5 shows the calculated spatially dependent thermophoretic effect as well as the concentration enhancement on the peak. The thermophoretic effect clearly will play a major role for S > 10−1. For mixtures of small-molecule liquids the Soret coefficient is typically on the order of S ∼ 10−3,48 and therefore thermodiffusion will play no role in the experiments described here.
Methods
Materials
Experiments were carried out on nitrobenzene, aniline, decane, hexadecane, cyclohexane, and methylene blue (Sigma Aldrich) and used as supplied. All samples were filtered before use using 0.2 mm hydrophilic polytetrafluoroethylene (PTFE) filters (Millipore) to remove dust. For all microscopy experiments, a sample thickness of 11.58 ± 0.19 μm was used, controlled by glass monodisperse particle standards (Whitehouse Scientific). Particles were sandwiched between borosilicate glass (VWR) and ruby mica discs, which were cleaned by rinsing in acetone, isopropyl alcohol, and distilled water, followed by drying in an oven at 150 °C for 30 min. The sample temperature was controlled to ±0.1 K using a Linkam THMS600 cryogenic microscopy stage. In the experiments, the samples were quenched from room temperature and held at a selected quench temperature.40,41Microscopy
Microscopy was carried out using an Olympus BX53 light microscope that features modular units for phase-contrast and fluorescence microscopy, and a custom unit allowing for simultaneous laser irradiation and microscopy. The primary laser used was a 785 nm continuous-wave diode laser (Thorlabs) producing a maximum power incident on the sample of 200 mW with an elliptical mode with a mean beam radius (at half height) of 2.4 μm (beam waist 4.1 μm) when using a ×10 objective. Phase-contrast microscopy converts small differences in optical path length into intensity, therefore it can be used as a measure of refractive index. Positive phase contrast has been used here and results in intensity scaling with refractive index for objects on the micrometre scale. Nitrobenzene strongly quenches many fluorescent dyes but the dye methylene blue is quenched relatively weakly. This produces contrast between the nitrobenzene-rich and decane-rich phases in fluorescence microscopy. Data were captured using the ImageJ add-on μManager and analysed primarily using ImageJ.Results
Laser-induced phase separation (LIPS)
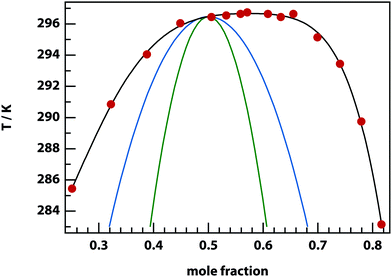
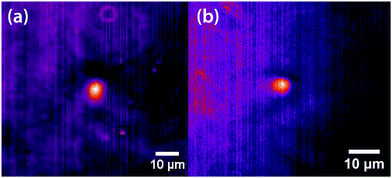
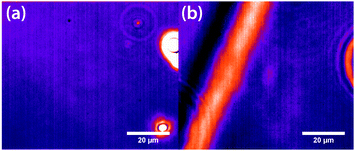
Experiments were carried out primarily using binary mixtures with a significant difference in refractive index (Δn). Mixtures of nitrobenzene and hexadecane were selected for the majority of experiments due to the high Δn (1.53749 and 1.43050 respectively) and low vapour pressures, in order to maintain consistent mole fractions during sample preparation and long experiments. The mixture is reported to have a bulk (upper consolute) critical temperature Tc = 309.69 K = 36.54 °C and critical mole fraction xc = 0.716.51 Our own experiments agree with this figure, with bulk Tc = 36.4 ± 0.2 °C, however, confinement effects in the 11 μm thick microscopy samples elevate the critical temperature to Tc = 37.3 ± 0.1 °C. An example of an experimentally determined phase diagram is shown in Fig. 6 for nitrobenzene–decane mixtures.Initial experiments were carried out 0.1 °C above the binodal at xc. When the 785 nm laser is focussed in the sample, a bright, diffuse droplet becomes visible when viewed using phase-contrast microscopy (Fig. 7). The bright spot indicates that the droplet is composed of a higher fraction of the high refractive-index component than the surrounding liquid.
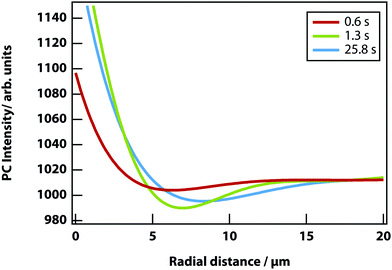
In addition, a dark region is observed surrounding the droplet, which is nitrobenzene-depleted. This depletion region appears a couple of seconds after the laser is switched on and then equilibrates with the rest of the sample. A radial distribution function (calculated from the image data) of a droplet, which is shown in Fig. 8 gives a full width half maximum (FWHM) of 1.7 μm at equilibrium and a depletion region at 7 μm after 1.3 s. The minimum of the radial distribution function shifts to larger values as a function of time as predicted by theory (see Fig. 4).
Fluorescence microscopy was carried out on mixtures of nitrobenzene and decane in order to corroborate the finding from phase-contrast microscopy that the droplet in the focus is nitrobenzene-rich.40,41 The dye methylene blue was used, as nitrobenzene weakly quenches its fluorescence by electron-transfer, giving good contrast between areas of high and low fractions of nitrobenzene. A dark spot in the focal area confirms that the droplet is composed of a higher fraction of nitrobenzene than the surrounding liquid.40,41
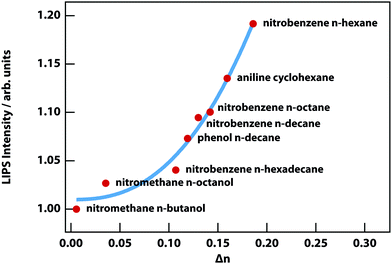
LIPS has so far been observed in the binary mixtures listed in Table 1, with the exception of the final entry where LIPS was too weak to be detected due to its small Δn, which is 3% of the nitrobenzene n-hexane mixture. Fig. 9 shows the two mixtures with the smallest Δn, from which it is clear that nitromethane–n-octanol is just barely detectable.
| Component 1 | Component 2 | Δn |
|---|---|---|
| Nitrobenzene | n-Hexane | 0.1812 |
| Aniline | Cyclohexane | 0.1594 |
| Nitrobenzene | n-Decane | 0.1452 |
| Nitrobenzene | n-Octane | 0.1430 |
| Phenol | n-Decane | 0.1190 |
| Nitrobenzene | n-Hexadecane | 0.1107 |
| Nitromethane | n-Octanol | 0.0355 |
| Nitromethane | n-Butanol | 0.0055 |
Fig. 10 shows the strength of LIPS, as a function of Δn, 0.1 °C above Tc for the mixtures listed in Table 1. The effect scales almost as the cube of Δn. This can be understood based on the quadratic dependence on Δn of the optical trap (see eqn (8)) combined with the linear dependence on Δn of phase-contrast microscopy.
The dynamics of LIPS was measured by chopping the laser beam and measuring the rise and decay of the LIPS signal (see Fig. 11). The time that it takes for the droplet to form and decay are broadly similar. For different nitrobenzene mixtures (see Table 2), there is no obvious relation between the dynamics and the viscosity (which determines the diffusion rate). However, concomitant changes in Δn (and therefore the depth of the optical trapping potential) are likely to mask any effect.
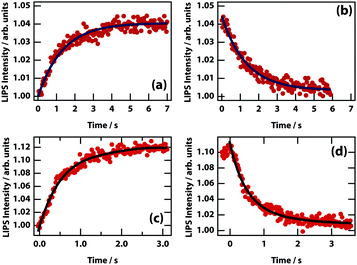 | ||
| Fig. 11 LIPS formation and decay curves. Dynamics are shown for mixtures of nitrobenzene hexadecane (a and b) and nitrobenzene octane (c and d). Times at 1/e of the minimum/maximum are listed in Table 2. | ||
| Component 2 | Viscosity (cP) | Formation (s) | Decay (s) |
|---|---|---|---|
| Octane | 1.10 | 0.60 | 0.87 |
| Decane | 1.31 | 1.31 | 1.68 |
| Hexadecane | 2.48 | 1.19 | 1.11 |
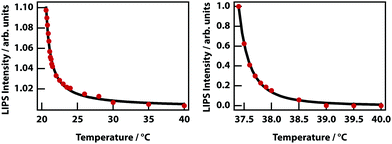
The theory predicts that LIPS follows a power law as a function of the difference in the temperature and the binodal temperature (see Fig. 3). LIPS temperature dependence was measured as a function of temperature above the critical point and is shown in Fig. 12 for two mixtures. These data can be fit to power laws of the form (T − T0)x, where x is −1.0 for nitrobenzene–octane and −2.4 for nitrobenzene–hexadecane broadly consistent with the theoretical prediction. The strength of LIPS depends not only on the temperature difference relative to Tc but also on the absolute value of the difference in mole fraction relative to xc.40,41
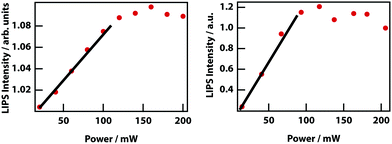
Higher laser power implies a deeper optical trap and therefore enhanced LIPS. Fig. 13 shows that at low powers, there is an approximately linear increase in magnitude of LIPS with power, consistent with eqn (10). At high laser powers and in mixtures with a relatively large Δn, the droplets become large enough that they are subject to the shade off effect, which is inherent in phase-contrast microscopy, resulting in a saturation of LIPS.
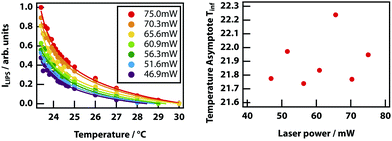
Finally, it was investigated whether the effective critical temperature (temperature asymptote) depends on laser power as predicted by theory (see Fig. 3). Unfortunately, the signal-to-noise ratio of the experiments is insufficient to establish this. Even by fixing the power law exponent to −1, it was not possible to determine any reasonable trend in the power-dependent temperature asymptotes (see Fig. 14)
LIPS and nucleation (LIPSaN)
Laser-induced nucleation experiments have a been carried out previously in a variety of metastable (supersaturated) solutions1–5,17,52 but a mechanistic understanding of the phenomenon has been lacking. We surmised that laser-induced nucleation was caused by optical trapping near a liquid–liquid critical point. This process would then be laser-induced phase separation and nucleation (LIPSaN).In the case of liquid–liquid demixing, there is a metastable region between the binodal and spinodal lines. In the metastable region phase separation occurs though a nucleation process identical (in principle) to that of crystal nucleation. Therefore, LIPSaN experiments were attempted on binary mixtures at temperatures and mole fractions in the metastable region. However, it was found that the metastable region is exceedingly narrow, causing spontaneous nucleation and phase separation to occur.
Nevertheless, LIPSaN could be demonstrated in a narrow mole fraction interval 0.62 < x < 0.69 for temperatures just above the binodal (see Fig. 15) giving rise to a spinodal decomposition pattern (Fig. 15(b)). Unexpectedly, LIPSaN in these mixtures occurs only once the laser has been switched off rather than on. This can be understood in terms of heating effects. When the tweezing laser is switched on, laser absorption will quickly heat the laser volume and some of the surrounding area (by ≤1.6 K, see above; Fig. 16(a)). On a slower timescale (approximately 30× more slowly, see above), determined by mass diffusion, LIPS will cause the formation of a nitrobenzene enriched droplet surrounded by a depleted volume (shown as a dot and a circle in Fig. 16(b)). When the laser is switched off, both the enriched droplet and the depleted volume will quickly cool (Fig. 16(c)). On a 30× longer timescale equilibrium will be restored (Fig. 16(d)). When such an experiment is carried out near the critical point, nothing happens as all points remain in the mixed region (Fig. 16(e)). When the starting point is at a high mole fraction and near the binodal, the depleted volume will drop into the unstable region below the spinodal when the laser is switched off (Fig. 16(f)). When the starting point is at low mole fraction and near the binodal, the enriched droplet will drop into the unstable region when the laser is switched off (Fig. 16(g)). Phase separation will cause this droplet to further enrich while shrinking at the same time, rendering it invisible because of the lever rule.
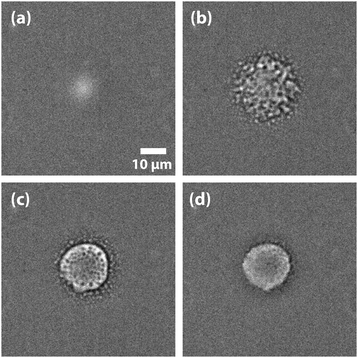 | ||
| Fig. 15 LIPS and nucleation (LIPSaN) experiments in nitrobenzene–decane. Experiments carried out in a metastable x = 0.632 nitrobenzene–decane mixture at T = 23.9 °C with a 120 mW 785 nm focussed laser, on for 30 s. When the laser is switched on a LIPS droplet forms (a) but only once the laser is switched off does nucleation occur (b), followed by Ostwald ripening (c) and (d).40,41 | ||
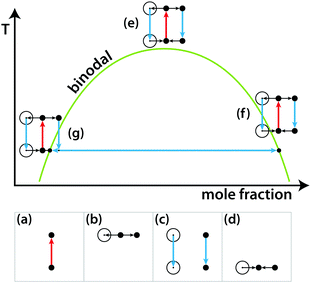 | ||
| Fig. 16 Schematic liquid–liquid phase diagram showing the combined effects of LIPS and heating. See text for explanation. | ||
Based on the mechanism shown in Fig. 16, the experimental results in Fig. 15 can be understood. Because it is the depleted region that triggers nucleation, the nucleating region is much larger than the LIPS spot. It also explains why the diameter of the LIPSaN droplet increases with exposure time and laser power.40,41
Finally, LIPSaN was investigated as a function of mole fraction.40,41 At lower mole fractions (closer to critical, x = 0.575) a large well-defined droplet nucleated, while at higher mole fractions, a cloud of smaller droplets is induced. As can be seen in Fig. 15(c) and (d), Ostwald ripening causes smaller sub-droplets to be subsumed into the main droplet. This effect cannot occur effectively further away from the critical point because of the lower density giving rise to the cloud of smaller droplets.
Discussion and conclusions
At a phase boundary the free energies of the two phases are identical and fluctuations in concentration or densities can be observed, particularly in the absence of an energy barrier between them. Fluctuations are strongest in proximity to critical points, such as near the upper consolute temperature (UCST) seen in the binary mixtures in this paper. We have demonstrated that these fluctuations can be harnessed using a laser, which generates a trapping potential that draws the high refractive index component of the mixture into the focus. In critical and near-critical mixed samples that are within ∼1 °C of the critical point, this potential forces phase separation. In metastable samples, the laser potential lowers the energy barrier to the separated state and can trigger nucleation.Photothermal separation has been documented in binary mixtures of molecular liquids53 and polymers,44,54,55 but relies on the system in question having a lower critical solution temperature (LCST), the opposite of the UCST present in the mixtures we have used. Bunkin et al. used such an LCST mixture and using a model based on the Navier–Stokes equation concluded that heat-induced barodiffusion (diffusion due to pressure) was the dominant mechanism.56 Any heating in an LCST system forces the mixture into the separated state, whereas heating in a UCST mixture moves it further into the mixed regime. As such, the mechanism of LIPS cannot be due to a direct heating effect.
One of the main mixture we have used, nitrobenzene–decane, has no electronic absorption bands at the laser wavelength of 785 nm (see Fig. S1, ESI†) ruling out the mechanism of resonant trapping of fluorescent molecules.57 Thermophoresis, or the Soret effect, is the diffusion of molecules in a mixture due to their preference to be in a region of high or low temperature, lowering the overall free energy. However, using our steady-state focal heating calculation and typical values of the Soret coefficient for small molecules,58 we conclude that the change in mole fraction is negligible relative to change due to LIPS.
LIPS is similar to the optical trapping of particles such as glass beads where, due to refraction within the particle, there is a small transfer of momentum that leads to a net restoring force towards the region of highest electric field.59 In optical trapping, the scattering force is also important as it pushes the particle out of the focus in the propagation direction of the laser beam. In order to trap particles in bulk liquid, the restoring force must be greater than or equal to the scattering force, which requires an objective lens with a numerical aperture >∼1.60 Our experimental setup requires a long working distance lens, which has a much lower numerical aperture of 0.3. As such in our experiments, the LIPS droplet is pushed against the lower microscope slide and not trapped in the strictest sense.
The LIPS and LIPSaN effects detailed here do not depend on the presence of pre-nucleation clusters that can be trapped and aggregated by the laser.61,62 Rather the laser generates a potential that lowers the free energy of the phase-separated state. The mixtures we used were chosen because their critical points are easily accessible and not hidden below a liquidus or above the boiling points of the components. Ultimately, this is a generic effect that applies to all mixtures.
The experiments presented here use LIPS and LIPSaN only to separate two liquids in a mixture near a liquid–liquid critical point. Nearly all liquid mixtures have a UCST although in most cases it will be hidden below the liquidus line. A good example is the aqueous sodium chloride solution, which—even though NaCl is highly soluble in water—has a hidden binodal and spinodal where an amorphous NaCl phase separates from water.63 The same holds true for aqueous protein solutions.29 However, in the case of proteins the position of the fluid–fluid critical point can be manipulated relatively easily using ionic strength and pH.64 Some protein solutions under some circumstances will show phase separation into a dense and a dilute–fluid phase and this is even observed in vivo.65,66 In cases where the UCST is below the liquidus, LIPS will produce a droplet with an enhanced concentration of one component liquid. This will either greatly increase the probability of nucleation through the greater concentration in a classical Gibbs nucleation process23,35 or force the production of a liquid-like droplet that is unstable with respect to crystallisation.67–69 Therefore, it is reasonable that LIPS is at the basis of most reported laser-induced crystal nucleation experiments (which would all be a form of LIPSaN).
Thus, LIPS is likely to be related to a string of recent laser-induced nucleation experiments claiming to use optical trapping of clusters,15,17,19,61,62,70–74 although these experiments could only be carried out at air–solution interfaces, implying that evaporation, Marangoni effects, and thermophoresis may play important roles as well. A repeat of these experiments in the bulk would be worthwhile, bearing in mind the possibility of a hidden liquid–liquid critical point enhancing concentration fluctuations. Bulk non-photochemical laser-induced nucleation (NPLIN) phenomena described by Garetz, Alexander, and others1–14,75,76 fit with our narrative as the final states have higher refractive indices than their precursor mixtures. There are two potential exceptions to this picture, the first being laser-induced bubble nucleation. Peters and co-workers reported NPLIN of gas bubbles from solutions of carbon dioxide in water.11 As a gas, CO2 has a much lower refractive index than water, which would be inconsistent with LIPS. The threshold pulse energy of the effect was reported to be independent of wavelength and purity of the chemicals, suggesting that heating does not play a role. Alexander and co-workers ran similar NPLIN experiments and found that filtering their solutions or thorough cleaning of glassware in acid increased the threshold for NPLIN and decreased the number of nucleation events.77 In any case, since our experiments show a depletion region which has a higher fraction of the low refractive-index component, this may be responsible for lowering the energy barrier to gas-bubble nucleation. The second potential exception to this rule is NPLIN of glacial acetic acid,4 as it is a pure liquid rather than a mixture. However, it is well established that pure liquids can exhibit liquid–liquid critical points, as observed in triphenyl phosphite,78–81n-butanol,82,83D-mannitol,84 and water.85 It may be the case that acetic acid exhibits a yet undocumented liquid–liquid critical point.
In summary, we have demonstrated that a cheap laser-diode can be used to induce phase separation and nucleation in near-critical binary liquid mixtures. The effect depends on both on a difference in refractive index and, more importantly, proximity to a liquid–liquid critical point. The theory presented here applies to laser-induced crystal nucleation and provides a framework for future research on the subject.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge discussions with Giovanni Volpe (University of Gothenburg) on the possible role of thermophoresis. We thank the Engineering and Physical Sciences Research Council (EPSRC) for support through grants EP/J004790/1, EP/J009733/1, and EP/N007417/1. This work was part funded by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 832703).References
- B. A. Garetz, J. E. Aber, N. L. Goddard, R. G. Young and A. S. Myerson, Phys. Rev. Lett., 1996, 77, 3475–3476 CrossRef CAS PubMed
.
- B. A. Garetz, J. Matic and A. S. Myerson, Phys. Rev. Lett., 2002, 89, 175501 CrossRef PubMed
.
- X. Sun, B. A. Garetz and A. S. Myerson, Growth, 2006, 6, 684–689 CrossRef CAS
.
- M. R. Ward, S. McHugh and A. J. Alexander, Phys. Chem. Chem. Phys., 2012, 14, 90–93 RSC
.
- N. Iefuji, R. Murai, M. Maruyama, Y. Takahashi, S. Sugiyama, H. Adachi, H. Matsumura, S. Murakami, T. Inoue, Y. Mori, Y. Koga, K. Takano and S. Kanaya, J. Cryst. Growth, 2011, 318, 741–744 CrossRef CAS
.
- Y. Liu, M. H. van den Berg and A. J. Alexander, Phys. Chem. Chem. Phys., 2017, 19, 19386–19392 RSC
.
- C. Duffus, P. J. Camp and A. J. Alexander, J. Am. Chem. Soc., 2009, 131, 11676–11677 CrossRef CAS
.
- W. Li, A. Ikni, P. Scouflaire, X. Shi, N. El Hassan, P. Gémeiner, J. M. Gillet and A. Spasojević-De Biré, Cryst. Growth Des., 2016, 16, 2514–2526 CrossRef CAS
.
- A. Usman, T. Uwada and H. Masuhara, J. Phys. Chem. C, 2011, 115, 11906–11913 CrossRef CAS
.
- T. Kosa, L. Sukhomlinova, L. Su, B. Taheri, T. J. White and T. J. Bunning, Nature, 2012, 485, 347–349 CrossRef CAS PubMed
.
- B. C. Knott, J. L. LaRue, A. M. Wodtke, M. F. Doherty and B. Peters, J. Chem. Phys., 2011, 134, 171102 CrossRef PubMed
.
- B. C. Knott, N. Duff, M. F. Doherty and B. Peters, J. Chem. Phys., 2009, 131, 224112 CrossRef PubMed
.
- B. C. Knott, M. F. Doherty and B. Peters, J. Chem. Phys., 2011, 134, 154501 CrossRef PubMed
.
- Y. Liu, M. R. Ward and A. J. Alexander, Phys. Chem. Chem. Phys., 2017, 19, 3464–3467 RSC
.
- K. I. Yuyama, T. Rungsimanon, T. Sugiyama and H. Masuhara, Cryst. Growth Des., 2012, 12, 2427–2434 CrossRef CAS
.
- T. Sugiyama, K. Yuyama and H. Masuhara, Acc. Chem. Res., 2012, 45, 1946–1954 CrossRef CAS PubMed
.
- K. Yuyama, T. Sugiyama and H. Masuhara, J. Phys. Chem. Lett., 2013, 4, 2436–2440 CrossRef CAS PubMed
.
- K. I. Yuyama, M. Ueda, S. Nagao, S. Hirota, T. Sugiyama and H. Masuhara, Angew. Chem., Int. Ed., 2017, 56, 6739–6743 CrossRef CAS PubMed
.
- H. Niinomi, T. Sugiyama, K. Miyamoto and T. Omatsu, Cryst. Growth Des., 2018, 18, 734–741 CrossRef CAS
.
- R. W. Bowman and M. J. Padgett, Rep. Prog. Phys., 2013, 76, 26401 CrossRef PubMed
.
- S. Bartkiewicz and A. Miniewicz, Phys. Chem. Chem. Phys., 2015, 17, 1077–1083 RSC
.
- D. Gebauer and H. Coelfen, Nano Today, 2011, 6, 564–584 CrossRef CAS
.
- R. J. Davey, S. L. M. Schroeder and J. H. Ter Horst, Angew. Chem., Int. Ed., 2013, 52, 2166–2179 CrossRef CAS PubMed
.
- H. Gebauer, D. Völkel and A. Cölfen, Science, 2008, 322, 1819–1822 CrossRef PubMed
.
- G. De With and N. A. J. M. Sommerdijk, Science, 2009, 587, 2007–2010 Search PubMed
.
- A. Dey, P. H. H. Bomans, F. A. Müller, J. Will, P. M. Frederik, G. De With and N. A. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1010–1014 CrossRef CAS
.
- P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. De Yoreo, P. M. Rodger and N. A. J. M. Sommerdijk, Proc. Natl. Acad. Sci. U. S. A., 2017, 201700342 Search PubMed
.
- A. E. S. Van Driessche, N. Van Gerven, P. H. H. Bomans, R. R. M. Joosten, H. Friedrich, D. Gil-Carton, N. A. J. M. Sommerdijk and M. Sleutel, Nature, 2018, 556, 89–94 CrossRef CAS PubMed
.
- P. R. ten Wolde and D. Frenkel, Science, 1997, 277, 1975–1978 CrossRef CAS PubMed
.
- J. Wedekind, L. Xu, S. V. Buldyrev, H. E. Stanley, D. Reguera and G. Franzese, Sci. Rep., 2015, 5, 1–7 Search PubMed
.
- L. Xu, S. V. Buldyrev, H. E. Stanley and G. Franzese, Phys. Rev. Lett., 2012, 109, 095702 CrossRef PubMed
.
- P. E. Bonnett, K. J. Carpenter, S. Dawson and R. J. Davey, Chem. Commun., 2003, 698–699 RSC
.
- M. Takasuga and H. Ooshima, Cryst. Growth Des., 2014, 14, 6006–6011 CrossRef CAS
.
- J. Mosses, D. A. Turton, L. Lue, J. Sefcik and K. Wynne, Chem. Commun., 2014, 50, 1–9 RSC
.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC
.
- A. F. Wallace, L. O. Hedges, A. Fernandez-martinez, P. Raiteri, J. D. Gale, G. A. Waychunas, S. Whitelam, J. F. Banfield and J. J. De Yoreo, Science, 2013, 692, 885–889 CrossRef
.
- A. Casner and J.-P. Delville, Phys. Rev. Lett., 2001, 87, 054503 CrossRef CAS
.
- R. D. Schroll, R. Wunenburger, A. Casner, W. W. Zhang and J. P. Delville, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef PubMed
.
- Y. Katsir and Y. Tsori, J. Phys.: Condens. Matter, 2017, 29, 63002 CrossRef PubMed
.
- F. Walton and K. Wynne, Nat. Chem., 2018, 10, 506–510 CrossRef CAS PubMed
.
- F. Walton and K. Wynne, Proc. SPIE, 2018, 10723, 107230O Search PubMed
.
-
R. A. L. Jones, Soft Condensed Matter, Oxford Univ. Press Inc., New York, 2002 Search PubMed
.
- H. Toyama, K. Yoshikawa and H. Kitahata, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 1–4 CrossRef PubMed
.
- J. P. Delville, C. Lalaude and A. Ducasse, Phys. A, 1999, 262, 40–68 CrossRef CAS
.
- P. F. Barbara, E. Aakesson, G. C. Walker, A. E. Johnson and N. E. Levinger, J. Phys. Chem., 2005, 96, 3728–3736 Search PubMed
.
- M. L. Cordero, E. Verneuil, F. Gallaire and C. N. Baroud, Phys. Rev. E: Stat., Nonlinear,
Soft Matter Phys., 2009, 79, 011201 CrossRef PubMed
.
- M. Benitez, Opt. Eng., 2018, 48, 1–8 Search PubMed
.
- M. Eslamian and M. Z. Saghir, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 1–11 Search PubMed
.
- S. Kedenburg, M. Vieweg, T. Gissibl and H. Giessen, Opt. Mater. Express, 2012, 2, 1588–1611 CrossRef CAS
.
- D. L. Camin, A. F. Forziati and F. D. Rossini, J. Phys. Chem., 1954, 58, 440–442 CrossRef CAS
.
-
J. Wang, PhD thesis, Univ. Maryl., 2006
.
- M. R. Ward and A. J. Alexander, Cryst. Growth Des., 2012, 12, 4554–4561 CrossRef CAS
.
- S.-A. Mukai, N. Magome, H. Kitahata and K. Yoshikawa, Appl. Phys. Lett., 2003, 83, 2557–2559 CrossRef CAS
.
- C. Crauste-thibierge, A. Petrosyan and S. Ciliberto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 052312 CrossRef
.
- J. Hofkens, J. Hotta, K. Sasaki, H. Masuhara and K. Iwai, Langmuir, 2002, 13, 414–419 CrossRef
.
- N. F. Bunkin, A. V. Lobeev, G. A. Lyakhov and Y. P. Svirko, Kvantovaya Elektron., 1996, 23, 62–66 CAS
.
- M. A. Osborne, S. Balasubramanian, W. S. Furey and D. Klenerman, J. Phys. Chem. B, 1998, 102, 3160–3167 CrossRef CAS
.
- S. Wiegand, J. Phys.: Condens. Matter, 2004, 16, R357–R379 CrossRef CAS
.
- S. E. S. Spesyvtseva and K. Dholakia, ACS Photonics, 2016, 3, 719–736 CrossRef CAS
.
-
M. Woerdemann, in Structured Light Fields, ed. M. Wördemann, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, pp. 5–26 Search PubMed
.
- C. S. Wu, P. Y. Hsieh, K. I. Yuyama, H. Masuhara and T. Sugiyama, Cryst. Growth Des., 2018, 18, 5417–5425 CrossRef CAS
.
- K. Yuyama, M. J. Islam, K. Takahashi, T. Nakamura and V. Biju, Angew. Chem., Int. Ed., 2018, 57, 13424–13428 CrossRef CAS PubMed
.
- H. Jiang, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Chem. Phys., 2019, 150, 1–23 Search PubMed
.
- Y. Wang, A. Lomakin, S. Kanai, R. Alex and G. B. Benedek, Langmuir, 2017, 33, 7715–7721 CrossRef CAS PubMed
.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 CrossRef CAS PubMed
.
- H. Le Ferrand, M. Duchamp, B. Gabryelczyk, H. Cai and A. Miserez, J. Am. Chem. Soc., 2019, 141, 7202–7210 CrossRef CAS PubMed
.
- J. F. Lutsko, Sci. Adv., 2019, 5, eaav7399 CrossRef CAS PubMed
.
- D. Gebauer and S. E. Wolf, J. Am. Chem. Soc., 2019, 141, 4490–4504 CrossRef CAS PubMed
.
- A. Ianiro, H. Wu, M. M. J. van Rijt, M. P. Vena, A. D. A. Keizer, A. C. C. Esteves, R. Tuinier, H. Friedrich, N. A. J. M. Sommerdijk and J. P. Patterson, Nat. Chem., 2019, 11, 320–328 CrossRef CAS
.
- J. R. Tu, A. Miura, K. I. Yuyama, H. Masuhara and T. Sugiyama, Cryst. Growth Des., 2014, 14, 15–22 CrossRef CAS
.
- K. Yuyama, J. George, K. G. Thomas, T. Sugiyama and H. Masuhara, Cryst. Growth Des., 2016, 16, 953–960 CrossRef CAS
.
- H. Niinomi, T. Sugiyama, M. Tagawa, K. Murayama, S. Harada and T. Ujihara, CrystEngComm, 2016, 18, 7441–7448 RSC
.
- K. Yuyama, K.-D. Chang, J.-R. Tu, H. Masuhara and T. Sugiyama, Phys. Chem. Chem. Phys., 2018, 20, 6034–6039 RSC
.
- H. Niinomi, T. Sugiyama, S. Uda, M. Tagawa, T. Ujihara, K. Miyamoto and T. Omatsu, Cryst. Growth Des., 2019, 19, 529–537 CrossRef CAS
.
- T. Tasnim, A. Goh, O. Gowayed, C. T. Hu, T. Y. Chen, J. E. Aber and B. A. Garetz, Cryst. Growth Des., 2018, 18, 5927–5933 CrossRef CAS
.
- A. J. Alexander and P. J. Camp, J. Chem. Phys., 2019, 150, 040901 CrossRef PubMed
.
- M. R. Ward, W. J. Jamieson, C. A. Leckey and A. J. Alexander, J. Chem. Phys., 2015, 142, 144501 CrossRef PubMed
.
- J. Mosses, C. D. Syme and K. Wynne, J. Phys. Chem. Lett., 2014, 6, 38–43 CrossRef PubMed
.
- K. Murata and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 7176–7185 CrossRef CAS PubMed
.
- M. Kobayashi and H. Tanaka, Nat. Commun., 2016, 7, 1–8 Search PubMed
.
- F. Walton, J. Bolling, A. Farrell, J. MacEwen, C. Syme, M. G. Jiménez, H. M. Senn, C. Wilson, G. Cinque and K. Wynne, DOI:10.26434/chemrxiv.9891491.v1.
- C. D. Syme, J. Mosses, M. González-Jiménez, O. Shebanova, F. Walton and K. Wynne, Sci. Rep., 2017, 7, 42439 CrossRef CAS PubMed
.
- R. Kurita and H. Tanaka, J. Phys.: Condens. Matter, 2005, 17, L293–L302 CrossRef CAS
.
- M. Zhu, J. Q. Wang, J. H. Perepezko and L. Yu, J. Chem. Phys., 2015, 142, 244504 CrossRef PubMed
.
- S. Woutersen, B. Ensing, M. Hilbers, Z. Zhao and C. A. Angell, Science, 2018, 359, 1127–1131 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01297d |
| This journal is © The Royal Society of Chemistry 2019 |