Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
DNA translocation to giant unilamellar vesicles during electroporation is independent of DNA size†
Shaurya
Sachdev
,
Aswin
Muralidharan
 ,
Dipendra K.
Choudhary
,
Dayinta L.
Perrier
,
Lea
Rems‡
,
Dipendra K.
Choudhary
,
Dayinta L.
Perrier
,
Lea
Rems‡
 ,
Michiel T.
Kreutzer
and
Pouyan E.
Boukany
,
Michiel T.
Kreutzer
and
Pouyan E.
Boukany
 *
*
Department of Chemical Engineering, Delft University of Technology, van der Maasweg 9, 2629 HZ, Delft, The Netherlands. E-mail: p.e.boukany@tudelft.nl
First published on 20th September 2019
Abstract
Delivery of naked DNA molecules into living cells via physical disruption of the membrane under electric pulses has potential biomedical applications ranging from gene electro-transfer, electro-chemotherapy, to gene therapy, yet the mechanisms involved in DNA transport remain vague. To investigate the mechanism of DNA translocation across the cell membrane, giant unilamellar vesicles (GUVs) were electroporated in the presence of DNA molecules keeping the size of the DNA molecules as a variable parameter. We experimentally determined the translocation efficiency for each size of the DNA molecule, to compare the results with the existing and conflicting theories of the translocation mechanism i.e. stochastic threading and bulk electrophoresis. We observed that the translocation efficiency is independent of DNA size (ranging from 25–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp, bp = base pairs), implying that DNA molecules translocate freely across the electro-pores in the lipid membrane in their native polymer conformation, as opposed to unravelling and threading through the electro-pore. Bulk electrophoretic mobility determines the relationship between translocation efficiency and the size of the DNA molecule. This research provides experimental evidence of the mechanistic understanding of DNA translocation across lipid membranes which is essential for devising efficient and predictable protocols for electric field mediated naked DNA delivery.
000 bp, bp = base pairs), implying that DNA molecules translocate freely across the electro-pores in the lipid membrane in their native polymer conformation, as opposed to unravelling and threading through the electro-pore. Bulk electrophoretic mobility determines the relationship between translocation efficiency and the size of the DNA molecule. This research provides experimental evidence of the mechanistic understanding of DNA translocation across lipid membranes which is essential for devising efficient and predictable protocols for electric field mediated naked DNA delivery.
1 Introduction
Physical disruption of the cell membrane and DNA transport are of fundamental interest in cell biology, biophysics and soft materials.1,2 Application of electric pulses to disrupt the cell membrane (electroporation) is a simple, easy and popular technique to deliver nucleic acids such as DNA (deoxyribonucleic acid) and RNA (ribonucleic acid) into living cells. The transport mechanism of these nucleic acids, especially DNA molecules, across the cell membrane during electroporation, is however poorly understood.3–5 The cell membrane is a complex entity comprising not only phospholipids and various lipid domains, but also inclusions such as membrane proteins and cholestrol.6 A dense cytoskeleton network known as actin cortex is also present underneath the cell membrane.7 Therefore, inferring the mechanism of DNA translocation across the cell membrane by conducting experiments on cells is inherently a complex and a challenging task due to simultaneous involvement of several cell membrane and cytoskeleton entities. An important step towards understanding the transport mechanism of DNA across the cell membrane is to decouple several cell membrane and cytoskeleton entities and obtain rudimentary knowledge about the transport process by using lipid vesicles as cell membrane models.5Experiments on lipid vesicles have revealed much needed insights into the mechanism of DNA electro-transfer across the cell membrane. For instance, Chernomordik et al. suggested that large native T7 DNA (∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp) and plasmid DNA (or pDNA ∼ 4700 bp) followed an endocytosis-like mechanism of translocation into large unilamellar vesicles (LUVs, mean diameter ∼ 500 nm) during electroporation.8 On the other hand, Lurquin et al. observed no endocytosis of DNA molecules (∼7600 bp) into giant unilamellar vesicles (GUVs, mean size ∼ 2.5–20 μm) during electroporation, suggesting a mechanism of direct entry (or transport) through the electro-pores formed during electroporation.9 To resolve this discrepancy, recently Portet et al. (2011) conducted experiments using GUVs (mean diameter ∼ 20 μm) and pDNA (∼4700 bp).10 Combining experiments with a proposed theoretical framework, they concluded direct entry of DNA molecules through electro-pores via electrophoresis as the mode of transport instead of electro-induced endocytosis. A similar mechanism of direct translocation of small interfering RNA through electro-pores was also observed during nano-second electroporation of GUVs.11 Investigating electroporation of GUVs in the presence of DNA molecules has thus been conducive in revealing how DNA molecules are transported across the cell membrane during electroporation. This was otherwise often challenging to unveil with experiments on living cells due to complexities associated with the coupling of the cell membrane and cytoskeleton entities.
000 bp) and plasmid DNA (or pDNA ∼ 4700 bp) followed an endocytosis-like mechanism of translocation into large unilamellar vesicles (LUVs, mean diameter ∼ 500 nm) during electroporation.8 On the other hand, Lurquin et al. observed no endocytosis of DNA molecules (∼7600 bp) into giant unilamellar vesicles (GUVs, mean size ∼ 2.5–20 μm) during electroporation, suggesting a mechanism of direct entry (or transport) through the electro-pores formed during electroporation.9 To resolve this discrepancy, recently Portet et al. (2011) conducted experiments using GUVs (mean diameter ∼ 20 μm) and pDNA (∼4700 bp).10 Combining experiments with a proposed theoretical framework, they concluded direct entry of DNA molecules through electro-pores via electrophoresis as the mode of transport instead of electro-induced endocytosis. A similar mechanism of direct translocation of small interfering RNA through electro-pores was also observed during nano-second electroporation of GUVs.11 Investigating electroporation of GUVs in the presence of DNA molecules has thus been conducive in revealing how DNA molecules are transported across the cell membrane during electroporation. This was otherwise often challenging to unveil with experiments on living cells due to complexities associated with the coupling of the cell membrane and cytoskeleton entities.
GUVs provide the opportunity to obtain precise and mechanistic understanding of DNA electro-transfer. For instance, in the experiments and the theoretical framework of Portet et al. (2011) it was assumed that the pores were large enough such that DNA molecules can translocate across the electro-pores in their native polymer conformation.10 In this scenario, the transport of DNA molecules should depend on the bulk electrophoretic mobility of DNA molecules. However, only one size (pDNA ∼ 4700 bp) was tested for the theoretical framework established. If pores are not large enough compared to the size of the DNA molecule (radius of gyration), Yu and Lin12 proposed a different theoretical model for DNA transport by considering that the pore is small enough to allow only a single base pair (bp) to pass through it at a time. In this scenario, the DNA molecules are not transported across the cell membrane in their native polymer conformation but rather translocate through the electro-pore one base pair at a time. This is equivalent to a single-file translocation or stochastic threading of DNA molecules across artificial nano-pores.13 According to this model, the DNA transport or translocation efficiency (TE) scales with the size of the DNA as TE ∼ N−1.5, where N represents the number of base pairs. Thus, by conducting systematic experiments on model cell membranes such as GUVs and varying the size of the DNA molecules, the diverse and conflicting theories can be tested in order to obtain a more accurate understanding of DNA transport across the cell membrane during electroporation.
In this research, GUVs are electroporated in the presence of DNA molecules of different sizes (25 bp, 100 bp, 500 bp, 1000 bp, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp, 15
000 bp, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp and 20
000 bp and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp) individually, in order to test the different mechanisms of DNA translocation i.e. the theoretical framework of Portet et al. (2011)10 that claims direct entry of the DNA molecules and the theoretical framework of Yu and Lin12 that claims single-file translocation of DNA molecules across the electro-pores. By comparing the experimental translocation efficiencies with the predictions from the theoretical frameworks, it was inferred that DNA molecules directly enter the GUVs during electroporation in their native configuration as proposed by Portet et al. (2011).10 The results of this study provide a mechanistic understanding of DNA translocation across an electro-pore which is not only necessary for understanding DNA translocation across real cell membranes, but also for predictable loading and dosage control of nucleic acids into vesicles using electroporation. Moreover, with such a diverse range of DNA sizes tested that span three orders of magnitude, these results can also be utilized to optimize loading of vesicles with small nucleic acids (such as siRNA, ∼20 bp) for gene silencing applications, and large nucleic acids (such as pDNA, ∼5000 bp) for gene therapeutic applications, using liposome mediated transfection.
000 bp) individually, in order to test the different mechanisms of DNA translocation i.e. the theoretical framework of Portet et al. (2011)10 that claims direct entry of the DNA molecules and the theoretical framework of Yu and Lin12 that claims single-file translocation of DNA molecules across the electro-pores. By comparing the experimental translocation efficiencies with the predictions from the theoretical frameworks, it was inferred that DNA molecules directly enter the GUVs during electroporation in their native configuration as proposed by Portet et al. (2011).10 The results of this study provide a mechanistic understanding of DNA translocation across an electro-pore which is not only necessary for understanding DNA translocation across real cell membranes, but also for predictable loading and dosage control of nucleic acids into vesicles using electroporation. Moreover, with such a diverse range of DNA sizes tested that span three orders of magnitude, these results can also be utilized to optimize loading of vesicles with small nucleic acids (such as siRNA, ∼20 bp) for gene silencing applications, and large nucleic acids (such as pDNA, ∼5000 bp) for gene therapeutic applications, using liposome mediated transfection.
2 Materials and methods
2.1 GUV preparation
The lipids used to prepare GUVs were 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine Rhodamine B sulfonyl) (ammonium salt) (Rhodamine-PE) and were purchased from Avanti Polar Lipids, Inc. The lipids were dissolved in chloroform (Sigma-Aldrich) at a mass concentration of 1 mg ml−1 and were stored at −20 °C. The lipid solutions were mixed, at room temperature, in order to achieve a concentration of 99.5 mol% DOPC and 0.5 mol% Rhodamine-PE. 20 μl of this lipid solution was deposited on the conducting side of two Indium Tin Oxide (ITO) slides (Sigma-Aldrich), separately. The lipids are then dried by placing these ITO slides in the vacuum. The ITO slides were then placed inside the cavity of a custom made Teflon chamber with the conducting sides facing each other and separated by a distance of 1.5 mm. The cavity of the Teflon chamber was filled with 1 ml of 240 mM aqueous sucrose solution. The electroformation procedure was followed to prepare the GUVs.14 A sinusoidal potential of 1.5 Vpp was applied to the ITO slides at a frequency of 10 Hz and for a period of 2 h. Subsequently, a square-wave potential of 1.225 V was applied for a period of 1 h and at a frequency of 5 Hz. An arbitrary-waveform generator (Agilent 33220A 20 MHz) was used for electroformation. After the electroformation procedure, the solution was diluted 20 times with 260 mM aqueous glucose solution to a final volume of 5 ml. With this procedure, GUVs were prepared having 240 mM aqueous sucrose solution on the inside and 260 mM aqueous glucose solution on the outside. This formulation was applied to generate GUVs with low membrane tension and avoid bursting of the GUVs during and after electroporation.2.2 DNA samples and staining procedure
To investigate the effect of biomolecule size, individual DNA fragments with 25 bp, 100 bp, 500 bp, 1000 bp, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp, 15
000 bp, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp and 20
000 bp and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp were purchased from Thermo Fisher Scientific Inc. under the brand of NoLimits DNA. For each DNA size, the stock vial consisted of 10 μg of DNA at a concentration of 0.5 μg μl−1 in 10 mM Tris–HCl (pH 7.6) and 1 mM EDTA. To visualize and quantify the DNA uptake, DNA molecules were stained in the stock vials using YOYO-1 dye (1 mM in DMSO from Thermo Fisher Scientific Inc.). The bp
000 bp were purchased from Thermo Fisher Scientific Inc. under the brand of NoLimits DNA. For each DNA size, the stock vial consisted of 10 μg of DNA at a concentration of 0.5 μg μl−1 in 10 mM Tris–HCl (pH 7.6) and 1 mM EDTA. To visualize and quantify the DNA uptake, DNA molecules were stained in the stock vials using YOYO-1 dye (1 mM in DMSO from Thermo Fisher Scientific Inc.). The bp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) YOYO-1 dye molecule staining ratio was 10
YOYO-1 dye molecule staining ratio was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to achieve a sufficient fluorescence signal-to-noise ratio, without significantly influencing the contour length of the DNA molecules.15,16 Staining was carried out on ice for a period of 1 hour.
1 to achieve a sufficient fluorescence signal-to-noise ratio, without significantly influencing the contour length of the DNA molecules.15,16 Staining was carried out on ice for a period of 1 hour.
2.3 Electropulsation of GUVs
Electropulsation was carried out in μ-Slide 4 Well Ibidi® chambers (Cat. No. 80426), to monitor the process of DNA uptake using an inverted confocal microscope. Custom made stainless steel electrodes with a 3 mm gap were placed inside 1 of the 4 chambers. 475 μl of 260 mM aqueous glucose solution was added to the chamber along with 2.5 μl of the stained DNA stock solution. 22.5 μl of solution from the Teflon chamber containing the GUVs was added into the μ-Slide 4 Well chamber. Care was taken to pipette the solution in between the electrodes. The final volume inside the μ-Slide 4 Well containing the electrodes was 500 μl and the DNA concentration was 2.5 μg ml−1. The electrodes were connected to the electropulsator (BetaTech Electro cell S20, France) to apply the electric field pulses. A voltage of 135 V was applied between the electrodes for a period of 5 ms. 10 such pulses were applied at a frequency of 0.33 Hz. These pulsing conditions have been routinely used for efficient transfer of DNA molecules in living cells or GUVs.3,10 This created an electric field (E0) of 0.45 kV cm−1. All experiments were done on GUVs having an initial diameter (Di) of ∼30 μm.2.4 Confocal image acquisition of DNA uptake
All the experiments were performed on a confocal microscope (ZEISS LSM 710, Germany) and the images were acquired using a 40× (1.3 NA oil immersion) objective. YOYO-1-labelled DNA molecules were excited using a 488 nm argon laser and the rhodamine-labelled GUVs were excited using a 543 nm helium–neon (He–Ne) laser. Both the lasers were used simultaneously for excitation. The emission filter for the YOYO-1 labelled DNA acquisition was set to 491–538 nm, while the emission filter for the rhodamine labelled GUVs was set to 569–797 nm. The resulting image was a combination of two separate channels i.e. the channel corresponding to the fluorescence from rhodamine-labelled GUVs (referred to as red channels) and the channel corresponding to YOYO-1-labelled DNA molecules (referred to as green channels). The scanning speed of the laser was adjusted to obtain a pixel dwell of 1.27 μs. The field of view consisted of 512 × 512 pixels spanning 212.55 × 212.55 μm2. The pixel depth was set to 16-bit and a line averaging of 2 was applied in order to improve the signal-to-noise ratio.2.5 Image processing
The diameter of the GUV was determined using the red channel and the mean fluorescence intensity of DNA molecules inside and outside the GUV was determined using the green channel. Both the channels were from the same frame or the image acquired using the confocal microscope. Multiple frames were captured and analysed to obtain transient information of the DNA uptake process. The red channel image was enhanced using the ‘imadjust()’ function in MATLAB® to optimize the detection of GUV as a circle and determine the corresponding diameter. The GUV was detected as a circle using the in-built function ‘imfindcircles()’ in MATLAB® that uses the Circular Hough Transform algorithm.17 The arguments used for the ‘imfindcircles()’ function were as follows; the enhanced red channel image on which the circle was to be detected, 20 and 50 pixels as the minimum and maximum radius, respectively, for the circle to be detected, and 0.94–0.96 as the ‘Sensitivity’ for optimal detection. Default values and settings were used for all other arguments. The radius and the center coordinates of the detected circle (GUV) returned by this function were superimposed on the green channel images to calculate the mean fluorescence intensity of the DNA molecules inside and outside of the GUVs. The inside of the GUVs corresponded to an area of a circle with 0.9 times the radius of the detected circle. The outside of the GUVs corresponded to an area that laid outside a circle with a radius 1.2 times that of the detected circle. The green channel images were not adjusted or enhanced for calculating the mean fluorescence intensity of DNA molecules.3 Results
In order to test the different models of DNA translocation across lipid bilayers (DNA translocation in their native polymer conformation through the electro-pore10 or DNA unravelling and threading through the electro-pore12), the experiments were performed on DNA molecules of the following sizes; 25 bp, 100 bp, 500 bp, 1000 bp, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp, 15
000 bp, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp and 20
000 bp and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp. The wide range of DNA sizes provided an opportunity to test these two different theories over three orders of DNA size. The DNA molecules were fluorescently labeled with YOYO-1 dye (1
000 bp. The wide range of DNA sizes provided an opportunity to test these two different theories over three orders of DNA size. The DNA molecules were fluorescently labeled with YOYO-1 dye (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 dye
10 dye![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
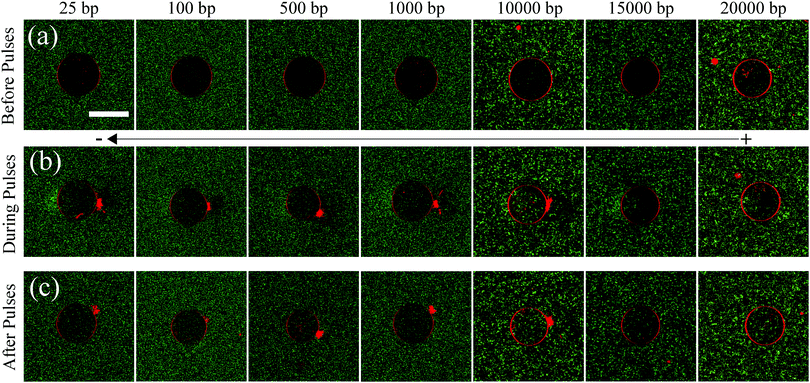
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bp staining ratio) in order to obtain the translocation efficiency as a ratio of the mean fluorescence intensity of DNA molecules inside and outside the GUV. GUVs were made of 99.5 mol% DOPC and 0.5 mol% Rhodamine-PE. Rhodamine-PE lipids were added as tracer lipids in order to detect the GUV during and after the application of electric field pulses, under the confocal microscope. The initial GUV diameter (Di) was chosen to be 30 μm for all the experiments and the electric field applied was 0.45 kV cm−1 (E0). This led to the generation of a trans-membrane potential (TMP) of ∼1 V, at the poles facing the electrodes, according to the simplified Schwan equation; TMP = 1.5E0Di/2.18 10 such electric field pulses were applied, each of 5 ms duration and at a frequency of 0.33 Hz. The concentration of DNA molecules was kept constant at 2.5 μg ml−1, for all experiments with different DNA sizes. These values are typically used in gene transfection protocols using electroporation,19 and also allowed sufficient uptake of DNA molecules by the GUVs to be quantified accurately, without the loss of stability of the GUVs post electroporation. The DNA uptake by GUVs during electroporation was recorded under a confocal microscope and is shown in Fig. 1. The figure consists of 3 rows and 7 columns showing uptake of DNA molecules corresponding to different DNA sizes. The first row (Fig. 1(a)) shows the images of GUVs before the electric field pulses were applied, for all DNA sizes considered. No fluorescence intensity corresponding to YOYO-1-labelled DNA molecules can be detected inside the GUVs before electroporation. The second row (Fig. 1(b)) shows images of GUVs and DNA uptake during the period of pulses. The DNA molecules can be seen to enter the GUVs from the cathode facing side of the electrode. The last row (Fig. 1(c)) shows the images of GUVs with the corresponding DNA uptake after the application of 10 pulses. All images are representative of typical experimental observations.
bp staining ratio) in order to obtain the translocation efficiency as a ratio of the mean fluorescence intensity of DNA molecules inside and outside the GUV. GUVs were made of 99.5 mol% DOPC and 0.5 mol% Rhodamine-PE. Rhodamine-PE lipids were added as tracer lipids in order to detect the GUV during and after the application of electric field pulses, under the confocal microscope. The initial GUV diameter (Di) was chosen to be 30 μm for all the experiments and the electric field applied was 0.45 kV cm−1 (E0). This led to the generation of a trans-membrane potential (TMP) of ∼1 V, at the poles facing the electrodes, according to the simplified Schwan equation; TMP = 1.5E0Di/2.18 10 such electric field pulses were applied, each of 5 ms duration and at a frequency of 0.33 Hz. The concentration of DNA molecules was kept constant at 2.5 μg ml−1, for all experiments with different DNA sizes. These values are typically used in gene transfection protocols using electroporation,19 and also allowed sufficient uptake of DNA molecules by the GUVs to be quantified accurately, without the loss of stability of the GUVs post electroporation. The DNA uptake by GUVs during electroporation was recorded under a confocal microscope and is shown in Fig. 1. The figure consists of 3 rows and 7 columns showing uptake of DNA molecules corresponding to different DNA sizes. The first row (Fig. 1(a)) shows the images of GUVs before the electric field pulses were applied, for all DNA sizes considered. No fluorescence intensity corresponding to YOYO-1-labelled DNA molecules can be detected inside the GUVs before electroporation. The second row (Fig. 1(b)) shows images of GUVs and DNA uptake during the period of pulses. The DNA molecules can be seen to enter the GUVs from the cathode facing side of the electrode. The last row (Fig. 1(c)) shows the images of GUVs with the corresponding DNA uptake after the application of 10 pulses. All images are representative of typical experimental observations.
A representative experiment describing the uptake of DNA molecules by the GUV during electroporation, for a DNA size of 100 bp, is shown in Fig. 2. Before the application of electric field pulses, Fig. 2(a), fluorescence from the DNA molecules (shown in green) could be seen to be homogeneously distributed outside the GUV (shown in red). The fluorescence intensity of DNA molecules outside the GUV corresponds to a concentration of 2.5 μg ml−1 and labelled as Iout. The negligible green fluorescence that could be seen inside the GUV was attributed to the sensor noise (Inoise). On the application of electric field pulses at t ∼ 0 s, the DNA molecules could be seen entering the GUV from the cathode facing side of the electrode. A simultaneous decrease in the GUV diameter was also observed. A representative snapshot of this process is shown in Fig. 2(b). After the application of electric field pulses, no uptake of DNA or a decrease in GUV diameter was observed. The final state of the GUV is shown in Fig. 2(c).
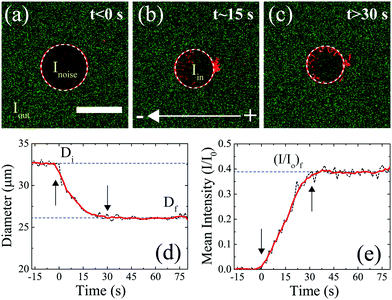 | ||
| Fig. 2 Quantifying the decrease in GUV diameter and the uptake of DNA molecules during electroporation. (a) State of the GUV before the application of electric field pulses (t < 0 s). The GUV is shown in red and the DNA molecules are shown in green. The GUV detected is shown using a white-dotted circle (see Section 2.5 in Materials and methods). The mean fluorescence intensity of DNA molecules outside the GUV is depicted as Iout corresponding to a concentration of 2.5 μg ml−1. The green fluorescence due to sensor noise found inside the GUV is labelled as Inoise. Scale bar = 30 μm. (b) State of the GUV during the application of electric field pulses (t ∼ 15 s). 10 pulses of an electric field amplitude of 0.45 kV cm−1 were applied, each of duration 5 ms and at a frequency of 0.33 Hz. This corresponds to a time frame of t ∼ 0 s to t ∼ 30 s. The mean fluorescence intensity inside the GUV due to uptake of DNA molecules during electroporation is depicted as Iin. (c) State of the GUV after the application of electric field pulses. For visualization purposes, the images shown in (a)–(c) are enhanced using the same adjustments as for Fig. 1. Detected GUV diameter and normalized mean fluorescence intensity I/I0 = (Iin − Inoise)/(Iout − Inoise), as a function of time, are plotted as black dotted lines in (d) and (e), respectively. The beginning and the end of pulses are marked by arrows. The solid red line represents smoothed data using the ‘smooth()’ function in MATLAB®. | ||
From these experiments, the transient data of the effect of electric field pulses on the GUVs and the simultaneous uptake of DNA molecules during electroporation could be extracted from the sequence of images captured for the process. Fig. 2(d) shows the GUV diameter as a function of time. Before the application of electric field pulses, the diameter was constant at ∼33 μm (labelled as Di). The initial diameter, Di, was calculated by taking the average of the diameters before the application of electric field pulses. During the application of electric field pulses (from t ∼ 0 s till t ∼ 30 s, as marked by arrows), the diameter decreased continuously. The decrease in diameter has been observed previously for fluid phase GUVs and is attributed to lipid loss during electroporation.20,21 After the application of electric field pulses, the diameter attained a steady-state value of ∼25 μm (labelled as Df). The final diameter, Df, was calculated by taking the average of the diameters after the application of pulses.
Similarly, the uptake of DNA by the GUV during electroporation was determined. The mean fluorescence intensity of the DNA molecules inside the GUV (Iin) was determined by calculating the mean fluorescence intensity of the DNA molecules inside a circle having a diameter corresponding to 0.9 times the detected GUV diameter (see Section 2.5 in Materials and methods). This was done to minimize edge effects. The initial mean fluorescence intensity corresponding to sensor noise (Inoise) was subtracted from the mean fluorescence intensity of the DNA molecules detected inside the GUV in each frame as I = Iin − Inoise. The sensor noise was also subtracted from the fluorescence intensity of DNA molecules outside the GUV (Iout) in each frame as I0 = Iout − Inoise. Iout corresponded to the mean fluorescence intensity of the DNA molecules outside a circle having a diameter corresponding to 1.2 times the detected GUV diameter. Normalized mean fluorescence intensity I/I0 was then plotted as a function of time as shown in Fig. 2(e). Before the application of electric field pulses, no DNA uptake could be observed inside the GUV. During application of electric field pulses (from t ∼ 0 s till t ∼ 30 s, as marked by arrows), the mean normalized fluorescence intensity continuously increased linearly. It finally reached a steady state value (I/I0)f = 0.38 after the end of the electric field pulses. This final steady state value (I/I0)f was calculated by taking the average of (I/I0) values after the application of electric field pulses. Other quantities such as DNA uptake time and the slope of normalized intensity (I/I0) vs. time during uptake of DNA by the GUV are shown in Section 1 of the ESI.†
The sequence of images representing the electroporation of GUVs were analysed for a number of experiments corresponding to different DNA sizes. The evolution of the diameter of the GUV and the fluorescence intensity corresponding to the uptake of DNA molecules were extracted as shown previously (see Fig. 2). The diameter ratio (Df/Di) was calculated for each DNA size and is shown in Fig. 3(a). The diameter of the GUVs did not decrease by more than ∼20%, after the application of electric field pulses. Similarly, the uptake of DNA molecules due to electroporation (I/I0)f from Fig. 2(e) was determined for each DNA size and is plotted in Fig. 3(b), as filled squares. Also plotted on the same figure are the theoretical predictions from Yu and Lin12 (solid line) and Portet et al. (2011)10 (dashed lines). For the theoretical prediction of Yu and Lin,12 the final probability of successful translocation (F–PST) was used as a measure for translocation efficiency, (I/I0)f, and for the theoretical prediction of Portet et al. (2011),10 the following equation was used from the proposed theoretical framework:
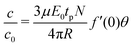 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 bp.22 For DNA sizes less than 400 bp, the electrophoretic mobility constantly decreased to a value of μ = 3.54 × 10−8 m2 S−1 V−1 for a DNA size of 27 bp.22 Using these values of electrophoretic mobility for the corresponding DNA sizes used in this work, and a flux factor of f′(0)θ = 0.26, the theoretical prediction according to eqn (1) is plotted in Fig. 3(b) as a dotted line corresponding to the legend; f′(0)θ = 0.26 TAE buffer. A value of μ = 3.75 × 10−8 m2 S−1 V−1 for the electrophoretic mobility and f′(0)θ = 0.26 for the flux factor was also used by Portet et al. (2011) for a DNA size of 4700 bp (pDNA).10
500 bp.22 For DNA sizes less than 400 bp, the electrophoretic mobility constantly decreased to a value of μ = 3.54 × 10−8 m2 S−1 V−1 for a DNA size of 27 bp.22 Using these values of electrophoretic mobility for the corresponding DNA sizes used in this work, and a flux factor of f′(0)θ = 0.26, the theoretical prediction according to eqn (1) is plotted in Fig. 3(b) as a dotted line corresponding to the legend; f′(0)θ = 0.26 TAE buffer. A value of μ = 3.75 × 10−8 m2 S−1 V−1 for the electrophoretic mobility and f′(0)θ = 0.26 for the flux factor was also used by Portet et al. (2011) for a DNA size of 4700 bp (pDNA).10
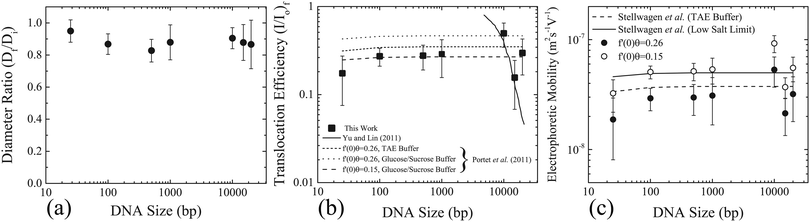 | ||
| Fig. 3 Size reduction of GUVs and DNA uptake as a function of DNA size. (a) The ratio of the final diameter (Df), after the application of the electric field pulses, to the initial diameter (Di), before the application of electric field pulses. The error bars represent the standard deviation. (b) Filled squares represent the translocation efficiency (I/I0)f as a function of the size of the DNA molecules. The error bars represent standard deviation. Also plotted are the theoretical predictions of the translocation efficiency from Yu and Lin (solid line),12 and Portet et al. (2011) (dashed line).20 (c) Electrophoretic mobility as a function of DNA size calculated using eqn (1) taking (c/c0) as (I/I0)f from (b). Two different values of the flux factor were used; f′(0)θ = 0.26, corresponding to filled black circles and f′(0)θ = 0.15 corresponding to open white circles. Electrophoretic mobilities determined from the literature (see Section 2 of the ESI† for detailed values) are also plotted for TAE buffer22 and low conductivitybuffers,25 as dashed and solid lines, respectively. | ||
The conductivity of the medium has been shown to influence the electrophoretic mobility of the DNA molecules.22–25 The buffers used in the current experiments consist of 260 mM glucose as the external medium and 240 mM sucrose as the internal medium. This corresponds to very low conductivity or ionic strength compared to TAE buffers. The electrophoretic mobility of DNA molecules in low conductivity buffers can be estimated by systematically reducing the ionic strength, as was done for dsA5 DNA molecules (20 bp).25 In this case, the electrophoretic mobility of dsA5 DNA at zero ionic strength was estimated to be μ = 4.6 × 10−8 m2 S−1 V−1, by the linear extrapolation of electrophoretic mobilities in the range of low ionic strength. A quantitatively similar increase in electrophoretic mobility was observed for dsA5 DNA molecules (20 bp) and pUC19 DNA molecules (2686 bp) with systematic reduction of ionic strength.24 Therefore, a similar quantitative increase in electrophoretic mobilities was considered for the sizes of the DNA molecules considered in this work corresponding to the low conductivity glucose and sucrose buffers. See Section 2 of the ESI† for the exact values of electrophoretic mobilities used, corresponding to TAE (Table ST1, ESI†) and the low conductivity sucrose and glucose buffers (Table ST2, ESI†), for the different DNA sizes in this work. The theoretical prediction according to eqn (1) with an increased electrophoretic mobility corresponding to the low conductivity buffers, and the same flux factor (f′(0)θ = 0.26), is shown in Fig. 3(b) as a dotted line with a legend; f′(0)θ = 0.26, glucose/sucrose buffer. Also shown in the same figure are the predictions from eqn (1) with the same increased electrophoretic mobility, however a low value of flux factor (f′(0)θ = 0.15) as a dashed line (legend; f′(0)θ = 0.15, glucose/sucrose buffer) which shows better agreement with the experimental values.
Based on the theoretical framework of Portet et al. (2011),10 the electrophoretic mobility can be back-calculated using eqn (1). Taking (c/c0) as (I/I0)f and using the electric field parameters from the experiments; E0 = 0.45 kV cm−1, N = 10, tp = 5 ms and R = 15 μm the electrophoretic mobility can be estimated for each size of the DNA molecule. These values are plotted in Fig. 3(c), as filled black and open white circles for f′(0)θ = 0.26 and f′(0)θ = 0.15, respectively. On the same figure, electrophoretic mobilities determined from the literature (see Section 2 of the ESI†) are also plotted for TAE buffer and low conductivity buffers, as dashed and solid lines, respectively. The close match between the experimentally determined electrophoretic mobilities and the values determined from the literature further validates the applicability of the theoretical framework of Portet et al. (2011)10 as the dominant mode of DNA translocation during electroporation of GUVs.
4 Discussion
To unravel the mechanism of DNA translocation through electro-pores in GUVs, the DNA size was varied keeping the pulsing parameters constant. The translocation efficiency or the amount of DNA transferred into the GUVs during electroporation as a function of the size of the DNA molecules could be compared to predictions from the theoretical frameworks of Yu and Lin12 and Portet et al. (2011).10 According to the stochastic model of Yu and Lin,12 the size of the electro-pore is small enough to allow only a single base-pair to translocate at a time. The final probability of successful translocation or F-PST (interpreted as the translocation efficiency, TE) should then decrease with the size of the DNA molecules (N), and in particular, should scale with the size of the DNA molecules as TE ∼ N−1.5. According to Fig. 3(b), no decrease in the translocation efficiency, (I/I0)f, was observed for the size of the DNA molecules tested. On the same figure, the prediction of Yu and Lin12 for the translocation efficiency as a function of size is plotted for a pulse duration of 5 ms as a solid line. The experimental results do not match the prediction of Yu and Lin,12 rendering the applicability of their model and mechanism of DNA translocation unlikely for electroporation of GUVs.The model of Portet et al. (2011)10 suggests that the DNA molecules can cross the electro-pores in their native polymer conformation, or that the electro-pores are large enough to allow the DNA molecules to cross freely. The bulk electrophoretic mobility governs the transport across the pores during electroporation. According to the theoretical framework adapted by Portet et al. (2011),10 the normalized increase in the concentration of DNA molecules inside the GUVs after the application of electric field pulses is given by eqn (1). The prediction is plotted in Fig. 3(b) for different values of electrophoretic mobility and flux factors f′(0)θ, as dashed lines. This prediction matches with the experimental values of normalized mean intensity of DNA molecules inside the GUVs, (I/I0)f, for values of electrophoretic mobilities of DNA molecules in glucose/sucrose buffer, and for a flux factor of f′(0)θ = 0.15. However, these values are slightly different from the values used in the theoretical framework of Portet et al. (2011).10
The electrophoretic mobility and the flux factor used in the theoretical framework of Portet et al. (2011) were μ = 3.75 × 10−8 m2 S−1 V−1 and f′(0)θ = 0.26.10 This value of electrophoretic mobility was measured for DNA molecules with size greater than 400 bp and for a TAE buffer (40 mM Tris, 1 mM EDTA, pH 8.0).22 The conductivity of TAE buffer is found to be in the range of 0.38–3.11 mS cm−1 depending upon the concentration of Tris (10–80 mM).23 The conductivity of the external buffer used by Portet et al. (2011) (260 mM glucose, 1 mM KH2PO4/K2HPO4, 1 mM NaCl, pH 7) was measured to be 0.45 mS cm−1.10 This lies within the range of conductivities of the TAE buffers used to measure the electrophoretic mobilities of DNA molecules. Addition of 2–50 mM NaCl to TAE buffers has shown to influence the value of the electrophoretic mobility, albeit only slightly for 2 mM NaCl.24 Therefore, ignoring the effects of addition of 1 mM NaCl to the KH2PO4/K2HPO4 buffer, a value of electrophoretic mobility of μ = 3.75 × 10−8 m2 S−1 V−1 seems to be an appropriate choice for a buffer adopted by Portet et al. (2011).10 The buffers used in this work correspond to 260 mM glucose as the external solution and 240 mM sucrose as the internal solution. The conductivities of 200 mM glucose and 200 mM sucrose solution were measured to be 0.0045 and 0.006 mS cm−1,26 respectively. The conductivity of 240 mM sucrose solutions was measured to be 0.015 mS cm−1.10 Thus, it can be assumed that the conductivities of the glucose and sucrose solutions used in this work are O(10−3–10−2) mS cm−1. For such low conductivity solutions, the electrophoretic mobilities are expected to be higher.22–25 Using values of electrophoretic mobilities corresponding to the low conductivity sucrose/glucose buffers (see Section 2 of the ESI† for precise values used) and a flux factor f′(0)θ = 0.26, the translocation efficiency or the normalized concentration according to eqn (1) plotted in Fig. 3(b) captures the qualitative trend, however it over-predicts the experimental translocation efficiency.
The value of the flux factor in the theoretical framework by Portet et al. (2011) was f′(0)θ = 0.26.10 The authors determined this value by comparing their experimental results with the theory. According to the theoretical framework, for conductivity ratios (external solution conductivity/internal solution conductivity) between 1 and 10, the experimentally determined flux factor f′(0)θ should lie between 0.1–0.5.10 The authors obtained a distribution of experimentally determined f′(0)θ, with a mean value of the distribution as 〈f′(0)θ〉 = 0.26, thus validating the theoretical framework for a DNA size of 4700 bp. According to Fig. 3(b), the theoretical prediction (eqn (1)) matches with the experimental translocation efficiencies in this work, for electrophoretic mobilities corresponding to low conductivity sucrose/glucose buffers, and for a flux factor value of f′(0)θ = 0.15. This value of flux factor f′(0)θ also lies between 0.1 and 0.5, suggesting the validity of the theoretical framework by Portet et al. (2011)10 for DNA sizes ranging from 25–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp.
000 bp.
A lower value of flux factor, f′(0)θ = 0.15 in this work, as opposed to f′(0)θ = 0.26 in Portet et al. (2011),10 could be due to multiple reasons. f′(0) depends on the conductivity ratio, and θ represents the angle that the permeabilized area, accessible to DNA translocation, subtends at the center of the GUV.10 A constant value of f′(0) = 2.34 rad−1 corresponding to a conductivity ratio of 1 was considered.10 A similar value of f′(0) = 3 rad−1 was obtained for the buffers, the electric field pulsing conditions and the GUV diameters corresponding to this work (see Section 3 of the ESI†). The distribution, as reported by Portet et al. (2011),10 thus arises due to different θ values corresponding to different permeabilized areas.10 The authors attributed this to different electric field intensities, pulse durations and GUV diameters considered which could lead to different permeabilized areas accessible to DNA translocation.10 Thus, f′(0)θ = 0.15 for the constant electric field pulsing conditions, the GUV diameters and the buffers used in this work could correspond to a value lying in the lower spectrum of the distribution reported by Portet et al. (2011).10
Considering f′(0) = 3 rad−1, a permeabilized area subtending an angle θ ∼ 2.9° (for f′(0)θ = 0.15) is obtained. Using Dperm = Rθc, where Dperm is the diameter of the permeabilized area (assuming a circular area), R is the radius of the vesicle and θc is the permeabilized angle θ in radians, a permeabilzed area with a diameter Dperm ∼ 0.75 μm is obtained for θ ∼ 2.9°. This permeabilized area could be considered as a single macropore. Although macropores are observed during the electroporation of GUVs,20,27 they are only observed during the last few μs of a ms pulse, and remain open for tens of milliseconds after the pulse ends.27 Since diffusion of DNA molecules is negligible compared to electrophoresis,10 majority of the DNA transport thus occurs during, and not after the pulse. However, the experiments in this work suggest a mode of transport where the pores are large enough during the electric field pulse to allow DNA molecules to translocate freely in their native polymer conformation. This implies that the pores formed are comparable to the coil size (or radius of gyration Rg) of the DNA molecules. The largest DNA molecule used in this work (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp) has an Rg ∼ 1 μm (see Section 4 of the ESI†), similar in size to the permeabilized area (Dperm ∼ 0.75 μm). Thus, a permeabilized area with diameter Dperm ∼ 0.75 μm can be considered as a macropore. When the size of electro-pores is smaller than Rg of the DNA molecules, DNA translocation across the membrane follows more complex mechanisms. For instance, DNA molecules form a DNA–membrane complex (for DNA sizes ≥ 25 bp) at the cell membrane of living cells under electropermeabilization conditions, which can influence the DNA translocation efficiency during electric pulses.3,28,29 These results, apart from providing a mechanistic understanding of DNA translocation, also provide information on the pore size during electroporation of GUVs.
000 bp) has an Rg ∼ 1 μm (see Section 4 of the ESI†), similar in size to the permeabilized area (Dperm ∼ 0.75 μm). Thus, a permeabilized area with diameter Dperm ∼ 0.75 μm can be considered as a macropore. When the size of electro-pores is smaller than Rg of the DNA molecules, DNA translocation across the membrane follows more complex mechanisms. For instance, DNA molecules form a DNA–membrane complex (for DNA sizes ≥ 25 bp) at the cell membrane of living cells under electropermeabilization conditions, which can influence the DNA translocation efficiency during electric pulses.3,28,29 These results, apart from providing a mechanistic understanding of DNA translocation, also provide information on the pore size during electroporation of GUVs.
5 Conclusions
The two theoretical frameworks proposed for DNA translocation, stochastic threading12 and bulk electrophoretic transfer10 were tested by varying the size of the DNA molecules and monitoring the translocation efficiency. It was determined that for the DNA sizes tested (ranging from 25–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bp), the DNA molecules can translocate freely through the electro-pores in their native polymer conformation, suggesting bulk electrophoretic transfer as the dominant mode of transport during electroporation of GUVs. For a given set of pulsing conditions, the bulk electrophoretic mobility of DNA molecules is the key parameter that determines the uptake during electroporation of GUVs. This mechanistic understanding of DNA translocation for model cell membranes not only allows a predictable loading of vesicles with a wide variety of DNA sizes, but provides also a basis for developing mechanistic models for more complex cell membranes,30 eventually approaching living cells.
000 bp), the DNA molecules can translocate freely through the electro-pores in their native polymer conformation, suggesting bulk electrophoretic transfer as the dominant mode of transport during electroporation of GUVs. For a given set of pulsing conditions, the bulk electrophoretic mobility of DNA molecules is the key parameter that determines the uptake during electroporation of GUVs. This mechanistic understanding of DNA translocation for model cell membranes not only allows a predictable loading of vesicles with a wide variety of DNA sizes, but provides also a basis for developing mechanistic models for more complex cell membranes,30 eventually approaching living cells.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Georg Pesch for critical reading of the manuscript and advice on COMSOL simulations. We acknowledge financial support from the European Research Council (ERC) under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant, Agreement No. 337820.Notes and references
- I. Hamley and V. Castelletto, Angew. Chem., Int. Ed., 2007, 46, 4442–4455 CrossRef CAS PubMed.
- L. Rems, D. Kawale, L. J. Lee and P. E. Boukany, Biomicrofluidics, 2016, 10, 043403 CrossRef PubMed.
- C. Rosazza, S. Haberl Meglic, A. Zumbusch, M.-P. Rols and D. Miklavcic, Curr. Gene Ther., 2016, 16, 98–129 CrossRef CAS.
- M. P. Stewart, R. Langer and K. F. Jensen, Chem. Rev., 2018, 118, 7409–7531 CrossRef CAS PubMed.
- D. L. Perrier, L. Rems and P. E. Boukany, Adv. Colloid Interface Sci., 2017, 249, 248–271 CrossRef CAS PubMed.
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CrossRef CAS PubMed.
- H. Lodish, J. E. Darnell, A. Berk, C. A. Kaiser, M. Krieger, M. P. Scott, A. Bretscher, H. Ploegh and P. Matsudaira, et al.,., Molecular cell biology, Macmillan, 2008 Search PubMed.
- L. V. Chernomordik, A. V. Sokolov and V. G. Budker, Biochim. Biophys. Acta, Biomembr., 1990, 1024, 179–183 CrossRef CAS.
- P. F. Lurquin and K. Athanasiou, Biochem. Biophys. Res. Commun., 2000, 267, 838–841 CrossRef CAS PubMed.
- T. Portet, C. Favard, J. Teissié, D. S. Dean and M.-P. Rols, Soft Matter, 2011, 7, 3872–3881 RSC.
- M. Breton, L. Delemotte, A. Silve, L. M. Mir and M. Tarek, J. Am. Chem. Soc., 2012, 134, 13938–13941 CrossRef CAS PubMed.
- M. Yu, W. Tan and H. Lin, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 2494–2501 CrossRef CAS PubMed.
- C. Dekker, Nat. Nanotechnol., 2007, 2, 209 CrossRef CAS PubMed.
- M. I. Angelova and D. S. Dimitrov, Faraday Discuss. Chem. Soc., 1986, 81, 303–311 RSC.
- K. Günther, M. Mertig and R. Seidel, Nucleic Acids Res., 2010, 38, 6526–6532 CrossRef PubMed.
- B. Kundukad, J. Yan and P. S. Doyle, Soft Matter, 2014, 10, 9721–9728 RSC.
- T. J. Atherton and D. J. Kerbyson, Image Vision Comput., 1999, 17, 795–803 CrossRef.
-
T. Kotnik, G. Pucihar and D. Miklav
![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) i
i![[c with combining breve]](https://www.rsc.org/images/entities/char_0063_0306.gif) , J. Membr. Biol., 2010, 236, 3–13 Search PubMed.
, J. Membr. Biol., 2010, 236, 3–13 Search PubMed. - J. C. Weaver, K. C. Smith, A. T. Esser, R. S. Son and T. Gowrishankar, Bioelectrochemistry, 2012, 87, 236–243 CrossRef CAS PubMed.
- T. Portet, F. C. i Febrer, J.-M. Escoffre, C. Favard, M.-P. Rols and D. S. Dean, Biophys. J., 2009, 96, 4109–4121 CrossRef CAS PubMed.
- D. L. Perrier, L. Rems, M. T. Kreutzer and P. E. Boukany, Sci. Rep., 2018, 8, 4758 CrossRef PubMed.
- N. C. Stellwagen, C. Gelfi and P. G. Righetti, Biopolymers, 1997, 42, 687–703 CrossRef CAS.
- N. C. Stellwagen, A. Bossi, C. Gelfi and P. G. Righetti, Anal. Biochem., 2000, 287, 167–175 CrossRef CAS PubMed.
- E. Stellwagen and N. C. Stellwagen, Electrophoresis, 2002, 23, 1935–1941 CrossRef CAS PubMed.
- E. Stellwagen and N. C. Stellwagen, Biophys. J., 2003, 84, 1855–1866 CrossRef CAS.
- K. A. Riske and R. Dimova, Biophys. J., 2005, 88, 1143–1155 CrossRef CAS PubMed.
- T. Portet and R. Dimova, Biophys. J., 2010, 99, 3264–3273 CrossRef CAS PubMed.
- C. Faurie, M. Rebersek, M. Golzio, M. Kanduser, J.-M. Escoffre, M. Pavlin, J. Teissie, D. Miklavcic and M.-P. Rols, J. Gene Med., 2010, 12, 117–125 CrossRef CAS PubMed.
- S. Sachdev, S. Feijoo Moreira, Y. Keehnen, L. Rems, M. T. Kreutzer and P. E. Boukany, Biochim. Biophys. Acta, Biomembr., 2019 Search PubMed , (under review).
- D. L. Perrier, A. Vahid, V. Kathavi, L. Stam, L. Rems, Y. Mulla, A. Muralidharan, G. H. Koenderink, M. T. Kreutzer and P. E. Boukany, Sci. Rep., 2019, 9, 8151 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1–S5 and Tables ST1–ST4. See DOI: 10.1039/c9sm01274e |
| ‡ Present address: Science for Life Laboratory, Department of Applied Physics, KTH Royal Institute of Technology, Tomtebodavägen 23, SE-171 65 Solna, Sweden. |
| This journal is © The Royal Society of Chemistry 2019 |