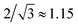Granular ionic crystals in a small nutshell

Abstract

Ordered two-dimensional arrangements of triboelectrically oppositely charged granular particles have been reported several times, but observations of bulk ordered binary granular particle packings are singular. We attribute this suppression of triboelectrically induced order to the concurrent behaviour of granular particles to pack densest due to gravity. We show that triboelectrically induced order robustly emerges in a container that does not allow for crystallization into a dense packing under gravity. It turns out that the triboelectrically ordered structure follows Pauling's predictions for atomic ionic crystals in many aspects, but also exhibits systematic deviations. We discuss how the emergence of order in an incommensurate container, the deviations from Pauling's predictions and the gravitational potential energy of the particles are connected.

---

1 Introduction

Materials from opposite ends of the dielectric triboelectric series oppositely charge in contact.¹ This behavior can be used to study self-assembly and crystallization of macroscopic particles. The ordered structures that emerge upon vibration of binary mixtures of granular particles in two-dimensional horizontal experiments had been studied in various publications.^2–8 The emergence of three-dimensional ordered structures, in contrast, has only been observed once in a study on humidity effects and segregation of vibrated Teflon (PTFE) and nylon (PA) spheres,⁹ to the best of the authors' knowledge. This minimal number of observed three-dimensional ordered structures caused by opposite triboelectric charging suggests existence of a mechanism that suppresses emergence of order by charging.

A potential reason might be gravity and agitation. Granular particles are macroscopic objects, which sediment and have to be mobilized by agitation. In studies on crystallization in bulk granular media the dominance of gravity or other external compression to drive formation of densest sphere packings has been worked out.^10–16 The emerging crystalline structures were found to minimize the gravitational potential energy and the kinetic energy from agitation for rectangular container geometries.^10,13,17

These findings suggest that crystallization of granular spheres into densest packings by gravity forms a deep energy minimum, that is hard to leave by interactions emerging from opposite charging. Emergence of order by triboelectric charging may consequently be best observed in a container that does not allow for crystallization by gravity, as the order process does not have to compete the formation of a densest packing.

We show with the experiments in Section 3.1 that a small spherical container does not allow for crystallization of monodisperse spheres by vibration under gravity alone. In contrast, a binary mixture of PTFE and PA spheres in this container geometry shows reproducible emergence of non-densely packed structures with long-ranged cubic order and local chemical order with vibration, i.e., a granular ionic crystal. When a container with flat walls is used instead of the spherical container, the binary mixture only shows emergence of long-range ordered hexagonal dense packings without chemical order.

The granular ionic crystal that forms in absence of the template by flat container walls is further investigated in Section 3.2. We show that the granular ionic crystal is to a large extent in agreement with Pauling's rules for atomic or molecular ionic crystals, but comprises systematic modification into a tetragonal phase by gravity.

2 Experimental

We used granular samples consisting of Teflon and nylon spheres. The spheres were bought from TIS Wälzkörpertechnologie with a diameter d of 2 mm. The polydispersity of the spheres is 50 μm according to the manufacturer, but the tomographic results indicated even less fluctuations of the sphere diameter. Before each experiment, the spheres were cleaned in ethanol and left to dry and consequently were filled into the container using a glass funnel. The different particle mixtures and container geometries used are explained further in the Sections 3.1 and 3.2.

We applied vertical vibrations to the sample using a Bruel & Kjaer LDS V721 vibrating table. The parameter of the sinusoidal agitation, amplitude A = 1 mm, frequency F = 23 Hz, and resulting acceleration of Γ = 2.1 g, were chosen to agitate the granular sample into a condensed, periodically compressed and expanded phase.^18,19 This behavior could be confirmed by inspection using the transparent container described below. The agitation was applied for 90 minutes, then the container was carefully removed from the vibrating table.

We recorded the resulting packing structure within the container using a GE phoenix nanotom μCT system. The particles' positions and material types were determined using the code presented by Weis and Schröter²⁰ with a modification to discriminate between PTFE and PA spheres. We employed the Voro++ code²¹ to obtain the Voronoi cells of the individual particles and consequently the local packing fractions ϕ_l and the Voronoi cell facets. We discard in the evaluation the particles touching the boundary of the evaluated volume and all particles touching a boundary particle.

The packing structures of the samples were characterized using the packing fraction ϕ_global, the average number of neighbors C, the radial distribution function g(r) and the q₄–q₆ bond orientational order parameter.²² The global packing fraction is calculated from the local packing fractions ϕ_lvia:

where N is the total number of spheres. C was determined by counting all particles within a cut-off distance of 1.05 d as neighbors. g(r) was determined by binning the positional distances in the sample into 1000 normalized bins. We determine C and g(r) as a global average as well as with respect to the chemical composition of the particles in the binary experiments. The q₄–q₆ bond orientational order analysis with an α = 2 facet weighting was used to distinguish and identify crystal structures underlying the arrangement of the spheres.²³

We measured the net charges on the granular spheres by picking up single spheres using polymethylpentene (PMP) tweezers and depositing them in a Faraday cup connected to a Keithley 6514 electrometer. The charges are determined from the height of the jumps in the recorded charge when a sphere is dropped into the cup, similar to our previous study.²⁴

The ionizing X-ray radiation of the tomographic setup affects the charging state of the spheres. The tomographic imaging thus always ended an experimental run. After imaging, the samples were removed, washed with ethanol and prepared for a next run as described above. The discharging effect of the radiation is further discussed in Section 4 and in the ESI.†

3 Results

3.1 Crystallization in a spherical nutshell

We want to create a situation where the container is not compatible with any space-filling crystal symmetry to minimize the tendency of the particles to take densest packings under gravity. We thus use a spherical aluminum container, a geometry which has the smallest possible interface among sample and container in addition to being incompatible with any space-filling crystal symmetry. Sandomirski and co-worker have shown in experiments with colloidal hard spheres that spherical walls only with curvature radii larger than 150 times the particle radii effectively enhance heterogeneous crystallization, while curvature radii less than 20 particle diameter effectively suppresses crystallization.²⁵ The spherical container used here has an inner radius of 20 mm, thus 20 times the particle radius, close to the reported limit of suppressing crystallization.

We put 2000 PTFE spheres in the container (‘monomer’ experiment), which corresponds to a volume filling of 25%. A slice from the tomographic reconstruction of the sample after vibration is displayed in Fig. 1(a). The sample has condensed after 90 minutes of vibration into a dense packing with a horizontal upper surface and without any apparent order. The spherical container thus effectively prevents formation of densest ordered arrangements of the spheres with gravity alone.

Fig. 1 Vertical slices through the tomographic reconstructions of the sphere packings after vibration. Gravity acts vertically, thus parallel to the image plane. The denser PTFE spheres appear brighter than the PA spheres in the reconstructions. The apparent radius reflects the position of the monosized spheres with respect to the image plane. A sedimented dense, but disordered packing of PTFE spheres is visible in (a) (‘monomer’ experiment). The spherical container geometry effectively prevent a crystalline packing of solid spheres. In the same geometry, (b) a mixture of PTFE and PA spheres forms a packing with apparent cubic symmetry with sorting of the PTFE and PA spheres after agitation (‘binary’ experiment). The ordered region is separated by a disordered layer from the container walls. The same mixture of particles exhibit a dense packing in the cuboidal container, (c) with apparent hexagonal symmetry, but no chemical order among the particles. The ordered pattern is commensurate to the wall visible at the left edge of the image.

We compare the results obtained in this first scenario to a sample consisting of 1000 PTFE and 1000 PA spheres (‘binary’ experiment) to establish the influence of the opposite triboelectric charging. The sample now exhibits a very different packing structure and morphology, see Fig. 1(b). The sample does not form a horizontal surface with vibration, but instead forms a pyramidal tip with flat facets. The packing of the spheres exhibit a rectangular pattern, while hexagonal close-packing is not observable. In addition, the sample exhibits sorting according to the chemical nature of the spheres, as an alternating pattern of bright PTFE spheres and darker PA spheres is visible. The ordered arrangement of the spheres is not commensurate to the spherical container walls and rests upon a disordered layer of spheres.

The spherical aluminum container of the binary experiment is replaced with a transparent cuboid container made out of poly(methyl methacrylate) (PMMA) with 50 mm side length in a third scenario (‘templated binary’ experiment). The spheres sediment in this setup into a polycrystalline hexagonally densest packing without chemical sorting of the particles. The packing structure is commensurate to the container walls, as the planes of particles are aligned with the container wall.

The samples thus exhibit apparently different structures in the three scenarios after vibration. The structural differences are quantified using the q₄–q₆-order metric‡ (see Fig. 2). The distributions of the q_l-values confirm the impressions from the tomographic reconstructions. Emergence of crystalline order among the solid spheres in the monomer experiment is effectively suppressed (Fig. 2a). The particles in the binary experiment are more homogeneously arranged, as their q_l scatter much less. The particles take an arrangement that is on average much closer to cubic symmetry than in the other two scenarios (Fig. 2b). The arrangement structure of the particles in the templated binary experiment can be identified as a HCP structure (Fig. 2c).

Fig. 2 The bond orientational order of the sphere positions in the three scenarios, given as position in the q₄–q₆-plane. The graphs on the x- and y-axis give the histograms of the q₄- and the q₆-parameter individually. The large symbols give the position of ideal hexagonal-close packed (HCP), face-centered cubic (FCC) and body-centered cubic (BCC) lattice sites in the q₄–q₆-plane. No order is apparent from the distribution of the q_l in the monomer experiment, (a). The particles in the binary experiment, (b), take arrangement structures which are less widely distributed and are closer to the ideal BCC values. The particles in the templated binary experiment, (c), apparently take a HCP arrangement structure with little noise. The value of the body-centered tetragonal T2 (BCT T2) structure is additionally marked in (b), see Section 3.2 for discussion.

The rectangular pattern with alternating spheres (Fig. 1) and the proximity of the q_l-values to the ideal BCC value (Fig. 2) suggests that a body-centered cubic (BCC) lattice forms the scaffold of the structure of the binary sample in the spherical container. This is further supported by the global parameters of the sample given in Table 1. We compare the global packing fraction ϕ_global and the global total average number of neighbors C_global to the values of the BCC, the T2-variation of the body-centered tetragonal (BCT), the random close-packed (RCP), and the hexagonal close-packed (HCP) hard sphere packing structure. The global packing fraction of the binary sample is in close agreement with the BCC hard sphere packing, while the packing fraction of the monomer experiment matches the value of a RCP hard sphere packing and the packing fraction of the templated binary packing approaches the value of the hexagonal dense FCC or HCP hard sphere packing.

Table 1 Global packing fraction ϕ_global and global total average number of neighbors C_global of the three experiments and for ideal hard sphere lattices. The packing fraction of the CsCl BCC structure is given for a size ratio between the two sphere species of one. Along with the global averages the average numbers of chemical homogeneous neighbors of PTFE spheres (C_TT) and of PA spheres (C_NN), the average number of chemical heterogeneous neighbors (C_TN) and the ratio of the number of PTFE spheres to the total number of spheres in the investigated volume N_T/(N_T + N_N) are given

Experiment	ϕ global	C global	C TT	C NN	C TN	N T/(NT + NN)
Monomer	0.641	8.1	—	—	—	1
Binary	0.678	9.1	1.26	1.26	7.87	0.50
Templated binary	0.704	11.3	4.7	5.0	6.6	0.48
CsCl (BCC)	0.68	8	0	0	8	0.5
BCT T2	0.698	10	2	2	8	0.5
RCP	0.64	6	—	—	—	—
HCP	0.74	12	—	—	—	—

---

The global total average numbers of neighbors C_global in the experimental packings follow the same trend. C_global in the binary sample is close to the expectation value from a BCC hard sphere lattice. The templated binary packing has an even higher number of neighbors than the binary packing, slightly lower than the ideal hexagonal packing value.

The local chemical order becomes apparent when the numbers of neighbors are calculated with sensitivity to the chemical nature of the spheres (C_TT, C_NN, and C_TN in Table 1). The binary experiment is composed nearly exclusively out of heterogeneous neighborhoods, i.e., contacts or close encounters among chemically dislike spheres. The templated binary sample does not have this extreme prevalence of heterogeneous neighborhoods, heterogeneous neighbors are only twice as probable as homogeneous neighbors.§ The ratio of the number of PTFE spheres to the total number of spheres in the investigated volume N_T/(N_T + N_N) shows some segregation in the templated binary experiment, as less PTFE spheres than PA spheres are found in the investigated volume.

3.2 The granular ionic crystal: a Pauling structure?

The results in Section 3.1 indicate that the binary sample in the incommensurate container takes a different structure than the monomer sample and than the binary sample in a container with flat walls. In Fig. 3 the tomographic reconstruction of the binary sample is rendered. The sample shape follows the spherical container at the bottom, while a pyramid with flat surfaces protrudes at the top. The ordered pattern with chemical sorting of the spheres extends horizontally and vertically throughout the sample, as can be seen from the quarter taken out of the reconstruction. It seems likely that design rules similar to ionic crystals define the arrangement structure of this ordered packing.

Fig. 3 Rendering of the sample from the binary experiment. PTFE spheres are displayed in red and PA spheres in grey. The sample follows the spherical container at the bottom, while a pyramid with flat surfaces protrude at the top. An ordered arrangement of the spheres extends throughout the sample, as can be seen from the quarter taken out in the upper left.

We estimate the charge on the spheres to transfer these rules from ionic crystals to the situation of the granular sphere packings in this study. We measure the charge on the spheres after vibrating by picking individual particles from the container with PMP tweezers and dropping them into a Faraday cup connected to an electrometer. This only allows for an estimate of the charge on the particles as handling of the particles with solid tweezers inevitably requires touching the particles and by this potentially generation or annihilation of charges.²⁴ The resulting charge distributions after measuring 60 particles is given in Fig. 4. The PTFE spheres and the PA spheres obviously charge oppositely, and the absolute value of the mean charge of the two sphere species nearly matches. If we assume that this charge is homogeneously distributed on each sphere surface and if we assume purely coulombic interaction between two spheres in contact, we get a force of F_q = (Q_PTFE·Q_PA)/(4πε₀d²) = 173 mN. In comparison, the gravitational force on the heavier PTFE spheres is F_g = m·g = 9.06 mg·9.81 m s⁻² = 90 mN, showing that the coulombic pair forces are on average about twice as high as the gravitational forces acting on a single sphere. The ordered structure in the spherical container must be strongly influenced by the triboelectric charging of the spheres, thus could justifiably be called an ionic crystal.

Fig. 4 Distribution of net charges on PTFE particles and PA particles after extraction from the binary sample vibrated in the spherical aluminum container. μ and the vertical dashed lines indicate the mean of the two charge distributions.

Pauling has worked out a set of semi-analytical rules that govern the structure of ionic crystals.²⁶ The first Pauling rule is purely geometrical, stating that the ions pack as hard spheres with radii given by their ionic radii. In an ionic crystal the electrostatic potential has to be minimal and the ions take a structure where the distance among the cations and anions is minimized and the distance among the anions is maximized. According to this rule, the ionic crystal structure will be determined by the ratio of the radii among the cations and the anions. The second Pauling rule is about electroneutrality, stating that the charge of each cation must balance the sum of the shared charge of the adjacent anions.

The experimental findings suggest that the binary sample could be idealized to consist of two spherical species of equal radii and with equal absolute mean charge value. The Pauling rules suggest the formation of the caesium chloride- (CsCl-) BCC structure for this situation of two ionic species of same charge with opposite sign and same radius.²⁶ In this structure a central ion is coordinated by 8 counterions, which form the edges of the cubic primitive cell. The apparent structure of the granular ionic crystal matches this expectation from the Pauling rules. We find cubic symmetry in the sample, a high prevalence of heterogeneous, i.e., counterionic, neighbors, and the packing fraction of a hard-sphere BCC structure.

3.3 Deviations from Pauling's prediction

Pauling's rules do not take into account gravity and a time evolution of the charge on the constituents of the structure. Deviations from the prediction of Pauling's rules in this granular case are thus likely. The forces emerging from the triboelectric charge can be expected to be large enough to overcome gravity, but they are still on the same order of magnitude (see Section 3.2). Also the charge has to build up or may be altered during the processing of the sample. Both effects make deviations likely.

A close inspection of the q₄–q₆-order parameter (see Fig. 2(b)) factually does reveal a systematic distortion of the crystal beyond random noise. Random noise alone would mostly reduce the mean q₆ value alone.²³ The simultaneous reduction of the mean q₄ value compared to the ideal BCC lattice value indicates a systematic difference in the arrangement structure of the spheres compared to the BCC lattice.

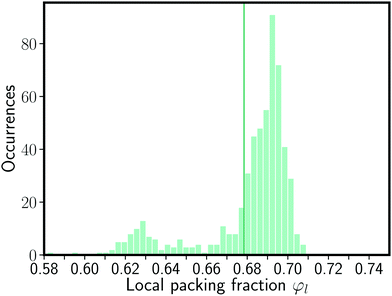
This indication of a systematic difference among the structure of the granular ionic crystal and a BCC lattice is further supported by the local neighborhood (see Table 1). The occurrence of homogeneous neighbors is not compatible with the CsCl BCC lattice. Finally, the distribution of local packing fractions (Fig. 5) shows that the global packing fraction of the sample of 0.678 is not the most likely packing fraction of the individual spheres. The mode of the distribution is 0.692, thus most of the spheres are packed denser than in a BCC hard sphere packing.

Fig. 5 Distribution of local packing fractions in the binary experiment, as obtained from the volumes of the Voronoi cells. The vertical line indicates the global packing fraction of the sample of 0.678. Locally, most spheres are packed denser than the global average.

A vertical cut through the reconstruction of the sample along an (100)-plane of the lattice reveals the nature of the systematic distortion of the BCC lattice (see inset in Fig. 6). The distance among horizontal planes shrinks with sample height, while at the same time the horizontal distance of the planes dilates. This vertical compaction of the sample is quantified in the main graph of Fig. 6. At the top of the sample the planes with the same chemical nature are compacted up to mechanical contact, thus particles with the same chemical nature and the same charging are pressed into contact at the expense of a horizontal dilation. The distances closer to the bottom of the sample are closer to the expectation value from the ideal CsCl BCC lattice.

Fig. 6 Systematic gravitational distortion of the granular ionic crystal. The inset shows a vertical cut through the sample along an (100)-plane, where the arrow indicates the direction of the gravitational acceleration g⃑. A compaction of the horizontal planes with sample height is visible, with an associated dilation of the sample in the horizontal direction. The main graph gives the vertical distance among either PTFE horizontal planes or PA horizontal planes (x-axis) as a function of the sample height (y-axis), both in units of particle diameter d. Lines are guides to the eye. The lowest planes have the largest vertical distance, but still less than the expectation value from a BCC lattice of . The distance shrinks with sample height up to mechanical contact of same-charged particles.

The granular ionic crystal thus exhibits an continuous change from a BCC-like arrangement at the bottom to a deformed cubic structure at the top. A BCC lattice which is compacted along one axis and is dilated along the other two axis forms a body-centered tetragonal (BCT) lattice. In particular, we find that a compaction up to the mechanical contact of the spheres underlying a hard-sphere BCC lattice forms the BCT T2 lattice.^27,28 In the compaction of a CsCl BCC lattice into a BCT T2 lattice counterions would thus come into contact. The observations in the granular crystal match these considerations. Most particles take a packing fraction higher than the BCC value and closer to the BCT T2 value (see Fig. 5), homogeneous neighbors occur (see Table 1), and the position of the BCT T2 lattice in the q₄–q₆-plane is closer to the experimental values than the BCC lattice position (see Fig. 2).

4 Discussion

We investigated the emergence of order in packings of granular particles with triboelectric charging. In particular, we investigated the role of the container geometry. The existing results on crystallization of monodisperse spheres suggested a dominance of gravity and the container geometry in the crystallization process. Even a selection of the emergent crystalline arrangement is possible with choosing a container commensurate to a certain crystal structure. We inferred, that an incommensurate container is beneficial to study the structure formation caused by triboelectric charging.

We could show that within a small spherical container crystallization is effectively suppressed. Even after 90 min of mobilization or 125 000 vibration cycles no signature of crystallization was detectable among the 2000 monomer spheres. This indicates that the disordered, loose packing with a packing fraction of 0.64 is the lowest potential energy state of hard spheres in this container. Exchanging one half of the spheres with spheres of the same size but made out of a material from the other end of the triboelectric series changes the picture. Now an ordered packing emerges robustly. This packing is a bit denser than the disordered packing, but a pyramidal tip emerges at the top, thus it does not minimize the gravitational potential. Putting this binary mixture in a rectangular container leads to the emergence of hexagonally densest packed spheres observed in earlier studies on crystallization of hard spheres, with an arrangement of the spheres nearly independent of their chemical nature.

These observations may be merged into an energy level picture. The lowest energy state of hard spheres in the spherical container has a high gravitational potential energy, as it is disordered and loosely packed. The lowest energy state of hard spheres in a rectangular container of commensurate dimensions is a hexagonally dense-packed state at a low gravitational potential. If during the course of vibration opposite triboelectric charges emerge, another potential demands minimization. In the case of the spherical container this minimization happens from a loose state, thus an arrangement according to a minimization of the coulombic interaction is possible with minimal increase in gravitational potential energy. In the case of the rectangular container the minimization of the coulombic interaction has to start from a dense state, and relaxation of repulsive and attractive interactions comes along with a gravitational potential energy penalty.

In the spherical container the particles can thus relax into a configuration that minimizes the electrostatic potential. The way how this happens is described by Pauling's rules for ionic crystals. Pauling's rules predict a CsCl BCC structure for the situation of the experiment of two ionic species of equal radius and equal but opposite charging. We find signatures of this prediction in the granular packing in the spherical container. The sample exhibits cubic symmetry and contacts among PA spheres or among PTFE spheres are rare.

However, the ionic crystalline arrangement of the granular spheres is still strongly affected by gravity. This supports the discussion on the potential energy above, and one may say that this makes this granular ionic crystalline arrangement ‘granular’. The horizontal crystal planes are vertically compressed, in the extreme up to mechanical contact of like-charged particles. It may be speculated that polarization helps to stabilize the contacts of the like-charged dielectric spheres.^8,29 The observed compression is surprisingly stronger at top of the packing than at the bottom. This is most likely caused by the lateral dilation that has to accompany the vertical compression. The rounded lower half of the granular ionic crystal is confined by the spherical container, thus it cannot dilate and the compression by gravity cannot compact the layer.

Another reasoning of the emergence of the granular ionic crystal in the spherical container is worth discussing. The structures described here are obtained after extended vibration. Thus a selection of packing structure may not only happen by energy minimization, but also by mechanical stability. The structures have to be mechanically stable to not be destroyed at each cycle of the vibrating table. The vibration using the spherical container may induce varying degrees of shear stress in the sample, while the vibration of the cuboidal container mainly vertically compress and dilate the sample. The packing structure of sample in the spherical container thus may have to be mechanically more robust to survive the vibration than the packing structure in the cuboidal container. Emerging crystalline structures thus may be frequently destroyed in the monomer experiment in the spherical container. In the binary experiment, a BCC packing structure is additionally mechanically stabilized by the attractive coulombic forces of heterogeneous neighbors. This additional stabilization does not emerge in HCP- or FCC-like structures, where homogeneous neighborhoods of like-charged particles have to be formed. The formation of a BCC structure in the spherical container may thus emerge from enhanced mechanical stability against the vibrations.

Time-resolved studies may help to rule out the two different lines of reasoning, the energy-level picture or the mechanical stability picture, by imaging of transiently formed structures. However, a practical note has to be made concerning time-resolved studies. It seems straight forward to do vibration studies on binary mixtures inside of the tomography setup. However, the ionizing X-rays affect the charging state of the particles. In the ESI† charge distributions of spheres in a plastic container are given before and after exposure to X-rays (see Fig. S3(a), ESI†). One can see that 60 minutes of X-ray radiation, a typical time for recording tomographic images, quarters the charge on the spheres. This effect has also affected the structures presented here. The radiograms of the binary sample show that particles from the surface of the packing and from the container walls have moved, most likely due to discharging by X-rays and gravity (see Fig. S3(b), ESI†).

Developing an approach for time-resolved studies is also required to investigate the nucleation and growth behavior of the granular ionic crystals. We made six runs using the binary sample in the spherical container. We thereby increased vibration time from 10 minutes to 90 minutes prior to taking the respective X-ray radiogram and consecutive preparation of the sample for the next run by washing. The granular ionic crystal with the pyramidal tip was only observed for the last three runs. It has to speculated, if this is only an effect of the extended vibration time, or if during the course of the experiment other parameters which we did not control, like temperature or humidity, had changed in favor of triboelectric charging.

We restrict the discussion of the experimental findings to the effects of container shape, gravitational potential energy, symmetric interparticle coulombic interactions, and mechanical stability. We believe that these are the main factors controlling the formation and structure of the granular ionic crystal. An elaborate discussion, especially regarding the details of the deviations from Pauling's rules and the formation of the BCT T2 structure, may involve additional factors:

The asymmetry of the absolute charges of the particles (see Fig. 4) may not be a measurement error induced by the tweezers, as assumed in the discussion above, but may reflect a real asymmetry in the charging of the particles. It may be speculated if the formation of the BCT T2 structure may be partially a response to such an asymmetry. However, the Pauling rules suggest an increase in the number of contacts among opposite-charged spheres with charge asymmetry, not an increase in like-charged contacts.²⁶ Assuming a charge asymmetry among the particles also highlights the influence of the container, which is not part of Pauling's rules. Charge conservation and an asymmetry among the charges of the particles requires that the container carries a significant charge. So the container may introduce a yet hard to predict influence on the charging of the granular particles. The granular particles are also not homogeneously charged objects, and the spatial distribution of surface charges on the particles may also affect the structure formation. Finally, granular particles have a material density in addition to the charge and the ionic radius considered as material parameter in Pauling's rules. The PTFE particles in the experiments presented here, for example, have a density and thus a weight nearly twice as high as the PA spheres.

The last issue may be addressed using coatings. The triboelectric charging of solid objects can be controlled by the surface chemistry.^30–32 This may lead to new approaches for structuring granular media even from monomer core particles. Coating half of the particles with a material prone to strong opposite triboelectric charging may enable the coulombic interaction required to induce structure formation. Particle core materials with low densities also lower the gravitational potential penalty for forming granular ionic crystals.

5 Conclusion

Monodisperse granular hard spheres do not show crystallization in a small spherical container, similar to findings in experiments with thermal colloids. Such a container geometry, incommensurate with space filling crystalline packings, allows for observation of ordered arrangements in binary granular samples with triboelectric charging. The structure of such a triboelectrically induced crystallization follows the predictions of Pauling's rules, and exhibits geometrical and chemical order. Still, this granular version of an ionic crystal is distorted by gravity. Gravity compacts the ideal CsCl BCC ionic crystal structure of the granular spheres into a BCT T2 structure, where like-charged spheres come into contact.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We like to thank Stephanie Oppelt for help with the charge measurements and Fan Yang for proof-reading the manuscript. Funding by the German Science Foundation DFG under BO 4174/2-1 and SP 714/12-1 is gratefully acknowledged.

References

1. S. P. Hersh and D. J. Montgomery, Text. Res. J., 1955, 15, 279–295.
2. B. A. Grzybowski, A. Winkleman, J. A. Wiles, Y. Brumer and G. M. Whitesides, Nat. Mater., 2003, 2, 241–245.
3. G. K. Kaufman, M. Reches, S. W. Thomas, J. Feng, B. F. Shaw and G. M. Whitesides, Appl. Phys. Lett., 2009, 94, 044102.
4. R. Cademartiri, C. A. Stan, V. M. Tran, E. Wu, L. Friar, D. Vulis, L. W. Clark, S. Tricard and G. M. Whitesides, Soft Matter, 2012, 8, 9771.
5. N. V. Shestopalov, G. Henkelman, C. T. Powell and G. J. Rodin, New J. Phys., 2009, 11, 053014.
6. N. V. Shestopalov, G. Henkelman and G. J. Rodin, J. Chem. Phys., 2011, 135, 154501.
7. Y. Wang, X. Y. Wei, S. Y. Kuang, H. Y. Li, Y. H. Chen, F. Liang, L. Su, Z. L. Wang and G. Zhu, ACS Nano, 2018, 12, 441–447.
8. E. B. Lindgren, B. Stamm, Y. Maday, E. Besley and A. J. Stace, Philos. Trans. R. Soc., A, 2018, 376, 20.
9. A. Schella, S. Herminghaus and M. Schröter, Soft Matter, 2017, 13, 394–401.
10. A. Panaitescu and A. Kudrolli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 032203.
11. O. Pouliquen, M. Nicolas and P. D. Weidman, Phys. Rev. Lett., 1997, 79, 3640–3643.
12. Y. Nahmad-Molinari and J. C. Ruiz-Suárez, Phys. Rev. Lett., 2002, 89, 264302.
13. O. Carvente and J. Ruiz-Suárez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011302.
14. M. Götz, T. Fey and P. Greil, J. Am. Ceram. Soc., 2012, 95, 95–101.
15. K. E. Daniels and R. P. Behringer, J. Stat. Mech.: Theory Exp., 2006, P07018.
16. F. Rietz, C. Radin, H. L. Swinney and M. Schröter, Phys. Rev. Lett., 2018, 120, 055701.
17. O. Carvente, G. G. Peraza-Mues, J. M. Salazar and J. C. Ruiz-Suárez, Granular Matter, 2012, 14, 303–308.
18. S. Luding, E. Clément, A. Blumen, J. Rajchenbach and J. Duran, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 49, 1634–1646.
19. S. Luding, E. Clément, A. Blumen, J. Rajchenbach and J. Duran, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1994, 50, 4113–4122.
20. S. Weis and M. Schröter, Rev. Sci. Instrum., 2017, 88, 051809.
21. C. Rycroft, Voro++: a three-dimensional Voronoi cell library in C++, Lawrence Berkeley National Lab. (LBNL), Berkeley, CA, 2009, Technical Report LBNL-1432E.
22. T. Aste, M. Saadatfar and T. Senden, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061302.
23. J. Haeberle, M. Sperl and P. Born, arXiv preprint arXiv:1906.08111, 2019.
24. J. Haeberle, A. Schella, M. Sperl, M. Schröter and P. Born, Soft Matter, 2018, 4987–4995.
25. K. Sandomirski, S. Walta, J. Dubbert, E. Allahyarov, A. Schofield, H. Löwen, W. Richtering and S. Egelhaaf, Eur. Phys. J.-Spec. Top., 2014, 223, 439–454.
26. L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026.
27. J. A. R. C. Clarke, Nature, 1972, 240, 408–410.
28. V. V. Dolivo-Dobrovol'skii, Crystallogr. Rep., 2002, 47, 723–726.
29. J. Qin, J. Li, V. Lee, H. Jaeger, J. J. de Pablo and K. F. Freed, J. Colloid Interface Sci., 2016, 469, 237–241.
30. W. J. Brennan, J. Lowell, M. C. O'Neill and M. P. W. Wilson, J. Phys. D: Appl. Phys., 1992, 25, 1513–1517.
31. L. S. McCarty, A. Winkleman and G. M. Whitesides, Angew. Chem., Int. Ed., 2007, 46, 206–209.
32. S. Wang, Y. Zi, Y. S. Zhou, S. Li, F. Fan, L. Lin and Z. L. Wang, J. Mater. Chem. A, 2016, 4, 1–7.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01272a

‡ Further characterization of these structural differences are given in the ESI.† The distributions of the local packing fractions ϕ_l and the radial distribution functions g(r) support the formation of a disordered random close-packed sphere packing in the monomer scenario and the formation of a hexagonal close-packed sphere packing in the templated binary scenario.

§ The differences in local chemical order are also apparent from the radial distribution functions given in the ESI.† The g(r) differ considerably for homogeneous and for heterogeneous distances in the binary sample, while they are essentially the same for the templated binary sample.

---