Bubbles nucleating on superhydrophobic micropillar arrays under flow

Abstract

When a supersaturated aqueous solution flows over a microstructured, hydrophobic surface, bubbles tend to nucleate. Here, we control heterogeneous nucleation of gas bubbles from supersaturated CO₂ solution. By designing the shape, size, and arrangement of hydrophobic micropillars and by adjusting the flow we obtain uniform nucleation patterns. It is possible to selectively turn nucleation on and off. We use laser scanning confocal microscopy to resolve nucleation in early stages at the micropillar–substrate intersection. Numerical simulations show a correlation between minute pressure drops behind micropillars and nucleation sites. Bubbles nucleate uniformly behind pillars of the same size. The flow profile further contributes to the uniform growth of the bubbles. We control heterogeneous nucleation by varying micropillar geometry or size, flow direction and rate. While nucleation behind square pillars is independent of the flow direction, nucleation behind round micropillars is coupled with the direction. Nucleation behind triangular micropillars is bifurcated. These observations pave the way for the replenishment of the gas layer entrapped in between hydrophobic surface features, needed for superhydrophobicity.

---

Introduction

Bubble formation by heterogeneous nucleation on surfaces is a highly relevant phenomenon in various academic and industrial applications. The creation of an air phase underwater changes the heat transfer between interfaces,^1,2 flow pattern close to the solid/liquid interface,³ tribological properties,⁴ chemical composition in the surrounding medium^5,6 and the superhydrophobic state of structured surfaces.^7,8 However, controlling the place and exact time of heterogeneous nucleation is elusive.⁹ This difficulty arises from the dependency of nucleation on local roughness,¹⁰ gas concentration in the solution¹¹ and pressure.¹² Various attempts were made in order to control nucleation of bubbles at the solid/liquid interface including the use of ultrasonic waves,⁸ surface cavities,⁹ temperature and surfactants,¹ and biphilic surfaces (chemically patterned hydrophobic/hydrophilic surfaces).¹³ These attempts, however, require high pressures, the use of distinctive chemical moieties or temperature regulation. As many natural and synthetic surfaces are structured,^14,15 it is of high interest to use the potency of morphology for controlling heterogeneous nucleation. Previous studies showed the power of geometry in nucleation of droplets from vapor^16–18 or solutions,¹⁹ and in shaping foams in 2D.²⁰ Yet, the impact of surface micromorphology and curvature on bubble nucleation under flow was not experimentally studied.

In this study, we designed superhydrophobic surfaces made of micropillars with varying size, position and shape. Using laser scanning confocal microscopy (LSCM), we were able to resolve the nucleation and growth of CO₂ bubbles from supersaturated aqueous solution. Nucleation is suppressed or induced based on the micropillar size and geometry. We show that the shape of the micropillars can change the nucleation site or whether nucleation occurs at all. Symmetry break in the micropillar size and arrangement gives rise to nucleation patterns, including bifurcation,²¹ and the size of surface features can either promote or suppress heterogeneous nucleation.

A central motivation focuses on finding a process which allows reestablishing the Cassie state of submerged superhydrophobic surfaces.²² Such surfaces have been demonstrated to reduce hydrodynamic drag,^23–27 used as membranes for gas exchange, such as in CO₂ capturing, and prevent biofilm formation.^28–33 These features, however, only exist in the so-called Cassie state, in which only the top faces of the characteristic protrusions of the rough surface are in direct contact with water. In between, a layer of air is maintained. In superhydrophobic submerged surfaces the lifetime of the Cassie state is limited by the hydrostatic pressure and dissolution of gas in water.^34,35 Therefore, finding methods to replenish or even rebuild the Cassie state is of high interest.³⁶ Exposing superhydrophobic surfaces to water, supersaturated with gas, holds a great promise for replenishing the Cassie state as it induces spontaneous nucleation and can be controlled as shown in this study.

Materials and methods

Micropillar surface

Micropillar surfaces are produced via photolithography. Clean glass slides (170 μm thick) are spin-casted with the negative photoresist SU-8 (3025, Microchem, Germany). After a pre-bake step (65 °C for 5 min, 95 °C for 10 min, 65 °C for 30 min, slowly cooling down to room temperature overnight), UV illumination (250 W, 25 s) through a chromium mask and post-baking (65 °C for 5 min, 95 °C for 10 min, 65 °C for 30 min, slowly cooling down to room temperature for 90 min) the samples were immersed in the developer solution (3 min). The non-crosslinked areas are rinsed off with 2-isopropanol. Finally, the samples were heated (150 °C for 30 min) and slowly cooled to room temperature overnight. After synthesis, micropillar surfaces are placed in a NaOH solution (0.1 M) overnight and coated with (1H,1H,2H,2H)-perfluorooctyl-trichlorosilane via chemical vapor deposition for 3 h. Then, vacuum is applied overnight to remove unreacted silanes. The resulting contact angle of the flat coated surface is 105° ± 3°.

Confocal microscopy and microfluidics

A microfluidic cell (ibidi GmbH) was used, together with a peristaltic pump to regulate flow through the chamber. The flow direction can be reversed by reversing the rotational direction of the pump. At the bottom of the microfluidic chamber a micropillar decorated surface was placed and sealed. The microfluidic chamber could be placed in an angle of up to 20° with respect to the pillar surface without leakage to occur. This misalignment was used in the experiments presented in Fig. 5. Consecutive nucleation cycles within each experiment differ by few seconds. The supersaturated solution was not diluted or mixed with other solutions of different concentration and the container was kept sealed during the experiment.

A laser scanning confocal microscope (Leica) was used to monitor the nucleation and growth of bubbles. CO₂ supersaturated solution (Rossmann GmbH, Germany) ([HCO₃⁻] = 325 mg L⁻¹, supersaturation levels 3–5) was flown through the chamber. Water soluble dye, N,N′-(2,6-diisopropylphenyl)-1,6,7,12-tetra-(1-methylpyridinium-3-yloxy)perylene-3,4,9,10-tetracarboxylic acid diimide tetramethane-sulfonate (WS-PDI) was added (5 μg mL⁻¹) to the supersaturated solution for 3D image reconstruction.

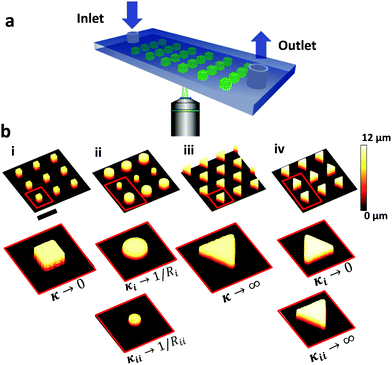
To analyze bubble nucleation, a hydrophobic glass slide covered with micropillar arrays of different shapes and arrangements was placed onto the bottom of a microfluidic cell. CO₂ supersaturated aqueous solution was pumped through the cell using a peristaltic pump, with flow rates in the range of 3–36 μL s⁻¹. The microfluidic cell was 450 μm high, 3.8 mm wide and 17 mm long. Bubble formation was imaged by a laser scanning confocal microscopy (LSCM) (Fig. 1a). Fig. 1b depicts confocal micrographs of the different micropillars designs in this study: (i) square, (ii) round with alternating diameter, (iii) triangular-uniformly oriented and (iv) triangles pointing in alternating directions.

Fig. 1 (a) The experimental setup: a microfluidic chamber monitored by a laser scanning confocal microscope. (b) Confocal micrographs of different micropillar surfaces used in this study: (i) square, (ii) round with alternating diameter, (iii) uniformly aligned triangles and (iv) triangles pointing in alternating directions. Scale bar: 100 μm.

Numerical simulations

Within numerical FEM simulations, pressure and velocity distributions are computed. The aim is to provide local pressure profiles at the start of bubble nucleation, close to the micro structures. The nucleation itself and bubble growth is not covered. Within a steady state approach no slip boundary conditions were applied at liquid/solid interfaces. The side walls of the fluidic cells are neglected and we assume a periodic flow behavior in the direction transversal to the main flow, i.e. identical flow fields in all rows of micropillars. Therefore, the model geometry comprises half a row of micropillars and symmetry boundary conditions are applied in transversal flow directions. The steady state Navier–Stokes equations have been solved using the FEM software package COMSOL.³⁷ The fluid volume in the layer of the micropillars has been meshed using prism cells with heights in micron and submicron ranges. The rest of the fluid volume has been meshed by tetrahedral cells with typical dimensions of a few microns close to the pillars up to about 30 microns far away. Overall, the meshes comprise typically between 200 000 and 300 000 volumetric cells. A parabolic flow profile has been applied at the inlet, whereas a constant pressure has been specified at the outlet. The fluid properties are set to those of water. By means of mesh sensitivity tests, it was assured that discretization errors are discernable.

Results and discussion

Square micropillars

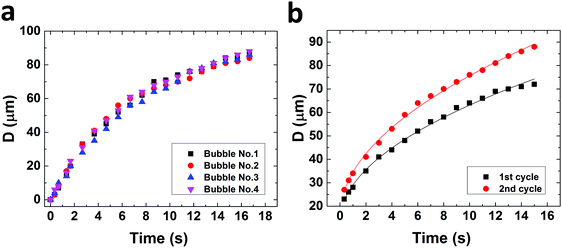
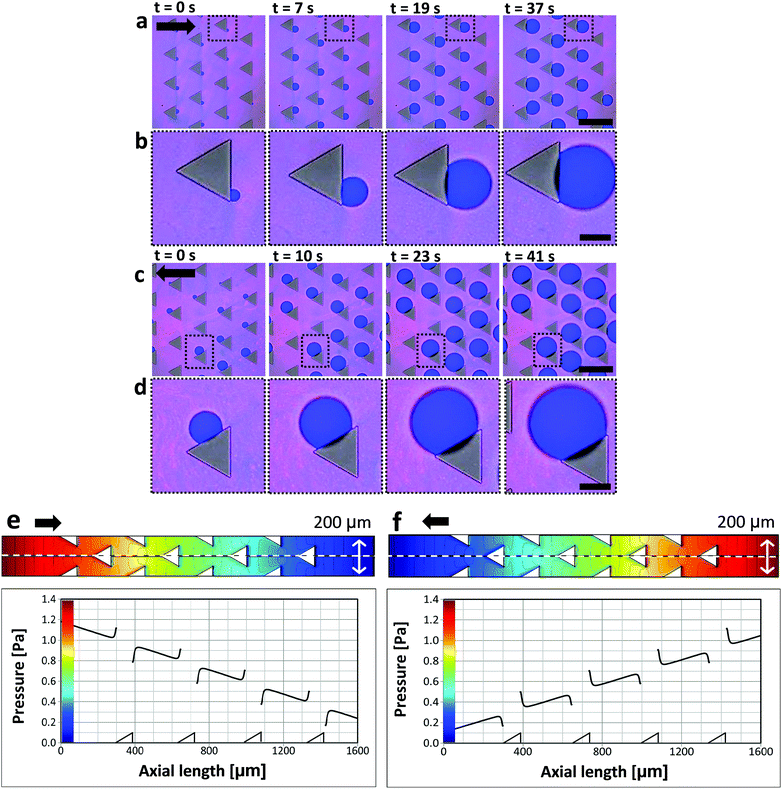
Bubbles nucleate preferentially behind the micropillars with respect to flow direction (Fig. 2). Nucleation is highly uniform and occurs simultaneously behind all micropillars. Bubbles nucleate preferentially at the intersection between the micropillar vertical rear wall and the bottom substrate (Fig. 2c). This observation agrees with free energy considerations.²² Reversing the flow direction results in reversing the nucleation site. In rare cases, three other scenarios were observed: (a) two bubbles nucleating at the same pillar, (b) bubbles nucleating, followed by shrinkage until dissolution and (c) no nucleation at all (Fig. S2 in the ESI†). In most experiments, however, uniform nucleation was observed.

Fig. 2 Confocal laser scanning micrographs of bubbles nucleation at square micropillars. CO₂ bubbles appear blue (reflection) while the surrounding aqueous medium appears pink and the micropillars appear green (see Experimental section). (a) Top view on multiple micropillars, the black arrow indicates the flow direction. Scale bar corresponds to 200 μm. Images are taken at the base of the micropillars focal plane. (b) Higher magnification of the area marked in dashed black line in (a). Scale bar corresponds to 50 μm. (c) 3D reconstruction from confocal z-stacks, depicting bubble nucleation and growth directly at the micropillar intersection with the planar surface. Pillars height is 10 μm and edge length 50 μm.

Once bubbles nucleate, they grow uniformly. Fig. 3a shows the contact diameter, D, of four bubbles behind four different square micropillars, growing within the same nucleation cycle. Minute variations in growth rate are attributed to local pinning due to changes in surface roughness. The experiment was repeated by reflowing saturated solution and air in cycles. In Fig. 3b the diameter of two bubbles growing in two consecutive cycles behind the same micropillar is compared. The second bubble grows faster than the first one although the volumetric flow rate, Q, was kept constant (18 μL s⁻¹). We have yet no good explanation for the observed faster growth of subsequent bubbles. Variation in growth rate may be attributed to local pressure variations between the cycles, or pressure fluctuations caused by the peristaltic pump. One may speculate that CO₂ molecules adsorbing to the solid surface survive the flushing and serve as a reservoir for the growth of the second bubble. It can, however, be estimated that one needs a much larger amount of CO₂ to noticeably affect a bubble than would be stored even in a dense monolayer of CO₂. To this end, let us consider the ideal gas law PV = nR̄T with P – pressure (Pa), V – volume (m³), n – number of moles (mol), R̄ – gas constant (m³ Pa mol⁻¹ K⁻¹) and T – temperature (K). We consider a bubble with contact radius of R = 50 μm (hence, corresponding contact diameter of D = 100 μm). To create a monolayer we estimate 10⁵ CO₂ molecules as an upper limit. This is negligible in comparison to the number of CO₂ molecules present in the bubble. Using the Young-Laplace equation ΔP = 2γ_bw/r (r – bubble radius) and the ideal gas law, we estimate that a bubble with a radius of r = 50 μm contains roughly 10¹² CO₂ molecules. Hence, surface adsorbed gas molecules do not alter the growth rate between consecutive growth cycles.

Fig. 3 Growth rate of bubbles nucleating behind square micropillars. (a) Four bubbles nucleating behind four pillars within one nucleation cycle. (b) Two bubbles nucleating behind the same micropillar over two consecutive nucleation cycles. D corresponds to the bubble contact diameter with the surface.

Fitted curves correspond to D(t) = 28.5·t^0.35 μm and D(t) = 33.8·t^0.35 μm, for the first and second cycles, respectively. Diffusion driven CO₂ bubble growth in moderately supersaturated aqueous solutions is given by r(t) ∝ t^0.5, with r – bubble radius and t – time.^12,38,40,41 Previous studies found that advective transport caused by growing bubbles in a non-confined environment may change the prefactor.^12,42 Here, however, advection is not only caused by the growing bubbles but is also a result of the forced flow in the microchannel. In addition, in our case the growth rates are one to two orders of magnitude larger in comparison with the reported rates by Enriquez et al.

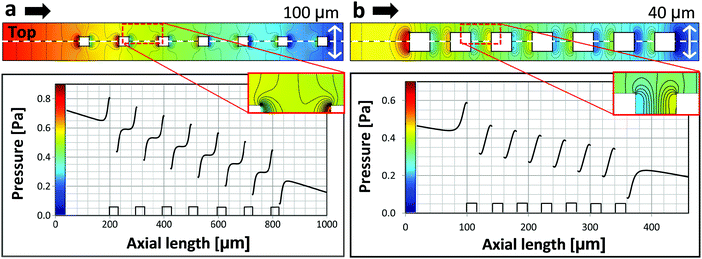
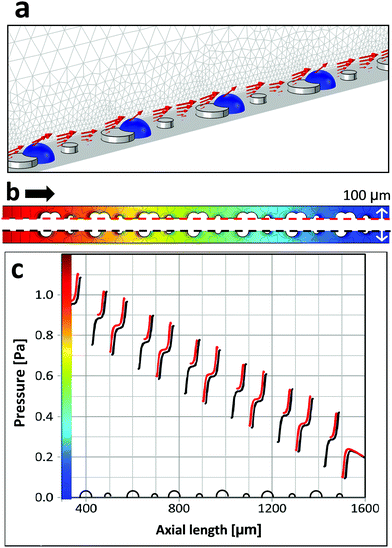
In order to analyze the local pressure distribution around micropillars, fluid dynamic simulations were used (Fig. 4). The overall flow is characterized by Reynolds numbers (Re) well below 10. Yet, in the layer of the micro structures characteristic velocities are well below the average velocity, and typical pillar dimensions are about 100 μm leading to local flow conditions with Re ≪ 1, i.e. creeping flow. Due to the small flow rates, total pressure drops across the microfluidic cell are about 3 Pa and below. The simulations show a local pressure drop behind micropillars in respect to flow direction and an increased pressure of comparable magnitude in front of them. Local pressure minima correlate with nucleation sites. We believe that this pressure variation suppresses nucleation before the micropillars and induces nucleation behind the pillars.

Fig. 4 Simulated pressure distribution within the microfluidic cell, for square micropillars under flow (average velocity u = 0.01 m s⁻¹). Flow direction is indicated by the black arrows. Upper figures show the color encoded pressure distribution at the bottom of the microchannel. Color legends are given in the graphs below. The pressure profiles presented in the lower graphs correspond to the line of symmetry (white dashed line). Insets show the pressure distribution between adjacent micropillars. The height of the micropillars is 10 μm in both cases. Edge length and spacing are 25 μm and 100 μm in (a) and 20 μm and 40 μm in (b), respectively. Pillars are sketched below the graph.

We examine the pressure distribution for square micropillars of two different dimensions: (a) edge length of 25 μm and spacing of 100 μm and (b) edge length of 20 μm and spacing of 40 μm. Black arrows indicate the flow direction. These two cases are important as they define the border between induced nucleation and nucleation suppression (Fig. S3 in the ESI†). The fact that bubble nucleation is observed in the scenario simulated in Fig. 4a and bubble nucleation is suppressed in the scenario in Fig. 4b indicates, that local pressure minima need to be sufficiently pronounced for nucleation to take place.

Dependence of bubble nucleation on flow direction and micropillar shape

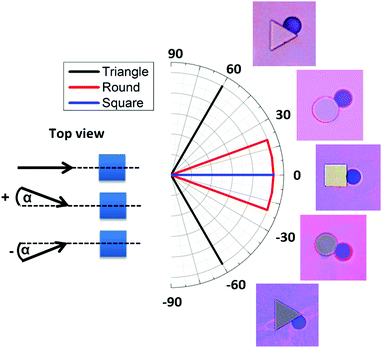
Behind square micropillars bubbles nucleate at the rear side, independently of the accessible incident flow direction within a range of α = −20…+20°. (Fig. 5). Here α is the flow angle of incidence. Behind cylindrical micropillars (50 μm diameter), the nucleation position corresponded to the flow angle of incidence for α = −20…+20°. Therefore, it is possible to direct bubble nucleation by adjusting the angle between the flow and the micropillars. For triangular micropillars, we observe a bifurcation transition to two possible nucleation sites. For an incident flow, shifted by α = 0…20°, nucleation and bubble growth occur at −60° with respect to flow direction, while for incident angles of α = −20…0° nucleation and growth occur at +60°.

Fig. 5 Direction of bubble growth with respect to flow angle of incidence, α, for triangular, round and square pillars. Left: Definition of angle of incidence, α. Right: Direction of bubble growth depending on flow direction in the range of α = −20…+20° with corresponding top view confocal micrographs (focal plane z = 0 μm).

To further demonstrate the impact of micropillar geometry on nucleation we use uniformly oriented triangular micropillars (Fig. 6). In the case where the base is oriented opposite to the flow direction, one nucleation site is observed behind the triangle base (Fig. 6a and b). However, when the flow direction is reversed the triangle base breaks the nucleation symmetry into two possible sites, left or right in downstream direction. Thus, the triangle base breaks the nucleation symmetry into two possible sites, left or right in downstream direction. One possible nucleation site is depicted in Fig. 6c and d. Minute deviations of the flow direction from the triangle median will induce nucleation on one edge of the triangle. Fluid dynamic simulations show that changing the flow direction reverses the pressure distribution and shifts the pressure drop around the triangle micropillar from the base to the side (Fig. 6e and f). The pressure profile along the symmetry (centre-) line of the triangular pillar row shows more or less identical local variations independent of the pillar orientation. In case of the reverse flow direction (Fig. 6c, d and f) bubbles do not nucleate right at the downstream vertex but on one side of the micropillar.

Fig. 6 Nucleation bifurcation depending on flow direction for triangular micropillars. (a) Triangular micropillars uniformly oriented. Black arrow indicates the flow direction. (b) Higher magnification of the area marked in a dashed black line in (a). (c) Flow direction is reversed using the same micropillars as in (a) and higher magnification of the area marked in a dashed black line (d). In all images the focal plane is the base of the micropillars. (e and f) Fluid dynamic simulations depicting the pressure distribution around triangular pillars, depending on the flow direction. Pillars are sketched below the graphs. Scale bars in (a and c) correspond to 200 μm, and in (b and d) to 50 μm.

Collective effects

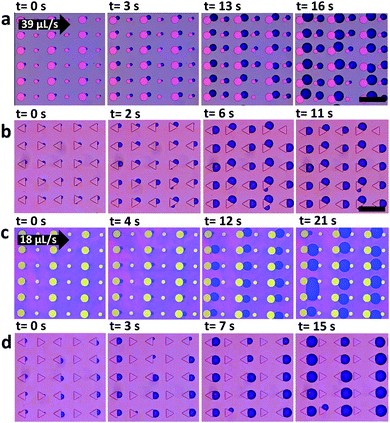
As can be seen in Fig. 6a and c bubbles do not nucleate behind all pillars. Already nucleated bubbles deplete CO₂ around them and tend to reduce the chance for nucleation of bubbles at neighboring micropillars. If a bubble does not nucleate initially, it is less probable to nucleate later. Such collective effects emerge when bubbles grow close to each other.^43,44 Growing bubbles compete for CO₂. An existing bubble acts as a CO₂ sink and can suppress the growth of adjacent bubbles.

We examine the possibility to induce bubble suppression and activation through arrangement of micropillars of different size or shape, depending on flow rate. Fig. 7 shows nucleation patterns for arrays of round micropillars with alternating diameter (a and c) and triangles pointing in alternating directions (b and d). Measurements were carried out at different flow velocities.

Fig. 7 Activation and suppression of bubbles under flow depending on micropillar geometry. Confocal micrographs (top view) of nucleation behind cylindrical micropillars with alternating diameter (a) and triangular micropillars of alternating orientation (b) under flow rate of Q = 39 μL s⁻¹. In (c and d) the flow rate is reduced to Q = 18 μL s⁻¹. Black arrows indicates the flow direction. All pillars are 10 μm high. Scale bar: 200 μm.

For volumetric flow of Q = 39 μL s⁻¹ (average velocity of u = 0.02 m s⁻¹) bubbles nucleated behind all round pillars (Fig. 7a). However, when the flow was reduced to Q = 18 μL s⁻¹ (u = 0.01 m s⁻¹) bubbles nucleated only behind larger micropillars (50 μm diameter). Nucleation was suppressed behind the smaller ones (20 μm diameter) (Fig. 7c). Similarly, for the triangular micropillars bubbles nucleated at both types of downstream edges, vertical and slanted (Fig. 7b) at 39 μL s⁻¹. When reducing the flow to Q = 18 μL s⁻¹ bubbles only nucleated at the vertical downstream edge while nucleation was suppressed at the slanted edges. Thus, the nucleation position can be selected by the flow rate.

Several mechanisms may be responsible for the observed flow rate dependence of bubble formation. We first consider cylindrical micropillars of alternating size (Fig. 7a and c). Fluid dynamic simulations reveal that local pressure drops behind 50 μm and 25 μm round micropillars are almost identical. For a pillar height of 10 μm and an average inlet velocity of 0.01 m s⁻¹ they are about ΔP = 0.15 Pa (Fig. S5, ESI†). Hence, differences in pressure drop are most likely not the reason for selective bubble nucleation. Fig. S3 in the ESI† shows nucleation occurs behind small and large pillars when their size is uniform. We therefore assume that initially bubble nucleation takes place behind all cylindrical pillars.

In this context we consider characteristic times associated with diffusive and advective CO₂ transport.⁴⁵ We, therefore, consider a local reduction in oversaturation due to CO₂ depletion around existing bubbles. The characteristic diffusion time of CO₂ molecules is given by t = x²/6D_CO2, with D_CO2 = 2 × 10⁻⁹ m² s⁻¹.⁴⁶ It takes a CO₂ molecule roughly 8 ms to equilibrate over a distance x = 10 μm (the height of the pillars) and 200 ms to equilibrate over 50 μm (the maximal diameter of micropillars). CO₂ molecules transported by advection, however, require roughly 20 ms to travel 10 μm or 100 ms to travel 50 μm for an average flow rate of 39 μL s⁻¹. For a flow rate of 18 μL s⁻¹ this time becomes longer: 40 and 200 ms, respectively. Thus, at the given geometries and flow rate diffusion and advection are at a critical balance.⁴⁷ While for low flow rates (18 μL s⁻¹ and below) diffusive supply of CO₂ may surpass advection, for higher flow rates (39 μL s⁻¹ and higher) advection adds to the CO₂ flux needed for bubbles to continue growing.

We also examine the hypothesis that a layer of adsorbed gas at the rear of the pillars may vary between the small and the large ones, leading to the observed selective nucleation. The thickness of this adsorbed gas layer becomes thicker at the front of the pillar (in respect to the flow direction) and thin out at the rear. In other words, an additional pressure drop behind the pillars, created in the wake of advected CO₂, may contribute to the selective nucleation behind pillars with specific size or geometry. While it is impossible to rule out this contribution, we consider our earlier estimation of the amount of gas adsorbed to the surface in order to show this effect may be neglected. The amount of CO₂ molecules needed for creating a monolayer at the surface of a bubble with contact radius R = 50 μm is smaller by seven orders of magnitude in comparison with the amount of CO₂ molecules the bubble contains. In addition, bubbles nucleate behind both the big and small pillars when their size is uniform (Fig. S3 in the ESI†). We therefore carefully conclude that this additional pressure drop cannot solely explain why bubbles grow behind specific pillars only.

For geometric reasons, bubbles of a given volume and with a given contact angle have a higher curvature (smaller radius of curvature) behind small pillars than behind large pillars. Thus, the capillary pressure in bubbles behind small pillars is higher than behind large pillars. If gas can diffuse and equilibrate between the two pillars, bubbles behind large pillars will grow at the expense of bubbles with small radius. We believe that this is the situation for low flow velocity. For high flow rates, diffusive transport is comparatively low and the process is dominated by advection. Still, also for larger flow rates it is observed that bubbles behind smaller pillars grow with a slightly lower rate (Fig. 7a).

Next, we consider whether a fluidic crosstalk could lead to suppression of bubble growth behind the smaller pillars. Could already nucleated bubbles influence the flow in such a way that nucleation behind neighboring micropillars is suppressed? To this end we simulate the flow field in the presence of bubbles behind the larger micropillars (Fig. 8). Within the steady state approach we examine to what extent are flow and pressure at the smaller pillars affected by the presence of bubbles at the larger pillars. Bubble growth and the gas flow within the bubbles are not taken into account in the simulations. In order to analyze the effect of the bubbles on the liquid flow the gas/liquid interfaces are regarded as free slip boundaries. It turns out that pressures behind smaller pillars are hardly affected by the presence of bubbles (Fig. 8b, c and Fig. S5, ESI†). Therefore, assuming laminar flow any fluidic crosstalk between adjacent pillars is unlikely.

Fig. 8 (a) Simulated flow in the presence of bubbles for round micropillars with alternating diameter of 50 μm and 25 μm, with interpillar spacing of 100 μm. Bubbles (blue) are attached to the larger micropillars, red arrows indicate the flow velocity. (b) Pressure distribution at the bottom of microchannel for two scenarios. Top: Half of a micropillar row with bubble attached to larger pillars; bottom: half of a micropillar row without bubbles. The color legend is provided in the graph below. (c) Pressure profiles along the symmetry-lines (red-dashed and black-dashed) shown in (b). The red curve denotes the pressure in the case with bubbles. Here, the larger gaps refer to the positions of pillars and bubbles. The black curve refers to the case without bubbles. Note: the latter is shifted by 10 μm for easier discrimination and comparison. All simulations results refer to an average velocity of u = 0.01 m s⁻¹ (flow direction is indicated by the black arrow in (b)). Pillars are sketched below the graph.

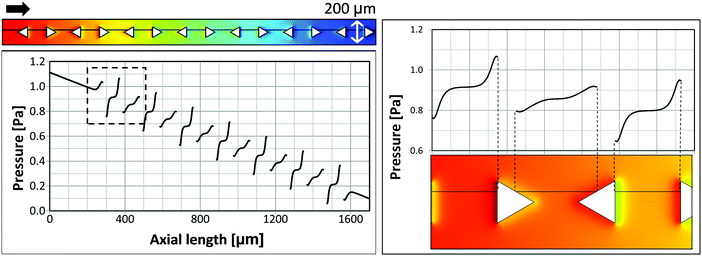
Finally, we examine the suppression of bubble nucleation at micropillars with triangular cross-section pointing in alternating directions as shown in Fig. 7d. Corresponding simulation results of the pressure distribution around triangular micropillars are shown in Fig. 9. The average flow velocity is u = 0.01 m s⁻¹, corresponding to Q = 18 μL s⁻¹ in the experiment. Because of surface energy bubbles tend to nucleate on concave nucleation sites or cavities rather than on convex sites.^39,48 In accordance with theory, we observe that bubble growth does not occur right at the downstream vertex and bubbles are shifted to either side (cf.Fig. 7b). Therefore, the pressure profile is shown along a line which is slightly off-centered (by 11.5 μm). The pressure shows pronounced local extrema close to the vertical triangle edges and less pronounced local extrema at the slanted edges. Experiments with low flow rate show bubble nucleation right at the positions where the pronounced local pressure minima are found (Fig. 9), i.e. backward facing vertical micropillar walls. Also from this observation it can be deduced that a certain critical local pressure minimum is needed to initiate or promote bubble nucleation.

Fig. 9 Simulated pressure for triangular micropillars (50 μm edge length) for an average velocity of u = 0.01 m s⁻¹ (flow direction is indicated by the black arrow). Top left: Pressure at the bottom of the microchannel. Bottom left: Pressure profile along the off-centered line shown in the graph above. Right: Close-up of pressure profile and color encoded pressure around triangular micropillars.

This conjecture is in accordance with experiments at higher flow rates, where bubble nucleation was observed at all backward facing micropillar walls, i.e. vertical and slanted walls (Fig. 7b). Generally, the flow within the layer of micropillars is characterized by Re ≪ 1 and the pressure is directly proportional to the flow rate, due to the linearity of the governing Stokes equation. Thus, also the local pressure variations and local minima are directly related to the flow rates. For a higher flow rate of Q = 39 μL s⁻¹ (Fig. 7b) the pressure profile shown in Fig. 9 has to be scaled by a factor of about two, which seemingly leads to all local pressure minima to be sufficiently pronounced.

Conclusions

Nucleation and growth of bubbles from oversaturated water solutions on hydrophobic micropillar arrays depend on the shape of surface features, the flow rate and direction. The pressure drop induced by the flow around the micropillars promotes nucleation behind the micropillars with respect to flow direction. Directly at the micropillar–substrate intersection the nucleation energy is the lowest and therefore takes place at this site, consistently. Nucleation behind square micropillars is independent of the flow direction. In contrast, nucleation behind cylindrical and triangular micropillars is flow direction sensitive. For cylindrical micropillars bubbles always nucleate behind micropillars. For triangular micropillars a bifurcation transition occurs: bubbles nucleate either to the left or right of the triangle apex. Breaking the symmetry of surface features allows inducing flow mediated activation and suppression of bubble nucleation. By adjusting the flow rate, one can suppress nucleation in specific sites, depending on the micropillar shape.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been supported by the German Research Foundation (DFG) under the individual project number 388761298. In addition, the authors acknowledge the support of the ERC advanced grant 340391-SUPRO.

References

1. H. J. Cho, J. P. Mizerak and E. N. Wang, Turning Bubbles on and off during Boiling Using Charged Surfactants, Nat. Commun., 2015, 6, 8599.
2. J. Kim, Review of Nucleate Pool Boiling Bubble Heat Transfer Mechanisms, Int. J. Multiphase Flow, 2009, 35(12), 1067–1076.
3. B. Shen, M. Yamada, S. Hidaka, J. Liu, J. Shiomi, G. Amberg, M. Do-Quang, M. Kohno, K. Takahashi and Y. Takata, Early Onset of Nucleate Boiling on Gas-Covered Biphilic Surfaces, Sci. Rep., 2017, 7(1), 2036.
4. X. Shen, S. L. Ceccio and M. Perlin, Influence of Bubble Size on Micro-Bubble Drag Reduction, Exp. Fluids, 2006, 41(3), 415–424.
5. G. Liger-Belair, G. Polidori and P. Jeandet, Recent Advances in the Science of Champagne Bubbles, Chem. Soc. Rev., 2008, 37(11), 2490–2511.
6. S. Shin, O. Shardt, P. B. Warren and H. A. Stone, Membraneless Water Filtration Using CO₂, Nat. Commun., 2017, 8, 15181.
7. S. Prakash, E. Xi and A. J. Patel, Spontaneous Recovery of Superhydrophobicity on Nanotextured Surfaces, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(20), 5508–5513.
8. B.-E. Pinchasik, H. Wang, H. Möhwald and H. Asanuma, Fully Reversible Transition between Cassie and Wenzel States via Acoustic Waves, Adv. Mater. Interfaces, 2016, 3(24), 1600722.
9. N. Bremond, M. Arora, C.-D. Ohl and Detlef Lohse, Controlled Multibubble Surface Cavitation, Phys. Rev. Lett., 2006, 96, 224501.
10. L. Wang, W. Zhang, X. Wang, J. Mi, J. Ma and Z. Du, The Mechanism of Roughness-Induced CO₂ Microbubble Nucleation in Polypropylene Foaming, Phys. Chem. Chem. Phys., 2017, 19(31), 21069–21077.
11. J. R. T. Seddon, E. S. Kooij, B. Poelsema, H. J. W. Zandvliet and Detlef Lohse, Surface Bubble Nucleation Stability, Phys. Rev. Lett., 2011, 106, 056101.
12. O. R. Enríquez, C. Sun, D. Lohse, A. Prosperetti and D. van der Meer, The Quasi-Static Growth of CO₂ Bubbles, J. Fluid Mech., 2014, 741.
13. C.-H. Choi, M. David, Z. Gao, A. Chang, M. Allen, H. Wang and C. Chang, Large-Scale Generation of Patterned Bubble Arrays on Printed Bi-Functional Boiling Surfaces, Sci. Rep., 2016, 6, 23760.
14. Z. Guo, W. Liu and B.-L. Su, Superhydrophobic Surfaces: From Natural to Biomimetic to Functional, J. Colloid Interface Sci., 2011, 353(2), 335–355.
15. T. Darmanin and F. Guittard, Superhydrophobic and Superoleophobic Properties in Nature, Mater. Today, 2015, 18(5), 273–285.
16. K.-C. Park, P. Kim, A. Grinthal, N. He, D. Fox, J. C. Weaver and J. Aizenberg, Condensation on Slippery Asymmetric Bumps, Nature, 2016, 531(7592), 78–82.
17. X. Fu, Z. Yao and P. Hao, Numerical Simulation of Condensation on Structured Surfaces, Langmuir, 2014, 30(46), 14048–14055.
18. R. Xiao, N. Miljkovic, R. Enright and E. N. Wang, Immersion Condensation on Oil-Infused Heterogeneous Surfaces for Enhanced Heat Transfer, Sci. Rep., 2013, 3, 1988.
19. H. Yu, S. Maheshwari, J. Zhu, D. Lohse and X. Zhang, Formation of Surface Nanodroplets Facing a Structured Microchannel Wall, Lab Chip, 2017, 17(8), 1496–1504.
20. Z. Huang, M. Su, Q. Yang, Z. Li, S. Chen, Y. Li, X. Zhou, F. Li and Y. Song, A General Patterning Approach by Manipulating the Evolution of Two-Dimensional Liquid Foams, Nat. Commun., 2017, 8, 14110.
21. Y. Shen, L. Hu, W. Chen and Xin Fu, Periodic and Aperiodic Bubbling in Submerged Gas-Liquid Jets through a Micro-Channel, Phys. Fluids, 2017, 29, 047104.
22. C. Shi, X. Cui, X. Zhang, P. Tchoukov, Q. Liu, N. Encinas, M. Paven, F. Geyer, D. Vollmer and Z. Xu, et al., Interaction between Air Bubbles and Superhydrophobic Surfaces in Aqueous Solutions, Langmuir, 2015, 31(26), 7317–7327.
23. K. Watanabe, Y. Udagawa and H. Udagawa, Drag Reduction of Newtonian Fluid in a Circular Pipe with a Highly Water-Repellent Wall, J. Fluid Mech., 1999, 381, 225–238.
24. E. Lauga and H. A. Stone, Effective Slip in Pressure-Driven Stokes Flow, J. Fluid Mech., 2003, 489, 55–77.
25. C.-H. Choi, U. Ulmanella, J. Kim, C.-M. Ho and C.-J. Kim, Effective Slip and Friction Reduction in Nanograted Superhydrophobic Microchannels, Phys. Fluids, 2006, 18(8), 087105.
26. J. P. Rothstein, Slip on Superhydrophobic Surfaces, Annu. Rev. Fluid Mech., 2010, 42(1), 89–109.
27. D. Schaffel, K. Koynov, D. Vollmer, H.-J. Butt and C. Schonecker, Local Flow Field and Slip Length of Superhydrophobic Surfaces, Phys. Rev. Lett., 2016, 116, 134501.
28. F. Geyer, C. Schönecker, H.-J. Butt and D. Vollmer, Enhancing CO₂ Capture Using Robust Superomniphobic Membranes, Adv. Mater., 2016, 29(5), 1603524.
29. M. Paven, P. Papadopoulos, S. Schöttler, X. Deng, V. Mailänder, D. Vollmer and H.-J. Butt, Super Liquid-Repellent Gas Membranes for Carbon Dioxide Capture and Heart–Lung Machines, Nat. Commun., 2013, 4, 2512.
30. G. McHale, M. I. Newton and N. J. Shirtcliffe, Immersed Superhydrophobic Surfaces: Gas Exchange, Slip and Drag Reduction Properties, Soft Matter, 2010, 6(4), 714–719.
31. D. E. M. Warsinger, J. Swaminathan, L. A. Maswadeh and J. H. Lienhard, Superhydrophobic Condenser Surfaces for Air Gap Membrane Distillation, J. Membr. Sci., 2015, 492, 578–587.
32. Y.-F. Lin, Q. Ye, S.-H. Hsu and T.-W. Chung, Reusable Fluorocarbon-Modified Electrospun PDMS/PVDF Nanofibrous Membranes with Excellent CO₂ Absorption Performance, Chem. Eng. J., 2016, 284, 888–895.
33. S. Pechook, K. Sudakov, I. Polishchuk, I. Ostrov, V. Zakin, B. Pokroy and M. Shemesh, Bioinspired Passive Anti-Biofouling Surfaces Preventing Biofilm Formation, J. Mater. Chem. B, 2015, 3(7), 1371–1378.
34. Y. Xiang, S. Huang, P. Lv, Y. Xue, Q. Su and H. Duan, Ultimate Stable Underwater Superhydrophobic State, Phys. Rev. Lett., 2017, 119(13), 134501.
35. Y. Li, D. Quéré, C. Lv and Q. Zheng, Monostable Superrepellent Materials, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(13), 3387–3392.
36. T. Verho, J. T. Korhonen, L. Sainiemi, V. Jokinen, C. Bower, K. Franze, S. Franssila, P. Andrew, O. Ikkala and R. H. A. Ras, Reversible Switching between Superhydrophobic States on a Hierarchically Structured Surface, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(26), 10210–10213.
37. COMSOL Multiphysics, Version 5.0, COMSOL, Inc, http://www.Comsol.Com.
38. S. F. Jones, G. M. Evans and K. P. Galvin, Bubble Nucleation from Gas Cavities - a Review, Adv. Colloid Interface Sci., 1999, 80, 27–50.
39. A. O. Maksimov, A. M. Kaverin and V. G. Baidakov, Heterogeneous Vapor Bubble Nucleation on a Rough Surface, Langmuir, 2013, 29(12), 3924–3934.
40. P. S. Epstein and M. S. Plesset, On the Stability of Gas Bubbles in Liquid-Gas Solutions, J. Chem. Phys., 1950, 18(11), 1505–1509.
41. P. Lv, H. Le The, J. Eijkel, A. Van den Berg, X. Zhang and D. Lohse, Growth and Detachment of Oxygen Bubbles Induced by Gold-Catalyzed Decomposition of Hydrogen Peroxide, J. Phys. Chem. C, 2017, 121(38), 20769–20776.
42. L. E. Scriven, On the Dynamics of Phase Growth, Chem. Eng. Sci., 1959, 10(1), 1–13.
43. S. Peng, T. L. Mega and X. Zhang, Collective Effects in Microbubble Growth by Solvent Exchange, Langmuir, 2016, 32(43), 11265–11272.
44. X. Zhu, R. Verzicco, X. Zhang and D. Lohse, Diffusive Interaction of Multiple Surface Nanobubbles: Shrinkage, Growth, and Coarsening, Soft Matter, 2018, 14(11), 2006–2014.
45. J. Atencia and D. J. Beebe, Controlled Microfluidic Interfaces, Nature, 2005, 437(7059), 648–655.
46. S. P. Cadogan, G. C. Maitland and J. P. M. Trusler, Diffusion Coefficients of CO₂ and N₂ in Water at Temperatures between 298.15 K and 423.15 K at Pressures up to 45 MPa, J. Chem. Eng. Data, 2014, 59(2), 519–525.
47. A. E. Kamholz and P. Yager, Theoretical Analysis of Molecular Diffusion in Pressure-Driven Laminar Flow in Microfluidic Channels, Biophys. J., 2001, 80(1), 155–160.
48. M. Iwamatsu, Line-Tension Effects on Heterogeneous Nucleation on a Spherical Substrate and in a Spherical Cavity, Langmuir, 2015, 31(13), 3861–3868.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01224a

---