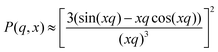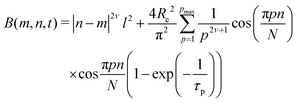Open Access Article
Open Access ArticleInner structure and dynamics of microgels with low and medium crosslinker content prepared via surfactant-free precipitation polymerization and continuous monomer feeding approach†
Tetyana
Kyrey
 *abc,
Judith
Witte
*abc,
Judith
Witte
 a,
Artem
Feoktystov
a,
Artem
Feoktystov
 b,
Vitaliy
Pipich
b,
Vitaliy
Pipich
 b,
Baohu
Wu
b,
Stefano
Pasini
b,
Baohu
Wu
b,
Stefano
Pasini
 b,
Aurel
Radulescu
b,
Aurel
Radulescu
 b,
Marcus U.
Witt
b,
Marcus U.
Witt
 c,
Margarita
Kruteva
c,
Margarita
Kruteva
 b,
Regine
von Klitzing
b,
Regine
von Klitzing
 c,
Stefan
Wellert
a and
Olaf
Holderer
c,
Stefan
Wellert
a and
Olaf
Holderer
 b
b
aInstitute of Chemistry, TU Berlin, Strasse des 17. Juni 124, 10623 Berlin, Germany. E-mail: t.kyrey@tu-berlin.de; Fax: +49 89 28910799; Tel: +49 89 28910799
bJülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH at Heinz Maier-Leibnitz Zentzum (MLZ), Lichtenbergstrasse 1, 85747 Garching, Germany
cDepartment of Physics, Soft Matter at Interfaces, Technical University Darmstadt, Alarich-Weiss-Straße 10, 64287 Darmstadt, Germany
First published on 17th July 2019
Abstract
The preparation of poly(N-isopropylacrylamide) microgels via classical precipitation polymerization (batch method) and a continuous monomer feeding approach (feeding method) leads to different internal crosslinker distributions, i.e., from core–shell-like to a more homogeneous one. The internal structure and dynamics of these microgels with low and medium crosslinker concentrations are studied with dynamic light scattering and small-angle neutron scattering in a wide q-range below and above the volume phase transition temperature. The influence of the preparation method, and crosslinker and initiator concentration on the internal structure of the microgels is investigated. In contrast to the classical conception where polymer microgels possess a core–shell structure with the averaged internal polymer density distribution within the core part, a detailed view of the internal inhomogeneities of the PNIPAM microgels and the presence of internal domains even above the volume phase transition temperature, when polymer microgels are in the deswollen state, are presented. The correlation between initiator concentration and the size of internal domains that appear inside the microgel with temperature increase is demonstrated. Moreover, the influence of internal inhomogeneities on the dynamics of the batch- and feeding-microgels studied with neutron spin-echo spectroscopy is reported.
1 Introduction
Stimuli-responsive polymers attract high research interest due to their responsiveness to external stimuli such as light, temperature and pH.1–6 Especially, microgels based on thermo-responsive poly(N-isopropylacrylamide) (PNIPAM) with a reversible temperature induced volume phase transition (VPT), which is close to physiological temperature (∼32 °C), serve as a model system for basic research and have been studied intensively.7–14 Below the volume phase transition temperature (VPTT), the polymer chains are swollen in water, while at higher temperatures (above the VPTT), the polymers partially release water molecules and a decrease of the particle size due to the chain collapse occurs.15Wu and co-authors16 showed that the crosslinker N,N′-methylenebisacrylamide (BIS) possesses faster consumption compared to NIPAM. Therefore, microgel preparation via classical precipitation polymerization (batch synthesis) leads to microgels with a crosslinker-rich core and a fluffier shell.17,18 Microgel preparation via a continuous monomer feeding approach (feeding synthesis) is assumed to lead to a more homogeneous crosslinker distribution.19–22 This was confirmed by a homogeneous elastic modulus and a homogeneous distribution of the embedded nanoparticles within the microgel.21 Properties of the microgel are closely related to their internal structure. A more homogeneous distribution of the crosslinker leads to a significantly higher swelling degree.22 The variation of the mesh size, which depends on the crosslinker distribution, plays a crucial role in the ability of the microgels to control drug delivery, i.e., the microgel matrix is used for loading of drugs into the polymer network.23 Thus, investigation and comparison of the internal structure of microgels prepared via batch and feeding methods are of high interest for the fundamental understanding of their properties and for further application.
So far, studies of the internal structure of microgels prepared via the continuous monomer feeding approach are very limited. Recent publications focused on studies of the microgel properties by means of optical microscopy or light scattering to prove the homogeneous crosslinker distribution in PNIPAM microgels.24–26 Such approaches do not give direct access to the internal structure and crosslinker distribution inside of the microgel. Neutron scattering methods can provide insight into the internal structure. The key advantage of the neutrons is the adjustable scattering contrast by using D2O as a solvent. Moreover, variation of the q-range permits the probing of the microgel structures in the nm to μm size range.
Earlier reported structural investigations of PNIPAM-based microgels prepared via classical precipitation polymerization in different solvents studied by means of atomic force microscopy (AFM), dynamic light scattering (DLS) and small-angle X-ray or neutron scattering (SAXS/SANS)9,27–31 give averaged information about the polymer density distribution inside the polymer microgels. For the structural characterization of the PNIPAM microgels, a core–shell or a core–fuzzy shell model is commonly used.6,17,29,32–34 In such models, the microgel has a homogeneous core with an uniform crosslinker distribution and a less dense shell with a polymer density gradient from the core to the outer surface.
The investigation of more complex microgels consisting of polymers with different VPTTs allows a more detailed description of the internal structure. M. Keerl and co-authors35 proposed a “dirty snowball” form factor for the description of the nanophase separated internal structure. In a copolymer microgel consisting of PNIPAM and PNIPMAM (N-isopropylmethacrylamide) at the transition temperature (30 °C), the PNIPAM domains (“dirt”) are collapsed and the PNIPMAM (“snowball”) is still in the swollen state. Wellert and co-authors36 used a model with two correlation lengths to describe the evolution of the internal structure of PEG-microgels during synthesis. Papagiannopoulos and co-authors37 reported on the formation of flower-like micelles below VPTT for triblock PS–PNIPAM–PS polymer microgels.
Hellweg and co-authors reported on investigations of the dynamics of macro- and microgels with low and medium crosslinker concentration. On a local scale, differences in the network dynamics between microgels and macrogels prepared via surfactant-free emulsion polymerisation were found.38 Moreover, a decrease of the collective diffusion coefficient of the microgels with the crosslinker concentration increase was obtained.10
Despite the number of works dedicated to the structural investigation of PNIPAM/BIS microgels and to the prediction of the influence of the microgel structure on their physico-chemical properties,39–41 the direct comparison of microgels with different internal crosslinker distributions is very limited.21
Recent investigations of the inner dynamics and network structure of PNIPAM microgels with different internal inhomogeneities with high cross-linker content (10 mol% BIS) were reported.42 It was shown that microgels prepared via the continuous monomer feeding approach possess a softer polymer network, i.e., polymer segments fluctuate as a Gaussian polymer chain in solvent. This leads to Zimm-type dynamics of the polymer chains. For the batch-microgels, on the other hand, due to the presence of a dense inner region, a dominant contribution of the cooperative density fluctuations was observed.
The internal structure of microgels in solvent is difficult to access. In the swollen state, below the VPTT, slight polymer density variations are mostly hidden by the low contrast in scattering experiments. And also, above the VPTT, microgels are mainly regarded as rather compact spherical particles.
In the current work, a detailed view of the inner microgel structure shall be provided, which reveals that the internal polymer network within a microgel exhibits a very rich structural and also dynamical complexity beyond a homogeneous average density variation from the centre to the shell.
The microgels revealed this complex internal structure and dynamics with a combination of small angle neutron scattering (SANS) and neutron spin echo (NSE) spectroscopy and dynamic light scattering (DLS).
2 Experimental
2.1 Materials
N-Isopropylacrylamide (≥99%) (NIPAM), N,N′-methylenebisacrylamide (≥99.5%) (BIS) and 2,2′-azobis(2-methylpropionamidine)dihydrochloride (97%) (AAPH) were purchased from Sigma-Aldrich (Munich, Germany). All chemicals were used as received. A Millipore Milli-Q Plus 185 purification system was used for water purification.2.2 Microgel synthesis
The different ways of crosslinker incorporation during microgel synthesis may lead to a different crosslinker distribution within the microgel network. Localisation of the crosslinker mostly in the central “core” part during the batch-synthesis43 and a more homogeneous distribution in the whole microgel volume obtained by the feeding approach22,25 are expected.The detailed description of the synthesis of the microgels via batch and feeding methods was described in previous work.42 Here, the amount of crosslinker was varied between 0.5 mol% and 5 mol%. NIPAM (1.688 g, 14.9 mmol (0.5 mol% BIS); 1.663 g, 14.7 mmol (2 mol% BIS); 1.613 g, 14.3 mmol (5 mol% BIS)), BIS (0.012 g, 0.075 mmol (0.5 mol% BIS); 0.046 g, 0.3 mmol (2 mol% BIS); 0.115 g, 0.75 mmol (5 mol% BIS)) and AAPH (0.25 mM for 1.7 mol% and 0.023 mM for 0.16 mol%) were used for the microgel preparation.
The preparation method aimed to obtain microgels of comparable size. The characterization of the actual particles is described in the Results.
For convenience, microgels prepared via the batch method are named b-MGx or batch-microgel and microgels prepared via the continuous monomer feeding approach are named f-MGx or feeding-microgel in the following, where x indicates the concentration of the crosslinker BIS in the microgel (0.5 mol%, 2 mol% or 5 mol%). In this series, all systems were prepared with 1.7 mol% initiator (AAPH). An additional sample with 0.16 mol% initiator is called b-MG0.5*. All concentrations were calculated from the component amount taken for the microgel preparation.
2.3 SANS
Small-angle neutron scattering (SANS) experiments were carried out on KWS-1,44,45 KWS-246,47 and KWS-348 instruments operated by the Jülich Centre for Neutron Science (JCNS) at the research reactor FRM II of the Heinz Maier-Leibnitz Zentrum (MLZ) in Garching, Germany. To probe a wide q-range, measurements were performed at sample-to-detector distances of 1.5, 8 and 20 m on KWS-1 (KWS-2) and 9.5 m on KWS-3 at wavelengths of 5 Å (Δλ/λ = 10%) and 12.8 Å (Δλ/λ = 20%), respectively. 1 mm Helma quartz cells were used. To probe the structure of the microgels below and above the VPTT, samples were thermostated at 20 and 50 °C on KWS-1 (KWS-2). On KWS-3, measurements were carried out in a temperature range of 20–50 °C. To achieve the best microgel–environment contrast, D2O was used as a solvent. For intensity calibration, empty cell and plexiglass were measured. For detailed information about the technical parameters of the instruments, see the corresponding references. Data treatment was performed with QtiKWS10 and SasView 4.1.2 software.2.4 NSE
In order to investigate the polymer dynamics, neutron spin-echo (NSE) experiments were carried out on a J-NSE49 “Phoenix” spectrometer operated by Jülich Centre for Neutron Science (JCNS) at the research reactor FRM II of the Heinz Maier-Leibnitz Zentrum (MLZ) in Garching, Germany. Measurements were performed in a q-range of 0.04–0.19 Å−1 at a wavelength of 8 Å probing Fourier times up to 40 ns. The samples were mounted in a thermostat-controlled sample environment at 20 °C. Helma quartz cells with a neutron pathway of 4 mm were used.2.5 DLS
For temperature-dependent dynamic light scattering (DLS) measurements, the microgel dispersions with a concentration of c = 0.1 mg mL−1 were measured using an LS instruments spectrometer equipped with a He–Ne laser (λ = 632.8 nm). Each autocorrelation function was measured for 45 s and temperatures between 20 and 50 °C were chosen. At each temperature, the scattering angle was varied between 30° and 100° in 5° steps. DLS data were fitted with a second-order cumulant.3 Results
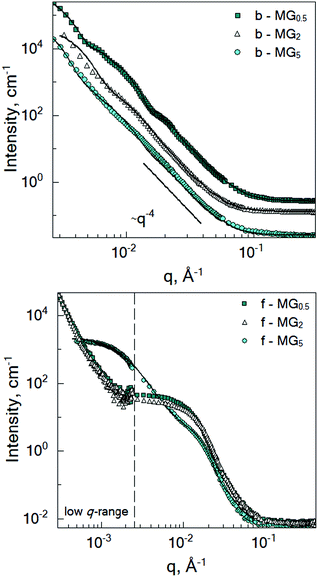
In order to investigate the influence of the amount of crosslinker (BIS) on the structure of microgels synthesised by the batch and feeding methods, small-angle neutron scattering experiments in a wide q-range (2 × 10−4–0.4 Å−1) at temperatures below and above the VPTT were performed.3.1 Structure of microgels below the VPTT
The microgel structure in the swollen state, according to Shibayama,31 was analysed in terms of the correlation length of the fluctuation and the frozen inhomogeneities, which become detectable below the VPTT, in our case at 20 °C. While the correlation length (ξ) and the frozen inhomogeneities (Ξ) characterize the crosslinker distribution within a microgel (Fig. 1), in the current work, the internal structure of the microgels was investigated based on the model first presented by Bastide and Leibler.50 The correlation length (ξ) corresponds to the thermal fluctuations of the polymer network and can be described with the Ornstein–Zernike function Ftherm(q) = Ioz/(1 + ξ2q2). The other length parameter Ξ is described with the Debye–Bueche function Ffroz(q) = Iinh/(1 + Ξ2q2)2 and corresponds to the characteristic size of the frozen inhomogeneities (or polymer islands, which do not swell). Hence, the fitting function of the scattering spectra of the microgels at 20 °C is: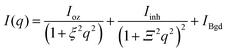 | (1) |
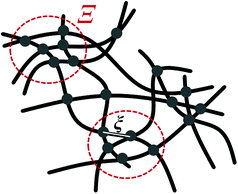 | ||
| Fig. 1 Internal microgel inhomogeneities with characteristic correlation lengths ξ and Ξ in the swollen state according to ref. 50. The dots represent inter-chain cross-links. Dashed-circles depict domains with frozen neighbour-junctions. | ||
| System | ξ, nm | Ξ, nm |
|---|---|---|
| b-MG0.5 | 3.5 | 170 |
| b-MG2 | 3.6 (0.6) | 86.6 (8.5) |
| b-MG5 | 3.6 | 82.6 |
| f-MG0.5 | 7.6 | 12.6 |
| f-MG2 | 8.7 | 19.8 |
| f-MG5 | 8.7 | 20.3 |
3.2 Structure of microgels above the VPTT
Fig. 3 shows the SANS curves of the collapsed batch- and feeding-microgels at 50 °C in D2O. The scattering signal of the batch-microgels measured above the VPTT significantly differs from the scattering signal of the feeding-microgels. Therefore, the model applied for the structural characterisation was modified according to the specifics of each microgel type (see below).While microgel b-MG5 possesses a rather monotonous decay of the scattering intensity with q, the scattering signal of the microgels with 0.5 and 2 mol% BIS (b-MG0.5 and b-MG2) shows more distinct features. Deviation of the experimental spectra from the Porod-like dependence is shown in Fig. S1 in the ESI.†
Initially, fuzzy-shell and core–shell models, which are often used for the characterization of systems similar to b-MGx,9,31,32 were applied, but no satisfying results were obtained, i.e., the fit curves do not describe the behaviour of the experimental curves in the whole q-range. Therefore, in the collapsed state, scattering spectra of the batch-microgels were fitted with a spheres-in-sphere (SiS) model:
| I(q, R, r) = I1P(q, R)S(q, R) + I2P(q, r)S(q, r) + IBgd | (2) |
where P(q, x) is the form factor of a sphere with a radius x (R – radius of microgel particle in first term, or r – radius of inner spherical object in second term), and IBgd takes into account the incoherent scattering. The scaling factors I1 and I2 allow us to estimate the number of small inner spherical objects per large particle, N*, accordingly to the procedure shown in the ESI.†
Due to the low concentration of polymer microgels in D2O, S(q, R) was taken as 1 (addition of the structure factor to the fit function does not influence the fit quality). Polydispersity of the particle radius was taken into account during the fitting procedure (values of 10–17% were obtained). Due to a low amount of spherical domains within one particle (see Discussion), the internal structure factor S(q, r) was taken as 1.
Fitting parameters, the hydrodynamic radii (RDLS) and the number (N*) of domains and their volume fraction within one particle (φ) are presented in Table 2. The volume fraction of the domains within the microgel particle was calculated as φ = N*r3/R3.
| System | C IN, mol% | R, nm | r, nm | R DLS, nm | N* | φ, % |
|---|---|---|---|---|---|---|
| b-MG0.5* | 0.16 | 113 | 40.6 | 121.6 | 2–6 | 9–28 |
| b-MG0.5 | 1.7 | 100 | 28.6 | 101 | 5–14 | 12–33 |
| b-MG2 | 1.7 | 93.9 | 21.7 | 94 | 4–11 | 5–14 |
| b-MG5 | 1.7 | 132.5 | 33.2 | 149 | 13–38 | 20–60 |
It should be noted that the chosen SiS model with the same size parameters also describes the b-MG0.5 SAXS curve, which due to better λ-resolutions of the method (in the restricted q-range) has even more pronounced features (see Fig. S2 in ESI†).
In the case of the batch-microgels, the core particle density seems to be so uncorrelated that no signatures of an internal structure factor contribution were detected, whereas for the feeding method, the structure factor plays an important role. Again, the whole microgel particle contains inhomogeneities made from the domains, but with a density of inhomogeneities such that the structure factor effects have to be considered. The second term of the fit function (eqn (2)) has to include contributions from the internal structure factor, which, according to Teixeira,51 can be written for randomly distributed domains with radius r′ organised in clusters as:
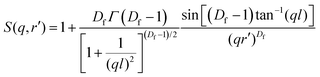 | (3) |
In the fitting procedure, a distribution of the particle size is necessary in order to damp the oscillations from the particle form factor of the sphere, thus a polydispersity factor of 0.29 was used. Parameters Df, l, and r′ were taken as free variables.
The fitting results are shown in Table 3.
| System | r′, nm | l, nm |
|---|---|---|
| f-MG0.5 | 15.8 | >400 |
| f-MG2 | 14.2 | >400 |
| f-MG5 | 12.5 | 47.1 |
3.3 Inter-microgel correlations
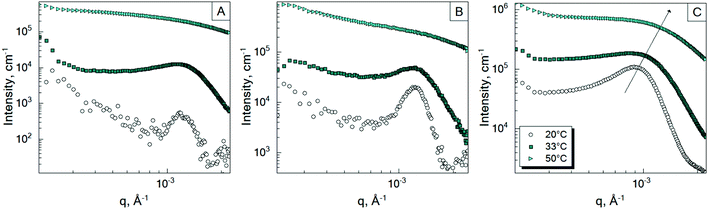
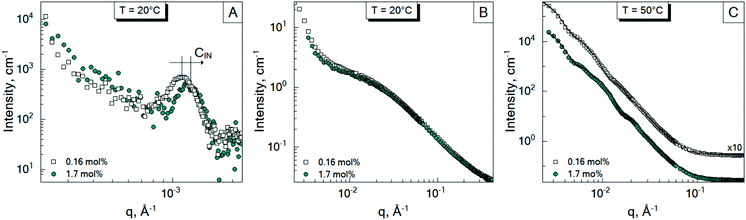
To investigate the inter-particle correlation in solution, a very small-angle neutron scattering (VSANS) experiment was performed in transmission geometry in a low q-range of 2 × 10−4–2.5 × 10−3 Å−1. Measurements were performed at temperatures from 20 °C to 50 °C. The scattering signal from the batch-microgels at 20 °C in this low q-range possesses clear peaks (Fig. 4), while the spectra of the feeding-microgels monotonously decrease as q increases, with exponent α (I(q) = Aq−α), which is 1.5, 1.9 and 2.5 for f-MG0.5, f-MG2 and f-MG5, respectively (see Fig. S4 in ESI†). An increase of α with the crosslinker concentration increase indicates the decrease of the number of polymer branching points and a softer and more flexible structure at lower CBIS (according to Hammouda,52α = 1.67 corresponds to the fully swollen chains and α = 3 corresponds to the clustered network).Fig. 4 represents selected scattering spectra of the systems of b-MGx at 20 °C, 33 °C and 50 °C. Spectra at 20 °C and 33 °C possess characteristic peaks that correspond to the inter-microgel distances. In the case of 5 mol% BIS, the peak position shifts to higher q with a higher temperature (Fig. 4C), whereas for systems with 0.5 and 2 mol% BIS, the position of these peaks, i.e., the distance between microgels, does not change with the temperature increase till 33.5 °C and vanishes from the presented q-range above the VPTT (Fig. 4A and B).
The position of each peak at 20 °C and values of a ∼ 2π/q*, which correspond to the inter-particle distances in real space, are listed in Table 4.
| System | C IN, mol% | q* × 10−3, nm−1 | a, nm | R DLS, nm |
|---|---|---|---|---|
| b-MG0.5* | 0.16 | 11 | 571.2 | 544.6 (22) |
| b-MG0.5 | 1.7 | 11.9 (1.8) | 528 | 265 |
| b-MG2 | 1.7 | 12.2 (1.3) | 515 | 313.4 |
| b-MG5 | 1.7 | 8.8 (2.3) | 714 | 350 |
The size of the microgels and the centre-to-centre distance (according to the obtained spectra in Fig. 4) decrease with increasing temperature more sharply for 0.5 and 2 mol% BIS, while for 5 mol% BIS, such a transition occurs within a broader temperature range. The different abilities of the b-MGx systems to change their size parameters are attributed to the topological constraints that are introduced into the polymer network, i.e., a lower crosslinking degree leads to a stronger polymer response to the temperature change close to the VPTT.53,54
3.4 Effect of initiator concentration
In Sections 3.1 and 3.2, the influence of the crosslinker concentration on the structural microgel parameters was presented. During the microgel synthesis, the initiator and crosslinker are commonly used. The initiator initiates the polymerisation reaction. Therefore, it was suggested that the amount of the initiator AAPH may also influence the internal structure of the microgels, i.e., the formation of the internal domains. In order to prove this, an additional experiment was performed. Since according to Fig. 3, the system b-MG0.5 has the most pronounced spectral features, it was chosen as a model system. Thus, microgels with 1.7 mol% and 0.16 mol% AAPH and 0.5 mol% BIS were prepared via batch precipitation polymerization and studied by means of SANS and VSANS at 20 °C and 50 °C.Fig. 5 represents the scattering spectra of both systems below (A and B) and above (C) the VPTT. It should be noted that the different amounts of the initiator do not influence significantly the scattering curves of microgels at 20 °C in the q-range of 0.01–0.4 Å−1 (Fig. 5B), i.e., the mesh size has the same value for both initiator concentrations. Whereas, at higher initiator concentration (CIN), the parameter a (corresponding to the peak position in Fig. 5A) is approximately two radii compared to the value obtained from DLS measurements for b-MG0.5, while for b-MG0.5*, a is comparable to the particle radius (see Table 2).
Fig. 5C represents the scattering spectra of b-MG0.5 and b-MG0.5* with 1.7 and 0.16 mol% AAPH, respectively, in the collapsed state. The parameters obtained in the fitting procedure according to the SiS model are listed in Table 2.
3.5 Internal dynamics
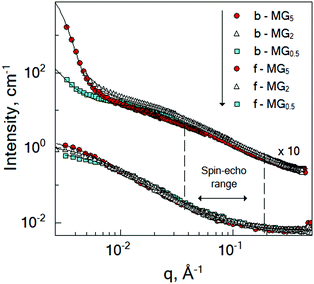
To probe the internal dynamics of the microgels in the swollen state, a neutron spin-echo (NSE) experiment was carried out at 20 °C. The microgel collapse at 50 °C causes the limitation of the free polymer chain motion. With initial dynamics investigations, the strong reduction of the coherent scattering intensity was observed (not presented here). This prevents the coverage of the wide q-range and makes the microgel dynamics investigation in the collapsed state not feasible. Normalized intermediate scattering functions (ISFs) of the microgels b-MG5 and f-MG5 measured in a q-range of 0.041–0.19 Å−1 at 20 °C are presented in Fig. 6.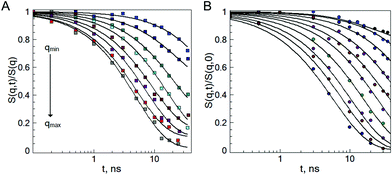 | ||
| Fig. 6 Normalized intermediate scattering function of the b-MG5 (A) and f-MG5 (B) microgels in the range qmin = 0.041 Å−1, qmax = 0.19 Å−1. Measurements were performed at 20 °C in D2O. Lines correspond to the fit with eqn (4). | ||
Earlier, Hellweg and co-authors10,11 showed that the NSE data of PNIPAM microgels with BIS concentrations of 1, 2 and 5% can be described by a single exponential function with two adjustable parameters (amplitude and relaxation rate). A decrease of the cooperative diffusion coefficient with the increase of the crosslinker concentration was observed. The application of this model to our systems does not give a good agreement with the experimental data over the whole q-range (for comparison of the different models to the experimental ISF, see the ESI†). Therefore, taking into account the presence of the static inhomogeneities obtained from SANS experiments, a model with a non-decaying component A(q)55–57 and a stretching exponent β = 0.85 was applied:
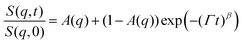 | (4) |
Plotting of the obtained relaxation rate divided by q2 as a function of q allows us to identify the different dynamic regimes and to estimate the diffusion coefficient of the microgels.
Fig. 7 shows that the diffusion coefficient Γ/q2 of the system b-MG5 fluctuates close to a constant value, while other systems have more complex behaviour, i.e., the relaxation rate Γ/q2 increases with increasing q; however, a clear single chain Zimm-dynamics was not observed either. Therefore, a single exponential function with β = 1 taking into account cooperative motions was applied only for the NSE-data of b-MG5. A cooperative diffusion coefficient Dc of (5.1 ± 0.1) × 10−11 m2 s−1 was found. A value for ξd of 3.4 nm was estimated using a pure solvent viscosity ηs(D2O, 20 °C) = 1.25 cP58 as ξd = kT/6πηsDc, where k is the Boltzmann constant, T is the temperature and ηs is the viscosity of the solvent. The value of ξd is in agreement with ξ from the SANS experiment.
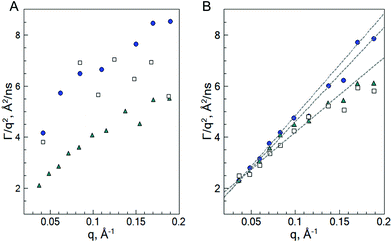 | ||
| Fig. 7 Γ/q2 as a function of q for the swollen (20 °C) b-MGx (A) and f-MGx (B) microgels with 5 mol% BIS (white squares), 2 mol% BIS (cyan triangles) and 0.5 mol% BIS (blue circles), according to the fit with eqn (4). Dashed lines indicate the deviation from the single dynamical regime. | ||
Taking into account the complex dependence of Γ/q2 on q for the microgels (except b-MG5) (see Fig. 7), we assume that a cooperative dynamics of the inner inhomogeneities influences the polymer chain dynamics, and therefore, for the characterisation of the dynamics behaviour of these systems, a full Zimm model was applied:29
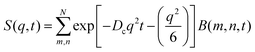 | (5) |
with a diffusion coefficient Dc and characteristic time
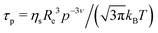 with the end-to-end distance of the polymer chain (set to the mesh size) Re and ν = 0.5.59 Thus, microgels were described with a single set of parameters with the full Zimm model including a diffusive contribution with Dc for the internal density fluctuations (the centre of mass diffusion of the whole particle is two orders of magnitude slower and does not contribute significantly in the present time window) and ηs as a second fit parameter. Since at the highest q, Γq2 levels slightly, i.e., the single chain dynamics becomes modified on a very local length scale, the diffusion coefficient was obtained from the medium q-range (see Fig. S6 in ESI†). The diffusion coefficient Dc and the solvent viscosity of each microgel sample obtained in the fit procedure are listed in Table 5.
with the end-to-end distance of the polymer chain (set to the mesh size) Re and ν = 0.5.59 Thus, microgels were described with a single set of parameters with the full Zimm model including a diffusive contribution with Dc for the internal density fluctuations (the centre of mass diffusion of the whole particle is two orders of magnitude slower and does not contribute significantly in the present time window) and ηs as a second fit parameter. Since at the highest q, Γq2 levels slightly, i.e., the single chain dynamics becomes modified on a very local length scale, the diffusion coefficient was obtained from the medium q-range (see Fig. S6 in ESI†). The diffusion coefficient Dc and the solvent viscosity of each microgel sample obtained in the fit procedure are listed in Table 5.
| Sample | η s, cP | D c, 10−11 m2 s−1 | D errc, 10−11 m2 s−1 |
|---|---|---|---|
| b-MG0.5 | 3.8 | 6.3 | (0.29) |
| b-MG2 | 3.2 | 2.8 | (0.15) |
| f-MG0.5 | 3.8 | 2.7 | (0.37) |
| f-MG2 | 4.6 | 2.3 | (0.54) |
| f-MG5 | 4.0 | 3.7 | (0.54) |
4 Discussion
Structure and dynamics investigation of PNIPAM based microgels showed the significant influence of the preparation process (i.e., crosslinker distribution within the microgels) and the amount of the crosslinker and initiator on the microgel features.4.1 Structural inhomogeneities below the VPTT
Addition of the crosslinker into the polymer solution, beside the formation of the polymer network, also leads to the formation of polymer network inhomogeneities. It was found that a continuous monomer feeding approach leads to microgels with a correlation length ξ of 7–9 nm in the swollen state, while microgels prepared via a batch method have ξ values of ∼4 nm. The obtained values correspond to the microgel mesh sizes reported in the literature.11,38,60 Thus, the polymers in the network of f-MGx are distributed more uniformly and behave like Gaussian chains in solution (exponents of the fractal Porod law of 1.5–2.5). The crosslinker in b-MGx is mostly localized in the core part of the particle. The f-MGx microgels do not have this crosslinker density gradient, but are more uniform in this respect. The length scale Ξ, which corresponds according to Shibayama31 to frozen inhomogeneities within a polymer network, indicates thus the characteristic size of the internal domains and increases with the increasing crosslinker concentration (12.6 nm at 0.5 mol% BIS and ∼20 nm at 2 and 5 mol% BIS). For batch-microgels, Ξ is much larger. They posses the opposite tendency: an increase of the BIS concentration leads to a decrease of the domain size Ξ (this relation is retained also above the VPTT, see below).It is interesting to note that a variation of the initiator concentration does not influence the mesh size of the microgels, but a decrease of the CIN by a factor of 10 leads to bigger microgels (544 nm vs. 265 nm). Moreover, the microgel b-MG0.5 with a higher initiator concentration has an inter-particle distance (a) that is approximately two particle radii compared to RDLS, while for the system b-MG0.5*, this parameter is comparable to the particle radius. We assume that a lower initiator concentration leads to the formation of softer microgels, which interpenetrate with each other. This penetration effect was also observed by Mohanty and co-authors.6 The authors showed that the averaged centre-to-centre distance of the microgels can be smaller than the initial unperturbed particle diameter due to their ability to interpenetrate.
At higher initiator concentration, the centre-to-centre distance a is close to 2RDLS, which means the microgels behave like hard spheres and only small interpenetration (few nanometres) or compression (both processes are possible) of the dangling ends occurs (2RDLS is slightly bigger than a). Our systems have much smaller concentrations than that reported in ref. 6; nevertheless, a similar behaviour is observed. Such similarities could be explained by the presence of aggregates in the microgel solution in the swollen state, in which microgels behave like a high density dispersion.
4.2 The sub-domain structure above the VPTT
An increase of the temperature above the VPTT leads to the collapse of the microgels, while the domain-like internal structure is retained.Since the initial application of the well-known models (core–shell and fuzzy-shell), which were reported in the literature, does not describe the experimental spectrum, the SiS model was applied to the batch-microgels at 50 °C.
The SiS model considers two possible explanations: (i) microgels with two different radii r and R coexist simultaneously, and (ii) microgels with radius R consist of smaller spherical domains with radius r. To find the right model, DLS measurements were performed. It was shown that all systems have only one relaxation mode corresponding to the hydrodynamic radius, whose value is close to the larger radius R in the SiS model. Thus, we conclude that microgels with radius R consist of smaller spherical domains with characteristic size r.
All spectra of b-MGx were analysed according to the SiS model with the assumption that independent of the crosslinker concentration, the internal part of the microgel particle has a domain-like structure. The latter can be clearly seen at the lowest BIS concentration, while an increase of the BIS amount may lead to a denser inner part of the particle and domains become less distinguishable in the SANS experiment. To our knowledge, such behaviour of the SANS spectrum (especially for 0.5 mol% BIS) was not detected earlier. For this point, there could be several reasons. According to Ikkai,61 the relation of the outer particle size to the domain size plays an important role in the ability of phase separation within one particle; the bigger the difference in sizes, the clearer the phase separation, i.e., domains become detectable. The other reason is a scattering contrast, i.e., the difference in scattering length density between the domain and surroundings. Here, the scattering from the microgel surface becomes more dominant (spectrum of b-MG5 exhibits Porod-like decay (see Fig. S1 in ESI†)) and domains that intersect or interpenetrate each other become indistinguishable in the SANS experiment.
Previously reported averaged polymer segment distributions within the core part of the core–shell PNIPAM microgels were also disputed by Matsui.62 Here, the authors showed that PNIPAM-based microgels may not always exhibit a uniform surface and may transform into an inhomogeneous raspberry-like structure upon heating. The formation of the internal domains (several tens of nanometres in size) was observed during the particle collapse. In ref. 63, with GISANS, a domain-like internal structure of the adsorbed PNIPAM microgels was shown. Very recently, the presence of higher crosslink density clusters within a PNIPAM microgel was shown in real space using high resolution fluorescence microscopy and dye tagging.64,65 Thus, according to these results, we conclude that domains remain at 50 °C even at higher crosslinker concentration. Moreover, the estimation of the domain number within one particle also confirms this assumption. From the relation of the scaling components I1 and I2 in eqn (2), where Ii = ϕiVi(Δρi)2 (ϕi is a volume concentration of the microgels with a volume Vi in the system volume V), the number of spherical domains (N*) of radius r inside the sphere of radius R was estimated (for details of the calculation, see the ESI†).
While the volume fraction of the domains ϕ of the batch-microgels with 0.5 mol% and 2 mol% BIS (<30%, see Table 2) is much smaller than it would be in the case of the dense packing of spherical objects, where the highest volume fraction is 74%,66 structure factor, i.e., domain–domain interaction, is negligible in contrast to the feeding-microgels. This means that for batch-microgels, no structure factor influence of the internal domains could be detected with SANS, in contrast to the feeding approach with its much higher internal domain density.
f-MGx microgels have a higher density of inhomogeneities requiring us to consider a structure factor contribution in the collapsed state. A higher BIS concentration leads to the formation of a rough fractal surface with an internal sub-domain structure, i.e., clusters consisting of domains of a radius of 12–15 nm are observed. The first term in eqn (2) can be neglected because of the size of the microgels and the influence of the structure factor contributions from eqn (3). From the very low q-region of the VSANS experiments, an agglomeration of microgels was visible, resulting in the large value of the fractal cut-off length l of the fractal structures and making it impossible to discern single large microgels.
According to the fit of f-MG5 at 50 °C, a fractal structure with the fractal dimension of 3.2 is formed. Small domains with radius (12.50 ± 0.01) nm (corresponding to inner domains with radius r of the b-MGx) build fractal-like clusters with a characteristic size of (47.1 ± 0.1) nm. This organization is similar to the batch-microgels, i.e., after the deswelling process, dense spherical islands are formed even by continuous monomer incorporation.
In the case of the lower crosslinker amount (0.5 mol% and 2 mol% BIS), a step-like scattering signal was obtained. Due to the difference in the size of the scattering objects (Guinier analysis) and the slope of the linear range, we conclude that the systems f-MG0.5 and f-MG2 have similar structures and can be characterized by a fractal-like structure with size >0.4 μm. In turn, these objects consist of smaller domains with a characteristic size of 15.8 nm (0.5 mol% BIS) and 14.2 nm (2 mol% BIS). The obtained scattering exponents are higher than 4. The same tendency was previously reported in ref. 13 and 53 and seems to indicate a dominant importance of the surface roughness in the probed q-range.67
Interestingly, parameters of the system f-MG2 in the swollen state are approx. equal to the parameters of f-MG5 (Table 3), while in the collapsed state, scattering curves, i.e., the characteristic parameters, of f-MG2 become identical to f-MG0.5 (Table 1).
It was shown that an increase of the initiator concentration changes the number of internal domains within a particle (Table 2). A higher CBIS leads to a denser packing of the particles and a decrease of the contrast between in- and out-domain regions. Thus, domains become difficult to distinguish (features of the SANS curves become less pronounced).
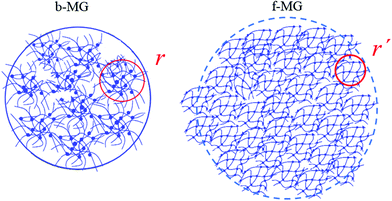 | ||
| Fig. 8 Microgel internal structure visualization. In the collapsed state, the sub-domain structure of the microgel becomes directly visible. | ||
With these results, we conclude that all microgels (prepared via batch and feeding methods) have an internal inhomogeneous structure below and above VPTT, while the parameters and distribution of such domains strongly depend on the preparation process (how crosslinker was introduced into the system) and the crosslinker and initiator concentration.
4.3 Polymer chain dynamics
Investigation by means of neutron spin-echo spectroscopy reveals that the domain-like internal structure of the microgels and the internal inhomogeneities due to the incorporated crosslinks significantly influence polymer dynamics. It should be noted that independent of the synthesis route and the crosslinker concentration, the clear Zimm-type dynamics was not observed.The b-MG5 microgel differs from the other investigated systems and Γ/q2 fluctuates around a constant value in the entire q-range, i.e., due to the dense polymer and crosslinker distribution in the core region of the microgels, cooperative network dynamics dominates. The same behaviour remains at a further CBIS increase (10 mol% BIS42) and is in agreement with previous investigations of PNIPAM systems with 5 mol% BIS.10 Diffusion like density fluctuations dominate here.
In turn, the other microgels possess more complex dynamic behaviour. It was found that in the low q-range, the dynamics deviates from single-chain motion. Only the batch-microgels with 0.5 mol% BIS possess Zimm-like dynamics over the q-range of the investigation. The same behaviour was previously reported for 0.26 mol% BIS in a PNIPAM gel.12 The low crosslinker amount and a continuous monomer feeding approach lead to the formation of the fluffy polymer structure, where single chain motion can be observed. Nevertheless, a non-homogeneous polymer distribution and the presence of the thermal and the frozen fluctuations (from SANS experiments) alter the polymer chain dynamics and their influence becomes non-negligible. Due to the non-monotonous increase of the relaxation rate in the presented q-range, a superposition of the different dynamics-types is assumed, i.e., independent of the internal crosslinker distribution, cooperative motion affects the single-chain dynamics in the presented q-range.
From the analysis with the full Zimm model, cooperative diffusion coefficients of (2.8–6.3) × 10−11 m2 s−1 for the batch-microgel and of (2.3–3.7) × 10−11 m2 s−1 for the feeding-microgels were obtained. The presence of a polymer network with a crowded environment leads to the increase of the solution viscosity compared to the viscosity of D2O (3.2–4.6 cP for microgels vs. 1.25 cP for heavy water). This tendency is in agreement with previous NSE investigations of microgels.29,42,56,68 At the highest q (0.17–0.19 Å−1), deviations from the Zimm model are obtained, whose origin is not yet clear, but seems to be rather diffusive-like. Here, we should note that due to the complex dynamics behaviour, further investigations in a higher q-range are necessary.
5 Conclusions
In the present work, the influence of the crosslinker distribution, i.e., synthesis (batch and feeding approaches), on the internal structure and dynamics of PNIPAM microgels was studied by means of dynamic light scattering, small-angle neutron scattering in a wide q-range and neutron spin-echo spectroscopy.The presence of an inhomogeneous polymer distribution within the microgel below VPTT was found for batch- as well as for feeding-microgels. However, the difference in the correlation lengths Ξ and ξ in the case of the feeding microgels is much lower than for the batch microgels, which indicates a more homogeneous internal structure of f-MGs compared to b-MGs. The changing of the crosslinker concentration influences the internal correlation parameter in different manners for batch- and feeding-microgels: with the increase of crosslinker concentration, Ξ increases in the case of f-MG systems and decreases in the case of b-MG systems. In turn, variation of the concentration of the initiator AAPH does not influence the correlation length ξ of the b-MG0.5 system at a constant crosslinker amount.
SANS measurements were used to improve the understanding of the inner microgel structure in the collapsed state. The presence of the internal domains inside the individual microgels even at 50 °C has been shown. An influence of the crosslinker and the initiator concentration on the internal structure of the microgels above VPTT was obtained. Namely, an increase of the initial crosslinker concentration leads to an increase of the internal domain size of b-MGx. The concentration of the initiator influences the fluffiness of the microgel and the internal domains. Moreover, an inhomogeneous distribution of the polymer segments above the VPTT with a fractal-like structure was also found for the microgels prepared via the continuous monomer feeding approach.
The influence of the crosslinker distribution and its initial concentration within one microgel on the dynamical properties of the microgels was observed. While for microgels prepared via the feeding approach, a segmental dynamics contributes for all crosslinker concentrations, Zimm dynamics was not found even at the lowest crosslinker amount of feeding-microgel, where it was expected. The higher crosslinker concentration in the case of microgels prepared via the batch method leads to a denser network and the cooperative dynamics dominates. Polymer interaction with the surrounding environment leads to an increase of the solution viscosity (compared to D2O viscosity) for all systems.
It was shown that microgels possess an inhomogeneous domain-like internal structure, which is preserved even above the VPTT. Different preparation procedures had a remarkable influence on the internal structure, and leave an imprint on the resulting segmental chain dynamics and density fluctuations. The feeding approach leads to a more homogeneous crosslinker distribution with larger correlation length ξ, but significantly smaller frozen inhomogeneity Ξ (below the VPTT) or smaller r (above the VPTT) compared to the batch microgels. Moreover, internal structural parameters strongly depend on the method of synthesis and the initial crosslinker concentration. The found inhomogeneities within the PNIPAM microgels give a detailed insight into the internal structure and dynamics of the microgels. Further investigations of the batch- and feeding-microgels with a more controlled variation of the synthesis components (series of initiator variation) are of high importance for further developments and knowledge driven design of smart thermo-responsive materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG) [Grants HO 5488/2-1 and WE 5066/3-1]. T. K., J. W. and S. W. thank JCNS and MLZ for the beam time and support to perform the neutron scattering measurements.Notes and references
- D. Suzuki, Y. Nagase, T. Kureha and T. Sato, J. Phys. Chem., 2014, 118, 2194–2204 CrossRef CAS PubMed.
- M. F. Schulte, A. Scotti, A. P. H. Gelissen, W. Richtering and A. Mourran, Langmuir, 2018, 34, 4150–4158 CrossRef CAS PubMed.
- A. Suzuki and T. Tanaka, Nature, 1990, 346, 345–347 CrossRef CAS.
- S.-k. Ahn, R. M. Kasi, S.-c. Kim and Y. Zhou, Soft Matter, 2008, 4, 1151–1157 RSC.
- W. Hong, X. Zhao and Z. Suo, J. Mech. Phys. Solids, 2010, 58, 558–577 CrossRef CAS.
- P. S. Mohanty, S. Nöjd, K. V. Gruijthuijsen, J. J. Crassous, M. Obiols-Rabasa, R. Schweins, A. Stradner and P. Schurtenberger, Sci. Rep., 2017, 7, 1487 CrossRef PubMed.
- B.-J. Niebuur, K.-L. Claude, S. Pinzek, C. Cariker, K. N. Raftopoulos, V. Pipich, M.-S. Appavou, A. Schulte and C. M. Papadakis, ACS Macro Lett., 2017, 6, 1180–1185 CrossRef CAS.
- D. Richter, M. Monkenbusch, A. Arbe and J. Colmenero, Adv. Polym. Sci., 2005, 174, 1–221 Search PubMed.
- S. Höfl, L. Zitzler, T. Hellweg, S. Herminghaus and F. Mugele, Polymer, 2007, 48, 245–254 CrossRef.
- T. Hellweg, K. Kratz, S. Pouget and W. Eimer, Colloids Surf., A, 2002, 202, 223–232 CrossRef CAS.
- M. Karg, S. Prévost, A. Brandt, D. Wallacher, R. von Klitzing and T. Hellweg, Prog. Colloid Polym. Sci., 2013, 140, 63–76 CAS.
- S. Koizumi, M. Monkenbusch, D. Richter and D. Schwahn, J. Chem. Phys., 2004, 121, 12721–12731 CrossRef CAS PubMed.
- A. Fernandez-Barbero, A. Fernandez-Nieves, I. Grillo and E. Lopez-Cabarcos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051803 CrossRef CAS PubMed.
- A. Meier-Koll, V. Pipich, P. Busch, C. M. Papadakis and P. Müller-Buschbaum, Langmuir, 2012, 28, 8791–8798 CrossRef CAS PubMed.
- M. Heskins and J. E. Guillet, J. Macromol. Sci., Part A: Pure Appl. Chem., 1968, 2, 1441–1455 CrossRef CAS.
- X. Wu, R. H. Pelton, A. E. Hamielec, D. R. Woods and W. Mcphee, Colloid Polym. Sci., 1994, 272, 467–468 CrossRef CAS.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- B. R. Saunders, Langmuir, 2004, 20, 3925–3932 CrossRef CAS PubMed.
- M. R. Islam and M. J. Serpe, Chem. Commun., 2013, 49, 2646–2648 RSC.
- Y. Liu, Y. Zhang and Y. Guan, Chem. Commun., 2009, 1867–1869 RSC.
- M. U. Witt, S. Hinrichs, N. Mo, S. Backes, B. Fischer and R. von Klitzing, J. Phys. Chem. B, 2019, 123, 2405–2413 CrossRef CAS PubMed.
- R. Acciaro, T. Gil and I. Varga, Langmuir, 2011, 27, 7917–7925 CrossRef CAS PubMed.
- M. Wei, Y. Gao, X. Li and M. J. Serpe, Polym. Chem., 2017, 8, 127–143 RSC.
- S. Seiffert, Macromol. Rapid Commun., 2012, 33(13), 1135–1142 CrossRef CAS PubMed.
- T. Still, K. Chen, A. M. Alsayed, K. B. Aptowicz and A. G. Yodh, J. Colloid Interface Sci., 2013, 405, 96–102 CrossRef CAS PubMed.
- H. Wolff, M. Kather, H. Breisig, W. Richtering, A. Pich and M. Wessling, ACS Appl. Mater. Interfaces, 2018, 10, 24799–24806 CrossRef CAS PubMed.
- M. Brugnoni, A. Scotti, A. A. Rudov, A. P. H. Gelissen, T. Caumanns, A. Radulescu, T. Eckert, A. Pich, I. I. Potemkin and W. Richtering, Macromolecules, 2018, 51, 2662–2671 CrossRef CAS.
- M. Karg and T. Hellweg, Curr. Opin. Colloid Interface Sci., 2009, 14, 438–450 CrossRef CAS.
- S. Maccarrone, C. Scherzinger, O. Holderer, P. Lindner, M. Sharp, W. Richtering and D. Richter, Macromolecules, 2014, 47, 5982–5988 CrossRef CAS.
- K. Kyriakos, M. Philipp, L. Silvi, W. Lohstroh, W. Petry, P. Müller-Buschbaum and C. M. Papadakis, J. Phys. Chem., 2016, 120, 4679–4688 CrossRef CAS PubMed.
- M. Shibayama, Polym. J., 2010, 43, 18–34 CrossRef.
- U. Gasser, J. S. Hyatt, J. J. Lietor-Santos, E. S. Herman, L. A. Lyon and A. Fernandez-Nieves, J. Chem. Phys., 2014, 141, 034901 CrossRef CAS PubMed.
- M. Dulle, S. Jaber, S. Rosenfeldt, A. Radulescu, S. Fo, P. Mulvaney and M. Karg, Phys. Chem. Chem. Phys., 2014, 17, 1354–1367 RSC.
- A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Nat. Commun., 2019, 10, 1418 CrossRef CAS PubMed.
- M. Keerl, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2009, 131, 3093–3097 CrossRef CAS PubMed.
- S. Wellert, A. Radulescu, A. Carl, R. V. Klitzing and K. Gawlitza, Macromolecules, 2015, 48, 4901–4909 CrossRef CAS.
- A. Papagiannopoulos, J. Zhao, G. Zhang and S. Pispas, Eur. Polym. J., 2014, 56, 59–68 CrossRef CAS.
- Y. Hertle, M. Zeiser, P. Fouquet, M. Maccarini and T. Hellweg, Z. Phys. Chem., 2014, 228, 1053–1075 CAS.
- W. Su, K. Zhao, J. Wei and T. Ngai, Soft Matter, 2014, 10, 8711–8723 RSC.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- M. Füllbrandt, R. von Klitzing and A. Schönhals, Soft Matter, 2013, 9, 4464–4471 RSC.
- J. Witte, T. Kyrey, J. Lutzki, A. M. Dahl, J. Houston, A. Radulescu, V. Pipich, L. Stingaciu, M. Kühnhammer, M. U. Witt, R. von Klitzing, O. Holderer and S. Wellert, Soft Matter, 2019, 15, 1053–1064 RSC.
- R. Pelton and P. Chibante, Colloids Surf., 1986, 20, 247–256 CrossRef CAS.
- A. V. Feoktystov, H. Frielinghaus, Z. Di, S. Jaksch, H. Kleines, A. Ioffe and D. Richter, J. Appl. Crystallogr., 2015, 48, 61–70 CrossRef CAS.
- H. M.-L. Zentrum, Journal of Large-scale Research Facilities, 2015, 1, A28 CrossRef.
- H. M.-L. Zentrum, Journal of Large-scale Research Facilities, 2015, 1, A29 CrossRef.
- A. Radulescu, V. Pipich, H. Frielinghaus and M.-S. Appavou, J. Phys.: Conf. Ser., 2012, 351, 012026 CrossRef.
- H. M.-L. Zentrum, Journal of Large-scale Research Facilities, 2015, 1, A31 CrossRef.
- S. Pasini, O. Holderer, T. Kozielewski, D. Richter and M. Monkenbusch, Rev. Sci. Instrum., 2019, 90, 043107 CrossRef CAS PubMed.
- J. Bastide and L. Leibler, Macromolecules, 1988, 21, 2647–2649 CrossRef CAS.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
- B. Hammouda, Probing nanoscale structures – the SANS toolbox, 2009, https://www.ncnr.nist.gov/staff/hammouda/the_SANS_toolbox.pdf.
- K. Kratz, T. Hellweg and W. Eimer, Polymer, 2001, 42, 6631–6639 CrossRef CAS.
- S. M. Hashmi and E. R. Dufresne, Soft Matter, 2009, 5, 3682–3688 RSC.
- A. Campanella, O. Holderer and K. N. Raftopoulos, Soft Matter, 2016, 12, 3214–3225 RSC.
- C. Scherzinger, O. Holderer, D. Richter and W. Richtering, Phys. Chem. Chem. Phys., 2012, 14, 2762–2768 RSC.
- A. M. Al-Baradi, S. Rimmer, S. R. Carter, J. P. de Silva, S. M. King, M. Maccarini, B. Farago, L. Noirez and M. Geoghegan, Soft Matter, 2018, 14, 1482–1491 RSC.
- G. Ulrych, Properties of liquid heavy water, http://hedhme.com/content_map/?link_id=22146article_id=532.
- B. Ewen, M. Mours, D. Richter, T. Shiga and H. Winter, Neutron spin echo spectroscopy. Viscoelasticity rheology, Springer-Verlag Berlin Heidelberg, 1997, pp. 1–248 Search PubMed.
- A. Habicht, W. Schmolke, G. Goerigk, F. Lange, K. Saalwächter, M. Ballauff and S. Seiffert, J. Polym. Sci., Part B: Polym. Phys., 2015, 53, 1112–1122 CrossRef CAS.
- F. Ikkai and M. Shibayama, Polymer, 2007, 48, 2387–2394 CrossRef CAS.
- S. Matsui, Y. Nishizawa, T. Uchihashi and D. Suzuki, ACS Omega, 2018, 3, 10836–10842 CrossRef CAS.
- T. Kyrey, J. Witte, V. Pipich, A. Feoktystov, A. Koutsioubas, E. Vezhlev, H. Frielinghaus, R. von Klitzing, S. Wellert and O. Holderer, Polymer, 2019, 169, 29–35 CrossRef CAS.
- E. Siemes, O. Nevskyi, D. Sysoiev, S. K. Turnhoff, A. Oppermann, T. Huhn, W. Richtering and D. Wöll, Angew. Chem., Int. Ed., 2018, 57, 12280–12284 CrossRef CAS PubMed.
- A. A. Karanastasis, Y. Zhang, G. S. Kenath, M. D. Lessard, J. Bewersdorf and C. K. Ullal, Mater. Horiz., 2018, 5, 1130–1136 RSC.
- D. A. Weitz, Science, 2004, 303, 968–969 CrossRef CAS PubMed.
- P. Wong, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 7417–7424 CrossRef CAS PubMed.
- K. Gawlitza, O. Ivanova, A. Radulescu, O. Holderer, R. von Klitzing and S. Wellert, Macromolecules, 2015, 48, 5807–5815 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01161g |
| This journal is © The Royal Society of Chemistry 2019 |