Using cavitation rheology to understand dipeptide-based low molecular weight gels

Abstract

The study of dipeptide-based hydrogels has been the focus of significant effort recently due to their potential for use in a variety of biomedical and biotechnological applications. It is essential to study the mechanical properties in order to fully characterise and understand this type of soft materials. In terms of mechanical properties, the linear elastic modulus is normally measured using traditional shear rheometry. This technique requires millilitre sample volumes, which can be difficult when only small amounts of gel are available, and can present difficulties when loading the sample into the machine. Here, we describe the use of cavitation rheology, an easy and efficient technique, to characterise the linear elastic modulus of a range of hydrogels. Unlike traditional shear rheometry, this technique can be used on hydrogels in their native environment, and small sample volumes are required. We describe our set-up and show how it can be used to probe and understand different types of gels. Gels can be formed by different triggers from the same gelator and this leads to different microstructures. We show that the data from the cavitational rheometer correlates with the underlying microstructure in the gels, which allows a greater degree of understanding of the gels than can be obtained from the bulk measurements.

---

Introduction

Low molecular weight gels are an attractive class of materials that are receiving significant attention. These gels result from the self-assembly of small molecules, called low molecular weight gelators (LMWG), into fibres.^1–4 The assembly process involves the cross-linking of the fibres to form a 3D network. This network is held by non-covalent interactions making these materials reversible. Hence, application of an external stimulus can result in the reverse gel-to-sol transition. LMWGs have been examined for a wide range of different potential applications including regenerative medicine,⁵ electronic devices,⁵ cell culture,⁶ and pollutant removal from environment.⁷

To understand the gels formed from LMWG, we need to understand the self-assembly process.^8–12 Depending on the final application, different mechanical properties are needed. It is possible to tune the final mechanical properties of low molecular weight gels, for example by controlling the volume fraction of the solvent and the temperature cycle used.¹³ It is crucial to fully characterise the mechanical properties to evaluate the applicability of these soft materials. Shear rheometry is one the most frequently used techniques to define the mechanical properties of complex fluids. This technique allows us to correlate the linear viscoelastic properties (LVE) of materials with their molecular structures and dynamics.¹⁴ Despite the usefulness of this technique, there are some limitations including the high cost of the instrument, potential difficulties loading the sample in the rheometer, evaporation issues¹⁵ and the sample volume required for measurements¹⁶ (on the order of millilitres). Sample volume is crucial when using soft biological systems, as they normally are available only in small quantities.¹⁷ Microrheology, “rheology on the micrometre length scale”, is one approach that attempts to overcome some of the limitations of the bulk rheology. It involves using microscopic probe particles to measure the mechanical properties on very small volumes (on the order of micro-litres).¹⁸ One of the main advantages of this approach is that it is a local probe, so can be used in heterogeneous systems where bulk rheology just gives an average distribution.¹⁷ However, it is necessary to add probe particles which may cause changes in the local microstructure being measured, and further only very soft materials can be measured.

As an alternative approach, Zimberlin et al.¹⁹ developed a new method, cavitation rheology, based on the cavitation phenomenon. This technique consists of growing an air bubble within a material and monitoring the maximum pressure, the critical pressure, P_c, that the material can stand before the material fails via the cavitation phenomenon.^19–36 The cavitation event can either be elastic or lead to fracture in the material.³⁰ This method has the advantage of being able to be conducted on gels of any shape in their native environment, whilst shear rheology requires precise isolated samples prepared in specific shapes and containers to be placed onto or into the rheometer.³⁷ It should be possible to use this on small volumes of material, although there will of course be a minimum volume before confinement effects become important. The maximum pressure the cavity can withstand corresponds to the elastic instability limit of the material, which can be related to the elastic modulus.¹⁹ This technique has been used for measuring the quantitative elastic properties of biological tissue in situ,²¹ and the results emphasise the differences in the elastic moduli before and after removal from the host.²¹

However, the lack of understanding of the relationship between the material properties obtained from shear and cavitation rheology leads to a restriction of its use in gels laboratories, particularly when comparing the gel modulus.³⁸ Zimberlin et al.³⁷ obtained the cavitation modulus, E_c, by modelling the gel as a neo-Hookean solid by using the equation²²

P_c = 5/6 E_c + 2γ/r

where γ is the surface tension of the solvent and r is the needle radius. Cavitation modulus derived from this model will depend on the mechanical properties of the material.¹⁹ Both the surface tension of the material and the needle radius will determine the critical pressure and, therefore, the cavitation modulus. Pavlovsky and co-workers used a correction factor to compare both shear and cavitation moduli, although they examined solutions and not gels.³⁹ Other researchers have looked at the correlation between modulus obtained from shear and cavitation rheology in a number of organogels.^26,27 Their results show cavitation moduli were always an order of magnitude greater than shear moduli. Bentz et al. reported recently a quantitative relationship, k_sc, between the gel modulus determined using shear and cavitation rheology for a series of model polymer gels.³⁸ This quantitative constant can be used to interconvert between shear storage (G′) and cavitation (E_c) modulus.

In this work, we examine the quantitative relationship between the shear storage modulus and cavitation modulus for a gelatine gel and gels formed from two different dipeptide low molecular weight gelators. We first describe an improved cavitation rheometer, validate this on model systems and then use our cavitation rheometer to understand and characterise dipeptide-based low molecular weight gels. Gels formed from the same gelator using different triggers results in different underlying microstructure. These differences directly translate into differences that can be determined using a combination of cavitation and bulk rheometry.

Results and discussion

Our cavitation rheology instrument was assembled following the description of Zimberlin et al.¹⁹ to quantify the pressure dynamics of a cavity within a soft material (Fig. 1). It includes a 10 mL Hamilton™ 1000 series Gastight syringe for air pumping mounted in a syringe pump (World Precision Instruments AL-1000). A high precision manometer (the Cavitation Rheology Analyser Box, or CRAB) with data logging capability was custom-built to control and record the pressure. A digital manometer was connected into the system via Y-junction and used to calibrate and double confirm pressure readings from the CRAB. The setup of the cavitation rheometer is fully described in the ESI† (Section II).

Fig. 1 (a) Experimental setup of our cavitation rheometer including all components: syringe pump (top right), a digital manometer (bottom right) and the sample (left); the left inset shows the needle inserted into the sample. (b) Diagram of experimental setup. (c) Experimental data for a cavitation example, where the maximum pressure recorded over time gives the critical pressure, P_c.

In a typical experiment, a needle was inserted into the sample, the syringe pump was turned on and a bubble started to grow within the material. The increase of pressure was then recorded by the CRAB, which digitises the signal from the system and translates it into pressure values. The maximum pressure recorded during the experiment is known as critical pressure, P_c (see experimental example in Fig. 1c). The experiment was finished after a drop in the pressure was recorded.

The depth at which the needle is inserted in the sample is critical for modulus measurement. There is an increase of the critical pressure as a function of the depth at which the needle is inserted within the material (Fig. S1, ESI†). Regarding this increase in P_c with depth, in experiments with water and glycerol mixtures, we found that the increase of needle immersion leads to a proportional increase in maximum bubble pressure as expected from increasing hydrostatic pressure with increasing depth (Fig. S2, ESI†). The proportionality constant relating the measured pressure to the calculated hydrostatic pressure for the liquid mixture under examination at a given depth was found to be ρg (ρ being the density, g the gravitational acceleration), in excellent agreement with the hydrostatic pressure equation (p = ρgh).

Given the need to control the needle immersion depth, a conductivity probe was designed in order to detect the contact of the needle tip with the sample surface (additional information is described in the ESI,† Section II.1.2.2.2.) and control axis movement of an Ormerod model 1 3D printer, which allows the precise positioning of the needle below the sample surface. A depth immersion of 1 mm is used throughout. The CRAB has a limited pressure operation and, as the pressure increases with depth immersion, using a small depth allows us to examine the greatest range of concentrations for each gelator. Three different samples are measured in all cases to ensure reproducibility and the needle is positioned in the middle of each sample to ensure any artefact is blocking or restricting the bubble growth.

Initially, gelatine gels were selected to validate our cavitation technique. P_c, using cavitation rheology (Fig. S3, ESI†), and G′, using shear rheology (Fig. S4, ESI†), were collected at different concentrations. Gelatine gels showed a frequency-independent behaviour and the storage moduli increased with concentration (Fig. S4, ESI†). Similarly, the critical pressure increased with concentration (Fig. S3, ESI†). Both shear and cavitation modulus showed a similar trend when compared at different concentrations (Fig. 2a), where values of both moduli increased with concentration. The cavitation moduli are an order of magnitude greater than shear moduli (Fig. 2a). There is an excellent correlation between both moduli (Fig. 2b), with a R² of 0.99. The value of the proportionality constant, k_sc, is 18.93 ± 0.53.

Fig. 2 (a) Storage shear moduli (black data) and cavitation moduli (purple data) as a function of concentration for gelatine gels. (b) Storage shear moduli against cavitation moduli for gelatine gels (R² = 0.99).

Next, PVA gels were selected in order to both further validate our technique and also to compare to the original work of Zimberlin et al.¹⁹ Gels are formed by the cross-linking of the PVA with borax.⁴⁰ These gels evolve with time, so in this experiment a series of samples were prepared and analysed at different times and measured just once. Both critical pressure and shear rheology modulus were measured as a function of time, t = 0 represents the time at which the solution of PVA was first synthesised.

PVA gels were frequency independent (Fig. S5, ESI†) and reproducible. The critical pressures also showed good reproducibility (Fig. S6, ESI†). A gel is not formed immediately; gelation takes some time. This can be seen from both the cavitation and shear rheology, where it takes around six days before a significant increase in either P_c or G′ is recorded (Fig. 3a). This is in agreement with the work of Zimberlin et al.¹⁹ From tan δ (G′′/G′, Fig. 3b), a gel has not formed until t = 6 days, from which point tan δ remains essentially constant. The pressure values collected before t = 6 days are linked to those of a viscous solution. Over time, physical cross-links occur in the polymer network, and a gradual increase in shear storage moduli is observed using shear rheology (Fig. 3a). However, that is not the case for data collected with the cavitation rheometer. The critical pressure increases up to t = 15 days broadly in line with the shear rheology data. However, after this time, the local pressure drops (Fig. 3a). We highlight here that the two techniques probe different length scales; shear rheology measures the elastic moduli of a bulk sample, while cavitation rheology quantifies a local point within the material. As such, we hypothesise that the underlying microstructure of the PVA gels starts to change after a certain time, which will just affect a local point in the material but will not affect the bulk elasticity. The agreement at earlier times shows the validity of the technique, especially when compared with the gelatine data above, whilst these latter data show the power of using both techniques to understand the gels at different length scales.

Fig. 3 (a) Storage shear moduli (black data) and critical pressure (purple data) as a function of time for PVA gels. (b) tan δ (black data) and critical pressure (purple data) as a function of time for PVA gels.

Having validated our cavitation rheology approach, we then moved to our area of interest, low molecular weight gels (LMWGs). We selected two different dipeptide-based gelators (Fig. 4a). We have previously reported in detail on gels formed from both of these^13,41,42 and so they represent good test cases. In both examples, the dipeptide is conjugated to an aromatic component at the N-terminus. These dipeptides are both very effective gelators and can be used to form gels in different ways. In all cases, a self-supporting gel was formed (Fig. 4b). Specifically, here two different methods were used to trigger the gelation of the dipeptide-based LMWG. The first method, the solvent trigger, consists of the dissolution of the gelator in a water-miscible solvent such as DMSO, followed by the addition of water.⁴³ The final pH of these hydrogels was typically around 3.36 and 3.73 for gels formed from 1 and 2 respectively. Gels form quickly by this method, and we have previously shown that this method leads to an underlying microstructure of spherulitic domains of fibres.¹³ Example spherulitic domains formed in gels of 1 and 2 respectively are shown in Fig. 4c and e.

Fig. 4 (a) Chemical structures of the gelator used; 1 (FmocLG); 2 (2NapFF). (b) Photograph of (left to right) a gel of 1 using DMSO, a gel of 1 using GdL, a gel of 2 using DMSO, and a gel of 2 using GdL. All gels at a concentration of 4 mg mL⁻¹. Scale bar represents 1 cm. (c–f) Confocal images of gels of 1 using a solvent trigger (c) and a pH trigger (d). Confocal images of gels 2 using a solvent trigger (e) and a pH trigger (f). All gels at a concentration of 4 mg mL⁻¹. The scale bars represent 20 μm in all cases.

1 and 2 were selected to use in our cavitation technique because of our understanding of the differences in the underlying microstructure. We would expect that differences in the microstructures would lead to different correlation k_sc constant values. Images for gels of 1 (Fig. S7, ESI†) and 2 (Fig. S8, ESI†) at different concentrations show that no changes are observed in the microstructure for the same trigger.

Gels of 1 were examined at different concentrations. Shear rheology data showed a frequency-independent behaviour when using solvent and pH triggers (Fig. S9 and S10, ESI,† respectively), with shear modulus increasing with concentration. This is typical for such gels. For gels formed by both triggers, cavitation analysis shows excellent reproducible data at all concentrations (Fig. S11 and S12, ESI†). Gels of 2 were analysed in the same way. Storage modulus (Fig. S13 and S14, ESI†) and critical pressure (Fig. S15 and S16, ESI†) were examined at different concentrations using the two different triggers. Both G′ and P_c increased with concentration. Storage modulus again showed a frequency-independent response in all cases and the critical pressure values were again reproducible.

Shear and cavitation moduli were evaluated as a function of concentration for gels of 1 and 2 using both triggers (Fig. 5). For gel 1, the shear and cavitation moduli show a similar trend with concentration for both triggers (Fig. 5a and b). Similarly, for gels formed from 2 with both triggers, both moduli show a good correlation (Fig. 5c and d).

Fig. 5 Shear moduli (black data) and cavitation moduli (purple data) as a function of concentration for gel 1 using (a) solvent-trigger and (b) pH-trigger and for gel 2 using (c) solvent-trigger and (d) pH-trigger.

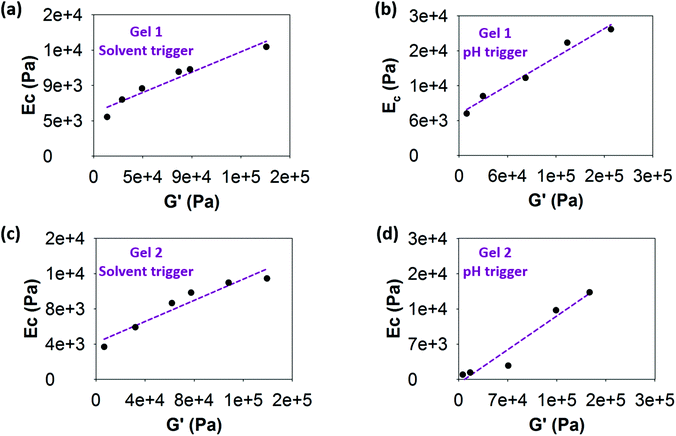
The relationship between both techniques is shown in Fig. 6, where the shear moduli are plotted against the cavitation moduli at different concentrations. The data show an excellent correlation fitting between both techniques in all cases with R² ranging from 0.92 to 0.98. The value of the constant k_sc is obtained from the slope of the linear regression in all cases. For gel 1, the value of k_sc was determined to be 0.06 ± 7.47 × 10⁻³ when using the solvent-trigger (Fig. 6a). A higher k_sc of 0.08 ± 7.41 × 10⁻³ was obtained when using the pH-trigger (Fig. 6b). Similar constant values were obtained for gel 2, with a k_sc of 0.06 ± 8.88 × 10⁻³ and 0.09 ± 13.75 × 10⁻³ for the solvent-trigger (Fig. 6c) and pH-trigger (Fig. 6d) respectively. Whilst similar in value, these are statistically different values. We note that the linear regression to the data does not go through the origin. We believe that this a result of there being a minimum gelation concentration below which no gels are formed and therefore it is not meaningful to effectively extrapolate to the value at zero concentration.

Fig. 6 Shear moduli plotted against cavitation moduli for gel of 1 using (a) a solvent trigger, (b) a pH trigger; and gel of 2 using (c) a solvent trigger and (d) a pH trigger. Slope of linear regression offer values of the constant k_sc. (R² = 0.94, 0.98, 0.92 and 0.94, respectively).

We believe that the differences in k_sc values for gels formed by the two triggers are due to the different underlying microstructures. What is notable here is the similarity in k_sc values for gel 1 and 2 when using the same trigger; the constant values collected for the same trigger are extremely similar in both LWMGs (Table 1).

Table 1 k _sc and deviation values for gel 1 and gel 2 using a solvent and pH trigger

LMWG	Trigger	Microstructure	k sc	Deviation
1	Solvent		0.06	±7.47 × 10^−3
2	Solvent		0.06	±8.88 × 10^−3
1	pH		0.08	±7.41 × 10^−3
2	pH		0.09	±13.75 × 10^−3

---

Varying the needle diameter has been used by some researchers to investigate the transition from cavitation to fracture in soft materials. The importance of using a specific needle size has been reported, as critical pressure is dependent on the needle diameter.^{22–24,27,34} Varying the needle size will affect the critical pressure, hence altering the cavitation modulus and consequently k_sc values. We examined for our gel 2 the effect of varying the needle diameter. Using a smaller needle diameter leads to differences in the gradient for cavitation modulus versus shear modulus. This affects k_sc values for both triggers (Fig. S17, ESI†).

We compared our k_sc values with those been reported in the literature. Surprisingly, our LMWG show the lowest values, not exceeding 0.1, while the constant values for other gels range from 3 to 40 (Fig. 7a). We link these considerable differences in k_sc values to the stiffness of the gels. For our LMWG systems the shear modulus is greater than the cavitation moduli (Fig. 7b), in contrast to what is been reported for other gels in the literature.^26,27 As k_sc is defined as the gradient between cavitation modulus (y-axis) versus shear modulus (x-axis), the greater the shear modulus, the lower the gradient and so the k_sc. We highlight that one example to expand on this. Fei et al. reported a 12-HSA gel with a stiffness of around 600 Pa and a critical pressure of around 5200 Pa.²⁶ For one of our gels, gel 1 using a solvent switch, the stiffness is around 20 000 Pa, whilst the critical pressure is roughly 5700 Pa. If we compare both gels, the critical pressures are very similar however the stiffness is much greater for our gel. We believe that there is an influence of the strain at which the gels break. The 12-HSA gel breaks at >10% strain, whilst our breaks at 3% strain (Fig. S18, ESI†). Similarly, all other LMWG show a critical strain no larger than 5% and stiffness in the order of 100 000 Pa, while gelatine and PVA-borax break at larger strains (around 800%) and the stiffness does not exceed 1000 Pa (Fig. S19, ESI†). Hence, whilst the absolute G′ is higher for ours LMWG, this is offset by the low breakage strain. It therefore seems likely that the value of P_c (and hence k_sc) depends on both the absolute modulus as well as the breakage strain.

Fig. 7 (a) Comparison our LMWGs k_sc values with others reported in the literature. (b) Elasticity values for shear (black data) and cavitation (purple data) moduli at 4 mg mL⁻¹ for gel 1 and gel 2 using the solvent-trigger (solid data) and pH-trigger (patterned data).

The cavitation rheology data give a greater insight into the networks that have been formed as compared to bulk rheology where the slight differences in absolute moduli are difficult to interpret. Understanding these differences is important; we have shown that the underlying microstructure links to the ability to 3D print such gels for example.⁴⁴

Conclusions

We have shown that cavitation rheology can be used to investigate our low molecular weight gel systems at the micrometre scale. Here we investigated the relationship between the shear moduli and the cavitation moduli for a range of different gels. We demonstrate that different k_sc values can be found for our gels depending on the trigger used, due to the differences in the underlying microstructure. The values are statistically different, and correlate with the structures that lead to the gel. We highlight that the values are very different to other gels examined here and elsewhere. This correlates with the significantly lower strains at which our gels break compared to other examples. Traditional shear rheology measures the bulk properties within the material while cavitation technique is clearly influenced by the mechanical properties at the micrometre length. Cavitation rheology is a powerful technique that can investigate in detail the microstructure of our LMWGs at a different scale that the traditional shear rheology cannot access. It should also be possible to use this technique to measure smaller volumes of gel than traditional rheology, as well as measuring patterned or otherwise inhomogeneous gels.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AMFC and LT thank the University of Glasgow for funding. CC acknowledges an Erasmus traineeship. DJA thanks the EPSRC for a Fellowship (EP/L021978/1), which funded BD. MarvinSketch 16.11.28.0 was used for naming chemical structures. We thank Finlay Walton (University of Glasgow) for help with the confocal microscope.

Notes and references

1. P. Terech and R. G. Weiss, Chem. Rev., 1997, 97, 3133–3160.
2. R. G. Weiss, J. Am. Chem. Soc., 2014, 136, 7519–7530.
3. N. M. Sangeetha and U. Maitra, Chem. Soc. Rev., 2005, 34, 821–836.
4. X. Du, J. Zhou, J. Shi and B. Xu, Chem. Rev., 2015, 115, 13165–13307.
5. A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002–8018.
6. E. V. Alakpa, V. Jayawarna, A. Lampel, K. V. Burgess, C. C. West, S. C. J. Bakker, S. Roy, N. Javid, S. Fleming, D. A. Lamprou, J. Yang, A. Miller, A. J. Urquhart, P. W. J. M. Frederix, N. T. Hunt, B. Péault, R. V. Ulijn and M. J. Dalby, Chem, 2016, 1, 298–319.
7. B. O. Okesola and D. K. Smith, Chem. Soc. Rev., 2016, 45, 4226–4251.
8. N. Singh, M. Kumar, J. F. Miravet, R. V. Ulijn and B. Escuder, Chem. – Eur. J., 2017, 23, 981–993.
9. Y. Lan, M. G. Corradini, R. G. Weiss, S. R. Raghavan and M. A. Rogers, Chem. Soc. Rev., 2015, 44, 6035–6058.
10. J. Raeburn, A. Zamith Cardoso and D. J. Adams, Chem. Soc. Rev., 2013, 42, 5143–5156.
11. E. R. Draper and D. J. Adams, Chem, 2017, 3, 390–410.
12. I. Ramos Sasselli, P. J. Halling, R. V. Ulijn and T. Tuttle, ACS Nano, 2016, 10, 2661–2668.
13. L. Chen, J. Raeburn, S. Sutton, D. G. Spiller, J. Williams, J. S. Sharp, P. C. Griffiths, R. K. Heenan, S. M. King, A. Paul, S. Furzeland, D. Atkins and D. J. Adams, Soft Matter, 2011, 7, 9721–9727.
14. M. Tassieri, M. Laurati, D. J. Curtis, D. W. Auhl, S. Coppola, A. Scalfati, K. Hawkins, P. R. Williams and J. M. Cooper, J. Rheol., 2016, 60, 649–660.
15. G. M. Newbloom, K. M. Weigandt and D. C. Pozzo, Macromolecules, 2012, 45, 3452–3462.
16. F. Del Giudice, M. Tassieri, C. Oelschlaeger and A. Q. Shen, Macromolecules, 2017, 50, 2951–2963.
17. V. Breedveld and D. J. Pine, J. Mater. Sci., 2003, 38, 4461–4470.
18. P. Cicuta and A. M. Donald, Soft Matter, 2007, 3, 1449–1455.
19. J. A. Zimberlin, N. Sanabria-DeLong, G. N. Tew and A. J. Crosby, Soft Matter, 2007, 3, 763–767.
20. J. A. Zimberlin and A. J. Crosby, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1423–1427.
21. J. A. Zimberlin, J. J. McManus and A. J. Crosby, Soft Matter, 2010, 6, 3632–3635.
22. S. Kundu and A. J. Crosby, Soft Matter, 2009, 5, 3963–3968.
23. J. Cui, C. H. Lee, A. Delbos, J. J. McManus and A. J. Crosby, Soft Matter, 2011, 7, 7827–7831.
24. J. Meid, F. Dierkes, J. Cui, R. Messing, A. J. Crosby, A. Schmidt and W. Richtering, Soft Matter, 2012, 8, 4254–4263.
25. M. S. Chin, B. B. Freniere, S. Fakhouri, J. E. Harris, J. F. Lalikos and A. J. Crosby, Plast. Reconstr. Surg., 2013, 131, 303e–305e.
26. P. Fei, S. J. Wood, Y. Chen and K. A. Cavicchi, Langmuir, 2015, 31, 492–498.
27. S. M. Hashemnejad and S. Kundu, Soft Matter, 2015, 11, 4315–4325.
28. L. E. Jansen, N. P. Birch, J. D. Schiffman, A. J. Crosby and S. R. Peyton, J. Mech. Behav. Biomed. Mater., 2015, 50, 299–307.
29. K. C. Bentz, S. E. Walley and D. A. Savin, Soft Matter, 2016, 12, 4991–5001.
30. S. B. Hutchens, S. Fakhouri and A. J. Crosby, Soft Matter, 2016, 12, 2557–2566.
31. J. Kang, C. Wang and S. Cai, Soft Matter, 2017, 13, 6372–6376.
32. T. Cohen and A. Molinari, Int. J. Solids Struct., 2015, 69–70, 544–552.
33. S. Raayai-Ardakani, Z. Chen, D. R. Earl and T. Cohen, Soft Matter, 2019, 15, 381–392.
34. A. Blumlein and J. J. McManus, J. Mater. Chem. B, 2015, 3, 3429–3435.
35. A. Blumlein, N. Williams and J. J. McManus, Sci. Rep., 2017, 7, 7346.
36. M. P. Milner and S. B. Hutchens, Extreme Mech. Lett., 2019, 28, 69–75.
37. J. A. Zimberlin, N. Sanabria-DeLong, G. N. Tew and A. J. Crosby, Soft Matter, 2007, 3, 763–767.
38. K. C. Bentz, N. Sultan and D. A. Savin, Soft Matter, 2018, 14, 8395–8400.
39. L. Pavlovsky, M. Ganesan, J. G. Younger and M. J. Solomon, Appl. Phys. Lett., 2014, 105, 114105.
40. E. Z. Casassa, A. M. Sarquis and C. H. Van Dyke, J. Chem. Educ., 1986, 63, 57.
41. C. Colquhoun, E. R. Draper, R. Schweins, M. Marcello, D. Vadukul, L. C. Serpell and D. J. Adams, Soft Matter, 2017, 13, 1914–1919.
42. D. J. Adams, M. F. Butler, W. J. Frith, M. Kirkland, L. Mullen and P. Sanderson, Soft Matter, 2009, 5, 1856–1862.
43. A. Mahler, M. Reches, M. Rechter, S. Cohen and E. Gazit, Adv. Mater., 2006, 18, 1365–1370.
44. M. C. Nolan, A. M. Fuentes Caparrós, B. Dietrich, M. Barrow, E. R. Cross, M. Bleuel, S. M. King and D. J. Adams, Soft Matter, 2017, 13, 8426–8432.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01023h

---