Open Access Article
Open Access ArticleNeutralisation rate controls the self-assembly of pH-sensitive surfactants†
Dominic W.
Hayward
 *ab,
Leonardo
Chiappisi
*ab,
Leonardo
Chiappisi
 ab,
Jyh Herng
Teo
b,
Sylvain
Prévost
ab,
Jyh Herng
Teo
b,
Sylvain
Prévost
 b,
Ralf
Schweins
b and
Michael
Gradzielski
b,
Ralf
Schweins
b and
Michael
Gradzielski
 *a
*a
aStranski-Laboratorium für Physikalische und Theoretische Chemie, Institut für Chemie, Technische Universität Berlin, Straße des 17. Juni 124, D-10623 Berlin, Germany. E-mail: hayward@ill.fr; michael.gradzielski@tu-berlin.de
bInstitut Laue-Langevin, 71 avenue des Martyrs, CS 20156, 38042 Grenoble cedex 9, France
First published on 14th October 2019
Abstract
The degree of ionisation of a weakly acidic surfactant can be continuously modified from nonionic to ionic by adjusting the pH. This property can be used to control the curvature and therefore the morphology of the self-assembled aggregates it forms in solution. Herein, we report the surprising phenomenon, observed in the alkyl ether oligo(ethylene oxide) carboxylate (CH3(CH2)11/13OEO4.5CH2COOH), whereby it is not only the pH but also the neutralisation rate that affects the aggregate morphology. Specifically, when the pH is increased slowly, up to 40 wt% of the surfactant remains in a long-lived vesicle state at high pH. This phenomenon was characterised in detail by small-angle neutron scattering and light scattering techniques. The cause of this phenomenon is thought to be related to a combination of polydispersity and the formation of acid-carboxylate dimers close to the pKa. The transition of these vesicles to the thermodynamically favoured micelles at high pH is inhibited by a high activation energy barrier and therefore only occurs very slowly. Increasing the NaCl concentration eliminates the presence of vesicles at high pH, demonstrating that the activation energy for the vesicle-to-micelle transition depends strongly on electrostatic interactions. These experiments show that the preparation pathway can be used to obtain different self-assembled structures at identical conditions via kinetic control. This phenomenon provides a useful tool for devising formulations where the properties of the system can be altered without changing the composition.
1 Introduction
Surfactants are low molecular weight amphiphiles that spontaneously self-assemble in aqueous solution. Depending on their chemical structure and environment, they can form a variety of different aggregate morphologies ranging from spherical and cylindrical micelles to planar lamellae and vesicles.1 The most common equilibrium morphology is that of spherical micelles and equilibration is generally achieved rapidly – typically in the millisecond to second regime. The kinetics of micelle formation are often described using two time constants, where the faster is associated with the exchange of single surfactant molecules and the slower with the complete disintegration of the aggregates.2 One therefore generally expects that micelles composed of low molecular weight surfactants will be in an equilibrated state shortly after their preparation or after a change of the solution conditions, such as temperature, pH or ionic strength.In the case of vesicles, which are much larger in size and have much higher aggregation numbers, formation via step-wise addition of individual molecules is statistically extremely unlikely. The kinetic processes that govern aggregation and disintegration are therefore rather different and in many cases difficult to elucidate precisely. In one system where the mechanism has been studied in detail, vesicle formation occurs via the growth of disklike micelles which then fuse and subsequently close into a spherical form.3–5 This process takes place on a timescale ranging from seconds to several hours, depending on the type of amphiphile present, and may be controlled by the addition of adulterants such as polymer surfactants, which act to stabilise the disc rims.6 Other vesicle transformation or ageing processes have been reported with equilibration times from a few days up to several months.7–9
The spontaneous formation of stable, or at least metastable, vesicles in single component surfactant solutions is uncommon and, for the most part, restricted to double-tailed molecules.10–12 Recently, spontaneous vesicle formation has also been reported in single-chain surfactants with phosphate13,14 or carboxylate head-groups.15–17 In this case, it is thought that the vesicles are composed of acid-soap dimers, whereby surfactant molecules with protonated and monoanionic headgroups undergo hydrogen bonding to form dimers with a single negative charge. Such systems are of interest, as the size and type of the aggregates depend both on the concentration of the surfactant14,15 and the pH of the solution,13,16–18 and could therefore be tuned to suit particular formulations or applications.
One such surfactant class, in which spontaneous vesicle formation has been observed, is the alkyl ether carboxylic acids (AECs). AECs are single-chained, weakly anionic surfactants with carboxylate head-groups. They are used in cosmetic and detergent formulations19 as well as in oil extraction techniques20 and are therefore industrially relevant and widely available. Of particular interest with regards to its self-assembly behaviour, is oligo-oxyethylene(4.5) lauryl ether carboxylic acid, which forms a mixture of vesicles and micelles at low pH (approx. 3–5)17,18 and exclusively micelles at high pH. As a result of this relatively well-known pH-responsive behaviour, this surfactant was previously used to test the concept of an in situ chemical reactor sample environment for small-angle neutron scattering (SANS) experiments.21 Here, in order to maximise the signal-to-noise ratio, particularly for the low-Q measurements, the pH of the aqueous surfactant solution was adjusted very slowly compared to the previous experiments (10 mL of 0.1 M NaOH added over 120 minutes vs. 0.1 mL of 10 M NaOH added over 1 s). In this case, a small fraction (∼1–2 wt%) of larger structures persisted in solution, even at high pH (∼10). Repeat measurements of the same samples after 24 hours yielded the same results, indicating that the resulting structures are at least metastable with respect to the expected dynamics of small-molecule, surfactant-based micelles. The results observed in ref. 21 are notable for two reasons: firstly, it is rather unusual to have two distinct, coexisting populations with different morphologies arising from a single type of surfactant molecule in solution. Secondly, pathway-dependent self-assembly is rare in simple surfactant systems.
As it was not clear how and why this type of complex behaviour should manifest in such an ostensibly simple system, this work has been undertaken to confirm that the effect is real (i.e. not an artefact arising from a particular measurement technique or a contaminated sample), to elucidate the effect in detail and to establish a possible mechanism. This study contains a detailed investigation on the effects of base addition-rate on the self-assembly behaviour of AECs with respect to: surfactant composition, base concentration, base composition and salt concentration. The results confirm the complexity of the phenomenon and are discussed in relation to possible explanations and potential routes by which this behaviour may be exploited.
2 Experimental
2.1 Materials
The surfactants AKYPO RLM 45 CA (C12E5Ac) and AKYPO RO 50 VG (C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac) were kindly donated by Kao Chemicals GmbH (Emmerich, Germany) and the surfactant NIKKOL ECT-7 (C13E7Ac) was donated by Nikko Chemicals (Tokyo, Japan). A generalised chemical structure of the surfactants is provided in Fig. 1 and the specific chemical structures of the individual materials is give in Fig. S1 in the ESI.† The nomenclature used in the abbreviations derives from that used for fatty acids, so the material Cx:yEzAc comprises: an alkyl chain with x carbons and y double bonds, a single oxygen followed by z ethylene oxide units and a CH2COOH carboxymethyl termination. As it may be relevant for the phenomena described in this work, it is instructive to briefly consider what is known about the composition of these materials. The surfactants are all produced in industrial quantities and are polydisperse in both alkyl chain length and number of ethylene oxide units. Molecules of AKYPO RLM 45 CA may have one of three different alkyl chain lengths (C12, C14 and C16) in the approximate ratio 2
1E5Ac) were kindly donated by Kao Chemicals GmbH (Emmerich, Germany) and the surfactant NIKKOL ECT-7 (C13E7Ac) was donated by Nikko Chemicals (Tokyo, Japan). A generalised chemical structure of the surfactants is provided in Fig. 1 and the specific chemical structures of the individual materials is give in Fig. S1 in the ESI.† The nomenclature used in the abbreviations derives from that used for fatty acids, so the material Cx:yEzAc comprises: an alkyl chain with x carbons and y double bonds, a single oxygen followed by z ethylene oxide units and a CH2COOH carboxymethyl termination. As it may be relevant for the phenomena described in this work, it is instructive to briefly consider what is known about the composition of these materials. The surfactants are all produced in industrial quantities and are polydisperse in both alkyl chain length and number of ethylene oxide units. Molecules of AKYPO RLM 45 CA may have one of three different alkyl chain lengths (C12, C14 and C16) in the approximate ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 and a distribution of ethylene oxide units centred around 4.5. Molecules of AKYPO RO 50 VG have alkyl chains C18
0.25 and a distribution of ethylene oxide units centred around 4.5. Molecules of AKYPO RO 50 VG have alkyl chains C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or C16 in the ratio 3
1 or C16 in the ratio 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and an ethylene oxide distribution centred around 5 units. Molecules of NIKKOL ECT-7 have alkyl chains of length C12, C13 or C14 in the ratio 2
1 and an ethylene oxide distribution centred around 5 units. Molecules of NIKKOL ECT-7 have alkyl chains of length C12, C13 or C14 in the ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and an ethylene oxide distribution centred around 7 units. Finally, due to the manner in which they are synthesised, the conversion from the ethoxylated alcohol to the carboxylic acid form may not be complete. The fraction of non-carboxymethylated chains is estimated to be approximately 10%.18,22,23 The materials were characterised by electrospray ionisation mass spectrometry (ESI-MS) (see Fig. S2, ESI†) and inductively coupled plasma optical emission spectrometry (ICP-OES) and unless otherwise stated, used as received. A summary of the materials used is given in Table 1. Sodium hydroxide, potassium hydroxide and sodium chloride were obtained from Sigma Aldrich (St. Louis, USA) and used as received. The D2O (>99.9%D) used for the preparation of samples for the SANS experiments was obtained from Euriso-top (Saint-Aubin, France).
2 and an ethylene oxide distribution centred around 7 units. Finally, due to the manner in which they are synthesised, the conversion from the ethoxylated alcohol to the carboxylic acid form may not be complete. The fraction of non-carboxymethylated chains is estimated to be approximately 10%.18,22,23 The materials were characterised by electrospray ionisation mass spectrometry (ESI-MS) (see Fig. S2, ESI†) and inductively coupled plasma optical emission spectrometry (ICP-OES) and unless otherwise stated, used as received. A summary of the materials used is given in Table 1. Sodium hydroxide, potassium hydroxide and sodium chloride were obtained from Sigma Aldrich (St. Louis, USA) and used as received. The D2O (>99.9%D) used for the preparation of samples for the SANS experiments was obtained from Euriso-top (Saint-Aubin, France).
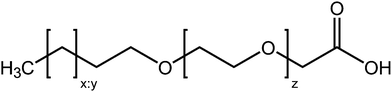 | ||
| Fig. 1 Generalised chemical structure of the surfactants used in this work. The surfactants differ from each other in three ways: the length of the alkyl chain (x), the number of double bonds in the alkyl chain (y) and the number of ethylene oxide units (z). The approximate structures of the individual materials are provided in Fig. S1 (ESI†). | ||
| Commercial name | Short form | Chemical formulaa | Molecular weight (g mol−1) | Active matter |
|---|---|---|---|---|
| a In the chemical formulae, EO = –(CH2CH2O)– has been used. | ||||
| AKYPO RLM 45 CA | C12E5Ac | CH3(CH2)11/13OEO4.5CH2COOH | 444 | 92% |
| AKYPO RO 50 VG | C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac 1E5Ac |
CH3(CH2)15/17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1OEO5CH2COOH 1OEO5CH2COOH |
544 | 91% |
| NIKKOL ECT-7 | C13E7Ac | CH3(CH2)12OEO7CH2COOH | 567 | Not given |
| Brij L4 | C12E4OH | CH3(CH2)12OEO4H | 362 | Not given |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac respectively), using ultrapure, deionised water (Milli-Q, 18.2 MΩ cm). With the exception of the ‘reverse-addition’ sample, all high pH samples were prepared in the same manner: a 40 mL vial was charged with 20 g of surfactant solution, the base (either NaOH or KOH) was added continuously via a syringe pump (33 DDS, Harvard Apparatus, USA) at the addition rates detailed in Table 2. For the ‘reverse addition’ sample, 0.5 mL of 1 M NaOH was added to 19.8 g deionised water in one portion, stirred for 5 minutes after which time, 0.2 g of unadulterated surfactant was added dropwise to the stirring solution. In the case of the salt-containing stock solutions, unless otherwise stated, the salt was added prior to the surfactant and the high-pH solutions were then prepared as previously.
1E5Ac respectively), using ultrapure, deionised water (Milli-Q, 18.2 MΩ cm). With the exception of the ‘reverse-addition’ sample, all high pH samples were prepared in the same manner: a 40 mL vial was charged with 20 g of surfactant solution, the base (either NaOH or KOH) was added continuously via a syringe pump (33 DDS, Harvard Apparatus, USA) at the addition rates detailed in Table 2. For the ‘reverse addition’ sample, 0.5 mL of 1 M NaOH was added to 19.8 g deionised water in one portion, stirred for 5 minutes after which time, 0.2 g of unadulterated surfactant was added dropwise to the stirring solution. In the case of the salt-containing stock solutions, unless otherwise stated, the salt was added prior to the surfactant and the high-pH solutions were then prepared as previously.
| Base concentration (mol L−1) | Volume (mL) | Addition time (s) | Addition rate (mol s−1) | Equivalent addition rate (molbase/molsurfactant/s) | ||
|---|---|---|---|---|---|---|
| C12E5Ac | C13E7Ac | C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac 1E5Ac |
||||
| 0.1 | 5 | 8 | 6.25 × 10−5 | 2.78 × 10−3 | ||
| 0.1 | 5 | 60 | 8.33 × 10−6 | 3.70 × 10−4 | ||
| 0.1 | 5 | 600 | 8.33 × 10−7 | 3.70 × 10−5 | ||
| 0.1 | 5 | 6000 | 8.33 × 10−8 | 3.70 × 10−6 | ||
| 0.1 | 5 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8.33 × 10−9 | 3.70 × 10−7 | ||
| 0.1 | 5 | 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8.33 × 10−10 | 3.70 × 10−8 | ||
| 1 | 0.5 | 8 | 6.25 × 10−5 | 2.78 × 10−3 | 3.40 × 10−3 | 3.55 × 10−3 |
| 1 | 0.5 | 60 | 8.33 × 10−6 | 3.70 × 10−4 | ||
| 1 | 0.5 | 600 | 8.33 × 10−7 | 3.70 × 10−5 | ||
| 1 | 0.5 | 6000 | 8.33 × 10−8 | 3.70 × 10−6 | 4.53 × 10−6 | 4.73 × 10−6 |
| 1 | 0.5 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8.33 × 10−9 | 3.70 × 10−7 | ||
| 1 | 0.5 | 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8.33 × 10−10 | 3.70 × 10−8 | ||
| 10 | 0.05 | 8 | 6.25 × 10−5 | 2.78 × 10−3 | ||
| 10 | 0.05 | 60 | 8.33 × 10−6 | 3.70 × 10−4 | ||
| 10 | 0.05 | 600 | 8.33 × 10−7 | 3.70 × 10−5 | ||
| 10 | 0.05 | 6000 | 8.33 × 10−8 | 3.70 × 10−6 | ||
2.2 Small-angle neutron scattering (SANS)
SANS measurements were carried out on the D11 instrument at the Institut Laue-Langevin (ILL) in Grenoble.24 Experiments were performed with a neutron wavelength of 6 Å and a path length of 2 mm at three sample-to-detector distances (SD): 1.5 m, 8 m and 39 m, covering the Q-range: 0.002–0.42 Å−1. Absolute intensities were obtained with reference to the secondary calibration standard, H2O (1 mm path length), which has a differential scattering cross-section of 0.983 cm−1 on the D11 instrument at λ = 6.0 Å. The raw data are available in the ILL data repository.25 For each measurement, the 2D detector data were integrated over the azimuthal angle (0–2π), and the D2O background was subtracted. Curves from the same sample at different SD were then combined and rebinned (the protocol for the rebinning algorithm is given in the ESI†). Finally, the data were fitted, in absolute units, to a two-component model18,21 consisting of a population of ellipsoidal core–shell micelles (interacting via a charged hard sphere structure factor) and a population of non-interacting, unilamellar, core–shell vesicles. A mass balance constraint ensured that all of the surfactant material known to be present in the sample is in either one or the other of these aforementioned aggregation states. Details of the model, are given elsewhere21 and the parameters used are given in the ESI.† At this point, it should be noted that, due to the existence of two polydisperse populations and the small weight fraction of the larger aggregates, the exact morphology of these aggregates could not be conclusively determined. However, as vesicles are known to exist at low pH16,18 and the small-angle scattering has previously been observed to vary continuously with increasing pH,21 consistent with a growing population of micelles and a shrinking population of vesicles, the description of the larger aggregates as vesicles has been adopted in this work.2.3 Light scattering
Static and dynamic light scattering experiments (SLS and DLS respectively) were conducted concurrently using an ALV light scattering instrument consisting of a CGS-3 goniometer, a HeNe laser operating at a wavelength of 632.8 nm and an LSE 5004 digital correlator. Prior to measurement, all samples were filtered using mixed cellulose ester membrane filters (Millipore Millex-AA, Merck Millipore Ltd, 0.8 μm pore size) to remove large dust particles. Measurements were performed in cylindrical cells (8 mm inner diameter) at 25 °C for scattering angles between 30° and 150°, covering the Q-range: 6 × 10−4–2.6 × 10−3 Å−1. For the SLS measurements, absolute intensities were obtained with reference to the toluene standard using the Rayleigh ratio 1.340 × 10−5 cm−1.The autocorrelation functions resulting from the DLS measurements were analysed using two methods: an indirect Laplace transformation of the correlation function to give a continuous size distribution,26 as well as a direct fit of the first-order field autocorrelation function using a double-exponential model to extract the decay constants.27 The field autocorrelation function g(1) was derived from the measured intensity autocorrelation function g(2)via the Siegert equation:28
| g(2) = 1 + β|g(1)|2 | (1) |
3 Results
3.1 SANS
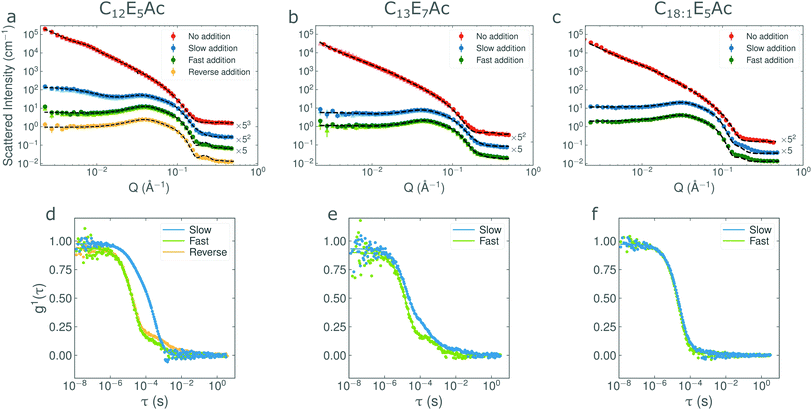
In order to verify the reproducibility of the addition-rate dependence effect, a fresh batch of C12E5Ac surfactant was used. Additionally, to investigate whether this effect also arises in other, analogous, AEC systems, two further surfactants were investigated: C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac and C13E7Ac. Surfactant solutions were prepared at 1 wt% in D2O, to which 0.5 mL of 1 M NaOD was added over either 8 seconds or 100 minutes (hereafter referred to as ‘fast’ and ‘slow’ additions respectively). As the number of molecules varied slightly between the different samples and surfactants used, an ‘equivalent addition rate’ was defined as the number of moles of base added per number of moles of surfactant present in solution per second (i.e. molar equivalents per second). The values are tabulated in Table 2. In addition, to investigate whether the effect could be attributed to irreversible chemical changes occurring in the surfactant as a result of reactions with the concentrated base, via alkaline hydrolysis for example, a sample was prepared in which the base was added prior to the surfactant. After initial measurements at 25 °C, all samples were also heated to 60 °C for 20 minutes, cooled to 25 °C and then remeasured. This was done in order to ascertain whether the self-assembled structures could be thermally ‘annealed’ into a thermodynamically favourable state. The resulting azimuthally-averaged scattering patterns are shown in Fig. 2(a–c), where the darker squares represent the initial measurements at 25 °C and the lighter triangles (almost entirely obscured behind the 25 °C data) represent the thermally ‘annealed’ samples. The parameters resulting from a non-linear least squares fit of the data to the two component model (consisting of ellipsoidal micelles and unilamellar vescicles), are given in Table 3. A comparison of the scattering patterns from the previous batch of C12E5Ac and the batch used in this work is shown in Fig. S3 (ESI†). The scattering patterns from both batches are identical.
1E5Ac and C13E7Ac. Surfactant solutions were prepared at 1 wt% in D2O, to which 0.5 mL of 1 M NaOD was added over either 8 seconds or 100 minutes (hereafter referred to as ‘fast’ and ‘slow’ additions respectively). As the number of molecules varied slightly between the different samples and surfactants used, an ‘equivalent addition rate’ was defined as the number of moles of base added per number of moles of surfactant present in solution per second (i.e. molar equivalents per second). The values are tabulated in Table 2. In addition, to investigate whether the effect could be attributed to irreversible chemical changes occurring in the surfactant as a result of reactions with the concentrated base, via alkaline hydrolysis for example, a sample was prepared in which the base was added prior to the surfactant. After initial measurements at 25 °C, all samples were also heated to 60 °C for 20 minutes, cooled to 25 °C and then remeasured. This was done in order to ascertain whether the self-assembled structures could be thermally ‘annealed’ into a thermodynamically favourable state. The resulting azimuthally-averaged scattering patterns are shown in Fig. 2(a–c), where the darker squares represent the initial measurements at 25 °C and the lighter triangles (almost entirely obscured behind the 25 °C data) represent the thermally ‘annealed’ samples. The parameters resulting from a non-linear least squares fit of the data to the two component model (consisting of ellipsoidal micelles and unilamellar vescicles), are given in Table 3. A comparison of the scattering patterns from the previous batch of C12E5Ac and the batch used in this work is shown in Fig. S3 (ESI†). The scattering patterns from both batches are identical.
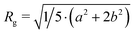 where a and b are the semi-minor and semi-major axes of the ellipsoid. With the exception of C12E5Ac slow addition sample, it was not possible to determine the vesicle radius with any degree of accuracy, as the weight fraction of surfactant in vesicle form was simply too low. For the purposes of comparing the fraction of surfactant in vesicle form, the vesicle radius was fixed at this value for all remaining fits. DLS measurements (see, for example, Fig. 3) show that this approximation is not unreasonable. All samples were prepared in D2O, with 1 M NaOD. The ‘slow’ addition rates were: 2.78 × 10−3, 3.40 × 10−3 and 3.55 × 10−3 eq. s−1 and the fast addition rates were: 3.70 × 10−6, 4.53 × 10−6 and 4.73 × 10−6 eq. s−1 for C12E5Ac, C13E7Ac and C18
where a and b are the semi-minor and semi-major axes of the ellipsoid. With the exception of C12E5Ac slow addition sample, it was not possible to determine the vesicle radius with any degree of accuracy, as the weight fraction of surfactant in vesicle form was simply too low. For the purposes of comparing the fraction of surfactant in vesicle form, the vesicle radius was fixed at this value for all remaining fits. DLS measurements (see, for example, Fig. 3) show that this approximation is not unreasonable. All samples were prepared in D2O, with 1 M NaOD. The ‘slow’ addition rates were: 2.78 × 10−3, 3.40 × 10−3 and 3.55 × 10−3 eq. s−1 and the fast addition rates were: 3.70 × 10−6, 4.53 × 10−6 and 4.73 × 10−6 eq. s−1 for C12E5Ac, C13E7Ac and C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac respectively. For the reverse addition sample, the base was added prior to the drop-wise addition of surfactant. Note that in the table, vesicle wt% corresponds to the weight fraction of surfactant in vesicle form
1E5Ac respectively. For the reverse addition sample, the base was added prior to the drop-wise addition of surfactant. Note that in the table, vesicle wt% corresponds to the weight fraction of surfactant in vesicle form
| Surfactant | Micelle Rg (nm) | Vesicle Rh (nm) | Vesicle wt% | N agg |
|---|---|---|---|---|
| C12E5Ac – Slow | 1.82 ± 0.06 | 26 ± 2 | 1.55 ± 0.06 | 197 |
| C12E5Ac – Fast | 1.71 ± 0.09 | 26 | 0.10 ± 0.01 | 96 |
| C12E5Ac – Reverse | 1.71 ± 0.07 | 26 | 0.03 ± 0.01 | 96 |
| C13E7Ac – Slow | 1.58 ± 0.13 | 26 | 0.14 ± 0.01 | 51 |
| C13E7Ac – Fast | 1.62 ± 0.04 | 26 | 0.10 ± 0.01 | 58 |
C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac – Slow 1E5Ac – Slow |
2.20 ± 0.03 | 26 | 0.15 ± 0.02 | 162 |
C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac – Fast 1E5Ac – Fast |
2.18 ± 0.04 | 26 | 0.01 ± 0.02 | 156 |
It is evident that the addition-rate effect for C12E5Ac is also present in the new sample and is not simply an artefact arising from a particular batch. The fit parameters show that the weight fraction of surfactant in vesicle form is over an order of magnitude higher for the slow-addition sample with respect to the fast-addition sample. This difference remains after the samples have been heated and cooled, which suggests that the structures formed are kinetically stable with respect to temperature (see Fig. 2). Scattering from the ‘reverse addition’ sample was very similar to the sample prepared by fast addition, suggesting that the differences in nanostructure cannot be ascribed to locally high base concentrations hydrolysing the surfactant during the addition.
Prior to the addition of the base, all of the surfactants show scattering characteristic of very large, locally flat structures such as bilayers or vesicles. This is consistent with previous scattering experiments18,21 and transmission electron microscopy studies.16 The initial pH of each of the initial solutions is approximately 2.6, corresponding to a degree of ionisation of 7%.
In Fig. 2b and c, it can be seen that the effects of base-addition-rate are much less pronounced in other, analogous, surfactants. Both the C13E7Ac and C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac solutions exhibit a slight upturn at Q ∼ 10−1 Å−1, indicating the presence of a small fraction of ‘larger’ structures. This feature is however, very weak compared to the one observed for the C12E5Ac slow-addition sample and the influence of the addition rate is barely perceptible. To highlight the differences between the samples, the ratio of the intensities from the fast and slow additions are compared in Fig. S4 (ESI†). Note that for the C12E5Ac and C13E7Ac, the addition speed also appears to affect the shape of the micelles.
1E5Ac solutions exhibit a slight upturn at Q ∼ 10−1 Å−1, indicating the presence of a small fraction of ‘larger’ structures. This feature is however, very weak compared to the one observed for the C12E5Ac slow-addition sample and the influence of the addition rate is barely perceptible. To highlight the differences between the samples, the ratio of the intensities from the fast and slow additions are compared in Fig. S4 (ESI†). Note that for the C12E5Ac and C13E7Ac, the addition speed also appears to affect the shape of the micelles.
To examine the reversibility of the addition-rate effect, a further two C12E5Ac solutions were prepared;
• Slow-addition of NaOD → addition of DCl → fast-addition of NaOD
• Fast-addition of NaOD → addition of DCl → slow-addition of NaOD
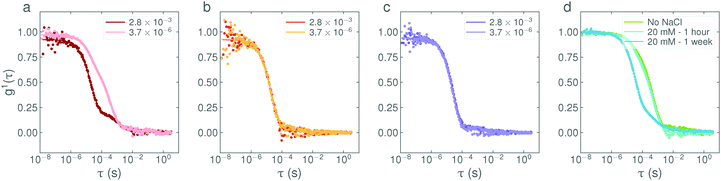
The SANS data from these samples is shown in Fig. S5 (ESI†). Two effects are immediately clear on comparison with Fig. 2a. Firstly, the nanostructures resulting from the two preparation routes are identical i.e. the addition-rate effect is no longer present. Secondly, the low-Q region is flat i.e. there are no-longer any larger structures in solutions. Both effects have been ascribed to the presence of an inert salt, in this case NaCl, formed by the neutralisation of HCl and NaOH (25 mM, – i.e. a slight molar excess with respect to the surfactant), screening the charged headgroups. The same effects are also observed by light scattering when NaCl is added either before or after the addition of NaOH (see Section 3.2.4). This strongly suggests that electrostatic interactions are key to understanding the morphology and stability of the self-assembled aggregates and ultimately, the underlying cause of the addition-rate effect.
3.2 Light scattering
The effects observed by small-angle scattering were investigated in further detail using light scattering methods. The DLS data are presented in three forms: the first-order field correlation function, an inverse Laplace transformation of the correlation function and the parameters resulting from fits of the correlation function to a bimodal exponential model of the form:g(1)(τ,Q) =A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−D1Q2τ) + (1 − A)exp(−D2Q2τ) exp(−D1Q2τ) + (1 − A)exp(−D2Q2τ) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
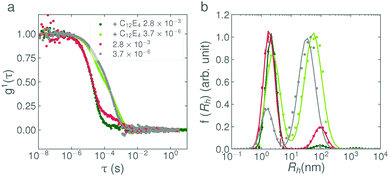
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac respectively. Despite the similar composition of the surfactants, the effect of the base addition-rate is clearly very different. In general, the results agree well with the observations from the small-angle scattering experiment; the C12E5Ac solutions shows a very pronounced addition-rate effect, whereas the C13E7Ac and C18
1E5Ac respectively. Despite the similar composition of the surfactants, the effect of the base addition-rate is clearly very different. In general, the results agree well with the observations from the small-angle scattering experiment; the C12E5Ac solutions shows a very pronounced addition-rate effect, whereas the C13E7Ac and C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac solutions do not. The data show that the C13E7Ac solutions do exhibit a slight rate-dependence, however the difference between the calculated weight fractions, as determined from the bimodal fit, is exceedingly small (∼0.06%). The C18
1E5Ac solutions do not. The data show that the C13E7Ac solutions do exhibit a slight rate-dependence, however the difference between the calculated weight fractions, as determined from the bimodal fit, is exceedingly small (∼0.06%). The C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
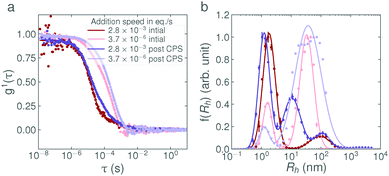
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac solutions exhibit no rate-dependent behaviour at all and the entirety of the surfactant is micellar form. At this point, it is also noting that the light scattering and neutron scattering techniques are each sensitive to slightly different aspects of the sample, as can be observed in Fig. 2. The intensity of the correlation function scales with the 6th power of the particle diameter and is therefore very sensitive to the presence of larger particles. SANS, on the other hand, is primarily sensitive to the volume of the scattering material and therefore the presence of vesicles is not highlighted as strongly. This effect can be seen in Fig. 2a and d. In Fig. 2d, the vesicle mode in the slow addition dominates the intensity, even though it only accounts for 2% of the surfactant volume. In Fig. 2a, the presence of vesicles can be seen by the upturn in intensity at low Q. For the fast and reverse addition samples, the amount of surfactant in vesicle form is approximately 50× less. In the DLS data, the vesicle modes are still clearly visible (even though only 0.1% of the sample is in vesicle form) whereas in the SANS data, this contribution is lost in the noise.
1E5Ac solutions exhibit no rate-dependent behaviour at all and the entirety of the surfactant is micellar form. At this point, it is also noting that the light scattering and neutron scattering techniques are each sensitive to slightly different aspects of the sample, as can be observed in Fig. 2. The intensity of the correlation function scales with the 6th power of the particle diameter and is therefore very sensitive to the presence of larger particles. SANS, on the other hand, is primarily sensitive to the volume of the scattering material and therefore the presence of vesicles is not highlighted as strongly. This effect can be seen in Fig. 2a and d. In Fig. 2d, the vesicle mode in the slow addition dominates the intensity, even though it only accounts for 2% of the surfactant volume. In Fig. 2a, the presence of vesicles can be seen by the upturn in intensity at low Q. For the fast and reverse addition samples, the amount of surfactant in vesicle form is approximately 50× less. In the DLS data, the vesicle modes are still clearly visible (even though only 0.1% of the sample is in vesicle form) whereas in the SANS data, this contribution is lost in the noise.
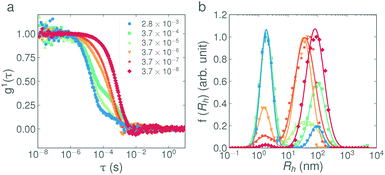
In Fig. 4a, the weight fraction of surfactant in vesicle form (based on eqn (2), full calculations shown in the ESI†) is shown for each base concentration and addition rate. Despite the variability in the data, the trend is again clear; the faster the addition rate of NaOH, the fewer larger structures are present in solution. The weight fractions of surfactant in vesicle form for the 2.8 × 10−3 eq. s−1 and 3.7 × 10−6 eq. s−1 additions of 1 M NaOH, as calculated from the DLS data, were found to be 0.06% and 2.2% respectively. This agrees well with the weight fractions found by SANS, as given in Table 3. Fig. 4b, shows the mean aggregation number as calculated from the plateau region of the static light scattering data (tabulated values are given in Table S2, SLS data are shown in Fig. S7, ESI†), and confirms the trends and sizes observed from the DLS data. For completeness, the mean aggregation numbers were also calculated from the SANS fit parameters in Table 3, the results (95 and 197 for the 2.8 × 10−3 eq. s−1 and 3.7 × 10−6 eq. s−1 of 1 M NaOH respectively) are broadly in agreement with the SLS data (46 and 167 respectively) and confirm that all three scattering techniques are showing a consistent, reproducible picture.
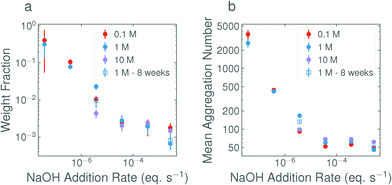 | ||
| Fig. 4 (a) Weight fractions of surfactant in vesicle form in 1 wt% solutions of C12E5Ac after the addition of NaOH at various concentrations and addition rates. Plots show an average of all measurements in the range 30°–150°. The weight fractions calculated at 30°, 90° and 150° are shown in Fig. S6 (ESI†). The values are calculated from fits to the bimodal exponential model in eqn (2) taking into account the relative volumes of the scatterers. (b) The mean aggregation numbers as calculated from the plateau of the corresponding static light scattering data (shown in Fig. S7, ESI†). | ||
For the 0.1 M and 1 M solutions, the base concentration appears to have little effect on the final structures. The suppression of larger structures in the case of the 10 M addition may be explained by considering the mechanics of the addition itself. The base was delivered via a 21 G needle (with a nominal inner diameter of 0.5 mm), which, due to the surface tension of the base at the tip of the needle, produces droplets with an average volume of ∼10 μL. In the case of the 10 M base, only 50 μL is added in total, equating to approx. 5 discrete drops. As a result of this ‘discretization’, the slower additions were in-fact a composed of a small number of very fast additions.
Finally, the influence of the base cation on the final nanostructure was investigated by performing the equivalent ‘fast’ and ‘slow’ additions (2.8 × 10−3 eq. s−1 and 3.7 × 10−6 eq. s−1 respectively) with KOH replacing NaOH. The results, given in Fig. S8 (ESI†), show that replacing the Na+ cation by K+ has little influence on the addition-rate effect, i.e. it appears not to be ion specific.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, surfactant
1, surfactant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) salt. Light scattering measurements, taken at total salt concentrations of 6 mM and 21 mM§ (i.e. molar ratios of approx. 4
salt. Light scattering measurements, taken at total salt concentrations of 6 mM and 21 mM§ (i.e. molar ratios of approx. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, surfactant
1, surfactant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) salt, respectively), are shown in Fig. 6. It can be seen that even at low concentrations, the presence of additional NaCl completely suppresses the appearance of larger structures at high pH and nullifies the addition-rate effect. The calculated diffusion coefficient of the structures is systematically affected by the presence of NaCl, decreasing from an initial value of D = 15.3 (10−12 m2 s−1) in the absence of NaCl to 12.7, 10.7 and 8.5 in the presence of 6 mM (i.e. a molar ratio of 4
salt, respectively), are shown in Fig. 6. It can be seen that even at low concentrations, the presence of additional NaCl completely suppresses the appearance of larger structures at high pH and nullifies the addition-rate effect. The calculated diffusion coefficient of the structures is systematically affected by the presence of NaCl, decreasing from an initial value of D = 15.3 (10−12 m2 s−1) in the absence of NaCl to 12.7, 10.7 and 8.5 in the presence of 6 mM (i.e. a molar ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, surfactant
1, surfactant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) salt), 21 mM (1
salt), 21 mM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, surfactant
1, surfactant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) salt) and 100 mM (1
salt) and 100 mM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.5, surfactant
4.5, surfactant![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) salt) NaCl respectively. This effect is most likely due to a decrease in the structure factor contribution, S(0), as the screening of micelle charges is increased. Curiously, when the NaCl is added after the addition of NaOH, it does not immediately disrupt the vesicles already present in solution but does act to reduce the relative amount of vesicles over time (see Fig. 6d) with a characteristic relaxation time of approximately 3 days.
salt) NaCl respectively. This effect is most likely due to a decrease in the structure factor contribution, S(0), as the screening of micelle charges is increased. Curiously, when the NaCl is added after the addition of NaOH, it does not immediately disrupt the vesicles already present in solution but does act to reduce the relative amount of vesicles over time (see Fig. 6d) with a characteristic relaxation time of approximately 3 days.
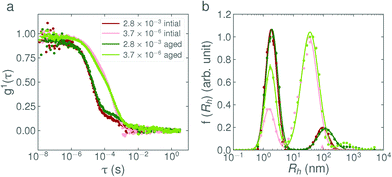
This interpretation was tested by preparing surfactant solution samples at pH values in the range 3.5–5.5 and allowing them to remain at this pH for 7 days before rapidly adding the remaining NaOH (via a single pipette addition) to bring them up to pH 10. The results of this test are given in Fig. S10 in the ESI.† Although a small increase in the vesicle fraction is observed for the sample maintained at pH 5.5, it is clear that the length of time spent close to the pKa is not the fundamental cause of the observed addition-rate phenomena.
4 Discussion
The phenomena described above, present something of a conundrum. On the one hand, the presence of a small fraction of unusual aggregates in aqueous solutions of industrial surfactants is far from unheard of. In most cases these could be easily dismissed as impurities or contaminants and would be deemed irrelevant. On the other hand, in this case, it is clear that:1. The presence or absence of these aggregates depends strongly on the preparation pathway.
2. This effect has been demonstrated on different batches of material using different experimental techniques.
3. The effects are significant (up to 40 wt%), systematic and reproducible.
The mystery is further deepened by the fact that the effects are either much weaker (C13E7Ac) or not found at all (C18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1E5Ac) in closely related materials of the same surfactant class. The pathway dependence appears not to be an ion-specific effect, as demonstrated by the near-identical findings with KOH and NaOH, but certainly has an ionic character, as shown by the absence of the effect in the presence of NaCl. Furthermore, the effect only diminishes very slowly, with a characteristic relaxation time of approximately 70 days, does not disappear on heating and cooling and is enhanced by the removal of water-soluble impurities. These observations do not lend themselves easily to a straightforward explanation or a conclusive interpretation, however, various possibilities are discussed below.
1E5Ac) in closely related materials of the same surfactant class. The pathway dependence appears not to be an ion-specific effect, as demonstrated by the near-identical findings with KOH and NaOH, but certainly has an ionic character, as shown by the absence of the effect in the presence of NaCl. Furthermore, the effect only diminishes very slowly, with a characteristic relaxation time of approximately 70 days, does not disappear on heating and cooling and is enhanced by the removal of water-soluble impurities. These observations do not lend themselves easily to a straightforward explanation or a conclusive interpretation, however, various possibilities are discussed below.
One possible culprit for the existence of two distinct self-assembled morphologies is the chemical polydispersity of the surfactant molecules. The C12E5Ac material not only contains a mixture of C12, C14 and C16 chains (in the approximate ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25), it also features a broad distribution of EO units (from 2 to 16, see Fig. S2 in the ESI†). The difference in size and solubility between headgroups containing 2 EO units and those containing 16 EO units is substantial and the presence of such a broad distribution will undoubtedly give rise to different self-assembly behaviour than would be present if the chain lengths were monodisperse. Indeed, it has previously been observed that the surfactant C12E10Ac does not form vesicles in aqueous solution, even at low pH.16,18 Furthermore, an investigation into surfactant mixtures of C18E20 and C18E100, revealed that although they generally form mixed micelles, the constituent surfactants segregate into separate structures when one of them undergoes a phase change.33 It is therefore not unreasonable to invoke polydispersity as an explanation for the mixture of vesicles and ellipsoidal micelles present at low pH. However, polydispersity on its own does not explain the appearance of long-lived vesicles at high pH or the addition-rate effect. It is also worth noting that C13E7Ac, which has a broadly similar (albeit slightly narrower) EO distribution, exhibits only a very weak addition-rate effect.
0.25), it also features a broad distribution of EO units (from 2 to 16, see Fig. S2 in the ESI†). The difference in size and solubility between headgroups containing 2 EO units and those containing 16 EO units is substantial and the presence of such a broad distribution will undoubtedly give rise to different self-assembly behaviour than would be present if the chain lengths were monodisperse. Indeed, it has previously been observed that the surfactant C12E10Ac does not form vesicles in aqueous solution, even at low pH.16,18 Furthermore, an investigation into surfactant mixtures of C18E20 and C18E100, revealed that although they generally form mixed micelles, the constituent surfactants segregate into separate structures when one of them undergoes a phase change.33 It is therefore not unreasonable to invoke polydispersity as an explanation for the mixture of vesicles and ellipsoidal micelles present at low pH. However, polydispersity on its own does not explain the appearance of long-lived vesicles at high pH or the addition-rate effect. It is also worth noting that C13E7Ac, which has a broadly similar (albeit slightly narrower) EO distribution, exhibits only a very weak addition-rate effect.
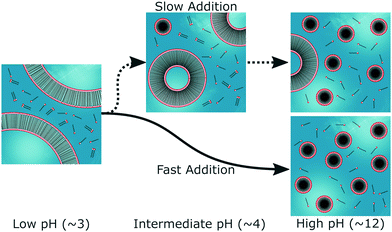
The pronounced effects of increasing the concentration of NaCl imply that electrostatic interactions play a crucial role in mediating this phenomenon; both those between neighbouring headgroups and those between the surface of the aggregates and the ionic species present in the solution. To understand why this may be the case, it may be instructive to consider the self-assembly process on a molecular level (Fig. 9). The reason why single-chain, weak-acid surfactant molecules can form vesicles, is thought to be due to their propensity to form ‘acid soaps’, i.e. acid-carboxylate dimers.13–15 The formation of vesicles tends to be centred on the pKa of the surfactant, as this is the point at which there is an equivalent amount of acidic and anionic surfactant molecules present in solution.16 Acid soaps are also found in the analogous case of fatty acids, where the formation of stable vesicles is only observed in this pH range.31,32 The hydrogen-bond between the resulting dimers can be very strong and has been shown to play a significant role in the self-assembly behaviour of n-alkyl carboxylic acids.34 In addition, bilayers or vesicles composed of acid-carboxylate dimers are anionic and have the capacity to sequester cations. This means the local pH in the vicinity of the vesicles may be up to 3 units below that of the bulk.35 The presence of acid-anion dimers therefore offers some clues regarding the longevity of vesicles up to higher pH values than might otherwise be expected.
Clearly, the above explanation is not complete. As the pH increases, the carboxylic headgroups of the surfactant should become deprotonated and the fraction of dimerised species should decrease. This, in turn, should lead to an increase in the electrostatic repulsion between the headgroups and naïvely, one would therefore expect all of the vesicles to eventually break apart. Despite extensive experimental efforts, the reasons why this does not occur when the pH is changed very slowly, are unclear. Furthermore, the acid-carboxylate hypothesis cannot explain the effect of NaCl on the self-assembly process. When NaCl is present prior to the addition of the base, even in small concentrations, it eliminates the presence of vesicles at high pH. However, it was seen in ref. 21 that when NaCl is present at low pH, it appears to initially promote the presence of monodisperse vesicles, before subsequently suppressing them at high pH (SANS data reproduced in Fig. S9, ESI†). These observations suggest that NaCl stabilises the vesicles at low pH but lowers the activation energy for vesicle disintegration at high pH.
5 Conclusions
It is postulated that these effects arise from a combination of the polydispersity in the length of the EO block and the propensity of single chain weak-acid surfactants to form acid-carboxylate dimers – a phenomenon also found in fatty acids.31,32 It is known that in conditions close to the pKa of the surfactant, the formation of stable vesicles occurs, however we have also shown that the effect is not simply related to the amount of time spent close to the pKa. Rather, the important parameter is the rate of change of pH; by slowing down the addition rate, a substantial fraction of vesicles (up to 40 wt%) is preserved. As the pH increases, the vesicle-to-micelle transition becomes inhibited and at pH 10, the structures are kinetically trapped in vesicle form with a relaxation time of approximately 70 days. The presence of NaCl facilitates the vesicle-to-micelle transition, potentially by disrupting the acid-carboxylate bond. This is not a complete explanation and further work is required to identify the exact mechanisms underlying this phenomenon. However, this effect could be very interesting both from a fundamental physical chemistry standpoint (e.g. as a model system to probe the vesicle-to-micelle transition) as well as from an applications perspective (e.g. as a mechanism for controlling the encapsulation and delivery of vesicle-borne cargo).Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the ILL for the allocated beamtime and the Partnership for Soft Condensed Matter (PSCM) for the use of their instruments. D. W. H. was supported by BMBF grant [05K16KT1] and L. C. acknowledges the TU-Berlin and the ILL for postdoctoral funding through a three-year cooperation agreement.References
- K. Holmberg, B. Jönsson, B. Kronberg and B. Lindman, Surfactants and Polymers in Aqueous Solution, John Wiley & Sons, Ltd, Chichester, UK, 2002 Search PubMed.
- E. A. G. Aniansson, S. N. Wall, M. Almgren, H. Hoffmann, I. Kielmann, W. Ulbricht, R. Zana, J. Lang and C. Tondre, J. Phys. Chem., 1976, 80, 905–922 CrossRef CAS.
- A. Shioi and T. A. Hatton, Langmuir, 2002, 18, 7341–7348 CrossRef CAS.
- J. Leng, S. U. Egelhaaf and M. E. Cates, Europhys. Lett., 2002, 59, 311–317 CrossRef CAS.
- T. M. Weiss, T. Narayanan, C. Wolf, M. Gradzielski, P. Panine, S. Finet and W. I. Helsby, Phys. Rev. Lett., 2005, 94, 1–4 CrossRef.
- K. Bressel, M. Muthig, S. Prevost, J. Gummel, T. Narayanan and M. Gradzielski, ACS Nano, 2012, 6, 5858–5865 CrossRef CAS.
- R. G. Laughlin, Colloids Surf., A, 1997, 128, 27–38 CrossRef CAS.
- E. Feitosa, G. Karlsson and K. Edwards, Chem. Phys. Lipids, 2006, 140, 66–74 CrossRef CAS PubMed.
- V. Guida, Adv. Colloid Interface Sci., 2010, 161, 77–88 CrossRef CAS PubMed.
- H. Madani and E. W. Kaler, Langmuir, 1990, 6, 125–132 CrossRef CAS.
- Y. Talmon, D. F. Evans and B. W. Ninham, Science, 1983, 221, 1047–1048 CrossRef CAS PubMed.
- J. E. Brady, D. F. Evans, B. Kachar and B. W. Ninham, J. Am. Chem. Soc., 1984, 106, 4279–4280 CrossRef CAS.
- P. Walde, M. Wessicken, U. Rädler, N. Berclaz, K. Conde-Frieboes and P. L. Luisi, J. Phys. Chem. B, 1997, 101, 7390–7397 CrossRef CAS.
- T. Sakai, M. Miyaki, H. Tajima and M. Shimizu, J. Phys. Chem. B, 2012, 116, 11225–11233 CrossRef CAS PubMed.
- T. Sakai, R. Ikoshi, N. Toshida and M. Kagaya, J. Phys. Chem. B, 2013, 117, 5081–5089 CrossRef CAS PubMed.
- A. Renoncourt, P. Bauduin, E. Nicholl, D. Touraud, J. M. Verbavatz, M. Dubois, M. Drechsler and W. Kunz, ChemPhysChem, 2006, 7, 1892–1896 CrossRef CAS PubMed.
- N. Vlachy, C. Merle, D. Touraud, J. Schmidt, Y. Talmon, J. Heilmann and W. Kunz, Langmuir, 2008, 24, 9983–9988 CrossRef CAS PubMed.
- L. Chiappisi, Adv. Colloid Interface Sci., 2017, 250, 79–94 CrossRef CAS PubMed.
- H. W. Stache, Anionic Surfactants: Organic Chemistry, Taylor & Francis, 1995 Search PubMed.
- G. Czichocki, H.-R. Holzbauer and C. Martens, Fett Wiss. Technol., 1992, 94, 66–73 CAS.
- D. W. Hayward, L. Chiappisi, S. Prévost, R. Schweins and M. Gradzielski, Sci. Rep., 2018, 8, 7299 CrossRef PubMed.
- D. Leinweber, U. Dahlmann and R. Kupfer, Process for the solvent-free preparation of ethercarboxylic acids having a low residual salt content, US Pat. 7208118, 2007 Search PubMed.
- T. A. Cripe, Process for making alkyl ethoxy carboxylates, US Pat. 5233087, 1993 Search PubMed.
- P. Lindner and R. Schweins, Neutron News, 2010, 21, 15–18 CrossRef.
- D. W. Hayward, L. Chiappisi, S. Prévost and R. Schweins, Internal time on D11, 2017, DOI:10.5291/ILL-DATA.INTER-354.
- S. Hansen, Eur. Biophys. J., 2018, 47, 179–184 CrossRef PubMed.
- H. Oikawa, Polymer, 1992, 33, 1116–1119 CrossRef CAS.
- A. J. F. Siegert, On the fluctuations in signals returned by many independently moving scatterers, Radiation Laboratory, Massachusetts Institute of Technology, 1943 Search PubMed.
- M. Shibayama, T. Karino and S. Okabe, Polymer, 2006, 47, 6446–6456 CrossRef CAS.
- S. Bucak, B. H. Robinson and A. Fontana, Langmuir, 2002, 18, 8288–8294 CrossRef CAS.
- K. Fontell and L. Mandell, Colloid Polym. Sci., 1993, 271, 974–991 CrossRef CAS.
- P. Walde, T. Namani, K. Morigaki and H. Hauser, Liposome Technology, Informa Healthcare, 2006, vol. I, pp. 1–19 Search PubMed.
- B. Plazzotta, J. Dai, M. A. Behrens, I. Furó and J. S. Pedersen, J. Phys. Chem. B, 2015, 119, 10798–10806 CrossRef CAS PubMed.
- R. Smith and C. Tanford, Proc. Natl. Acad. Sci. U. S. A., 1973, 70, 289–293 CrossRef CAS PubMed.
- T. H. Haines, Proc. Natl. Acad. Sci. U. S. A., 1983, 80, 160–164 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00950g |
| ‡ From the SANS results, it can be seen that there is a structure factor peak, which has been ascribed to electrostatic interactions between the smaller, micellar components. To account for this, in each case a structure factor correction, 1/S (Q → 0), has been applied to the smaller of the radii obtained by DLS as quoted in the text. |
| § Including the 1 mM present in the as received surfactant. |
| This journal is © The Royal Society of Chemistry 2019 |