Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamics of individual Brownian rods in a microchannel flow†
Andreas
Zöttl
 *ab,
Kira E.
Klop
c,
Andrew K.
Balin
b,
Yongxiang
Gao
cd,
Julia M.
Yeomans
*ab,
Kira E.
Klop
c,
Andrew K.
Balin
b,
Yongxiang
Gao
cd,
Julia M.
Yeomans
 b and
Dirk G. A. L.
Aarts
c
b and
Dirk G. A. L.
Aarts
c
aInstitute for Theoretical Physics, TU Wien, Wiedner Hauptstraße 8-10, Wien, Austria. E-mail: andreas.zoettl@tuwien.ac.at
bThe Rudolf Peierls Centre for Theoretical Physics, University of Oxford, Clarendon Lab., Parks Rd., Oxford, OX1 3PU, UK
cDepartment of Chemistry, Physical and Theoretical Chemistry Laboratory, University of Oxford, Oxford, OX1 3QZ, UK
dInstitute for Advanced Study, Shenzhen University, Nanhai Avenue 3688, Nanshan District, Shenzhen, 518060, China
First published on 9th July 2019
Abstract
We study the orientational dynamics of heavy silica microrods flowing through a microfluidic channel. Comparing experiments and Brownian dynamics simulations we identify different particle orbits, in particular in-plane tumbling behavior, which cannot be explained by classical Jeffery theory, and we relate this behavior to the rotational diffusion of the rods. By constructing the full, three-dimensional, orientation distribution, we describe the rod trajectories and quantify the persistence of Jeffery orbits using temporal correlation functions of the Jeffery constant. We find that our colloidal rods lose memory of their initial configuration in about a second, corresponding to half a Jeffery period.
Understanding the physics of a micron-scale, elongated particle moving in viscous flows is widely relevant. Examples include the effect of shape on nano-particle assisted drug delivery,1 the dynamics of flowing suspensions of bacteria,2 nanoengineering optically anisotropic devices3 and the processing of food and pastes.4 The orientational behavior of a single, non-Brownian, ellipsoidal rod in a simple shear flow was analyzed theoretically in a classic paper by Jeffery in 19225 who found that the orientation of an axisymmetric ellipsoid undergoes a periodic motion on the unit sphere. Assuming that the flow is in the x direction and that the shear gradient is along z (see also Fig. 1(a) for non-uniform shear), the specific orbit a particle follows is determined by its aspect ratio λ, the shear rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and the Jeffery constant
and the Jeffery constant 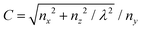 which depends on the initial orientation of the rod and ranges from −∞ to ∞. Here, the unit vector n = nx
which depends on the initial orientation of the rod and ranges from −∞ to ∞. Here, the unit vector n = nx![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + nyŷ + nzẑ points along the long axis of the particle. For C = ±∞ the rod rotates in the xz-plane. It is oriented along the direction of flow for most of the time, but periodically “tumbles”, i.e. flips its orientation by 180°. For smaller values of C, the motion has a finite y-component, and looks very similar to the trajectory of the paddles of a kayak if viewed from the side, hence the term “kayaking” for these orbits. At C = 0, the rod orients along the y-direction and only rotates around its long axis. This last type of motion is called “log-rolling”, and has been shown to be unstable for rod-shaped particles.6 Experiments on single rods, carried out in the non-Brownian regime, have demonstrated the applicability of Jeffery's ideas.7
+ nyŷ + nzẑ points along the long axis of the particle. For C = ±∞ the rod rotates in the xz-plane. It is oriented along the direction of flow for most of the time, but periodically “tumbles”, i.e. flips its orientation by 180°. For smaller values of C, the motion has a finite y-component, and looks very similar to the trajectory of the paddles of a kayak if viewed from the side, hence the term “kayaking” for these orbits. At C = 0, the rod orients along the y-direction and only rotates around its long axis. This last type of motion is called “log-rolling”, and has been shown to be unstable for rod-shaped particles.6 Experiments on single rods, carried out in the non-Brownian regime, have demonstrated the applicability of Jeffery's ideas.7
Subsequent research has shown how the many perturbations present in flowing channels can affect the reproducibility and longevity of the orbits. For example, even small deviations from a perfect axisymmetric rod shape can lead to the appearance of doubly periodic and chaotic orbits, and these have been studied both theoretically and experimentally.8–10 The proximity of channel walls,11–15 inertia6 and the viscoelasticity of the shearing fluid16 have also been shown to perturb the Jeffery solution. Furthermore, noise may also affect the orbits: for smaller rods, where Brownian motion (i.e. thermal noise) is relevant, there has been work using rheo-optical techniques to measure rod distributions,17,18 and these have been compared to theoretical predictions and Brownian dynamics simulations.19–22 However, we are not aware of any existing experiments tracking individual trajectories of highly Brownian rods under shear.
With the advent of improved imaging techniques such experiments are now possible and here we describe observations of the individual trajectories of rods which are about 3 microns in length as they move through microchannels under Poiseuille flow. Orbits are modified substantially in the presence of strong thermal noise which affects the orientational motion of individual rods. In particular we find that, for rods a few microns in length, Jeffery orbits can only be observed at very large shear rates, and that the persistence of Jeffery orbits is very sensitive to the size of the rods. Reconstructing the full three-dimensional distribution of orientations we quantify the competition between Jeffery rotation and strong rotational Brownian motion which leads to fast decorrelation of the orientational state of a rod. We quantify this in terms of the decay of the temporal autocorrelation of the Jeffery ‘constant’: whereas 30 μm rods are well described by neglecting rotational diffusion,7 rods of 3.3 μm typically do not complete even a single complete Jeffery rotation. Using Brownian dynamics simulations we show that Brownian noise, Jeffery rotation, and gravity are sufficient to explain the experimental results.
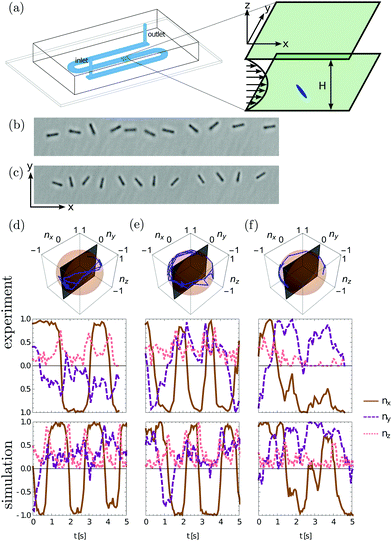
Silica rods with length 3–4 μm, diameter 0.5–0.7 μm and average aspect ratio λ = 5.523 were dispersed in deionized water. The concentration of rods was 10 particles per nl at most, such that the particles were far apart and did not interact with each other. The rods were not perfectly symmetric but bullet-shaped, with one end being a spherical cap while the other end was straight.24 Microfluidic devices with a simple, unbranched channel, of height H = 10 μm and width 300 μm, were prepared using standard soft-lithography techniques for PDMS. The channel consisted of two bends which were purely to increase the length of the channel, so that the rods had enough time to settle and reach a steady state before being imaged. Particles were imaged in the centre of the second straight segment, such that the effect of the bends as well as the lateral side walls could be neglected. Channels were plasma cleaned before use and a flow was achieved by imposing a pressure difference between the inlet and outlet tubes. As the silica rods sediment easily, the rods were expected to be distributed around the bottom wall of the channel.
The system was imaged in the xy-plane, using a Zeiss LSM 5 Exciter in bright field mode, with a 63 × 1.4 NA oil-immersion objective. Image series of 1000 frames with a rate of 10 frames per second were recorded using a Ximea MQ042MG-CM CMOS camera, see Video S1 of the ESI.† Particles were thus tracked through time and their positions, orientations in the xy-plane, ϕ = arctan(ny/|nx|), and lengths Lp projected to the xy plane determined in each frame using image analysis techniques. In total we analyzed the data for 115 rods which were tracked for at least for 25 frames or 2.5 s.
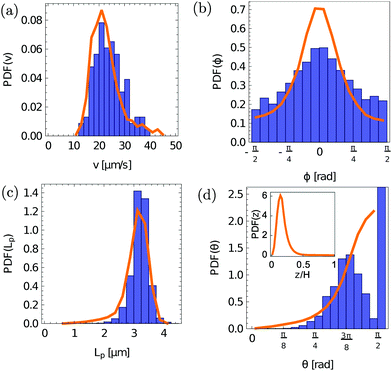
The instantaneous and average velocity of each particle was determined by calculating the distance travelled in a frame or complete track respectively, and dividing by the time. The instantaneous velocity was found to be relatively constant for all particles, changing by no more than a few μm s−1 throughout the time the particle was tracked. In contrast, the mean velocities of individual rods are spread in a range of 10–40 μm s−1 and peaked around 25 μm s−1, see Fig. 2(a). As the width and length of the channels are much larger than their height, the flow profile was comparable to a Hele-Shaw flow,25i.e. a plane Poiseuille flow in the xz-plane, whereas the flow velocity was constant in the xy-plane except close to the side walls. The particles flowing through the channels therefore experienced a non-uniform, asymmetric shear in the xz-plane, see Fig. 1(a). Since in Poiseuille flow the velocity of rods is connected to the lateral position in the channel, we conclude that different rods move at different average distances from the bottom surface but stay at almost constant height for individual tracks.
Examples of rod behavior, illustrated in Fig. 1, show clearly that the orientational behavior of the rods did not follow simple Jeffery orbits. For some rods Jeffery-like kayaking behavior was observed (Fig. 1(c)) where the rod's orientation nx occasionally flipped by approximately 180° while ny remained either positive or negative (Fig. 1(d) and Video S2 of the ESI†). However, most of the rods were able to change the sign of ny dynamically so that the rods then tumbled in the xy plane (see Fig. 1(b), (e) and Video S3 of the ESI†), which is not possible for non-Brownian Jeffery orbits. Other trajectories showed even more irregular motion where no clear oscillation could be identified (see for example Fig. 1(f)). Simple Jeffery tumbling motion in the xz plane was not observed.
Fig. 2(b) shows the time-and ensemble averaged distribution for the angle ϕ which characterizes the rod orientation in the xy-plane. The distribution is peaked and almost symmetric around zero, meaning the particles are most likely to align with the flow-direction. The lengths Lp of the rods projected to the xy plane are plotted in Fig. 2(c). The distribution peaks around 3.1 μm and does not have a sharp cut-off to larger lengths due to the polydispersity of the rods and due to effects coming from the finite resolution of the image analysis. The width of the distribution to smaller lengths stems from the out-of-plane orientation of rods.
While the angle ϕ can be extracted directly from the tracked rods in the xy-plane, determining the out-of-plane angle θ = arcsin|nz| is less obvious. The length of the rod in the z direction is unknown and cannot be simply extracted from Lp due to the small polydispersity in the length L of our rods. Following ref. 23, θ is calculated using 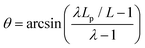 . Since it is not possible to measure the length L of each individual rod, we use L = 3.3 μm, the average rod length, for all rods. Hence, θ can only be estimated, and it is possible that Lp > L. In this case we always assume that the rod is aligned in the xy-plane, where θ = π/2. In Fig. 2(d) we show the distribution of θ which includes the artificial peak at θ = π/2. Note that while we can fully determine the orientation components nx and ny, which lie in the range (−1,1), we can estimate nz = sin
. Since it is not possible to measure the length L of each individual rod, we use L = 3.3 μm, the average rod length, for all rods. Hence, θ can only be estimated, and it is possible that Lp > L. In this case we always assume that the rod is aligned in the xy-plane, where θ = π/2. In Fig. 2(d) we show the distribution of θ which includes the artificial peak at θ = π/2. Note that while we can fully determine the orientation components nx and ny, which lie in the range (−1,1), we can estimate nz = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ only up to a sign, and we chose nz > 0, see Fig. 1.
θ only up to a sign, and we chose nz > 0, see Fig. 1.
The observed orientational behavior of the silica rods deviates in many ways from Jeffery's theory. The most obvious difference lies in the aperiodicity of the dynamics and the apparent random jumping between orbits characterized by different values of the Jeffery constant C. The Brownian motion of the rods changes their orientation in such a way that they move continually from one orbit to another, leading to randomness in the orientational dynamics.
In order to identify the relative importance and interplay of shear rate, Brownian noise, gravity and confinement, we performed Brownian dynamics (BD) simulations of an ellipsoid in Poiseuille flow using the experimental parameters. A rod is approximated by a prolate ellipsoid of length L = 3.3 μm, width W = 0.6 μm, aspect ratio λ = 5.5 and volume V = 0.62 μm3. We approximate the parallel and perpendicular translational (D‖ and D⊥) and rotational (Dr) diffusion coefficients of a rod at room temperature and water viscosity using analytic expressions for a prolate ellipsoid,26 which gives D‖ = 0.39 μm2 s−1, D⊥ = 0.29 μm2 s−1, Dr = 0.21 s−1. Since the rods are approximately 90% heavier than water, they experience a density difference Δρ = 900 kg m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 resulting in a typical sedimentation velocity vs = VΔρg/γs = 0.46 μm s−1, where γs is a typical friction coefficient estimated as γs = 2kBT/(D‖ + D⊥). The corresponding gravitational Péclet number27α = VΔρgL/kBT = 4.2, or, equivalently, the sedimentation length is Lsed = L/α = 0.7 μm. Hence Lsed + L/2 can be interpreted as the typical length a rod is away from the bottom wall due to thermal fluctuations and steric effects. We neglect hydrodynamic interactions with the wall as these are sufficiently small that they will have only a minor effect on the rod's orientation dynamics.28
23 resulting in a typical sedimentation velocity vs = VΔρg/γs = 0.46 μm s−1, where γs is a typical friction coefficient estimated as γs = 2kBT/(D‖ + D⊥). The corresponding gravitational Péclet number27α = VΔρgL/kBT = 4.2, or, equivalently, the sedimentation length is Lsed = L/α = 0.7 μm. Hence Lsed + L/2 can be interpreted as the typical length a rod is away from the bottom wall due to thermal fluctuations and steric effects. We neglect hydrodynamic interactions with the wall as these are sufficiently small that they will have only a minor effect on the rod's orientation dynamics.28
The rod moves in a planar Poiseuille flow vf characterized by a wall shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . We use the experimental channel dimensions and do not allow the rod to penetrate the walls. Brownian dynamics simulations are used to calculate the rod position r and orientation n:
. We use the experimental channel dimensions and do not allow the rod to penetrate the walls. Brownian dynamics simulations are used to calculate the rod position r and orientation n:
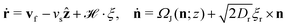 | (1) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) accounts for the translational diffusion of the rod (for details see ref. 29), ΩJ(n;z) is Jeffery's reorientation rate which depends linearly on the local shear rate
accounts for the translational diffusion of the rod (for details see ref. 29), ΩJ(n;z) is Jeffery's reorientation rate which depends linearly on the local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) l(z) =
l(z) = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (1 − 2z/H), and ξ and ξr denote Gaussian white noise.
(1 − 2z/H), and ξ and ξr denote Gaussian white noise.
We perform simulations for different wall shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , averaging over 5000 rods with random initial conditions for each value of the shear. We find, as expected, that after equilibration all the rods are distributed in the lower half of the channel because of sedimentation due to gravity, see inset of Fig. 2(d). The shear rate
, averaging over 5000 rods with random initial conditions for each value of the shear. We find, as expected, that after equilibration all the rods are distributed in the lower half of the channel because of sedimentation due to gravity, see inset of Fig. 2(d). The shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) could be inferred from measurements of the distribution of particle velocities: using
could be inferred from measurements of the distribution of particle velocities: using ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 18 s−1 results in a velocity distribution that matches the experiments very well (see the orange curve in Fig. 2(a)). This value is used to create all of the simulation results shown in Fig. 2 and 3. We note that without including the sedimentation of the rods the velocity distribution cannot be reproduced.
= 18 s−1 results in a velocity distribution that matches the experiments very well (see the orange curve in Fig. 2(a)). This value is used to create all of the simulation results shown in Fig. 2 and 3. We note that without including the sedimentation of the rods the velocity distribution cannot be reproduced.
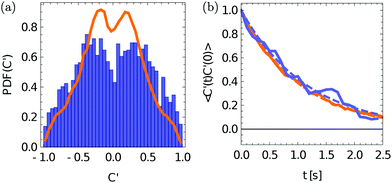 | ||
| Fig. 3 (a) Distribution of modified Jeffery constants C′. Color code as in Fig. 2. (b) Temporal auto-correlation function of C′ including exponential fits (blue: experiments; orange: simulations). | ||
We identify the same qualitative orientational behavior as observed in the experiments, as shown by the examples in Fig. 1(d)–(f). As a more quantitative comparison we compare the orientation distributions for the angles ϕ and θ in Fig. 2(b) and (d), obtaining the same trends as in the experiments. The peak for ϕ is more pronounced in the simulations which could result from the small shape asymmetry of the rods. The distribution for θ essentially captures the experimental values, but does not show the artificial sharp peak at θ = π/2. We also compare the distributions of projected rod lengths Lp in Fig. 2(c). The simulations reproduce the experiments well if we assume that the rod length L is normally distributed with standard deviation σ = 0.25 μm.
Brownian motion gives an explanation for the xy-tumbling motion, which is not predicted by Jeffery theory, and which has not been observed for anisotropic particles. If the rods follow a kayaking trajectory with a large amplitude, they come very close to aligning with the x-axis after each flip. In a Jeffery orbit a rod spends most of its time in this flow-aligned orientation. Similarly here the particle will spend some time performing Brownian motion around the flow-aligned direction, which could pull it to the other side of the x-axis before it starts another kayaking cycle, effectively making it tumble in the xy-plane. This is confirmed by our simulations, and an example trajectory is shown in Fig. 1(e).
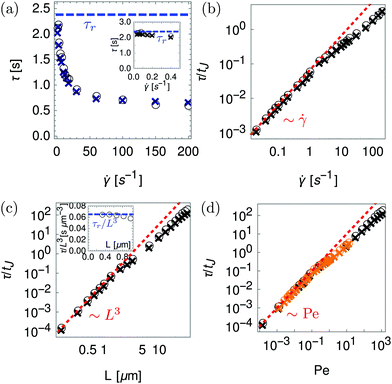
To quantify the competition between periodic Jeffery orbits and the influence of noise we determine the instantaneous Jeffery “constants” C(t) from both experiments and simulations. For convenience we use a modified Jeffery constant C′ = sign(C)/(1 + |C|) which maps to the interval C′ ∈ {−1,1} where C′ = 0 corresponds to C = ±∞ (rotation in xz plane) and C′ = ±1 to C = 0 (log rolling). The particle- and time-averaged distributions of C′, which are shown in Fig. 3(a), match reasonably well between experiments and simulations. In particular they show maxima in the distributions around C′ ∼ ±0.25. To determine the persistence of a Jeffery orbit, we compute the temporal C′ auto-correlation function 〈C′(t)C′(0)〉 which decays approximately exponentially as exp(−t/τ) (Fig. 3(b)). The decay time τ ≈ 1 s agrees very well between experiments (τ = 1.16 s) and simulations (τ = 1.05 s).
It is instructive to compare τ to the Jeffery oscillation period tJ = 2π(λ + λ−1)/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.98 s. τ/tJ gives the number of Jeffery oscillations a rod performs before losing information about its Jeffery orbit state. Since in our system τ/tJ ≈ 0.5 the rod does not even finish one turn before its state decorrelates, reiterating that we do not observe clear Jeffery orbits in the experiments or simulations.
= 1.98 s. τ/tJ gives the number of Jeffery oscillations a rod performs before losing information about its Jeffery orbit state. Since in our system τ/tJ ≈ 0.5 the rod does not even finish one turn before its state decorrelates, reiterating that we do not observe clear Jeffery orbits in the experiments or simulations.
In Fig. 4(a) we show the dependence of the Jeffery decorrelation time τ on the wall shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . We observe that τ decreases with increasing
. We observe that τ decreases with increasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) meaning that stronger shear leads to faster decorrelation. Interestingly, τ is smaller than the rotational diffusion time τr = 1/(2Dr) = 2.38 s (dashed blue curve in Fig. 4(a)) but approaches τr for vanishing shear rates (see inset of Fig. 4(a)), when the system is essentially governed by Brownian fluctuations only. Thus, at higher rates there is a competition between the relatively fast rotation on the unit sphere helping the fluctuations to faster decorrelate the memory of the Jeffery orbits and faster shear rates, and hence rotation rates, helping rods to finish Jeffery rotations before they are fully decorrelated. This can be seen in Fig. 4(b), where we plot τ per Jeffery reorientation time tJ which increases linearly with
meaning that stronger shear leads to faster decorrelation. Interestingly, τ is smaller than the rotational diffusion time τr = 1/(2Dr) = 2.38 s (dashed blue curve in Fig. 4(a)) but approaches τr for vanishing shear rates (see inset of Fig. 4(a)), when the system is essentially governed by Brownian fluctuations only. Thus, at higher rates there is a competition between the relatively fast rotation on the unit sphere helping the fluctuations to faster decorrelate the memory of the Jeffery orbits and faster shear rates, and hence rotation rates, helping rods to finish Jeffery rotations before they are fully decorrelated. This can be seen in Fig. 4(b), where we plot τ per Jeffery reorientation time tJ which increases linearly with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) for small
for small ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , and sub-linearly for higher
, and sub-linearly for higher ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , in accordance with Fig. 4(a), since tJ ∼
, in accordance with Fig. 4(a), since tJ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1. This indicates that only very large shear rates of
−1. This indicates that only very large shear rates of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102 s−1) would allow clear Jeffery orbits to be observed for several oscillations in experiments using our rods. Indeed such clear orbits have been observed for tumbling bacterial cell bodies in strong shear.30
(102 s−1) would allow clear Jeffery orbits to be observed for several oscillations in experiments using our rods. Indeed such clear orbits have been observed for tumbling bacterial cell bodies in strong shear.30
We also analyze the dependence of τ/tJ on the rod length L while keeping the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 18 s−1 and L/H = 0.33 constant. Fig. 4(c) shows a strong dependence on the rod length. For example, 10 μm long rods would already perform about 10 persistent oscillations. Again, for very small lengths L the orientational dynamics is mainly governed by rotational Brownian noise since τr ∼ L3. Indeed we show in the inset of Fig. 4(c) that τ ∼ L3 and that τ approaches τr for rod lengths on the order of L ≲ 500 nm.
= 18 s−1 and L/H = 0.33 constant. Fig. 4(c) shows a strong dependence on the rod length. For example, 10 μm long rods would already perform about 10 persistent oscillations. Again, for very small lengths L the orientational dynamics is mainly governed by rotational Brownian noise since τr ∼ L3. Indeed we show in the inset of Fig. 4(c) that τ ∼ L3 and that τ approaches τr for rod lengths on the order of L ≲ 500 nm.
The fact that for both small ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and small L the dynamics is governed by Brownian fluctuations, while for large
and small L the dynamics is governed by Brownian fluctuations, while for large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and L the dynamics becomes deterministic, can be captured by the rotational Péclet number Pe = τr/tJ = f(λ)
and L the dynamics becomes deterministic, can be captured by the rotational Péclet number Pe = τr/tJ = f(λ)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /Dr with f(λ) = [4π(λ + λ−1)]−1 which compares the rotational diffusion time with the Jeffery reorientation time. For our rods the shape function f(λ) = f(5.5) = 0.014 and our experiments are performed at Pe = 1.2. (Note that a common alternative definition of Pe omits this shape function.)
/Dr with f(λ) = [4π(λ + λ−1)]−1 which compares the rotational diffusion time with the Jeffery reorientation time. For our rods the shape function f(λ) = f(5.5) = 0.014 and our experiments are performed at Pe = 1.2. (Note that a common alternative definition of Pe omits this shape function.)
We plot the results for both varying shear rate and varying rod length, as discussed in Fig. 4(a)–(c), as a function of Pe in Fig. 4(d). Indeed the data for varying ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (shown in orange) and varying L (shown in black) collapses to a single curve. As expected, for very small Pe, τ ∼ Pe.
(shown in orange) and varying L (shown in black) collapses to a single curve. As expected, for very small Pe, τ ∼ Pe.
Finally we note that these results are not a consequence of gravity- and noise-induced cross-streamline migration or the steric interaction with the walls: keeping the z position of the particles fixed, for example at z = 0.2H, does not modify the results significantly, as shown in Fig. 4.
We have studied colloidal rods flowing in a plane Poiseuille flow, and observed particles performing stochastic kayaking and xy-tumbling motions. The latter behavior is not modelled within Jeffery theory, but can be explained by the Brownian nature of the rods. Rods are able to switch between different states, and their dynamics can be quantified by the Jeffery constant and its temporal correlations. Based on our findings, it would be interesting to study in the future the influence of the Brownian motion on denser suspensions of colloidal rods.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported through funding from the ERC Advanced Grant 291234 MiCE. A. Z. acknowledges funding from the Austrian Science Fund (FWF) through a Lise-Meitner Fellowship (Grant No. M 2458-N36), and from the European Union through a Marie Skłodowska Curie Intra-European Fellowship (G.A. No. 653284). Y. G. acknowledges financial support from the General Program of the National Natural Science Foundation of China (Project no. 11774237).Notes and references
- E. Blanco, H. Shen and M. Ferrari, Nat. Biotechnol., 2015, 33, 941 CrossRef CAS PubMed.
- G. Junot, N. Figueroa-Morales, T. Darnige, A. Lindner, R. Soto, H. Auradou and E. Clément, Europhys. Lett., 2019, 126, 44003 CrossRef.
- D. Fry, B. Langhorst, H. Kim, E. Grulke, H. Wang and E. K. Hobbie, Phys. Rev. Lett., 2005, 95, 038304 CrossRef CAS PubMed.
- E. Dickinson, Annu. Rev. Food Sci. Technol., 2015, 6, 211–233 CrossRef CAS PubMed.
- G. B. Jeffery, Proc. R. Soc. London, Ser. A, 1922, 102, 161–179 CrossRef.
- J. Einarsson, F. Candelier, F. Lundell, J. R. Angilella and B. Mehlig, Phys. Rev. E, 2015, 91, 041002 CrossRef CAS PubMed.
- J. Einarsson, A. Johansson, S. K. Mahato, Y. N. Mishra, J. R. Angilella, D. Hanstorp and B. Mehlig, Acta Mech., 2013, 224, 2281–2289 CrossRef.
- E. J. Hinch and L. G. Leal, J. Fluid Mech., 1979, 92, 591–607 CrossRef.
- A. L. Yarin, O. Gottlieb and I. V. Roisman, J. Fluid Mech., 1997, 340, 83–100 CrossRef.
- J. Einarsson, B. M. Mihiretie, A. Laas, S. Ankardal, J. R. Angilella, D. Hanstorp and B. Mehlig, Phys. Fluids, 2016, 28, 013302 CrossRef.
- A. Hijazi and A. Khater, Comput. Mater. Sci., 2001, 22, 279 CrossRef CAS.
- M. Zurita-Gotor, J. Bławzdziewicz and E. Wajnryb, J. Rheol., 2007, 51, 71 CrossRef CAS.
- A. Atwi, A. Khater and A. Hijazi, Polymer, 2013, 54, 1555 CrossRef CAS.
- E. Holmstedt, H. O. Akerstedt, T. S. Lundstrom and S. M. Hogberg, J. Fluids Eng., 2016, 138, 081203 CrossRef.
- S. Monjezi, J. D. Jones, A. K. Nelson and J. Park, Nanomaterials, 2018, 8, 130 CrossRef PubMed.
- D. Z. Gunes, R. Scirocco, J. Mewis and J. Vermant, J. Non-Newtonian Fluid Mech., 2008, 155, 39 CrossRef CAS.
- P. L. Frattini and G. G. Fuller, J. Fluid Mech., 1986, 168, 119 CrossRef CAS.
- D. Xie, M. Lista, G. G. Qiao and D. E. Dunstan, J. Phys. Chem. Lett., 2015, 6, 3815 CrossRef CAS PubMed.
- E. J. Hinch and L. G. Leal, J. Fluid Mech., 1973, 57, 753 CrossRef.
- A. Hijazi and M. Zoaeter, Eur. Polym. J., 2002, 38, 2207 CrossRef CAS.
- B. D. Leahy, D. L. Koch and I. Cohen, J. Fluid Mech., 2015, 772, 42 CrossRef CAS.
- D. Palanisamy and W. K. den Otter, J. Chem. Phys., 2018, 148, 194112 CrossRef PubMed.
- Y. Gao, A. K. Balin, R. P. Dullens, J. M. Yeomans and D. G. Aarts, Phys. Rev. Lett., 2015, 115, 248301 CrossRef PubMed.
- A. Kuijk, A. van Blaaderen and A. Imhof, J. Am. Chem. Soc., 2011, 133, 2346–2349 CrossRef CAS PubMed.
- P. Tabeling, Introduction to Microfluidics, Oxford University Press, Oxford, 2005 Search PubMed.
- S. Kim and S. J. Karila, Microhydrodynamics: Principles and Selected Applications, Dover Publications Inc., Mineaola, New York, 2005 Search PubMed.
- M. Enculescu and H. Stark, Phys. Rev. Lett., 2011, 107, 058301 CrossRef PubMed.
- C. Pozrikidis, J. Fluid Mech., 2005, 541, 105–114 CrossRef.
- D. Matsunaga, F. Meng, A. Zöttl, R. Golestanian and J. M. Yeomans, Phys. Rev. Lett., 2017, 119, 198002 CrossRef PubMed.
- T. Kaya and H. Koser, Phys. Rev. Lett., 2009, 103, 138103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00903e |
| This journal is © The Royal Society of Chemistry 2019 |