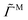Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhanced diffusion and magnetophoresis of paramagnetic colloidal particles in rotating magnetic fields
Zachary M.
Sherman
 a,
Julia L.
Pallone
a,
Randall M.
Erb
b and
James W.
Swan
*a
a,
Julia L.
Pallone
a,
Randall M.
Erb
b and
James W.
Swan
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: jswan@mit.edu; Tel: +1 (617) 324-7359
bDepartment of Mechanical and Industrial Engineering, Northeastern University, Boston, MA 02115, USA
First published on 5th August 2019
Abstract
Dispersions of paramagnetic colloids can be manipulated with external magnetic fields to assemble structures via dipolar assembly and control transport via magnetophoresis. For fields held steady in time, the dispersion structure and dynamic properties are coupled. This coupling can be problematic when designing processes involving field-induced forces, as particle aggregation competes against and hinders particle transport. Time-varying fields drive dispersions out-of-equilibrium, allowing the structure and dynamics to be tuned independently. Rotating the magnetic field direction using two biaxial fields is a particularly effective mode of time-variation and has been used experimentally to enhance particle transport. Fundamental transport properties, like the diffusivity and magnetophoretic mobility, dictate dispersions' out-of-equilibrium responses to such time-varying fields, and are therefore crucial to understand to effectively design processes utilizing rotating fields. However, a systematic study of these dynamic quantities in rotating fields has not been performed. Here, we investigate the transport properties of dispersions of paramagnetic colloids in rotating magnetic fields using dynamic simulations. We find that self-diffusion of particles is enhanced in rotating fields compared to steady fields, and that the self-diffusivity in the plane of rotation reaches a maximum value at intermediate rotation frequencies that is larger than the Stokes–Einstein diffusivity of an isolated particle. We also show that, while the magnetophoretic velocity of particles through the bulk in a field gradient decreases with increasing rotation frequency, the enhanced in-plane diffusion allows for faster magnetophoretic transport through porous materials in rotating fields. We examine the effect of porous confinement on the transport properties in rotating fields and find enhanced diffusion at all pore sizes. The confined and bulk values of the transport properties are leveraged in simple models of magnetophoresis through tortuous porous media.
Introduction
Electric and magnetic fields are useful for manipulating dispersions containing polarizable dielectric and paramagnetic colloids and nanoparticles. The field induces dipole and higher-order polarization moments within the particles, which interact with the polarization moments induced within other particles. This can be used to faciliate self-assembly of structures aligned with the field1,2 as well as modulate their macroscopic material properties on-the-fly.3–5 If the field is held steady in time, the dispersion can only respond by relaxing toward thermodynamic equilibrium, so its structure and dynamics are coupled. This coupling can be problematic when designing processes involving field-induced forces. For example, large interparticle dipolar forces that drive self-assembly of photonic crystals also tend to cause kinetic arrest;6,7 large field strengths that drive rapid magnetophoresis lead to particle aggregation that reduces mobility in porous media.8 If energy is supplied to vary the field in time, the dispersion is driven out of equilibrium. Unlike its equilibrium counterpart, the dispersion structure and dynamics can be tuned independently and optimized for a target application.9 Several types of field modulation have been investigated including toggling the field on and off6,7,10–16 and switching the field's polarity,17–22 but a particularly effective mode is rotating the field direction.23 The dipolar interactions among particles drive them to align in the field direction, forming chains that rotate with the field. This has been used to enhance mixing at the micron scale,24,25 amplify signals from biochemical sensors,26–28 propel artificial microswimmers,29–31 and assemble magnetic “conveyor-belts” to transport cargo.32Many researchers have considered paramagnetic nanoparticles as a means to transport drugs and molecules for targeted therapeutic applications.8,12,20,33 The nanoparticles can be localized to a specific site using magnetic field gradients to guide the particles magnetophoretically. In many cases, the target sites (e.g., tumor cells) are surrounded by dense, porous tissue through which the particles must navigate. It is advantageous to use large field strengths and large gradients to increase the flux of particles to the target site. If the field orientation is held steady during magnetophoresis, the dipole moments induced in the paramagnetic particles attract one another and the particles aggregate into long chains. The aggregate size can be much larger than the characteristic pore size, hindering the particles' mobility through the tissue or even preventing penetration into the tissue entirely. Soheilian, Erb, and coworkers proposed using rotating magnetic fields to suppress particle aggregation during magnetophoresis.8 The dispersed nanoparticles fit within the pores and readily navigated the tortuous porous network in rotating fields, so the flux of particles was greatly enhanced over magnetophoresis with a steady field. Fig. 1 illustrates these differences between magnetophoresis with steady and rotating fields. Understanding the transport of paramagnetic particles in rotating fields will facilitate their use for promising targeted therapeutic applications.
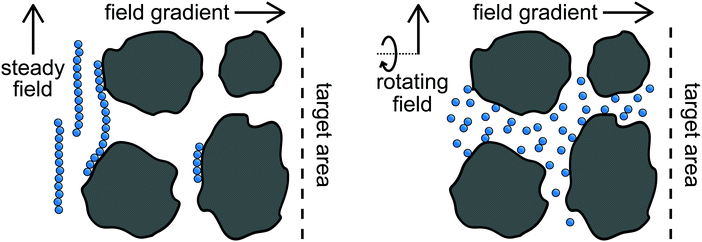 | ||
| Fig. 1 Schematic of magentophoresis in steady (left) and rotating (right) fields through a porous material. | ||
The case of individual chains at very dilute concentrations in a rotating field has been thoroughly investigated theoretically, computationally, and experimentally.25,34–42 At low rotation frequencies, the chains rotate at the same frequency as the field, but lag behind it. The steady-state lag angle balances the magnetic torque driving rotation with the viscous torque opposing it.34,38,39 The magnetic and viscous forces vary along the chain, causing the chain to adopt a slight “S” shape as it rotates.39 As the rotation frequency increases, the viscous shear forces along the chain overpower the attractive intrachain dipolar forces holding the chain together. The chain can break up with increasing frequency to reduce its drag while still rotating synchronously at the field frequency,35,36,43 or the chain can rotate asynchronously with the field and have complicated breakup and orbiting dynamics.8,44–47
Concentrated suspensions at very large rotation frequencies have also been investigated.48–57 When the rotation frequency is much larger than the characteristic diffusion time of the particles, the particles experience an effectively steady interparticle potential. This interaction is isotropically attractive in the plane of rotation and repulsive out of the plane of rotation, and the functional form is identical to that of regular dipolar interactions of half-strength oriented out-of-plane, but with the sign of attractions and repulsions switched (i.e., an “opposite” dipole interaction).48 High-frequency rotating fields are especially effective at forming large, two-dimensional sheets of particles in experiments.50,51,55,56 The complete phase diagram in high-frequency fields has been computed in simulations and reveals that the equilibrium phases are three-dimensional crystals.52
The dynamics and transport properties of concentrated dispersions of polarizable particles in rotating fields at intermediate frequencies have not been reported. Because many of the applications of such dispersions are governed by their out-of-equilibrium response to rotating fields, understanding the transport properties is crucial to effectively utilize rotating fields in practice. In this work, we use Brownian dynamics simulations to investigate diffusion and magnetophoretic transport of a three-dimensional dispersion of spherical, polarizable particles driven by a two-dimensional rotating magnetic field. Though either magnetic or electric fields can be used for rotation, magnetic fields are more common in experiments because their effects on the dispersion are easier to control, as electric fields can generate unwanted currents, electroosmotic flows, and electrochemical reactions. In this simulation study, we interpret our results from the perspective of a magnetic field-driven experiment. However, the mathematical treatment of either class of experiments is identical, so our results can apply to both rotating magnetic and electric fields. First, we describe our simulation method which takes into account many-bodied, mutual polarization among the particles as well many-bodied, hydrodynamic interactions. Next, we describe the steady-state response of the dispersion as a function of various system parameters. We quantify the long-time self-diffusivity of the particles, which is enhanced in rotating fields over steady fields. Then, we compute the magnetophoretic mobility of the particles in the bulk and propose a simple model to calculate the mobility in porous media. Finally, we elucidate the effect of porous confinement on the diffusion and magnetophoretic transport in porous media.
Simulation method
At the colloidal scale, the equations of motion for the position xi of a spherical particle i of mass mi are described by the Langevin equation,58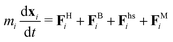 | (1) |
| xi(t + Δt) = xi(t) + ui(t)Δt | (2) |
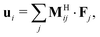 | (3) |
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) =
= ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) H·
H·![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) , where
, where ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) ≡ [u1, u2,…, uN]T is a list of the N particle velocities,
≡ [u1, u2,…, uN]T is a list of the N particle velocities, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ≡ [F1, F2,…, FN]T is a list of particle forces,
≡ [F1, F2,…, FN]T is a list of particle forces, ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) H is the grand hydrodynamic mobility tensor whose ijth block entries are MHij, and the T superscript indicates transposition. An approximation for MHij is the Rotne–Prager–Yamakawa tensor,
H is the grand hydrodynamic mobility tensor whose ijth block entries are MHij, and the T superscript indicates transposition. An approximation for MHij is the Rotne–Prager–Yamakawa tensor,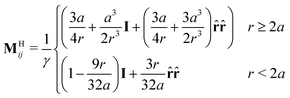 | (4) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ≡ r/r, and γ ≡ 6πηa is the Stokes drag of a sphere of radius a in a solvent of viscosity η.61MHij can be succinctly written in periodic geometries with its Fourier-space representation
≡ r/r, and γ ≡ 6πηa is the Stokes drag of a sphere of radius a in a solvent of viscosity η.61MHij can be succinctly written in periodic geometries with its Fourier-space representation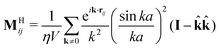 | (5) |
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) ]T is the wavevector, k ≡ |k|,
]T is the wavevector, k ≡ |k|, ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ≡ k/k, Lx, Ly, and Lz are the dimensions of the periodic simulation cell, and V ≡ LxLyLz is its volume.62 This far-field representation of the hydrodynamic mobility tensor treats each particle as a regularized point force plus a point quadrupole generating a Stokeslet that entrains the other particles. Because this is the dominant contribution to the hydrodynamic interactions, we neglect higher order force moments (e.g., torques and stresslets) for computational efficiency. The set of stochastic Brownian forces
≡ k/k, Lx, Ly, and Lz are the dimensions of the periodic simulation cell, and V ≡ LxLyLz is its volume.62 This far-field representation of the hydrodynamic mobility tensor treats each particle as a regularized point force plus a point quadrupole generating a Stokeslet that entrains the other particles. Because this is the dominant contribution to the hydrodynamic interactions, we neglect higher order force moments (e.g., torques and stresslets) for computational efficiency. The set of stochastic Brownian forces ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) B ≡ [FB1,FB2,…,FBN]T satisfies
B ≡ [FB1,FB2,…,FBN]T satisfies〈![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) B〉 = 0, 〈 B〉 = 0, 〈![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) B B![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) B〉 = 2kBT( B〉 = 2kBT(![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) H)−1/Δt H)−1/Δt | (6) |
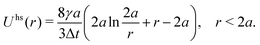 | (7) |
We refer to the above method of handling hydrodynamic interactions as the “HI model”. We also consider the “freely draining” (FD) model, which neglects interparticle hydrodynamic interactions, MHij = 0 for i ≠ j, so that the drag on each particle is decoupled from all of the others and equal to the Stokes drag, MHii = I/γ. In this case, the hard sphere potential takes a different form Uhs(r) = γ(r − 2a)2/4Δt.64 For this work, we always use the HI model unless the FD model is specifically referenced.
For the interparticle magnetic polarization forces, we use a mutual dipole model, where the dipole moment induced in one particle is affected by the fields generated from the dipole moments induced in all the other particles. The magnetic forces are many-bodied and first require finding the unknown particle dipoles by solving
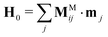 | (8) |
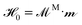 , where
, where 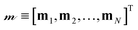 is a list of particle dipoles,
is a list of particle dipoles, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 0 ≡ [H0, H0,…, H0]T is the external field repeated N times, and
0 ≡ [H0, H0,…, H0]T is the external field repeated N times, and ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) M is the grand potential tensor whose ijth block entries are MMij. An approximation for MMij is
M is the grand potential tensor whose ijth block entries are MMij. An approximation for MMij is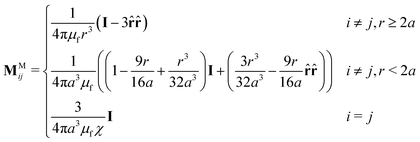 | (9) |
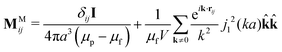 | (10) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) M is inverted at each time step to find the unknown particle dipoles as
M is inverted at each time step to find the unknown particle dipoles as 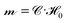 , where
, where ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ≡ (
≡ (![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) M)−1 is called the grand capacitance tensor. The inversion is performed numerically using an iterative scheme GMRES68 with a spectrally-accurate Ewald method to compute
M)−1 is called the grand capacitance tensor. The inversion is performed numerically using an iterative scheme GMRES68 with a spectrally-accurate Ewald method to compute 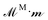 .9,69 Then, the force on a particle i is
.9,69 Then, the force on a particle i is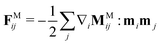 | (11) |
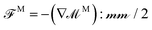 , where
, where ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) M ≡ [FM1,FM2,…, FMN]T.67,70
M ≡ [FM1,FM2,…, FMN]T.67,70
The external field rotates in the xy-plane with frequency ν
H0(t) = H0[cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt, sin ωt, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt, 0], ωt, 0], | (12) |
This description for the magnetic interactions assumes the magnetization of a particle is linearly dependent on the local field. This is a good approximation for small field strengths, but the dipole moment eventually saturates to a finite value at large field strengths. Above the saturation field, the particles can no longer mutually polarize one another and a constant dipole model can be descriptive of the suspension. Such a model is not considered here, and we assume the field strength is small enough to be in the linear limit. The magnitude of the susceptibility |χ| controls how strong mutual polarization among particles is relative to the polarization due solely to the external field H0. This qualitatively changes the many-body description of the dispersion and has a substantial effect on the phase behavior.67 Here, we focus on the limit of “perfectly susceptible” particles with χ = 3 and μp → ∞. We could have picked an arbitrary χ value, but this limiting case at the maximum possible |χ| lets us easily probe the effects of mutual polarization. Real suspensions have χ < 3, so mutual polarization is not as strong as those observed in our simulations. Truncating polarization moments at the dipole level in eqn (9) and (10) is accurate when particles are well separated, but higher-order moments become important as particles move close together. In fact for perfectly susceptible particles, the force between a pair at contact and the dipole moments for a chain of particles in contact diverges if an infinite number of moments are accounted for.65,73 It is possible to include this divergence with “lubrication-like” pairwise interactions.65 However, this divergence is not realized in real systems because particles never come into true contact and other surface forces dominate particle interactions on these short length scales. Because we only include dipole moments, all forces and dipoles are finite at contact. The interactions are regularized as the particles overlap, r < 2a, so that they remain solutions to the governing magnetostatic equations but stay finite as r → 0.67 The level of detail we have included in the simulations reproduces the phase behavior observed in experiments with steady fields.67
The natural nondimensionalization scheme scales lengths by the particle radius a, energies by the thermal energy kBT, time by the bare diffusion time τD ≡ 6πηa3/kBT, and external field by 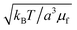 . Other quantities are nondimensionalized by combinations of these four, such as dipoles scaled by
. Other quantities are nondimensionalized by combinations of these four, such as dipoles scaled by 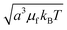 (i.e., a3μf times the field scale). A tilde is used to indicate the nondimensionalized version of a dimensional quantity, for example frequency
(i.e., a3μf times the field scale). A tilde is used to indicate the nondimensionalized version of a dimensional quantity, for example frequency ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) =ντD. We choose a time step of Δ
=ντD. We choose a time step of Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 10−3 for frequencies
= 10−3 for frequencies ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ≤ 10, which is short enough to resolve dynamics within a single rotation. For higher frequencies
≤ 10, which is short enough to resolve dynamics within a single rotation. For higher frequencies ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) > 10, we decrease the time step to Δ
> 10, we decrease the time step to Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 10−4. For all simulations, we use N = 8000 particles in a cubic, periodic simulation box. Limited testing with larger system sizes of N = 64
= 10−4. For all simulations, we use N = 8000 particles in a cubic, periodic simulation box. Limited testing with larger system sizes of N = 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 did not change our results. We first thermalized the dispersion for 100τD with no applied field to obtain a random configuration. The rotating field is then turned on, and the dispersion is allowed to equilibrate for 500–2500τD. Data is then collected and averaged over 100–2500τD. The wide range of simulation times was required for simulations at low frequencies, which needed long acquisition times to resolve full rotation cycles. Simulations at larger frequencies equilbrated quickly and only needed short data acquisition times. Snapshots depicting the simulation geometry and typical configurations are shown in Fig. 2.
000 did not change our results. We first thermalized the dispersion for 100τD with no applied field to obtain a random configuration. The rotating field is then turned on, and the dispersion is allowed to equilibrate for 500–2500τD. Data is then collected and averaged over 100–2500τD. The wide range of simulation times was required for simulations at low frequencies, which needed long acquisition times to resolve full rotation cycles. Simulations at larger frequencies equilbrated quickly and only needed short data acquisition times. Snapshots depicting the simulation geometry and typical configurations are shown in Fig. 2.
Steady-state
In a steady, nonrotating field, particles align and form chains in the direction of the applied field. At low field strengths![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 and volume fractions ϕ, there is an equilibrium distribution of chain lengths whose mean Nc increases as the field or volume fraction increases.4 Because the particles mutually polarize each other as they chain, there is a distribution of dipole moments whose mean m also increases in magnitude m ≡ |m| with
0 and volume fractions ϕ, there is an equilibrium distribution of chain lengths whose mean Nc increases as the field or volume fraction increases.4 Because the particles mutually polarize each other as they chain, there is a distribution of dipole moments whose mean m also increases in magnitude m ≡ |m| with ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 and ϕ.67 For sufficiently large field strengths and volume fractions, chain–chain interactions drive crystallization, and the dispersion reaches fluid/body-centered tetragonal (BCT) crystal coexistence.67,74
0 and ϕ.67 For sufficiently large field strengths and volume fractions, chain–chain interactions drive crystallization, and the dispersion reaches fluid/body-centered tetragonal (BCT) crystal coexistence.67,74
At sufficiently low densities and low field strengths, the chains are much shorter than the interchain distance, and the dispersion in rotating fields can be described by the well-studied single chain results.25,34–42 For small rotation frequencies, the equilibrium distribution of chain lengths and dipole strengths in steady fields is not perturbed much, but the viscous drag on the chains causes them to lag behind the field by an angle θ. For a straight chain of length Nc and rotation frequency ν, the lag angle is that which balances the total magnetic torque driving the rotation, ΓMtot = Nc|m × H0| ∼ Nc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ, with the hydrodynamic torque opposing it, ΓHtot ∼ νNc3, and the lag angle goes as sin
2θ, with the hydrodynamic torque opposing it, ΓHtot ∼ νNc3, and the lag angle goes as sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θ ∼ νNc2, increasing with rotation frequency.39 Because the chain length and dipole strength are relatively constant, the magnetic torque increases with ν. As the frequency becomes too large, increasing the lag angle cannot provide enough magnetic torque to sustain the rotation. Instead, the chain breaks up to lower its hydrodynamic torque, so the magnetic torque attains a maximum value at intermediate frequencies around where chains begin to break up. This breakup hinders mutual polarization and the dipole strength m of each particle drops with rotation frequency.
2θ ∼ νNc2, increasing with rotation frequency.39 Because the chain length and dipole strength are relatively constant, the magnetic torque increases with ν. As the frequency becomes too large, increasing the lag angle cannot provide enough magnetic torque to sustain the rotation. Instead, the chain breaks up to lower its hydrodynamic torque, so the magnetic torque attains a maximum value at intermediate frequencies around where chains begin to break up. This breakup hinders mutual polarization and the dipole strength m of each particle drops with rotation frequency.
At larger ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 and ϕ, several other factors complicate theoretical analysis. Chains of size Nc sweep out discs of radius aNc, and interchain interactions become important when these discs overlap. Because Nc can become quite large as
0 and ϕ, several other factors complicate theoretical analysis. Chains of size Nc sweep out discs of radius aNc, and interchain interactions become important when these discs overlap. Because Nc can become quite large as ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 and ϕ increase, especially for low frequencies, chain–chain interactions are important even at small volume fractions. Hydrodynamic flows generated within the dispersion as the chains rotate contribute additional shear forces that may affect chain break up. As chains bump into each other, they can break apart, reform, and assemble into different kinds of structures like platelets, sheets, and three-dimensional crystals (as seen in Fig. 2), so even the concept of “rotating chains” may not be appropriate for many real dispersions in rotating fields.51–53
0 and ϕ increase, especially for low frequencies, chain–chain interactions are important even at small volume fractions. Hydrodynamic flows generated within the dispersion as the chains rotate contribute additional shear forces that may affect chain break up. As chains bump into each other, they can break apart, reform, and assemble into different kinds of structures like platelets, sheets, and three-dimensional crystals (as seen in Fig. 2), so even the concept of “rotating chains” may not be appropriate for many real dispersions in rotating fields.51–53
Fig. 3 shows several steady-state quantities, the average cluster size Nc, the average dimensionless particle dipole strength 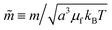 , and the average dimensionless magnetic torque per particle
, and the average dimensionless magnetic torque per particle 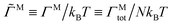 in dispersions with different volume fractions, field strengths, and rotation frequency. Particles were considered part of the same cluster if they were within a threshold distance of 2.1a of any other particle in the cluster, and then the cluster sizes were averaged over the set of observed clusters to obtain Nc. ΓM was computed from the mean dipole m as ΓM = |m × H0|. Note that this is the total magnetic torque on the entire dispersion normalized by the number of particles. An individual paramagnetic particle does not rotate due to this magnetic torque alone because the particle's induced magnetic moment rotates freely. At low field strengths (
in dispersions with different volume fractions, field strengths, and rotation frequency. Particles were considered part of the same cluster if they were within a threshold distance of 2.1a of any other particle in the cluster, and then the cluster sizes were averaged over the set of observed clusters to obtain Nc. ΓM was computed from the mean dipole m as ΓM = |m × H0|. Note that this is the total magnetic torque on the entire dispersion normalized by the number of particles. An individual paramagnetic particle does not rotate due to this magnetic torque alone because the particle's induced magnetic moment rotates freely. At low field strengths (![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ≤ 1.05 for the dispersion at ϕ = 0.005 and
0 ≤ 1.05 for the dispersion at ϕ = 0.005 and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ≤ 0.9 for the dispersion at ϕ = 0.05), the trends of the steady-state quantities are similar to the dilute, single chain trends discussed above. At higher field strengths, the complicated interchain interactions become important and the steady-state quantities are not described by the single-chain model. At very low frequencies, the rotation does not generate enough shear force to break chains apart, but rather helps chains “find” one another and facilitates the formation of platelets and crystalline sheets. In some cases, the mean cluster size is larger for the rotating fields than steady fields, where chains can only coalesce due to fluctuation- or defect-driven interactions, which aren't particularly long-ranged.74,75 Thermodynamically, there is no preference for chains to coalesce in-plane or out-of-plane, but rotation enhances the rate of in-plane aggregation so the formation of platelets and sheets in the low frequency regime is a kinetic effect. These kinetic signatures were also observed in experiments of paramagnetic particles,35 where the steady-state chain length was larger in low-frequency rotating fields than steady fields, as well as simulations of particles with permanent dipoles,76 that formed large sheets similar to Fig. 2 at low rotation frequencies. The dipole strength of crystalline configurations is significantly larger than that of chains for highly susceptible particles, so there are also cases where the dipole in rotating fields of low frequency is larger than that in steady fields.67 These crystal platelets and sheets rotate with the field, which requires large magnetic torques, even at low frequencies. This can be avoided in experiments by using slightly incommensurate frequencies in a biaxial field setup,53 randomly fluctuating the field orientation,51 or switching the rotation periodically between clockwise and counterclockwise.55,56 As the frequency increases, chains break up before they coalesce in the plane of rotation, and the mean cluster size drops, accompanied by drops in the dipole strength and magnetic torque, suppressing aggregation altogether as
0 ≤ 0.9 for the dispersion at ϕ = 0.05), the trends of the steady-state quantities are similar to the dilute, single chain trends discussed above. At higher field strengths, the complicated interchain interactions become important and the steady-state quantities are not described by the single-chain model. At very low frequencies, the rotation does not generate enough shear force to break chains apart, but rather helps chains “find” one another and facilitates the formation of platelets and crystalline sheets. In some cases, the mean cluster size is larger for the rotating fields than steady fields, where chains can only coalesce due to fluctuation- or defect-driven interactions, which aren't particularly long-ranged.74,75 Thermodynamically, there is no preference for chains to coalesce in-plane or out-of-plane, but rotation enhances the rate of in-plane aggregation so the formation of platelets and sheets in the low frequency regime is a kinetic effect. These kinetic signatures were also observed in experiments of paramagnetic particles,35 where the steady-state chain length was larger in low-frequency rotating fields than steady fields, as well as simulations of particles with permanent dipoles,76 that formed large sheets similar to Fig. 2 at low rotation frequencies. The dipole strength of crystalline configurations is significantly larger than that of chains for highly susceptible particles, so there are also cases where the dipole in rotating fields of low frequency is larger than that in steady fields.67 These crystal platelets and sheets rotate with the field, which requires large magnetic torques, even at low frequencies. This can be avoided in experiments by using slightly incommensurate frequencies in a biaxial field setup,53 randomly fluctuating the field orientation,51 or switching the rotation periodically between clockwise and counterclockwise.55,56 As the frequency increases, chains break up before they coalesce in the plane of rotation, and the mean cluster size drops, accompanied by drops in the dipole strength and magnetic torque, suppressing aggregation altogether as ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) gets large. Because the high-frequency limit results in an effectively steady, “opposite dipole” interaction, aggregation can only be suppressed for field strengths below the crystal phase boundary, where there is a thermodynamic driving force for sheet formation.52 The strength of the dipolar attractions decreases as the interactions become time-averaged. For a constant dipole model (no mutual polarization), the strength of the high-frequency attraction is exactly one-half of the strength of attractions in a steady field.48 For mutual dipole models, the strength of the high-frequency attraction is even lower than one-half of the steady case, since anisotropy of the structures with the field in the steady case give a huge mutual polarization boost compared to the more isotropic configuration in the rotating case.53,67 If the field is sufficiently large, particles form sheets and crystallize at any rotation frequency, owing to thermodynamic phase boundaries in the low-frequency (dipole) and high-frequency (“opposite dipole”) limits, and particle aggregation cannot be prevented with rotation.
gets large. Because the high-frequency limit results in an effectively steady, “opposite dipole” interaction, aggregation can only be suppressed for field strengths below the crystal phase boundary, where there is a thermodynamic driving force for sheet formation.52 The strength of the dipolar attractions decreases as the interactions become time-averaged. For a constant dipole model (no mutual polarization), the strength of the high-frequency attraction is exactly one-half of the strength of attractions in a steady field.48 For mutual dipole models, the strength of the high-frequency attraction is even lower than one-half of the steady case, since anisotropy of the structures with the field in the steady case give a huge mutual polarization boost compared to the more isotropic configuration in the rotating case.53,67 If the field is sufficiently large, particles form sheets and crystallize at any rotation frequency, owing to thermodynamic phase boundaries in the low-frequency (dipole) and high-frequency (“opposite dipole”) limits, and particle aggregation cannot be prevented with rotation.
Fig. 3 also compares the average cluster sizes in dispersions with long-ranged hydrodynamic interactions (HI) and those without (FD), where the drag on each particle is simply the Stokes drag. We find that the mean cluster size, average particle dipole, and magnetic torque are similar for both models, with the mean cluster size being a bit larger for the FD model at low frequencies. In the FD model, each particle in an aggregate feels Stokes drag, and the total drag of the aggregate goes as Nc, the number of particles in the aggregate, regardless of aggregate shape. With long-ranged HI, the drag on an aggregate goes as N1/dc, where d is the aggregate's fractal dimension.64,77,78 Solvent flows around the object, so particles on the interior of the aggregate feel little drag compared to those on the exterior. Because the particles align with the rotating field, the fractal dimension is close to d ≈ 1, especially at early times, and the aggregates feel similar drag whether HI are included or not. Additionally, the solvent can reach each particle and the distribution of drag force along the aggregates is similar in both HI and FD models, so break up occurs at similar frequencies. Therefore, we expect the steady-state quantities to be similar whether or not HI are included, as observed in our simulations.
Diffusivity
On sufficiently long time scales, the motion of particles is diffusive and the mean squared displacement of a particle grows linearly in time,| 〈r(τ)r(τ)〉 = 2D∞sτ | (13) |
| 〈r‖2(τ)〉 = 4D‖τ, 〈r⊥2(τ)〉 = 2D⊥τ, | (14) |
| 〈(rx(τ) + ry(τ))rz(τ)〉 = 4D‖,⊥τ, | (15) |
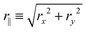 is the in-plane displacement and r⊥ ≡ |rz| is the out-of-plane displacement. It is convenient to consider these diffusivities relative to the Stokes–Einstein diffusivity D0 ≡ kBT/6πηa of an isolated particle,
is the in-plane displacement and r⊥ ≡ |rz| is the out-of-plane displacement. It is convenient to consider these diffusivities relative to the Stokes–Einstein diffusivity D0 ≡ kBT/6πηa of an isolated particle, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ ≡ D‖/D0,
‖ ≡ D‖/D0, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ⊥ ≡ D⊥/D0,
⊥ ≡ D⊥/D0, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖,⊥ ≡ D‖,⊥/D0. We observe that the cross diffusivity
‖,⊥ ≡ D‖,⊥/D0. We observe that the cross diffusivity ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖,⊥ is always very small, so diffusive motion in the plane of rotation is decoupled from diffusive motion out of plane, and only the diagonal elements of D∞s are nonzero. Fig. 4 shows
‖,⊥ is always very small, so diffusive motion in the plane of rotation is decoupled from diffusive motion out of plane, and only the diagonal elements of D∞s are nonzero. Fig. 4 shows ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ and
‖ and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ⊥ for different volume fractions, field strengths, and rotation frequencies.
⊥ for different volume fractions, field strengths, and rotation frequencies.
A particle's self-diffusivity is related to its drag γH (which is generally different than the Stokes drag γ) via the Einstein relation D = kBT/γH. When particles are aggregated, their self-diffusivity is constrained by the self-diffusivity of the aggregate, which moves as a single unit. Because the fractal dimension is d≈1, the drag on aggregates increase linearly with their lengths, and the self-diffusivity of the particles is small. Fig. 4 shows that, at low frequencies, both ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ and
‖ and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ⊥ decrease as the field increases since the aggregate size increases with field. As chains break up in the rotating field, the aggregates become smaller and the self-diffusivity of the particles increases. Both
⊥ decrease as the field increases since the aggregate size increases with field. As chains break up in the rotating field, the aggregates become smaller and the self-diffusivity of the particles increases. Both ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ and
‖ and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ⊥ increase as the rotation frequency increases. At large frequencies, both self-diffusivities approach the self-diffusivity of a hard sphere suspension, D0(1 − 2.1ϕ) at small ϕ, which is a bit less than D0 of an isolated particle due to hydrodynamic and steric interactions.79,80 If the field strength is too large, significant crystallization occurs for all rotation frequencies, and the self-diffusivities are small and relatively independent of
⊥ increase as the rotation frequency increases. At large frequencies, both self-diffusivities approach the self-diffusivity of a hard sphere suspension, D0(1 − 2.1ϕ) at small ϕ, which is a bit less than D0 of an isolated particle due to hydrodynamic and steric interactions.79,80 If the field strength is too large, significant crystallization occurs for all rotation frequencies, and the self-diffusivities are small and relatively independent of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) .
.
For intermediate field strengths, there is a maximum in ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ at intermediate frequencies. Not only is the maximum
‖ at intermediate frequencies. Not only is the maximum ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ larger than the hard sphere self-diffusivity at high rotation frequencies, it is also larger than
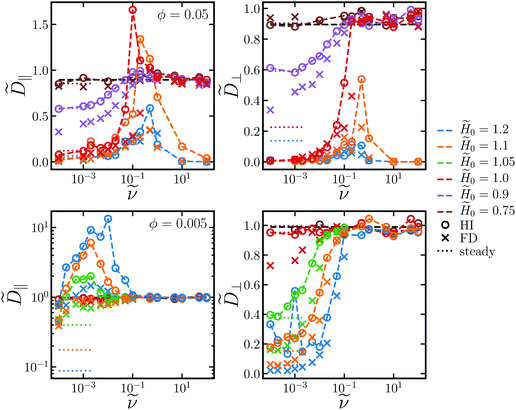
‖ larger than the hard sphere self-diffusivity at high rotation frequencies, it is also larger than ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 0. Thus, the rotating field facilitates faster diffusion for a range of frequencies. This diffusivity peak is observed for all volume fractions between ϕ = 0.005 and ϕ = 0.05. The frequency
0. Thus, the rotating field facilitates faster diffusion for a range of frequencies. This diffusivity peak is observed for all volume fractions between ϕ = 0.005 and ϕ = 0.05. The frequency ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) * at the peak
* at the peak ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖* is fairly independent of field strength for the field strengths investigated. Fig. 5 shows that
‖* is fairly independent of field strength for the field strengths investigated. Fig. 5 shows that ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) * increases as a power law with increasing ϕ, while
* increases as a power law with increasing ϕ, while ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖* decreases with ϕ. A power law fit yields
‖* decreases with ϕ. A power law fit yields ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) * ∼ ϕ2.0, and the peak frequency is quadratic in volume fraction in at least the range ϕ = 0.005–0.05. As the volume fraction increases, aggregation competes against diffusion, and the peak self-diffusivity
* ∼ ϕ2.0, and the peak frequency is quadratic in volume fraction in at least the range ϕ = 0.005–0.05. As the volume fraction increases, aggregation competes against diffusion, and the peak self-diffusivity ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖* drops as does the window where
‖* drops as does the window where ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ > D0. In fact, if ϕ or
‖ > D0. In fact, if ϕ or ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 become too large, bulk crystallization occurs and the diffusivity remains small for all rotation frequencies. The out-of-plane diffusivity does not have a maximum and increases monotonically to the hard-sphere result as frequency increases.
0 become too large, bulk crystallization occurs and the diffusivity remains small for all rotation frequencies. The out-of-plane diffusivity does not have a maximum and increases monotonically to the hard-sphere result as frequency increases.
The scaling of ν* ∼ ϕ2 can be explained by considering chains of Nc particles that sweep out disks of volume Vd = 2a3πNc2 as they rotate. If there are Nd = N/Nc of these disks, the disk volume fraction is ϕd = NdVd/V ∼ NNc/V ∼ Ncϕ, where ϕ = 4πa3N/3V is the particle volume fraction. From the balance of magnetic and shear forces, the chain length decreases with frequency as Nc ∼ ν−1/2,35,39 so ϕd ∼ ν−1/2ϕ. We hypothesize that the peak frequency occurs when ϕd ∼ 1, where the disks begin to overlap. Thus, the critical frequency goes as ν* ∼ ϕ2, consistent with the scaling we observe in the simulations.
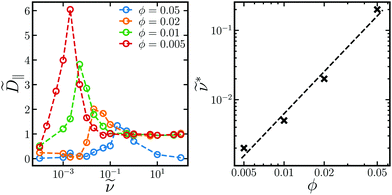
Enhanced diffusion above D0 can have contributions from two sources, illustrated in Fig. 6. First, the “interchain mechanism”, aggregates can exchange particles as they break up and reform in the rotating field. Particles can “hop” from chain to chain and be shuttled along due to interparticle forces alone. Second, the “hydrodynamic mechanism”, as the chains rotate they generate flow fields that entrain and move other particles around. Each chain functions as a magnetic “stir bar” that produces mixing flows in the dispersion. Fig. 4 compares the diffusivities in dispersions with (HI) and without (FD) long-ranged hydrodynamic interactions. When hydrodynamic interactions are turned off, the diffusivity peak disappears and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ increases monotonically with
‖ increases monotonically with ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) to the hard-sphere value at high frequencies. From the steady-state quantities in Fig. 3, the structures in the two models are fairly similar, so the qualitative differences in diffusivities is not solely a result of differences in structure. Without HI, enhanced diffusion can only be due to the interchain mechanism, since the solvent flows in the hydrodynamic mechanism are absent. Even though particles in the FD model assemble into large rotating chains and platelets that strongly interact, this does not lead to fast diffusive transport. Because we do not observe enhanced diffusion when HI are turned off, we conclude that the enhanced diffusion above D0 is due mainly to hydrodynamic mixing flows. As
to the hard-sphere value at high frequencies. From the steady-state quantities in Fig. 3, the structures in the two models are fairly similar, so the qualitative differences in diffusivities is not solely a result of differences in structure. Without HI, enhanced diffusion can only be due to the interchain mechanism, since the solvent flows in the hydrodynamic mechanism are absent. Even though particles in the FD model assemble into large rotating chains and platelets that strongly interact, this does not lead to fast diffusive transport. Because we do not observe enhanced diffusion when HI are turned off, we conclude that the enhanced diffusion above D0 is due mainly to hydrodynamic mixing flows. As ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) increases, the aggregates rotate faster, increasing mixing, but they also break up and become smaller, decreasing mixing. Therefore, there is an optimal frequency range that balances these competing effects and yields the maximum in
increases, the aggregates rotate faster, increasing mixing, but they also break up and become smaller, decreasing mixing. Therefore, there is an optimal frequency range that balances these competing effects and yields the maximum in ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ we observe in Fig. 4 and 5. This mixing mechanism is consistent with experimental observations of enhanced tracer diffusion of noninteracting tracer particles in a dispersion with rotating paramagnetic chains.24,25 Because the tracer particles are not magnetically responsive, enhanced diffusion above the tracer's Stokes–Einstein diffusivity is due solely to the hydrodynamic flow mechanism. Our results show that this is true even for self-diffusion of paramagnetic particles, whose motion due to solvent flows overpowers motion due to interparticle forces.
‖ we observe in Fig. 4 and 5. This mixing mechanism is consistent with experimental observations of enhanced tracer diffusion of noninteracting tracer particles in a dispersion with rotating paramagnetic chains.24,25 Because the tracer particles are not magnetically responsive, enhanced diffusion above the tracer's Stokes–Einstein diffusivity is due solely to the hydrodynamic flow mechanism. Our results show that this is true even for self-diffusion of paramagnetic particles, whose motion due to solvent flows overpowers motion due to interparticle forces.
We observe that ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ⊥ ≤
⊥ ≤ ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ for the entire field and frequency range. Particles have attractive interactions in the plane of rotation but purely repulsive interactions out of plane. Thus, particles tend to move more within the same plane parallel to the rotation than they do orthogonally to it. Additionally, hydrodynamic mixing flows mostly have the same orientation as the rotating field driving it, so these flows push particles around within the plane of rotation. Finally, the bare diffusivity of an isolated chain is larger in the direction of its long axis than in the orthogonal direction.77 Because the long axis is always oriented in the plane of rotation, the bare chain diffusivity contributes more to in-plane motion than to out-of-plane motion.
‖ for the entire field and frequency range. Particles have attractive interactions in the plane of rotation but purely repulsive interactions out of plane. Thus, particles tend to move more within the same plane parallel to the rotation than they do orthogonally to it. Additionally, hydrodynamic mixing flows mostly have the same orientation as the rotating field driving it, so these flows push particles around within the plane of rotation. Finally, the bare diffusivity of an isolated chain is larger in the direction of its long axis than in the orthogonal direction.77 Because the long axis is always oriented in the plane of rotation, the bare chain diffusivity contributes more to in-plane motion than to out-of-plane motion.
Magnetophoretic mobility
Polarizable particles will move in a nonuniform field via magnetophoresis. Here, we consider a rotating field with a small spatial gradient oriented arbitrarily. If the components of the applied field gradient ∇H0 are small compared to H0/a, the steady-state structure of the dispersion is only weakly perturbed by the magnetophoretic forces. In this case, the average phoretic velocity can be computed from the steady-state structure with no field gradient. The magnetophoretic force on a particle i, FPi, is equal to the dot product of its dipole mi with the field gradient, FPi = (∇H0)·mi ≡ G(Ĥ0·mi), where G = ∇H0 and Ĥ0 ≡ H0/H0. Because the dispersion's structure and dipole moment are induced by the field and align with it, the absolute field direction is not important and only its magnitude matters. We do not need to consider the field gradient tensor ∇H0, which has both the field and gradient directions, but rather the field gradient vector G = ∇H0, which has only the gradient direction and the field magnitude. This would not be true for an arbitrary, permanent structure or dipole in a field gradient, for which both the field direction and the gradient direction matter.The dipoles are determined from the steady-state configuration at zero field gradient by computing 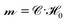 , and the set of phoretic forces
, and the set of phoretic forces 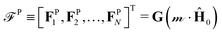 produce velocities
produce velocities ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) =
= ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) H·
H·![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) P. The average phoretic velocity
P. The average phoretic velocity 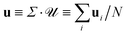 , where Σ is a summation tensor, can then be written as
, where Σ is a summation tensor, can then be written as
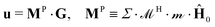 | (16) |
![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) P0 = 4πχ
P0 = 4πχ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0I/3 ≡
0I/3 ≡ ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) 0I. M0 increases with both χ and H0, and, unlike
0I. M0 increases with both χ and H0, and, unlike ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 0,
0, ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) 0 is not normalized to 1 in our choice of dimensionless units.
0 is not normalized to 1 in our choice of dimensionless units.
In the rotating field, the field gradient G can point either in the plane of rotation or out of plane. We observe that the gradient in-plane does not produce an appreciable velocity out of plane and vice versa, so MP only has two non-zero, diagonal elements, MP‖ and MP⊥, like the self-diffusivity
| u‖ = MP‖G‖, u⊥ = MP⊥G⊥ | (17) |
![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) 0 at large
0 at large ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) due to mutual polarization. Because the hydrodynamic mobility tensor is isotropic for the FD model, both
due to mutual polarization. Because the hydrodynamic mobility tensor is isotropic for the FD model, both ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥ =
⊥ = ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ‖. For the HI model however, like the self-diffusivities,
‖. For the HI model however, like the self-diffusivities, ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥ ≤
⊥ ≤ ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ‖ for the entire field and frequency range due to increased drag in the direction orthogonal to the field. When particles are aggregated, the magnetophoretic force on each particle contributes to the total magnetophoretic force on the aggregate, FP ∼ Nc. The drag on the aggregate only scales with the aggregate's characteristic length γH ∼ Nc1/d.64,77,78 In the limiting case where the particles aggregate into chains with fractal dimension d = 1, it would seem like these effects should cancel out as the chains break up with increasing rotation frequency, and the magnetophoretic mobility should remain constant. However, the dipole strength, which contributes to the magnetophoretic force, decreases as the aggregates break up. Additionally, because the magnetophoretic forces on each particle are oriented in the same direction, the hydrodynamic flows from each particle in an aggregate entrain the others and decrease the drag on the aggregate. This particular drag-reduction mode is very strong for our hydrodynamic model, which treats each particle as an isolated point force and point quadrupole. If an aggregate is treated as a rigid collection of particles constrained to move together, which may be appropriate given the strong interparticle forces, the rigidity constraints significantly increase the drag, so the drag reduction may not be quite so dramatic.81,82 Such a refined hydrodynamic model was not implemented here. If the particles form platelets and sheets (d ≈ 2) or crystals (d ≈ 3), the mobility decreases even faster as the aggregates break up, with the rate increasing the larger the fractal dimension. Compared to the FD model, where the drag on each particle is constant, the in-plane mobilities are significantly larger in the HI model. At low volume fractions, the out-of-plane mobility is also larger for the HI model, but fall below the values for the FD model at larger volume fractions. These effects cause the magnetophoretic mobility to decrease with increasing frequency and decreasing field. Therefore, in the bulk, particles can generally be magnetophoretically transported more quickly in steady fields than in rotating fields.
‖ for the entire field and frequency range due to increased drag in the direction orthogonal to the field. When particles are aggregated, the magnetophoretic force on each particle contributes to the total magnetophoretic force on the aggregate, FP ∼ Nc. The drag on the aggregate only scales with the aggregate's characteristic length γH ∼ Nc1/d.64,77,78 In the limiting case where the particles aggregate into chains with fractal dimension d = 1, it would seem like these effects should cancel out as the chains break up with increasing rotation frequency, and the magnetophoretic mobility should remain constant. However, the dipole strength, which contributes to the magnetophoretic force, decreases as the aggregates break up. Additionally, because the magnetophoretic forces on each particle are oriented in the same direction, the hydrodynamic flows from each particle in an aggregate entrain the others and decrease the drag on the aggregate. This particular drag-reduction mode is very strong for our hydrodynamic model, which treats each particle as an isolated point force and point quadrupole. If an aggregate is treated as a rigid collection of particles constrained to move together, which may be appropriate given the strong interparticle forces, the rigidity constraints significantly increase the drag, so the drag reduction may not be quite so dramatic.81,82 Such a refined hydrodynamic model was not implemented here. If the particles form platelets and sheets (d ≈ 2) or crystals (d ≈ 3), the mobility decreases even faster as the aggregates break up, with the rate increasing the larger the fractal dimension. Compared to the FD model, where the drag on each particle is constant, the in-plane mobilities are significantly larger in the HI model. At low volume fractions, the out-of-plane mobility is also larger for the HI model, but fall below the values for the FD model at larger volume fractions. These effects cause the magnetophoretic mobility to decrease with increasing frequency and decreasing field. Therefore, in the bulk, particles can generally be magnetophoretically transported more quickly in steady fields than in rotating fields.
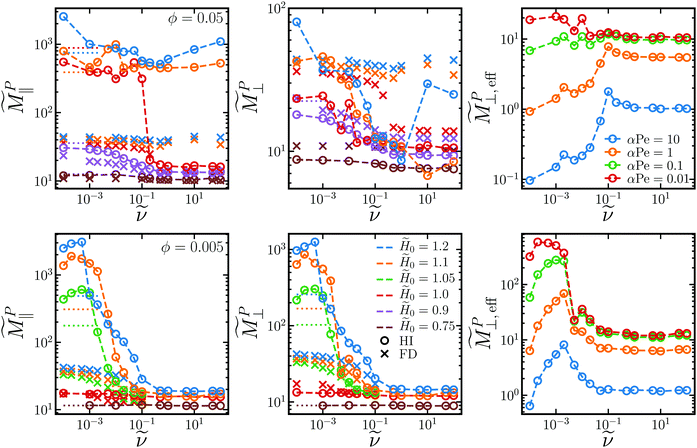 | ||
Fig. 7 Small-gradient magnetophoretic mobility in the plane of rotation ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ‖ (left column) and out of the plane of rotation ‖ (left column) and out of the plane of rotation ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥ (middle column) as a function of rotation frequency ⊥ (middle column) as a function of rotation frequency ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) for two different volume fractions ϕ = 0.05 (top row) and ϕ = 0.005 (bottom row) and several different field strengths for two different volume fractions ϕ = 0.05 (top row) and ϕ = 0.005 (bottom row) and several different field strengths ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 (different colors). Circles correspond to simulations with long-ranged hydrodynamic interactions (HI) while crosses neglect these in the freely draining (FD) model. The values for steady fields (with HI) at 0 (different colors). Circles correspond to simulations with long-ranged hydrodynamic interactions (HI) while crosses neglect these in the freely draining (FD) model. The values for steady fields (with HI) at ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 0 are shown with dotted lines. The effective out-of-plane magnetophoretic mobility in porous media = 0 are shown with dotted lines. The effective out-of-plane magnetophoretic mobility in porous media ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥,eff (right column) at ⊥,eff (right column) at ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 1.0 (top) and 0 = 1.0 (top) and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 1.1 (bottom) for different values of αPe (different colors) from eqn (18). 0 = 1.1 (bottom) for different values of αPe (different colors) from eqn (18). | ||
This is not necessarily the case in porous media, as illustrated in Fig. 1. Soheilian, Erb, and coworkers showed that the magnetophoretic flux of paramagnetic colloids through synthetic porous tissue in steady fields was smaller than that in rotating fields.8 The large aggregates formed in steady fields had difficultly navigating the small tortuous pores, while aggregation was suppressed in rotating fields allowing individual particles to more easily pass through the porous network. We can derive a simple phenomenological model to explain this observation. Consider a porous material of length L illustrated in Fig. 8. In a gradient of strength G⊥ oriented out of the plane of rotation, the particles can travel that distance magnetophoretically in a minimum time t = L/u⊥, where u⊥ = MP⊥G⊥ is the magnetophoretic velocity in the bulk. However, because the porous material is tortuous, particles cannot move straight through the material. We imagine that, as particles travel phoretically in the gradient direction, they run into obstacles of characteristic length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Because the phoretic force is directed toward an obstacle, the only way the particle can get around it is diffusively, which takes a time t =
. Because the phoretic force is directed toward an obstacle, the only way the particle can get around it is diffusively, which takes a time t = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/D‖. The relevant diffusivity is D‖, as diffusion is taking place orthogonally to the out-of-plane gradient. Diffusion in the gradient direction D⊥ does not help traverse the obstacle because it is directed towards and away from the obstacle and is usually negligible compared to the phoretic forces. If there are No such obstacles across the length L, the total time to traverse the porous material is t = L/u⊥ + No
2/D‖. The relevant diffusivity is D‖, as diffusion is taking place orthogonally to the out-of-plane gradient. Diffusion in the gradient direction D⊥ does not help traverse the obstacle because it is directed towards and away from the obstacle and is usually negligible compared to the phoretic forces. If there are No such obstacles across the length L, the total time to traverse the porous material is t = L/u⊥ + No![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/D‖. Thus, the effective phoretic velocity through the porous material is u⊥,eff = u⊥/(1 + No
2/D‖. Thus, the effective phoretic velocity through the porous material is u⊥,eff = u⊥/(1 + No![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2u⊥/LD‖). If the gradient is directed in the plane of rotation instead, the relevant phoretic velocity is u‖ while the relevant diffusivity is D⊥, and the effective phoretic velocity is u‖,eff = u‖/(1 + No
2u⊥/LD‖). If the gradient is directed in the plane of rotation instead, the relevant phoretic velocity is u‖ while the relevant diffusivity is D⊥, and the effective phoretic velocity is u‖,eff = u‖/(1 + No![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2u‖/LD⊥). Therefore, the effective magnetophoretic mobility in the porous material is
2u‖/LD⊥). Therefore, the effective magnetophoretic mobility in the porous material is
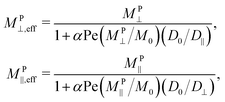 | (18) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /L is a dimensionless function of the tortuosity and porosity of the porous network (through No/L and
/L is a dimensionless function of the tortuosity and porosity of the porous network (through No/L and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) and the Péclet number Pe ≡
) and the Péclet number Pe ≡ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) M0G/D0 depends on the field strength (through M0) and the field gradient. Fig. 7 shows the effective mobility in porous materials of different αPe as a function of
M0G/D0 depends on the field strength (through M0) and the field gradient. Fig. 7 shows the effective mobility in porous materials of different αPe as a function of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) . If the porous material has high porosity and low tortuousity, there are very few, small obstacles and α is small. Particles do not need to diffuse much in the direction orthogonal to the field and can pass nearly straight through the porous network phoretically, so (18) simplifies to MPi,eff ≈ MPi. The Péclet number is small if the gradient or field is weak. In this case, for any pore geometry, diffusion around obstacles is fast compared to magnetophoresis in the gradient direction, so transport is limited by magnetophoresis and again (18) simplifies to MPi,eff ≈ MPi. In this latter case, diffusion in the gradient direction may become important, and a more complicated model might be needed. Because both MP‖ and MP⊥ decrease with increasing ν, the effective porous mobility in steady fields is larger than that in rotating fields and decreases with ν. For porous networks with low porosity and high tortuousity in strong fields and field gradients, αPe is large and diffusion orthogonal to the gradient dominates the transport, so (18) reduces to MPi,eff ≈ DiM0/αPe
. If the porous material has high porosity and low tortuousity, there are very few, small obstacles and α is small. Particles do not need to diffuse much in the direction orthogonal to the field and can pass nearly straight through the porous network phoretically, so (18) simplifies to MPi,eff ≈ MPi. The Péclet number is small if the gradient or field is weak. In this case, for any pore geometry, diffusion around obstacles is fast compared to magnetophoresis in the gradient direction, so transport is limited by magnetophoresis and again (18) simplifies to MPi,eff ≈ MPi. In this latter case, diffusion in the gradient direction may become important, and a more complicated model might be needed. Because both MP‖ and MP⊥ decrease with increasing ν, the effective porous mobility in steady fields is larger than that in rotating fields and decreases with ν. For porous networks with low porosity and high tortuousity in strong fields and field gradients, αPe is large and diffusion orthogonal to the gradient dominates the transport, so (18) reduces to MPi,eff ≈ DiM0/αPe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D0. Both D‖ and D⊥ increase with ν, and the phoretic velocity through porous material in rotating fields is larger than in steady fields. In fact, because
D0. Both D‖ and D⊥ increase with ν, and the phoretic velocity through porous material in rotating fields is larger than in steady fields. In fact, because ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ has a maximum at intermediate rotation frequency, so does MP⊥,eff at large αPe, and the fastest transport through porous media occurs at intermediate frequencies. These trends are consistent with the experimental results of Soheilian et al. of magnetophoresis through porous media in rotating fields, so it is possible their experiments live in the large αPe regime.8 This kind of model was also used to explain enhanced diffusion of charged species through porous media in rotating electric fields compared to steady fields.83 In that case, the electrophoretic driving force changed direction over time allowing the charged species to navigate around obstacles phoretically. This is similar, but of a different nature, than our setup here, where the magnetophoretic driving force (i.e., the field gradient) is constant in time, and particles navigate around obstacles diffusively with a diffusivity enhanced by the rotating field.
‖ has a maximum at intermediate rotation frequency, so does MP⊥,eff at large αPe, and the fastest transport through porous media occurs at intermediate frequencies. These trends are consistent with the experimental results of Soheilian et al. of magnetophoresis through porous media in rotating fields, so it is possible their experiments live in the large αPe regime.8 This kind of model was also used to explain enhanced diffusion of charged species through porous media in rotating electric fields compared to steady fields.83 In that case, the electrophoretic driving force changed direction over time allowing the charged species to navigate around obstacles phoretically. This is similar, but of a different nature, than our setup here, where the magnetophoretic driving force (i.e., the field gradient) is constant in time, and particles navigate around obstacles diffusively with a diffusivity enhanced by the rotating field.
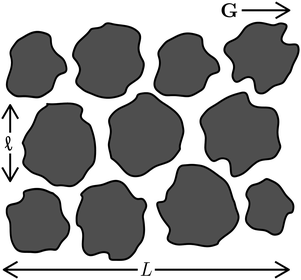 | ||
Fig. 8 Schematic of magnetophoresis in a field gradient G through a model porous material of length L composed of No obstacles of size ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . . | ||
This simple model does not consider the effects of the pore walls on the magnetophoretic mobility. Steric interactions, for example, can prevent aggregates from entering the pores at all if the pore size is smaller than the aggregate size, and the flux through the material will be smaller than expected,8 as in Fig. 1. Hydrodynamic interactions with the wall tend to slow both diffusive and phoretic motion of particles as the confining walls get closer together.84,85 Thermodynamic interactions with the wall (e.g., van der Waals, electrostatic, hydrophobic/philic) modify particle motion, with attractions tending to hinder particle travel through pores. Amin et al. showed in vivo that paramagnetic particles aggregated and stuck to vessel walls in mice during magnetophoresis in steady fields leading to poor transport.20 This could be suppressed by flipping the direction of the applied field gradient in time to detach particles from walls and increase the transport rate, a different but analogous strategy to the setup discussed here. Finally, modes of transport through walls, like endocytosis which is particularly important for transport in biological systems, are not considered here but can be enhanced using time-dependent fields to suppress particle aggregation during magnetophoresis.12
As a first attempt to understand these wall effects, we simulated dispersions in a rigid cage scaffold of pore size h, depicted in Fig. 9, as a simple model for transport in a porous material exposed to rotating fields with no field gradient. Because the channels through the cage are straight, the cage has very low tortuousity and does not look like the model in Fig. 8 we proposed to derive eqn (18). However, the cage is simple with a single defining parameter, the pore size h, and allows us to examine the effect of confinement on the transport properties. To observe the dynamics in (18), we would need to apply a field gradient and simulate magnetophoresis directly, which is beyond the scope of this work. The cage is composed of beads of the same size as the paramagnetic particles, rigidly constrained together. The cage is fixed in place and its walls interact sterically and hydrodynamically with the particles, with no other cage/particle interactions (e.g., magnetic dipole, attractions, etc.). A modification to our hydrodynamic model is needed to ensure the particles composing the cage remain rigidly constrained, which is discussed in detail elsewhere.81,82,86 Like our previous bulk calculations, we computed the long-time self diffusivity from the mean-squared displacement (15) and the low-gradient magnetophoretic mobility from eqn (16), both shown in Fig. 9.
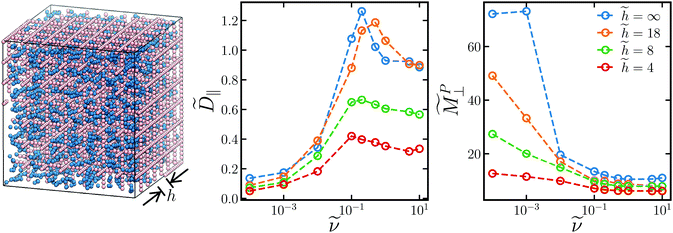 | ||
Fig. 9 (left) Snapshot of simulation of paramagnetic colloids (blue) in a rigid scaffold (pink) of pore size ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ≡ h/a (measured from the edges of the scaffold particles) exposed to a rotating magnetic field of the same orientation as in Fig. 2. The long-time, in-plane self-diffusivity ≡ h/a (measured from the edges of the scaffold particles) exposed to a rotating magnetic field of the same orientation as in Fig. 2. The long-time, in-plane self-diffusivity ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ (middle) and low-gradient, out-of-plane magnetophoretic mobility ‖ (middle) and low-gradient, out-of-plane magnetophoretic mobility ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥ (right) as a function of rotation frequency ⊥ (right) as a function of rotation frequency ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) at a field strength at a field strength ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 1.0 and volume fraction ϕ = 0.05 with respect to pore volume for different pore sizes (different colors). 0 = 1.0 and volume fraction ϕ = 0.05 with respect to pore volume for different pore sizes (different colors). | ||
As expected, both ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ and
‖ and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥ decrease with decreasing pore size due to steric and hydrodynamic hinderance from the walls. The trends in
⊥ decrease with decreasing pore size due to steric and hydrodynamic hinderance from the walls. The trends in ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ‖ and
‖ and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ⊥ with rotation frequency ν remain the same as the bulk trends for all pore sizes. The out-of-plane magnetophoretic mobility decreases with rotation frequency, while the in-plane diffusivity increases with frequency until it reaches a maximum value.
⊥ with rotation frequency ν remain the same as the bulk trends for all pore sizes. The out-of-plane magnetophoretic mobility decreases with rotation frequency, while the in-plane diffusivity increases with frequency until it reaches a maximum value. ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ⊥ and
⊥ and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) ‖ (not shown) also follow the same trends as the bulk for all pore sizes. Because these transport quantities take into account wall effects, they may be the appropriate ones to use in eqn (18) for porous media with pore size
‖ (not shown) also follow the same trends as the bulk for all pore sizes. Because these transport quantities take into account wall effects, they may be the appropriate ones to use in eqn (18) for porous media with pore size ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Because confinement does not qualitatively change the trends in
. Because confinement does not qualitatively change the trends in ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i and
i and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) i, our earlier analysis for the effective porous mobility
i, our earlier analysis for the effective porous mobility ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) i,eff using bulk values for
i,eff using bulk values for ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i and
i and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) i still holds. In particular, the effective magnetophoretic mobility in porous media of low porosity and high tortuousity (large α) is larger in rotating fields than that in steady fields.
i still holds. In particular, the effective magnetophoretic mobility in porous media of low porosity and high tortuousity (large α) is larger in rotating fields than that in steady fields.
Our results for the steady-state and transport quantities in the bulk and under confinement, along with our simple expressions (18) for transport in porous media, can help to optimize particle transport in experimental applications. We investigated how changing three main parameters, the field strength H0, rotation frequency ν, and volume fraction ϕ, affected particle transport in rotating magnetic fields. For example, increasing H0 generally increases the magnetophoretic mobility (Fig. 7). However, if H0 is too high, particle aggregation cannot be suppressed with rotation and the effective mobility MPi,eff through porous media is low. This is especially important when considering steric interactions with pore walls, because particles may not enter the pores at all if the aggregate size is larger than the pore size, as in Fig. 1. The optimal field strength to maximize particle flux through porous materials should lie just below the crystallization boundary, which decreases with ϕ. For small, tortuous pores where transport is diffusion-limited, the flux can be maximized at intermediate ν for which D‖ has a maximum (Fig. 4). The frequency at the peak diffusivity scales as ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) * ∼ ϕ2 (Fig. 5). The larger ϕ, the more particles there are to contribute to the flux, but D‖ decreases with ϕ. The window of frequencies where enhanced diffusion is observed shrinks as ϕ increases, so finding this window experimentally at large ϕ might be challenging. Intermediate field strengths and frequencies, where aggregates have broken up sufficiently to enter pores while retaining enhanced diffusion above D0 are ideal for magnetophoresis through porous media. The dynamics in this regime are complicated, and experiments have shown transient chaos in particle motion at intermediate frequencies.47 This time-dependent chaos could have important effects on particle transport that aren't incorporated into our analysis. In any case, the magnetophoretic flux through porous media in rotating fields can be optimized at intermediate
* ∼ ϕ2 (Fig. 5). The larger ϕ, the more particles there are to contribute to the flux, but D‖ decreases with ϕ. The window of frequencies where enhanced diffusion is observed shrinks as ϕ increases, so finding this window experimentally at large ϕ might be challenging. Intermediate field strengths and frequencies, where aggregates have broken up sufficiently to enter pores while retaining enhanced diffusion above D0 are ideal for magnetophoresis through porous media. The dynamics in this regime are complicated, and experiments have shown transient chaos in particle motion at intermediate frequencies.47 This time-dependent chaos could have important effects on particle transport that aren't incorporated into our analysis. In any case, the magnetophoretic flux through porous media in rotating fields can be optimized at intermediate ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0,
0, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , and ϕ. Such an optimization is predicted in the effective mobility calculations in Fig. 7. For certain αPe regimes in porous materials, we have identified some ϕ,
, and ϕ. Such an optimization is predicted in the effective mobility calculations in Fig. 7. For certain αPe regimes in porous materials, we have identified some ϕ, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0, and
0, and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) that can yield around 2–10-fold increases in the magnetophoretic flux in rotating fields over steady fields. This is consistent with the enhancement observed in experiments.8
that can yield around 2–10-fold increases in the magnetophoretic flux in rotating fields over steady fields. This is consistent with the enhancement observed in experiments.8
Conclusion
Because rotating magnetic fields drive paramagnetic colloids and nanoparticles out of equilibrium, they can overcome many of the challenges associated with assembling and transporting particles in steady fields. However, fundamental transport properties of particles in rotating fields, crucial to dictating responses to the time-varying field, had not been characterized in terms of experimental parameters. In this work, we used Brownian dynamics simulations to study dispersions of paramagnetic colloids in rotating magnetic fields. The simulations included both many-bodied long-ranged hydrodynamic interactions as well as many-bodied mutual polarization among particles. We found that, in the bulk, both the self-diffusivities in plane and out of plane of the rotation increase with rotation frequency as particle aggregation is suppressed. The in-plane diffusivity has a maximum at intermediate frequencies above the Stokes–Einstein diffusivity of an isolated particle. Thus, the rotation frequency can be optimized to enhance self-mixing. Although the magnetophoretic mobility in the bulk is larger for steady fields than in rotating fields, we derived a simple phenomenological model for the effective magnetophoretic mobility in porous media that shows the mobility is larger in rotating fields than in steady fields for porous media of large tortuousity and low porosity. The model requires only bulk transport properties and physical characteristics of the porous geometry and can be used to maximize magnetophoretic transport through porous materials. Finally, we examined the effect of porous confinement on the transport quantities and found no qualitative difference in their trends with respect to rotation frequency. Our results can be leveraged to design and implzement efficient transport processes in rotating magnetic fields.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank support from NASA (Grant No. 80NSSC18K0162).References
- T. Gong, D. T. Wu and D. W. M. Marr, Langmuir, 2003, 19, 5967–5970 CrossRef CAS.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS PubMed.
- J. Ge and Y. Yin, Angew. Chem., Int. Ed., 2011, 50, 1492–1522 CrossRef CAS PubMed.
- A. P. Gast and C. F. Zukoski, Adv. Colloid Interface Sci., 1989, 30, 153–202 CrossRef CAS.
- J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710 RSC.
- J. W. Swan, P. A. Vasquez, P. A. Whitson, E. M. Fincke, K. Wakata, S. H. Magnus, F. D. Winne, M. R. Barratt, J. H. Agui, R. D. Green, N. R. Hall, D. Y. Bohman, C. T. Bunnell, A. P. Gast and E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16023–16028 CrossRef CAS PubMed.
- Z. M. Sherman and J. W. Swan, ACS Nano, 2019, 13, 764–771 CrossRef CAS PubMed.
- R. Soheilian, Y. S. Choi, A. E. David, H. Adbi, C. E. Maloney and R. M. Erb, Langmuir, 2015, 31, 8267–8274 CrossRef CAS PubMed.
- Z. M. Sherman, H. Rosenthal and J. W. Swan, Langmuir, 2018, 34, 1029–1041 CrossRef CAS PubMed.
- J. H. E. Promislow and A. P. Gast, Langmuir, 1996, 12, 4095–4102 CrossRef CAS.
- J. H. E. Promislow and A. P. Gast, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 642–651 CrossRef CAS.
- K. A. Min, M. C. Shin, F. Yu, M. Yang, A. E. David, V. C. Yang and G. R. Rosania, ACS Nano, 2013, 7, 2161–2171 CrossRef CAS PubMed.
- J. W. Swan, J. L. Bauer, Y. Liu and E. M. Furst, Soft Matter, 2014, 10, 1102–1109 RSC.
- J. W. Swan, P. A. Vasquez and E. M. Furst, Phys. Rev. Lett., 2014, 113, 138301 CrossRef PubMed.
- J. L. Bauer, Y. Liu, M. J. Kurian, J. W. Swan and E. M. Furst, J. Chem. Phys., 2015, 143, 074901 CrossRef PubMed.
- J. L. Bauer, M. J. Kurian, J. Stauffer and E. M. Furst, Langmuir, 2016, 32, 6618–6623 CrossRef CAS PubMed.
- S. O. Lumsdon, E. W. Kaler and O. D. Velev, Langmuir, 2004, 20, 2108–2116 CrossRef CAS PubMed.
- M. Mittal, P. P. Lele, E. W. Kaler and E. W. Furst, J. Chem. Phys., 2008, 129, 064513 CrossRef PubMed.
- M. Z. Bazant, in Electrokinetics and Electrohydrodynamics of Microsystems, ed. A. Ramos, Springer, 2011 Search PubMed.
- F. U. Amin, A. K. Hoshiar, T. D. Do, Y. Noh, S. A. Shah, M. S. Khan, J. Yoon and M. O. Kim, Nanoscale, 2017, 9, 10619–10632 RSC.
- A. Kaiser, A. Snezhko and I. S. Aranson, Sci. Adv., 2017, 3, 1601469 CrossRef PubMed.
- G. Kokot and A. Snezhko, Nat. Commun., 2018, 9, 2344 CrossRef PubMed.
- R. M. Erb, J. J. Martin, R. Soheilian, C. Pan and J. R. Barber, Adv. Funct. Mater., 2016, 26, 3859–3880 CrossRef CAS.
- S. L. Biswal and A. P. Gast, Anal. Chem., 2004, 76, 6448–6455 CrossRef CAS PubMed.
- T. Franke, L. Schmid, D. A. Weitz and A. Wixforth, Lab Chip, 2009, 9, 2831–2835 RSC.
- A. K. Vuppu, A. A. Garcia, M. A. Hayes, K. Booksh, P. E. Phelan, R. Calhoun and S. K. Saha, J. Appl. Phys., 2004, 96, 6831–6838 CrossRef CAS.
- B. H. McNaughton, R. R. Agayan, R. Clarke, R. G. Smith and R. Kopelman, Appl. Phys. Lett., 2007, 91, 224105 CrossRef.
- S. Y. Park, H. Handa and A. Sandu, Nano Lett., 2010, 10, 446–451 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- F. Qiu, S. Fujita, R. Mhanna, L. Zhang, B. R. Simona and B. J. Nelson, Adv. Funct. Mater., 2015, 25, 1666–1671 CrossRef CAS.
- D. Du, E. Hilou and S. L. Biswal, Soft Matter, 2018, 14, 3463–3470 RSC.
- F. Martinez-Pedrero and P. Tierno, Phys. Rev. Appl., 2015, 3, 051003 CrossRef.
- F. Li, W. Nie, F. Zhang, G. Lu, C. Lv, Y. Lv, W. Bao, L. Zhang, S. Wang, X. Gao, W. Wei and H.-Y. Xie, ACS Cent. Sci., 2019, 5, 796–807 CAS.
- S. Melle, G. G. Fuller and M. A. Rubio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 4111–4117 CrossRef CAS PubMed.
- S. Melle, O. G. Calderón, M. A. Rubio and G. G. Fuller, J. Non-Newtonian Fluid Mech., 2002, 102, 135–148 CrossRef CAS.
- S. Melle, O. G. Calderón, G. G. Fuller and M. A. Rubio, J. Colloid Interface Sci., 2002, 247, 200–209 CrossRef CAS PubMed.
- S. Melle, O. G. Calderón, M. A. Rubio and G. G. Fuller, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 041503 CrossRef PubMed.
- S. L. Biswal and A. P. Gast, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 041406 CrossRef PubMed.
- I. Petousis, E. Homburg, R. Derks and A. Dietzel, Lab Chip, 2007, 7, 1746–1751 RSC.
- S. Krishnamurthy, A. Yadav, P. E. Phelan, R. Calhoun, A. K. Vuppu, A. A. Garcia and M. A. Hayes, Microfluid. Nanofluid., 2008, 5, 33–41 CrossRef CAS.
- Y. Gao, M. A. Hulsen, T. G. Kang and J. M. J. den Toonder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041503 CrossRef CAS PubMed.
- A. Vázquez-Quesada, T. Franke and M. Ellero, Phys. Fluids, 2017, 29, 032006 CrossRef.
- A. K. Vuppu, A. A. Garcia and M. A. Hayes, Langmuir, 2003, 19, 8646–8653 CrossRef CAS.
- G. Helgesen, P. Pieranski and A. T. Skjeltorp, Phys. Rev. Lett., 1990, 64, 1425–1428 CrossRef PubMed.
- A. C. H. Coughlan and M. A. Bevan, Phys. Rev. E, 2016, 94, 042613 CrossRef PubMed.
- A. C. H. Coughlan and M. A. Bevan, J. Chem. Phys., 2017, 147, 074903 CrossRef PubMed.
- H. Abdi, R. Soheilian, R. M. Erb and C. E. Maloney, Phys. Rev. E, 2018, 97, 032601 CrossRef CAS PubMed.
- T. C. Halsey, R. A. Anderson and J. E. Martin, Int. J. Mod. Phys. B, 1996, 10, 3019–3027 CrossRef.
- J. E. Martin, R. A. Anderson and C. P. Tigges, J. Chem. Phys., 1998, 108, 7887–7900 CrossRef CAS.
- J. E. Martin, E. Venturini, J. Odinek and R. A. Anderson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 61, 2818–2830 CrossRef CAS.
- M. E. Leunissen, H. R. Vutukuri and A. van Blaaderen, Adv. Mater., 2009, 21, 3116–3120 CrossRef CAS.
- F. Smallenburg and M. Dijkstra, J. Chem. Phys., 2010, 132, 204508 CrossRef PubMed.
- J. E. Martin and A. Snezhko, Rep. Prog. Phys., 2013, 76, 126601 CrossRef PubMed.
- D. Du, D. Li, M. Thakur and S. L. Biswal, Soft Matter, 2013, 9, 6867–6875 RSC.
- K. Müller, N. Osterman, D. Babič, C. Likos, J. Dobnikar and A. Nikoubashman, Langmuir, 2014, 30, 5088–5096 CrossRef PubMed.
- T. Mohorič, G. Kokot, N. Osterman, A. Snezhko, A. Vilfan, D. Babič and J. Dobnikar, Langmuir, 2016, 32, 5094–5101 CrossRef PubMed.
- H. Wang, T. Mohorič, X. Zhang, J. Dobnikar and J. Horbach, Soft Matter, 2019, 15, 4437–4444 RSC.
- W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, 1989 Search PubMed.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831 CrossRef CAS.
- A. M. Fiore, F. B. Usabiaga, A. Donev and J. W. Swan, J. Chem. Phys., 2017, 146, 124116 CrossRef PubMed.
- D. M. Heyes and J. R. Melrose, J. Non-Newtonian Fluid Mech., 1993, 46, 1–28 CrossRef CAS.
- Z. Varga, G. Wang and J. Swan, Soft Matter, 2015, 11, 9009–9019 RSC.
- R. T. Bonnecaze and J. F. Brady, Proc. R. Soc. A, 1990, 430, 285–313 CrossRef CAS.
- E. E. Keaveny and M. R. Maxey, J. Comput. Phys., 2008, 227, 9554–9571 CrossRef.
- Z. M. Sherman, D. Ghosh and J. W. Swan, Langmuir, 2018, 34, 7117–7134 CrossRef CAS PubMed.
- R. Freund, G. H. Golud and N. M. Nachtigal, Acta Numer., 1991, 1, 57–100 CrossRef.
- D. Lindbo and A.-K. Tornberg, J. Comput. Phys., 2011, 230, 8744–8761 CrossRef.
- R. T. Bonnecaze and J. F. Brady, J. Chem. Phys., 1992, 96, 2183–2202 CrossRef CAS.
- J. A. Anderson, C. D. Lorenz and A. Travessat, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- D. J. Jeffrey, J. Inst. Maths Appl., 1978, 22, 337–351 CrossRef.
- E. M. Furst and A. P. Gast, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 6916–6925 CrossRef CAS PubMed.
- T. C. Halsey and W. Toor, J. Stat. Phys., 1990, 61, 1257–1281 CrossRef.
- S. Jäger and S. H. L. Klapp, Soft Matter, 2011, 7, 6606–6616 RSC.
- S. Kim and S. J. Karrila, Microhydrodynamics: Principles and Selected Applications, Dover Publications, 2005 Search PubMed.
- Z. Varga and J. Swan, Soft Matter, 2016, 12, 7670–7681 RSC.
- G. K. Batchelor, J. Fluid Mech., 1983, 131, 155–175 CrossRef CAS.
- J. F. Brady, J. Fluid Mech., 1994, 272, 109–133 CrossRef CAS.
- G. Wang, Z. Varga, J. Hofmann, I. E. Zarraga and J. W. Swan, J. Phys. Chem. B, 2018, 122, 2867–2880 CrossRef CAS PubMed.
- G. Wang, A. M. Fiore and J. W. Swan, J. Rheol., 2019, 63, 229–245 CrossRef CAS.
- S.-Y. Kim, J. H. Cho, E. Murray, N. Bakh, H. Choi, K. Ohn, L. Ruelas, A. Hubbert, M. McCue, S. L. Vassallo, P. J. Keller and K. Chung, Proc. Natl. Acad. Sci. U. S. A., 2015, 46, E6274–E6283 CrossRef PubMed.
- J. W. Swan and J. F. Brady, Phys. Fluids, 2010, 22, 103301 CrossRef.
- J. W. Swan and J. F. Brady, J. Fluid Mech., 2011, 687, 254–299 CrossRef CAS.
- J. W. Swan and G. Wang, Phys. Fluids, 2016, 28, 011902 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |

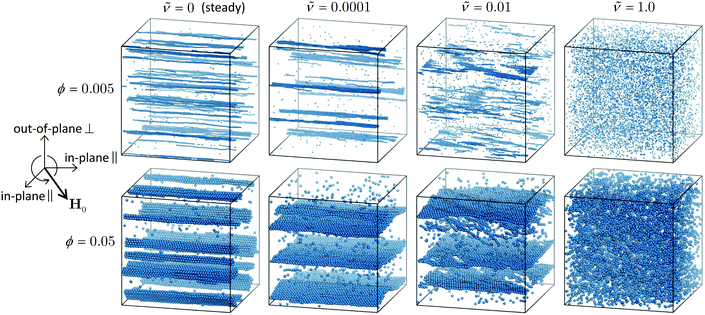
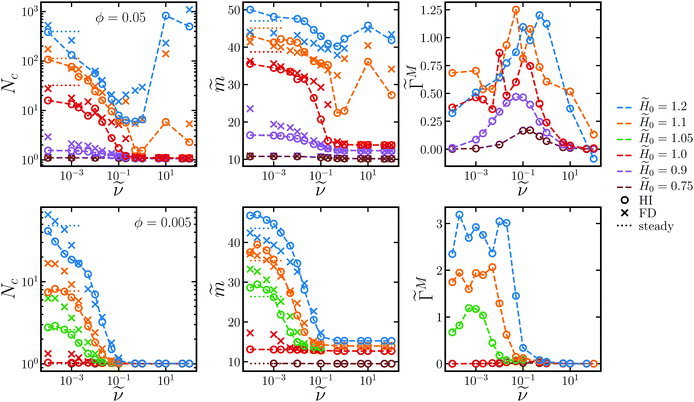
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif)