Open Access Article
Open Access ArticleModeling the magnetostriction effect in elastomers with magnetically soft and hard particles†
Pedro A.
Sánchez
 *ab,
Oleg V.
Stolbov
*ab,
Oleg V.
Stolbov
 c,
Sofia S.
Kantorovich
c,
Sofia S.
Kantorovich
 bd and
Yuriy L.
Raikher
bd and
Yuriy L.
Raikher
 c
c
aWolfgang Pauli Institute, Oskar-Morgenstern-Platz 1, 1090 Wien, Austria. E-mail: pedro.sanchez@univie.ac.at
bUral Federal University, Lenin av. 51, 620000, Ekaterinburg, Russia
cLaboratory of Physics and Mechanics of Soft Matter, Institute of Continuous Media Mechanics, Russian Academy of Sciences (Ural Branch), Perm, Russia
dUniversity of Vienna, Sensengasse 8, 1090, Vienna, Austria
First published on 19th August 2019
Abstract
We analyze theoretically the field-induced microstructural deformations in a hybrid elastomer, that consists of a polymer matrix filled with a mixture of magnetically soft and magnetically hard spherical microparticles. These composites were introduced recently in order to obtain a material that allows the tuning of its properties by both, magnetically active and passive control. Our theoretical analysis puts forward two complementary models: a continuum magnetomechanical model and a bead-spring computer simulation model. We use both approaches to describe qualitatively the microstructural response of such elastomers to applied external fields, showing that the combination of magnetically soft and hard particles may lead to an unusual magnetostriction effect: either an elongation or a shrinking in the direction of the applied field depending on its magnitude. This behavior is observed for conditions (moderate particle densities, fields and deformations) under which the approximations of our models (linear response regime, negligible mutual magnetization between magnetically soft particles) are physically valid.
1 Introduction
Magnetic elastomers (MEs) consist of highly elastic polymer matrices filled with magnetic microparticles.1–6 The presence of the latter makes these materials to change their physical properties as a response to external magnetic fields.7–10 Thanks to this characteristic, MEs are promising candidates for numerous technological applications, as for example in pressure and acceleration sensors, adaptive damping devices and vibration absorbers, magnetically controlled actuators or soft robotics.11–18Field-induced changes in the properties of MEs are produced by internal rearrangements of the embedded magnetic particles.5,19 Such rearrangements are mechanically limited by the polymer matrix, as particles have to deform the latter in order to change their position and/or orientation within the sample. Therefore, the structure and properties of these materials is the result of the balance between magnetic interactions and mechanical constraints. In many practical cases, matrix deformations are elastic and the original structure is recovered after switching off the field. Consequently, MEs may exhibit, among other interesting field-induced responses, giant magnetorheological effects (i.e., very large increases of their elastic moduli under fields)9,20–22 as well as large magnetostriction effects (i.e., notable changes in the shape of the sample)20,23–25 frequently reversible and associated to shape memory effects.26,27
The complex microstructure of MEs, that is responsible for their properties and technological advantages, also represents a hard scientific challenge for their fundamental characterization. In general, all studies emphasize the complex interplay between the interparticle interactions and their rearrangements, on one side, and the particle-matrix mechanical coupling on the other. Despite macroscopic magnetorheological or magnetostriction effects are relatively easy to measure experimentally, their connection to microscopic properties (i.e., properties at the micrometer scale) is still far from being fully understood. Optical properties of MEs make experimental observations of their microstructural transformations rather difficult. Both, optical microscopy26–30 and X-ray tomography31–33 techniques are used for such purpose, but up to date there is still a lack of insight on the dynamics of the internal transformations. Recent approaches try to overcome such limitations by applying particle tracking methods.19,34,35
In order to connect microscopic properties and macroscopic response of MEs, considerable theoretical efforts have been performed in recent years. Numerous analytical and numerical models with different levels of resolution have been introduced. Being one of the most interesting properties of these materials, many of such approaches are addressed to the modeling of magnetostriction effects.36–44 Most of these models are based on mean-field and continuum descriptions of the magnetomechanical coupling inside the material. This makes feasible to reach time and length scales large enough to allow the direct modeling of macroscopic properties. However, these approaches require strong simplifications at the microscopic level that should be chosen very carefully in order to attain a proper representation of the experimental system.
As an alternative approach, particle-based computer simulation models have been also introduced very recently for the modeling of MEs. Closely related to computer models of magnetic fluids and gels,45–51 they can incorporate in a more natural way relevant microscopic details at the cost of being much more computationally expensive. This makes unavoidable the use of some simplifications. Usually, one has to ignore the atomistic details of the polymer matrix, taking some type of coarse-grained representation for it. Most simple approaches use an implicit representation, assuming affine deformations.52 Numerous models use elastic springs to represent the mechanical constraints of the polymer matrix on the magnetic particles, either based on some fixed reference frame33,35 or on an interconnected network of particles and springs.45,47,48,50,53–55 Explicit bead-spring monomer representations of the polymers, as the ones used in some models of magnetic gels,56–59 still seem too expensive to provide useful insights on MEs. Another important simplification required by these models is the treatment of the magnetic properties of the embedded particles. Apart from few exceptions,45 particle-based simulation models usually rely on representing them as beads with point magnetic dipoles.
In parallel with the efforts undertaken on their characterization, current investigations on MEs include the design of materials with enhanced and more sophisticated properties. A recently developed strategy combines particles of different sizes and magnetic properties in order to obtain a material whose behavior can be controlled actively and passively.60–62 Specifically, the complex magnetic filler is composed of relatively large microparticles of a magnetically hard (MH) material mixed with a fraction of smaller, magnetically soft (MS) microparticles. The result is an elastomer that combines magnetically hard and soft properties. The physical phenomena exhibited by such magnetically hard + soft elastomers (HSMEs) are necessarily more complex than the corresponding to simpler composites: in one hand, both MH and MS particles respond to external fields (active control); on the other hand, MH particles are able to get magnetized and keep a remanent magnetic moment that influences the surrounding MS particles even at zero external field (passive control). The obvious drawback of such an increased sophistication is the harder challenge implied in reaching a proper understanding of HSMEs, compared to the already complex modeling of conventional MEs.
In this work we present an approach for the modeling of HSMEs based on a qualitative analysis of the microscopic behavior of these materials. Such analysis is used to develop two complementary models: the first is a continuum magnetomechanical description of the system, whereas the second uses a bead-spring coarse-grained representation to perform extensive computer simulations. The qualitative agreement of the results provided by both models, that are based on different sets of approximations, is a strong indication of the physical feasibility of the characteristic microscopic behavior they predict: for an appropriate orientation of the external field, local microscopic particle rearrangements may contribute to a macroscopic elongation or shrinking of the sample depending on the field strength. To our best knowledge, this behavior has never been observed nor predicted for simple MEs.
The paper is organized as follows: in Section 2 we present our qualitative description of the microscopic properties of HSMEs; in Section 3 we introduce the continuum model; details of the bead-spring model and the computer simulations are described in Section 4; the comparison of results from both models are presented in Section 5; finally, a summary of conclusions is included in Section 6.
2 System of interest
Up to date, HSMEs have been prepared experimentally by using either spherical61 or anisometric63 MH particles. Here we focus only on the first case. Due to their internal structure, such spherical MH particles require a rather strong magnetic field in order to acquire a significant magnetization. After being magnetized, they behave as single-domain particles with a rather high coercive force and a magnetic moment well aligned with the direction of the initial magnetizing field. Typical experimental magnitudes for these parameters are presented in Section S1 of the ESI.† In the following we discuss qualitatively the properties one can expect from HSMEs samples created with such particles.2.1 Elastomers with magnetically hard and soft particles
In an initially prepared HSME, all the embedded particles—both magnetically soft and magnetically hard—are non-magnetized and, thus, the composite does not bear any intrinsic magnetically induced stresses. At this stage, from the viewpoint of mechanical measurement, a HSME is equivalent to any conventional composite with a solid filler of the same size distribution.The situation changes when a just-made HSME is subjected to a strong external field; this field is removed afterwards and, in fact, could be applied in a form of a short pulse. The point is that the amplitude of the field should be greater that the coercive force of the majority of the MH particles. Such a magnetic initialization transforms the MH particles in permanent micromagnets and entails arising of a set of magnetostatic interactions in the composite. One can distinguish three types of those: (i) the MH particles interact with each other as permanent magnetic dipoles, (ii) each MS particle, having acquired a magnetic moment induced by the fields of neighboring MH particles, interacts with the latter, and, finally (iii) all the MS particles interact with each other.
All these interactions produce forces that depend on relative positions of the particles and orientations of their magnetic moments. These forces strive to displace (re-group) the particles as to reduce the magnetostatic energy of the assembly. However, as the particles have to move either with (in case of strong adhesion) or through (in case of weak adhesion) the matrix, any particle displacement induces restoring elastic forces counteracting the magnetic ones. Evidently, the resulting state of a HSME sample is established as a result of balancing of all the intrinsic magnetic and elastic forces. An external magnetic field ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 imposed on such a system, as long as it is not extremely strong, does not affect the matrix, but it perturbs the magnetic moments of the particles. In MS particles both, the magnitude and orientation of their magnetic moments are affected by
0 imposed on such a system, as long as it is not extremely strong, does not affect the matrix, but it perturbs the magnetic moments of the particles. In MS particles both, the magnitude and orientation of their magnetic moments are affected by ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0, since these particles readily magnetize along the direction of the net local field. A MH particle, however, does not change substantially its magnetic moment,
0, since these particles readily magnetize along the direction of the net local field. A MH particle, however, does not change substantially its magnetic moment, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) h after becoming magnetized, unless the applied field opposes
h after becoming magnetized, unless the applied field opposes ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) h and reaches the magnitude of the coercive force, Hc. In that case, the particle magnetic moment can invert its orientation. For example, for materials like SmCo5 and NdFeB (that are typical magnetic fillers in MEs) the value of Hc can be many hundreds of Oe. By that,
h and reaches the magnitude of the coercive force, Hc. In that case, the particle magnetic moment can invert its orientation. For example, for materials like SmCo5 and NdFeB (that are typical magnetic fillers in MEs) the value of Hc can be many hundreds of Oe. By that, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 alters the distribution of intrinsic magnetic forces in the HSME and makes the system to seek a configuration that delivers the magneto-elastic balance under new conditions. As a result, the sample responds to the applied field by both, microstructural and overall shape changes.
0 alters the distribution of intrinsic magnetic forces in the HSME and makes the system to seek a configuration that delivers the magneto-elastic balance under new conditions. As a result, the sample responds to the applied field by both, microstructural and overall shape changes.
2.2 Qualitative description
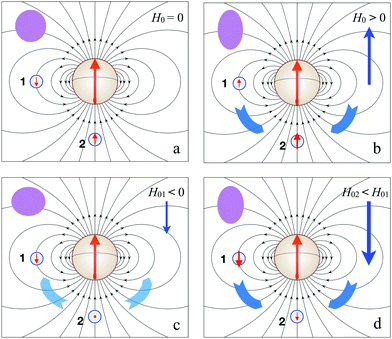
To understand the specific effects caused by MH (large) particles settled amidst MS (small) ones, we focus on a minimal element of the HSME sample. This element comprises a single magnetized MH spherical particle enveloped by an elastic shell, in which the MS particles are embedded. In the following discussion, we assume this elastic shell to be ideally incompressible and to posses a moderate stiffness, enough to not allow for too large displacements of the MS particles and not too strong to totally hinder such displacements. In other words, we assume that even under the maximal field envisaged in the problem, the elastic forces attain the level necessary to balance the magnetic ones at relatively small shifts of the MS particles from their initial positions. Indeed, if the elasticity of the matrix is very low, then the magnetic forces would work virtually without resistance, so that the shell with the MS particles would become an analogue of a magnetic fluid droplet and would readily stretch along the field.Fig. 1 shows four sketches of a HSME elementary volume that illustrate its qualitative behavior under different conditions. For clarity, all MS particles are represented by only two reference ones: (1) is located at a point along the axis defined by the magnetic moment of the MH particle (i.e., at one of the ‘poles’ of the MH particle), and (2) lies on a perpendicular axis (i.e., at the ‘equator’ plane), both at the same distance from the MH center.
When no external field is applied, (H0 = 0, Fig. 1a), the MS particles experience only the field of the MH one. As these particles are isotropically magnetically polarizable, their induced magnetic moments point along the local direction of this field, so that the arising dipolar forces are attractive for both of them. From that, one concludes that the MS particle in position 1 and its neighborhood as well as the MS particle in position 2 and the others around it, would strive to approach the MH core along the respective radial directions, entraining the matrix with them. However, due to the incompressibility of the shell, the particles of group 1 cannot approach the MH core in the ‘equatorial’ plane without simultaneously pushing the particles of group 2 away from the MH core along the ‘polar’ direction. Likewise, the particles of group 2 cannot move nearer the MH core along the ‘polar’ axis without pushing the particles of group 1 to the periphery of ‘equatorial’ zone. Therefore, the stresses generated by the representing MS particles 1 and 2 in Fig. 1a attempt to displace the shell in opposing directions. Our qualitative analysis cannot determine to what extent those displacements would compensate, but it definitely shows that the shape changes of the shell at H0 = 0 are minimal.
Under an external field parallel to the dipole moment of the MH particle, that we define as positive (H0 > 0, Fig. 1b), the stress balance is shifted in favor of the ‘polar’ group of MS particles. This is due to the fact that the applied field and the field of the central dipole point in the same direction at the ‘polar’ region, whereas they point in opposite directions in the ‘equator’ zone. In case the MS particles would be mechanically unconstrained, 1 would be repelled and 2 would be attracted by the MH one. However, the elastic network actually couples their displacements and constrains the distance that any MS particle can move away from the central one. The only way to obey this coupled and constrained repulsion from the ‘equator’ zone and attraction from the ‘polar’ region is the effective migration of MS particles from the ‘equator’ to the ‘poles’ (thick arrows in the sketch). As a consequence, the sample tends to stretch along the field direction, not by simply following the direction of the local dipolar forces but by effect of the local depletion/accumulation of MS particles.
In case the applied field is negative—i.e., it is antiparallel to the central dipole moment—even for field strengths lower than the coercive force one needs to consider how it might affect the MH particle. In principle, one may expect the latter to rotate in order to align with the direction of the field, so the magnetic energy is minimized. However, this can only come at the cost of increasing the elastic energy of the matrix. From simple considerations one can show that the antiparallel orientation is actually mechanically stable for field strengths not larger than a critical value, Hr, lower than the coercive force but still not weak, 0 ≪ |Hr| < |Hc|. Therefore, we may justly assume that for any negative applied field H0 that meets Hc < Hr < H0 < 0, the MH particle will not experience any reorientation of its dipole moment, neither by internal switching nor by rigid rotation. In Section S1 of the ESI† we present an estimation of the validity conditions of this behavior and show that they are fulfilled for the range of field values under which the main effects predicted by our models take place. This condition is assumed for the rest of this qualitative discussion.
In order to analyze the effect of negative fields on the MS particles, one can distinguish two cases. For a field strength comparable to the dipolar field of the MH particle at the ‘polar’ region (Fig. 1c), the magnetic moments of the MS particles there tend to vanish, whereas in the ‘equator’ their magnetization becomes stronger. In this situation, the energy of the particles in position 2 is lower than that in position 1, and the MS particles tend to migrate from the ‘poles’ to the ‘equator’. The accompanying displacements of their polymer environment tend to produce axial shrinking of the sample. Under negative applied fields strong enough to impose the orientation of all induced dipoles in the sample (Fig. 1d), the MS particles in the ‘polar’ position are repelled form the MH core, whereas the MS particles in the ‘equator’ are attracted to it. Both tendencies affect the incompressible matrix in the same way, and the sample stretches in the direction of the applied field.
Under decrease of the applied field from strong negative to zero, the sample reversibly passes the states d–c–b–a of Fig. 1. Therefore, the presented qualitative analysis surmises that under applied field cycle, deformational response of the model HSME element is non-monotonic: it displays stretching as well as shrinking, thus, changing its shape from prolate to oblate and back. This scenario is certainly interesting: it suggests that, due to their mixed magnetic content, HSMEs might display non-trivial field-induced macroscopic shape alternation. Moreover, the presence of the MH core makes the shape change non-symmetrically: i.e., under a sinusoidal applied field, the eccentricities attained by the sample in the positive and negative half-periods would be different.
The presented considerations, being to high extent qualitative, are by no means an ultimate proof of the effect. Besides, they neglect some possibly important details. In particular, the magnetic interactions between the MS particles are not taken into account and, as well, the entrainment of the matrix by the particles is just implied and not even outlined. To verify the validity of the conclusions made, in next Sections we perform a formal analysis of the system comparing the results provided by two different models. The first model is a continuum description of the system in which the polymer shell filled with MS particles is represented as a layer of deformable magnetizable structureless medium. In the second approach, we perform a numerical modeling using computer simulations with a bead-spring representation of the particles and the polymer matrix.
3 Continuum analytical modeling approach
3.1 Magnetostatic problem
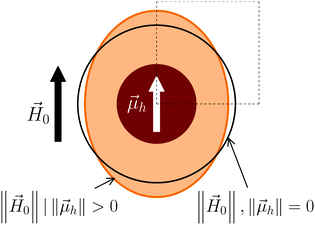
We consider the minimal HSME element described above, placed in an external homogeneous magnetic field,![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0. The continuum representation of such element consists of magnetically hard core (r < r1) and magnetically soft shell r1 < r < r2. Without loss of generality,
0. The continuum representation of such element consists of magnetically hard core (r < r1) and magnetically soft shell r1 < r < r2. Without loss of generality, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 points along Oz axis. The magnetically soft shell is assumed to have a magnetic susceptibility, χ, whereas the magnetically hard core has a magnetization,
0 points along Oz axis. The magnetically soft shell is assumed to have a magnetic susceptibility, χ, whereas the magnetically hard core has a magnetization, 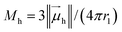 , also coaligned with Oz. In this geometry, shown in Fig. 2, the magnetostatic problem can be formulated as
, also coaligned with Oz. In this geometry, shown in Fig. 2, the magnetostatic problem can be formulated as![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) = = ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 − ∇ψ, Δψ = 0, 0 − ∇ψ, Δψ = 0, | (1) |
 | (2) |
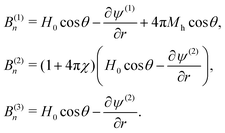 | (3) |
Let us seek for the solution in the form of spherical functions under the condition ψ(i) < ∞, i = 1, 2, 3 once r → 0 or r → ∞:
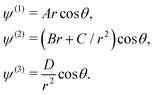 | (4) |
The resulting system of equations to find coefficients A, B, C, D, has the form:
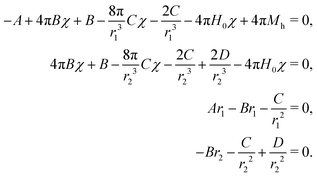 | (5) |
Solving system (5) leads to the following expressions for the coefficients:
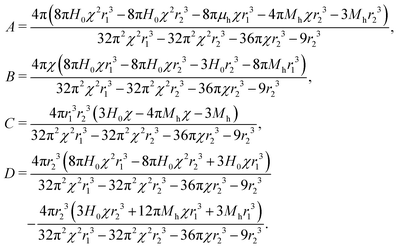 | (6) |
3.2 Elastic problem
Having obtained the solution of the magnetostatic problem, i.e., having found the distribution of the magnetic field inside the magnetically soft shell, one can calculate how the shell would deform under the influence of resulting magnetic forces. In order to do that, we need to formulate the equations for a magneto-elastic medium, respecting the balance between magnetic and elastic forces:∇·![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) + + ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) ·∇ ·∇![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) = 0, = 0, | (7) |
![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) denotes the stress tensor and
denotes the stress tensor and ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) the magnetization vector. In case of equilibrium, the pressure on both sides of the outer border Γ, whose external normal vector is denoted via
the magnetization vector. In case of equilibrium, the pressure on both sides of the outer border Γ, whose external normal vector is denoted via ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) , should be the same. Thus, one obtains:
, should be the same. Thus, one obtains:![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) · ·![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) |Γ = 2πMn2 |Γ = 2πMn2![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) |Γ, |Γ, | (8) |
![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) with displacement vector
with displacement vector ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) as
as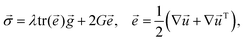 | (9) |
![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) is unity tensor, G stands for the shear modulus, and Lamé coefficient λ characterizes the compressibility of the material, which is related to its volume elastic modulus as K = λ + 2G/3.
is unity tensor, G stands for the shear modulus, and Lamé coefficient λ characterizes the compressibility of the material, which is related to its volume elastic modulus as K = λ + 2G/3.
Assuming linear magnetization law ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) = χ
= χ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) , the equality
, the equality 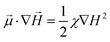 holds true. Note that experimental measurements show that the response of MEs for moderate fields (up to ca. 2 kOe) and strains (at least up to 10%) is essentially linear (see, for instance, ref. 64). As we will see below, the most interesting behavior in our results fits within such moderate values.
holds true. Note that experimental measurements show that the response of MEs for moderate fields (up to ca. 2 kOe) and strains (at least up to 10%) is essentially linear (see, for instance, ref. 64). As we will see below, the most interesting behavior in our results fits within such moderate values.
We will use the variational formulation of the magnetoelastic problem (principle of virtual work). In order to obtain the latter, we have to multiply eqn (8) and (9) by δ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) and integrate:
and integrate:
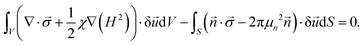 | (10) |
Employing Gauss–Ostrogradsky theorem, after simplifications, we come to a so-called weak formulation:
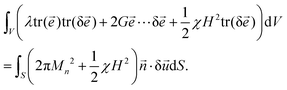 | (11) |
The Dirichlet boundary conditions write:
uρ|ρ=0 = 0, uz|z=0 = 0, ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) |r=r1 = 0, |r=r1 = 0, | (12) |
4 Coarse-grained simulation modeling
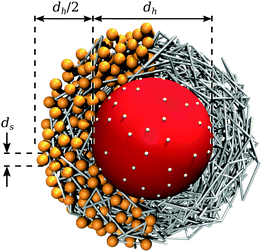
We use a minimal bead-spring modeling approach in order to represent the magnetic and elastic coupling within the HSME elementary unit, analyzing its magnetoelastic behavior by means of molecular dynamics (MD) simulations. Fig. 3 shows a sketch of the HSME elementary unit in our simulation model. It corresponds to the initial configuration of one of the simulation runs.The central MH particle is represented as a sphere of diameter dh, whose position and orientation are fixed in space. It is surrounded by Ns MS particles, also modelled as spheres of diameter ds. On the surface of the central particle there are Na spots at randomly distributed fixed locations that serve as anchoring points. These anchoring points and the centers of the MS particles are crosslinked by elastic springs, forming a highly connected network that mimics the elastic properties of the polymer matrix. In this way, MS particles are able to move under the combined effect of their magnetic interactions and the mechanical constrains imposed by the springs. The crosslinks with the anchoring points keep the network of springs and MS particles mechanically coupled to the surface of the MH one.
Note that the choice of a spherical symmetry for the elementary unit is not intended to provide a quantitative representation of the macroscopic deformations of a sample composed of many of such units. Our goal here is only the qualitative modeling of such deformations on the basis of local rearrangements occurring in the vicinity of the MH particles. To this regard, the main artifact associated to this approach is the fact that the MS particles in the most external layer have a relatively higher degree of anisotropy in their elastic constraints than the inner ones (i.e., a lower average number of bonding springs). However, the volume of the shell is large enough to comprise several inner layers of MS particles, so that the ones belonging to the external surface are less than 15% of the total. Under the condition of a relatively low concentration of MH particles in the sample, it is reasonable to assume that the qualitative local behavior of the system is well captured by our modeling approach. Nevertheless, one can consider reasonable the qualitative extrapolation of the local deformations to the overall deformation of a macroscopic sample.
In the following sections we introduce the interactions governing our simulation model and a description of the simulation protocol we employed.
4.1 Model interactions
Since we use a MD simulation approach, in order to keep numerical stability we need to avoid discontinuities in the interaction potentials. Besides this technical reason, we also assume that solid particles within the elastomer will be always surrounded by a layer of polymer material of finite thickness that elastically hinders actual close contact between them. This is a reasonable assumption at least for not very high particle densities. Therefore, the central MH particle and the surrounding MS ones are conveniently represented as soft-core spheres with an excluded volume determined by a truncated and shifted Lennard-Jones pair interaction, also known as Weeks–Chandler–Andersen (WCA) potential:65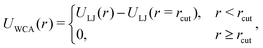 | (13) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j‖ is the current center-to-center distance between the pair of interacting beads i and j, U(r) = 4εLJ[(d/r)12 − (d/r)6] is the conventional Lennard-Jones potential, rc is a truncation distance set to rc = 21/6d in order to make the interaction purely repulsive, and d is the center-to-center excluded distance, that depends on the characteristic diameter of each bead, di and dj, as d = (di + dj)/2.
j‖ is the current center-to-center distance between the pair of interacting beads i and j, U(r) = 4εLJ[(d/r)12 − (d/r)6] is the conventional Lennard-Jones potential, rc is a truncation distance set to rc = 21/6d in order to make the interaction purely repulsive, and d is the center-to-center excluded distance, that depends on the characteristic diameter of each bead, di and dj, as d = (di + dj)/2.
As we pointed above, the polymer matrix that constrains the movement of the MS particles around the MH one is represented implicitly as a single network of elastic springs connecting all MS particles and anchoring points on the surface of the central one. A similar simple approach was introduced very recently to model the magnetoelastic response of thin film elastomeric coatings.55 Each spring i corresponds to a simple harmonic potential:
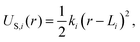 | (14) |
The magnetization dynamics of MS particles is much faster than the dynamics of the mechanical deformation of the polymer matrix. This imposes the use of some approximation for the treatment of their magnetic properties. Our simple approach is to represent the magnetic properties of both, MH and MS particles, by point magnetic dipoles located at their centers. Therefore, any pair of magnetized particles i and j, without regard to their MH or MS nature, interacts by means of the conventional dipole–dipole potential:
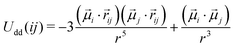 | (15) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij =
ij = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j is the vector connecting their centers and r = ‖
j is the vector connecting their centers and r = ‖![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij‖. Here, we will assign to the central MH particle either a zero magnetic moment or a moment with fixed orientation and length,
ij‖. Here, we will assign to the central MH particle either a zero magnetic moment or a moment with fixed orientation and length, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) h = (0,0,μh). The dipole moment of each MS particle i,
h = (0,0,μh). The dipole moment of each MS particle i, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) i, will be induced by the net external field at the position of its center,
i, will be induced by the net external field at the position of its center, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) i, according to
i, according to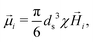 | (16) |
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) i = i = ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 + 0 + ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) (i)h, (i)h, | (17) |
![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 is any eventually applied uniform external field, that here will be taken as having only a component in the z axis,
0 is any eventually applied uniform external field, that here will be taken as having only a component in the z axis, ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) 0 = (0,0,H0), and
0 = (0,0,H0), and ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) (i)h is the dipolar field created by the central MH particle at the position of the MS one, that is defined as
(i)h is the dipolar field created by the central MH particle at the position of the MS one, that is defined as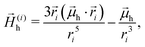 | (18) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i is the vector connecting the center of the MH particle to the center of the polarized one and ri = ‖
i is the vector connecting the center of the MH particle to the center of the polarized one and ri = ‖![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i‖. Therefore, with this approximation we are disregarding the mutual magnetic induction between the MS particles when calculating their induced dipoles. However, their dipole–dipole interactions, either with the central MH particle and the mutual ones, are fully taken into account by means of expression (15). Mutual magnetization between MS is important at very short, nearly close contact interparticle distances, whereas at larger distances the point dipole representation provides a good approximation.66 As pointed above, here we assume that effective close contact between MS particles is prevented by the surrounding polymer material, thus the point dipole approximation can be considered a reasonable approach for a qualitative characterization of the system. Finally, according to this representation, MS particles also experience the Zeeman interaction with applied external fields. Since such interaction corresponds to induced dipoles, it is one half the conventional Zeeman potential energy:67
i‖. Therefore, with this approximation we are disregarding the mutual magnetic induction between the MS particles when calculating their induced dipoles. However, their dipole–dipole interactions, either with the central MH particle and the mutual ones, are fully taken into account by means of expression (15). Mutual magnetization between MS is important at very short, nearly close contact interparticle distances, whereas at larger distances the point dipole representation provides a good approximation.66 As pointed above, here we assume that effective close contact between MS particles is prevented by the surrounding polymer material, thus the point dipole approximation can be considered a reasonable approach for a qualitative characterization of the system. Finally, according to this representation, MS particles also experience the Zeeman interaction with applied external fields. Since such interaction corresponds to induced dipoles, it is one half the conventional Zeeman potential energy:67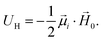 | (19) |
4.2 Simulation approach
We perform MD simulations of the model described above using open boundaries and a Langevin thermostat. The latter introduces friction and stochastic terms, that follow the conventional fluctuation–dissipation rules, in the translational and rotational Newtonian equations of motion. This is a usual strategy to represent implicitly the effects of the thermal fluctuations of liquid background fluids in coarse-grained simulations.68,69 Even though in elastomeric materials such liquid background is absent, it is still convenient to keep a small degree of thermal fluctuations in this type of coarse-grained MD simulations in order to ease the mechanical relaxation of the system, preventing it from being kinetically trapped into highly stressed configurations.55 This is achieved by setting a non zero but relatively rather low value for the thermal energy in the system. The system of units and the set of parameter values used here are discussed in the next Section.Each simulation run consists of several steps that we briefly describe here. Further details can be found in Section S2 of the ESI.† First, an initial configuration is prepared by fixing inside the simulation box the MH particle, with its Na surface anchoring points, and placing randomly the Ns magnetizable particles uniformly distributed inside a shell of thickness dh/2 around the former, so that the volume fraction within the shell is ρs = Ns(ds/dh)3/7. The MS particles and anchoring points are then crosslinked by randomly selecting elements from a list of candidate pairs, consisting of either two particles or one particle and one anchoring point, whose center-to-center distance is not larger than an arbitrary cutoff, dcut. The components of each selected pair are bonded with a spring with potential (14). The equilibrium length of such spring, Li, is set to be equal to the center-to-center distance of the pair at the moment of creating the bond. In this way, a subsequent significant deformation of the network structure due to purely mechanical effects from the springs is prevented, ensuring that changes in the overall density of particles will be moderate and only induced by magnetic interactions. Following similar approaches to the build up of spring networks,35 here we take the elastic constant of each spring, ki, to be proportional to its corresponding equilibrium length, Li. Additionally, in order to ease the fitting of the model, we also rescale its value with the average equilibrium length of all springs in the system, 〈L〉:
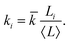 | (20) |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) is simply the average of all spring constants, playing the role of a fitting parameter that determines the overall rigidity of the network. After each spring is added to the system, the total amount of bonds assigned to each element of the pair is checked. Whenever a particle or anchoring point gets bonded to an arbitrary maximum amount of neighbors, smax, all the candidate pairs to which it belongs are removed from the list. In this way, large inhomogeneities in the distribution of springs across the network is prevented. This crosslinking procedure is iterated until the list of candidate pairs is exhausted. At that point, if any MS particle remains unbonded, smax/2 bonds with different randomly selected close particles or anchoring points are set on it in order to ensure the complete connectivity of the elastic network. In Section S3 of the ESI† we show an example of typical distribution of elastic constants set with this procedure.
is simply the average of all spring constants, playing the role of a fitting parameter that determines the overall rigidity of the network. After each spring is added to the system, the total amount of bonds assigned to each element of the pair is checked. Whenever a particle or anchoring point gets bonded to an arbitrary maximum amount of neighbors, smax, all the candidate pairs to which it belongs are removed from the list. In this way, large inhomogeneities in the distribution of springs across the network is prevented. This crosslinking procedure is iterated until the list of candidate pairs is exhausted. At that point, if any MS particle remains unbonded, smax/2 bonds with different randomly selected close particles or anchoring points are set on it in order to ensure the complete connectivity of the elastic network. In Section S3 of the ESI† we show an example of typical distribution of elastic constants set with this procedure.
It is important to underline that, in difference with the continuum model, this approach does not impose the strict incompressibility of the shell. However, for moderate deformations, the changes in the volume enclosed by the implicit boundary are expected to be also not very large. Once the initial configuration is prepared, the dipole moment of the central particle, μh, and the external field, H0, are set and the MD run is performed, letting the system to relax until all net displacements of the MS particles are vanished and only very small fluctuations due to the residual thermal noise remain, indicating that the elastic network structure has reached a stationary configuration. Finally, the properties of such relaxed network structure are analyzed.
4.3 Nondimensional units and sampled parameters
In both, continuum analytical calculations and computer simulations with coarse-grained models, it is convenient to use a system of reduced—i.e., dimensionless—units that makes all parameters of interest to vary within a similar domain of values, typically close to unity. This ensures the numerical stability and accuracy of the calculations, eases the comparison with other models and allows the representation of any system that keeps the same ratios of physical quantities, independently from their absolute values. In the following, reduced quantities will be denoted with a tilde symbol, so that![[X with combining tilde]](https://www.rsc.org/images/entities/i_char_0058_0303.gif) will indicate the value of the physical quantity X in our system of reduced units.
will indicate the value of the physical quantity X in our system of reduced units.
As a reference, typical available HSME samples are synthesized with MH particles of diameter dh ≈ 50 μm and saturation magnetization of Mh ≈ 800 G, combined with volume fractions of around ρs ≈ 0.3 of MS particles with diameter ds ≈ 5 μm and very high magnetic susceptibility, close to the limiting value χ ≈ 3/4π ≈ 0.24, embedded into polymer matrices with a typical shear modulus of G ≈ 105 dyn per cm3.61,70 A natural choice for the reduced units of length is the size of the smallest particles in the system, ds, so that ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) s = 1 and
s = 1 and ![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) h = 10. For continuum analytical calculations it is very convenient to take the square root of the shear modulus as the reference scale for the magnetic parameters—i.e., magnetic field, magnetization and magnetic moment—so that
h = 10. For continuum analytical calculations it is very convenient to take the square root of the shear modulus as the reference scale for the magnetic parameters—i.e., magnetic field, magnetization and magnetic moment—so that 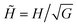 ,
, 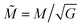 and
and 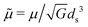 , respectively. This choice fully defines our system of reduced units. For instance, sampling reduced strengths of the external field in the range
, respectively. This choice fully defines our system of reduced units. For instance, sampling reduced strengths of the external field in the range ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ∈ [0,10] corresponds to a moderate physical range of up to 3.16 × 103 Oe, that is one order or magnitude lower than the experimental saturation field used, for instance, in ref. 33 for HSME samples of this type. Accordingly, the reduced magnetic moment of the central particle, whenever it is magnetized, is taken as
0 ∈ [0,10] corresponds to a moderate physical range of up to 3.16 × 103 Oe, that is one order or magnitude lower than the experimental saturation field used, for instance, in ref. 33 for HSME samples of this type. Accordingly, the reduced magnetic moment of the central particle, whenever it is magnetized, is taken as ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 1324.6, that corresponds to approximately 5.24 × 10−5 emu. From this, one can estimate that the maximum reduced magnetic moment induced in any given MS particle by the combined action of the applied external field and the field created by the central particle is approximately
h = 1324.6, that corresponds to approximately 5.24 × 10−5 emu. From this, one can estimate that the maximum reduced magnetic moment induced in any given MS particle by the combined action of the applied external field and the field created by the central particle is approximately ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) s ≲ 20, or 8 × 10−7 emu. Finally, in Section S1 of the ESI† we deduced the critical value of the external field that, applied in antiparallel orientation with respect to the dipole of the central particle, would lead to an inversion of the latter. This is Hr ≈ −1.5 × 103 Oe, or
s ≲ 20, or 8 × 10−7 emu. Finally, in Section S1 of the ESI† we deduced the critical value of the external field that, applied in antiparallel orientation with respect to the dipole of the central particle, would lead to an inversion of the latter. This is Hr ≈ −1.5 × 103 Oe, or ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) r ≈ −4.7.
r ≈ −4.7.
Besides defining a system of reduced units, we need to set explicitly a number of parameters in order to perform the simulations. The total amount of MS particles required to fill the shell with the chosen volume fraction, ρs = 0.3, is Ns = 2100. For the amount of anchoring points on the surface of the central particle we take Na = 99, that is the amount of MS particles needed to fill, with the same ρs, a thinner shell of reduced thickness 1. The specific value of the strength of the soft core interaction (13) between particles, εLJ, is irrelevant as long as it prevents too much overlap. For simplicity, we take ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) LJ = 1. For the thermal energy in the system we use a very low value,
LJ = 1. For the thermal energy in the system we use a very low value, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = 0.001, that proved to be convenient for the relaxation of this type of bead-spring systems.55 In difference with the continuum model, the shear modulus of the network of springs and small particles in the simulation model is not a simple free parameter. Reasonably, one can expect it to depend on the amount of springs and their distributions of elastic constants and equilibrium lengths, which in turn depend on the parameters smax, dcut and
= 0.001, that proved to be convenient for the relaxation of this type of bead-spring systems.55 In difference with the continuum model, the shear modulus of the network of springs and small particles in the simulation model is not a simple free parameter. Reasonably, one can expect it to depend on the amount of springs and their distributions of elastic constants and equilibrium lengths, which in turn depend on the parameters smax, dcut and ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) . Concerning the maximum amount of bonds per particle, smax, the larger would be its value, the more isotropic would tend to be the spatial constraining of the particles, but also the higher would be the computational load. As a compromise between computational efficiency and isotropy, here we take smax = 6. Regarding the crosslinking cutoff distance, dcut, in one hand very long bond lengths would seem too unrealistic in a network-like representation of the polymer matrix; on the other hand, we want most of the crosslinked particles to reach their maximum amount of crosslinks. After checking different values, we take dcut = 6ds as one that reasonably satisfies both conditions. Finally, we are left with
. Concerning the maximum amount of bonds per particle, smax, the larger would be its value, the more isotropic would tend to be the spatial constraining of the particles, but also the higher would be the computational load. As a compromise between computational efficiency and isotropy, here we take smax = 6. Regarding the crosslinking cutoff distance, dcut, in one hand very long bond lengths would seem too unrealistic in a network-like representation of the polymer matrix; on the other hand, we want most of the crosslinked particles to reach their maximum amount of crosslinks. After checking different values, we take dcut = 6ds as one that reasonably satisfies both conditions. Finally, we are left with ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) as the only fitting parameter for the elastic properties of the shell. In order to obtain an estimation of the value of
as the only fitting parameter for the elastic properties of the shell. In order to obtain an estimation of the value of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) that corresponds to the target shear modulus, we use the model of Kot and coworkers for the elastic properties of a simple mass-spring random network.71 According to this model, the bulk modulus of such a network is given by
that corresponds to the target shear modulus, we use the model of Kot and coworkers for the elastic properties of a simple mass-spring random network.71 According to this model, the bulk modulus of such a network is given by
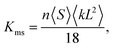 | (21) |
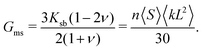 | (22) |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) corresponding to a given shear modulus
corresponding to a given shear modulus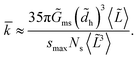 | (23) |
![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 〉 ≈ 20 and 〈
〉 ≈ 20 and 〈![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) 3〉 ≈ 93, that gives
3〉 ≈ 93, that gives ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) ≈ 0.4. We also tested several values of
≈ 0.4. We also tested several values of ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) between 0.1 and 1.0 (see Section S4 in the ESI†), observing that actually
between 0.1 and 1.0 (see Section S4 in the ESI†), observing that actually ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = 0.4 provides the best matching between the continuum and the bead-spring models. Therefore, in the next section we will discuss only the simulation results obtained with this value. Such results correspond to averages over 20 independent runs. All computer simulations in this study have been performed with the ESPResSo 3.3.1 simulation package.72
= 0.4 provides the best matching between the continuum and the bead-spring models. Therefore, in the next section we will discuss only the simulation results obtained with this value. Such results correspond to averages over 20 independent runs. All computer simulations in this study have been performed with the ESPResSo 3.3.1 simulation package.72
5 Results and discussion
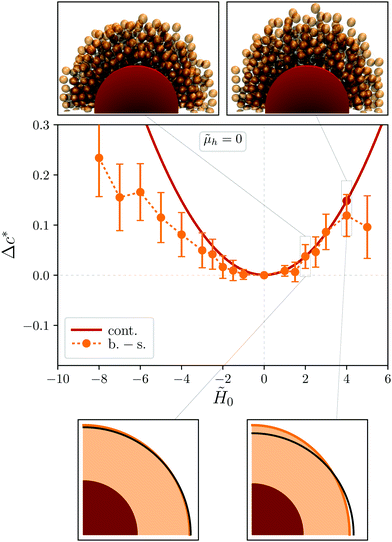
We start the discussion by considering the simplest case, that is when the central particle in the HSME elementary unit is nonmagnetic:![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0. The first task is to find a way to characterize the expected magnetically induced deformations of the elastic matrix to directly compare the continuum and the bead-spring models. Whereas in the former the outer edge of the matrix is perfectly defined and the deformations are easy to visualize, in the bead-spring model no explicit outer boundary exists (see Fig. 3) since it is rendered by the discrete positions of MS particles. To find commensurate terms for that comparison, we define a virtual boundary of the bead-spring system as follows. First, the convex hull of all particles in the system is calculated. Then, by assuming that under any moderate deformation the elastic shell keeps an ellipsoidal profile, we perform a least-squares fit of an ellipsoid to that convex hull.
h = 0. The first task is to find a way to characterize the expected magnetically induced deformations of the elastic matrix to directly compare the continuum and the bead-spring models. Whereas in the former the outer edge of the matrix is perfectly defined and the deformations are easy to visualize, in the bead-spring model no explicit outer boundary exists (see Fig. 3) since it is rendered by the discrete positions of MS particles. To find commensurate terms for that comparison, we define a virtual boundary of the bead-spring system as follows. First, the convex hull of all particles in the system is calculated. Then, by assuming that under any moderate deformation the elastic shell keeps an ellipsoidal profile, we perform a least-squares fit of an ellipsoid to that convex hull.
Fig. 4 shows two examples of relaxed configurations of the bead-spring system corresponding to ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0 and two values of the external field,
h = 0 and two values of the external field, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 0 (left) and
0 = 0 (left) and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 4 (center). The size of the MS particles is scaled by 0.5 in order to ease the visualization. Each configuration is surrounded by its virtual boundary, calculated with the fitting procedure described above and plotted as a semitransparent surface. The fitted ellipsoid corresponding to
0 = 4 (center). The size of the MS particles is scaled by 0.5 in order to ease the visualization. Each configuration is surrounded by its virtual boundary, calculated with the fitting procedure described above and plotted as a semitransparent surface. The fitted ellipsoid corresponding to ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 4 is also plotted separately (right). In both cases, the ellipsoid envelops the “cloud” of particles rather well.
0 = 4 is also plotted separately (right). In both cases, the ellipsoid envelops the “cloud” of particles rather well.
Taking advantage of the “ellipsoid terms” we introduced, the deformations of the shell boundary are characterized by means of a single parameter, defined as Δc* = 〈(c − c0)/c0〉, where c is the distance from the center of the MH particle to the point where the outer shell boundary intersects with the axis parallel to the external field, c0 is the value of that distance when ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0 and
h = 0 and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 0, and angle brackets denote the average over independent runs. Note that Δc* is positive for longitudinal expansion of the boundary and negative in opposite case.
0 = 0, and angle brackets denote the average over independent runs. Note that Δc* is positive for longitudinal expansion of the boundary and negative in opposite case.
Fig. 5 shows the dependence of Δc* on ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 for both models at
0 for both models at ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0. Note that the sign of
h = 0. Note that the sign of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 indicates its orientation with respect to the reference axis. As follows from this plot, the continuum model predicts a parabolic expansion of the system boundary along the field. The curve is perfectly symmetric with respect to the point
0 indicates its orientation with respect to the reference axis. As follows from this plot, the continuum model predicts a parabolic expansion of the system boundary along the field. The curve is perfectly symmetric with respect to the point ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 0, that corresponds to the unperturbed system. Within the interval
0 = 0, that corresponds to the unperturbed system. Within the interval ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ∼ [−2,2], i.e., at low fields, the characteristic function Δc*(
0 ∼ [−2,2], i.e., at low fields, the characteristic function Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) obtained for the bead-spring model obeys rather well the parabolic law. For stronger fields, as the statistical fluctuations in the bead-spring model increase, the deviations from the parabolla become more significant. However, the qualitative behavior of both models remains the same: the axial elongation of the system grows independently of the orientation of the field. This elongation is clearly visible in the configuration snapshots selected from both models that are included in Fig. 5. An important difference in such snapshots is, however, that the shrinking in the direction perpendicular to the field observed in the continuum model is indistinguishable in the bead-spring system.
0) obtained for the bead-spring model obeys rather well the parabolic law. For stronger fields, as the statistical fluctuations in the bead-spring model increase, the deviations from the parabolla become more significant. However, the qualitative behavior of both models remains the same: the axial elongation of the system grows independently of the orientation of the field. This elongation is clearly visible in the configuration snapshots selected from both models that are included in Fig. 5. An important difference in such snapshots is, however, that the shrinking in the direction perpendicular to the field observed in the continuum model is indistinguishable in the bead-spring system.
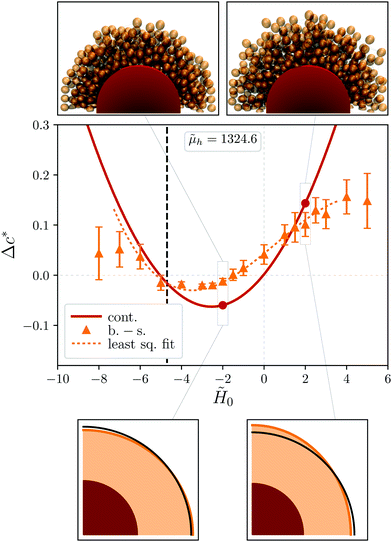
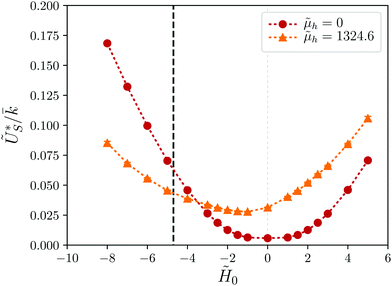
Fig. 6 shows the results on Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) obtained when the central particle in the system has permanent moment
0) obtained when the central particle in the system has permanent moment ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 1324.6. In this case the results of both models, although qualitatively similar, are quantitatively rather different. In both approaches, the essential effect of the magnetic field of the MH particle is to shift the minimum of the parabolic profile to negative values. For the continuum model, this is Δcmin* ≈ −0.06 for
h = 1324.6. In this case the results of both models, although qualitatively similar, are quantitatively rather different. In both approaches, the essential effect of the magnetic field of the MH particle is to shift the minimum of the parabolic profile to negative values. For the continuum model, this is Δcmin* ≈ −0.06 for ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ≈ −2.54. In this case, as discussed in Section 2.2, the incompressibility of the elastic shell and the attractive effect of the MH particle, when its field is the only cause of the magnetization of the MS ones, makes the net deformation of the boundary model very small: for
0 ≈ −2.54. In this case, as discussed in Section 2.2, the incompressibility of the elastic shell and the attractive effect of the MH particle, when its field is the only cause of the magnetization of the MS ones, makes the net deformation of the boundary model very small: for ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 0, Δc* ≈ 0.002. However, the corresponding deformation in the bead-spring model is much stronger, being approximately Δc* ≈ 0.04. Besides that, the position of the minimum of Δc*(
0 = 0, Δc* ≈ 0.002. However, the corresponding deformation in the bead-spring model is much stronger, being approximately Δc* ≈ 0.04. Besides that, the position of the minimum of Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0), as obtained from a weighted least-squares fit of the simulation data to cubic splines, is located at a stronger external field,
0), as obtained from a weighted least-squares fit of the simulation data to cubic splines, is located at a stronger external field, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ≈ −3.48, yielding a weaker deformation (Δcmin* ≈ −0.026) than the continuum model. Another important fact is that the deformation curve of the bead-spring model is not symmetric with respect to its minimum: at relatively large negative fields it has a more steep slope than at positive ones. Finally, it is very important to underline that the main part of the changes from longitudinal expansion to shrinking and back, observed in both models for a range of negative fields, correspond to fields weaker than the critical field for the switching of the orientation of the central dipole,
0 ≈ −3.48, yielding a weaker deformation (Δcmin* ≈ −0.026) than the continuum model. Another important fact is that the deformation curve of the bead-spring model is not symmetric with respect to its minimum: at relatively large negative fields it has a more steep slope than at positive ones. Finally, it is very important to underline that the main part of the changes from longitudinal expansion to shrinking and back, observed in both models for a range of negative fields, correspond to fields weaker than the critical field for the switching of the orientation of the central dipole, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) r = −4.7 (see thick vertical dashed line), thus they can be considered as physically feasible. According to the crossing between the curves Δc*(
r = −4.7 (see thick vertical dashed line), thus they can be considered as physically feasible. According to the crossing between the curves Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) and
0) and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 =
0 = ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) r, the switching would happened, as we increase the strength of the antiparallel field, far after the shell reaches its maximum longitudinal shrinking, only slightly before it recovers a symmetrical shape. Note that, consequently, the points corresponding to
r, the switching would happened, as we increase the strength of the antiparallel field, far after the shell reaches its maximum longitudinal shrinking, only slightly before it recovers a symmetrical shape. Note that, consequently, the points corresponding to ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 <
0 < ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) r can be considered unphysical.
r can be considered unphysical.
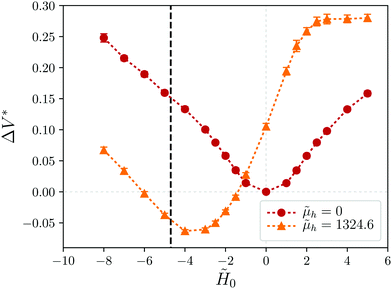
The discrepancies between the models, especially when the central particle is magnetized, are not surprising due to the different assumptions established for each approach. One of the key differences is the incompressibility of the shell, that is a condition strictly imposed in the continuum model and absent in the bead-spring network representation. The good agreement between the fitted shear modulus of the latter and the one predicted by the model of Kot and coworkers,71 where Poisson ratio of a significantly compressible system is used, indicates that volume changes might influence considerably the bead-spring simulation results. In order to check this, we calculated the volumes of the fitted ellipsoids, Ṽ = 4πã![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif)
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) /3, and analyzed their relative change, defined analogously to the longitudinal deformation parameter as ΔV* = 〈(Ṽ − Ṽ0)/Ṽ0〉, where Ṽ0 is the volume corresponding to
/3, and analyzed their relative change, defined analogously to the longitudinal deformation parameter as ΔV* = 〈(Ṽ − Ṽ0)/Ṽ0〉, where Ṽ0 is the volume corresponding to ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0 and
h = 0 and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 0.
0 = 0.
Fig. 7 shows the dependence of ΔV* on the applied field for both investigated magnetizations of the central particle. The relative volume change is significant, growing to about 25% for the strongest sampled elongations. In the case ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0, the change is symmetric with respect to the reference value at
h = 0, the change is symmetric with respect to the reference value at ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 0 and remains rather moderate within the low field interval,
0 = 0 and remains rather moderate within the low field interval, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ∼ [−2,2]. This explains the good agreement with the continuum model observed for Δc*(
0 ∼ [−2,2]. This explains the good agreement with the continuum model observed for Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) in such interval. However, for
0) in such interval. However, for ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 1324.6 the magnitude of ΔV* varies over a wide interval. Opposite to what was observed for the slope of Δc*(
h = 1324.6 the magnitude of ΔV* varies over a wide interval. Opposite to what was observed for the slope of Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0), the change of ΔV*(
0), the change of ΔV*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) is substantial in the interval
0) is substantial in the interval ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ∼ [−2,2] but weakens for stronger negative fields. This indicates that relatively large elongations predicted by the continuum model at low fields are smeared in the bead-spring system by volume changes. The region of longitudinal shrinking, signaled by negative values of Δc* in the region of physical validity of the models,
0 ∼ [−2,2] but weakens for stronger negative fields. This indicates that relatively large elongations predicted by the continuum model at low fields are smeared in the bead-spring system by volume changes. The region of longitudinal shrinking, signaled by negative values of Δc* in the region of physical validity of the models, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 >
0 > ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) r = −4.7, approximately corresponds to a general decrease of the volume. Moreover, the respective minima of Δc*(
r = −4.7, approximately corresponds to a general decrease of the volume. Moreover, the respective minima of Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) and ΔV*(
0) and ΔV*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) correspond to similar values of field, close to
0) correspond to similar values of field, close to ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ≈ −3.75.
0 ≈ −3.75.
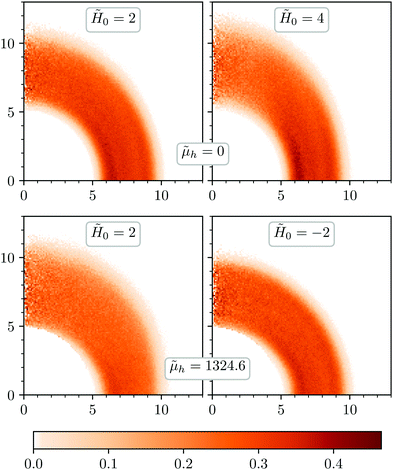
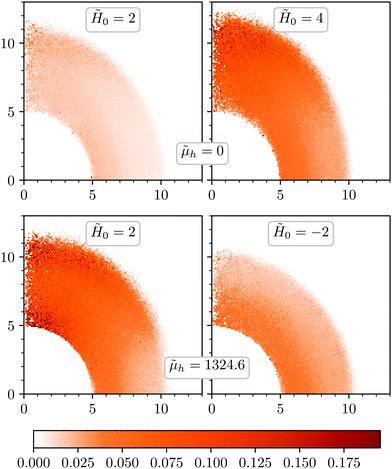
Another important assumption in the continuum model is that the distribution of MS particles is uniform and constant without regard to shell shape. However, the bead-spring model does not only allow changes in the volume of the shell, but also in the local density of MS particles. Fig. 8 presents a set of color scale ‘heat maps’ of the local volume fraction of MS particles, corresponding to the same values of external field selected for the snapshots of Fig. 5 and 6. These distributions have been calculated by sampling the volume fraction inside spheres of diameter 1.5ds randomly located within the shell. Here, as in the continuum model results, we take advantage of the symmetries of the system and show only one quadrant of the two-dimensional projection of the distributions. As expected, longitudinal expansion of the shell with ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 at
0 at ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0 and its longitudinal shrinking under
h = 0 and its longitudinal shrinking under ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 < 0 can also be clearly observed in these maps. More interesting is the fact that in all these examples the ‘equatorial’ zone (i.e., the region close to the transverse plane) has a relatively high fraction of particles, with a weak but distinguishable indication of radial layering. The latter is signaled by dark stripes, that are present in all cases at least at a distance from the surface of the central particle around ∼2
0 < 0 can also be clearly observed in these maps. More interesting is the fact that in all these examples the ‘equatorial’ zone (i.e., the region close to the transverse plane) has a relatively high fraction of particles, with a weak but distinguishable indication of radial layering. The latter is signaled by dark stripes, that are present in all cases at least at a distance from the surface of the central particle around ∼2![[d with combining tilde]](https://www.rsc.org/images/entities/i_char_0064_0303.gif) s. Such layering indicates that the MS particles form chains fairly well aligned with the external field direction.
s. Such layering indicates that the MS particles form chains fairly well aligned with the external field direction.
For ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0 (Fig. 8, upper row), the moderate change of volume associated to the field-induced longitudinal expansion of the shell leads to a significant transverse shrinking. This enhances the layering in the ‘equatorial’ zone, that shows another dense stripe close to the external boundary.
h = 0 (Fig. 8, upper row), the moderate change of volume associated to the field-induced longitudinal expansion of the shell leads to a significant transverse shrinking. This enhances the layering in the ‘equatorial’ zone, that shows another dense stripe close to the external boundary.
When the central particle is magnetized and the external field is parallel to its magnetic moment, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 > 0 (Fig. 8, lower left plot), the shell elongation undergoes without its significant transverse shrinking, even though the external region has a very low density. As a consequence, there is a relatively large increase of the total virtual volume. The cause of this effect is that in the ‘equatorial’ zone the field of the central particle and the external one point in opposite directions, thus making the net field very low. Under such conditions, large local rearrangements of particles are hardly possible and a much weaker layering is observed. In the ‘polar’ region (i.e., close to the longitudinal axis) the shell elongates similarly to the case
0 > 0 (Fig. 8, lower left plot), the shell elongation undergoes without its significant transverse shrinking, even though the external region has a very low density. As a consequence, there is a relatively large increase of the total virtual volume. The cause of this effect is that in the ‘equatorial’ zone the field of the central particle and the external one point in opposite directions, thus making the net field very low. Under such conditions, large local rearrangements of particles are hardly possible and a much weaker layering is observed. In the ‘polar’ region (i.e., close to the longitudinal axis) the shell elongates similarly to the case ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0. The only difference is that the ‘polar caps’ of the magnetized MH particle become attractive to the MS particles, and the inner boundary of the shell shifts slightly towards it.
h = 0. The only difference is that the ‘polar caps’ of the magnetized MH particle become attractive to the MS particles, and the inner boundary of the shell shifts slightly towards it.
In case the applied field is antiparallel to the central dipole (Fig. 8, lower right plot), is the ‘equatorial’ zone of the shell the one that behaves similarly to the case ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0. An actual shrinking of the outer boundary can neither be distinguished there. In the ‘polar’ zone, as long as the external field does not become dominant, the surface of the MH particle remains attractive, pulling the inner boundary of the shell closer. However, the net field is too weak to induce formation of chains, and the total thickness of the shell at that region does not increase. Therefore, the small longitudinal shrinking one can observe comes mainly from the shift of the shell rather than from a local change in thickness.
h = 0. An actual shrinking of the outer boundary can neither be distinguished there. In the ‘polar’ zone, as long as the external field does not become dominant, the surface of the MH particle remains attractive, pulling the inner boundary of the shell closer. However, the net field is too weak to induce formation of chains, and the total thickness of the shell at that region does not increase. Therefore, the small longitudinal shrinking one can observe comes mainly from the shift of the shell rather than from a local change in thickness.
The bead-spring model also makes straightforward the analysis of the field-induced changes of elastic energy in the system. Fig. 9 shows the elastic energy (14) averaged over all springs and independent runs, 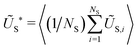 , scaled with the average elastic constant,
, scaled with the average elastic constant, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = 0.4. For
= 0.4. For ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0, the stress of the spring network is negligible in the low field range,
h = 0, the stress of the spring network is negligible in the low field range, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ∼ [−2,2], with a significant growth only at stronger fields. This evidences that the spring network experiences slight rearrangements of the MS particles as a response to weak homogeneous external fields, without large changes of volume or mechanical stress. In this way, it follows rather well the ideal behavior predicted by the continuum model. However, the presence of the nonuniform field of the central particle when it is magnetized sets the spring network under significant stress for any applied external field. Under these conditions, local particle rearrangements are more difficult and the shell responds to the external field mainly by collective displacements that entail more moderate changes of internal stress. The minimum of elastic energy is then located at negative values of
0 ∼ [−2,2], with a significant growth only at stronger fields. This evidences that the spring network experiences slight rearrangements of the MS particles as a response to weak homogeneous external fields, without large changes of volume or mechanical stress. In this way, it follows rather well the ideal behavior predicted by the continuum model. However, the presence of the nonuniform field of the central particle when it is magnetized sets the spring network under significant stress for any applied external field. Under these conditions, local particle rearrangements are more difficult and the shell responds to the external field mainly by collective displacements that entail more moderate changes of internal stress. The minimum of elastic energy is then located at negative values of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0, close to the point
0, close to the point ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 ≈ −1.4 where the curves Δc*(
0 ≈ −1.4 where the curves Δc*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) and ΔV*(
0) and ΔV*(![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0) cross zero (see Fig. 6 and 7).
0) cross zero (see Fig. 6 and 7).
Finally, it is also interesting to examine the spatial distribution of elastic energies of the springs. This gives a notion of the local stress at different points of the elastic shell. This property is calculated in a similar way to the procedure employed to obtain the density distributions. The only difference is that in this case we look at the elongations of the springs connected to the particles inside the sampling volume. The local elastic energy is then calculated as the sum of values given by expression (14) for such elongations, scaled by ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) = 0.4. Fig. 10 shows color maps for these distributions, corresponding to the same parameter sets of Fig. 8.
= 0.4. Fig. 10 shows color maps for these distributions, corresponding to the same parameter sets of Fig. 8.
For ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0, the distribution maps confirm the contrast between the low overall stress induced by a weak field,
h = 0, the distribution maps confirm the contrast between the low overall stress induced by a weak field, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 2 (upper left plot), and by a larger one,
0 = 2 (upper left plot), and by a larger one, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 4 (upper right plot), observed in Fig. 9. The qualitative similarity between the spatial distributions presented in the upper row of Fig. 10 is quite understandable, as they correspond to the same type of shell deformation, i.e., to the shell expansion along the field. The common trait of these distributions is the existence of a region of low stress in the ‘equatorial’ zone and of high stress in the ‘polar’ one, in both cases close to the outer boundary of the shell.
0 = 4 (upper right plot), observed in Fig. 9. The qualitative similarity between the spatial distributions presented in the upper row of Fig. 10 is quite understandable, as they correspond to the same type of shell deformation, i.e., to the shell expansion along the field. The common trait of these distributions is the existence of a region of low stress in the ‘equatorial’ zone and of high stress in the ‘polar’ one, in both cases close to the outer boundary of the shell.
For ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 1324.6 (Fig. 10, lower row), the difference between the distributions obtained for
h = 1324.6 (Fig. 10, lower row), the difference between the distributions obtained for ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = 2 (lower left plot) and
0 = 2 (lower left plot) and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) 0 = −2 (lower right plot) is not only quantitative but also qualitative, since they correspond to elongation and shrinking, respectively. For elongation, the distribution is very similar to the one observed for
0 = −2 (lower right plot) is not only quantitative but also qualitative, since they correspond to elongation and shrinking, respectively. For elongation, the distribution is very similar to the one observed for ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) h = 0, with the addition of another region of relative high stress close to the attracting ‘polar cap’ of the MH particle. Under inverse field, however, the overall stress is relatively lower and its distribution totally changes. The highest elastic energy concentrates within an inner layer around the MH particle, whereas the lowest energy is observed in the outer region of the shell, being slightly lower close to the ‘polar’ zone. This supports the interpretation discussed above on the shrinking of the shell being caused by the attraction of the MS particles to the ‘poles’ of the MH one.
h = 0, with the addition of another region of relative high stress close to the attracting ‘polar cap’ of the MH particle. Under inverse field, however, the overall stress is relatively lower and its distribution totally changes. The highest elastic energy concentrates within an inner layer around the MH particle, whereas the lowest energy is observed in the outer region of the shell, being slightly lower close to the ‘polar’ zone. This supports the interpretation discussed above on the shrinking of the shell being caused by the attraction of the MS particles to the ‘poles’ of the MH one.
6 Conclusions
We presented a theoretical characterization of microstructural magnetostriction effects in a novel type of complex magnetic elastomers, made of a mixture of small (magnetically soft) and large (magnetically hard) microparticles, all embedded in a relatively stiff polymer matrix.We based our characterization on a qualitative description of the behavior of a minimal microstructural element of the material, consisting of a single central magnetically hard particle surrounded by an elastic incompressible shell, that is filled with magnetically soft particles. From simple considerations, we deduced that the elastic shell experiences an elongation in the direction of an applied external field when the latter is parallel to the magnetic moment of the central particle. When external field and central dipole moment are antiparallel, a nonmonotonic behavior is expected: for weak applied fields, the shell should shrink along the field direction, reaching a maximum degree of shrinking and subsequent decrease as the field strength approaches the critical field for the reversal of the magnetic moment of the central particle. This indicates that such complex hybrid elastomers can provide a unique opportunity to create a material that expands and shrinks along a given axis, combining its active and passive magnetic control.
In order to validate our qualitative considerations, we performed a formal analysis of the elastomer element by means of two complementary theoretical models, based on different approximations. First one is a continuum analytical description of the magnetoelastic system. It assumes ideal incompressibility of the elastic shell and a uniform distribution of magnetically soft particles within it, without regard of deformations. The second model, designed for molecular dynamics simulations, is a bead-spring representation of the system. It includes explicit particles carrying point magnetic dipoles and an implicit random network of polymers, modelled as harmonic springs connecting the particles. In this latter representation the shell is not incompressible, but local variations of density of the particles it contains are taken into account in a natural way.
Results from both models confirm the initial qualitative picture. The continuum model predicts a parabolic function for the longitudinal deformation of the shell as a function of the applied field strength. For a non magnetized central particle, the deformation corresponds only to expansions along the applied field axis. When the central dipole is introduced, the minimum of the parabolla shifts and the shell longitudinally shrinks for an interval of weak antiparallel applied fields. The bead-spring model shows in general a good qualitative agreement with the continuum one. The agreement is even quantitative for the case of zero central dipole and weak applied fields. For other conditions, quantitative differences arise due to effects of the compressibility of the shell. Results of the bead-spring model also provide distributions of particle densities and elastic stresses in the shell. We found indications of radial layering of the particles in the region near the transverse plane. Finally, mechanical stresses tend to concentrate in the ‘pole’ regions of the shell when it elongates, whereas the stronger stress is found in a symmetric layer next to the internal boundary of the shell when it shrinks.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. A. S. and S. S. K. acknowledge support by the DFG grant OD 18/24-1, by the Act 211 of the Government of the Russian Federation, contract No. 02.A03.21.0006, and by the FWF START-Projekt Y 627-N27. S. S. K. also acknowledges RFBR Grant 19-52-12028. O. V. S. and Yu. L. R. acknowledge support by RFBR projects 17-41-590160 and 19-52-12045, respectively. Computer simulations were carried out at the Vienna Scientific Cluster.References
- J. M. Ginder, M. E. Nichols, L. D. Elie and J. L. Tardiff, Smart Structures and Materials 1999: Smart Materials Technologies, 1999, pp. 131–138 Search PubMed.
- A. Fuchs, Q. Zhang, J. Elkins, F. Gordaninejad and C. Evrensel, J. Appl. Polym. Sci., 2007, 105, 2497–2508 CrossRef CAS.
- G. Filipcsei, I. Csetneki, A. Szilágyi and M. Zrínyi, Magnetic Field-Responsive Smart Polymer Composites, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 137–189 Search PubMed.
- Ubaidillah, J. Sutrisno, A. Purwanto and S. A. Mazlan, Adv. Eng. Mater., 2015, 17, 563–597 CrossRef CAS.
- S. Odenbach, Arch. Appl. Mech., 2016, 86, 269–279 CrossRef.
- M. Shamonin and E. Y. Kramarenko, Novel Magnetic Nanostructures, Elsevier, 2018, pp. 221–245 Search PubMed.
- M. R. Jolly, J. D. Carlson, B. C. Muñoz and T. A. Bullions, J. Intell. Mater. Syst. Struct., 1996, 7, 613–622 CrossRef CAS.
- Z. Varga, G. Filipcsei and M. Zrínyi, Polymer, 2006, 47, 227–233 CrossRef CAS.
- A. V. Chertovich, G. V. Stepanov, E. Y. Kramarenko and A. R. Khokhlov, Macromol. Mater. Eng., 2010, 295, 336–341 CrossRef CAS.
- A. Boczkowska and S. Awietjan, Advanced Elastomers – Technology, Properties and Applications, InTech, Rijeka, 2012, ch. 6 Search PubMed.
- J. D. Carlson and M. R. Jolly, Mechatronics, 2000, 10, 555–569 CrossRef.
- H.-X. Deng, X.-L. Gong and L.-H. Wang, Smart Mater. Struct., 2006, 15, N111 CrossRef.
- T. L. Sun, X. L. Gong, W. Q. Jiang, J. F. Li, Z. B. Xu and W. H. Li, Polym. Test., 2008, 27, 520–526 CrossRef CAS.
- W. Li and X. Zhang, Recent Pat. Mech. Eng., 2008, 1, 161–166 CrossRef CAS.
- H. Böse, R. Rabindranath and J. Ehrlich, J. Intell. Mater. Syst. Struct., 2012, 23, 989–994 CrossRef.
- J. Thévenot, H. Oliveira, O. Sandre and S. Lecommandoux, Chem. Soc. Rev., 2013, 42, 7099–7116 RSC.
- Y. Li, J. Li, W. Li and H. Du, Smart Mater. Struct., 2014, 23, 123001 CrossRef.
- T. I. Becker, V. Böhm, J. Chavez Vega, S. Odenbach, Y. L. Raikher and K. Zimmermann, Arch. Appl. Mech., 2019, 89, 133–152 CrossRef.
- T. Gundermann and S. Odenbach, Smart Mater. Struct., 2014, 23, 105013 CrossRef.
- J. M. Ginder, S. M. Clark, W. F. Schlotter and M. E. Nichols, Int. J. Mod. Phys. B, 2002, 16, 2412–2418 CrossRef CAS.
- S. S. Abramchuk, D. A. Grishin, E. Y. Kramarenko, G. V. Stepanov and A. R. Khokhlov, Polym. Sci., Ser. A, 2006, 48, 138–145 CrossRef.
- A. Stoll, M. Mayer, G. J. Monkman and M. Shamonin, J. Appl. Polym. Sci., 2014, 131, 39793 CrossRef.
- S. Bednarek, J. Magn. Magn. Mater., 2006, 301, 200–207 CrossRef CAS.
- X. Guan, X. Dong and J. Ou, J. Magn. Magn. Mater., 2008, 320, 158–163 CrossRef CAS.
- G. V. Stepanov, E. Y. Kramarenko and D. A. Semerenko, J. Phys.: Conf. Ser., 2013, 412, 012031 CrossRef.
- S. Abramchuk, E. Kramarenko, G. Stepanov, L. V. Nikitin, G. Filipcsei, A. R. Khokhlov and M. Zrínyi, Polym. Adv. Technol., 2007, 18, 883–890 CrossRef CAS.
- G. V. Stepanov, S. S. Abramchuk, D. A. Grishin, L. V. Nikitin, E. Y. Kramarenko and A. R. Khokhlov, Polymer, 2007, 48, 488–495 CrossRef CAS.
- C. Bellan and G. Bossis, Int. J. Mod. Phys. B, 2002, 16, 2447–2453 CrossRef CAS.
- G. V. Stepanov, D. Y. Borin, Y. L. Raikher, P. V. Melenev and N. S. Perov, J. Phys.: Condens. Matter, 2008, 20, 204121 CrossRef CAS PubMed.
- H.-N. An, S. J. Picken and E. Mendes, Soft Matter, 2012, 8, 11995–12001 RSC.
- D. Günther, D. Y. Borin, S. Günther and S. Odenbach, Smart Mater. Struct., 2012, 21, 015005 CrossRef.
- M. Schümann, D. Y. Borin, S. Huang, G. K. Auernhammer, R. Müller and S. Odenbach, Smart Mater. Struct., 2017, 26, 095018 CrossRef.
- P. A. Sánchez, T. Gundermann, A. Dobroserdova, S. S. Kantorovich and S. Odenbach, Soft Matter, 2018, 14, 2170–2183 RSC.
- T. Borbáth, S. Günther, D. Y. Borin, T. Gundermann and S. Odenbach, Smart Mater. Struct., 2012, 21, 105018 CrossRef.
- G. Pessot, M. Schümann, T. Gundermann, S. Odenbach, H. Löwen and A. M. Menzel, J. Phys.: Condens. Matter, 2018, 30, 125101 CrossRef PubMed.
- G. Diguet, E. Beaugnon and J. Y. Cavaillé, J. Magn. Magn. Mater., 2009, 321, 396–401 CrossRef CAS.
- O. V. Stolbov, Y. L. Raikher and M. Balasoiubc, Soft Matter, 2011, 7, 8484–8487 RSC.
- A. Zubarev, Physica A, 2013, 392, 4824–4836 CrossRef CAS.
- Y. Han, A. Mohla, X. Huang, W. Hong and L. E. Faidley, Int. J. Appl. Mech., 2015, 7, 1550001 CrossRef.
- P. Metsch, K. A. Kalina, C. Spieler and M. Kästner, Comput. Mater. Sci., 2016, 124, 364–374 CrossRef CAS.
- D. Romeis, V. Toshchevikov and M. Saphiannikova, Soft Matter, 2016, 12, 9364–9376 RSC.
- D. Romeis, P. Metsch, M. Kästner and M. Saphiannikova, Phys. Rev. E, 2017, 95, 042501 CrossRef PubMed.
- O. V. Stolbov and Y. L. Raikher, Arch. Appl. Mech., 2018, 89(1), 63–76 CrossRef.
- D. Romeis, V. Toshchevikov and M. Saphiannikova, Soft Matter, 2019, 15, 3552–3564 RSC.
- M. R. Dudek, B. Grabiec and K. W. Wojciechowski, Rev. Adv. Mater. Sci., 2007, 14, 167–173 CAS.
- D. S. Wood and P. J. Camp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011402 CrossRef PubMed.
- M. A. Annunziata, A. M. Menzel and H. Löwen, J. Chem. Phys., 2013, 138, 204906 CrossRef PubMed.
- M. Tarama, P. Cremer, D. Y. Borin, S. Odenbach, H. Löwen and A. M. Menzel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042311 CrossRef PubMed.
- A. M. Menzel, Phys. Rep., 2015, 554, 1–45 CrossRef CAS.
- G. Pessot, H. Löwen and A. M. Menzel, J. Chem. Phys., 2016, 145, 104904 CrossRef PubMed.
- R. Weeber, M. Hermes, A. M. Schmidt and C. Holm, J. Phys.: Condens. Matter, 2018, 30, 063002 CrossRef PubMed.
- D. Ivaneyko, V. P. Toshchevikov, M. Saphiannikova and G. Heinrich, Macromol. Theory Simul., 2011, 20, 411–424 CrossRef CAS.
- G. Pessot, P. Cremer, D. Y. Borin, S. Odenbach, H. Löwen and A. M. Menzel, J. Chem. Phys., 2014, 141, 124904 CrossRef PubMed.
- D. Ivaneyko, V. Toshchevikov and M. Saphiannikova, Soft Matter, 2015, 11, 7627–7638 RSC.
- P. A. Sánchez, E. S. Minina, S. S. Kantorovich and E. Y. Kramarenko, Soft Matter, 2019, 15, 175–189 RSC.
- R. Weeber, S. Kantorovich and C. Holm, Soft Matter, 2012, 8, 9923–9932 RSC.
- R. Weeber, S. Kantorovich and C. Holm, J. Magn. Magn. Mater., 2015, 383, 262–266 CrossRef CAS.
- A. V. Ryzhkov, P. V. Melenev, C. Holm and Y. L. Raikher, J. Magn. Magn. Mater., 2015, 383, 277–280 CrossRef CAS.
- A. V. Ryzhkov, P. V. Melenev, M. Balasoiu and Y. L. Raikher, J. Chem. Phys., 2016, 145, 074905 CrossRef PubMed.
- D. Y. Borin and G. V. Stepanov, J. Optoelectron. Adv. Mater., 2013, 15, 249–253 CAS.
- J. Linke, D. Y. Borin and S. Odenbach, RSC Adv., 2016, 6, 100407–100416 RSC.
- D. Borin, G. Stepanov and E. Dohmen, Arch. Appl. Mech., 2019, 89, 105–117 CrossRef.
- G. V. Stepanov, D. Y. Borin, A. V. Bakhtiiarov and P. A. Storozhenko, Smart Mater. Struct., 2017, 26, 035060 CrossRef.
- T. Mitsumata, S. Ohori, A. Honda and M. Kawai, Soft Matter, 2013, 9, 904–912 RSC.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- A. M. Biller, O. V. Stolbov and Y. L. Raikher, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 023202 CrossRef CAS PubMed.
- L. D. Landau and E. M. Lifshitz, Electrodynamics of continuous media, 1963 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1st edn, 1987 Search PubMed.
- D. Frenkel and B. Smit, Understanding molecular simulation, Academic Press, 2002 Search PubMed.
- G. V. Stepanov, A. V. Chertovich and E. Y. Kramarenko, J. Magn. Magn. Mater., 2012, 324, 3448–3451 CrossRef CAS.
- M. Kot, H. Nagahashi and P. Szymczak, Visual Computer, 2015, 31, 1339–1350 CrossRef.
- A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Roehm, P. Košovan and C. Holm, Meshfree Methods for Partial Differential Equations VI, Springer Berlin Heidelberg, 2013, vol. 89, pp. 1–23 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Quantitative considerations of magneto-mechanical properties of spherical MH particles embedded in an elastic matrix; details of the simulation protocol; example distribution of elastic constants; fitting of the simulation model. See DOI: 10.1039/c9sm00827f |
| This journal is © The Royal Society of Chemistry 2019 |