Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interplay of motility and polymer-driven depletion forces in the initial stages of bacterial aggregation†
Michael K.
Porter
 a,
Asher
Preska Steinberg
a,
Asher
Preska Steinberg
 a and
Rustem F.
Ismagilov
a and
Rustem F.
Ismagilov
 *ab
*ab
aDivision of Chemistry & Chemical Engineering, California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA. E-mail: rustem.admin@caltech.edu
bDivision of Biology & Biological Engineering, California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA
First published on 23rd August 2019
Abstract
Motile bacteria are often found in complex, polymer-rich environments in which microbes can aggregate via polymer-induced depletion forces. Bacterial aggregation has many biological implications; it can promote biofilm formation, upregulate virulence factors, and lead to quorum sensing. The steady state aggregation behavior of motile bacteria in polymer solutions has been well studied and shows that stronger depletion forces are required to aggregate motile bacteria as compared with their nonmotile analogs. However, no one has studied whether these same trends hold at the initial stages of aggregation. We use experiments and numerical calculations to investigate the polymer-induced depletion aggregation of motile Escherichia coli in polyethylene glycol solutions on short experimental timescales (∼10 min). Our work reveals that in the semi-dilute polymer concentration regime and at short timescales, in contrast to what is found at steady state, bacterial motility actually enhances aggregate formation by increasing the collision rate in viscous environments. These unexpected findings have implications for developing models of active matter, and for understanding bacterial aggregation in dynamic, biological environments, where the system may never reach steady state.
Introduction
Bacteria thrive in a wide range of biological and ecological contexts and play important roles in the human gut, soil, wastewater sludge, and other complex environments. In these environments, bacterial motility has implications for biofilm formation and virulence. For example, in the gut, Salmonella typhimurium uses its flagella to burrow through the intestinal mucus layer and penetrate the host epithelium, causing infection.2 Certain species of Pseudomonas aeruginosa require motility to form biofilms, such as those found on medical devices.3 Microbial motility is further influenced by polymers, which are abundant in many environments.4 For example, in the gut, polymers are secreted by the host5–8 and dietary fibers are ingested regularly.1 In wastewater treatment plants, sludge used to collect microbes and particulate waste also contains polymers.9,10Polymers are well known to aggregate bacteria, which is important because aggregation precedes biofilm formation,11 correlates with altered gene expression,3,12 including antibiotic-resistance genes,13 and induces phenotypic changes such as quorum sensing.14 Polymers can bind to bacteria via specific chemical interactions and cause aggregation through agglutination. These interactions are found in biological settings such as the gut, where mucins,5 immunoglobulins,6 and other host-secreted proteins7 can aggregate bacteria via chemically mediated interactions. Polymers can also aggregate microbes via depletion forces. This mechanism of aggregation does not depend on microbes binding to specific chemical functional groups but is instead only a function of the physical parameters of the polymer (molecular weight (MW), hydrodynamic radius) and bacteria size.15–17 In the presence of non-adsorbing polymers such as polyethylene glycol (PEG), bacteria aggregate through depletion interactions, which occur when two bacteria approach each other at a close enough distance that the polymer is excluded from the space between the bacteria, a region called the depletion zone.13 The difference in polymer concentration between the depletion zone and the bulk solution results in an osmotic pressure difference that generates an attractive force between bacteria. Because depletion forces depend on the physical properties of polymers and bacteria, these forces can drive bacterial aggregation irrespective of bacterial surface chemistry. In the case of nonmotile bacteria (which are not auto-aggregating) in solutions of non-adsorbing polymers, the only driving forces for aggregation are polymer-induced depletion forces.17,18 However, for motile bacteria in solutions of non-adsorbing polymers, there are forces due to the motility of the bacteria and due to depletion forces; the competition between these forces determines the steady-state aggregation behavior.18 At sufficient polymer concentrations and long time scales, when the system reaches steady state, polymer-induced depletion attractions between bacteria can result in aggregation (i.e., phase separation18). The addition of motility has been found to require significantly stronger depletion attraction to achieve the aggregation as compared with nonmotile bacteria.18 Active matter is an area of intense research, and the field is currently working on a unified theoretical framework to understand these systems.19,20 In particular, the aggregation behavior of motile bacteria in polymeric solutions at long time scales is widely studied;18,21–24 however, to our knowledge there are no published studies on aggregation at short time scales.
The initial stages of aggregate formation are of particular interest because microbial responses to aggregation (e.g., upregulation of quorum sensing and virulence pathways) occur on short time scales (tens of minutes) and would be influenced by the initial stages of aggregation. Furthermore, the initial stages of aggregation are particularly relevant for biological systems where the system may never reach steady state; for example, in the gastrointestinal (GI) tract where food and ingested material are constantly in transit.1,25 In these environments, aggregate formation is constantly disrupted because of shear, peristaltic contractions, and other forces, making early aggregate formation relevant to these biological systems.
In this study, we investigate how motility influences the polymer-induced depletion aggregation of bacteria at short time scales (t ∼ 10 min). We quantify this experimentally by using confocal fluorescence microscopy to measure the size distribution of bacterial aggregates in PEG solutions with molecular weights and concentrations relevant to the murine small intestine.1 Furthermore, we develop an understanding of which physical parameters influence the initial formation of these aggregates. We use a physical model for motile bacteria in PEG solutions that focuses on the balance of depletion and swim forces as well as the effective diffusivity of the bacteria.
Experimental
Bacteria cell culture
Overnight cultures of naturally motile E. coli K12 MG1655 (ATCC 47076) were prepared in liquid lysogeny broth (LB) culture incubated at 35 °C to mid-exponential phase. These cultures were combined to reach the desired cell concentration for the experiment (109 cells per mL). Cells were first centrifuged at 4.8 kG for 10 min and then resuspended in motility buffer (MB; 10 mM potassium phosphate buffer, 0.1 mM EDTA, pH 7.0) to stain with SYTO 9 (live, ex/em 480/500 nm). Following staining, cells were centrifuged again to wash out excess stain. To obtain nonmotile E. coli, cells were treated with 0.5% (75 mM) sodium azide in MB after washing.Confocal microscope imaging and bacterial aggregation in polyethylene glycol (PEG)
All images and z-stacks were obtained using a Zeiss LSM 800 confocal fluorescence microscope (488 nm excitation, detection at 490–540 nm). Each stack was 200 × 200 × 45 μm in volume and contained about 135 slices. Nonmotile and motile E. coli K12 were prepared and stained using the method described above. PEG solutions were prepared by dissolving four times the overlap concentration into MB (for motile conditions) or by using MB with 0.5% sodium azide (for nonmotile condition). A range of 10 kDa, 100 kDa, and 1 MDa PEG solutions were achieved by serial dilution. A 5 μL aliquot of each respective PEG solution was combined with 0.5 μL E. coli for a final cell concentration of 109 cells per mL. We pipetted 2 μL of each combined suspension into an imaging chamber made from SecureSeal imaging spacer (Electron Microscopy Sciences; 0.12 mm depth and 9 mm diameter) and a glass slide, and the top of the chamber was immediately sealed with a #1.5 glass coverslip. A single z-stack of each PEG dilution sample was taken approximately 10 min after the imaging chamber was sealed. Each biological replicate was conducted with a new bacterial cell culture.FIJI macro imaging and empirical bootstrapping
All imaging analysis was performed as previously described in ref. 1.Measuring mean-squared displacement (MSD) of E. coli
E. coli K12 were cultured and prepared as described above. The final cell concentration was diluted to 5 × 108 cells per mL when added to each PEG solution in MB. A Leica DMI6000 with a Visitech Infinity3 confocal microscope was used to obtain 20 s videos of the cells at about 16 frames per s.Videos were analyzed using an ImageJ plugin developed by the MOSAIC group for 2D/3D particle tracking using an algorithm developed in ref. 26. At least 1000 bacteria were analyzed per condition. Data output from the ImageJ plugin was further analyzed and the mean square displacement (MSD) was calculated using MATLAB code used in ref. 27 in conjunction with an in-house script. (Script will be provided by request.)
Estimating overlap concentration for PEG
The polymer overlap concentration cP* was estimated using the following relation:28,29 | (1) |
Estimating solution viscosity
We estimated the solution viscosity via a virial expansion:28| η = ηs(1 + [η]cP + kH[η]2cP2 +⋯) | (2) |
Results and discussion
Measuring E. coli aggregation at short time scales
To understand how motility affects the depletion-driven aggregation of bacteria at short time scales, we measured the initial formation of bacterial aggregates. As a model organism, we used E. coli K12 MG1655. This naturally motile strain of E. coli displays “run and tumble” dynamics, and can be rendered nonmotile by treating with 0.5 wt% sodium azide.32,33 This method of rendering cells nonmotile has been used before in research focusing on the flagellar motility of E. coli.32 Plating showed that the azide treatment killed nearly all of the cells 1 h after the initial treatment (Fig. S1, ESI†). To ensure we selected biologically relevant physical parameters for our experiments, we used data from our previous gel permeation chromatography experiments on luminal fluid from the murine small intestine to determine the range of the polymer molecular weights and concentrations.1 In these previous experiments, the polymers we found in the murine small intestine ranged in size from a few kDa to a few MDa.1 Therefore, we chose to tune the depletion potential in this work with polymers within this size range. As our test polymer, we chose to use PEG solutions in a motility buffer (MB, 0.1 mM EDTA, 10 mM potassium phosphate, pH 7.0). PEG is a linear, chemically inert polymer33,34 that is well characterized in inducing depletion forces in passive colloid solutions.35–42 We used a range of 1 MDa PEG concentrations (0.05–6.5 mg mL−1) to adjust the depletion potential and rheology of the solution, which span both the dilute and semi-dilute polymer concentration regimes (the transition between these regimes is denoted by the overlap concentration, cP* = 1.6 mg mL−1 (see calculations in Experimental)). We also measured bacterial aggregation in 10 kDa and 100 kDa PEG near their respective overlap concentrations (cP* = 8.5 mg mL−1 and 85 mg mL−1 for 100 kDa and 10 kDa PEG, respectively). We previously detected polymers of a similar size and concentration in the murine small intestine.1 A motility buffer control was implemented to confirm that the cells were not auto-aggregating and that the aggregation measured in each sample containing PEG was the result of the PEG in the solution.To quantify the initial aggregation of bacteria, we measured the volume-weighted average aggregate sizes (N) using fluorescence confocal microscopy (Fig. 1a). After mixing the E. coli with the PEG, the bacterial suspension was placed into an imaging chamber, and sealed with a glass coverslip to eliminate drifting and evaporation effects. Z-stacks of cells in solutions of PEG at various concentrations were obtained after 10 min to focus on the behavior on short timescales (Fig. 1b and c). Separate experiments were performed for motile and nonmotile cells. Imaging at short timescales also reduces the effects of sedimentation from gravity.43 Imaging analysis was performed (using an ImageJ pipeline that we developed previously1) to count each object, measure the volumes of each aggregate, and normalize by the singlet volume to obtain the volume-weighted average aggregate size.
In these experiments, we found that nonmotile bacterial aggregation in the presence of 1 MDa PEG (Fig. 2a) was qualitatively consistent with depletion-driven aggregation with similar trends observed at half (Fig. 2b) and double (Fig. 2c) the bacterial concentration. Additionally, we tested the effect of changing PEG MW and found trends that were qualitatively consistent with depletion-driven aggregation (Fig. S2, ESI†); the extent of aggregation generally decreased with MW. Nonmotile E. coli aggregated less in the presence of PEG 100 kDa (Fig. S2b, ESI†) as compared to in the presence of PEG 1 MDa (Fig. 2a) and no aggregation was observed in the presence of PEG 10 kDa. Somewhat counterintuitively, as the 1 MDa PEG concentration increased, aggregate size increased up to a limit and then started decreasing. We previously measured similar aggregation profiles with particles in PEG solutions;1 the shape of those profiles was at least in part attributed to the increase in solution viscosity, which hindered the Brownian motion of the particles, limiting the inter-particle collisions that initiate aggregation. We suspect that a similar mechanism may be at play for the nonmotile bacteria in this study. The depletion attractions increase as a function of polymer concentration due to the contribution of osmotic pressure, which is mirrored by the increasing aggregate size of the nonmotile bacteria in the dilute PEG concentration regime (eqn (3) and (4)). We observed that as the PEG concentration increased and approached the semi-dilute concentration regime, the aggregate sizes became larger. In the semi-dilute regime, the depletion attractions continued to increase with the increase in PEG concentration, but the range of these attractions decreased with PEG concentration. At PEG concentrations far above the overlap concentration, we observed a decrease in aggregate sizes. The use of sodium azide to render E. coli nonmotile could alter cell surface properties in a manner that affects their depletion-driven aggregation. However, due to their lack of aggregation in the motility buffer control and the aggregation curve being qualitatively similar to bioinert particles in similar polymer solutions,1 we assume that this effect is minimal. We hypothesized that at higher PEG concentrations, the enhanced viscosity decreased inter-bacterial collisions, thus hindering aggregate formation.
 | ||
| Fig. 2 A comparison of the aggregation of motile and nonmotile E. coli K12 at a range of concentrations of 1 MDa PEG. Volume-weighted average aggregate sizes (Vol Wt Avg Size) of nonmotile and motile E. coli K12 for serial dilutions of 1 MDa PEG using a bacteria concentration of 1 × 109 CFU mL−1 (a) and for E. coli at half (b) and twice (c) this concentration. Aggregate sizes were measured 10 min after cells were mixed with PEG. Volume-weighted average sizes in terms of bacteria per aggregate (N) are plotted against polymer mass concentration (cP) in mg mL−1. Vertical error bars are 95% empirical bootstrap confidence intervals using the bootstrapping protocol described in [Imaging analysis] in Methods of ref. 1. Data for each PEG concentration were compiled from at least four (a), at least three (b), or at least two (c) biological replicates in these experiments (where a replicate is a new bacterial culture). For each concentration of PEG, each replicate was obtained from one z-stack that was comprised of about 135 slices. | ||
Motile bacteria demonstrated different aggregation trends compared with their nonmotile analogs. In the PEG 1 MDa solutions, we observed no aggregation in the dilute PEG concentration regime, but at cP = 0.8 mg mL−1, motile E. coli abruptly began to aggregate, and continued to aggregate through the semi-dilute polymer concentration regime (Fig. 2a). Similar trends were observed when we halved (Fig. 2b) or doubled (Fig. 2c) the bacterial concentrations. In the lower MW PEG solutions, we found minimal aggregation for the motile bacteria in PEG 100 kDa (Fig. S2b, ESI†) and no aggregation for motile bacteria in PEG 10 kDa (Fig. 2a). Because the main physical difference between the motile and nonmotile bacteria is their motion, we hypothesized that the differences in depletion attractions required to aggregate motile versus nonmotile bacteria at short time scales are due to cell motility. Previously, researchers have modeled the steady-state depletion aggregation of motile bacteria by assuming that the swim force produced by bacterial motility directly counteracts the depletion force.18 We hypothesized that a similar framework could be applied here; the swim force counteracts the depletion force at low PEG concentrations, negating any attractive force to aggregate the cells. Therefore, a stronger depletion force, or higher PEG concentration, is necessary to aggregate the motile bacteria to the same extent as the nonmotile bacteria. Support for this hypothesis was experimentally demonstrated at cP = 0.4 mg mL−1 whereby we observed the nonmotile bacteria aggregate but the motile do not.
Effective potentials describe E. coli aggregation in the dilute polymer concentration regime
To investigate the interplay of swim and depletion forces that give rise to the differences in the observed aggregation behavior between motile and nonmotile bacteria, we began by using effective potentials to describe aggregation in the dilute polymer concentration regime. We focused on explaining the discrepancy in aggregation at cP = 0.4 mg mL−1, where we observed substantial aggregation of nonmotile bacteria but no aggregation of motile bacteria (Fig. 3a). In The dilute regime, nonmotile bacterial aggregation increased with the PEG polymer concentration from the osmotic pressure contribution in the depletion potential (Fig. 3b). The effective potential between nonmotile bacteria can be described by the Asakura–Oosawa depletion potential:15,16,44 | (3) |
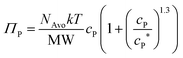 | (4) |
 | (5) |
 | ||
| Fig. 3 Effective potentials describe aggregation of motile and nonmotile E. coli in the dilute concentration regime of PEG 1 MDa. (a) The volume-weighted average aggregate size (Vol Wt avg size, N) are plotted for both motile and nonmotile E. coli at cP = 0.4 mg mL−1 PEG. The box plots depict the 95% empirical bootstrap confidence intervals of the Vol Wt avg size calculated using the method described in the “Imaging analysis” section of the Methods of ref. 1. The line bisecting the box is the 50th percentile; the upper and lower edges of the box are the 25th and 75th percentile respectively; and the whiskers are the 2.5th and 97.5th percentiles. Data were compiled from at least three biological replicates. (b) A schematic of nonmotile bacteria (orange) in PEG (purple) solution at 0 min and at (c) 10 min. The PEG is excluded from the inter-bacterial volume inducing an effective potential (brown dotted line) due to depletion (pink arrows). (d) A schematic of motile bacteria (blue) in PEG (purple) solution at 0 min and at (e) 10 min. Although the PEG induces the same depletion potential (pink arrows) at a given concentration, the swim force (white arrows) from the bacterial motility decreases both the well depth and the range, reducing their effective potential (blue dotted line) and preventing aggregation in the dilute PEG concentration regime. (f) The effective potential at contact (Umin/kT) is plotted for motile and nonmotile E. coli against PEG concentration (mg mL−1). The vertical black dotted lines at cP = 0.4 and cP = 1.6 mg mL−1 denote the potential minima taken from the complete potentials plotted in (g) and (h), respectively. (g) The full effective potential (Ueff/kT) is plotted against distance from the bacterial surface for both motile and nonmotile E. coli at cP = 0.4 mg mL−1 PEG. (h) The full effective potential (Ueff/kT) is plotted against distance from the bacterial surface for both motile and nonmotile E. coli at cP = 1.6 mg mL−1 PEG. | ||
We found that motile bacteria do not aggregate at low PEG concentrations until a certain PEG concentration threshold is reached (Fig. 3c). To estimate the effective potential of motile bacteria and the effect of the swim force on the aggregation of motile bacteria, we used a previously established theoretical framework.18 We began by considering the forces that bacteria experience in solution. This model accounts for the swim force that arises from bacterial motility and the polymer-induced depletion force. The swim force can be described from the ellipsoid approximation to the Stokes–Einstein drag coefficient:17,54
 | (6) |
 | (7) |
 | (8) |
In the dilute polymer concentration regime, we observed that the aggregation trends for both motile and nonmotile bacteria were qualitatively consistent with expectations based on the changes of the minima of their respective effective potentials (Ueff(r = 0)) at each PEG concentration (Fig. 3d). For nonmotile bacteria, the effective potential consists of only the depletion potential, which increases with polymer concentration. Our observations of the aggregation of nonmotile bacteria were qualitatively consistent with what is predicted from the depletion potential. In contrast, for motile bacteria, theoretical calculations suggest that swim force will exceed the depletion force at low polymer concentrations, resulting in no effective potential. Our experimental observations were consistent with these calculations; we saw no aggregation in motile bacteria at PEG 1 MDa concentrations less than 0.8 mg mL−1. This effect is further illustrated by looking at the shape of the effective potentials for motile and nonmotile bacteria at cP = 0.4 mg mL−1 (Fig. 3e). For nonmotile bacteria, the total depletion range spans about 120 nm from the bacteria surface, and at inter-bacterial contact, the depletion well is at its minimum at approximately −5kT. In contrast, theory suggests that the swim force of motile bacteria will completely dominate over the depletion potential, resulting in no net attractive potential. The predicted lack of net attractions between motile bacteria is supported experimentally as we did not observe aggregation of motile bacteria at cP ≤ 0.4 mg mL−1; the depletion forces are simply not strong enough to compete with the swimming force of the motile bacteria to induce aggregation.
At cp > 0.4 mg mL−1 and as the polymer concentration enters the semi-dilute regime, effective potentials are insufficient to explain the experimentally observed aggregation results. At cP = 1.6 mg mL−1 (overlap concentration), where both motile and nonmotile E. coli aggregate, the depletion potential is strong enough to induce attractions between motile bacteria (Fig. 3f). Beyond the overlap concentration, in which the solution enters the semi-dilute regime, the magnitude of the effective potential minima continues to increase (Fig. 3d). Based on these predictions, we expect to see greater aggregation of nonmotile bacteria in the semi-dilute regime. However, in our experiments, we observed that aggregation actually began to decrease for the nonmotile bacteria at PEG concentrations of >0.8 mg mL−1 (Fig. 2a). Because the theory did not match with our experimental observations at these short time scales, it suggests that effective potentials are insufficient to explain the observed aggregation behavior at PEG concentrations greater than 0.8 mg mL−1. We therefore proposed an alternate explanation for bacterial aggregation in the semi-dilute polymer concentration regime that relies on effective diffusivity. We test this hypothesis next.
Reduction in bacterial diffusivity explains aggregation in the semi-dilute polymer concentration regime where effective potentials are insufficient
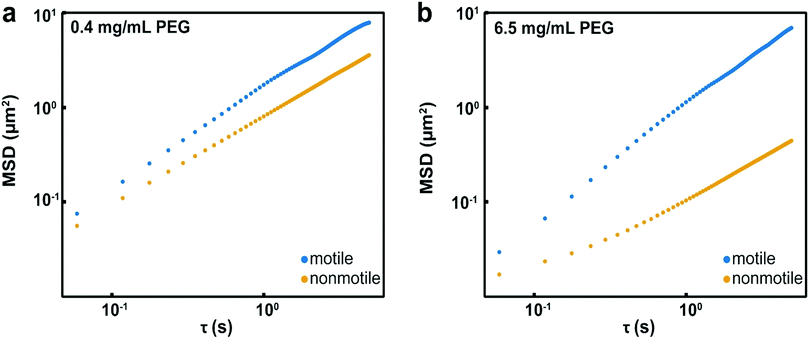
We hypothesized that in the semi-dilute concentration regime, the higher solution viscosity limits Brownian motion more appreciably than it limits bacterial motility. If this were the case, one would expect a reduced collision frequency among nonmotile bacteria leading to reduced aggregation at short time scales in viscous environments. In contrast, because motile bacteria are able to swim in viscous environments,4 their rate of collision would remain high and they would aggregate at short time scales even in highly viscous environments.To test our hypothesis, we compared the displacement of both motile and nonmotile E. coli in the dilute concentration regime (cP = 0.4 mg mL−1) and in the semi-dilute concentration regime (6.5 mg mL−1) by measuring their MSD (Fig. 4a). The MSD (in μm2) is defined as MSD(τ) = 〈|r(t0 + τ) − r(t0)|2〉, where r (in μm) is a vector describing the position of the bacteria at a given time scale τ (in s). At cP = 0.4 mg mL−1, where nonmotile bacteria aggregate but motile do not, displacement of both motile and nonmotile cells is high. At this PEG concentration, we had already established that the depletion force is strong enough to aggregate nonmotile bacteria but is not strong enough to overcome the swim force induced by the motile cells. Although motile cells are likely undergoing more collisions due to their motility, there are insufficient attractions to initiate aggregation. The displacement of the nonmotile bacteria at cP = 6.5 mg mL−1 was substantially lower than their displacement at cP = 0.4 mg mL−1, supporting the assertion that their collision frequency, and therefore aggregation rate, was decreased. The displacement of motile bacteria at this PEG concentration was much larger than the nonmotile bacteria, confirming that the higher viscosity did not impede movement and therefore collisions (Fig. 4b). The higher collision frequency of the motile bacteria, combined with the high depletion potential at the cP = 6.5 mg mL−1 PEG concentration, resulted in aggregation of the motile bacteria (Fig. 2). These results suggest that the at short time scales, aggregation becomes kinetically limited and is controlled by collision frequency of bacteria and their aggregates.
Conclusions
Bacterial aggregation often occurs in complex physiological environments such as the gastrointestinal tract or the lungs; in these settings it is important to understand the initial formation of aggregates before physiological factors such as peristalsis or swallowing play a role. Bacterial aggregation is thought to be the first step in colonization and biofilm formation; therefore, understanding the mechanism by which aggregates initially form could reveal important patterns in these processes. In this paper, we investigated how the interplay of swim forces that arise from motility and polymer-induced depletion forces influence bacterial aggregation. It has been reported previously that, at steady state, E. coli aggregate in the presence of non-adsorbing polymers, due to polymer-induced depletion forces.18 At steady state, an effective potential incorporating contributions from swim forces and depletion forces adequately describes the aggregation behavior of the system,18 wherein motility diminishes depletion-driven aggregation. Thus, polymers in greater quantities and/or sizes (i.e., a stronger depletion potential) are required for motile bacteria to aggregate compared with their nonmotile analogs. Here, we investigated the effect of bacterial motility on aggregation at short time scales (before the system reaches steady state).We found that, in contrast to what has been demonstrated at steady state, at short time scales, motility can actually enhance aggregation, resulting in the formation of aggregates that are larger than those formed by nonmotile bacteria under the same conditions. For polymer-induced depletion forces to result in bacterial aggregation at short time scales, two conditions must be met: (i) sufficient inter-bacterial attractions, and (ii) sufficient inter-bacterial collisions. In the dilute polymer concentration regime, swimming competes with depletion to reduce the effective potential of a bacteria, resulting in less aggregation. Above the overlap concentration, motility allows the bacteria to overcome kinetic hindrances that may otherwise prevent aggregation at high viscosity environments, resulting in an increase in aggregation.
Future work should explore whether differences in motility impact aggregation of microbes and microbial physiology in more complex environments, e.g., in the gastrointestinal tract and the lungs. Beyond bacterial aggregation, this work may inform other studies of the behavior of active matter at early timescales.
Conflicts of interest
The technology described in this publication is the subject of a patent application filed by Caltech.Acknowledgements
This work was funded in part by the Army Research Office (ARO) Multidisciplinary University Research Initiative (MURI) contract #W911NF-17-1-0402, the Jacobs Institute for Molecular Engineering for Medicine, an NSF Graduate Research Fellowship DGE-144469 (to APS), and a Center for Environmental Microbial Interactions (CEMI) Caldwell Graduate Fellowship (to APS). We thank Andres Collazo and the Beckman Imaging Facility for help with imaging, and we thank Natasha Shelby for contributions to writing and editing this manuscript.References
- A. Preska Steinberg, S. S. Datta, T. Naragon, J. C. Rolando, S. R. Bogatyrev and R. F. Ismagilov, eLife, 2019, 8, e40387 CrossRef PubMed.
- B. Stecher, S. Hapfelmeier, C. Muller, M. Kremer, T. Stallmach and W. D. Hardt, Infect. Immun., 2004, 72, 4138–4150 CrossRef CAS PubMed.
- G. A. O'Toole and R. Kolter, Mol. Microbiol., 1998, 30, 295–304 CrossRef PubMed.
- A. E. Patteson, A. Gopinath, M. Goulian and P. E. Arratia, Sci. Rep., 2015, 5, 15761 CrossRef CAS PubMed.
- S. Puri, J. Friedman, D. Saraswat, R. Kumar, R. Li, D. Ruszaj and M. Edgerton, Pathogens, 2015, 4, 752–763 CrossRef CAS PubMed.
- K. Moor, M. Diard, M. E. Sellin, B. Felmy, S. Y. Wotzka, A. Toska, E. Bakkeren, M. Arnoldini, F. Bansept, A. D. Co, T. Voller, A. Minola, B. Fernandez-Rodriguez, G. Agatic, S. Barbieri, L. Piccoli, C. Casiraghi, D. Corti, A. Lanzavecchia, R. R. Regoes, C. Loverdo, R. Stocker, D. R. Brumley, W. D. Hardt and E. Slack, Nature, 2017, 544, 498–502 CrossRef CAS PubMed.
- J. H. Bergstrom, G. M. Birchenough, G. Katona, B. O. Schroeder, A. Schutte, A. Ermund, M. E. Johansson and G. C. Hansson, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13833–13838 CrossRef PubMed.
- M. Caldara, R. S. Friedlander, N. L. Kavanaugh, J. Aizenberg, K. R. Foster and K. Ribbeck, Curr. Biol., 2012, 22, 2325–2330 CrossRef CAS PubMed.
- A. Ramesh, D. J. Lee and S. G. Hong, Appl. Microbiol. Biotechnol., 2006, 73, 219–225 CrossRef CAS PubMed.
- H. Liu and H. H. P. Fang, J. Biotechnol., 2002, 95, 249–256 CrossRef CAS PubMed.
- K. Hojo, S. Nagaoka, T. Ohshima and N. Maeda, J. Dent. Res., 2009, 88, 982–990 CrossRef CAS PubMed.
- L. Laganenka, R. Colin and V. Sourjik, Nat. Commun., 2016, 7, 12984 CrossRef CAS PubMed.
- P. R. Secor, L. A. Michaels, A. Ratjen, L. K. Jennings and P. K. Singh, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10780–10785 CrossRef CAS PubMed.
- C. Solano, M. Echeverz and I. Lasa, Curr. Opin. Microbiol., 2014, 18, 96–104 CrossRef CAS PubMed.
- S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 140901 CrossRef.
- S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS.
- G. Dorken, G. P. Ferguson, C. E. French and W. C. Poon, J. R. Soc., Interface, 2012, 9, 3490–3502 CrossRef PubMed.
- J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. E. Cates, D. Marenduzzo, A. N. Morozov and W. C. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057 CrossRef CAS PubMed.
- S. C. Takatori and J. F. Brady, Curr. Opin. Colloid Interface Sci., 2016, 21, 24–33 CrossRef CAS.
- A. P. Solon, Y. Fily, A. Baskaran, M. E. Cates, Y. Kafri, M. Kardar and J. Tailleur, Nat. Phys., 2015, 11, 673–678 Search PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 Search PubMed.
- M. E. Cates and J. Tailleur, EPL, 2013, 101, 20010 Search PubMed.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- J. D. Huizinga and W. J. Lammers, Am. J. Physiol.: Gastrointest. Liver Physiol., 2009, 296, G1–G8 CrossRef CAS PubMed.
- I. F. Sbalzarini and P. Koumoutsakos, J. Struct. Biol., 2005, 151, 182–195 CrossRef CAS PubMed.
- G. Yongxiang and M. L. Kilfoil, Opt. Express, 2009, 17, 4685–4704 CrossRef PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, New York, 2003 Search PubMed.
- A. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118 CrossRef CAS.
- J. K. Armstrong, R. B. Wenby, H. J. Meiselman and T. C. Fisher, Biophys. J., 2004, 87, 4259–4270 CrossRef CAS PubMed.
- K. W. Ebagninin, A. Benchabane and K. Bekkour, J. Colloids Interface Sci., 2009, 336, 360–367 CrossRef CAS PubMed.
- C. V. Gabel and H. C. Berg, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8748–8751 CrossRef CAS PubMed.
- M. T. Valentine, Z. E. Perlman, M. L. Gardel, J. H. Shin, P. Matsudaira, T. J. Mitchison and D. A. Weitz, Biophys. J., 2004, 86, 4004–4014 CrossRef CAS PubMed.
- Y. Y. Wang, S. K. Lai, J. S. Suk, A. Pace, R. Cone and J. Hanes, Angew. Chem., Int. Ed., 2008, 47, 9726–9729 CrossRef CAS PubMed.
- B. Vincent, J. Edwards, S. Emmett and A. Jones, Colloids Surf., 1985, 18, 261–281 CrossRef.
- C. Cowell, R. Li-In-On and B. Vincent, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 337–347 RSC.
- B. Vincent, P. F. Luckham and F. A. Waite, J. Colloids Interface Sci., 1980, 73, 508–521 CrossRef CAS.
- J. Clarke and B. Vincent, J. Colloids Interface Sci., 1981, 82, 208–216 CrossRef CAS.
- R. I. Feigin and D. H. Napper, J. Colloids Interface Sci., 1980, 75, 525–541 CrossRef CAS.
- B. Vincent, J. Clarke and K. Barnett, Colloids Surf., 1986, 17, 51–65 CrossRef CAS.
- A. P. Gast and L. Leibler, Macromolecules, 1986, 19, 686–691 CrossRef CAS.
- A. Jones and C. Valeriani, Colloids Surf., 1989, 42, 113–138 CrossRef CAS.
- C. Allain, M. Cloitre and M. Wafra, Phys. Rev. Lett., 1995, 74, 1478 CrossRef CAS PubMed.
- A. Vrij, Pure Appl. Chem., 1976, 48, 471–483 CAS.
- S. Kawaguchi, G. Imai, J. Suzuki, A. Miyahara, T. Kitano and K. Ito, Polymer, 1997, 38, 2885–2891 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, OUP Oxford, New York, 2003 Search PubMed.
- L. Cai, Structure and function of airway surface layer of the human lungs & mobility of probe particles in complex fluids, The University of North Carolina at Chapel Hill, 2012 Search PubMed.
- W. Burchard, Biomacromolecules, 2001, 2, 342–353 CrossRef CAS PubMed.
- V. Prasad, Weakly Interacting Colloid Polymer Mixtures, Harvard University, 2002 Search PubMed.
- C. Tanford, Physical Chemistry of Macromolecules, Wiley, New York, 1961 Search PubMed.
- H. Lee, R. M. Venable, A. D. Mackerell, Jr. and R. W. Pastor, Biophys. J., 2008, 95, 1590–1599 CrossRef CAS PubMed.
- J. F. Joanny, L. Leibler and P. G. De Gennes, J. Polym. Sci., 1979, 17, 1073–1084 CAS.
- R. Verma, J. C. Crocker, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 1998, 81, 4004 CrossRef CAS.
- W. Yan and J. F. Brady, Soft Matter, 2015, 11, 6235–6244 RSC.
- M. E. Cates, Rep. Prog. Phys., 2012, 75, 042601 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00791a |
| This journal is © The Royal Society of Chemistry 2019 |