Open Access Article
Open Access ArticleThe intimate relationship between cavitation and fracture†
Shabnam
Raayai-Ardakani
 a,
Darla Rachelle
Earl
a and
Tal
Cohen
a,
Darla Rachelle
Earl
a and
Tal
Cohen
 *ab
*ab
aDepartment of Civil and Environmental Engineering, MIT, 77 Massachusetts Avenue, Cambridge, MA, USA
bDepartment of Mechanical Engineering, MIT, 77 Massachusetts Avenue, Cambridge, MA, USA. E-mail: talco@mit.edu
First published on 1st May 2019
Abstract
Nearly three decades ago, the field of mechanics was cautioned of the obscure nature of cavitation processes in soft materials [A. Gent, Cavitation in rubber: a cautionary tale, Rubber Chem. Technol., 1990, 63, 49–53]. Since then, the debate on the mechanisms that drive this failure process is ongoing. Using a high precision volume controlled cavity expansion procedure, this paper reveals the intimate relationship between cavitation and fracture. Combining a Griffith inspired formulation for crack propagation, and a Gent inspired formulation for cavity expansion, we show that despite the apparent complexity of the fracture patterns, the pressure–volume response follows a predictable path. In contrast to available studies, both the model and our experiments are able to track the entire process including the unstable branch, by controlling the volume of the cavity. Moreover, this minimal theoretical framework is able to explain the ambiguity in previous experiments by revealing the presence of metastable states that can lead to first order transitions at onset of fracture. The agreement between the simple theory and all of the experimental results conducted in PDMS samples with shear moduli in the range of 25–246 [kPa] confirms that cavitation and fracture work together in driving the expansion process. Through this study we also determine the fracture energy of PDMS and show its significant dependence on strain stiffening.
When pushed to its extremes, a solid will usually fail by one of two mechanisms; cavitation or fracture. The former refers to the spontaneous growth of pre-existing defects within the body, while the latter is characterized by splitting the material to form new surface area. Fracture is something that we experience often, from the shattering of a window or a cellphone screen and to the splitting of a piece of fruit. Cavitation, on the other hand, is not as mundane, nonetheless it is ubiquitous. Theories of cavitation have been used to explain extreme phenomena that occur over various length scales; from the formation of craters by meteorite impact,1,2 volcanic eruptions,3,4 underground explosions,5–8 and penetration phenomena;9,10 to the exposure of seeds in ripening crop,‡ and to morphogenesis processes that occur in crucial stages of embryonic development.11,12 Moreover, cavitation is employed in medical applications to enhance drug delivery, and to treat cancer,13–15 it has been indicated as a primary mechanism of damage in traumatic brain injury,16–18 and has been shown to provide a means for probing of local material properties in soft and biological materials.19–23
Although cavitation and fracture have been traditionally considered separately, it is well known that one can lead to the other. In ductile metals, growth and coalescence of voids is commonly accepted as the primary mechanism of fracture.24–28 In rubbers and highly deformable materials, however, there is no agreement as to which mechanism is activated at every instance29 and the debate is ongoing.30 On the one hand, an extensive body of literature has been devoted to investigation of cavitation as a purely elastic phenomenon.31–35 On the other hand, the same phenomenon has been consistently considered in the literature as a fracture process.36–41 In a recent study, Poulain et al.,30 were able to observe the process at high spatial and temporal resolutions and conclude that “internal damage in soft material should be viewed as a fracture phenomenon”.
While the general debate in the literature revolves around the question: Is it cavitation or fracture?, in this work we show that the two mechanisms are intimately coupled and inseparable. Additionally we show that the fully coupled behaviour can be captured analytically.
A major challenge in experimentally studying the formation of internal cavities/cracks is in controlling the process while clearly capturing the form of the cavity/crack in the bulk. Additionally, these processes are known to be highly sensitive to initial imperfections.41–43 In available studies,30,40 neither the volume of the cavity nor the applied load have been controlled throughout the process. Hence, formation of the cavity/crack occurs abruptly and available models focus on determining the onset of fracture. Recent advances have been pushing the experimental capability into high speed fracture phenomena44 and employing phase separation for identification of the crack initiation.45
In the present work, by controlling the volume of the cavity/crack as it expands within a transparent PDMS sample, we are able to obtain precise measurements of pressure (p) versus volume (V) throughout the process not only at the initiation of the crack but also throughout the crack propagation. This is achieved by our custom designed experimental setup,22 which functions as a volume controlled syringe pump (see schematic illustration in Fig. 1). We fabricate cuboid PDMS samples of various shear moduli, in the range of 25–246 [kPa], as achieved by varying the base to cross-linking agent ratios, and we inflate a cavity/crack at the tip of the needle at a constant volumetric rate.§ The fabrication protocol and experimental procedure are detailed in ESI.1.† The shear moduli of the samples were measured using the method discussed in our previous work.22 For samples exhibiting strain stiffening, we fit our experimental results to a Gent model.46
Even if viewed solely as a fracture process, the expansion behaviour observed in our experiments, is extremely complex. To demonstrate this, after performing the volume controlled experiment to a predefined volume, we drain the injected fluid and replace it with a fast curing polymeric material (polyvinyl siloxane) and ‘freeze’ the shape of our cavities/cracks as described in ESI.1.†
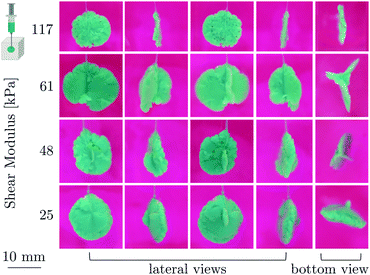
Images of representative cavities/cracks that have been ‘frozen’ using this method are shown in Fig. 1 for samples of different shear moduli (μ). It is apparent that the intricate patterns that form vary considerably between the specimens and even within the same cavity/crack, they can have several protrusions, and regions of different surface roughness. These differences may be attributed to the presence of initial imperfections created in the injection process. Nonetheless, if considering only the aspect ratio of the cavities/cracks, it is observed that stiffer specimens take forms of higher aspect ratio (additional images can be found in ESI.3,† Fig. SI.3.1–SI.3.5).
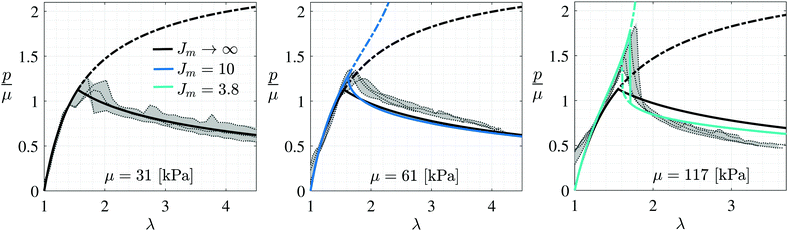
Despite the intricacy observed in Fig. 1, the pressure–volume response exhibits astonishing order. In Fig. 2 we show representative results for three different values of the shear moduli (additional curves can be found in ESI.4,† Fig. SI.4.1). The pressure is shown as a function of the effective stretch, λ = (V/V0)1/3 = a0/A0, where V0 is the volume of the initial defect, A0 is the effective radius of the initial defect, and a0 is the effective radius of the cavity/crack (see Fig. 3a for illustration, and the ESI.1,† for experimental details). This effective stretch provides a meaningful dimensionless measure for the cavity expansion that is independent of the initial volume. The response can be divided into three stages. At the initial stage of inflation, all of the experimental curves follow a similar path, then departure from that path is apparent at a peak value, but does not occur at the same point for each test. Nonetheless, as expansion progresses, the curves seem to resume a shared path. In this process the peak value of cavity pressure represents the stability limit. If the volume is not constrained, any pressure above this peak value would result in complete rupture of the specimen. As observed in Fig. 2, for stiffer samples the peak value increases and is followed by a steeper decline.
Although the experimental observations indicate that this process is highly sensitive to initial imperfections, the conforming of the experimental curves to similar trends, in all but an intermediate range, suggests that a theoretical model can potentially aid in determining which mechanism drives this process (cavitation, fracture, or both).
Prediction of the expansion path
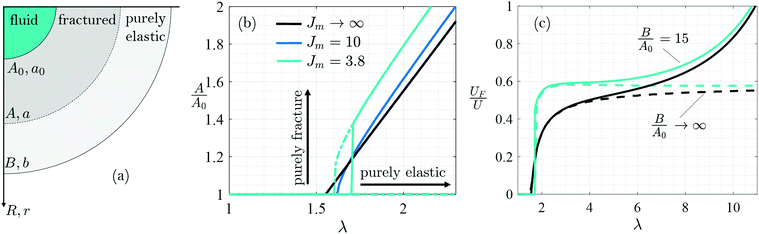
Complementary to the previous analyses of fracture initiation,37,41,47 here we assume that the deformation of the sample can be divided into two distinct zones that border at an effective radius that is denoted by A in the undeformed configuration and by a in the deformed configuration (Fig. 3a). The deformation in the external region is assumed to be purely elastic and spherically symmetric. Limiting our discussion to incompressible materials, the kinematics of the deformation in this region are fully defined as a function of the circumferential stretch at the boundary λa = a/A. Considering bodies of finite dimension we also write the circumferential stretch at the external boundary as λb = b/B where the effective external radius of the body is B in the undeformed and b in the deformed configuration (it will be shown later that the dimension of the body does not effect the response). By integrating the elastic energy density over the volume of the body, the total elastic energy can be written, after some algebra, as in ref. 22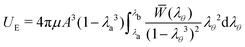 | (1) |
![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) (λθ) depends only on the shear modulus (μ), and the local value of the circumferential stretch (λθ = r/R), where r and R represent the radial coordinate in the current and reference configurations, respectively (Fig. 3a).
(λθ) depends only on the shear modulus (μ), and the local value of the circumferential stretch (λθ = r/R), where r and R represent the radial coordinate in the current and reference configurations, respectively (Fig. 3a).
The internal region R ∈ [A0,A] is assumed to undergo a fracture process. While available theories37,38,48 consider cracks of specific shapes (for example penny shape), here by assuming an effective spherical region undergoing the fracture process, we eliminate the need for any assumption on the shape or number of protrusions present at the cavity surface. To estimate the energy invested in creating surface area within the fractured region, we employ an augmented Griffith49 type approach to account for the spherical nature of the deformation and the effect of strain stiffening
| UF = 2π(A2 − A02)Gcf(λa). | (2) |
The total energy invested in the expansion process is the sum of the two energies U = UE + UF and takes the dimensionless form
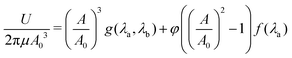 | (3) |
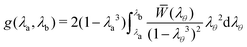 | (4) |
Note that due to incompressibility, for a given imposed expansion a0, the stretches λa and λb depend on the initial dimensions of the body A0, B, and on the location of the boundary A ∈ [A0B]. It is expected that for a given imposed expansion a0, the equilibrium location of the boundary (A) will minimize the total energy, such that ∂U/∂A = 0 and ∂2U/∂A2 > 0. Additional extrema may appear at the physical boundaries. An extramum at A = A0 corresponds to the purely elastic solution, while an extramum at A = B corresponds to complete failure.
Assuming that the fractured material is no longer capable of resisting the deformation, the cavity pressure can be estimated by considering only the elastic region and can be obtained by the derivative p = −∂UE/∂V, which can be simplified to the form
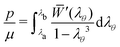 | (5) |
Note that in contrast to the above approach, earlier theoretical models have been limited to determining the onset of fracture.40,41,47,50 Here we solve for the entire process by controlling the volume of the cavity.
To obtain a prediction of the expansion process, it remains to choose a constitutive relation. A natural choice is the neo-Hookean response, for which ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) = (I1 − 3)/2 where for the present deformation, the first invariant of the left Cauchy–Green deformation tensor is I1 = 2λθ2 + λθ−4. To account for strain stiffening that can appear due to limiting chain extensibility, this relation can be extended using the Gent model46 to write
= (I1 − 3)/2 where for the present deformation, the first invariant of the left Cauchy–Green deformation tensor is I1 = 2λθ2 + λθ−4. To account for strain stiffening that can appear due to limiting chain extensibility, this relation can be extended using the Gent model46 to write ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) = (Jm/2)ln(1 − (I1 − 3)/Jm). Locking of the polymer network appears as a singularity when I1 − 3 = Jm. At the limit Jm → ∞, the Gent model reduces to the neo-Hookean model.
= (Jm/2)ln(1 − (I1 − 3)/Jm). Locking of the polymer network appears as a singularity when I1 − 3 = Jm. At the limit Jm → ∞, the Gent model reduces to the neo-Hookean model.
With the above formulation, for a given elastic response, prediction of the expansion process depends only on φ. As a first step we consider the neo-Hookean response, which is commonly adopted to model PDMS. For simplicity we choose f(λa) = 1 in (3). In all figures (i.e.Fig. 2 and Fig. SI.4.1 in ESI.4†) the neo-Hookean prediction is represented by the black solid and dashed-dotted curves. Unless indicated otherwise, all of the results have been derived for samples with B/A0 = 15, as in the experiments.
It is already worth noting that all of the theoretical predictions have been made with a single value of the dimensionless measure of surface energy φ = 1.
Comparing between the experimental curves and the neo-Hookean prediction for samples with μ ≤ 48 [kPa] (see Fig. 2 and Fig. SI.4.1 in ESI.4†) reveals a notable agreement. Recall that no fitting parameters are used (other than setting φ = 1). Focusing on the initial range of inflation (before the peak pressure) it is apparent that as the shear modulus increases, the experimental curves exhibit stiffening behaviour that is not captured by the neo-Hookean model, and that the increases in the peak pressures are followed by steeper gradients. The Gent model (as shown by the coloured curves) is able to capture the stiffening response within the elastic region and indicates that as the shear modulus increases (or equivalently the cross-linking increases) the elastic network can endure less stretching before locking (as indicated by the decreasing values of Jm). The good agreement between the experimental curves and the theoretical predictions in early stages of inflation before arriving at the peak pressure, confirms that within this range response is purely elastic. (Within this range the minimum energy solution is at the boundary A = A0).
To account for the fact that stiffening increases the energetic cost of fracturing as previously discussed,37,41 we have included the function f(λa) in (3). Based on the experimental results, at the neo-Hookean limit Jm → ∞ this function should take the value f(λa) = 1, while at the other limit, if the locking stretch is approached (Jm → I1 − 3) the energy required to fracture becomes singular. Although different functional forms can be employed, in view of the Gent model, a natural choice is
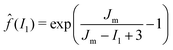 | (6) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (2λa2 + λa−4). Note that Jm in the above equation is found from the elastic portion of the experimental curves.
(2λa2 + λa−4). Note that Jm in the above equation is found from the elastic portion of the experimental curves.
Now, without any additional fitting parameters, we apply the above formulation along with (6) to the entire range of expansion. As observed, this simple model is able to capture the response over the entire range of shear moduli (Fig. SI.4.1 in ESI.4†). Perhaps the most remarkable result is that it brings further insight into the physics of the problem by giving rise to first order transitions between metastable states (shown by the dashed-dotted coloured lines). Note that the metastable path for fracture corresponds to a local minimum in the energy U, that appears while the global minimum corresponds to the purely elastic path with A = A0. At a critical expansion, the purely elastic solution is no longer a global minimum and fracture initiates (A > A0) (representative curves for the energy landscape are shown in ESI.5,† Fig. SI.5.1). As observed, these transitions become more pronounced for stiffer materials and explain the sudden drops in pressure. Since a first order transition requires excess energy, the onset of fracture in stiffer materials varies significantly among the different tests. Nonetheless, the curves eventually unite and resume similar trends.
Cavitation or fracture?
With the new understanding of this phenomenon, we can now return to answer the original question: Is it cavitation or fracture? To do so, we first examine the propagation of the fracture front (A) throughout the expansion process on a phase diagram, as shown in Fig. 3b. In this plane, travelling in the horizontal direction corresponds to purely elastic expansion, while processes that involve only fracture without cavity expansion travel in the vertical direction. As observed, initially all curves travel along the horizontal line in a purely elastic process with A = A0. At a critical expansion (λc), departure from the horizontal path is observed and becomes more abrupt as stiffening increases. Eventually all curves follow a path that is driven by the simultaneous action of both mechanisms. For materials with Jm = 3.8 the metastable path departs earlier (i.e. λ < λc), a first order transition is then observed between the purely elastic expansion and a finitely fractured state. The transition corresponds to fracturing without any elastic effects, but then cavity expansion is resumed. Overall, throughout the process, expansion can abruptly switch between different mechanisms.Now that it is clear that both mechanisms can be simultaneously activated, another means for determining which mechanism is more dominant, is by considering the fraction of energy invested in each. In Fig. 3c we plot the fraction of energy that has been invested in fracturing (for Jm = 3.8 and Jm → ∞). We find that within a large range of expansions λ < 4 the fraction of energy invested in fracture does not exceed 60%. It is only when the effective fracture radius approaches the external boundary of the body that fracture engulfs, as observed for the curves with B/A0 = 15.
Often, the debate between cavitation and fracture revolves around the fact that fracture is associated with an initial length scale41,47 (i.e. the size of an initial defect or a notch), while cavitation theories exclude that information by considering the limit in which the initial defect is sufficiently small compared to the size of the body. In this case B/A0 → ∞, or equivalently λb = 1 (as seen from the incompressibility constraint). As shown in ESI.5,† Fig. SI5.2, the present model is practically insensitive to the ratio B/A0 within a large range of expansion ratios. Hence, the formulation in eqn (1)–(5) can be recast in an even simpler form by substituting λb = 1.
Finally, we recall that all of the theoretical predictions have been calculated using φ = 1. This is a surprising result given the observed sensitivity to the shear modulus (μ) and that the value of φ directly determines both the point of departure from the purely elastic response and the trend of the curve at large strains. Nonetheless, φ = 1 is shown to provide good agreement with experiments in all cases. Hence, for the PDMS samples used in this work Gc = μA0 is proportional to the shear modulus. With A0 ≈ 1 [mm] we find that Gc is in the range of 25–250 [J m−1]. Since in the present formulation Gc is calculated per effective unit area S = 2π(A2 − A02), which can be thought of as the minimal surface area needed to advance the fracture front from A0 to A, a geometric correction should be included in comparing the present value of Gc with values measured via alternative methods.
The energy release rate (per effective unit area) is obtained by directly differentiating (1) with λb = 1, which takes the simple form ![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) E = −∂UE/∂S = μA
E = −∂UE/∂S = μA![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) (λa). To obtain the critical value at onset of fracture (when A = A0), we substitute in this relation the critical stretch λc, as determined from the energy minimization. It is observed from our experiments (Fig. 2 and more in ESI.4,† Fig. SI.4.1), that at the neo-Hookean limit λc ≈ 1.55 which leads to
(λa). To obtain the critical value at onset of fracture (when A = A0), we substitute in this relation the critical stretch λc, as determined from the energy minimization. It is observed from our experiments (Fig. 2 and more in ESI.4,† Fig. SI.4.1), that at the neo-Hookean limit λc ≈ 1.55 which leads to ![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) E = μA0(= Gc). For increasing material stiffening, fracturing requires significantly higher levels of
E = μA0(= Gc). For increasing material stiffening, fracturing requires significantly higher levels of ![[U with combining dot above]](https://www.rsc.org/images/entities/i_char_0055_0307.gif) E, as shown in ESI.5,† Fig. SI.5.3.
E, as shown in ESI.5,† Fig. SI.5.3.
Several studies have considered the relationship between the critical fracture energy release rate (Gc) and the shear modulus (μ). The classical model of Lake and Thomas51 considers chain scission as the dominant mechanism of fracture and predicts that critical energy release rate follows a scaling of the form Gc ∝ μ−1/2. Recently, Mao and Anand52 suggested that if fracture occurs by both cross-link stretching and scission, the scaling is Gc ∝ μ1/2. Based on recent experiments and in accord with the classical models, Hutchens et al.40 proposed a phenomenological power law model in the form Gc ∝ μn. They report a range of the powers n ≈ 0.08–3 for a few representative polymer systems. Noting the variations in the power n in the previous literature, here, for PDMS samples we obtain a linear dependence (n = 1). Another key point to highlight is that our experiments clearly demonstrate a strong dependence of the critical fracture energy release rate on the stiffening behaviour of the material (Jm).
Conclusion
To summarize, we have shown that in soft materials cavitation and fracture co-operate to drive failure. This observation is facilitated by a controlled experimental procedure of cavity expansion, that allows us to both examine the cavity/crack patterns, and to measure the pressure–volume response with high precision. These tests are conducted on a family of PDMS samples with shear moduli in the range of 25–246 [kPa]. A simple theory based on energetic arguments is shown to agree with all of the experiments while revealing that occurrence of abrupt pressure drops is a manifestation of a first order transition between metastable states, which may arise when material stiffening is significant. In exposing the existence of metastable states, this study explains the source of the significant dependence on initial imperfections, even in the absence of surface tension effects. Additionally, an effective measure of the critical fracture energy release rate is directly found from these experiments and is shown to be linearly proportional to the shear modulus, while exhibiting significant sensitivity to strain stiffening, which appears in these materials due to locking of the polymer chains at large stretches.Finally, while elucidating the basic mechanisms involved in formation of cavities/cracks in soft materials, the present work gives rise to a multitude of additional open questions. A natural next step is to extend this work to additional soft materials, to determine the microscopic mechanisms that lead to the dependence of fracture energy on stiffening of the polymer network, and to include surface tension effects that may become significant for smaller initial defects. It remains to be determined if similar interactions between cavitation and fracture appear in stiff materials, such as ductile metals. Reminiscent of viscous fingering phenomena, our fracture patterns are characterized by various length scales and surface roughness. Additional work is needed to explain and perhaps, control, the formation of these elusive patterns. Finally, it is worth noting that the theoretical framework presented here, applies equivalently to situations in which tension is applied remotely. Although we have not been able to confirm experimentally that remote tension will result in similar expansion processes, nature has provided us with some examples (see ESI.2,† Fig. SI.2.1).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge the support of the Army Research Office and Dr Ralph A. Anthenien, Program Manager.References
- J. N. Goodier, On the mechanics of indentation and cratering in solid targets of strain-hardening metal by impact of hard and soft spheres, Stanford Research Institute Menlo Park, CA, 1964 Search PubMed.
- H. Melosh and G. Collins, Nature, 2005, 434, 157 CrossRef CAS PubMed.
- R. Sulpizio and S. Massaro, Front. Earth Sci., 2017, 5, 18 Search PubMed.
- M. Davydov, V. Kedrinskii, A. Chernov and K. Takayama, J. Appl. Mech. Tech. Phys., 2005, 46, 208–215 CrossRef CAS.
- P. Chadwick, A. D. Cox and H. G. Hopkins, Phil. Trans. R. Soc. Lond. A, 1964, 256, 235–300 CrossRef.
- C. F. Chyba, P. J. Thomas and K. J. Zahnle, Nature, 1993, 361, 40 CrossRef.
- T. Cohen, R. Masri and D. Durban, J. Appl. Mech., 2010, 77, 041009 CrossRef.
- T. Cohen and D. Durban, J. Appl. Mech., 2013, 80, 011017 CrossRef.
- M. Forrestal and D. Tzou, Int. J. Solids Struct., 1997, 34, 4127–4146 CrossRef.
- R. Sobeski and G. Urgessa, Int. J. Prot. Struct., 2015, 6, 43–64 CrossRef.
- E. Hoijman, D. Rubbini, J. Colombelli and B. Alsina, Nat. Commun., 2015, 6, 7355 CrossRef CAS PubMed.
- A. Navis and C. M. Nelson, Semin. Cell Dev. Biol., 2016, 139–147 CrossRef PubMed.
- C. C. Coussios and R. A. Roy, Annu. Rev. Fluid Mech., 2008, 40, 395–420 CrossRef.
- A. K. Wood and C. M. Sehgal, Ultrasound Med. Biol., 2015, 41, 905–928 CrossRef PubMed.
- E. P. Stride and C. C. Coussios, Proc. Inst. Mech. Eng., Part H, 2010, 224, 171–191 CrossRef CAS PubMed.
- T. El Sayed, A. Mota, F. Fraternali and M. Ortiz, Comput. Methods Appl. Mech. Eng., 2008, 197, 4692–4701 CrossRef.
- R. S. Salzar, D. Treichler, A. Wardlaw, G. Weiss and J. Goeller, J. Neurotrauma, 2017, 34, 1589–1602 CrossRef PubMed.
- J. Goeller, A. Wardlaw, D. Treichler, J. O'Bruba and G. Weiss, J. Neurotrauma, 2012, 29, 1970–1981 CrossRef PubMed.
- J. A. Zimberlin, N. Sanabria-DeLong, G. N. Tew and A. J. Crosby, Soft Matter, 2007, 3, 763–767 RSC.
- A. J. Crosby and J. J. McManus, Phys. Today, 2011, 64, 62–63 CrossRef.
- T. Cohen and A. Molinari, Int. J. Solids Struct., 2015, 69, 544–552 CrossRef.
- S. Raayai-Ardakani, Z. Chen, D. R. Earl and T. Cohen, Soft Matter, 2019, 15, 381–392 RSC.
- J. B. Estrada, C. Barajas, D. L. Henann, E. Johnsen and C. Franck, J. Mech. Phys. Solids, 2018, 112, 291–317 CrossRef.
- H. Rogers, Trans. Metall. Soc. AIME, 1960, 218, 498–506 Search PubMed.
- F. A. McClintock, J. Appl. Mech., 1968, 35, 363–371 CrossRef.
- V. Tvergaard, J. Mech. Phys. Solids, 1982, 30, 265–286 CrossRef.
- M. Ashby, F. Blunt and M. Bannister, Acta Metall., 1989, 37, 1847–1857 CrossRef CAS.
- V. Tvergaard and A. Needleman, Acta Metall., 1984, 32, 157–169 CrossRef.
- A. Gent, Rubber Chem. Technol., 1990, 63, 49–53 CrossRef.
- X. Poulain, V. Lefèvre, O. Lopez-Pamies and K. Ravi-Chandar, Int. J. Fract., 2017, 205, 1–21 CrossRef CAS.
- C. Horgan and D. Polignone, Appl. Mech. Rev., 1995, 48, 471–485 CrossRef.
- J. M. Ball, Philos. Trans. R. Soc., A, 1982, 306, 557–611 CrossRef.
- R. Stringfellow and R. Abeyaratne, Mater. Sci. Eng., A, 1989, 112, 127–131 CrossRef.
- H. Hang-Sheng and R. Abeyaratne, J. Mech. Phys. Solids, 1992, 40, 571–592 CrossRef.
- A. Gent and P. Lindley, Proc. R. Soc. London, Ser. A, 1959, 249, 195–205 Search PubMed.
- G. H. Lindsey, J. Appl. Phys., 1967, 38, 4843–4852 CrossRef CAS.
- Y.-Y. Lin and C.-Y. Hui, Int. J. Fract., 2004, 126, 205–221 CrossRef CAS.
- V. Lefèvre, K. Ravi-Chandar and O. Lopez-Pamies, Int. J. Fract., 2015, 192, 1–23 CrossRef.
- S. Kundu and A. J. Crosby, Soft Matter, 2009, 5, 3963–3968 RSC.
- S. B. Hutchens, S. Fakhouri and A. J. Crosby, Soft Matter, 2016, 12, 2557–2566 RSC.
- A. Gent and C. Wang, J. Mater. Sci., 1991, 26, 3392–3395 CrossRef.
- A. Gent and D. Tompkins, J. Polym. Sci., Part A-2, 1969, 7, 1483–1487 CrossRef CAS.
- O. Lopez-Pamies, M. I. Idiart and T. Nakamura, J. Mech. Phys. Solids, 2011, 59, 1464–1487 CrossRef.
- M. P. Milner and S. B. Hutchens, Extreme Mech. Lett., 2019, 28, 69–75 CrossRef.
- J. Y. Kim, Z. Liu, B. M. Weon, C.-Y. Hui, E. R. Dufresne and R. W. Style, 2018, arXiv preprint, arXiv:1811.00841.
- A. Gent, Rubber Chem. Technol., 1996, 69, 59–61 CrossRef CAS.
- M. L. Williams and R. A. Schapery, Int. J. Fract. Mech., 1965, 1, 64–72 CrossRef CAS.
- J. Kang, C. Wang and S. Cai, Soft Matter, 2017, 13, 6372–6376 RSC.
- A. A. Griffith and M. Eng, Philos. Trans. R. Soc., A, 1921, 221, 163–198 CrossRef.
- M. Williams and R. Schapery, Int. J. Fract. Mech., 1965, 1, 64–72 CrossRef CAS.
- G. J. Lake and A. G. Thomas, Proc. R. Soc. London, Ser. A, 1967, 300, 108–119 CAS.
- Y. Mao and L. Anand, J. Appl. Mech., 2018, 85, 081008 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00570f |
| ‡ See Fig. SI.2.1 in ESI.2.† |
| § Note that the diameter of the needle is chosen to be sufficiently large so that surface tension effects can be neglected. The rate of inflation is sufficiently slow such that the process is quasi-static and no rate dependence is observed. |
| ¶ This particular functional form has been found through a trial and error procedure and fits well to all of our experimental data. |
| This journal is © The Royal Society of Chemistry 2019 |