The role of stickiness in the rheology of semiflexible polymers

Abstract

Semiflexible polymers form central structures in biological material. Modelling approaches usually neglect influences of polymer-specific molecular features aiming to describe semiflexible polymers universally. Here, we investigate the influence of molecular details on networks assembled from filamentous actin, intermediate filaments, and synthetic DNA nanotubes. In contrast to prevalent theoretical assumptions, we find that bulk properties are affected by various inter-filament interactions. We present evidence that these interactions can be merged into a single parameter in the frame of the glassy wormlike chain model. The interpretation of this parameter as a polymer specific stickiness is consistent with observations from macro-rheological measurements and reptation behaviour. Our findings demonstrate that stickiness should generally not be ignored in semiflexible polymer models.

---

Introduction

Semiflexible polymers play a central role in biological systems as major building blocks of intracellular scaffolds and extracellular matrices. Among the most abundant semiflexible cytoskeletal biopolymers are filamentous actin (F-actin) and intermediate filaments (IF).^1,2 Network structures formed by these polymers exhibit unique viscoelastic properties, which cannot be easily deduced from the well-established theoretical frameworks for linear flexible polymers or rigid rods.³ Classical polymer physics theories typically try to avoid details of molecular properties and mostly reduce semiflexible polymers to their size and stiffness in order to establish universal models. Networks are modelled either as entangled networks, as in the tube model,^4–6 or as cross-linked networks as in the affine model.⁷ Many features of the tube model, such as the scaling of the plateau modulus with monomer concentration and the behaviour of single filaments within a network, indeed fit very well to the experimental data for F-actin.^4,8 The affine model has been demonstrated to predict the correct scaling of the plateau modulus in terms of concentration and cross-linker density for cross-linked F-actin,^9,10 but also for vimentin and keratin IF in the presence of MgCl₂.^11–13

In reality, however, biopolymers without added cross-linkers already display adhesive interactions partially screened by electrostatic repulsion.^14–17 For F-actin, minor impurities and ageing effects are reported to cause a strong batch-to-batch variation of the network properties.^6,18 IF networks feature pronounced hydrophobic interactions causing a weak concentration scaling of the network stiffness and a pronounced strain-stiffening in the non-linear deformation regime.^19–21 These effects can neither be explained by the tube nor by the affine deformation model. Furthermore, recent experimental studies on F-actin and DNA-based semiflexible polymers present evidence that central predictions of the tube model in respect to the persistence length l_p might be false.^22,23

Here, we employ the natural filaments F-actin, vimentin and keratin IF as well as purely artificial double-crossover DNA nanotubes (DX tubes) in order to investigate the influence of (unspecific) adhesive interactions on the rheology of semiflexible polymer networks. DX tubes are used as an additional synthetic semiflexible polymer model-system based on the self-assembly of DNA tiles.^24,25 These tubes, with a diameter between 7 and 20 nm, a persistence length of around 4 μm, a contour length of several micrometers, and a negative surface charge, were chosen for their similarity to the biopolymers under investigation (see Table S1 of ESI†).

Experimental

Protein preparation

Monomeric actin (G-actin) was obtained with an acetone powder prep from rabbit muscle, purified, and stored at −80 °C in G-Buffer (2 mM sodium phosphate buffer pH 7.5, 0.2 mM ATP, 0.1 mM CaCl₂, 1 mM DTT, 0.01% NaN₃) as described previously.²⁶ Small sample volumes were thawed and kept on ice no longer than one day before experiments. The polymerization to F-actin was always induced by adding 1/10 volume fraction of 10 times concentrated F-buffer (20 mM sodium phosphate buffer pH 7.5, 1 M KCl, 10 mM MgCl₂, 2 mM ATP, 10 mM DTT) to the final sample solution. F-actin was fluorescently labelled by polymerizing G-actin at 5 μM in a 1 : 1 ratio with phalloidin–tetramethylrhodamine B isothiocyanate (Phalloidin-TRITC – Sigma-Aldrich Co., USA).

Recombinant human keratins K8 and K18 were expressed, purified and prepared as described in ref. 27 and 28. Briefly, proteins were expressed in E. coli, purified and stored in 8 M urea at −80 °C. Before use, K8 and K18 were mixed in equimolar ratios and renatured by dialysis against 8 M urea, 2 mM Tris–HCl (pH 9.0) and 1 mM DTT with stepwise reduction of the urea concentration (6 M, 4 M, 2 M, 1 M, 0 M). Each dialysis step was done for 20 min at room temperature, then the dialysis was continued overnight against 2 mM Tris–HCl, pH 9.0, 1 mM DTT at 4 °C. The dialysed protein was kept on ice for a maximum of four days. The final protein concentration was determined by measuring the absorption at 280 nm using a DU 530 UV/vis Spectrophotometer (Beckman Coulter Inc., USA). Assembly of keratin was initiated by addition of an equal volume of 18 mM Tris–HCl buffer (pH 7.0) to renatured keratins resulting in a final buffer condition of 10 mM Tris–HCl (pH 7.4).

Human vimentin was obtained from recombinant expression in E. coli and purified from inclusion bodies as described by Herrmann et al.²⁹ Before the assembly into filaments, the purified vimentin was dialysed in a stepwise fashion from 8 M urea against a 2 mM sodium phosphate buffer at pH 7.5 and kept on ice for a maximum of four days.³⁰ Polymerization was induced as described for actin. Fluorescent labelling was performed with Alexa Fluor 488 C5 Maleimide (Thermo Fisher Scientifc Inc., USA) as described by Winheim et al.³¹ The only modification was the removal of excess dye by elution over PD-10 Desalting Columns (GE Healthcare, USA). Unlabelled vimentin monomers were mixed with about 10% labelled monomers before dialysis to obtain fluorescently labelled filaments.

Double-crossover DNA nanotubes

All oligomers for hybridization of the DNA nanotubes were adapted from Ekani-Nkodo et al.²⁵ (Table S2 of ESI†) and purchased from Biomers.net with HPLC purification. In order to assemble a nanotube network of a desired concentration the required strands (SE1–SE5) were mixed in equimolar concentration in an assembly buffer containing 40 mM Tris–acetate, 1 mM EDTA and 12.5 mM Mg²⁺ (pH 8.3). The concentration of each stock solution was confirmed spectrophotometrically by a NanoDrop 1000 (Thermo Fisher Scientifc Inc., USA) at a wavelength of 260 nm. These strands were hybridized in a TProfessional Standard PCR Thermocycler (Core Life Sciences Inc., USA) by denaturation for 10 min at 90 °C and complementary base pairing for 20 h between 80 °C and 20 °C by lowering the temperature by 0.5 K every 10 min. After hybridization DNA nanotubes were stored at room temperature. For visualization the oligomer SE3 was modified with the fluorescent Cyanine dye 3 with two additional spacer thymine bases in between. DNA nanotubes were labelled by partially or fully replacing the unlabelled oligo SE3 by SE3-Cy3.

Shear rheology

Shear rheology measurements were performed with a strain controlled ARES rheometer (TA Instruments, USA) equipped with a 40 mm plate–plate geometry at a gap width of 140 μm. Biopolymer solutions were mixed on ice and assembled directly on the rheometer for 2 h at 25 °C (Actin, Vimentin) or 20 °C (K8/18). Hybridized DX tubes were carefully placed on the rheometer and allowed to equilibrate for 2 h at 20 °C. To prevent both evaporation and artefacts from interfacial elasticity, samples were surrounded with sample buffer and sealed by a cap equipped with wet sponges. A dynamic time sweep with short measurements every 60 s at frequency of 1 Hz and a strain of 5% was used to record filament assembly and equilibration. G*(ω) was measured with a dynamic frequency sweep ranging from 0.01 Hz to 80 Hz at a strain of 5%. Fitting was performed with a self-written script in Mathematica (Wolfram Research, USA).

The differential shear modulus K = dσ/dγ was obtained from transient step rate measurements at strain rates of 0.025 s⁻¹, 0.1 s⁻¹, and 0.25 s⁻¹ directly after G*(ω) measurements. The resulting stress–strain curves were smoothed with a spline fit in MATLAB (MathWorks, USA) and K was defined as the gradient of stress σ divided by the gradient of strain γ.

Mesh size

The mesh size of a semiflexible polymer network can be estimated by assuming a simple cubic network of rigid rods with the mass per length m_L and the protein concentration c: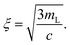with m_L = 2.66 × 10⁻¹¹ g m⁻¹, for F-actin,³² 4.40 × 10⁻¹¹ g m⁻¹ for DX tubes,²⁴ 5.48 × 10⁻¹¹ g m⁻¹ for vimentin IF^27,33 and 3.15 × 10⁻¹¹ g m⁻¹ for keratin K8/K18 IF³⁴ the employed concentrations (c_actin = 0.5 g l⁻¹, c_DX = 1.0 g l⁻¹, c_vimentin = 1.0 g l⁻¹, c_keratin = 0.5 g l⁻¹) should lead to networks with similar mesh sizes (ξ_actin = 0.40 μm, ξ_DX = 0.36 μm, ξ_vimenin = 0.41 μm, ξ_keratin = 0.43 μm).

Reptation measurements

Samples for single filament observations were prepared and analysed as described previously.³⁵ Both fluorescently labelled actin and vimentin were polymerized for one hour at room temperature. Labelled filaments were gently mixed with unlabelled monomers to a molar ratio between 1 : 2000 and 1 : 20 000 and polymerized for one hour at 37 °C. (±)-6-Hydroxy-2,5,7,8-tetramethylchromane-2-carboxylic acid (Trolox – Sigma-Aldrich Co., USA) was added to a final concentration of 2 mM as an anti-photobleaching agent due to its radical scavenging and antioxidant activities. Labelled DX tubes were carefully pipetted into an unlabelled DX tube network containing no anti-photobleaching agents. The mixtures of labelled filaments embedded in an unlabelled network were placed between two glass slides, as described by Golde et al.³⁶ F-actin samples were kept at room temperature for one hour prior to observation. Specimen with pure vimentin were polymerized directly in the sample chamber for two hours at room temperature. DX tube samples were left to equilibrate overnight at room temperature.

Images of the embedded tracer filaments were recorded via an epifluorescence microscope (Leica DM-IRB, 100× oil objective, NA 1.35 – Leica Camera AG, Ger) equipped with a CCD camera (Andor iXon DV887 – Andor Technology Ltd, UK). At least 10 filaments were captured in each sample with a frame rate of 10 Hz for 10 s. These filaments were chosen to be well away from the glass surface and had to lie within the focal plane to enable 2D tracking. Filament tracking was performed with the freely available ImageJ plugin JFilament (http://imagej.nih.gov/ij/).

All images of a single filament were summed up and a mean tube backbone was tracked from this overlay. For the MSD, the filament centre was defined as the point at the backbone with an equal distance to both ends. Its movement was analysed as a projection on the tangent vector of the tube backbone at the corresponding position. Our definition of the filament centre is susceptible to fluctuations of the contour length caused by tracking errors and filament ends moving out of focus. Thus, we compared the MSD of the filament centre to the MSD of the contour length over time divided by 4. Filaments with a non-constant MSD of the contour length were excluded from analysis. For filaments where both the MSD of the contour length and the MSD of the filament centre are constant and comparably small, the latter is only an upper bound of the actual filament movement.

Contour length

The contour length of DX tubes was determined as the median length of more than 100 DX tubes adsorbed on a glass surface. The histogram of the contour length of F-actin, vimentin IF and DX tubes is presented in Fig. S1 (ESI†). The contour length of keratin K8/18 IF was assumed to have the same value as vimentin IF. This assumption is justified by the observation that keratin and vimentin IF have a very similar length distribution for longer times despite a faster initial annealing of keratin IF.³⁷

Results and discussion

Linear rheology

Fig. 1 displays typical results for F-actin (0.5 g l⁻¹), DX tubes (1 g l⁻¹), vimentin (1 g l⁻¹) and keratin K8/K18 (0.5 g l⁻¹) IF networks. The monomer concentrations were chosen in order to have a comparable mesh size (see Experimental). All networks feature a storage modulus G′ that appears flat, but in fact behaves like a weak power law. F-actin and DX tubes display a beginning cross-over between G′ and the loss modulus G′′ while the cross-over frequency for vimentin and keratin IF has been previously shown to appear at frequencies higher than probed by macro-rheology.²⁰ The cross-over of G′ and G′′ denotes the transition from network properties dominated by filament interactions for low frequencies to the high frequency regime dominated by single filament behaviour.³⁸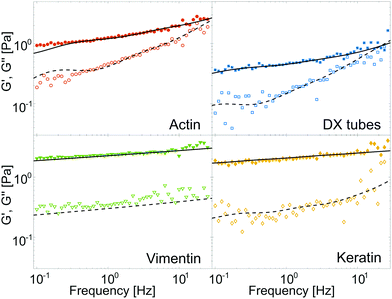

Fig. 1 Typical storage modulus G′ (solid symbols) and loss modulus G′′ (open symbols) versus frequency. Black lines are the result of fitting G′ (solid) and G′′ (dashed) simultaneously with eqn (3) of the GWLC. Although the curves roughly resemble a rubber plateau, they in fact follow a weak power law. The cross-over frequency between G′ and G′′ significantly varies for different polymer types.

In order to enable a quantitative comparison of different polymers and samples, we characterized the shear modulus via an approximation of the elastic modulus by a local power law G′(ω) ∝ ω^α with exponent α in the frequency regime below the cross-over. For IF, the local power law exponent α is around 0.07 and it is about twice as large for F-actin and DX tubes with α ≈ 0.14 (Fig. S2 of ESI†). Additionally, we display the loss factor tan(ϕ) = G′′/G′ at a fixed frequency of 1 Hz. This frequency was chosen to avoid experimental noise in the low frequency regime while still maintaining a frequency independent loss factor for most samples (Fig. S3 of ESI†). The loss factor has a strong sample to sample variation for F-actin (tan(ϕ) = 0.40 ± 0.11) and decreases over DX tubes and vimentin to keratin (tan(ϕ) = 0.11 ± 0.02), meaning the networks become more elastic (Fig. S2 of ESI†).

We recently demonstrated that α and tan(ϕ) of composite networks of actin and vimentin filaments have intermediate values in comparison to pure networks.³⁵ They can be tuned simply by the ratio of actin and vimentin filaments in the network. However, both the tube and the affine model predict only a flat plateau for frequencies below the cross-over.^4,6,7 These models are typically used to compare only the scaling predictions of the network stiffness with experimental data.^{4–7,9,10,22,23,39–44} To our knowledge, a study by Schmidt et al. presents the sole fit of the tube model to a measured frequency dependence of G′ and G′′ and shows only a rough agreement.⁴⁵ Thus, we need a different model for explaining the actual frequency dependence of the complex shear modulus.

The observed weak power laws are reminiscent of soft glassy systems and have been shown to be a main feature of micro-rheological experiments in cells, as well.⁴⁶ A phenomenological model providing a description of the weak power law behaviour on a network level is the glassy wormlike chain model (GWLC) established by Kroy and Glaser.⁴⁷ This model is an extension of the wormlike chain (WLC), the minimal model of a semiflexible polymer. The constituting idea is that the mode relaxation times τ_n of all eigenmodes of (half-)wavelength λ and modenumber n that are longer than a characteristic interaction length Λ are stretched exponentially:

Here, N_n = λ_n/Λ − 1 is the number of interactions per length λ. ε is the stretching parameter controlling how strong the modes are slowed down. The assumption of an exponential stretching is directly supported by the experimental observation of logarithmic tails of the dynamic structure factor in F-actin solutions.⁴⁸ The complex linear shear modulus in the high frequency regime is:

G*(ω) = Λ/(5ξ²χ(ω)), (3)

where ξ is the mesh size and χ(ω) is the micro-rheological, linear response function to a point force at the ends of the GWLC at frequency ω. The specific model used for this study has been comprehensively described previously³⁵ and more details are presented in the ESI.†

We can fit eqn (3) directly to the macro-rheological data in the linear regime for each sample. The fit parameters are the mesh size ξ, the interaction length Λ and the stretching parameter ε. All other parameters were fixed to literature values or experimentally obtained (see Table S1 of ESI†). Λ is determined by the cross-over frequency ω_Λ = 2π⁵l_pk_BT/(ζ_⊥Λ⁴) with transverse drag coefficient ζ_⊥. For the fitting of the IF networks, Λ is assumed to be below, but of the same order of magnitude as Λ for F-actin and DX tubes to account for a larger ω_Λ (Fig. S4, ESI†). ε is the parameter that defines the functional dependence of G*(ω) for frequencies ω < ω_Λ. ξ is used as a free fit parameter to obtain the correct network stiffness because it only shifts the magnitude of G* without any influence on the functional dependency.

We then compare ε with the local power law exponent α and the loss factor tan(ϕ) (Fig. 2). It is worth noting that α, tan(ϕ) and ε are directly connected in the theory and their relation can be approximated analytically for ε ≫ 1 as presented in ref. 49. The comparison reveals that a small loss factor correlates with a small power law exponent. Moreover, we find significant differences in ε between all polymer types with mean values ± standard deviation of 6.7 ± 2.7 for actin, 13.4 ± 2.8 for DX tubes, 24.9 ± 1.7 for vimentin and 31.8 ± 7.2 for K8/K18 (Fig. S2 of ESI†).

Fig. 2 Local power law exponent of G′ ∝ ω^α (open symbols) and loss factor tan(ϕ) = G′′/G′ (solid symbols) versus stretching parameter ε. Each pair of data points represents one sample. The exponent was obtained from fitting G′ with a power law for frequencies smaller than the cross-over between G′ and G′′. The loss factor was obtained from fitting tan(ϕ) locally with a power law at a frequency of 1 Hz. ε is the result from fitting the complex shear modulus G* to eqn (3) for each sample. Dashed lines are the numerical results of an exemplary G_GWLC* where all parameters except ε are fixed.

Stretching parameter ε as stickiness

The original study by Kroy and Glaser suggests the interpretation of ε as a kinetic “stickiness” parameter.⁴⁷ε can be thought of as the height of the free energy barriers of unspecific filament-to-filament interactions in units of k_BT.⁴⁸ Later interpretations suggest a test polymer that can bind and unbind to “sticky” entanglement points by overcoming the energy barrier, which slows the contributions from long-wavelength bending modes during relaxation.⁵⁰ In the following, we will demonstrate that ε appears indeed as a polymer specific stickiness that combines all filament-to-filament interactions into one number.

A look at the molecular details of biopolymers suggests several adhesive interactions as plausible candidates for sticky interactions. Since semiflexible biopolymers are relatively massive multi-molecular assemblies, errors such as misfoldings or hydrophobic loops,⁵¹ which can cause inter-filament interactions, are expected to occur in general on a purely stochastic basis.

F-actin has been used as the model system for entangled semiflexible polymers for decades and exhibits the smallest ε. The main protein interactions are electrostatic forces due to a negative surface charge resulting in a repulsive potential shielded by ions in the buffer solution. Larger ion concentrations lead to attractive electrostatic forces causing counterion cloud condensation. The ion concentrations used for this study, however, are well below this transition and attractive ion effects can be ruled out.¹⁶ The reason for an ε > 1 are most likely minor impurities and ageing effects that have been shown to cause batch-to-batch variations of reconstituted F-actin networks.^6,18 These batch-to-batch variations are already suggested to be a consequence of very small amounts of cross-links by Morse.⁶ A different ε for different batches is further supported by the observation, that different actin preparations lead to different power law exponents of G′.¹⁸ In contrast, different rheometers used for the same preparation changed the magnitude, but not the power law exponent of G′.

DX tubes seem to be similar to F-actin in regards to their polyelectrolyte properties. It would be very interesting to compare the effective electrostatic charge with ε quantitatively. A calculation of the effective electrostatic charge of DX tubes, however, is non-trivial due to the cross-over DNA tiles structure and the relative dielectric constant of the medium that depends on the unknown effective ion concentration in the buffer.^52,53 The comparison of F-actin and double stranded DNA¹⁶ suggests a higher charge density of DX tubes, which in turn is shielded by a higher Mg²⁺ concentration in the buffer. Thus, the higher ε of DX tubes is more likely a consequence of the sub-fraction of stuck filaments. This can be explained by mishybridization during the assembly leading to filament connections that are independent of electrostatic interactions.

The large ε of IF can be explained by their dominant hydrophobic interactions.^19,20 These interactions are partially mitigated by electrostatic repulsion between vimentin IF¹⁵ leading to a smaller ε in comparison to keratin. Keratin IF also have a tendency to form bundled and even clustered network structures at comparably low densities.^54,55 Bundling and clustering, however, should not appear at the protein concentration and buffer conditions employed.^12,13

The experimental data can be further compared to the model by calculating an exemplary G_GWLC*. The model parameters are fixed to contour length L = 18 μm, l_p = 4 μm, Λ = 1 μm, and ξ = 0.2 μm, resembling intermediate values of the experimental results. By only varying ε, the obtained G_GWLC*(ε) are analysed for each ε in the same way as the rheological data.

Remarkably, the resulting curves for α_GWLC(ε) and tan(ϕ)_GWLC(ε) can already be viewed as a master curve for the experimental data without any rescaling, although L, l_p, Λ and ξ differ for every polymer type (Fig. 2). A better agreement between experimental data and the GWLC can be reached by calculating G_GWLC*(ε) for each polymer (Fig. S5 of ESI†).

In contrast to α and tan(ϕ), ε is significantly different for all four polymers (Fig. S2 of ESI†). Thus, ε is not only the key parameter of the GWLC, but it might be a key factor for deriving a universal master curve that unifies systems with fundamentally different molecular details as well. It appears as a very robust quantity for characterizing the linear rheological behaviour of semiflexible polymer networks and seems to provide a more universal description of network properties than the pseudo plateau modulus G₀.

In principle, it would be very interesting to further contemplate the role of the persistence length l_p, especially with regard to the studies that question the established scaling predictions of the stiffness of entangled semiflexible polymer networks with l_p.^22,23 In the GWLC, l_p is not only a pre-factor of the micro-rheological response functions χ(ω), but influences the relaxation time τ and may influence the interaction length Λ as well. While l_p varies between 0.5 μm for keratin K8/K18^20,56 and 9 μm for F-actin,⁵⁷ we are limited in the analysis by the unknown specific relation between l_p and Λ. Unfortunately, this relation cannot be deduced from our data (see ESI† for a more detailed discussion). Thus, we cannot dissect the role of l_p independent of the other network parameters. However, the agreement between experimental data and the exemplary G_GWLC* suggests that, under certain conditions, stickiness might be more important for network properties than l_p.

Non-linear rheology

In contrast to the linear regime, it is well-known that the behaviour of F-actin and IF at large deformations is drastically different to each other.^58,59 To investigate these differences, the GWLC can be extended to the non-linear regime with the pre-tension dependent linear modulus as a simplified model. The differential shear modulus K = dσ/dγ, defined as the derivative of stress σ over strain γ, can be measured with a [small gamma, Greek, dot above]-protocol as described previously³⁵ (see ESI† for details). Although K is measured in dependency of γ as in Fig. S6 of ESI,† it can be displayed over σ to enable a comparison with the model (Fig. 3).

Fig. 3 Differential shear modulus K = dσ/dγ rescaled by its value in the linear regime K_linversus stress σ. Solid lines are single measurements. Dotted lines are replicated curves with the non-linear extension of the GWLC. F-actin and DX tubes have a similar behaviour with weak to no strain-stiffening. Strain-stiffening is more pronounced for vimentin IF while keratin IF have the highest peak value K_max at a much larger σ. F-actin and vimentin IF data reproduced from ref. 35.

With this method, we are able to replicate K for F-actin, DX tubes and vimentin filament networks (Fig. 3 and Table S1 of ESI†). The initial softening of vimentin IF can be captured by an additional bond-breaking mechanism as described previously.³⁵ For keratin K8/K18, we can shift the peak of K to the correct σ, but underestimate K_max by an order of magnitude. The phenomenology of keratin IF is potentially based on strong filament interactions as well as a small l_p leading to two different slopes for K due to a cross-over from a bending to a stretching dominated regime. This behaviour is better described by a triangular lattice model for physiological cross-linked networks.⁶⁰ Keratin IF act as some kind of limiting case for the applicability of the GWLC in the non-linear regime. The observation that the polymer with the largest ε behaves more like a cross-linked network supports the interpretation of ε as stickiness.

Recent modelling approaches on reversibly cross-linked networks predict a qualitatively similar behaviour of the non-linear regime in comparison to the GWLC.⁶¹ However, there is still a flat plateau in the linear regime. We can only speculate that introducing multiple relaxation times might enable a connection of reversible cross-links and the proposed stickiness.

Stickiness in reptation

The constituting idea of the GWLC in eqn (2) can be implemented using an effective mode dependent friction transversal to the filament ζ_n = ζ_⊥exp(N_nε) for λ_n > Λ as well. If this increase of the transversal friction is indeed caused by sticky interactions, this should also increase the longitudinal friction and slow down the reptation of single filaments within the network. To test this reasoning, we observed embedded fluorescent tracer filaments and analysed the mean-squared displacement (MSD) of the filament centre parallel to the tangent vector as described previously.^22,35 Unfortunately, this technique is not applicable for keratin because there is no live stain for native keratin IF leading to their exclusion from the following analysis. For the following examination, the “tube” is simply the space formed by the geometrical constraints due to the surrounding filaments that can be probed by a test polymer.⁶²

A quantitative comparison between different polymer networks can be achieved by looking at the MSD at τ = 2 s, where the MSD is in a weak power law regime, rescaled by the tube width a (Fig. 4).^63,64 In this regime, the MSD is independent of the polymer length. We use the MSD instead of the more common longitudinal diffusion coefficient because there is no diffusion for the stick-slip like systems investigated here.

Fig. 4 (a) MSD of the filament centre parallel to the tube rescaled by tube width a versus lag time τ. The lines are the median of all observed filaments with n ≥ 10. (b) Distribution of MSD at lag time τ = 2 s rescaled by tube width a. Each data point is a single filament. The black cross denotes the median and illustrates that the overall motility decreases from F-actin over DX tubes to vimentin IF.

Both F-actin and DX tubes reveal a strong filament-to-filament variation with similar distributions. The distribution of vimentin IF is dominated by significantly smaller values in comparison to both F-actin (p = 1.6 × 10⁻³) and DX tubes (p = 3.1 × 10⁻²) (Fig. 4(b) and Fig. S7 of ESI†). The main difference between F-actin and DX tubes is that some DX tubes have a flat MSD. This implies that they are stuck at their respective position and hints at mishybridization during the assembly process. Such a behaviour was not observed for F-actin (Fig. S7 of ESI†).

In the tube model, the MSD (τ = 2 s)/a is expected to increase for smaller persistence lengths because the mode of transportation is dominated by filament undulations in this time regime.⁶³ Here, we see the exact opposite behaviour. This means the assumption behind the persistence length scaling is either violated or overwritten by an additional factor like the proposed effective friction.

The motion of the tracer filaments could potentially be influenced by the attached fluorescent dye. However, the labelling alone does not seem to impede filament motion in networks.^8,22,65 Thus, the decrease of the MSD (τ = 2 s)/a from F-actin over DX tubes to vimentin IF while ε increases, supports the interpretation of ε as a polymer stickiness, which increases the longitudinal friction and slows down filament motion.

Recent Brownian dynamics simulations of entangled solutions of semiflexible polymers by Lang and Frey demonstrate, that polymer relaxation might have to be considered as a many-body effect with dynamic correlations instead of a diffusive motion along a tube.⁶⁶ Their simulations demonstrate that varying friction coefficients strongly influence the interplay of a tracer polymer with its surrounding. This friction is not necessarily the same as the proposed sticky interactions. Including stickiness, however, could provide further insight into relaxation processes within a network that seem to be more complicated than assumed by the tube model. The sticky reptation model for flexible polymers by Leibler et al.⁶⁷ could potentially be a basis for such a model. However, it is unclear to us if it can be adapted for semiflexible polymers due to fundamental differences between both systems. The GWLC in the presented form is independent of this discussion because it is only a high frequency approximation without low frequency relaxation mechanisms of any kind.

Conclusion

Considering the discussed limitations, it is remarkable that the GWLC captures most of the linear and non-linear macro-rheological properties of the semiflexible polymer networks investigated here. The stretching parameter ε is more than a simple free fit parameter. Our results consistently support the interpretation of ε as a polymer specific stickiness that strongly affects rheological characteristics and might be able to overwrite scaling predictions in classical semiflexible polymer theories. The different magnitudes of stickiness for F-actin and IF may help to get a better understanding of their roles in living cells. Cells are able to modify network structures with numerous binding proteins, especially for F-actin. However, inherent sticky interactions such as hydrophobic interactions for IF, would limit the ability to further tune network properties. At the same time, the high stickiness of IF contributes to their non-linear behaviour and possibly influences cell properties under large deformations. We expect that the GWLC can also be used to analyse other sticky semiflexible polymers such as the recently investigated temperature dependent hydrophobic interactions in α-synuclein fibril networks.¹⁷ While the simplistic phenomenological nature of the GWLC diminishes some explanatory power, it shows that inter-filament stickiness impacts semiflexible polymer networks and should be considered in polymer models aiming to fully describe the dynamics of such systems. The large size and high complexity of semiflexible polymers makes filament misfolding and impurities likely, even for supposedly interactionless proteins like F-actin. Including stickiness as a universal feature in semiflexible polymers means a paradigm shift in classical polymer physics because it allows to unify systems that where to date treated either as purely entangled or chemically cross-linked. This approach might help to further explain and resolve the current discrepancies between established models and experimental data.^22,23

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully thank Tatjana Wedig (DKFZ) for technical assistance with vimentin and keratin procedures, and Klaus Kroy for fruitful discussions. Furthermore, we acknowledge funding by the Deutsche Forschungsgemeinschaft for M. G. (DFG-1116/14-1) and H. H. (HE 1853/11-1) and by the European Research Council (ERC-741350).

References

1. F. Huber, J. Schnauß, S. Rönicke, P. Rauch, K. Müller, C. Fütterer and J. Käs, Adv. Phys., 2013, 62, 1–112.
2. H. Herrmann, H. Bär, L. Kreplak, S. V. Strelkov and U. Aebi, Nat. Rev. Mol. Cell Biol., 2007, 8, 562–573.
3. C. P. Broedersz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995–1036.
4. H. Isambert and A. C. Maggs, Macromolecules, 1996, 29, 1036–1040.
5. B. Hinner, M. Tempel, E. Sackmann, K. Kroy and E. Frey, Phys. Rev. Lett., 1998, 81, 2614–2617.
6. D. C. Morse, Macromolecules, 1998, 31, 7044–7067.
7. F. C. MacKintosh, J. Käs and P. A. Janmey, Phys. Rev. Lett., 1995, 75, 4425–4428.
8. J. Käs, H. Strey, J. X. Tang, D. Finger, R. Ezzell, E. Sackmann and P. A. Janmey, Biophys. J., 1996, 70, 609–625.
9. M. L. Gardel, J. H. Shin, F. C. MacKintosh, L. Mahadevan, P. Matsudaira and D. A. Weitz, Science, 2004, 304, 1301–1305.
10. R. Tharmann, M. M. A. E. Claessens and A. R. Bausch, Phys. Rev. Lett., 2007, 98, 088103.
11. Y.-C. Lin, N. Y. Yao, C. P. Broedersz, H. Herrmann, F. C. MacKintosh and D. A. Weitz, Phys. Rev. Lett., 2010, 104, 058101.
12. A. Leitner, T. Paust, O. Marti, P. Walther, H. Herrmann and M. Beil, Biophys. J., 2012, 103, 195–201.
13. P. Pawelzyk, H. Herrmann and N. Willenbacher, Soft Matter, 2013, 9, 8871–8880.
14. R. Piazza, Curr. Opin. Colloid Interface Sci., 2004, 8, 515–522.
15. M. Schopferer, H. Bär, B. Hochstein, S. Sharma, N. Mücke, H. Herrmann and N. Willenbacher, J. Mol. Biol., 2009, 388, 133–143.
16. P. A. Janmey, D. R. Slochower, Y.-H. Wang, Q. Wen and A. Cēbers, Soft Matter, 2014, 10, 1439–1449.
17. S. A. Semerdzhiev, S. Lindhoud, A. Stefanovic, V. Subramaniam, P. van der Schoot and M. M. Claessens, Phys. Rev. Lett., 2018, 120, 208102.
18. J. Xu, W. H. Schwarz, J. A. Käs, T. P. Stossel, P. A. Janmey and T. D. Pollard, Biophys. J., 1998, 5, 2731–2740.
19. S. Yamada, D. Wirtz and P. A. Coulombe, J. Struct. Biol., 2003, 143, 45–55.
20. P. Pawelzyk, N. Mücke, H. Herrmann and N. Willenbacher, PLoS One, 2014, 9, e93194.
21. J. Block, V. Schroeder, P. Pawelzyk, N. Willenbacher and S. Köster, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853, 3053–3064.
22. C. Schuldt, J. Schnauß, T. Händler, M. Glaser, J. Lorenz, T. Golde, J. A. Käs and D. M. Smith, Phys. Rev. Lett., 2016, 117, 197801.
23. M. Tassieri, Macromolecules, 2017, 50, 5611–5618.
24. P. W. K. Rothemund, A. Ekani-Nkodo, N. Papadakis, A. Kumar, D. K. Fygenson and E. Winfree, J. Am. Chem. Soc., 2004, 126, 16344–16352.
25. A. Ekani-Nkodo, A. Kumar and D. K. Fygenson, Phys. Rev. Lett., 2004, 93, 268301.
26. B. Gentry, D. Smith and J. Käs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 031916.
27. H. Herrmann, M. Häner, M. Brettel, S. A. Müller, K. N. Goldie, B. Fedtke, A. Lustig, W. W. Franke and U. Aebi, J. Mol. Biol., 1996, 264, 933–953.
28. H. Herrmann, T. Wedig, R. M. Porter, E. B. Lane and U. Aebi, J. Struct. Biol., 2002, 137, 82–96.
29. H. Herrmann, L. Kreplak and U. Aebi, Methods Cell Biol., 2004, 78, 3–24.
30. N. Mücke, T. Wedig, A. Bürer, L. N. Marekov, P. M. Steinert, J. Langowski, U. Aebi and H. Herrmann, J. Mol. Biol., 2004, 340, 97–114.
31. S. Winheim, A. R. Hieb, M. Silbermann, E.-M. Surmann, T. Wedig, H. Herrmann, J. Langowski and N. Mücke, PLoS One, 2011, 6, e19202.
32. A. C. Steven, J. F. Hainfeld, B. L. Trus, J. S. Wall and P. M. Steinert, J. Biol. Chem., 1983, 258, 8323–8329.
33. U. Wickert, N. Mücke, T. Wedig, S. A. Müller, U. Aebi and H. Herrmann, Eur. J. Cell Biol., 2005, 84, 379–391.
34. H. Herrmann, M. Häner, M. Brettel, N.-O. Ku and U. Aebi, J. Mol. Biol., 1999, 286, 1403–1420.
35. T. Golde, C. Huster, M. Glaser, T. Händler, H. Herrmann, J. A. Käs and J. Schnauß, Soft Matter, 2018, 14, 7970–7978.
36. T. Golde, C. Schuldt, J. Schnauß, D. Strehle, M. Glaser and J. Käs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 044601.
37. N. Mücke, S. Winheim, H. Merlitz, J. Buchholz, J. Langowski and H. Herrmann, PLoS One, 2016, 11, e0157451.
38. F. Gittes and F. C. MacKintosh, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, R1241–R1244.
39. K. Kroy and E. Frey, Phys. Rev. Lett., 1996, 77, 306–309.
40. D. C. Morse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 031502.
41. M. L. Gardel, M. T. Valentine, J. C. Crocker, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2003, 91, 158302.
42. J. Liu, M. L. Gardel, K. Kroy, E. Frey, B. D. Hoffman, J. C. Crocker, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2006, 96, 118104.
43. M. Tassieri, R. M. L. Evans, L. Barbu-Tudoran, G. N. Khaname, J. Trinick and T. A. Waigh, Phys. Rev. Lett., 2008, 101, 198301.
44. M. Atakhorrami, G. Koenderink, J. Palierne, F. MacKintosh and C. Schmidt, Phys. Rev. Lett., 2014, 112, 088101.
45. F. G. Schmidt, B. Hinner, E. Sackmann and J. X. Tang, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5509–5517.
46. B. Fabry, G. N. Maksym, J. P. Butler, M. Glogauer, D. Navajas and J. J. Fredberg, Phys. Rev. Lett., 2001, 87, 148102.
47. K. Kroy and J. Glaser, New J. Phys., 2007, 9, 416.
48. C. Semmrich, T. Storz, J. Glaser, R. Merkel, A. R. Bausch and K. Kroy, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20199–20203.
49. K. Kroy and J. Glaser, AIP Conf. Proc., 2009, 1151, 52–55.
50. L. Wolff, P. Fernandez and K. Kroy, New J. Phys., 2010, 12, 053024.
51. L. Feng, E. Kim, W. L. Lee, C. J. Miller, B. Kuang, E. Reisler and P. A. Rubenstein, J. Biol. Chem., 1997, 272, 16829–16837.
52. G. S. Manning, Biophys. Chem., 1978, 9, 65–70.
53. G. S. Manning, J. Phys. Chem. B, 2007, 111, 8554–8559.
54. J. Kayser, H. Grabmayr, M. Harasim, H. Herrmann and A. R. Bausch, Soft Matter, 2012, 8, 8873–8879.
55. J. Deek, F. Hecht, L. Rossetti, K. Wißmiller and A. R. Bausch, Acta Biomater., 2016, 43, 218–229.
56. T. Lichtenstern, N. Mücke, U. Aebi, M. Mauermann and H. Herrmann, J. Struct. Biol., 2012, 177, 54–62.
57. H. Isambert, P. Venier, A. C. Maggs, A. Fattoum, R. Kassab, D. Pantaloni and M. F. Carlier, J. Biol. Chem., 1995, 270, 11437–11444.
58. P. A. Janmey, U. Euteneuer, P. Traub and M. Schliwa, J. Cell Biol., 1991, 113, 155–160.
59. C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194.
60. C. P. Broedersz and F. C. MacKintosh, Soft Matter, 2011, 7, 3186–3191.
61. J. Plagge, A. Fischer and C. Heussinger, Phys. Rev. E, 2016, 93, 062502.
62. M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988, vol. 73.
63. R. Granek, J. Phys. II, 1997, 7, 1761–1788.
64. T. C. B. McLeish, Adv. Phys., 2002, 51, 1379–1527.
65. M. Keshavarz, H. Engelkamp, J. Xu, O. I. van den Boomen, J. C. Maan, P. C. M. Christianen and A. E. Rowan, J. Phys. Chem. B, 2017, 121, 5613–5620.
66. P. Lang and E. Frey, Nat. Commun., 2018, 9, 494.
67. L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00433e

---