Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Poynting effect of brain matter in torsion†
Valentina
Balbi
 *a,
Antonia
Trotta
*a,
Antonia
Trotta
 b,
Michel
Destrade
b,
Michel
Destrade
 ab and
Aisling
Ní Annaidh
ab and
Aisling
Ní Annaidh
 b
b
aSchool of Mathematics, Statistics and Applied Mathematics, NUI Galway, University Road, Galway, Ireland. E-mail: vbalbi@nuigalway.ie; v.balbiv@gmail.com
bSchool of Mechanical & Materials Engineering, University College Dublin, Belfield, Dublin 4, Ireland
First published on 13th June 2019
Abstract
We investigate experimentally and model theoretically the mechanical behaviour of brain matter in torsion. Using a strain-controlled rheometer, we perform torsion tests on fresh porcine brain samples. We quantify the torque and the normal force required to twist a cylindrical sample at constant twist rate. Data fitting gives a mean value for the shear modulus of μ = 900 ± 312 Pa and for the second Mooney–Rivlin parameter of c2 = 297 ± 189 Pa, indicative of extreme softness. Our results show that brain always displays a positive Poynting effect; in other words, it expands in the direction perpendicular to the plane of twisting. We validate the experiments with finite element simulations and show that when a human head experiences a twisting motion in the horizontal plane, the brain can experience large forces in the axial direction.
1 Introduction
The brain is an extremely soft and fragile tissue, making it hard to test experimentally using the standard protocols in place for soft matter such as elastomers or rubbers.1 The inflation test is not appropriate for obvious reasons. The uni-axial tensile test requires a dogbone geometry and clamping, which cannot be realised in practice for brain tissue; instead, the end faces of a cylinder have to be glued to the tension plates, which leads rapidly to an inhomogeneous deformation.2,3 The compression test can achieve homogeneous deformation with lubrication of the plates, but only up to about 10% strain, after which it starts to bulge out.4 By contrast, the simple shear test works well5,6 up to a 45° tilting angle leading to a maximal stretch of more than 60%. Similarly, as we show in this paper, the torsion test can be implemented readily for brain matter.Simple shear and torsion tests are particularly useful to study the Poynting effect, a typical nonlinear phenomenon displayed by soft solids. When sheared or twisted, those materials tend to elongate (positive Poynting effect7) or contract (negative Poynting effect8) in the direction perpendicular to the shearing or twisting plane. This phenomenon has been observed for brain matter in simple shear tests.6 However, a practical limitation of simple shear tests is that to date there are no shearing devices able to measure and quantify the normal force, which limits the determination of material parameters.
An alternative test is torsion. It can be performed by glueing a cylindrical sample between two parallel plates and then applying a twist to the sample by rotating one plate with respect to the other. In the past, torsion tests on brain matter have been performed using a rheometer, at constant strain rates (from 0.05 to 1 s−1),9 to measure the elastic properties of the tissue and to investigate its viscoelastic behaviour dynamically over a range of frequencies (20–200 Hz).10 A comprehensive summary of the results of mechanical tests on brain tissue can be found in two recent reviews.11,12 However, in these studies, only the torques were recorded. Moreover, torsion was modelled as simple shear, an equivalence that, as we show in the ESI,† is only valid locally. To our knowledge, the role played by the normal forces arising during torsion of brain matter has not been investigated yet.
In this work, we perform torsion tests on cylindrical porcine brain samples and measure the torque and the axial force required to twist the samples at a constant twist rate of 300 rad m−1 s−1. In Section 2, we describe the experimental protocols for preparing and testing the brain specimens. In Section 3, we present the collected and filtered data and describe the filtering strategy adopted to keep meaningful experimental measurements. We then accurately model the data with the Mooney–Rivlin model in Section 4 and obtain material parameters of brain matter that compare well with those found from other tests. To further validate the analytical modelling, we implement finite element (FE) simulations in Abaqus to mimic the experiments and finally, we use the estimated mechanical parameters to simulate a rotational head impact.
Our main finding is that brain matter exhibits the normal Poynting effect, i.e. it tends to expand along its axis when twisted.13 As noted by Rivlin,7 the Poynting effect is a nonlinear elastic effect par excellence and cannot be explained by the linearised theory. It was present in all the cylindrical samples we tested, and when we simulated the rapid twisting of a head in a finite element model, we found that large vertical stresses developed in the whole brain also.
2 Materials and methods
In this section, we give a brief description of the procedure for preparation and testing of the brain samples.2.1 Tissue preparation
Two fresh porcine heads from freshly killed 22-week-old mixed sex pigs were obtained from a BRC-regulated (British Retail Consortium) food processing facility (Dawn Pork & Bacon, Waterford, Ireland). The animals did not die for this study; therefore, we did not need to require ethical approval from the Ethics Committee at University College Dublin.The scalp was removed using a scalpel and the cranial bone was removed using an oscillating saw. Following removal of the skull, the meninges tissue was removed using surgical scissors. Finally, following resection of connective and vascular tissue and separation from the spinal cord, the undamaged brain was placed in phosphate buffered saline (PBS) solution.
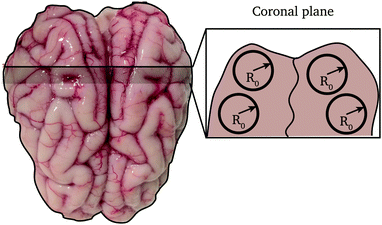
The brains had an average (maximum) length, width and height of 7.5 ± 0.3 cm, 6.4 ± 0.3 cm and 3 ± 0.3 cm, respectively. From each brain, three slices of approximately 15 mm were obtained from the frontal, parietal and occipital portions, respectively. Then, a stainless steel cylindrical punch of 20 mm diameter was used to remove up to four cylinders from each slice (depending on the available surface of the slice) as shown in Fig. 2. Each long cylindrical sample was then cut to samples of approximately 10 mm using a scalpel and template. The exact height of the specimen was measured again prior to testing. A total of 9 mixed grey and white matter samples were then used for testing and modelling in this study. After extraction, the cylindrical samples were placed in PBS solution in multi-well plates of 20 mm diameter and placed in a fridge for less than 2 hours while all samples were prepared.
2.2 Mechanical testing
A Discovery HR2 Hybrid rheometer with parallel plates was used for all mechanical testing. This device has a torque resolution of 0.1 nN m and a normal force resolution of 0.5 mN. To enable easy removal and to protect the platens, masking tape was applied to both faces of the parallel plates,3,4,6 and then the samples were glued rigidly to the tape using a high viscosity glue. The tape thickness (≤1 mm) is negligible compared to the height of the samples. All testing was performed at room temperature (23°–25°) and the samples were kept hydrated until the beginning of the test. A cylindrical Peltier plate with radius rp = 10 mm was used. The rheometer was controlled through the TRIOS Software (v4.3.1). Each of the 9 samples was tested once. The test consisted of a single stress growth step: a ramp test, where the upper plate is rotated at a constant twist rate for a duration of 10 s. The distance H between the top plate and the bottom of the instrument was adjusted until the normal force was zero at the beginning of each test. The twist rate (angular velocity of the upper plate per unit height) was![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) = 300 rad m−1 s−1. The testing protocol was validated on silicon gel samples (see the ESI,† for details).
= 300 rad m−1 s−1. The testing protocol was validated on silicon gel samples (see the ESI,† for details).
3 Experimental results
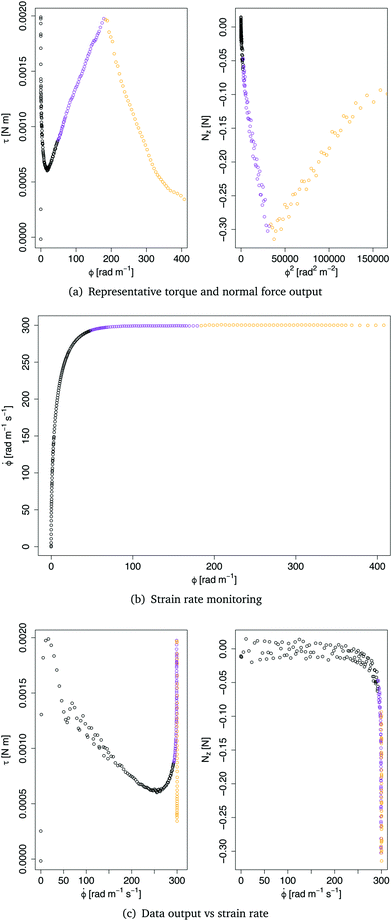
In this section, we describe the filtering procedure required to get a clean set of data, ready for model fitting and parameter estimation.Fig. 3 shows a set of typical output data from the rheometer. In Fig. 3(a), the torque τ and the normal force Nz are plotted against the twist ϕ and the twist squared, respectively. The output twist ϕ in the plots is the angle of rotation α per unit length ϕ = α/H. From the data shown in Fig. 3(a), we identify three regions, for both the torque and the force data: (i) a noisy region (in black), at the very beginning of the test; (ii) a linear region (in purple) bounded by a maximum (minimum), and (iii) a decaying region (in orange) towards the end of the experiment.
The initial noisy region is due to the delay time of the instrument in reaching a constant twist rate. The plot in Fig. 3(b) shows the twist rate against the twist and clearly highlights the initial region where the upper plate is accelerating to reach the constant twist rate ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) = 300 rad m−1 s−1. The plots in Fig. 3(c) further show that some data were actually generated at twist rates lower than 300 rad m−1 s−1. Only the data generated at 300 rad m−1 s−1 were thus considered in the following analysis.
= 300 rad m−1 s−1. The plots in Fig. 3(c) further show that some data were actually generated at twist rates lower than 300 rad m−1 s−1. Only the data generated at 300 rad m−1 s−1 were thus considered in the following analysis.
The other filtering criterion is the breaking point of the sample, which is identified clearly by a steep drop and rise in the plots of Fig. 3(a), indicating that an irreversible change in the mechanical response of the tissue occurred. Therefore, all data points after the breaking point were discarded.
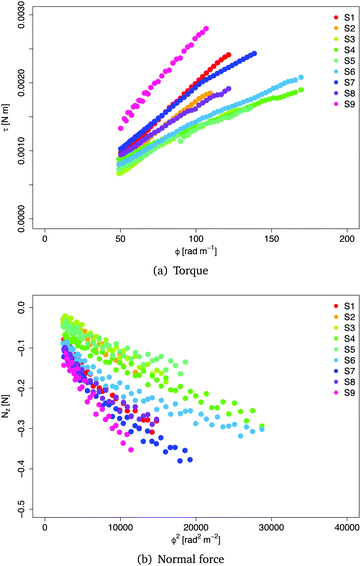
The remaining “good” data obtained from nine samples S1,…,S9 are shown in Fig. 4. Note that the rheometer reported positive values for the normal force, showing that the samples tend to expand axially during the twist (positive Poynting effect). Here, we changed the sign of the data to be consistent with the modelling approach presented in the next section.
4 Modelling
To fit the experimental data and get a quantitative estimation of the behaviour of the brain in torsion, we first analyse the data, and then reproduce the mechanical tests theoretically. Finally, we perform finite element simulations in Abaqus.4.1 Theory
Here, we calculate the torque τ and the normal force Nz required to maintain a cylindrical sample of initial radius R0 and initial height L0 in a state of torsion.As mentioned in Section 2.2, the normal force was set to zero before commencing each test. However, the force transducer of the HR2 rheometer has a sensitivity of 0.01 N, so that variations of the force within that range are not detected by the instrument. We therefore expect that the sample undergoes a small contraction prior to the transducer picking up a meaningful value for the force. Mathematically, we superpose an axial contraction to the actual rotation so that the total deformation is written in cylindrical coordinates as follows:
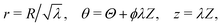 | (1) |
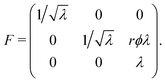 | (2) |
We are interested in the elastic behaviour of brain matter, which we assume to be isotropic and incompressible. In view of the linear dependence of the torque with respect to the twist and of the normal force with respect to the twist squared highlighted by the results in Fig. 4, we conclude that the constitutive behaviour of the brain must14 be modelled with a Mooney–Rivlin strain energy function:6,15
| W = c1(I1 − 3) + c2(I2 − 3), | (3) |
| σ = 2c1B − 2c2B−1 − pI, | (4) |
The principal stretches are the square roots of the eigenvalues of B. The intermediate stretch 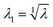 is associated with the radial direction, and the maximum and minimum stretches λ2 and λ3 are obtained by solving the following equations:
is associated with the radial direction, and the maximum and minimum stretches λ2 and λ3 are obtained by solving the following equations:
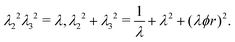 | (5) |
The elastic equilibrium of the deformation is translated as the following problem:
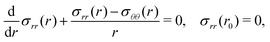 | (6) |
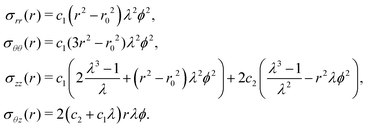 | (7) |
These formulas were first established by Rivlin,7 see Appendix A for details.
Now, the torque 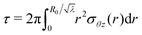 and the normal force
and the normal force 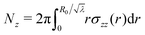 that have to be applied to the cylinder to maintain the deformation in (1) are:
that have to be applied to the cylinder to maintain the deformation in (1) are:
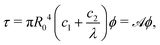 | (8) |
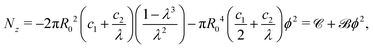 | (9) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ,
, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) , and
, and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) are introduced, the parameters c1 and c2 are linked by the following relations:
are introduced, the parameters c1 and c2 are linked by the following relations: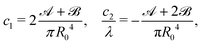 | (10) |
2![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (λ3 − 1) − (λ3 − 1) − ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) R02λ2 = 0. R02λ2 = 0. | (11) |
Note, as expected for the Mooney–Rivlin model, the linear dependence of the torque on the twist and of the normal force on the twist squared, see (8) and (9).
Because the shear modulus μ = 2(c1 + c2) is positive, it follows that ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and −
and −![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) are positive when λ < 1 (when the cylinder is contracted prior to the twist). The coefficient
are positive when λ < 1 (when the cylinder is contracted prior to the twist). The coefficient ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) is associated with the Poynting effect displayed by the sample (
is associated with the Poynting effect displayed by the sample (![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) < 0 corresponds to the normal Poynting effect) and is due almost entirely to the twist, whereas the coefficient
< 0 corresponds to the normal Poynting effect) and is due almost entirely to the twist, whereas the coefficient ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) accounts for the pre-stretch only. When λ = 1, i.e. in pure torsion, we have
accounts for the pre-stretch only. When λ = 1, i.e. in pure torsion, we have ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = πR04(c1 + c2),
= πR04(c1 + c2), ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = −πR04(c1/2 + c2), and
= −πR04(c1/2 + c2), and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) = 0. The values of λ in Table 2 show that the samples S2 and S3 experience less than 1% pre-stretch; hence, for those two samples,
= 0. The values of λ in Table 2 show that the samples S2 and S3 experience less than 1% pre-stretch; hence, for those two samples, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) provides an effective measure of the exact Poynting effect, i.e. in the absence of a normal compressive force, the samples would expand axially.
provides an effective measure of the exact Poynting effect, i.e. in the absence of a normal compressive force, the samples would expand axially.
4.2 Parameter estimation
To fit the data in Fig. 4, we use the open-source software RStudio (version 1.1.383). The function lm (from the package stats) allows us to perform a linear regression on the data sets {ϕ,τ} and {ϕ2,Nz}. By calling the function lm on the set {ϕ,τ}, we obtain the coefficient![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) from eqn (8) and the linear regression on {ϕ2,Nz} gives us the coefficients
from eqn (8) and the linear regression on {ϕ2,Nz} gives us the coefficients ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) and
and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) appearing in eqn (9).
appearing in eqn (9).
Moreover, the fit on {ϕ2,Nz} uses a weighted (with respect to ϕ2) least squares method. The weights are given by the values of ϕ2, which increase over time as the test progresses. Therefore, data collected at the beginning of the test (which are more uncertain) are weighted less than those collected at the end of the test. Finally, we input the coefficients ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ,
, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) and
and ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) into eqn (10) to get the elastic parameters c1 and c2.
into eqn (10) to get the elastic parameters c1 and c2.
The results of the linear regression are shown in Table 1. The mean values for the elastic parameters are μ = 900 Pa and c2 = 297 Pa, respectively. The dimensions of the nine samples after the compression are summarised in Table 2, where the length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and radius r0 are given for each sample, as well as the pre-stretch computed from (11) and the maximum values of the highest principal stretch λmax2, attained at breaking point close to the top face.
0 and radius r0 are given for each sample, as well as the pre-stretch computed from (11) and the maximum values of the highest principal stretch λmax2, attained at breaking point close to the top face.
| Sample | μ [Pa] | c 2 [Pa] | R τ 2 | R N z 2 |
|---|---|---|---|---|
| S1 | 1232.50 | 294.45 | 0.999 | 0.946 |
| S2 | 1092.31 | 235.84 | 0.998 | 0.939 |
| S3 | 766.95 | 310.60 | 0.988 | 0.966 |
| S4 | 491.14 | 201.22 | 0.996 | 0.958 |
| S5 | 656.96 | 59.68 | 0.988 | 0.87 |
| S6 | 644.59 | 113.75 | 0.994 | 0.92 |
| S7 | 952.36 | 347.26 | 0.993 | 0.947 |
| S8 | 803.12 | 401.41 | 0.997 | 0.925 |
| S9 | 1460.17 | 710.29 | 0.995 | 0.962 |
| Mean ± SD | 900 ± 312 | 297 ± 189 |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = λL0 (measured by the instrument), the radius r0 = λ−1/2R0 of the nine samples and the maximum value of the greatest principal stretch λ2 before sample breaking
0 = λL0 (measured by the instrument), the radius r0 = λ−1/2R0 of the nine samples and the maximum value of the greatest principal stretch λ2 before sample breaking
| Sample | λ | ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 [mm] 0 [mm] |
r 0 [mm] | λ max2 |
|---|---|---|---|---|
| S1 | 0.93 | 12.62 | 10.36 | 1.82 |
| S2 | 0.99 | 16.02 | 10.05 | 1.73 |
| S3 | 0.99 | 15.92 | 10.05 | 1.81 |
| S4 | 0.89 | 12.95 | 10.59 | 2.14 |
| S5 | 0.94 | 13.26 | 10.31 | 1.85 |
| S6 | 0.85 | 14.19 | 10.84 | 2.04 |
| S7 | 0.89 | 9.51 | 10.59 | 1.87 |
| S8 | 0.89 | 12.22 | 10.59 | 1.68 |
| S9 | 0.95 | 10.14 | 10.26 | 1.69 |
4.3 Computational validation
We performed brain torsion simulations using ABAQUS Standard 6.14-1 to validate our analytical modelling of the deformation.The initial cylindrical geometry of the sample was obtained by setting the radius R0 = 10 mm and the height L0 = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/λ, calculated according to Table 2. We used a mesh of 78
0/λ, calculated according to Table 2. We used a mesh of 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 750 hexahedral elements (C3D8) with hybrid formulation to reproduce exact incompressibility and we assigned the Mooney–Rivlin model with material parameters in Table 1 to account for hyperelasticity.
750 hexahedral elements (C3D8) with hybrid formulation to reproduce exact incompressibility and we assigned the Mooney–Rivlin model with material parameters in Table 1 to account for hyperelasticity.
To simulate the twist, we first defined a reference point at the centre of the top surface of the cylinder, which we then coupled with all points on the surface, and finally, we assigned a rotational displacement around the longitudinal axis (ramp form of amplitude 3 rad) whilst setting the other degrees of freedom to zero. The bottom surface of the cylinder was encastred. The output variables were the resultant axial force (RF3) and torque (RM3).
To perform the simulations, we chose two specimens: S1 and S2. An additional step, prior to the torsion, was added to simulate the 7% pre-compression (see Table 2) undergone by S1.
The results are shown in Fig. 5. We see that the numerical simulations validate the predictions of the analytical model described in Section 4.1. The torque and the normal force calculated in Abaqus are consistent with the analytical predictions and the measured data for both cases with and without pre-compression (S1 and S2, respectively). We note that there is a small mismatch between the analytical and the numerical normal force for S1. This is due to the longitudinal bulging of the sample occurring during the 7% pre-compression phase, which results in a non-homogeneous deformation along the axis of the cylinder.
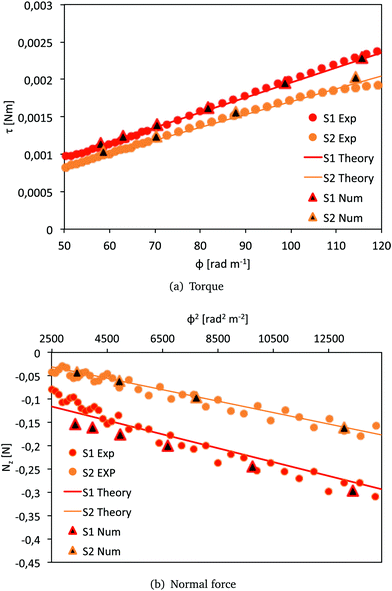 | ||
| Fig. 5 Comparison of the resultant torque τ and normal force Nz for S1 and S2. Results of the numerical simulations in Abaqus (triangles), analytical predictions with the models (8) and (9) (solid lines) and experimental data (red circles for S1 and orange circles for S2). | ||
5 Discussion and conclusions
Here, we note that the results presented in Table 1 show that cylindrical samples of brain matter with initial radius R0 = 10 mm twisted at a twist rate![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) = 300 rad m−1 s−1 behave as Mooney–Rivlin materials with a shear modulus μ = 900 ± 312 Pa. This value is in the same range of values found by Rashid et al.16 when a block of porcine brain matter was sheared at a shear rate of
= 300 rad m−1 s−1 behave as Mooney–Rivlin materials with a shear modulus μ = 900 ± 312 Pa. This value is in the same range of values found by Rashid et al.16 when a block of porcine brain matter was sheared at a shear rate of 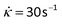 , estimated to be conducive to diffuse axonal injury.17,18 Moreover, from Table 2, we note that the values of the principal stretch (greatest stretch) λ2 at the breaking point are in the range of 1.67–2.14, which corresponds to extensions of 67% to 114%. These values of strain are well above the estimated axonal strain thresholds associated with diffuse axonal injury (>0.05)19 and to white matter damage in the optical nerve (>0.34).20
, estimated to be conducive to diffuse axonal injury.17,18 Moreover, from Table 2, we note that the values of the principal stretch (greatest stretch) λ2 at the breaking point are in the range of 1.67–2.14, which corresponds to extensions of 67% to 114%. These values of strain are well above the estimated axonal strain thresholds associated with diffuse axonal injury (>0.05)19 and to white matter damage in the optical nerve (>0.34).20
In addition, here, we are able to directly estimate the second Mooney–Rivlin coefficient c2 from the normal force data and thus provide a direct measure of the Poynting effect. This quantity cannot be measured from shear stress data alone, although its sign (positive for porcine brain matter) can be deduced by piercing a hole in one of the platens.6 We note also that in contrast to simple shear, where a neo-Hookean material (c2 = 0) does not display the Poynting effect,6 the same material does have a non-zero normal force in torsion.21
Finally, it should be noted that the influences of tissue orientation and anisotropy have not been considered in this study, as the 9 tested samples were all excised from slices in the coronal plane. The orientation of axons within the white matter might play a role in determining the constitutive behaviour of the brain at different length-scales.22,23 Testing of brain samples excised from different planes could therefore provide useful information on the effect of anisotropy both at the micro and macro scales.
Another limitation of the study is that all tests were performed at room temperature. Although a general consensus on the matter has not been reached yet, discussions on the effect of temperature on brain stiffness can be found in ref. 24–26.
Our conclusion is that brain matter exhibits a real and large Poynting effect in torsion, which is bound to lead to the development of large normal forces in an impacted brain.
In order to investigate the existence and magnitude of axial forces during twisting head impacts, we used Abaqus/Explicit to simulate a rotational impact with the University College Dublin Brain Trauma Model (UCDBTM) developed by Horgan and Gilchrist.27
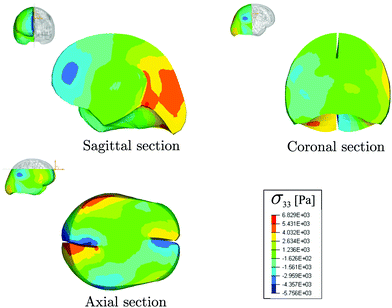
We applied a rotational acceleration in the axial plane to the centre of gravity of the head, peaking at 2170 rad s−2. This value of rotational acceleration is in the range of accelerations experienced in boxing.28 We used the mean values of the estimated parameters μ and c2 in Table 1 to model the mechanical behaviour of the brain matter. In Fig. 6, the distribution of the axial stress component σ33 (where σ is the Cauchy stress) throughout the brain is shown for a rotational angle of α = 0.52 rad. The three sections in the sagittal, coronal and axial planes, respectively, highlight areas where the stress reaches peaks of magnitude in the thousands of Pa. These values indicate that vertical stresses developing during a rotational head impact are of the same order of magnitude as the stiffness μ and are five to ten times larger than the shear stress component σ23, even when the hydrostatic pressure is removed, see ESI,† for more details.
Therefore, the high normal stresses developing during rotational impacts could potentially contribute to traumatic brain injury (TBI) during this type of impact. The results presented in this work thus open the path towards further studies to quantify the role played by normal forces in TBI, in particular with a view to defining more accurate threshold criteria for TBI.
Conflicts of interest
There are no conflicts to declare.Appendix A
By integrating the first of (6) together with the initial condition, we obtain: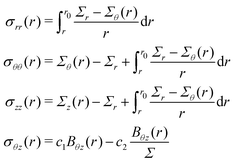 | (12) |
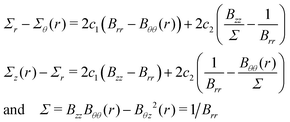 | (13) |
Then, by substituting (2) into (13) and then into (12) we obtain (7).
Acknowledgements
We thank Badar Rashid for Fig. 1(a–c); David McManus for help with the dissection of pig heads; Xiaolin Li for technical assistance with the rheometer; Christiane Görgen for help with fitting in RStudio; and Giuseppe Saccomandi for insightful discussions on the modelling of torsion. The work has received funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie grant agreements No. 705532 (Valentina Balbi and Michel Destrade) and No. 642662 (Antonia Trotta and Aisling Ní Annaidh).Notes and references
- British Standards, British Standards Institution, 2012, BS 903-0:2012.
- K. Miller and K. Chinzei, J. Biomech., 2002, 35, 483–490 CrossRef PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, Comput. Mater. Sci., 2012, 64, 295–300 CrossRef.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2012, 10, 23–38 CrossRef PubMed.
- B. Donnelly and J. Medige, J. Biomech. Eng., 1997, 119, 423–432 CrossRef CAS PubMed.
- M. Destrade, M. Gilchrist, J. G. Murphy, B. Rashid and G. Saccomandi, Int. J. Non Linear Mech., 2015, 75, 54–58 CrossRef.
- R. S. Rivlin, Philos. Trans. R. Soc., A, 1949, 242, 173–195 CrossRef.
- P. A. Janmey, M. E. McCormick, S. Rammensee, J. L. Leight, P. C. Georges and F. C. MacKintosh, Nat. Mater., 2007, 6, 48 CrossRef CAS PubMed.
- L. E. Bilston, Z. Liu and N. Phan-Thien, Biorheology, 2001, 38, 335–345 CAS.
- K. B. Arbogast and S. S. Margulies, J. Biomech., 1998, 31, 801–807 CrossRef CAS PubMed.
- S. Chatelin, A. Constantinesco and R. Willinger, Biorheology, 2010, 47, 255–276 Search PubMed.
- A. Goriely, M. G. Geers, G. A. Holzapfel, J. Jayamohan, A. Jérusalem, S. Sivaloganathan, W. Squier, J. A. van Dommelen, S. Waters and E. Kuhl, Biomech. Model. Mechanobiol., 2015, 14, 931–965 CrossRef PubMed.
- J. H. Poynting, Proc. R. Soc. London, Ser. A, 1909, 82, 546–559 CrossRef.
- R. Mangan, M. Destrade and G. Saccomandi, Extreme Mech. Lett., 2016, 9, 204–206 CrossRef.
- K. Mendis, R. Stalnaker and S. Advani, J. Biomech. Eng., 1995, 117, 279–285 CrossRef CAS PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2013, 28, 71–85 CrossRef PubMed.
- B. Morrison III, H. L. Cater, C. Wang, F. C. Thomas, C. T. Hung, G. A. Ateshian and L. E. Sundstrom, Stapp Car Crash Journal, 2003, 47, 93–105 Search PubMed.
- B. Morrison III, H. L. Cater, C. D. Benham and L. E. Sundstrom, J. Neurosci. Methods, 2006, 150, 192–201 CrossRef PubMed.
- Y. C. Yap, A. E. King, R. M. Guijt, T. Jiang, C. A. Blizzard, M. C. Breadmore and T. C. Dickson, PLoS One, 2017, 12, e0176997 CrossRef PubMed.
- A. C. Bain and D. F. Meaney, J. Biomech. Eng., 2000, 122, 615–622 CrossRef CAS PubMed.
- C. O. Horgan and J. G. Murphy, J. Elasticity, 2015, 118, 127–140 CrossRef.
- S. Budday, G. Sommer, C. Birkl, C. Langkammer, J. Haybaeck, J. Kohnert, M. Bauer, F. Paulsen, P. Steinmann and E. Kuhl, et al. , Acta Biomater., 2017, 48, 319–340 CrossRef CAS PubMed.
- J. Van Dommelen, T. Van der Sande, M. Hrapko and G. Peters, J. Mech. Behav. Biomed. Mater., 2010, 3, 158–166 CrossRef CAS PubMed.
- M. Hrapko, J. Van Dommelen, G. Peters and J. Wismans, J. Biomech. Eng., 2008, 130, 031003 CrossRef CAS PubMed.
- J. Van Dommelen, M. Hrapko and G. Peters, Mechanosensitivity of the Nervous System, Springer, 2009, pp. 249–279 Search PubMed.
- B. Rashid, M. Destrade and M. D. Gilchrist, J. Mech. Behav. Biomed. Mater., 2012, 14, 113–118 CrossRef PubMed.
- T. J. Horgan and M. D. Gilchrist, International Journal of Crashworthiness, 2003, 8, 353–366 CrossRef.
- T. Walilko, D. C. Viano and C. A. Bir, Br. J. Sports Med., 2005, 39, 710–719 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00131j |
| This journal is © The Royal Society of Chemistry 2019 |