Open Access Article
Open Access ArticleShear melting and recovery of crosslinkable cellulose nanocrystal–polymer gels†
Abhinav
Rao
a,
Thibaut
Divoux
 bc,
Gareth H.
McKinley
bc,
Gareth H.
McKinley
 a and
A. John
Hart
a and
A. John
Hart
 *a
*a
aDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: ajhart@mit.edu
bCentre de Recherche Paul Pascal, CNRS UMR 5031 – 115 avenue Schweitzer, 33600 Pessac, France
cMultiScale Material Science for Energy and Environment, UMI 3466 CNRS-MIT, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA
First published on 30th April 2019
Abstract
Cellulose nanocrystals (CNC) are naturally-derived nanostructures of growing importance for the production of composites having attractive mechanical properties, and offer improved sustainability over purely petroleum-based alternatives. Fabrication of CNC composites typically involves extrusion of CNC suspensions and gels in a variety of solvents, in the presence of additives such as polymers and curing agents. Most studies so far have focused on aqueous CNC gels, yet the behavior of CNC–polymer gels in organic solvents is important to their wider processability. Here, we study the rheological behavior of composite polymer–CNC gels in dimethylformamide, which include additives for both UV and thermal crosslinking. Using rheometry coupled with in situ infrared spectroscopy, we show that under external shear, CNC–polymer gels display progressive and irreversible failure of the hydrogen bond network that is responsible for their pronounced elastic properties. In the absence of cross-linking additives, the polymer–CNC gels show an instantaneous but partial recovery of their viscoelasticity upon cessation of flow, whereas, the presence of additives allows the gels to recover over much longer timescale via van der Waals interactions. By exploring a broad range of shear history and CNC concentrations, we construct master curves for the temporal evolution of the viscoelastic properties of the polymer–CNC gels, illustrating universality of the observed dynamics with respect to gel composition and flow conditions. We find that polymer–CNC composite gels display a number of the distinctive features of colloidal glasses and, strikingly, that their response to the flow conditions encountered during processing can be tuned by chemical additives. These findings have implications for processing of dense CNC–polymer composites in solvent casting, 3D printing, and other manufacturing techniques.
1 Introduction
Colloidal gels are percolated networks of attractive particles and/or polymers.1–3 Despite encompassing a wide variety of compositions and architectures, colloidal gels share the common feature of a primarily elastic mechanical response under small strains.4–6 As such, they are used to design soft solid materials with applications including foodstuff, bio-compatible materials, highly stretchable electronics and soft robotics.7–12 More recently, colloidal gels have enabled the production of novel materials via direct ink writing, a versatile additive manufacturing technique in which shear-thinning fluids are deposited by extrusion through a nozzle.13–15 Extrusion disrupts the gel's equilibrium microstructure until it yields and reorganizes to accommodate the flow process. The response of the gel after it is subjected to a strong flow depends on the nature of interactions among the colloidal particles. Either the gel accumulates damage under shear until it is irreversibly destroyed (gel collapse), or the gel recovers after flow cessation, and eventually re-forms a percolated network, given a sufficiently long period of rest. These two types of behavior allow us to distinguish between colloidal gels that experience an irreversible yielding transition,16–19 and colloidal gels that can be rejuvenated due to the shear-reversible nature of the interparticle attractive interactions such as van der Waals or depletion interactions.20–23 The recovery step of the latter category of gels has been termed “rheological aging” and the kinetics of such phenomena are a complex function of the volume fraction, the nature of the interparticle interactions and the shear history.24–29 Being able to tailor the yielding, flow and recovery of colloidal gels is crucial to achieving the desired shape, mechanical integrity and microstructure in direct-write 3D printing and molding.30,31 Such a task becomes even more challenging when designing colloidal gels as precursors for composite materials, as their rheology strongly depends on the physical and chemical properties of multiple components as well as the chemistry of the solvent. Each of these factors can affect the interparticle interactions and consequently the viscoelastic properties. For instance, the presence of charged species has been shown to alter the liquid to gel transition in LAPONITE® suspensions.32–35 Suspensions and gels of cellulose nanocrystals are a compelling case in point, as they display a wide variety of solvent-mediated interparticle interactions including van der Waals attraction, hydrogen bonding and electrostatic repulsion.36,37Cellulose nanocrystals (CNCs) are rod-like nanostructures consisting of repeating glucose units, and are a subject of growing interest as key ingredients of green composites due to their mechanical and chemical properties, as well as their sustainability and biocompatibility.37–40 CNCs are used as fillers for a variety of thermoplastics, thermosets and hydrogels, resulting in improved mechanical properties and temperature stability.41,42 Methods used for processing CNC composites include solvent-casting, coagulation and spinning, as well as melt extrusion.43–45 More recently, bulk CNC-based structures have been produced by direct-ink writing.46,47 Consequently, the rheological properties of these composites, and especially the interplay of yielding, flow and recovery are strongly connected to our ability to manufacture CNC-based materials with the desired microstructure and properties.
CNCs are most commonly produced by sulfuric acid hydrolysis of wood fibers, which leaves residual sulfate groups on the CNCs, resulting in a negative surface charge.37 This allows the formation of colloidal CNC suspensions with relatively high concentrations, stabilized by electrostatic repulsion.48 Moreover, CNCs also form intermolecular hydrogen bonds between surface hydroxyl groups, which results in a sol/gel transition as evidenced by the emergence of a yield stress and a sharp increase in the storage modulus at sufficiently high CNC concentration.37,49 The gel microstructure and concentration at which gelation occurs are dependent on the pH and ionic strength of the solvent, the presence of screening charges, as well as the aspect ratio and polydispersity of the CNCs.50–53 The rod-like shape of CNCs and the presence of surface charges also favor the formation of liquid crystal phases, which can give the gels a local crystalline order.36,54,55 The case of aqueous CNC gels has been the most documented: the addition of charge-screening ions results in attractive van der Waals interparticle interactions leading to a broad range of rheological behavior depending on whether the gel is dominated by repulsive or attractive interactions.56–58 Under external shear, the storage modulus of aqueous CNC gels decreases irreversibly as the gel is subject to increasing strain amplitude, and the CNCs are irreversibly rearranged.59 A recent study on aqueous CNC gels under extrusion flow visualized by polarized light imaging, has shown that above the yield stress, CNCs display shear-induced alignment that is not trivially controlled by the macroscopic strain applied to the gel.60 This last result illustrates the complexity of the rheological behavior of CNC gels and calls for a more in-depth investigation into the flows of CNC gels over a wide range of timescales. Studies on CNC gels have typically been limited to aqueous solvents, whereas the industrial-scale production of CNC/polymer composites requires precursors that are chemically more complex, and which may include oligomers, polymers, and crosslinking agents that necessitate organic solvents. Moreover, the mechanisms driving the microstructural changes associated with yielding in CNC gels are not thoroughly understood.
In this article, we study the rheological properties of polymer–CNC gels, in an organic solvent. We first show that these gels experience a progressive and irreversible decrease of their elastic properties under external shear. Using rheology coupled with time-resolved Fourier Transform Infrared Spectroscopy (FTIR), we find that degradation of the elastic properties of the gel is caused by the progressive decrease of the density of hydrogen bonds between the CNCs. Such shear-melting of the gel microstructure is irreversible because the hydrogen bonds are not restored after flow cessation due to strong electrostatic repulsion and the effect of crowding. By contrast, we show that the addition of relatively small amounts of UV and thermal curing agents to the gel leads to a partially shear-reversible behavior. The UV-curable gels also display a progressive thixotropic decrease of their elastic properties upon external shear, but once the flow is stopped, the gels exhibit a partial recovery of their elastic properties. Applying a series of successive shear-melting steps, and monitoring the viscoelastic recovery of the gels after each step, we explore the dynamics of the gel recovery over a very broad range of cumulative strains. First, we show that the yield stress measured after each period of shear decreases logarithmically with increasing accumulated strain. Second, we reveal how the series of recovery curves, which follow each period of shear, can be scaled onto a universal master curve, providing key insights about the evolution in the gel microstructure. While each period of shear leads to an irreversible decrease of the total number of hydrogen bonds, the CNCs also interact via attractive van der Waals interactions (made possible by the curing agent, which plays the role of charge screening) and these attractive interactions are responsible for the partial recovery process. This scenario, which is confirmed by in situ rheo-FTIR measurements is robust and illustrated over a broad range of CNC concentrations. Finally, we mimic the typical rheological behavior associated with extrusion-based 3D printing of the polymer–CNC gels by performing creep experiments at stresses close to the yield stress. We show that, in the presence of the crosslinking additives, the gels display a rapid recovery following the nonlinear creep flow, suggesting that the curing agent can be used as a control parameter to tune the mechanical integrity of polymer–CNC gels for use in direct ink writing.
2 Experimental
UV curable CNC gels (UV-CG) were prepared by first dissolving an epoxide oligomer, a photoinitiator, and a thermal crosslinker in dimethylformamide (DMF). The oligomer is poly(bisphenol-a-co-epichlorohydrin)diglycidyl ether (Mn ∼ 355 g mol−1), the cationic photoinitiator is triarylsulfonium hexafluorophosphate (50% in propylene carbonate) and the thermal crosslinker is 4-aminophenyl sulfone. All reagents were obtained from Sigma Aldrich. Freeze-dried CNC powder (Celluose Lab, New Brunswick, Canada) is added to the mixture and then dispersed by probe sonication at 40% amplitude for 15 seconds (750 W Sonics Vibra Cell). Reference composite gels (CG) were prepared using the same process, with the exception of adding the photoinitiator and thermal crosslinker. In all the gels, the mass ratio of the epoxide oligomer to the CNCs is 10%, and the mass of the cationic photoinitiator is 10% of the mass of the epoxide oligomer. The amine to epoxide molar ratio is 0.4. The mass fractions of the crosslinkers are selected to allow UV curing of millimeter thick layers within a few minutes, and accelerated thermal curing at lower temperatures.Sonication induces the initial microstructure of the gels, and has been used to break down aggregates of nanoparticles in a variety of colloidal systems, resulting in improved interfacial properties.61,62 Here, probe sonication breaks down the freeze-dried CNC powder into smaller nanoparticles, resulting in a large number of hydroxyl (OH) groups available for hydrogen bonding. After sonication, the average width of the CNCs is around 2.5 nm as measured by dynamic light scattering, and the average length is around 100 nm (see ESI,† Fig. S1 and S2). Sonication also generates a complex flow pattern that drives the large-scale association of CNCs efficiently, leading to the formation of the gel.
Standard rheological tests are performed with a stress-controlled rheometer (AR-G2, TA Instruments) with a 40 mm diameter parallel-plate geometry equipped with a solvent trap. The lower plate (stator), includes a Peltier module, which is used to maintain the sample temperature at 25 °C. In addition, simultaneous rheology and Fourier-Transform Infrared Spectroscopy (FTIR) measurements are performed with a stress-controlled rheometer (HAAKE MARS, Thermo Fisher) equipped with a Rheonaut module. The rheometer has a 35 mm diameter upper plate (rotor) and the infrared laser is directed into the sample via an Attenuated Total Reflectance (ATR) crystal of surface area 1 mm2, located in the lower plate of the shear cell (stator). The ATR crystal is positioned at a radial position corresponding to 50% of the plate diameter, to ensure that the sampled region (which extends between 3 and 10 μm from the stator) experiences a sufficiently intense local shear flow, while avoiding edge effects. A background IR spectrum is obtained prior to loading each sample, and spectra are collected at 0.1 Hz and synchronized with the rheology data.
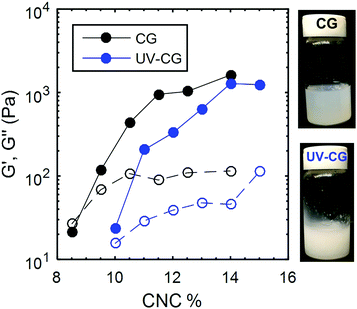
The range of CNC concentrations explored was selected such that the polymer–CNC composite always formed a gel when left undisturbed after the sonication step. For CNC content lower than 8 wt%, we do not observe gelation with the sonication parameters described above, while for CNC content larger than 15 wt%, the kinetic arrest occurs during the sonication step before the individual CNCs are fully dispersed. Fig. 1 summarizes the changes in the linear viscoelastic properties of the CG and the UV-CG gels, showing the values of the elastic and viscous moduli (G′ and G′′ resp.) as a function of the CNC mass fraction. For both types of composite gels, G′ and G′′ are increasing functions of the CNC mass fraction within the window 8 wt% to 15 wt%. Moreover, G′ saturates at CNC content larger than 11 wt% for CG gels (15 wt% for UV-CG gels). This behavior contrasts with the typical power-law-like increase broadly reported for colloidal gels, which involve van der Waals and depletion interactions.6,63 For these CNC gels, such saturation may result from the geometric constraints associated with the hydrogen bonding between neighboring CNCs. Indeed, hydrogen bonds behave as localized patchy interactions with limited attraction range.64 This interpretation is consistent with the finding that the elastic modulus of both types of gels, with and without crosslinkers is limited by the same asymptotic value of G′ ≲ 2000 Pa. Comparing the FTIR spectra of pristine UV-curable and composite gels, the effect of the crosslinkers is identified to be physical rather than chemical. The comparison is described in detail in ESI,† Fig. S3. Finally, the physical appearance of the gels are pictured in Fig. 1. The composite gels are translucent, whereas the UV-curable gels are opaque, indicating that the UV curable gels have a coarser microstructure than the reference composite gels. Further insight into the transparency of the composite gels is obtained by small angle X-ray scattering measurements of the composite gels and reveals long-range order and clustering, characteristic of locally aligned nematic domains (Fig. S4, ESI†).
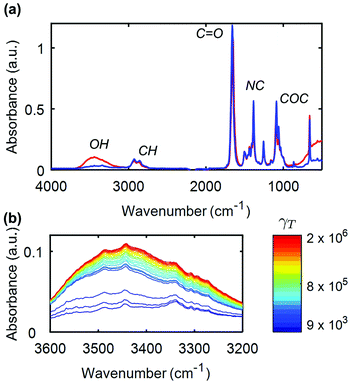
FTIR-coupled rheometry allows us to monitor the evolution of the composite gel microstructure under external shear. A representative mid-IR spectrum of a 14 wt%. UV-curable gel is illustrated in Fig. 2a. The most prominent peak between 1600 and 1700 cm−1 arises from the carbonyl bond in DMF, while the peak at about 1380 cm−1 is attributed to the NC bond in DMF.65 The peak at about 1100 cm−1 is due to the pyranose ring, which forms the backbone of the CNC. Finally, the broad peak, which spans between 3200 and 3600 cm−1 is the signature of the free hydroxyl (OH) groups in the gel.66 This is the primary peak of interest during rheology experiments, as a reduction in the number of hydrogen bonds between the CNCs, results in a growth of the peak intensity due to the increase in concentration of free OH groups.66–68 As an illustrative example, we show in Fig. 2b the evolution of this peak for increasing cumulative strain γT during a creep test at σ = 105 Pa. Here, the cumulative strain is defined as the total integrated strain applied on a given sample over one or more cycles of flow. The dimensionless parameter αOH,
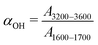 | (1) |
3 Results and discussion
3.1 Shear melting of UV curable gels
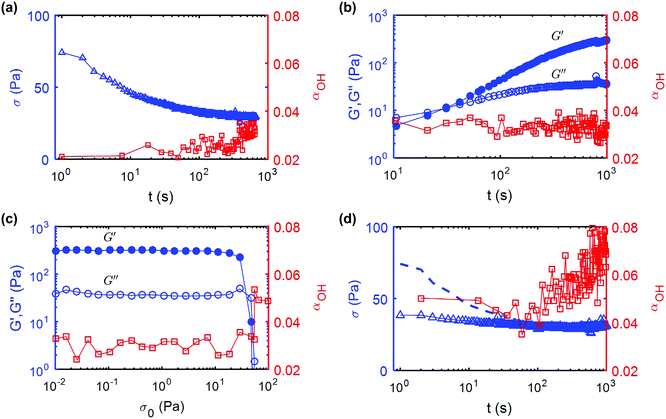
To quantify the evolution of UV curable CNC gels under external shear, we repeat recursively the same protocol, which consists of three steps: (i) a steady flow at high shear rate to partially degrade the gel microstructure, (ii) a period of rest during which we monitor the gel recovery via small amplitude oscillations; and (iii) an oscillatory stress sweep to estimate the yield stress of the gel. We illustrate that sequence in detail in Fig. 3 for a 11 wt%. UV curable CNC gel. We first apply a constant shear rate of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1 over a fixed duration, here of 660 s but more generally chosen between 10 s and 1000 s to control the total strain experienced by the sample. This breaks a fraction of the hydrogen bonds present in the gel. The flow is then stopped by decreasing the shear rate from
= 500 s−1 over a fixed duration, here of 660 s but more generally chosen between 10 s and 1000 s to control the total strain experienced by the sample. This breaks a fraction of the hydrogen bonds present in the gel. The flow is then stopped by decreasing the shear rate from ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1 to
= 500 s−1 to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 s−1 over 10 s. Under constant external shear, the stress σ, slowly decreases in time, while the structural parameter αOH computed from the IR spectrum displays a progressive increase from 0.02 to 0.035 (Fig. 3a).
= 0 s−1 over 10 s. Under constant external shear, the stress σ, slowly decreases in time, while the structural parameter αOH computed from the IR spectrum displays a progressive increase from 0.02 to 0.035 (Fig. 3a).
Following the end of the preshear, the storage and loss modulus of the gel are monitored by small amplitude oscillatory shear for a period of 1000 s (Fig. 3b). Right after flow cessation, we find that G′ < G′′, indicating that the gel has been fluidized by the applied shear. After about 30 s, G′ becomes larger than G′′, which indicates that the gel rebuilds, and after 100 s, G′ asymptotically increases to a value such that G′ ≫ G′′. During this recovery phase, αOH remains constant, αOH ≃ 0.03, indicating that the hydrogen bonds broken during the period of high shear do not re-form, and that hydrogen bonding between CNCs cannot be responsible for the elastic recovery of the gel. This is the principal reason why we use the term “shear melting” to describe the step of high shear rate. To determine the yield stress of the gel after recovery, we perform an oscillatory stress sweep of increasing amplitude from σ0 = 10−2 Pa to 100 Pa (Fig. 3c). At low stress values, the gel displays primarily an elastic behavior characterized by G′ ≫ G′′, up to the yield point where G′ abruptly drops and G′′ exhibits a local maximum. We use the crossing point of G′ and G′′ to define the yield stress σc of the gel. Simultaneous measurement of αOH shows that the number of hydrogen bonds remains constant all the way to the yield stress, at which point αOH then increases abruptly to about 0.05, which indicates that the yielding and flow results in a supplemental loss of hydrogen bonds.
Following the stress-sweep, we repeat for a second time a shear melting step, i.e. a shear flow at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1. The evolution of the shear stress and value of αOHversus time during the second shear melting cycle are shown in Fig. 3d. For reference, the shear stress measured during the first shear melting step is shown by a dashed line. The initial value of the shear stress in the second cycle is seen to be significantly lower than that measured in the first cycle. Furthermore, αOH increases from 0.05, measured at the end of the stress sweep, to about 0.08. This data is consistent with our hypothesis that the shear-melting and yielding of the UV-curable gel results in an irreversible degradation of some hydrogen bonds in the gel, and that the hydrogen bonds do not re-form even during the extended recovery period.
= 500 s−1. The evolution of the shear stress and value of αOHversus time during the second shear melting cycle are shown in Fig. 3d. For reference, the shear stress measured during the first shear melting step is shown by a dashed line. The initial value of the shear stress in the second cycle is seen to be significantly lower than that measured in the first cycle. Furthermore, αOH increases from 0.05, measured at the end of the stress sweep, to about 0.08. This data is consistent with our hypothesis that the shear-melting and yielding of the UV-curable gel results in an irreversible degradation of some hydrogen bonds in the gel, and that the hydrogen bonds do not re-form even during the extended recovery period.
The time-dependent recovery of the elastic modulus of the UV-curable CNC gels can be attributed to weak van der Waals attractive interactions between the CNCs. Since van der Waals attractions are local, they allow rapid gelation due to the formation of a percolating jammed network, and a subsequent time-dependent increase in the modulus due to further development of a glassy network.25 This behavior is enabled because the crosslinkers in the UV curable CNC gels inhibit, or screen the electrostatic repulsion between the CNCs generated by their residual surface charges. The cationic photoinitiator is a complex of the form ArS+ PF6−, where Ar represents a phenyl group. The polyamine curing agent is also polar (Lewis base) and has a structure of the form (R-NH2)2SO2, where R is a hydrocarbon group. The polar curing agents in the UV-curable gels cause an analogous charge screening effect to that of sodium chloride in aqueous CNC suspensions.36,56 The effect of charge-stabilization of colloids in relatively non-polar solvents has been shown to be significant, with a balance of interparticle potentials similar to polar solvents.69 However, in the absence of charge screening, the reference composite gels do not show an increase in G′ after a sequence of high shear rate, i.e. G′ recovers instantaneously due to crowding and electrostatic repulsion but does not display subsequent time dependence. (see ESI,† Fig. S5).
To further understand the differences in the recovery of these two classes of gels, several cycles of shear melting and recovery were imposed following the protocol described above in Fig. 3. The temporal evolution of G′ during the recovery that follows each shear-melting sequence are reported in Fig. 4a for a 11 wt%. UV-curable gel (the corresponding evolution in G′′ is shown in ESI,† Fig. S6). After each period of high shear, the elastic modulus G′ initially increases rapidly, before slowly approaching an asymptotic value. The successive recovery curves however, reach lower G′ values for increasing cumulative strain. A reduction in G′ after each period of shear was also observed in the composite gels, however they display negligible time-dependence in the recovery (Fig. S7, ESI†). These results once again show that irreversible degradation of the hydrogen bonds occurs during shear-melting steps.
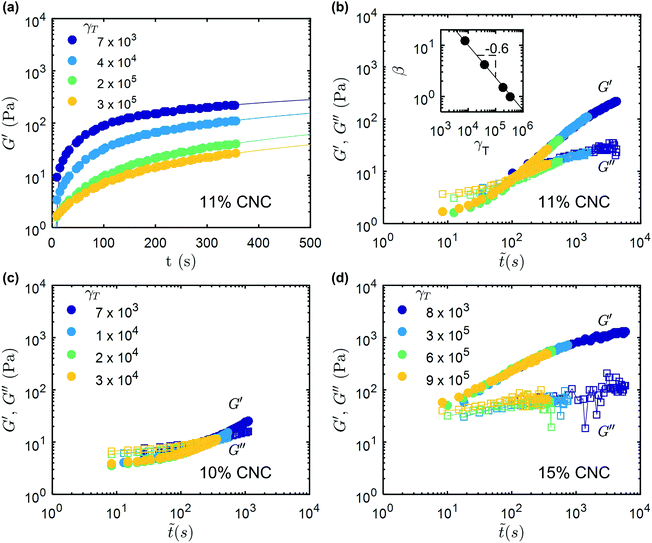 | ||
Fig. 4 Viscoelastic recovery of UV curable CNC gels: (a) recovery of the elastic modulus G′ versus time after repeated shear-melting steps for a UV curable gel with 11 wt% CNC. The cumulative strain, γT experienced by the sample before each recovery step is indicated on the graph. The fits correspond to the best power-law fits described by eqn (2). (b) Master curve for both the elastic modulus G′ (filled symbols) and the viscous modulus G′′ (open symbols) versus a rescaled time axis ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = βt. Inset: Variation of the rescaling parameter β vs. cumulative strain γT. The line corresponds to a power-law fit β = kγζT with an exponent ζ = −0.63 ± 0.03 and a prefactor k = 3362. (c and d) Show similar master curves to that reported in (b) on the same axes scales, for UV-curable gels with respectively lower and higher CNC content, i.e. 10 wt% and 15 wt% respectively. The rescaling factors for (c) and (d) are shown in ESI,† Fig. S8. = βt. Inset: Variation of the rescaling parameter β vs. cumulative strain γT. The line corresponds to a power-law fit β = kγζT with an exponent ζ = −0.63 ± 0.03 and a prefactor k = 3362. (c and d) Show similar master curves to that reported in (b) on the same axes scales, for UV-curable gels with respectively lower and higher CNC content, i.e. 10 wt% and 15 wt% respectively. The rescaling factors for (c) and (d) are shown in ESI,† Fig. S8. | ||
The time evolution of G′ in the UV-curable gels is well described by the following power-law function:
| G′(t) = Gr′ + atb | (2) |
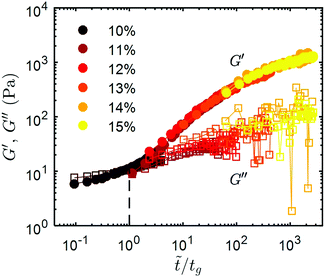
Indeed, all the recovery curves presented in Fig. 4a, which are determined after various cumulative strains, γT, can be rescaled into a single master curve in a logarithmic representation, by translating the recovery curves along the horizontal (time) axis by introducing the following timescale ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = βt, where β is a scaling factor. The same rescaling factor is also used for G′′. Fig. 4b shows the master recovery curve for the 11 wt% CNC gel, and the corresponding rescaling factor β decreases as a power-law with increasing γT (inset in Fig. 4b). At low γT, the gel recovers rapidly and G′ exceeds G′′ immediately following the shear-melting step. As γT increases, the recovery dynamics of G′ and G′′ trace the master curve, and the rate of recovery becomes progressively slower. At large cumulative strain, G′ is observed to be smaller than G′′ immediately after flow-cessation, and to recover slowly thereafter. This observation is robust and master recovery curves were also determined for UV-curable gels with 10 wt% and 15 wt% CNCs (Fig. 4c and d respectively). The rescaling factors for the 10 wt% and 15 wt% gels also follow similar power laws to the 11 wt% gel, and are shown in ESI,† Fig. S8. At low CNC concentration (10 wt%), a lower strain is required to fluidize the gel and the recovery is significantly slower. Consistently, at higher CNC concentration (15 wt%), the elasticity of the gel recovers much faster, with G′ > G′′ almost instantly upon flow cessation for the entire range of cumulative strain explored. Furthermore, the recovery profiles obtained for UV-curable gels with different concentrations, after the same shear history (γT = 7 × 103), can all be combined into a global master curve by normalizing the time axis by a characteristic time, tg, defined as the crossing point of G′ and G′′ (Fig. 6). This sets a common reference point for all the recovery curves, regardless of the CNC concentration of the gel. The global master curve illustrates the universality of the shear-melting and recovery behavior of the UV-curable gels under non-linear external shear.
= βt, where β is a scaling factor. The same rescaling factor is also used for G′′. Fig. 4b shows the master recovery curve for the 11 wt% CNC gel, and the corresponding rescaling factor β decreases as a power-law with increasing γT (inset in Fig. 4b). At low γT, the gel recovers rapidly and G′ exceeds G′′ immediately following the shear-melting step. As γT increases, the recovery dynamics of G′ and G′′ trace the master curve, and the rate of recovery becomes progressively slower. At large cumulative strain, G′ is observed to be smaller than G′′ immediately after flow-cessation, and to recover slowly thereafter. This observation is robust and master recovery curves were also determined for UV-curable gels with 10 wt% and 15 wt% CNCs (Fig. 4c and d respectively). The rescaling factors for the 10 wt% and 15 wt% gels also follow similar power laws to the 11 wt% gel, and are shown in ESI,† Fig. S8. At low CNC concentration (10 wt%), a lower strain is required to fluidize the gel and the recovery is significantly slower. Consistently, at higher CNC concentration (15 wt%), the elasticity of the gel recovers much faster, with G′ > G′′ almost instantly upon flow cessation for the entire range of cumulative strain explored. Furthermore, the recovery profiles obtained for UV-curable gels with different concentrations, after the same shear history (γT = 7 × 103), can all be combined into a global master curve by normalizing the time axis by a characteristic time, tg, defined as the crossing point of G′ and G′′ (Fig. 6). This sets a common reference point for all the recovery curves, regardless of the CNC concentration of the gel. The global master curve illustrates the universality of the shear-melting and recovery behavior of the UV-curable gels under non-linear external shear.
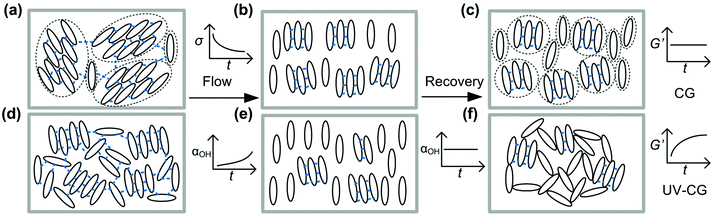
Combining the insights from in situ FTIR measurements and rheology, we can now discuss the mechanism of shear-melting and recovery, as well as illustrate the universality of the gel recovery in this shear-sensitive, weakly attractive system, with respect to cumulative strain and CNC concentration. Fig. 7 shows a schematic of the postulated microstructural evolution during shear melting and recovery of both UV-curable and composite gels. The composite gel initially has a glassy microstructure, composed of aligned domains of CNCs (Fig. 7a). As we increase the strain applied to the composite gel, an increasing number of hydrogen bonds are irreversibly broken (increasing αOH), and more CNCs are free to be rearranged by the local flow field (Fig. 7b). CNCs in the composite gels are balanced by van der Waals attraction and electrostatic repulsion. The recovery of G′ is almost instantaneous upon cessation of flow due to the strong electrostatic repulsion between CNCs. But subsequent microstructural changes would require slow, long-range, cooperative movement of the CNCs, which are not favorable due the effect of crowding. Thus, negligible time evolution is observed in G′ after flow cessation and the hydrogen bonds are irreversibly broken and do not re-form (constant αOH). Each cycle of shear flow results in a gel with smaller clusters and fewer hydrogen bonds, as illustrated in Fig. 7c. After shear flow, the gel also has a comparatively lower G′ (Fig. S7, ESI† and a lower yield stress (Fig. S9, ESI†)), relative to its initial state.
The UV-curable gels do not possess the long-range order of the composite gels, as evidenced by their more opaque color. This is because the electrostatic charges that drive long-range alignment of CNCs into nematic domains are screened. Rather, the elasticity of the gels is attributed to a percolating network of hydrogen bonds and van der Waals attractions between the CNCs (Fig. 7d). Unlike low concentration CNC suspensions that form phase separated gels upon the addition of salt, these gels are formed due to a sufficiently high concentration of CNCs resulting in a structure that is closer to that of an attractive glass.56,70 During shear flow, the percolating interactions are broken, permitting flow and reorganization of the CNCs (Fig. 7e). The UV-curable gels display a partial recovery of G′ over time, at a rate that decreases with increasing accumulated strain. This result suggests that the strongly hydrogen-bonded network of CNCs is progressively replaced by clusters of CNCs that interact via weak van der Waals attractive forces (Fig. 7d).
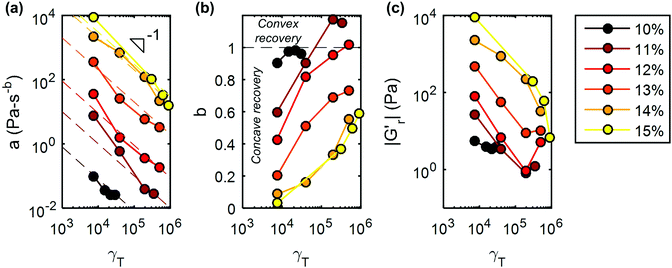
A striking feature seen in the recovery of the 11 wt%. UV-curable gel is that G′ versus time is initially concave at low γT before transitioning to a convex shape at large γT (Fig. 4b). The recovery exponent, b, is less than 1 at small strains (γT = 7 × 103) and greater than 1 at larger strains (Fig. 5b). At small strains, the concave recovery curve reflects the rapid initial recovery of the CNCs, which are trapped in local “cages” formed by their neighbors. As the accumulated strain increases, the shape of the viscoelastic recovery becomes increasingly convex, indicating that the recovery is initially slow, but accelerates after a quiescent period. Correspondingly, G′′ is initially greater than G′ suggesting that the gel is fluidized, permitting the CNCs to flow either individually or in clusters. Combining these observations, we deduce that recovery after the application of large strains may first involve hydrodynamic rearrangements of the CNCs, followed by rapid percolation of van der Waals bonded clusters of CNCs.
These distinctions in the dynamics of viscoelastic recovery are also observed by comparing gels of different CNC concentrations after similar shear histories. On the one hand, the 10 wt% CNC gel breaks down at low strains, with a recovery exponent b ∼ 1, and a recovery rate a ≪ 1, indicative of very slow recovery. On the other hand, the 15 wt% CNC gel exhibits a highly concave (b < 1) recovery profile at low strains. While b approaches 1 at higher strains, a is about 4 orders of magnitude larger than that observed for the 10 wt% gel, suggesting a more rapid recovery. Moreover, the initial portion of the recovery of the 15 wt% gel remains rapid even at high strains, most likely because the loading of CNCs is sufficient for rapid clustering to take place via van der Waals interactions. As a result, the initial percolation takes place too rapidly in the 15 wt% gel to be measured experimentally, and G′ > G′′ at all times greater than 8.5 s (the first recorded data point) during the recovery.
Further emphasizing the universality of the recovery dynamics, the rate parameter a can be directly compared across gels with different CNC concentrations without normalization, although the final value of G′ after recovery increases with CNC concentration. This is because the value of G′ corresponding to the crossover of G′ and G′′ during recovery is almost identical for all the gels, about 20 Pa. This indicates that all the gels pass through a similar minimal percolated state during the recovery step. While the cumulative shearing strain γT increases from 7 × 103 to 5 × 105, a decreases monotonically from 7.5 to 0.02 for the 11 wt% gel. With increasing γT, more hydrogen bonds are broken allowing hydrodynamic re-ordering of the CNCs, and resulting in smaller clusters. The dependence of the aggregation rate on cluster size is widely observed in attractive colloidal gels.71 Illustrating that lowering the CNC concentration has a similar effect to increasing γT, the initial rate of recovery at γT = 8 × 103, is 0.1 Pa s−b (b ∼ 0.9) for a 10 wt% CNC gel and 8500 Pa s−b (b ∼ 0.05) for a 15 wt% CNC gel. An analogous regulation of recovery behavior is seen in aging silica gels, where temperature, rather than the accumulated strain, alters the dynamics of particle aggregation following shear melting.72 More generally, the universality we demonstrate via the master curves in Fig. 4 and 6 is consistent with the theory that fluidization of a colloidal glass by shear is analogous to decreasing the colloidal volume fraction or increasing the thermal energy of the system.73
The evolution of the yield stress, σc (Fig. 8) with cumulative strain for the UV-curable gels, was determined by performing a stress sweep of the form shown in Fig. 3c following each recovery step. The yield stress is defined as the minimum applied stress amplitude for which G′ < G′′. The initial yield stress of the gel increases with increasing CNC concentration, except for 14 wt% and 15 wt% gels, which display a similar yield stress. This result is in agreement with the existence of a plateau in the dependence of the elastic modulus with the CNC concentration, for weight fractions larger than 14% (Fig. 1). For increasing γT, the UV-curable gels display a monotonic decrease in the yield stress following a logarithmic dependence in γT. For the lowest concentration explored (10 wt%), the gel becomes fully fluidized, i.e. it no longer exhibits a yield stress for a cumulative strain of γT ≃ 3 × 104. Note that shear-induced irreversible rearrangements of CNCs were reported in aqueous suspensions using light scattering techniques.59 However, we demonstrate for the first time that the irreversibility of the yielding process is linked to the loss of hydrogen bonds between the CNCs, and that partial recovery of elastic properties of the gels is made possible by the charge-screening effect of the crosslinkers, leading to the formation of a percolated network mediated by van der Waals attractions.
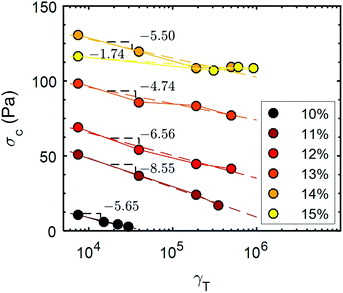 | ||
Fig. 8 Yield stress, σc, of UV-curable CNC gels for different CNC concentrations ranging between 10% and 15 wt% versus cumulative strain γT. Each yield stress was obtained by performing a stress sweep at a frequency of f = 1 Hz. See Fig. 3(c) for the measurement of the first point of the 11 wt% data set. The dashed lines correspond to the best fit of the data with a logarithmic function: σc = σ(0)c + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γT), where σ(0)c and B serve as free parameters. The values of B obtained from the fit are reported on the graph. ln(γT), where σ(0)c and B serve as free parameters. The values of B obtained from the fit are reported on the graph. | ||
3.2 Creep flows of composite gels
While shear-rate controlled rheometry provides valuable insight into the irreversible shear melting of the gels, flow during processing of CNC composites often occurs under constant external stress, and therefore over different timescales. For instance, shear-induced rearrangements of CNCs during pressure-driven extrusion through a nozzle have been shown to take place over time scales up to 103 s.60 In a pressure-controlled extruder, the time over which a gel experiences a high shear stress is dependent on the geometry of the nozzle. Flow occurs when the stress at the wall of the nozzle reaches the yield stress.74 Therefore, a creep test performed with a rheometer, at a stress close to the yield stress, mimics the dynamic response of the gel during flow through an extruder.We first consider the case of the UV-curable gel at two different concentrations: 12 wt% and 14 wt% CNCs. The protocol is the following: the gel is subject to a 60 s pre-shear at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 500 s−1 to erase the shear history from loading the gels into the rheometer. The gel is allowed to recover for 103 s, before being subjected to a stress sweep, which allows us to determine the yield stress of the gel (see ESI,† Fig. S10). The stress value, σ used to perform the creep test is then chosen to be close to the yield stress, σ/σc ≃ 0.99. The creep tests on the 12 wt% and 14 wt% gel were performed at σ = 65 Pa and σ = 105 Pa respectively, and the strain response is reported as a function of time in Fig. 9a. The initial creep is slower for the 14 wt% gel compared to the 12 wt% due to the higher elastic modulus of the material, but both gels accumulate a large total strain of about γT ∼ 106 over 1000 s. The strain for the 12 wt% CNC gel grows as a power law of time: γ(t) ∼ t0.96, whereas the 14 wt% gel shows a decelerating strain response. This result points toward a fluid-like behavior for the 12 wt% gel and a more viscoelastic solid-like response for the 14 wt% gel.75 Indeed, this behavior is confirmed by the gels' response following the creep test (Fig. 9b and c). Upon cessation of flow, the 12 wt% gel is fully fluidized (G′′ < G′), and the gel rebuilds within about 100 s. Note that both G′ and G′′ experience an increase during the recovery. By contrast, the 14 wt% gel shows a solid-like behaviour (G′ < G′′) immediately upon cessation of flow, which strongly suggests that the percolated network formed by the CNCs linked by hydrogen bonds still spans the whole sample. We attribute this difference to the denser microstructure of the 14 wt% gel. Furthermore, the viscoelastic recovery for the 14 wt% gel only affects G′, while G′′ is relatively constant, which suggests that the rebuilding of the percolated microstructure proceeds without an increase in the viscous dissipation. The corresponding changes in the hydrogen bond density between the CNCs are monitored with FTIR by following the evolution of αOH during the creep and recovery tests. The results are consistent with the previous observations and confirm our rheological findings: αOH increases monotonically during the creep test, i.e. hydrogen bonds between CNC particles are progressively destroyed under shear (Fig. 9d). Finally, αOH remains constant during the recovery period, at a value equal to that reached at the end of the creep test, which means that the disruptions in the hydrogen bonds are not reversible during the rest period (Fig. 9e and f). The elastic recovery in both 12 wt% and 14 wt% gels are therefore related to weak van der Waals attractive interactions between the CNCs.
= 500 s−1 to erase the shear history from loading the gels into the rheometer. The gel is allowed to recover for 103 s, before being subjected to a stress sweep, which allows us to determine the yield stress of the gel (see ESI,† Fig. S10). The stress value, σ used to perform the creep test is then chosen to be close to the yield stress, σ/σc ≃ 0.99. The creep tests on the 12 wt% and 14 wt% gel were performed at σ = 65 Pa and σ = 105 Pa respectively, and the strain response is reported as a function of time in Fig. 9a. The initial creep is slower for the 14 wt% gel compared to the 12 wt% due to the higher elastic modulus of the material, but both gels accumulate a large total strain of about γT ∼ 106 over 1000 s. The strain for the 12 wt% CNC gel grows as a power law of time: γ(t) ∼ t0.96, whereas the 14 wt% gel shows a decelerating strain response. This result points toward a fluid-like behavior for the 12 wt% gel and a more viscoelastic solid-like response for the 14 wt% gel.75 Indeed, this behavior is confirmed by the gels' response following the creep test (Fig. 9b and c). Upon cessation of flow, the 12 wt% gel is fully fluidized (G′′ < G′), and the gel rebuilds within about 100 s. Note that both G′ and G′′ experience an increase during the recovery. By contrast, the 14 wt% gel shows a solid-like behaviour (G′ < G′′) immediately upon cessation of flow, which strongly suggests that the percolated network formed by the CNCs linked by hydrogen bonds still spans the whole sample. We attribute this difference to the denser microstructure of the 14 wt% gel. Furthermore, the viscoelastic recovery for the 14 wt% gel only affects G′, while G′′ is relatively constant, which suggests that the rebuilding of the percolated microstructure proceeds without an increase in the viscous dissipation. The corresponding changes in the hydrogen bond density between the CNCs are monitored with FTIR by following the evolution of αOH during the creep and recovery tests. The results are consistent with the previous observations and confirm our rheological findings: αOH increases monotonically during the creep test, i.e. hydrogen bonds between CNC particles are progressively destroyed under shear (Fig. 9d). Finally, αOH remains constant during the recovery period, at a value equal to that reached at the end of the creep test, which means that the disruptions in the hydrogen bonds are not reversible during the rest period (Fig. 9e and f). The elastic recovery in both 12 wt% and 14 wt% gels are therefore related to weak van der Waals attractive interactions between the CNCs.
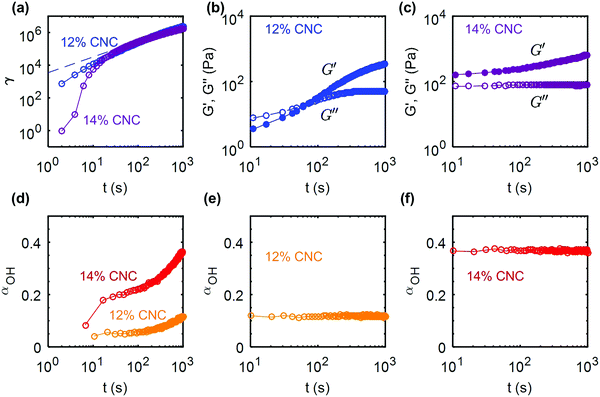 | ||
| Fig. 9 Creep and recovery of UV curable (UV-CG) gels: (a) shear strain γ versus time during creep flow at σ = 65 Pa for the 12 wt% gel and σ = 105 Pa for the 14 wt% CNC gel. These stress values were chosen to be close to the respective yield stresses, (σ/σc ≃ 0.99) of each gel (see ESI,† Fig. S10 for the determination of the yield stress). The dashed line corresponds to the best power-law fit of the data γ(t) ∝ t0.96 for the 12 wt% gel. (b and c) Elastic and viscous modulus versus time, measured by small amplitude oscillatory shear of amplitude σ0 = 0.5 Pa and frequency f = 1 Hz for the 12 wt% and the 14 wt% gel respectively. Evolution of the IR peak ratio parameter αOHversus time during (d) the creep flow and (e) and (f) the recovery of the 12 wt% and 14 wt% gels. | ||
Creep experiments coupled to FTIR measurements were also performed on the 9.3 wt% and the 12.5 wt% composite gels at σ = 100 Pa and σ = 120 Pa respectively. These stress values are again chosen to be comparable to the yield stress of the samples (see ESI,† Fig. S10 for the determination of the yield stress). The creep response γ(t,σ) of both gels are reported in Fig. 10a on a logarithmic scale. Similar to the UV-curable gels, the strain of the 9.3 wt% composite gel shows a power-law increase as a function of time: γ(t) ∼ t1.19, whereas the 12.5 wt% CNC gel shows a decelerating flow. The key difference between the composite gel, which does not contain additives and the UV-curable gel (shown in Fig. 9) is visible in the response following the creep test (Fig. 10b and c). The absence of photoinitiator dramatically changes the recovery after flow. As we observed in the strain-controlled experiments, the recovery of G′ is partial due to the irreversibly broken hydrogen bonds, and quasi-instantaneous due to the rapid arrest of the CNCs clusters experiencing electrostatic repulsion. These features are the hallmark of glassy dynamics.76 Therefore, our observations find a natural framework in the context of Soft Glassy Rheology, for which analogous effects have been reported, e.g.; in LAPONITE® gels, where charge screening results in a transition from slow cooperative rearrangements of the particles, to rapid recovery.77 Finally for the 12.5 wt% composite gels, we note that αOH remains constant during the creep test, due to the fact that the stress selected for the creep test is not sufficiently larger than the yield stress (Fig. 10d). As a result, the total accumulated strain is insufficient to generate a significant change in αOH. However, the evolution of the strain still suggests that the sample is elastically deformed and flows largely as a plug (Fig. 10a). Such a rheological response is favorable to retain the mechanical integrity of the gel during extrusion processing such as in direct-write printing.
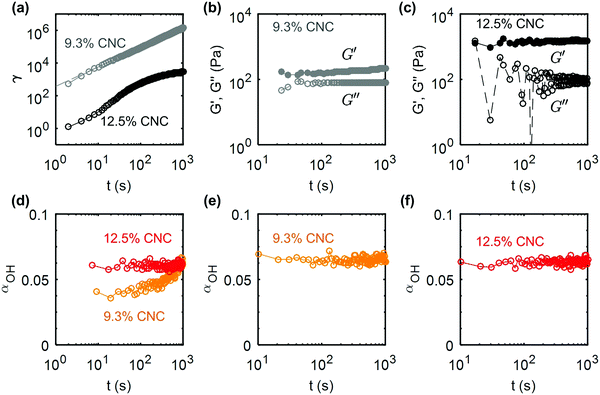 | ||
| Fig. 10 Creep and recovery of the composite (CG) gels: (a) shear strain γ versus time during creep flow at σ = 100 Pa (σ/σc ≃ 1.71) for a 9.3 wt% CNC gel and σ = 120 Pa (σ/σc ≃ 0.86) for a 12.5 wt% CNC gel. Refer to ESI,† Fig. S10 for the determination of the yield stress. The dashed line corresponds to the best power-law fit of the data for the 9.3 wt% gel: γ(t) ∝ t1.19. (b and c) Elastic and viscous modulus versus time, measured by small amplitude oscillatory shear of amplitude σ0 = 0.5 Pa and frequency f = 1 Hz for the 9.3 wt% and the 12.5 wt% CNC gel respectively. (d–f) Evolution of the IR peak ratio parameter αOHversus time during (d) the creep flow and (e and f) the structural recovery of the 9.3 wt% and the 12.5 wt% CNC gels showing no change in the OH peak. | ||
4 Conclusions
We have explored a set of formulations of CNC–polymer composite gels for the synthesis of UV-curable nanocomposites. This formulation involves the introduction of crosslinking additives, which confer tunable rheological properties upon the CNC gel, while enabling UV curing of highly filled CNC–polymer composites. Dispersion of CNCs in DMF by sonication results the formation of strong gels via hydrogen bonding between the CNCs. Using FTIR coupled with rheometry, we found that these hydrogen bonds are irreversibly broken by external shear, and that the density of hydrogen bonds increases monotonically with increasing cumulative strain. External shear thus plays the role of “shear-melting” in CNC–polymer gels, and for sufficiently large strains, brings the gel into a fully fluidized state, which shows a partial and quasi-instantaneous recovery upon flow cessation. The level of recovery decreases for increasing cumulative strain. The presence of crosslinking additives screens the electrostatic repulsive interactions between the CNCs, which then interact mainly through van der Waals attractive interactions, resulting in a time-dependent, power-law recovery of viscoelastic properties upon flow cessation. Revealing universality of this behavior with respect to shear history and CNC concentration, we identified master curves that represent the recovery dynamics of the gels, for a broad range experimental parameters. Furthermore, the CNC composite gels display rheological phenomena similar to those observed in model colloidal gels, and furthermore, these behaviors can be tuned with additives such as crosslinking agents. This offers a unique opportunity to control the properties of CNC–polymer composite gels through applied shear, and for the application of these gels as precursors for solid nanocomposites. Therefore, this work should have a broad impact on the production of CNC-based materials, including by 3D printing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Nate Crawford (Thermo Fisher) for access to the Rheonaut instrument and assistance with the measurements; Crystal Owens for performing the DLS measurement; and Sébastien Manneville for insightful discussions. Financial support was provided by the Procter & Gamble Company.References
- A. H. Krall and D. A. Weitz, Phys. Rev. Lett., 1998, 80, 778–781 CrossRef CAS.
- E. Dickinson, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 1983, 80, 3 RSC.
- E. Stiakakis, D. Vlassopoulos, C. N. Likos, J. Roovers and G. Meier, Phys. Rev. Lett., 2002, 89, 208302 CrossRef CAS PubMed.
- R. T. Bonnecaze and M. Cloitre, in Micromechanics of Soft Particle Glasses, ed. M. Cloitre, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 117–161 Search PubMed.
- A. Zaccone, H. Wu and E. Del Gado, Phys. Rev. Lett., 2009, 103, 208301 CrossRef PubMed.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775 CrossRef CAS PubMed.
- S. Lin, H. Yuk, T. Zhang, G. A. Parada, H. Koo, C. Yu and X. Zhao, Adv. Mater., 2016, 28, 4497–4505 CrossRef CAS PubMed.
- H. Yuk, S. Lin, C. Ma, M. Takaffoli, N. X. Fang and X. Zhao, Nat. Commun., 2017, 8, 14230 CrossRef CAS PubMed.
- T. Gibaud, N. Mahmoudi, J. Oberdisse, P. Lindner, J. S. Pedersen, C. L. P. Oliveira, A. Stradner and P. Schurtenberger, Faraday Discuss., 2012, 158, 267 RSC.
- J. P. Gong, Science, 2014, 344, 161–162 CrossRef CAS PubMed.
- J. Thiele, Y. Ma, S. M. C. Bruekers, S. Ma and W. T. S. Huck, Adv. Mater., 2014, 26, 125–148 CrossRef CAS PubMed.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216 CrossRef CAS PubMed.
- J. R. Raney, B. G. Compton, J. Mueller, T. J. Ober, K. Shea and J. A. Lewis, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 1198–1203 CrossRef CAS PubMed.
- J. Mueller, J. R. Raney, K. Shea and J. A. Lewis, Adv. Mater., 2018, 1705001 CrossRef PubMed.
- J. A. Lewis and G. M. Gratson, Mater. Today, 2004, 7, 32–39 CrossRef CAS.
- D. Bonn, Science, 1998, 280, 265–267 CrossRef PubMed.
- M. Leocmach, C. Perge, T. Divoux and S. Manneville, Phys. Rev. Lett., 2014, 113, 038303 CrossRef PubMed.
- M. Lefranc and E. Bouchaud, Extreme Mech. Lett., 2014, 1, 97–103 CrossRef.
- B. Keshavarz, T. Divoux, S. Manneville and G. H. McKinley, ACS Macro Lett., 2017, 6, 663–667 CrossRef CAS.
- C. Derec, G. Ducouret, A. Ajdari and F. Lequeux, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061403 CrossRef PubMed.
- G. Ovarlez and P. Coussot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011406 CrossRef CAS PubMed.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- E. Moghimi, A. R. Jacob, N. Koumakis and G. Petekidis, Soft Matter, 2017, 13, 2371–2383 RSC.
- V. Viasnoff and F. Lequeux, Phys. Rev. Lett., 2002, 89, 065701 CrossRef PubMed.
- A. S. Negi and C. O. Osuji, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031404 CrossRef PubMed.
- Y. M. Joshi and G. Petekidis, Rheol. Acta, 2018, 57, 521–549 CrossRef CAS.
- L. Cipelletti and L. Ramos, J. Phys.: Condens. Matter, 2005, 17, R253–R285 CrossRef CAS.
- P. Chaudhuri and L. Berthier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2017, 95, 060601 CrossRef PubMed.
- M. Bouzid, J. Colombo, L. V. Barbosa and E. Del Gado, Nat. Commun., 2017, 8, 15846 CrossRef CAS PubMed.
- B. C. Yu and F. F. Lange, Adv. Mater., 2001, 13, 276–280 CrossRef CAS.
- J. A. Lewis, J. E. Smay, J. Stuecker and J. Cesarano, J. Am. Ceram. Soc., 2006, 89, 3599–3609 CrossRef CAS.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- R. Angelini and B. Ruzicka, Colloids Surf., A, 2015, 483, 316–320 CrossRef CAS.
- R. Angelini, E. Zaccarelli, F. A. de Melo Marques, M. Sztucki, A. Fluerasu, G. Ruocco and B. Ruzicka, Nat. Commun., 2014, 5, 4049 CrossRef CAS PubMed.
- K. Suman and Y. M. Joshi, Langmuir, 2018, 34, 13079–13103 CrossRef CAS PubMed.
- J. P. F. Lagerwall, C. Schütz, M. Salajkova, J. Noh, J. Hyun Park, G. Scalia and L. Bergström, NPG Asia Mater., 2014, 6, e80 CrossRef CAS.
- R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Chem. Soc. Rev., 2011, 40, 3941 RSC.
- Y. Habibi, L. A. Lucia and O. J. Rojas, Chem. Rev., 2010, 110, 3479–3500 CrossRef CAS PubMed.
- D. N. S. Hon, Cellulose, 1994, 1, 1–25 CrossRef CAS.
- H. J. Kim, S. Park, S. H. Kim, J. H. Kim, H. Yu, H. J. Kim, Y.-H. Yang, E. Kan, Y. H. Kim and S. H. Lee, J. Mol. Catal. B: Enzym., 2015, 122, 170–178 CrossRef CAS.
- J. J. Fallon, B. Q. Kolb, C. J. Herwig, E. J. Foster and M. J. Bortner, J. Appl. Polym. Sci., 2018, 46992 Search PubMed.
- F. Khelifa, Y. Habibi, L. Bonnaud and P. Dubois, ACS Appl. Mater. Interfaces, 2016, 8, 10535–10544 CrossRef CAS PubMed.
- L. Tang and C. Weder, ACS Appl. Mater. Interfaces, 2010, 2, 1073–1080 CrossRef CAS PubMed.
- W. J. Lee, A. J. Clancy, E. Kontturi, A. Bismarck and M. S. P. Shaffer, ACS Appl. Mater. Interfaces, 2016, 8, 31500–31504 CrossRef CAS PubMed.
- K. Ben Azouz, E. C. Ramires, W. Van den Fonteyne, N. El Kissi and A. Dufresne, ACS Macro Lett., 2012, 1, 236–240 CrossRef CAS.
- G. Siqueira, D. Kokkinis, R. Libanori, M. K. Hausmann, A. S. Gladman, A. Neels, P. Tingaut, T. Zimmermann, J. A. Lewis and A. R. Studart, Adv. Funct. Mater., 2017, 1604619 CrossRef.
- S. Huan, R. Ajdary, L. Bai, V. Klar and O. J. Rojas, Biomacromolecules, 2018, 20, 635–644 CrossRef PubMed.
- T. Abitbol and E. D. Cranston, Handbook of Green Materials, World Scientific, 2014, pp. 37–56 Search PubMed.
- D. Liu, X. Chen, Y. Yue, M. Chen and Q. Wu, Carbohydr. Polym., 2011, 84, 316–322 CrossRef CAS.
- C. Honorato-Rios, A. Kuhnhold, J. R. Bruckner, R. Dannert, T. Schilling and J. P. F. Lagerwall, Front. Mater., 2016, 3, 21 Search PubMed.
- J. R. Bruckner, A. Kuhnhold, C. Honorato-Rios, T. Schilling and J. P. F. Lagerwall, Langmuir, 2016, 32, 9854–9862 CrossRef CAS PubMed.
- A. E. Way, L. Hsu, K. Shanmuganathan, C. Weder and S. J. Rowan, ACS Macro Lett., 2012, 1, 1001–1006 CrossRef CAS.
- M. Nordenström, A. Fall, G. Nyström and L. Wågberg, Langmuir, 2017, 33, 9772–9780 CrossRef PubMed.
- D. Gray and X. Mu, Materials, 2015, 8, 7873–7888 CrossRef CAS PubMed.
- E. E. Ureña-Benavides, G. Ao, V. A. Davis and C. L. Kitchens, Macromolecules, 2011, 44, 8990–8998 CrossRef.
- Y. Xu, A. D. Atrens and J. R. Stokes, Soft Matter, 2018, 14, 1953–1963 RSC.
- A. Dorris and D. G. Gray, Cellulose, 2012, 19, 687–694 CrossRef CAS.
- H. Guo, S. Ramakrishnan, J. L. Harden and R. L. Leheny, J. Chem. Phys., 2011, 135, 154903 CrossRef PubMed.
- B. Derakhshandeh, G. Petekidis, S. Shafiei Sabet, W. Y. Hamad and S. G. Hatzikiriakos, J. Rheol., 2013, 57, 131–148 CrossRef CAS.
- M. K. Hausmann, P. A. Rühs, G. Siqueira, J. Läuger, R. Libanori, T. Zimmermann and A. R. Studart, ACS Nano, 2018, 12, 6926–6937 CrossRef CAS PubMed.
- I. M. Mahbubul, T. H. Chong, S. S. Khaleduzzaman, I. M. Shahrul, R. Saidur, B. D. Long and M. A. Amalina, Ind. Eng. Chem. Res., 2014, 53, 6677–6684 CrossRef CAS.
- V. S. Nguyen, D. Rouxel, R. Hadji, B. Vincent and Y. Fort, Ultrason. Sonochem., 2011, 18, 382–388 CrossRef CAS PubMed.
- V. Prasad, V. Trappe, A. D. Dinsmore, P. N. Segre, L. Cipelletti and D. A. Weitz, Faraday Discuss., 2003, 123, 1–12 RSC.
- Nonappa and O. Ikkala, Adv. Funct. Mater., 2018, 28, 1704328 CrossRef.
- A. Shastri, A. K. Das, S. Krishnakumar, P. J. Singh and B. N. Raja Sekhar, J. Chem. Phys., 2017, 147, 224305 CrossRef PubMed.
- M. R. K. Sofla, R. J. Brown, T. Tsuzuki and T. J. Rainey, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2016, 7, 035004 Search PubMed.
- T. Kondo, Cellulose, 1997, 4, 281 CrossRef CAS.
- Y. Hishikawa, E. Togawa and T. Kondo, ACS Omega, 2017, 2, 1469–1476 CrossRef CAS.
- M. F. Hsu, E. R. Dufresne and D. A. Weitz, Langmuir, 2005, 21, 4881–4887 CrossRef CAS PubMed.
- Y. Xu, A. D. Atrens and J. R. Stokes, J. Colloid Interface Sci., 2017, 496, 130–140 CrossRef CAS PubMed.
- L. Cipelletti, S. Manley, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 2000, 84, 2275–2278 CrossRef CAS PubMed.
- A. S. Negi, C. G. Redmon, S. Ramakrishnan and C. O. Osuji, J. Rheol., 2014, 58, 1557–1579 CrossRef CAS.
- C. Eisenmann, C. Kim, J. Mattsson and D. A. Weitz, Phys. Rev. Lett., 2010, 104, 035502 CrossRef PubMed.
- J. A. Lewis, Adv. Funct. Mater., 2006, 16, 2193–2204 CrossRef CAS.
- H. K. Chan and A. Mohraz, J. Rheol., 2014, 58, 1419–1439 CrossRef CAS.
- P. J. Lu and D. A. Weitz, Annu. Rev. Condens. Matter Phys., 2013, 4, 217–233 CrossRef CAS.
- H. Tanaka, S. Jabbari-Farouji, J. Meunier and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 021402 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02647e |
| This journal is © The Royal Society of Chemistry 2019 |