 Open Access Article
Open Access ArticleEffect of microchannel structure and fluid properties on non-inertial particle migration†
R. V.
Maitri
a,
S.
De
ab,
S. P.
Koesen
a,
H. M.
Wyss
 c,
J.
van der Schaaf
d,
J. A. M.
Kuipers
a,
J. T.
Padding
c,
J.
van der Schaaf
d,
J. A. M.
Kuipers
a,
J. T.
Padding
 e and
E. A. J. F.
Peters
e and
E. A. J. F.
Peters
 *a
*a
aMultiphase Reactors Group, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, P. O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: e.a.j.f.peters@tue.nl
bShell India Markets Private Limited, Shell Technology Centre Bangalore, India
cMicrosystems Group, Department of Mechanical Engineering, Eindhoven University of Technology, P. O. Box 513, 5600 MB Eindhoven, The Netherlands
dChemical Reactor Engineering Group, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, P. O. Box 513, 5600 MB Eindhoven, The Netherlands
eIntensified Reaction and Separation Systems, Department of Process and Energy, Delft University of Technology, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands
First published on 12th March 2019
Abstract
In this work, we investigate the influence of channel structure and fluid rheology on non-inertial migration of non-Brownian polystyrene beads. Particle migration in this regime can be found in biomedical, chemical, environmental and geological applications. However, the effect of fluid rheology on particle migration in porous media remains to be clearly understood. Here, we isolate the effects of elasticity and shear thinning by comparing a Newtonian fluid, a purely elastic (Boger) fluid, and a shear-thinning elastic fluid. To mimic the complexity of geometries in real-world application, a random porous structure is created through a disordered arrangement of cylindrical pillars in the microchannel. Experiments are repeated in an empty channel and in channels with an ordered arrangement of pillars, and the similarities and differences in the observed particle focusing are analyzed. It is found that elasticity drives the particles away from the channel walls in an empty microchannel. Notably, particle focusing is unaffected by curved streamlines in an ordered porous microchannel and particles stay away from pillars in elastic fluids. Shear-thinning is found to reduce the effect of focusing and a broader region of particle concentration is observed. It is also noteworthy that the rheological characteristics of the fluid are not important for the particle distribution in a randomly arranged pillared microchannel and particles have a uniform distribution for all suspending fluids. Moreover, discussion on the current discrepancy in the literature about the equilibrium positions of the particles in a channel is extended by analyzing the results obtained in the current experiments.
1 Introduction
Particle migration in a suspending fluid is encountered in many natural and industrial processes. The understanding of particle migration is important to improve industrial processes such as hydraulic fracturing for shale gas production or drug delivery in biomedical engineering. Microfluidic devices are specifically appealing to get an insight into these processes due to precise control of the surrounding environment and its cost effectiveness. The devices used to study these processes are generally referred to as miniaturized total analysis systems (μTAS) or lab on a chip (LoC) devices and are often used to perform a proof-of-concept of new approaches.1The application of microfluidics to study processes in the oil & gas industry such as enhanced oil recovery (EOR) using polymer/foam/nanoparticle/surfactant floods, hydraulic fracturing, microbial enhanced recovery, heavy oil extraction, etc. are reviewed by Lifton.2 Barbati et al.3 emphasize the importance of milli- and microfluidic scale experiments to gain more insight into fluid–proppant interactions for hydraulic fracturing dynamics. Microfluidics is attractive for the oil & gas industry because the length scales are comparable to those of porous rock structures. Microfluidic techniques are also widely used for biomedical applications.1 Nam et al.4 used a microfluidic setup with a viscoelastic fluid to separate malaria parasites from red blood cells by exploiting the size difference. Furthermore, Nagrath et al.5 used microchip technology for isolating tumor cells in cancer patients. In summary, these studies illustrate that in-depth understanding of the separation of cells from bodily fluids can be obtained using microchannels with complex fluids.
The particle migration in a carrying fluid depends on hydrodynamic effects such as inertia and fluid rheology, and also on particle–particle interactions and the particles’ size and shape. Particles do not migrate laterally in Stokes flow in a Newtonian fluid as the non-inertial equations are linear and are reversible in the case of a velocity reversal.6 Hence, the presence of non-linear effects such as inertia or elasticity are important to achieve a non-uniform distribution of particles. Segré and Silberberg7 studied the particle migration in a cylindrical tube in an inertial flow and found that particles tend to form a ring at a distance of around 0.6R from the central axis of the tube. This is the so-called ‘tubular pinch’ effect. In the absence of inertia, viscoelasticity can also trigger particle migration in a lateral direction. In a viscoelastic fluid, the primary reason for lateral particle migration is the normal stress difference (N1 = τxx − τyy) and its spatial gradient.8 The magnitude of the first normal stress indicates the tension in streamlines and is generally higher in regions of high shear rate. For example, N1 is mainly generated near the four walls in a rectangular cross-section channel and it is weaker at the centre and corners. A pronounced non-uniform distribution of particles in the channel is obtained in the regions of weak first normal stress differences. Shear-thinning behaviour in viscoelastic fluids is observed to push particles towards channel walls.9 Conversely, particles in a constant viscosity elastic (Boger) fluid seem to avoid the near wall region including corners10 but Yang et al.11 reported the presence of particles near the corners, using the same fluid as that of ref. 10. The reason for the discrepancy was speculated to be a difference in the microchannel material by Del Giudice et al.,10 however, more studies are needed to establish agreement among researchers. Also in a recent review on this subject, this issue is described as an open question.12
There are several experimental and numerical studies investigating the particle migration in a square, rectangular or circular channel. However, in porous microchannels only very few experimental or numerical studies have been performed. There are some studies that were carried out on Newtonian fluid flow through ordered porous media.13–15 Huang et al.13 proposed a microfluidic device with a periodic array of obstacles for continuous particle separation according to their sizes. Frechette and Drazer14 studied the directional locking of non-Brownian particles with varying sizes, also in periodic arrays. He et al.15 studied the dispersion of nanoparticles in regular arrays of nanoposts for highly confined flows. All these studies discussed particle migration in periodic arrays of pillars in Newtonian fluids and there are even fewer studies that study particle migration with non-Newtonian fluids.16–18 Jacob et al.17 investigated the particle dispersion of 2 μm particles in a Newtonian and shear-thinning elastic fluid (HPAM) and they presented an analysis of the influence of elastic instabilities. However, due to the presence of both elasticity and shear-thinning properties in HPAM, the effect of each property could not be studied separately.
In this paper, we study the influence of fluid rheology and channel structure on the non-inertial migration of non-Brownian particles. We have tried to isolate the elastic and shear-thinning effects by comparing the particle distribution in a Newtonian fluid, a Boger fluid (elastic), and HPAM (elastic and shear-thinning). To investigate the influence of the structure, experiments were performed in a rectangular microchannel without pillars, with an ordered array of pillars, and with a random array of pillars.
2 Materials and methods
2.1 Microfluidic setup
The microfluidic setup consists of multiple components including a syringe pump, microchannel, microscope and a camera. A KR analytical syringe pump (Fusion 200 Touch, KR analytical Ltd, UK) was used to push the fluid in a controlled manner into the microchannel. Rectangular microchannels made from polydimethylsiloxane (PDMS) were used in this work. The particle migration in the channels was observed with a Zeiss Axio Observer D1 inverted microscope and the series of images was captured with a high-speed Redlake Motion Pro X-4 camera with the number of frames per second (fps) ranging from 30 to 5000, depending on the flow rate. All the experiments were performed at room temperature.2.2 Microfluidic devices
The microchannels used in the current experiments were prepared using standard soft lithography techniques.19 The inverse channel design was fabricated by photolithography, using an SU-8 photoresist on a silicon wafer. The elastomer was prepared by mixing PDMS pre-polymer with a curing agent in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w ratio and pouring on the silicon wafer mold. The membrane was cured overnight at 65 °C. Subsequently, the PDMS layer was carefully removed from the wafer and cut into separate pieces, with each piece containing one channel. After punching holes for in- and outlets, the prepared PDMS pieces and upper layer were activated by plasma and bonded together. After baking, the microchannel was ready for use. The microchannel preparation was performed at the Microfab Lab at TU Eindhoven.
1 w/w ratio and pouring on the silicon wafer mold. The membrane was cured overnight at 65 °C. Subsequently, the PDMS layer was carefully removed from the wafer and cut into separate pieces, with each piece containing one channel. After punching holes for in- and outlets, the prepared PDMS pieces and upper layer were activated by plasma and bonded together. After baking, the microchannel was ready for use. The microchannel preparation was performed at the Microfab Lab at TU Eindhoven.
The microchannels used in our experiments have different configurations. The inside of the rectangular cross section channels consists of either (i) no pillars, (ii) an ordered arrangement of pillars, or (iii) a random arrangement of pillars. The channels without pillars will be referred to as ‘empty channels’ hereafter. For pillared microchannels with an ordered arrangement, pillars are present in a staggered manner as shown in Fig. 1. The porosity (ε) of the unit cell considered in Fig. 1 can be taken as the overall porosity of the microchannel. If the pillar diameter is dp and yp is the centre to centre distance between pillars, the porosity can be computed from eqn (1).
 | (1) |
We chose two porosities for the random channels, namely 0.81 and 0.95. For these channels, the arrangement of pillars was selected such that the minimum centre to centre distance between the pillars is 74 μm and 80 μm, respectively. These distances were used to avoid jamming in the case of a very narrow gap. Neighbouring pillars will have surface to surface distances around 5dp–6dp. The required information about the geometry of the microchannels considered in this study is summarized in Table 1.
| Pillar arrangement | Width, w (μm) | Height, h (μm) | Length, l (mm) | y p (μm) | δ L (μm) | d p (μm) | Porosity (ε) |
|---|---|---|---|---|---|---|---|
| No pillars | 60 | 70 | 60 | — | 64.6 | — | 1.0 |
| Ordered | 1000 | 70 | 40 | 210.0 | 114.2 | 50 | 0.95 |
| Ordered | 1000 | 70 | 40 | 96.7 | 70.3 | 50 | 0.76 |
| Random | 1000 | 70 | 40 | 80 (minimum) | 114.2 | 50 | 0.95 |
| Random | 1000 | 70 | 40 | 74 (minimum) | 80.3 | 50 | 0.81 |
2.3 Fluids
In this work, three suspending fluids were used. First, a glycerol–water mixture (F1) was used with 60 wt% of glycerol where the effective viscosity of the solution is 10.7 mPa s. A second fluid (F2) with elastic properties was prepared by mixing 2000 ppm of polyacrylamide (PAM, 5–6 MDa) in a water–glycerol (60 wt% glycerol) solution. Shear thinning elastic fluids (F3 and F4) were prepared by dissolving 160 ppm of hydrolyzed polyacrylamide HPAM3330 (8 MDa) and HPAM3630 (20 MDa) in demineralized water, respectively. The viscosity of the fluids was measured using an Anton Paar MCR 302 series rheometer. The shear rheology of these fluids is shown in Fig. 2. Rheology data of these fluids are fit to the Carreau–Yasuda model as represented by eqn (2) and the important parameters are reported in Table 2. The change in viscosity for the PAM solution is small compared to that of the HPAM solution and, hence, it will be referred to as a Boger fluid. | (2) |
| Label | Fluid | Elasticity | η 0 (Pa s) | λ (s) | n | a |
|---|---|---|---|---|---|---|
| F1 | Water–glycerol mixture | × | 0.0107 | — | — | — |
| F2 | PAM | ✓ | 0.0361 | 3.67 × 10−2 ± 3.2 × 10−3 | 0.817 ± 5.5 × 10−3 | 1.42 ± 0.15 |
| F3 | HPAM3330 | ✓ | 0.6467 | 6.41 × 100 ± 2.2 × 10−1 | 0.316 ± 1.2 × 10−2 | 1.92 ± 0.08 |
| F4 | HPAM3630 | ✓ | 0.8512 | 3.11 × 101 ± 6.6 × 10−1 | 0.321 ± 7.4 × 10−3 | 2.62 ± 0.13 |
2.4 Particles
For the experiments, non-Brownian polystyrene particles of 5 mm were used. These particles were obtained from Sigma-Aldrich and the standard deviation in the particle size is less than 0.1 mm, which corresponds to a 2% coefficient of variation. The density of these particles is 1050 kg m−3, which is close to a fluid density of 1000 kg m−3. The sedimentation velocity calculations according to Stokes's law show that the sedimentation effect is moderately present for the lowest flow rate and is negligible for all other flow rates. The particles were suspended in the solutions and mixed properly using a magnetic stirrer for a sufficient time. The volume fraction of particles in the solution was around 0.02 wt%.The particle distribution was measured using a particle tracking technique. Information on the particle distribution in the channel was obtained using the positions of the particles. Series of images were used and the static disturbances in the image were removed during post-processing of the experimental images. A given image was divided in the width direction into multiple bands parallel to each other. The position of vectors, which gives the count of particles, was used to compute the fraction of particles (ϕ(i)) in the ith band,
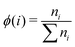 | (3) |
The post-processing of images and the particle fraction computations were performed using DaVis software by LaVision. The particle fraction for the experiments is demonstrated using a 3D plot. For this, the y-direction is chosen as the direction along the width of the channel. The centre of the channel in the width direction is chosen as the origin and the off-centre distances are made dimensionless by dividing the real distance by the half-width of the channel (w/2).
3 Non-dimensional parameters
The relative magnitude of different forces can be expressed in terms of non-dimensional numbers. The ratio of inertial to viscous forces is represented by the Reynolds number (Re), | (4) |
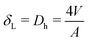 | (5) |

Another important dimensionless number is the Weissenberg number (Wi), which is the ratio of the fluid relaxation time (λ) to the characteristic time scale of the flow (λf). There are different available choices for λf. One of them is the ratio of the average axial velocity and the transverse length scale (δL) and it roughly represents the inverse of the shear rate in the channel. This choice is primarily used in the current study. Another choice would be to calculate the flow time scale as the residence time of the fluid in the channel (λf = tres = l/u) and it is denoted here by De. With this choice, we will get an idea if the viscoelastic fluid attains sufficient time to relax in the channel. De ≪ 1 shows that the viscoelastic fluid gets multiple relaxation cycles whereas De ≫ 1 means that the fluid relaxation time is much larger than the time taken by a fluid element to travel from the inlet to the outlet. The expressions of the discussed numbers are given by eqn (6) and (7).
 | (6) |
 | (7) |
Another non-dimensional parameter is the elasticity number (El), which is the ratio of the Weissenberg number to the Reynolds number. This number signifies the dominance of elastic forces over inertial forces.
 | (8) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102) for F2 and El ∼
(102) for F2 and El ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (104) for F4 for an empty channel. For a microchannel with an ordered arrangement of pillars (ε = 0.95) El ∼
(104) for F4 for an empty channel. For a microchannel with an ordered arrangement of pillars (ε = 0.95) El ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10) for F2 and El ∼
(10) for F2 and El ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (103) for F4, whereas for a low porosity microchannel (ε = 0.76) El ∼
(103) for F4, whereas for a low porosity microchannel (ε = 0.76) El ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (102) for F2 and El ∼
(102) for F2 and El ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (104) for F4. It can be noted that the elasticity number for HPAM is generally two orders of magnitude higher than PAM for all structures.
(104) for F4. It can be noted that the elasticity number for HPAM is generally two orders of magnitude higher than PAM for all structures.
4 Results
As a first step, we investigate the particle focusing in an empty channel for three different types of fluids as detailed in Table 2 (F3 and F4 have similar properties of shear-thinning and elasticity). Snapshots of the particle distribution in the mentioned fluids are presented in Fig. 3. The particle distribution is found to be uniform for the Newtonian fluid (F1) as shown in Fig. 3a. This experiment was repeated for multiple flow rates and the same uniform distribution is observed. This is expected since no non-linear effects of inertia or viscolasticity are present in the fluid. However, the particle distribution in a viscoelastic fluid is dependent on the flow rate, which changes the Weissenberg number. The results are analyzed by plotting the particle fraction values along the width of the channel. The particle distribution is mostly uniform in a Boger fluid (F2) at a lower Weissenberg number, similar to that in a Newtonian fluid (F1). This can be seen in the particle fraction plot in Fig. 4a. For Wi = 0.01, observations show a small particle-free zone at the wall and a slight preference for particles at a finite distance from the wall. This observation is similar to the findings of Leshansky et al.20 and is attributed to non-hydrodynamic forces (e.g. electrostatic repulsion). A Boger fluid at a low Weissenberg number acts basically as a Newtonian fluid due to weak elastic forces. As the Weissenberg number is increased, enhanced focusing of particles at the channel centre is observed. A monotonic increase in focusing at the centre can be clearly seen in Fig. 4a for Wi = 0.01–49.1. Similar experiments were performed in shear-thinning elastic fluids (F3 and F4) as well. HPAM3330 (F3) was used for experiments of Wi = 1–40 and HPAM3630 (F4) was used for Wi = 95.5–19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100. The use of two different fluids allows us to achieve a low Weissenberg number using F3 due to its lower relaxation time and a high Weissenberg number due to a higher relaxation time of F4. The particle fraction along the channel width with varying Weissenberg number is shown in Fig. 4b. In this case, similar to the Boger fluid, particles are uniformly distributed for a low Weissenberg number. However with increasing flow rate, particles seem to show two distinct peaks near walls up to Wi = 95.5. Focusing of particles at the centre of the channel is predominantly obtained at Wi = 191 & 1910. The centreline focusing weakens if the Weissenberg number is increased further. At the highest Weissenberg number of 19
100. The use of two different fluids allows us to achieve a low Weissenberg number using F3 due to its lower relaxation time and a high Weissenberg number due to a higher relaxation time of F4. The particle fraction along the channel width with varying Weissenberg number is shown in Fig. 4b. In this case, similar to the Boger fluid, particles are uniformly distributed for a low Weissenberg number. However with increasing flow rate, particles seem to show two distinct peaks near walls up to Wi = 95.5. Focusing of particles at the centre of the channel is predominantly obtained at Wi = 191 & 1910. The centreline focusing weakens if the Weissenberg number is increased further. At the highest Weissenberg number of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100, the particle distribution is again quite uniform, similar to the situation at the lowest Weissenberg number. The onset of the centreline focusing is achieved at much lower Weissenberg numbers in F2 compared to that in F4. Moreover, this focusing in F2 does not weaken even at the highest flow rate. It is interesting to point out that for higher Weissenberg numbers, particles do not tend to stay near the wall in F2 (flat profile of the particle fraction near the wall at Wi = 49.1), however particles are found near walls even for the best focusing scenario in F4.
100, the particle distribution is again quite uniform, similar to the situation at the lowest Weissenberg number. The onset of the centreline focusing is achieved at much lower Weissenberg numbers in F2 compared to that in F4. Moreover, this focusing in F2 does not weaken even at the highest flow rate. It is interesting to point out that for higher Weissenberg numbers, particles do not tend to stay near the wall in F2 (flat profile of the particle fraction near the wall at Wi = 49.1), however particles are found near walls even for the best focusing scenario in F4.
 | ||
| Fig. 4 Experimental results for the particle fraction in an empty rectangular microchannel in (a) the Boger fluid (F2) and (b) the shear-thinning elastic fluids (F3 + F4). | ||
Next, we studied the particle migration in an orderly arraged pillared microchannel. In these experiments, three fluids (F1, F2 and F4) act as a suspending fluid and microchanels with two different porosities (ε = 0.95 and 0.76) are used. For the ε = 0.95 channel, the particle fraction is calculated by dividing the channel in the width direction into multiple bins. Snapshots of the particle distribution at a given flow rate are shown in Fig. 5. The particle distribution for F1 is again uniform for all flow rates. The particle fractions for suspending fluids F2 and F4 are plotted for various Weissenberg numbers and are presented in Fig. 6. The PAM solution (F2) shows Newtonian behaviour at lower Weissenberg numbers, however, focusing of particles is observed at higher Weissenberg numbers. Fig. 6a shows the distribution of the particle fraction along the width direction. Representative snapshots for non-uniformly and uniformly distributed particles in F2 are shown in Fig. 5b and c, respectively. For the case of focused particle transport (Wi = 3.2), specifically two lanes of particles between two pillars are observed. The distance of each particle lane from the neighbouring pillar is around 0.25 times the total distance between adjacent pillars, which demonstrates the highly symmetric distribution of particles. The width of no-particle zones (also, the distance between two adjacent particle lanes) is 0.5 times the pillar surface–surface distance. A similar trend is observed for the low porosity microchannel at Wi = 3.3 (Fig. 1a and 2a in the ESI†). For F4, particles travel in distinct lanes for Wi = 6.8, which indicates focused particle migration. Similar observations are made for higher Weissenberg numbers till Wi = 683, as seen in Fig. 6b. It should be noted that the focusing in F2 is sharper than that in F4. This can be observed also from the difference in the particle distributions in Fig. 5c and d. Another important observation is that the particles are uniformly distributed at the highest Weissenberg number of 1367. This observation is again similar to that of an empty channel. This is quite interesting since the curved streamlines don't have a significant effect on the particle focusing and the results are the same compared to those of an empty microchannel. The particles focus such that they are going through a curved empty microchannel. These experiments are also performed in a low porosity (ε = 0.76) microchannel and the observations are similar to that of the high porosity channel experiments. Readers are referred to the ESI† for snapshots and particle fraction graphs. The particle fraction in a low porosity channel does not reveal the focusing phenomenon as clearly as in a high porosity microchannel, like in Fig. 6. If the particle trend is observed in Fig. 5c, there are always horizontal strips where particles are not observed within the whole image. For low porosity microchannels, these pillars are very close to each other and highly tortuous paths of particles are such that the particle-free horizontal strips are very narrow (Fig. 1 in the ESI†).
 | ||
| Fig. 6 Experimental results for the particle fraction in an orderly arranged pillared microchannel of porosity ε = 0.95: (a) the Boger fluid (F2) and (b) HPAM3630 (F4). | ||
Next, we performed experiments in microchannels with randomly arranged pillars. The particle distribution is uniform and well distributed for not only Newtonian fluids but also for viscoelastic fluids F2 and F4 (Fig. 7). These experiments were repeated for multiple flow rates and porosities (ε = 0.81 and 0.95), however, focusing of particles is not observed. This is interesting, as the underlying length scales and porosities are very much similar to those of a pillared microchannel with a regular arrangement of pillars but the observed behaviors are markedly different.
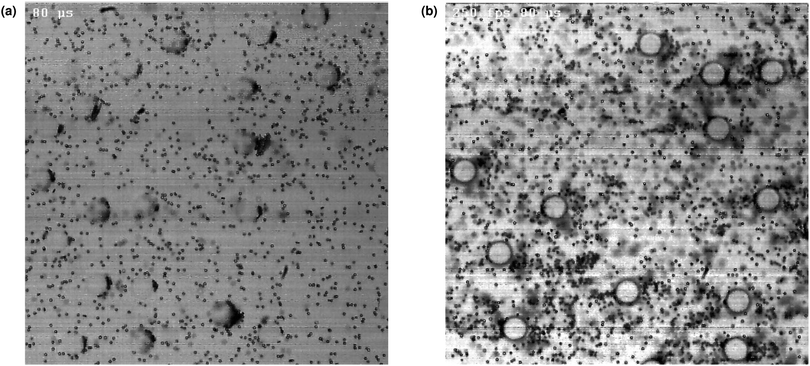 | ||
| Fig. 7 Instantaneous snapshots of experiments in a randomly arranged pillared microchannel of porosity ε = 0.95: (a) the Boger fluid (F2) at Wi = 3.2 and (b) HPAM3630 (F4) at Wi = 683. | ||
5 Discussion
Particles suspended in a Newtonian fluid flowing through an empty rectangular channel show a uniform distribution in Stokes flow. This is due to the absence of any non-linear effects due to either inertia or viscoelasticity. The equations of motion are linear in this situation and are invariant under velocity reversal.6 Due to the (almost) constant viscosity, the velocity profile in a Boger fluid (F2) is similar to that in a Newtonian fluid. The velocity of the fluid increases gradually from the channel wall to its centre and the shear rate is minimal at the centre and increases towards the walls. In viscoelastic fluids, the first normal stress difference, N1 = τxx − τyy, as well as its spatial gradient, is the driving force for particle migration. N1 is generally dependent on the shear rate and it is higher in the higher shear rate regions. The relevant dimensionless number for the particle migration is presented in eqn (S10) of the ESI.† The first normal stress difference and its gradient will be minimal at the centre (low shear rate region) and will increase towards the walls. Hence, particles tend to stay at the centre of a channel. In Fig. 4a, the particle distribution shows a peak at a finite distance from the wall and particle-free zones near the wall. Although the particle-free zone is reasoned to be due to non-hydrodynamic repulsive forces,20 particle migration towards the centre will be caused by elastic forces (negligible inertia, Re = 1.2 × 10−4). The relevant dimensionless number k(∼(l/w)β2Wi) signifies the lateral migration distance (non-dimensionalized with the half-width, w/2) near the outlet of the channel. For Wi = 0.01, k has a value of around 0.07, which demonstrates that the length of the channel is not enough to drive the particles towards the centre. The velocity for a shear-thinning elastic fluid (F4) increases sharply near the wall and has a much flatter profile around the centre compared to the velocity profile in a constant viscosity fluid. Therefore, the shear rate is high near the wall and low around the centre of the channel and a similar trend is also observed in the first normal stress difference. Therefore the particles are pushed to the region of lower N1, that is the centre of a channel. However, it can be observed from Fig. 4b that a few particles still are found near the wall even at Weissenberg numbers for which focusing is observed. The reason for this can be explained in terms of a strong shear-thinning effect due to the high shear rate near the wall, which reduces the viscosity and, consequently, reduces elastic forces and increases inertial forces.9 Another important observation is that particles do not focus exactly at the centre in F4 but there is a spread around the centre. This could be explained based on the flat velocity profile in the near centre region because the lower shear rates cause a lower first normal stress difference and its gradient at the centre and region around it. Therefore focusing is less sharp in F4 than in F2 (Fig. 3b and c).In the literature, there is a discrepancy between the results of Yang et al.11 and Del Giudice et al.10 for particle migration in a Boger fluid. Yang et al.11 reported that a considerable amount of particles migrate towards the corners in a Boger fluid whereas Del Giudice et al.10 found only a single focusing location, which is at the centre of the channel. This discrepancy was attributed to a difference in the channel materials used (PDMS bonded with glass11vs. PMMA bonded with PMMA10) since the same solution of polyvinylpyrrolidone (PVP, a Boger fluid) was used in these studies. As our PAM solution is also a Boger fluid, the particle migration phenomenon seems to support the observation of Del Giudice et al.10 of a single equilibrium point at the centre of the channel. We have used a PDMS channel bonded with glass and polystyrene particles, which is same as that of Yang et al.11 Hence the reasoning of the difference in the material does not seem to account for the discrepancy. However, these results strengthen the idea that particles predominantly stay near the centre of the channel at higher Weissenberg numbers in Boger fluids with El ≫ 1.
In an orderly arranged pillared microchannel, a Newtonian fluid shows a uniform distribution of particles as expected (Fig. 5a). Fig. 5c shows distinct lanes of particles with a periodic structure in a Boger fluid at Wi = 3.2. Particles are also observed to stay away from pillars. This behaviour can be explained with arguments similar to those used in the discussion of results in an empty rectangular channel. Due to a high shear rate near the pillars, the first normal stress difference is also higher and it reduces as we move away from the pillar. However, as the distance is increased from one pillar, we approach the neighbouring pillar, which also has a high shear near its surface. Therefore, particles form quite a symmetric structure by maintaining an optimum distance from pillars to stay in the low shear region. The tendency of particles to stay away from the wall is a bit weaker in a shear-thinning elastic fluid (F4) where few particles are observed near pillars. However, it should be noted that particles are still found to travel in distinct lanes for Wi = 683 (Fig. 5d). The presence of particles near pillars is due to the shear-thinning effect, which reduces the fluid viscosity by weakening the elastic force. The focusing width is a bit more wide compared to that in F2 and it could again be explained by the fact that a flatter velocity can be expected away from the pillar and, hence, the small shear rate region is spread out similarly to that in an empty microchannel.
Another important pattern to study is the lane switching of particles. In the Newtonian fluid (F1), particles stay in a given lane and do not switch from one lane to another. A similar observation is made for all experiments in F2 but with more focused transport. For F4, particles stick to lanes until the Weissenberg number reaches Wi = 683, however, lane switching is observed at Wi = 1367. The phenomenon of switching lanes can be best viewed in the video given as ESI.† The lane switching behaviour is due to elastic instabilities in shear-thinning elastic fluids at high Weissenberg numbers.17,21,22 In shear-thinning elastic fluids, a higher Weissenberg number compared to a Boger fluid is required for focusing of particles due to opposing effect of shear-thinning and elasticity. However, above a certain Weissenberg number elastic instabilities promote the uniform distribution of particles by lane switching. Hence, there is an intermediate range of Weissenberg numbers for which particle focusing is observed in shear-thinning elastic fluids. We did not observe lane switching in a Boger fluid due to elastic instability even at the maximum Weissenberg number of 3.2.
Elastic instabilities also seem to be a reason for the uniform distribution of particles in F4 at Wi > 1910 in an empty channel. Another reason could be a high flow rate of the fluid such that the length of the channel is not sufficient for focusing. Romeo et al.23 proposed a dimensionless number for particle migration in a cylindrical channel which takes care of the fluid and flow properties along with the geometrical parameter. This parameter was modified for the square channel by Del Giudice et al.10 and is the same as the derived expression (eqn (S10) in the ESI†). For higher Weissenberg numbers, a smaller length is sufficient for the migration of particles towards the centre. However, the hypothesis we have is that if the fluid relaxation time is higher than the residence time of the fluid in the channel, the fluid does not get enough time to sufficiently focus the particles laterally. The Deborah number (eqn (7)) is the parameter which measures the relaxation time compared to the average residence time of the fluid in a channel. For Wi = 1910, De ≈ 2 and above this De focusing seems to fade away. Another reason for this could be a slight effect of inertia in F4 as Re ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1.0) for Wi = 9550 and 19
(1.0) for Wi = 9550 and 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100. Moreover the flow rate is very high for these Wi numbers and the shear rate near the wall is higher than 1500 s−1. At this shear rate, the fluid is almost in the Newtonian regime and the polymer has a negligible effect on the lateral migration of particles. For the Boger fluid, De ≪ 1 even for the highest Weissenberg number and hence very good focusing is observed.
100. Moreover the flow rate is very high for these Wi numbers and the shear rate near the wall is higher than 1500 s−1. At this shear rate, the fluid is almost in the Newtonian regime and the polymer has a negligible effect on the lateral migration of particles. For the Boger fluid, De ≪ 1 even for the highest Weissenberg number and hence very good focusing is observed.
In a microchannel with a random arrangement of pillars, the particle distribution is uniform not only in a Newtonian fluid but also in elastic fluids (F2 and F4) for all flow rates. This reveals that the existence of a periodic structure of pillars which gives a periodic flow structure is important for focusing of particles when elastic forces are present. The absence of focusing due to elastic effects can be attributed to a random distribution of high and low shear regions which contributes to the strong lateral migration of particles.
6 Conclusions
In this paper, we studied the particle migration in microchannels. The effect of fluid elasticity and shear-thinning on particle migration is investigated by isolating these effects through the use of multiple fluids. Suspending fluids used are (i) a water–glycerol mixture (a Newtonian fluid), (ii) an aqueous solution of 160 ppm HPAM (an elastic and shear-thinning fluid), and (iii) a water–glycerol solution of 2000 ppm of PAM (a Boger fluid, elastic and weakly shear-thinning). We have also investigated the effect of channel structure on the particle migration.First, experiments are performed in a 60 mm long rectangular channel with a cross section of 60 mm × 70 mm. The particle distribution in the Newtonian fluid is found to be quite uniform in the width direction. Particles don't prefer a specific position in the channel for all the flow rates considered. Similar behaviour is also observed for HPAM and PAM at lower Weissenberg numbers. For PAM, at higher Weissenberg numbers, particles seem to focus predominantly at the centre of the channel. This focusing gets sharper with increasing Weissenberg number. Particles focus at the centre in HPAM as well with few particles near the wall with increasing Weissenberg number, however, focusing at the centre is a bit weaker than in PAM. Quite interestingly, above a certain Weissenberg number, focusing reduces, causing a broader particle distribution in HPAM. We attribute this to a too short residence time of the fluid in the channel to be effective in focusing the particles. The Boger fluid yields a better focusing compared to the shear thinning elastic fluid.
Next, pillared microchannels with an orderly arrangement of pillars are used. Unlike in an empty rectangular channel, straight streamlines are not present. Hence, we tried to investigate the effect of curved streamlines on the particle migration. For the Newtonian fluid, the observation is the same as in the rectangular channel, demonstrating well distributed particles. For PAM, quite interestingly, particles are seen to travel in lanes, followed by curved streamlines at Weissenberg numbers of around 1 or higher. This focusing seems to get sharper with increasing Weissenberg number. For Wi > 1, particles stick to a lane and do not cross over from one lane to another. In the HPAM solution, particles seem to be again well distributed at lower Weissenberg numbers. With increasing Weissenberg numbers, the particles predominantly stay away from the pillars with few particles near the pillar surface. This focusing is seen to vanish after a certain value of the Weissenberg number due to elastic instabilities. The particles are well distributed for Wi ∼ ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (103) because particles switch from one lane to another in the channel promoting mixing of particles. Hence, shear-thinning elastic fluids can promote focusing within an intermediate range of Weissenberg numbers, above and below which a uniform distribution is observed.
(103) because particles switch from one lane to another in the channel promoting mixing of particles. Hence, shear-thinning elastic fluids can promote focusing within an intermediate range of Weissenberg numbers, above and below which a uniform distribution is observed.
In a randomly arranged pillared microchannel, the Newtonian fluid again shows that particles are well distributed. Moreover, HPAM and PAM could not promote focusing of particles at a specific location. These results are confirmed by varying the porosity of the channel as well. This result is particularly interesting since the simplified structure of microchannels is used generally as a proof-of-concept of real world applications, like enhanced oil recovery. However, simplified cases may not always capture the full picture and the results could be substantially different, as observed in our experiments. Therefore, the use of microchannels will be useful only if we mimic the porous structure along with the fluid rheology as closely as possible.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank Prof. Niels Deen for his help in the post-processing of the experimental results using Davis. This work is supported by the programme ‘Computational Sciences for Energy Research (CSER)’ of the Foundation for Fundamental Research on Matter (FOM), which is now part of the Netherlands Organisation for Scientific Research Institutes (NWO-I). This research is also co-financed by Shell Global Solutions International B.V.References
- E. K. Sackmann, A. L. Fulton and D. J. Beebe, Nature, 2014, 507, 181–189 CrossRef CAS PubMed.
- V. A. Lifton, Lab Chip, 2016, 16, 1777–1796 RSC.
- A. C. Barbati, J. Desroches, A. Robisson and G. H. McKinley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 415–453 CrossRef CAS PubMed.
- J. Nam, Y. Shin, J. K. S. Tan, Y. B. Lim, C. T. Lim and S. Kim, Lab Chip, 2016, 16, 2086–2092 RSC.
- S. Nagrath, L. V. Sequist, S. Maheswaran, D. W. Bell, D. Irimia, L. Ulkus, M. R. Smith, E. L. Kwak, S. Digumarthy, A. Muzikansky, P. Ryan, U. J. Balis, R. G. Tompkins, D. A. Haber and M. Toner, Nature, 2007, 450, 1235–1239 CrossRef CAS PubMed.
- R. G. Cox and S. G. Mason, Annu. Rev. Fluid Mech., 1971, 3, 291–316 CrossRef.
- G. Segré and A. Silberberg, Nature, 1961, 189, 209–210 CrossRef.
- B. P. Ho and L. G. Leal, J. Fluid Mech., 1976, 76, 783–799 CrossRef.
- G. Li, G. H. McKinley and A. M. Ardekani, J. Fluid Mech., 2015, 785, 486–505 CrossRef CAS.
- F. Del Giudice, G. Romeo, G. D'Avino, F. Greco, P. A. Netti and P. L. Maffettone, Lab Chip, 2013, 13, 4263–4271 RSC.
- S. Yang, J. Y. Kim, S. J. Lee, S. S. Lee and J. M. Kim, Lab Chip, 2011, 11, 266–273 RSC.
- D. Yuan, Q. Zhao, S. Yan, S.-Y. Tang, G. Alici, J. Zhang and W. Li, Lab Chip, 2018, 18, 551–567 RSC.
- L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CrossRef CAS PubMed.
- J. Frechette and G. Drazer, J. Fluid Mech., 2009, 627, 379–401 CrossRef.
- K. He, S. T. Retterer, B. R. Srijanto, J. C. Conrad and R. Krishnamoorti, ACS Nano, 2014, 8, 4221–4227 CrossRef CAS PubMed.
- F. Babayekhorasani, D. E. Dunstan, R. Krishnamoorti and J. C. Conrad, Soft Matter, 2016, 12, 5676–5683 RSC.
- J. D. Jacob, R. Krishnamoorti and J. C. Conrad, Phys. Rev. E, 2017, 96, 1–13 CrossRef PubMed.
- N. Debnath, M. Hassanpourfard, R. Ghosh, J. Trivedi, T. Thundat, M. Sadrzadeh and A. Kumar, Soft Matter, 2017, 13, 8698–8705 RSC.
- Y. Xia and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 550–575 CrossRef CAS PubMed.
- A. M. Leshansky, A. Bransky, N. Korin and U. Dinnar, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef PubMed.
- H. Bodiguel, J. Beaumont, A. Machado, L. Martinie, H. Kellay and A. Colin, Phys. Rev. Lett., 2015, 114, 1–5 CrossRef PubMed.
- S. De, J. van der Schaaf, N. G. Deen, J. A. Kuipers, E. A. Peters and J. T. Padding, Phys. Fluids, 2017, 29, 113102 CrossRef.
- G. Romeo, G. D'Avino, F. Greco, P. A. Netti and P. L. Maffettone, Lab Chip, 2013, 13, 2802–2807 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02348d |
| This journal is © The Royal Society of Chemistry 2019 |



![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)

