Open Access Article
Open Access ArticleImage-based analysis of uniaxial ring test for mechanical characterization of soft materials and biological tissues
Eline E.
van Haaften
 ab,
Mark C.
van Turnhout
ab,
Mark C.
van Turnhout
 a and
Nicholas A.
Kurniawan†
a and
Nicholas A.
Kurniawan†
 *ab
*ab
aDepartment of Biomedical Engineering, Eindhoven University of Technology, The Netherlands
bInstitute for Complex Molecular Systems, Eindhoven University of Technology, The Netherlands
First published on 25th March 2019
Abstract
Uniaxial ring test is a widely used mechanical characterization method for a variety of materials, from industrial elastomers to biological materials. Here we show that the combination of local material compression, bending, and stretching during uniaxial ring test results in a geometry-dependent deformation profile that can introduce systematic errors in the extraction of mechanical parameters. We identify the stress and strain regimes under which stretching dominates and develop a simple image-based analysis approach that eliminates these systematic errors. We rigorously test this approach computationally and experimentally, and demonstrate that we can accurately estimate the sample mechanical properties for a wide range of ring geometries. As a proof of concept for its application, we use the approach to analyze explanted rat vascular tissues and find a clear temporal change in the mechanical properties of these explants after graft implantation. The image-based approach can therefore offer a straightforward, versatile, and accurate method for mechanically characterizing new classes of soft and biological materials.
1 Introduction
Mechanical characterization of ring-shaped materials traditionally employ uniaxial ring test, where the specimen is mounted between two arms and subjected to extension through a prescribed movement of the arms. The distance between the arms and the force required to apply the arm movement are recorded and used to calculate the material properties. The simplicity of the method makes it attractive for the characterization of a wide range of materials, ranging from ring-shaped hydrogels1 to food products.2 Indeed, the uniaxial ring test is the official standard for tensile testing of elastomers (ASTM D 1414),3 established for use by the O-ring industry.4More recently, uniaxial ring test has also found a large application area in the mechanical characterization of biological tissues and biomaterials. In particular, uniaxial ring test has been increasingly shown to be the method of choice for the assessment of mechanical properties of blood vessels and blood vessel substitutes, due to its ability to mimic the physiological loading in the circumferential direction.5–7 Moreover, uniaxial ring test allows mechanical characterization of small and delicate vascular specimens, for which other testing methods such as uniaxial tensile test of cut-out sample strips and biaxial test of planar samples are unfeasible or can introduce undesired measurement artifacts.8–11 As such, biomedical researchers have started to explore the usefulness of uniaxial ring test for the mechanical measurement of small blood vessels,12 vascular grafts,12,13 tissue-engineered vascular constructs,14,15 and even arterial tissues.7 Such mechanical assessments are important not only for improving the design of vascular constructs and developing mathematical models,16,17 but also for understanding and diagnosing various vascular diseases.18,19
One key challenge that commonly arises in the uniaxial ring test is the extraction of useful material parameters from the raw measurement data. A typical approach is by fitting the force vs. arm distance (or pin displacement) data to a linear function, from which the Young's modulus of the material is inferred. However, in a uniaxial ring test, the initial force response recorded on the pins contains a mixed contribution from bending and stretching forces, as the ring is deformed to a straight shape. Furthermore, as we shall show in this article, during this initial bending stage, pin displacements are not a suitable measurement metric for material stretches. These effects make accurate and reliable material parameters estimation from force–displacement curves a challenge.
We propose that there exists a stretch regime under which the bending and stretching contributions can be sufficiently separated, so that the material properties can be accurately estimated from a uniaxial ring test without using inverse analysis. This knowledge will greatly expand the use of the uniaxial ring test method for the characterizations of new classes of materials, especially when the material behavior is not a priori known, for example in the context of soft hydrogels and biological materials.
In this work, we demonstrate that deformation above a certain critical stretch in uniaxial ring tests is effectively dominated by stretching, thereby allowing accurate estimation of material mechanical stiffness. We further propose a simple image-based approach that both exploits this idea and circumvents the current problem with stretch estimation from pin displacement. We validate our approach computationally and experimentally through a direct comparison with uniaxial tensile testing measurements, and quantify how various parameters such as ring geometry can affect the analysis and outcomes. Finally, we show a proof of concept where we apply the method to characterize the temporal change in the mechanical properties as a result of tissue formation and scaffold degradation in explants from aortic interposition grafts in rats.
2 Materials and methods
In a uniaxial ring test, a ring-shaped specimen is stretched by two pins that move in opposite directions. We first assess the merit of our approach numerically and investigate how experimental parameters affect the extraction of the sample stiffness Ering. We then propose an image-based tracking algorithm to estimate sample stretch in uniaxial ring experiments and we compare our estimate of Ering against the Young's modulus that we measured in uniaxial tensile tests on the same material.2.1 Computational method
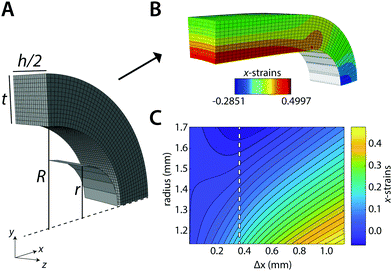
All finite element (FE) simulations were performed with Simulia Abaqus 6.14-1 (Dassault Systèmes Simulia Corp., Providence, RI, USA). The ring is meshed with 20-node quadratic brick elements (C3D20RH) that are kept approximately equal in size (determined with initial mesh convergence tests) for all simulations. We use an isotropic compressible Neo-Hookean material model for the ring with strain energy potential function:
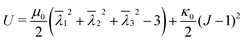 | (1) |
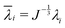 the deviatoric principal stretches, J the determinant of the deformation gradient tensor F, and κ0 the compression modulus. The shear modulus μ0 and compression modulus κ0 are derived from the Young's modulus E and Poisson's ratio ν as:
the deviatoric principal stretches, J the determinant of the deformation gradient tensor F, and κ0 the compression modulus. The shear modulus μ0 and compression modulus κ0 are derived from the Young's modulus E and Poisson's ratio ν as: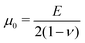 | (2) |
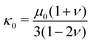 | (3) |
We calculate the stress σring for the ring in each displacement increment using σring = F/A, where F is the reaction force on the pin. A is the cross-sectional area of the ring in the yz-symmetry plane, as obtained from the coordinates and displacements of the highest node on the outer perimeter and those of the opposite node in the inner perimeter of the ring.
Because of sample bending during the uniaxial ring test, pin displacement is not suitable for the assessment of ring stretches. Instead, we use the stretch of the outer perimeter of the ring λOP, calculated for each increment in the simulation, as a measurement metric of ring stretch. We further propose that at sufficiently large pin displacements, sample deformation is dominated by stretching. Therefore, we anticipate that: (1) λOP becomes linear in pin displacements; and (2) stresses in the ring become linear in λOP (in the symmetry plane between the pins). Following these premises, we estimate the Young's modulus of the ring that is being tested, Ering, as:
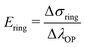 | (4) |
In practice, the initial bending also results in compressive strains in the yz-symmetry plane of the ring. We use the strains in x-direction over this plane to find the point of maximum compression: λ±. For λOP > λ±, all the strains over this cross section monotonically increase in the simulations (Fig. 1C, dashed line). We then estimate Ering with ΔλOP = 2.5%, starting at λ± + 2.5%:
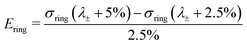 | (5) |
| Symbol | Property | Unit | Parameter space |
|---|---|---|---|
| R | Inner ring radius | mm | [0.5–2.5] |
| h/R | Ring height to radius | — | [0.2–4.0] |
| t/R | Ring thickness to radius | — | [0–1] |
| r/R | Pin radius to radius | — | [0.1–0.9] |
| E | Young's modulus | MPa | [0.1–5.1] |
| ν | Poisson's ratio | — | [0–0.475] |
We investigate the effects of the explored parameters on λ± and Ering with a multiple linear regression model. Buckingham π theorem was used to define a nondimensional equation by constructing the following dimensionless groups out of the dimensioned variables:
 | (6) |
| y = a1 + a2π2 + a3π3 + a4π4 + a5ν + error | (7) |
2.2 Experimental method
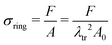 | (8) |
| λtr = 1 − ν(λOP − 1) | (9) |
| Group | h (mm) | R (mm) | t (mm) | t/R (−) |
|---|---|---|---|---|
| 1 | 0.69 ± 0.00 | 0.92 ± 0.01 | 0.48 ± 0.02 | 0.52 ± 0.02 |
| 2 | 0.68 ± 0.00 | 0.97 ± 0.01 | 0.29 ± 0.03 | 0.30 ± 0.03 |
| 3 | 0.67 ± 0.01 | 1.43 ± 0.01 | 0.27 ± 0.03 | 0.19 ± 0.02 |
To compare the uniaxial ring test results against traditional uniaxial tensile data, dogbone shaped samples (n = 4) from the same material were uniaxially stretched in the biaxial tensile tester at the same crosshead speed of 10 mm min−1. Before mounting the sample, graphite particles were applied onto the surface facilitating optical strain analysis by digital image correlation (using LabJoy software, Fig. 4B). Assuming isotropic material properties, the Poisson's ratio was derived from the slopes of the longitudinal and transverse stretch, up to a longitudinal stretch of 1.2 (eqn (9)). Similar to the ring tests, we calculate the ratio between σ and λ over a 2.5% stretch range, starting at λ = 2.5%:
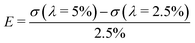 | (10) |
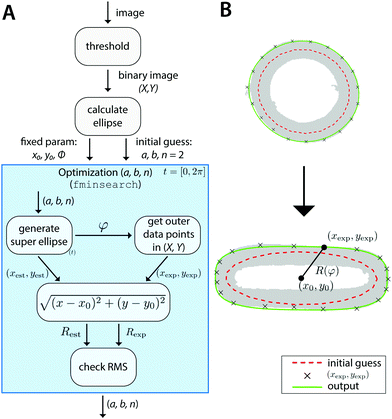
In short, the image is converted into a binary image with sample coordinates (X, Y). For the image of the undeformed samples, this set of coordinates is fitted with an ellipse to calculate the center of mass (i.e. x0, y0), the major and minor axes a and b, and the orientation ϕ. However, at larger stretches, an ellipse cannot accurately describe the outline of the sample. Therefore, a shape parameter n is introduced, which transforms the ellipse into a super ellipse. We use the fit of the ordinary ellipse as an initial guess for this super ellipse. The parameters x0, y0 and ϕ are fixed, and with those we fit the parametric form of the super ellipse:
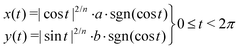 | (11) |
We select a number of points on the outer perimeter of (X,Y) and compare their distance to the center of mass with the distance of the estimated super ellipse to the center of mass. With the fminsearch function in Matlab, we minimize the root-mean-square (RMS) of the differences in distances between the sample points and the corresponding super ellipse points. Using this approach, any number of data points can be generated and used to calculate the RMS. Here, t is discretized into 20 points between 0 and 2π, resulting in excellent shape-fitting results (Fig. 2B).
This algorithm, schematically depicted in Fig. 2A, is implemented in Matlab and is made freely accessible viahttps://gitlab.tue.nl/stem/orlab.
2.3 Measurements of ex vivo biological samples
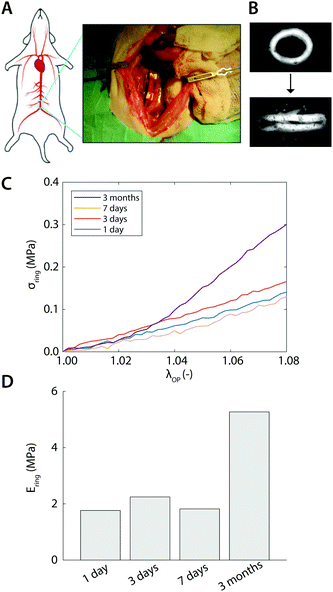
As a proof of concept, explants from aortic interposition grafts in rats were subjected to the uniaxial ring test to characterize the temporal change in mechanical properties as a result of de novo tissue formation and scaffold degradation. Briefly, the vascular scaffolds (2 mm inner diameter, 280 μm thickness, 5 μm fibers) were prepared from supramolecular polycaprolactone-based elastomeric polymers20 using electrospinning. The extremities were shielded by an impenetrable Gore-Tex strip to prevent anastomotic ingrowth. The Gore-Tex shielded scaffolds were then implanted as abdominal aorta interposition grafts in rats for up to 3 months. All animal experiments were reviewed and approved by the Institutional Animal Care and Use Committee of the University of Utrecht, The Netherlands, and conform to the guidelines for the use of laboratory animals as formulated by the Dutch Law on animal experimentation. For a detailed description of the in vivo study, the reader is referred to Bonito21 At selected time points, ring-shaped explants were harvested, snap-frozen in liquid nitrogen, and stored at −80 °C until analysis. All mechanical tests were performed in a phosphate-buffered saline bath at 37 °C and analyzed according to the method presented in Section 2.2.3 Results
3.1 Simulations of uniaxial ring test
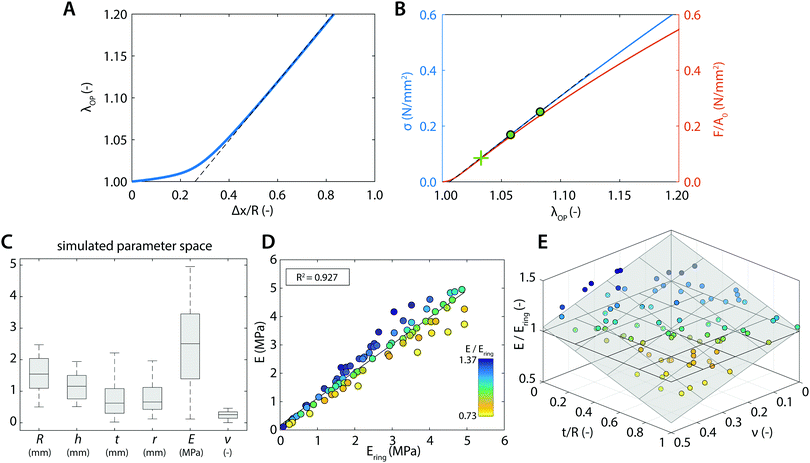
We first tested our assumption that for large pins displacements λOP indeed becomes linear with pin displacements Δx (Fig. 3A); and that the estimate of ring tensile stress σring from pin reaction forces and ring cross sectional area becomes linear with λOP (Fig. 3B, blue). This validates our use of λOP and σring in the analysis. Note that the pin reaction force itself (uncorrected for area changes) does not necessarily become linear in λOP (Fig. 3B, red). The strain contour plots show that, due to bending of the ring shape during uniaxial ring test, the material undergoes local compression and tension (Fig. 1B and C). However, at large pin displacements, tensile strains become linear over the entire cross section of the ring.We next asked whether the point of maximum compression is influenced by the geometry of the ring samples and the pin, as well as the Poisson's ratio of the sample. To rigorously test this, we run a large number of simulations with varying experimental parameters and statistically analyzed the results using a multiple linear regression model to find the key parameters that sensitively affect the deformation mode. For the point of maximum compression in the simulations we find:
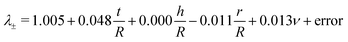 | (12) |
| λ ± = | 1.005 | +0.048t/R | +0.000h/R | −0.011r/R | +0.013ν | + error |
|---|---|---|---|---|---|---|
| 95% CI | 0.999 1.011 | 0.043 0.053 | −0.002 0.003 | −0.017 −0.005 | 0.002 0.025 | |
| SS/SStot | 0.751 | 0.002 | 0.026 | 0.011 | 0.212 | |
| p | 0.000 | 0.000 | 0.769 | 0.001 | 0.027 | |
| n = 100 | R a 2 = 0.773 |
These results suggest that for r/R ≪ 1 the variation in λ± can be largely attributed to variation in the thickness of the ring t/R. When we apply a post hoc linear regression analysis, we find that:
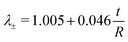 | (13) |
Not all simulations converged up to stretches of λ± + 5%, which is necessary for our analysis of Ering (eqn (5)). Therefore we could only use 85 out of the 100 simulations that we ran, but this did not introduce a noteworthy bias in the uniform distribution of the tested parameter space (Fig. 3C). From these 85 simulations, we find for the relationship between the actual Young's modulus E and the estimated Young's modulus Ering:
| E = 0.950Ering + 0.169 | (14) |
As can be seen from eqn (14), Ering overestimates the actual E by 5% on average. For the remaining, small variation on this overestimation, we find (Table 4):
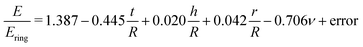 | (15) |
| E/Ering = | 1.387 | −0.445t/R | +0.020h/R | +0.042r/R | −0.706ν | + error |
|---|---|---|---|---|---|---|
| 95% CI | 1.338 1.437 | −0.492 −0.340 | 0.001 0.040 | −0.019 0.103 | −0.807 −0.604 | |
| SS/SStot | 0.557 | 0.007 | 0.003 | 0.306 | 0.128 | |
| p | 0.000 | 0.000 | 0.038 | 0.170 | 0.000 | |
| n = 85 | R a 2 = 0.856 |
These results indicate that the remaining variation can be best explained by t/R and ν: for larger t/R and ν, Ering tends to become larger with respect to the actual E (Fig. 3E).
3.2 Experimental validation
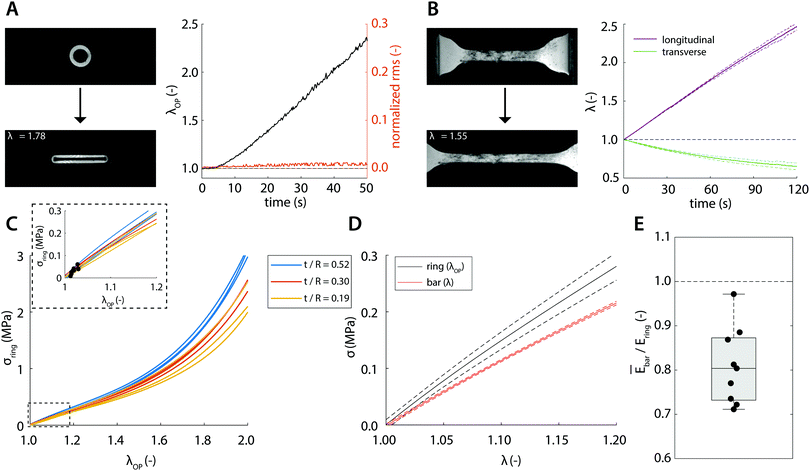
Having established a method to accurately estimate material stiffness and eliminate systematic errors due to measurement geometry and sample mechanical properties, we now test this method experimentally. Using our tracking algorithm, an estimation of the outer perimeter stretch could be obtained with a root-mean-square below 1.5% of the estimated perimeter throughout the entire analysis (Fig. 4A). The stretch-time relation in Fig. 4A further confirms that the relation between λOP and pin displacement is initially nonlinear, but eventually becomes linear for large deformations. To compute the stresses, we normalize the recorded forces to true area (eqn (8) and (9)) with the Poisson's ratio that we measured in the uniaxial tensile tests (Fig. 4B, ν = 0.41). Since our simulation results show that sample geometry, particularly t/R affects sample deformation and therefore the estimation of the material mechanical properties, we tested rubber samples with varying sample geometries in the uniaxial ring test. The resulting experimental stress–stretch curves of the ring-shaped samples indeed corroborate the computational findings: for smaller t/R, the computed stresses tend to become smaller (Fig. 4C).To directly compare the uniaxial ring test results against the ‘conventional’ uniaxial tensile test of the same material, we plot the average stress–stretch relations measured using the two techniques (Fig. 4D). It can be qualitatively observed that the curves are close to each other and that the computed stresses measured in the ring tests are slightly but consistently larger compared to those in the tensile tests. To make a quantitative comparison, we take into account the point of maximum compression λ±, which is estimated viaeqn (13) and highlighted in the inset of Fig. 4C. Using eqn (4), Ering is estimated and compared against the average stiffness of the tensile test (Fig. 4E). We find that the stiffness estimated from the ring test (1.46 ± 0.15 MPa) agrees closely with the actual stiffness (1.17 ± 0.02 MPa), with only a minor discrepancy as predicted by our simulation results.
3.3 Uniaxial ring test of aortic grafts
With the established experimental method, we tested the mechanical properties of abdominal aorta interposition grafts that were implanted in rats for up to 3 months (Fig. 5A and B). At each explantation time point, the grafts exhibited a typical t/R ratio of around 0.2. The results show a clear temporal change in the mechanical behavior, especially between the early time points (up to 7 days) and the late time point (3 months, Fig. 5C). This change in mechanical behavior is consistent with the idea that initially the graft response is dominated by the properties of the scaffold, which is gradually degraded and replaced by the newly formed, stiffer vascular tissue. The extracted Ering increases by a factor of >2 over the tested period, reflecting this stiffening trend (Fig. 5D).4 Discussion
Uniaxial ring testing is a common method to identify material properties, including Young's modulus, yield stress and strain, and ultimate tensile stress and strain.6,22–24 Furthermore, in the context of biomedical materials, clinically-important parameters such as burst pressure and compliance are also typically estimated from ring test data, through the application of Laplace's law, to characterize the functionality of (tissue engineered) vascular grafts.25–27 In many of these applications, however, the pin-to-pin distance is used as the deformation metric for estimating the sample mechanical properties. As we show here, this approach, though simple, is inherently problematic as the deformation of the ring-shaped sample involves a combination of local compression, bending, and stretching. As a result, derivations of stretch are often highly susceptible to systematic errors. Moreover, the deformation profile and the relative contributions of stretching and bending are strongly affected by the sample and pin geometry and therefore difficult to identify, making the experimental force–strain relations hard to interpret.In the present study, we offer a straightforward and accurate approach to estimate material stiffness from uniaxial ring test measurements. The simplicity of the approach is based on the notion that the contributions of sample bending and stretching in the force response can be well delineated from geometry alone, and thereby the outer perimeter stretch of the ring, λOP, can be used as a valid deformation metric (i.e., instead of using the pin-to-pin distance). We develop a robust and freely-accessible algorithm for quantifying λOP from the measurement images and rigorously validate the approach computationally and experimentally.
The numerical simulations confirmed (1) that for large deformations, outer perimeter stretch λOP becomes linear with pin displacement; and (2) that for large deformations, the estimated ring stress from pin reaction forces and cross sectional area σring becomes linear in λOP (Fig. 1B and 3A, B). Similarly, this linear behavior for large deformations was also confirmed in our experiments (Fig. 4A). The numerical simulations further showed that quantification of Ering based on λOP is in very good agreement with the actual stiffness E (eqn (4)). Extensive survey over a large parameter space shows that the actual stiffness is typically 5% lower than estimated by Ering (eqn (14)), with outliers of up to ≈30% (Fig. 3E).
In the calculation of Ering, we take into account that in the initial phase of the ring test the deformation is dominated by bending. With regard to this, our simulations revealed a simple empirical relation between the point of maximum compression (i.e., monotonic extension over the entire cross section of the ring) and ring geometry (i.e., t/R), independent of the intrinsic material properties (eqn (13)). Although ν (as a measure of incompressibility) and r/R (which affects the extent of ring bending) also contribute to this relation, their effects are negligible compared to t/R (<2.5% vs. 75%, Table 3), particularly when we consider that these effects are also limited by the possible range of the parameters: in general 0 < ν < 0.5, and by definition 0 < r/R < 1. Using this relation, the stretch-dominating region in the ring test data can be identified and used to calculate a valid first-order, linear stiffness of the material (i.e., E) without time-consuming and complex inverse analysis methods.
We emphasize that our proposed image-based analysis is optimally suited for the accurate extraction of this linear stiffness, which is particularly valuable in the field of vascular tissue engineering and biology. Extension of the approach to estimate other, non-linear parameters of soft tissues (for instance by a Fung material model) is possible, but inevitably requires an inverse analysis of some kind, because these parameters cannot be directly calculated from the slope of the σ–λ±-curve.
The results from the simulations thus allow us to proceed with the experimental validation, where we tested ring-shaped and dog-bone-shaped samples from the same material. Taking into account the point of maximum compression for the calculation of Ering, we found that the actual stiffness, as determined from the uniaxial tensile test, is typically 20% lower than Ering, as determined from ring test data (Fig. 4E). This overestimation of E is larger than the 5% overestimation found by the simulations (eqn (14)) and can likely be attributed to experimental noise, which is common to all mechanical tests (e.g., noise on force and displacement transducers, pixel discretization of the images, sample irregularities). In fact, due to the geometry and symmetry of uniaxial ring tests, the signal-to-noise ratio of ring tests is expected to be higher than that of conventional tensile tests.
It can be observed that previous studies that use the ring test approach to estimate burst pressures have also consistently shown to overestimate the actual burst pressure by between 25% and >400%.25 Although these values cannot be directly compared to our results, it supports the idea that the ring-test method has a tendency to overestimate material properties. In fact, our simulations and experiments reveal that the degree of overestimation by Ering is related to the geometry of the ring, t/R, and to the compressibility of the ring, ν (Fig. 3E and 4C): the larger these ratios, the larger the tendency to overestimate the stiffness. However, since Poisson's ratios of biological tissues typically fall in the narrow range of 0.3 < ν < 0.5, t/R remains the most relevant variable to account for. Based on this, we conclude that the accuracy of the method becomes better for relatively thin-walled ring samples, and that for a given t/R, the method is very sensitive to detect differences in stiffness. Therefore, it is recommended to always take into account this geometrical effect when comparing data from rings with different geometrical properties.
Finally, we applied the method, as an exemplary proof of concept, to measure the mechanical properties of ring-shaped vascular explants from rat aortic grafts. Given the agreement between the experimental and computational analysis, it is expected that the actual stiffness of the explants is slightly lower than the values reported in Fig. 5. Despite this, the temporal changes in mechanical properties, as a result of tissue formation and scaffold degradation, remain evident, illustrating the merit of this approach.
5 Conclusions
In conclusion, we have shown how the uniaxial ring test can be used to mechanically characterize soft materials and biological tissues, without the need for time consuming and complex inverse analysis methods. We offer a simple image-based analysis approach to determine the deformations in the tissue and provide an empirical relation to identify the stretch-dominating region of the force curve. This makes the uniaxial ring test a very attractive research tool for various research lines involving characterization of ring-shaped materials, even when the material behavior is not a priori known, including in the field of vascular tissue engineering and biology.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
The authors would like to thank Dr Sandra Loerakker for her comments on the Finite Element modeling, as well as Dr Valentina Bonito and Dr Anthal Smits for sharing the raw data of the mechanical tests on the explants. We acknowledge support from the Netherlands's Ministry of Education, Culture, and Science (Gravitation program “Materials-Driven Regeneration”).References
- J. H. Wu, P. F. Li, C. L. Dong, H. T. Jiang, B. Xue, X. Gao, M. Qin, W. Wang, B. Chen and Y. Cao, Nat. Commun., 2018, 9, 620 CrossRef PubMed.
- H. Jung and W. B. Yoon, J. Food Sci., 2017, 82, 2894–2900 CrossRef CAS PubMed.
- A. International, Annual Book of ASTM Standards; Section 9: RUBBER, ASTM International, Conshohocken, USA, 2008, vol. 09.02 Rubber Products, Industrial Specifications and Related Test Methods; Gaskets; Tires Search PubMed.
- J. R. Davis, Tensile Testing, ASM International, Materials Park, OH, 2nd edn, 2004 Search PubMed.
- M. J. Mulvany and W. Halpern, Nature, 1976, 260, 617–619 CrossRef CAS PubMed.
- D. Seliktar, R. A. Black, R. P. Vito and R. M. Nerem, Ann. Biomed. Eng., 2000, 28, 351–362 CrossRef CAS PubMed.
- R. A. Macrae, K. Miller and B. J. Doyle, Strain, 2016, 52, 380–399 CrossRef.
- T. H. Petersen, E. A. Calle, M. B. Colehour and L. E. Niklason, Cells Tissues Organs, 2012, 195, 222–231 CrossRef CAS PubMed.
- E. Claes, J. M. Atienza, G. V. Guinea, F. J. Rojo, J. M. Bernal, J. M. Revuelta and M. Elices, Conf. Proc. IEEE Eng. Med. Biol. Soc., 2010, 2010, 3792–3795 CAS.
- A. V. Kamenskiy, Y. A. Dzenis, S. A. J. Kazmi, M. A. Pemberton, I. I. Pipinos, N. Y. Phillips, K. Herber, T. Woodford, R. E. Bowen, C. S. Lomneth and J. N. MacTaggart, Biomech. Model. Mechanobiol., 2014, 13, 1341–1359 CrossRef PubMed.
- J. T. Keyes, D. G. Haskett, U. Utzinger, M. Azhar and J. P. Vande Geest, J. Biomech. Eng., 2011, 133, 075001 CrossRef PubMed.
- M. Stoiber, B. Messner, C. Grasl, V. Gschlad, H. Bergmeister, D. Bernhard and H. Schima, Exp. Mech., 2015, 55, 1591–1595 CrossRef.
- C. Grasl, H. Bergmeister, M. Stoiber, H. Schima and G. Weigel, J. Biomed. Mater. Res., Part A, 2010, 93, 716–723 Search PubMed.
- T. Shazly, A. Rachev, S. Lessner, W. S. Argraves, J. Ferdous, B. Zhou, A. M. Moreira and M. Sutton, Exp. Mech., 2015, 55, 41–51 CrossRef CAS.
- J. J. Stankus, L. Soletti, K. Fujimoto, Y. Hong, D. A. Vorp and W. R. Wagner, Biomaterials, 2007, 28, 2738–2746 CrossRef CAS PubMed.
- E. E. van Haaften, C. V. C. Bouten and N. A. Kurniawan, Cells, 2017, 6, 19 CrossRef PubMed.
- G. A. Holzapfel, J. Theor. Biol., 2006, 238, 290–302 CrossRef PubMed.
- G. S. Kassab, J. R. Soc., Interface, 2006, 3, 719–740 CrossRef PubMed.
- F. Safshekan, M. Tafazzoli-Shadpour, M. Abdouss and M. B. Shadmehr, Materials, 2016, 9, 456 CrossRef PubMed.
- V. Bonito, A. I. Smits, O. J. Goor, B. D. Ippel, A. Driessen-Mol, T. J. Münker, A. W. Bosman, T. Mes, P. Y. Dankers and C. V. Bouten, Acta Biomater., 2018, 71, 247–260 CrossRef CAS PubMed.
- V. Bonito, PhD thesis, Eindhoven University of Technology, 2018.
- L. Soffer, X. Wang, X. Zhang, J. Kluge, L. Dorfmann, D. L. Kaplan and G. Leisk, J. Biomater. Sci., Polym. Ed., 2008, 19, 653–664 CrossRef CAS PubMed.
- B. C. Isenberg and R. T. Tranquillo, Ann. Biomed. Eng., 2003, 31, 937–949 CrossRef PubMed.
- H. Ahn, Y. M. Ju, H. Takahashi, D. F. Williams, J. J. Yoo, S. J. Lee, T. Okano and A. Atala, Acta Biomater., 2015, 16, 14–22 CrossRef CAS PubMed.
- G. Konig, T. N. McAllister, N. Dusserre, S. A. Garrido, C. Iyican, A. Marini, A. Fiorillo, H. Avila, W. Wystrychowski, K. Zagalski, M. Maruszewski, A. Linthurst, L. Cierpka, L. M. De and N. L'Heureux, Biomaterials, 2009, 30, 1542–1550 CrossRef CAS PubMed.
- R. Gauvin, M. Guillemette, T. Galbraith, J.-M. Bourget, D. Larouche, H. Marcoux, D. Aubé, C. Hayward, F. A. Auger and L. Germain, Tissue Eng., Part A, 2011, 17, 2049–2059 CrossRef PubMed.
- J. Johnson, D. Ohst, T. Groehl, S. Hetterscheidt and M. Jones, J. Tissue Sci. Eng., 2015, 6, 1000151 Search PubMed.
Footnote |
| † Department of Biomedical Engineering, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: kurniawan@tue.nl |
| This journal is © The Royal Society of Chemistry 2019 |