Open Access Article
Open Access ArticleMono-patchy zwitterionic microcolloids as building blocks for pH-controlled self-assembly
Fatemeh Naderi
Mehr
 *ab,
Dmitry
Grigoriev
a,
Nikolay
Puretskiy
a and
Alexander
Böker
*ab,
Dmitry
Grigoriev
a,
Nikolay
Puretskiy
a and
Alexander
Böker
 *ab
*ab
aFraunhofer Institute for Applied Polymer Research IAP, D-14476 Potsdam-Golm, Germany. E-mail: fatemeh.naderi.mehr@iap.fraunhofer.de; alexander.boeker@iap.fraunhofer.de
bChair of Polymer Materials and Polymer Technologies, University Potsdam, D-14476 Potsdam-Golm, Germany
First published on 14th February 2019
Abstract
A directional molecular interaction between microcolloids can be achieved through pre-defined sites on their surface, “patches”, which might make them follow each other in a controlled way and assemble into target structures of more complexity. In this article, we report the successful generation and characterization of mono-patchy melamine–formaldehyde microparticles with oppositely charged patches made of poly(methyl vinyl ether-alt-maleic acid) or polyethyleneimine via microcontact printing. The study of their self-aggregation behavior in solution shows that by change of pH, particle dimers are formed via attractive electrostatic force between the patchy and non-patchy surface of the particles, which reaches its optimum at a specific pH.
Introduction
Recently, patchy particles have been attracting growing attention in material science due to their asymmetrical surface properties. Compared to colloidal particles with uniform properties, they have the advantage that their anisotropy can be used for bottom-up self-assembly to build new functional materials.1–3A directional chemical or physical interaction between patchy particles leads to the formation of specific complex structures, e.g., multi-layers, polymer-like chains, DNA or RNA string like helices, which are understood and predicted theoretically by a variety of works over the past years.4–7 R. Guo and his co-workers showed in the results of their simulation that the presence of three patches on the surface of each building block is needed to achieve DNA-like helices. Furthermore, size and spatial distribution of patches play a crucial role in the final configuration, e.g., diameter of the helices.8,9
It was shown in theoretical works of E. Bianchi and her group that patchy particles could be self-assembled to clusters whose morphology depends on size and number of patches for different types of patchy particles, such as DNA- or protein-like systems. They used either Monte Carlo simulations or developed ideas for optimization based on evolutionary algorithms.10–15
Preparation of multi patchy particles with more than two patches in a one-step process was realized by colloidal fusion or sandwich microcontact printing.16,17 Among a number of established approaches for fabrication of patchy particles, microcontact printing (μCP) is a gentle, cheap and efficient method, which ensures the transfer of the ink molecules to the colloids via polydimethylsiloxane (PDMS) stamps with high reproducibility with respect to the patch parameters.18 In addition, μCP allows to precisely control most of the parameters influencing the patch properties, like ink concentration, ink layer thickness on the stamp, stamping force and duration, adhesion of the ink to the stamp and particle surfaces, polarity and quality of the auxiliary solvent used for the release of patchy particles, etc.
On the other hand, relatively small yield of resulting patchy particles and significant technical difficulties of this method in the application to the sub-micrometer particles or for the production of patchy particles with more than two patches can be seen as its disadvantages.19–21
As mentioned above, a localized well-defined patch-to-patch interaction, e.g., attractive or repulsive electrostatic interactions serve as driving force for the formation of superstructures.22–26 Despite a variety of theoretical investigations on quantification of the interactions between charged patchy or non-patchy particles, so far there have not been many experimental studies in this regard.27–34
For example, inverse patchy colloids (IPC) were considered as a new type of heterogeneously charged particles in theoretical and experimental investigations.33,35,36 The term “inverse” here refers to the repulsive interactions between patches and attractive interactions between patchy and patch-free regions of the particles. In the work of P. D. J. Van Oostrum, silica patchy particles with two identically positively charged patches on their poles made of APTES and a negatively charged equatorial belt were prepared. Their electrostatic interactions and self-assembly to the clusters were studied using simulation methods.37,38 It was also reported by O. Cayre that one positively charged patch made of ODTAB could be generated on negatively charged sulfate latex particles using μCP.39
The successful attachment of multi-patches made of positively charged PEI on the surface of negatively charged silica particles using flat and wrinkled PDMS stamps was reported.27,40–43
Conceiving the idea of using patchy particles for biological applications tends to more investigations on patchy particles made of bio-organic substrates, which are compatible with living systems. In this sense, microcolloids such as polymer particles with epoxy groups were functionalized via covalent bonding of positively charged amino groups on their surface, e.g., proteins and enzymes.21,44,45
The strength of electrostatic interactions between patchy particles can be controlled by an effective charge heterogeneity between patchy and non-patchy surfaces. To this end, a specific ion is bound to the surface of patch or particle.38,46 For example, the surface charge density of patch can be changed by its proton-binding; hence the aggregation of patchy particles in solution can be manipulated by pH-regulation in protic media to initiate particle-assembly in a desired way.
In simulations using charged patchy particle models (CCPM), it was also found that the electrostatic interactions between patchy proteins can be controlled by change of ionic strength.40,47,48
Here we put our major effort on the reproducible preparation and characterization of mono-patchy polymeric melamine formaldehyde (MF) microparticles with oppositely charged patches, made of poly(methyl vinyl ether-alt-maleic acid) (PMVEMA) or polyethyleneimine (PEI), via microcontact printing. Further, we study the self-aggregation behavior of mono-patchy particles as a function of pH for each type of patches. Between a diversity of possible aggregation forms, the statistical analysis of predominantly formed particle dimers via patch–patch, particle–particle, and patch–particle interactions was performed. Finally, these results were compared with theoretical calculation of the electrostatic force between patchy particles, based on a simplified model.
Results and discussion
Oppositely charged patches
To generate mono-patchy particles with positively or negatively charged patches, the MF microparticles are very suitable due to their isoelectric point (IEP) at almost neutral pH. Comparison of the zeta-potential of the MF particles in water and ethanol–water (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10), showed the IEPs at pH 7.1 and 8.9 respectively (Fig. 1). PMVEMA and PEI, as strong and multivalent polyelectrolytes, induce a considerable electrostatic attraction to the MF particles, which results in the creation of patchy particles with a good yield and patches with a high surface charge density and stability.
10), showed the IEPs at pH 7.1 and 8.9 respectively (Fig. 1). PMVEMA and PEI, as strong and multivalent polyelectrolytes, induce a considerable electrostatic attraction to the MF particles, which results in the creation of patchy particles with a good yield and patches with a high surface charge density and stability.
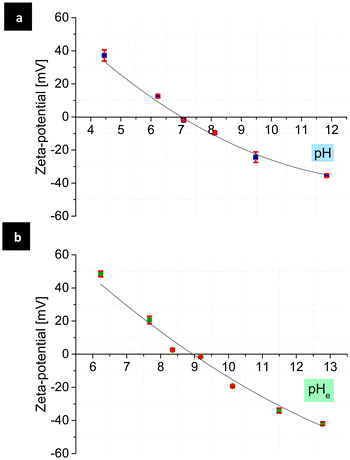 | ||
Fig. 1 Zeta-potential of the MF particles as a function of pH in water (a), pHe in water–ethanol (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) (b) and the corresponding IEPs at pH 7.1 and pHe 8.9 in water and ethanol–water, respectively. 10) (b) and the corresponding IEPs at pH 7.1 and pHe 8.9 in water and ethanol–water, respectively. | ||
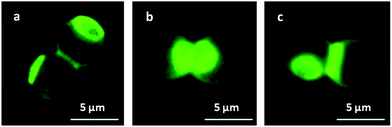
The successful attachment of PMVEMA and PEI onto the surface of the MF particles was confirmed by fluorescence microscopy (Fig. 2).
Patch thickness and the yield of μCP
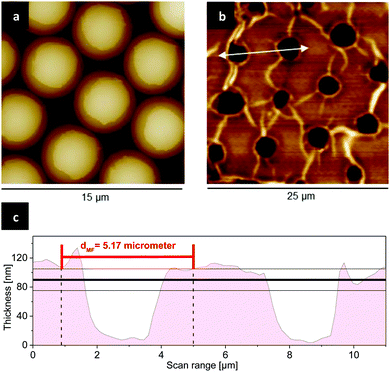
AFM analysis of the stamp and patchy particles after μCP and subsequent release in acetone yields reliable information about the thickness and the form of resulted patches. Patchy particles with patches made of PMVEMA were fixed on a PDMS stamp, and scanned with AFM (Fig. 3a).The release of patchy particles in a solvent occurs, because the adhesion of PMVEMA to the MF particles is stronger than its adhesion to the PDMS stamp due to the attractive electrostatic interaction at their interfaces. Here the polarity of solvent used for release plays a key role in the thickness of resulted patches. For example, ethanol can dissolve PMVEMA so well, that the cohesion of PMVEMA in the film layer is weaker than its adhesion to the MF particles, which results in the reduced thickness of patches. In contrast to ethanol, in a bad solvent for the respective polyelectrolyte ink, e.g., acetone the thickness of the patches increases. AFM images of the PDMS stamp after release in acetone show circular holes. These reveal that large parts of the polyelectrolyte ink layer were disrupted from the stamp and transferred as patches to the particles surface (Fig. 3b and c). This is in agreement with previous findings.20
With the assumption that the average depth of these holes is equal to the thickness of resulting patches after release, the thickness obtained from the measurements of 100 holes in PMVEMA film (Mw 1980 kDa) was found to be 90 ± 15 nm.
The thickness of patches and the percentage of patchy particles relative to the total number of particles (yield of μCP) were influenced by the concentration and the molecular weight of polymeric inks. For calculation of the yield, a small sample of obtained patchy particles was observed by fluorescence microscopy, and the particles were manually counted. To check, if this sample represents the whole batch, a hemocytometer was also used for counting smaller subsections of the whole sample and keeping the overall number of all particles in the same range and compared the results. Both statistics are found to be in good agreement. The hemocytometer ensures that the counted number of particles is representative for the whole batch.
With increasing the concentration of PEI from 1 to 3 wt%, the yield rises from 75 to 85%. In contrast to PEI, in case of using PMVEMA, the higher the concentration, the lower is the thickness of patch and the yield of patchy particles. Increasing the concentration of PMVEMA solution up to 3 wt% decreases its pH value to 2.0, which is very close to the isoelectric point of SiO2 layer on the top of the PDMS stamp (Fig. 4).
As a result, the adhesion of PMVEMA to PDMS is stronger than its adhesion to the MF particles, which reduces the yield from 84 to 24% (Table 1).
| Conc. (wt%) | PMVEMA | PEI | ||
|---|---|---|---|---|
| Thickness (nm) | Yield (%) | Thickness (nm) | Yield (%) | |
| 1 | 21 ± 3 | 76 | 25 ± 3 | 75 |
| 2 | 49 ± 4 | 84 | 46 ± 3 | 79 |
| 3 | 86 ± 3 | 24 | 76 ± 2 | 85 |
The increased density of functional carboxyl and amino groups, and the reduced solubility of high molecular weight polymeric inks during the release result in a higher yield as well as larger thickness of resulted patches, which is independent of the type of polymer. Preparation of patchy particles using PMVEMA with approximately two times higher molecular weight (Mw 1980 kDa) than (Mw 600–1000 kDa) leads to the formation of patches with about 25% higher thickness.
This effect has also been mirrored in the yield of patchy particles. A ten times higher molecular weight of PMVEMA with a concentration of 2 wt% causes an improvement in the yield from 84 to 90%.
PDMS treatment with ethanol
To study the effect of PDMS oligomers on its surface polarity, the stamps were treated with ethanol after completion of cross-linking. The residual non-cross-linked oligomers in the PDMS can diffuse to the surface of the stamp and decrease the efficiency of plasma activation, i.e., reduce the hydrophilicity.49As a result, the adhesion of the ink to the PDMS stamp is weaker than its adhesion to the MF particles, which leads to the creation of patches with larger thickness. On the contrary, the treatment causes increased adhesion of the ink to PDMS stamp and decreased thickness of patches, subsequently (Fig. 5a). Comparison of the thickness of PEI patches made by μCP with treated and untreated PDMS shows a difference of ca. 30 nm. The yield of μCP with treated and untreated stamps were 76 and 79% respectively, which means that the modification of adhesion properties of the PDMS stamp does not affect the yield significantly (Fig. 5b and c).
The treatment with ethanol as a polar solvent for dissolving the remaining oligomers was carried out for 6 hours. In this period the weight of PDMS stamps was increased about 5% due to its swelling through uptake of ethanol. After removing the stamps from ethanol, their weight was decreasing over the next 6 hours because of ethanol release and evaporation. In the end, after a total time of 12 hours, the ratio of the final weight of PDMS stamp to its initial weight (Wend/W0) was 99% that reveals the presence of quite small amounts of non-cross-linked oligomers, which were dissolved and removed (Fig. 6).50–52
The electrostatic interactions and force between patchy particles at different pH
Depending on the pH of the solution, patches made of PMVEMA or PEI carry negative or positive charges, respectively. As mentioned above (see Fig. 1), from the measurement of zeta-potential of the MF particles as a function of pH can be assumed that the surface charge of the MF particles can also vary in a wide range of negative, neutral and positive values.Therefore, at specific pH mono-patchy particles can be considered as simple, small dipoles, which are forced to aggregate in the solution due to their opposite surface charges. For example, in a moderately basic pH range, the surface of the MF particles is negatively, and the patches made of PEI are positively charged due to their increased dissociation degree.
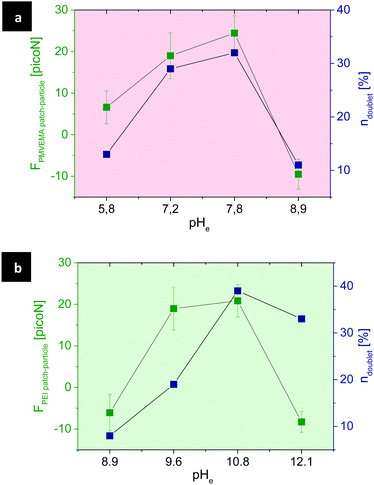
Apart from single patchy particles and multi-particulate aggregates, some possible types of dimers were formed via patch–patch, particle–particle, and patch–particle interactions. Quantitative analysis of these dimers at different pH was carried out with the aim of assessing the controlled self-assembly of patchy particles in solution (Fig. 7).
Statistics show that patchy particles are predominantly assembled to dimers due to patch–particle interactions for both types of patches made of PMVEMA or PEI (Table 2).
| PMVEMA | ||||
|---|---|---|---|---|
| pHe | n particle–patch | n patch–patch | n particle–particle | n tot |
| 8.9 | 112 (53%) | 11 (5%) | 87 (42%) | 210 (100%) |
| 7.8 | 167 (82%) | 6 (3%) | 31 (15%) | 204 (100%) |
| PEI | ||||
|---|---|---|---|---|
| pHe | n particle–patch | n patch–patch | n particle–particle | n tot |
| 8.9 | 222 (65%) | 18 (5%) | 105 (30%) | 345 (100%) |
| 10.8 | 300 (86%) | 10 (3%) | 38 (11%) | 348 (100%) |
The interplay between the charges of the polymer patches and the surface of the MF particles leads – at a specific pH – to a maximum in the number of dimers formed via patch–particle interactions.
To quantify the interactions between mono-patchy particles, a simplified model based on the theory developed by Hoffmann, Bianchi and Likos was used (Appendix). According to this model, the interactions between mono-patchy colloids in the equilibrium state can be related solely to electrostatic forces (eqn (1)).
 | (1) |
The localized charges, Qparticle and Qpatch, can be calculated using eqn (2).53
 | (2) |
 | (3) |
The surface charge of patches rises by increasing the dissociated fraction of polymer molecules, i.e., protonation of PEI and deprotonation of PMVEMA. The statistic of dimers formed via patch–particle interaction was in reasonable accordance with the theoretically estimated electrostatic force between patchy and non-patchy surfaces of particles (Fig. 9).
Despite the repulsive interactions between identically charged surfaces, other less frequently observed dimers were also formed via patch–patch and particle–particle interactions (Fig. 7). This might be a result of different non-electrostatic interactions, such as van der Waals forces or the formation of hydrogen bonds. During the dimer formation, collision of individual particles is required. If their kinetic energy is high enough to overcome the electrostatic repulsion between two surfaces of the same sign, formation of dimers driven by the above-mentioned forces could take place.
Self-aggregation behavior of patchy particles in a solution with an increased ionic strength
It is well-known that electrostatic interactions between charged objects (ions, particles, etc.) in electrolyte media are strongly influenced by ionic strength, i.e., by electrolyte concentration.In order to prove the effect of this factor on the electrostatically driven aggregation of patchy particles, a saturated solution of NaCl in ethanol–water (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) was added to the dispersion of each type of mono-patchy particles.
10) was added to the dispersion of each type of mono-patchy particles.
For a quantitative analysis of the self-aggregation of mono-patchy particles before and after addition of NaCl, a small sample of arbitrary number of the obtained particles was observed by fluorescence microscopy, and the particles were counted manually (Table 3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) before and after the addition of NaCl. The percentage of single particles proportional to the total number of particles significantly increases
10) before and after the addition of NaCl. The percentage of single particles proportional to the total number of particles significantly increases
| +NaCl | PMVEMA | PEI | ||
|---|---|---|---|---|
| n single | n aggregates | n single | n aggregates | |
| Before | 20 (4%) | 468 (96%) | 64 (13%) | 427 (87%) |
| After | 267 (51%) | 256 (49%) | 273 (53%) | 246 (47%) |
The dissociation of salt in ethanol–water medium leads to screening of electrostatic attractive interactions between the patchy particles. In accordance with this, the statistics, made on the basis of the microphotographs, show that the fraction of single patchy particles, compared to the aggregates fraction strongly increased after addition of salt.
Experimental
Materials
Poly(methyl vinyl ether alt maleic acid) (PMVEMA) with Mw of 216 and 1980 kDa, branched poly(ethyleneimine) (PEI) with Mw of 600–1000 kDa, fluorescein isothiocyanate, rhodamine 6G, and bromoiodomethane were supplied by Sigma Aldrich. Melamine formaldehyde particles with the average size of 5.17 ± 0.09 μm were synthesized by microparticles GmbH.The PDMS kit, Sylgard 184 – silicone elastomer, contained the monomer and curing agent was obtained by Dow Corning. The standard buffers for calibration and adjustment of pH were obtained by Mettler Toledo.
Preparation of inked PDMS and monolayer of particles
To synthesize PDMS, a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of monomer and crosslinker was poured into a rectangular Petri dish to form a polymer matrix with a thickness of approx. 3 mm.
1 mixture of monomer and crosslinker was poured into a rectangular Petri dish to form a polymer matrix with a thickness of approx. 3 mm.
After letting the mixture rest over night to remove air bubbles, it was heated up to 80 °C for 2 hours. Then the crosslinked PDMS was cut into 1 cm × 1 cm stamps and stored in a closed container for later use.
The glass object carrier was also cut into 1 cm × 1 cm pieces, cleaned with ethanol in an ultrasonic bath for 5 minutes and dried in a nitrogen flow. In order to improve the wettability of the substrates, PDMS stamp and object carrier were treated with air plasma for 1 minute at 0.2 mbar and a power of 100 and 300 W respectively. Then the stamp was spin-coated with 60 μL of the polymer ink at 4000 rpm for 1 minute, whereas the concentration of the inks was varied from 1 to 3 wt% (Table 2). The monolayer of the MF particles was prepared via drop casting of 5 μL of a 1 wt% aqueous particle dispersion on the object carrier and subsequent drying under nitrogen flow at RT for 10 minutes.
Microcontact printing for the creation of patchy particles
In this procedure, a polydimethylsiloxane (PDMS) stamp, coated with the polymeric ink, was pressed against a monolayer of the MF particles. The obtained patchy particles were released in acetone or ethanol in an ultrasonic bath for 15 minutes.Then the dispersion of patchy particles was centrifuged for 3 minutes at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, the supernatant was removed, and the particles were washed three times in ethanol at 8000 rpm for 3 minutes. After the wash procedure, they were collected in an Eppendorf tube for the further characterization.
000 rpm, the supernatant was removed, and the particles were washed three times in ethanol at 8000 rpm for 3 minutes. After the wash procedure, they were collected in an Eppendorf tube for the further characterization.
PDMS treatment with ethanol
Three PDMS stamp samples were treated in a container filled with ethanol for a total time period of 6 hours (Fig. 4a). During each measurement, samples were taken out of ethanol, dabbed with a lint-free tissue and weighted, while the used ethanol was replaced with fresh ethanol. After this time, the samples were moved to a clean Petri dish and weighted every 15 minutes for further 2 hours. The last measurement was then performed 4 hours later.Microscopy
A stock solution of fluorescent dye in ethanol with a concentration of 5 μg ml−1 was initially prepared. 20 μl of this solution was added to the suspension of patchy particles in 80 μl ethanol and after 15 minutes centrifuged at 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 3 minutes. The supernatant was removed, and patchy particles were washed three times in ethanol at 8000 rpm for 3 minutes. For the imaging, a Leica DMi8 microscope at the magnifications of 20, 40 and 63 was used, and the resulted images were processed via LAS X software provided by Leica.
000 rpm for 3 minutes. The supernatant was removed, and patchy particles were washed three times in ethanol at 8000 rpm for 3 minutes. For the imaging, a Leica DMi8 microscope at the magnifications of 20, 40 and 63 was used, and the resulted images were processed via LAS X software provided by Leica.
Zeta-potential measurement
A Nano ZS90 of Malvern was used to measure the zeta-potential of the MF particles at 25 °C and different pH. As dispersant water and ethanol–water (90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) were chosen. The resulted values were processed by the Zetasizer-NanoApplication and averaged from three independent measurements.
10) were chosen. The resulted values were processed by the Zetasizer-NanoApplication and averaged from three independent measurements.
Preparation of ethanol-buffer at different pH
The aggregation behavior of patchy particles was investigated in ethanol-buffer solutions at different pHe. A specialized electrode for the ethanol-based solution named EtOH-Trode was supplied by Metrohm. The calibration was carried out using water-based buffers at 25 °C and pH 4, 7 and 10.To prepare the calibration solutions, ethanol was mixed with buffers at 10, 30, 50, 70, 80, 90 wt% for each pH. The concentration of ethanol in the dispersion of patchy particles for studying of their self-aggregation behavior in the solution at different pH was maintained at 90 wt%. The pH values of media were measured before using.
Conclusions and outlook
In this work, we generated zwitterionic mono-patchy MF microparticles with positively or negatively charged patches made of PEI or PMVEMA, respectively. The effects of the concentration and the molecular weight of the polymeric ink and the influence of the modification of the adhesion surface properties of PDMS stamp on the yield and thickness of patches were studied.The self-aggregation behavior of patchy particles via electrostatic interactions was controlled by changing the pH, i.e., the charge difference between patchy and non-patchy surfaces of particles. At specific pH, where more than the half of ink molecules are dissociated, and the zeta-potential of the MF particles is increased, the number of mono-patchy particle-dimers via patch–particle interaction rises to a maximum. This dependence of patchy particles self-assembly on the pH value in the dispersion medium can be satisfactorily described by the simplified model accounting only for electrostatic interactions between patches and particles taken as point charges.
Additionally, changing the ionic strength of the media by addition of salt led to an increased population of single patchy particles, which also confirms a main contribution of electrostatic forces in interactions between patchy particles.
Future studies involve the preparation and self-assembly behavior of di-patchy MF particles with two oppositely charged patches made of PMVEMA and PEI.
Conflicts of interest
There are no conflicts of interest to declare.Appendix
Sabapathy and co-workers have used a pair potential for the interaction between two mono-patchy IPCs derived on the basis of potential equation proposed by Hoffmann, Bianchi and Likos.14,25,34 | (A1) |
Further simplification of this equation is possible taking into account the analysis made in the ref. 25. These authors calculated the electrostatic interaction energy of a pair of IPC particles at a fixed separation distance and at different orientations and showed that this energy is only weakly dependent on the kink angle between interacting IPCs in aggregates: the value of this function grows only by 50% in the physically reasonable range of kink angles from 50 to 120 degrees. Thus, the contribution of the orientation factor Qij to the entire interaction potential between IPCs is also quite low compared to the pH-dependent electrostatic interaction and with the pH-dependent effect of the ionic charge density distribution in the medium and thus can be neglected, i.e.,
 | (A2) |
The term in the factorized potential accounting for the effect of the ions double layer could be simplified taking into account the very small thickness of the patches compared to the radius of the microparticles (IPCs), i.e. we can approximate that rij in (A2) is practically equal to σ (where σ denotes the radius of patchy IPCs according to the ref. 14). This approximation is valid because the statistics of the various particle aggregation shapes was made on the basis of the microscopic observations for equilibrium states and therefore did not consider any parameters related to the aggregation kinetics when the patchy particles approach each other and rij is sufficiently larger than σ and can change dynamically during the aggregate formation.
Since,
 | (A3) |
After taking this derivative and substituting one gets:
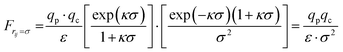 | (A4) |
Therefore, the final form of the simplified expression for the interaction force between patch and colloidal particle contains only the Coulomb term.
Acknowledgements
The authors would like to thank S. Grunst and Dr M. Pinnow for their help and advice with SEM-imaging and M. Zimmermann for helpful discussions. This work was financially supported by the European Research Council ERC in the framework of the project Replicoll.References
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed.
- E. W. Edwards, D. Wang and H. Möhwald, Macromol. Chem. Phys., 2007, 208, 439–445 CrossRef CAS.
- S. C. Glotzer, M. J. Solomon and N. A. Kotov, AIChE J., 2004, 50, 2978–2985 CrossRef CAS.
- L. Feng, R. Dreyfus, R. Sha, N. C. Seeman and P. M. Chaikin, Adv. Mater., 2013, 25, 2779–2783 CrossRef CAS PubMed.
- F. Sciortino, E. Bianchi, J. F. Douglas and P. Tartaglia, J. Chem. Phys., 2007, 126, 194903 CrossRef PubMed.
- S. Ferrari, E. Bianchi and G. Kahl, Nanoscale, 2017, 9, 1956–1963 RSC.
- S. Ferrari, G. Kahl and E. Bianchi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 43 CrossRef PubMed.
- R. Guo, J. Mao, X.-M. Xie and L.-T. Yan, Sci. Rep., 2014, 4, 7021 CrossRef PubMed.
- S. Jiang and S. Granick, Langmuir, 2009, 25, 8915–8918 CrossRef CAS PubMed.
- E. Bianchi, C. N. Likos and G. Kahl, Nano Lett., 2014, 14, 3412–3418 CrossRef CAS PubMed.
- E. Bianchi, C. N. Likos and G. Kahl, ACS Nano, 2013, 7, 4657–4667 CrossRef CAS PubMed.
- E. Bianchi, P. Tartaglia, E. La Nave and F. Sciortino, J. Phys. Chem. B, 2007, 111, 11765–11769 CrossRef CAS PubMed.
- E. Bianchi, G. Doppelbauer, L. Filion, M. Dijkstra and G. Kahl, J. Chem. Phys., 2012, 136, 214102 CrossRef PubMed.
- E. Bianchi, G. Kahl and C. N. Likos, Soft Matter, 2011, 7, 8313–8323 RSC.
- E. Bianchi, B. Capone, G. Kahl and C. N. Likos, Faraday Discuss., 2015, 181, 123–138 RSC.
- Z. Gong, T. Hueckel, G.-R. Yi and S. Sacanna, Nature, 2017, 550, 234 CrossRef PubMed.
- L. Sanchez, P. Patton, S. M. Anthony, Y. Yi and Y. Yu, Soft Matter, 2015, 11, 5346–5352 RSC.
- Y. Yi, L. Sanchez, Y. Gao and Y. Yu, Analyst, 2016, 141, 3526–3539 RSC.
- M. Zimmermann, D. Grigoriev, N. Puretskiy and A. Böker, RSC Adv., 2018, 8, 39241–39247 RSC.
- M. Zimmermann, D. John, D. Grigoriev, N. Puretskiy and A. Böker, Soft Matter, 2018, 14, 2301–2309 RSC.
- T. Kaufmann, M. T. Gokmen, C. Wendeln, M. Schneiders, S. Rinnen, H. F. Arlinghaus, S. A. F. Bon, F. E. Du Prez and B. J. Ravoo, Adv. Mater., 2010, 23, 79–83 CrossRef PubMed.
- A. M. Yake, C. E. Snyder and D. Velegol, Langmuir, 2007, 23, 9069–9075 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Langmuir, 2008, 24, 355–358 CrossRef CAS PubMed.
- L. Hong, A. Cacciuto, E. Luijten and S. Granick, Langmuir, 2008, 24, 621–625 CrossRef CAS PubMed.
- M. Sabapathy, R. Ann Mathews K and E. Mani, Phys. Chem. Chem. Phys., 2017, 19, 13122–13132 RSC.
- R. Hieronimus, S. Raschke and A. Heuer, J. Chem. Phys., 2016, 145, 064303 CrossRef.
- J. Lekner, Proc. R. Soc. A, 2012, 468, 2829 CrossRef.
- E. Bichoutskaia, A. L. Boatwright, A. Khachatourian and A. J. Stace, J. Chem. Phys., 2010, 133, 024105 CrossRef PubMed.
- I. N. Derbenev, A. V. Filippov, A. J. Stace and E. Besley, Soft Matter, 2018, 14, 5480–5487 RSC.
- C. N. Likos, R. Blaak and A. Wynveen, J. Phys.: Condens. Matter, 2008, 20, 494221 CrossRef.
- Y. V. Kalyuzhnyi, E. Bianchi, S. Ferrari and G. Kahl, J. Chem. Phys., 2015, 142, 114108 CrossRef PubMed.
- S. Ferrari, E. Bianchi, Y. V. Kalyuzhnyi and G. Kahl, J. Phys.: Condens. Matter, 2015, 27, 234104 CrossRef PubMed.
- E. G. Noya, I. Kolovos, G. Doppelbauer, G. Kahl and E. Bianchi, Soft Matter, 2014, 10, 8464–8474 RSC.
- N. Hoffmann, Magnetic and Electrostatic Interactions of Colloids and Polyelectrolytes, PhD thesis, Heinrich-Heine University Duesseldorf, Duesseldorf, 2006 Search PubMed.
- M. Stipsitz, G. Kahl and E. Bianchi, J. Chem. Phys., 2015, 143, 114905 CrossRef PubMed.
- E. G. Noya and E. Bianchi, J. Phys.: Condens. Matter, 2015, 27, 234103 CrossRef PubMed.
- E. Bianchi, P. D. J. van Oostrum, C. N. Likos and G. Kahl, Curr. Opin. Colloid Interface Sci., 2017, 30, 8–15 CrossRef CAS.
- P. D. J. van Oostrum, M. Hejazifar, C. Niedermayer and E. Reimhult, J. Phys.: Condens. Matter, 2015, 27, 234105 CrossRef CAS PubMed.
- O. Cayre, V. N. Paunov and O. D. Velev, J. Mater. Chem., 2003, 13, 2445–2450 RSC.
- C. Yigit, J. Heyda, M. Ballauff and J. Dzubiella, J. Chem. Phys., 2015, 143, 064905 CrossRef PubMed.
- H. Ohshima, E. Mishonova and E. Alexov, Biophys. Chem., 1996, 57, 189–203 CrossRef CAS PubMed.
- E. B. Lindgren, H.-K. Chan, A. J. Stace and E. Besley, Phys. Chem. Chem. Phys., 2016, 18, 5883–5895 RSC.
- D. John, M. Zimmermann and A. Böker, Soft Matter, 2018, 14, 3057–3062 RSC.
- P. Seidel and B. J. Ravoo, Macromol. Chem. Phys., 2016, 217, 1467–1472 CrossRef CAS.
- T. Tigges, D. Hoenders and A. Walther, Small, 2015, 11, 4540–4548 CrossRef CAS PubMed.
- C. E. Felder, J. Prilusky, I. Silman and J. L. Sussman, Nucleic Acids Res., 2007, 35, W512–W521 CrossRef PubMed.
- A. I. Abrikosov, B. Stenqvist and M. Lund, Soft Matter, 2017, 13, 4591–4597 RSC.
- C. Yigit, J. Heyda and J. Dzubiella, J. Chem. Phys., 2015, 143, 064904 CrossRef PubMed.
- S. Yunus, C. de C. de Looringhe, C. Poleunis and A. Delcorte, Surf. Interface Anal., 2007, 39, 922–925 CrossRef CAS.
- Y. Ding, S. Garland, M. Howland, A. Revzin and T. Pan, Adv. Mater., 2011, 23, 5551–5556 CrossRef CAS PubMed.
- A. L. Briseno, M. Roberts, M.-M. Ling, H. Moon, E. J. Nemanick and Z. Bao, J. Am. Chem. Soc., 2006, 128, 3880–3881 CrossRef CAS PubMed.
- A. Jain, P. Bharadwaj, S. Heeg, M. Parzefall, T. Taniguchi, K. Watanabe and L. Novotny, Nanotechnology, 2018, 29, 265203 CrossRef PubMed.
- P. Attard, D. Antelmi and I. Larson, Langmuir, 2000, 16, 1542–1552 CrossRef CAS.
- B. Chen, X. Zhao, Y. Liu, B. Xu and X. Pan, RSC Adv., 2015, 5, 1398–1405 RSC.
- C. Duran, Y. Jia, Y. Hotta, K. Sato and K. Watari, J. Mater. Res., 2005, 20, 1348–1355 CrossRef CAS.
- Z. Wang, Z. Ni, D. Qiu, G. Tao and P. Yang, J. Anal. At. Spectrom., 2005, 20, 315–319 RSC.
- R. Benavente, M. D. Salvador, M. C. Alcázar and R. Moreno, Ceram. Int., 2012, 38, 2111–2117 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |